常见函数的梯度、海赛矩阵
预备知识: 方向导数与梯度、海赛矩阵及泰勒公式[1]
![预备知识: 方向导数与梯度、海赛矩阵及泰勒公式[1]](https://img.taocdn.com/s3/m/a965e0818762caaedd33d4f0.png)
特别地,在(10.4.7)式中,取 u 为各坐标轴的单位方向向量,则方向导数就是偏导数.如
果 n = 1 , u 是坐标轴 x 轴的单位方向向量,则一元函数的方向导数就是导数.
方向导数都存在,且有
Du f ( x0 , y0 ) = fx′( x0 , y0 ) cosα + f y′ ( x0 , y0 ) cos β ,
其中 cosα , cos β 为向量 u 的方向余弦.
(10.4.2)
证 因函数 f (x, y) 在点 P0 ( x0 , y0 ) 可微,则
( ) f
u
x
Q(x, y)
图 10.4.2 方向导数 Du f (x0 , y0 ) 的几何意义
2.方向导数的计算
直接利用定义式(10.4.1)来计算方向导数是很不方便的,下面的定理给出了用偏导数计 算方向导数的一个简便的公式.
定理 10.4.1 设函数 f (x, y) 在点 P0 ( x0 , y0 ) 可微,那么函数在该点沿任意方向向量 u 的
(10.4.5)
Du f (x, y, z) = ∇f (x, y, z) ⋅u0. 这表明,方向导数是函数梯度在方向向量 u 上的投影.
(10.4.6)
例 3 求 函 数 f (x, y) = x2 y + 2 y 在 点 (2, −1) 处 的 梯 度 以 及 函 数 在 该 点 处 沿 方 向
152
lim
h→0
f
( x0
+ h cosα ,
y0
+ h cos β ) −
h
f
( x0, y0 )
=
fx′( x0 , y0 ) cosα
Байду номын сангаас
海塞矩阵在多元函数条件极值中的应用

2005年12月安阳工学院学报Dec .2005第6期(总第18期)Journal of Anyang I nstitute of Technol ogy No .6(Gen .No .18)3收稿日期:2005-12-20作者简介:张丽丽(1978-),女,河南偃师人,河南财经学院讲师,主要从事数值计算方向的研究。
海塞矩阵在多元函数条件极值中的应用张丽丽 王军民 耿向平(河南财经学院河南郑州450002)摘 要:本文提出了利用海塞矩阵计算多元函数条件极值的一种新方法,并结合几个例子分类讨论这种方法在实际问题中的应用,同时针对一篇已经发表的文章,我们指出了它的问题,并运用本文所列方法,给出了正确的解法。
关键词:海塞矩阵;多元函数;条件极值;稳定点中图分类号:O175.27 文献标识码:A 文章编号:1673-2928(2005)06-0079-03 《数学分析》是大多数高校的必开课程,有着十分重要的基础作用,多元函数的极值问题又是这门课程里面非常重要的部分,而且在实践中应用非常广泛,对它的研究就显得十分必要。
本文首先介绍多元函数极值问题的一些理论,然后分类讨论不同约束条件下的求解方法,这些方法具有一定的普遍性,同时针对一篇已经发表的文章,我们指出了其中一个例子解法中的错误,并采用本文的方法,给出正确的解题方法。
在《数学分析》[1]教材中,多元函数有如下定义:设n 元函数y =f (x )=f (x 1,x 2,Λ,x n )定义于区域D 中,且点P 0(x 01,x 02,Λ,x 0n )是这区域内的一点。
若在点P 0的某邻域内,恒有f (x )<f (P 0)(或f (x )>f (P 0))则称函数f (x )在点P 0处有极大值(或极小值)。
本文若无特殊说明,均假定函数f (x )在点P 0(x 01,x 02,Λ,x 0n )的某邻域内连续,且二阶偏导数也连续。
下面我们给出稳定点和海塞矩阵的定义。
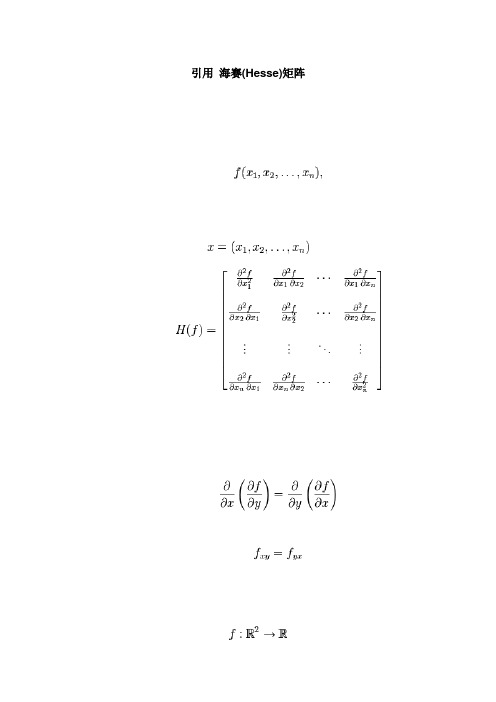
海森矩阵(Hessianmatrix或Hessian)

海森矩阵(Hessianmatrix或Hessian)
在中,海森矩阵(Hessian matrix 或 Hessian)是⼀个⾃变量为向量的实值函数的⼆阶组成的,此函数如下:
如果f所有的⼆阶导数都存在,那么f的海森矩阵即:
H(f)ij(x) = D i D j f(x)
其中,即
(也有⼈把海森定义为以上矩阵的)海森矩阵被应⽤于⽜顿法解决的⼤规模优化问题。
混合偏导数和海森矩阵的对称性
海森矩阵的混合偏导数是海森矩阵⾮主对⾓线上的元素。
假如他们是连续的,那么求导顺序没有区别,即
上式也可写为
在正式写法中,如果f函数在区域D内连续并处处存在⼆阶导数,那么f的海森矩阵在D区域内为。
在→的函数的应⽤
给定⼆阶导数连续的,海森矩阵的⾏列式,可⽤于分辨f的临界点是属于还是。
对于f的临界点 (x0,y0) ⼀点,有,然⽽凭⼀阶导数不能判断它是鞍点、局部极⼤点还是局部极⼩点。
海森矩阵可能解答这个问题。
H > 0 :若,则(x0,y0)是局部极⼩点;若,则(x0,y0)是局部极⼤点。
H < 0 :(x0,y0)是鞍点。
H = 0 :⼆阶导数⽆法判断该临界点的性质,得从更⾼阶的导数以考虑。
海森矩阵及其应用

海森矩阵及其应⽤海森矩阵在数学中, 海森矩阵(Hessian matrix或Hessian)是⼀个⾃变量为向量的实值函数的⼆阶偏导数组成的⽅块矩阵, 此函数如下:f(x1,x2…,xn)如果ff的所有⼆阶导数都存在, 那么ff的海森矩阵即:H(f)ij(x)=DiDjf(x)其中x=(x1,x2…,xn)x=(x1,x2…,xn), 即H(f)H(f)为:海森矩阵在⽜顿法中的应⽤⼀般来说, ⽜顿法主要应⽤在两个⽅⾯, 1, 求⽅程的根; 2, 最优化.1), 求解⽅程并不是所有的⽅程都有求根公式, 或者求根公式很复杂, 导致求解困难. 利⽤⽜顿法, 可以迭代求解.原理是利⽤泰勒公式, 在x0x0处展开, 且展开到⼀阶, 即f(x)=f(x0)+(x–x0)f'(x0)f(x)=f(x0)+(x–x0)f′(x0),求解⽅程f(x)=0f(x)=0, 即f(x0)+(x–x0)f'(x0)=0f(x0)+(x–x0)f′(x0)=0, 求解x=x1=x0–f(x0)/f'(x0)x=x1=x0–f(x0)/f′(x0), 因为这是利⽤泰勒公式的⼀阶展开, f(x)=f(x0)+(x–x0)f'(x0)f(x)=f(x0)+(x–x0)f′(x0)处并不是完全相等, ⽽是近似相等, 这⾥求得的x1x1并不能让f(x)=0f(x)=0, 只能说f(x1)f(x1)的值⽐f(x0)f(x0)更接近f(x)=0f(x)=0, 于是乎, 迭代求解的想法就很⾃然了, 可以进⽽推出xn+1=xn–f(xn)/f'(xn)xn+1=xn–f(xn)/f′(xn), 通过迭代, 这个式⼦必然在f(x∗)=0f(x∗)=0的时候收敛. 整个过程如下图:2), 最优化在最优化的问题中, 线性最优化⾄少可以使⽤单纯形法(或称不动点算法)求解, 但对于⾮线性优化问题, ⽜顿法提供了⼀种求解的办法.假设任务是优化⼀个⽬标函数ff, 求函数ff的极⼤极⼩问题, 可以转化为求解函数ff的导数f'=0f′=0的问题, 这样求可以把优化问题看假设任务是优化⼀个⽬标函数ff, 求函数ff的极⼤极⼩问题, 可以转化为求解函数ff的导数f'=0f′=0的问题, 这样求可以把优化问题看成⽅程求解问题(f'=0f′=0). 剩下的问题就和第⼀部分提到的⽜顿法求解很相似了.这次为了求解f'=0f′=0的根, 把f(x)f(x)的泰勒展开, 展开到22阶形式:f(x+Δx)=f(x)+f′(x)Δx+12f′′(x)Δx2f(x+Δx)=f(x)+f′(x)Δx+12f″(x)Δx2这个式⼦是成⽴的, 当且仅当 ΔxΔx ⽆限趋近于0时, f(x+Δx)=f(x)f(x+Δx)=f(x), 约去这两项, 并对余项式f′(x)Δx+12f”(x)Δx2=0f′(x)Δx+12f”(x)Δx2=0对ΔxΔx求导(注: f'(x)f′(x), f”(x)f”(x)均为常数项. 此时上式等价与: f′(x)+f′′(x)Δx=0f′(x)+f″(x)Δx=0求解:Δx=−f′(xn)f′′(xn)Δx=−f′(xn)f″(xn)得出迭代公式:xn+1=xn−f′(xn)f′′(xn),n=0,1,...xn+1=xn−f′(xn)f″(xn),n=0,1,...⼀般认为⽜顿法可以利⽤到曲线本⾝的信息, ⽐梯度下降法更容易收敛(迭代更少次数), 如下图是⼀个最⼩化⼀个⽬标⽅程的例⼦, 红⾊曲线是利⽤⽜顿法迭代求解, 绿⾊曲线是利⽤梯度下降法求解.在上⾯讨论的是22维(xx坐标维度 + yy坐标维度)情况, ⾼维情况的⽜顿迭代公式是:xn+1=xn−[Hf(xn)]–1∇f(xn),n≥0。
现代设计理论与方法复习题

现代设计理论与方法一、填空题1、常用的现代设计方法有 、 、 和 。
2、构成优化问题的数学模型的三要素分别是 、 和 。
3、在优化算法的基本迭代公式中,指的是 。
4、可靠性设计中常用的分布函数有 、 和 。
5、求总体刚度矩阵的方法主要由两种:一是 ,即根据总体刚度系数的定义求解;另一种方法是 ,即由各单元刚度矩阵求总体刚度矩阵。
6、弹性力学中平面问题有 和 两种。
7、作业对象一般可分为 、 和 三大类。
8、功能原理方案综合常用形态学矩阵,矩阵的行代表 ,矩阵的列代表 。
9、广义的设计指的是对发展过程的安排,包括发 、 、 和 。
10、常用的优化算法有 、 、 和 。
11、零件可靠性设计时,通过联结方程建立 、 和 三者的关系。
12、设计经历了 、 、 和 四个发展阶段。
13、使用鲍威尔法求解二维优化问题,初始搜索方向可设成 和 。
14、函数在点处的梯度为 ,海塞矩阵为 。
15、平面三节点三角形单元 个自由度。
16、常用的评价决策方法有 , , 和 。
17、弹性力学基本方程包括 、 和 。
二、选择题三、名词解释 1、可靠度:2、不可靠度或失效概率:3、失效率: k k k k d x x α+=+1k α()54,21222121+-+=x x x x x x f ⎥⎦⎤⎢⎣⎡=420X5、狭义设计:6、优化设计的过程:7、计算机辅助设计:8、价值工程:四、简答题1.现代设计、传统设计的区别与联系。
2.可靠性设计有何特点?3.简述共轭梯度法的基本流程。
4.可靠性设计包括哪些内容,各有什么方法?5.运用系统化设计方法进行原理方案设计的主要步骤?6.简述有限法分析的基本过程。
7.作业对象包括哪些?8.什么是系统化设计?步骤?9.现代产品设计的一般进程(技术系统)10.设计发展的阶段11.可靠性设计与传统设计的区别12.现代设计方法的特点。
13.分功能(功能元)求解的方法主要有哪些?五、计算题1、试用算子进行模糊综合评价来评定某学生毕业设计的成绩。
Hessian矩阵

引用海赛(Hesse)矩阵microfisher的海赛(Hesse)矩阵海色矩阵在数学中,海色矩阵是一个自变量为向量的实值函数的二阶偏导数组成的方块矩阵,此函数如下:如果f所有的二阶导数都存在,那么f的海色矩阵即:H(f)ij(x) = DiDjf(x)其中,即(也有人把海色定义为以上矩阵的行列式)海色矩阵被应用于牛顿法解决的大规模优化问题。
混合偏导数和海色矩阵的对称性海色矩阵的混合偏导数是海色矩阵主对角线上的元素。
假如他们是连续的,那么求导顺序没有区别,即上式也可写为在正式写法中,如果f函数在区域D内连续并处处存在二阶导数,那么f的海色矩阵在D区域内为对称矩阵。
在R^2→R 的函数的应用给定二阶导数连续的函数,海色矩阵的行列式,可用于分辨f的临界点是属于鞍点还是极值。
对于f的临界点(x0,y0)一点,有,然而凭一阶导数不能判断它是鞍点、局部极大点还是局部极小点。
海色矩阵可能解答这个问题。
H > 0 :若,则(x0,y0)是局部极小点;若,则(x0,y0)是局部极大点。
H < 0 :(x0,y0)是鞍点。
H = 0 :二阶导数无法判断该临界点的性质,得从更高阶的导数以泰勒公式考虑。
Hessian矩阵是多维变量函数的二阶偏导数矩阵,H(i,j)=d^2(f)/(d(xi)d(xj))它是对称的。
如果是正定的的可用导数=0的变量组确定它的极小值,负定的确定它的极大值,否则无法确定极值。
1.极值(极大值或极小值)的定义设有定义在区域D Rn上的函数 y=f(x)=f(x1,...,xn) . 对于区域D的一内点x0=(x10,...,xn0),若存在x0的一个邻域UD,使得f(x)≤f(x0) x∈U则称x0是f(x)的极大点,f(x0)称为f(x)的极大值.相反,如f(x)≥f(x0) x∈U则称x0是f(x)的极小点,f(x0)称为f(x)的极小值.2.海赛(Hessian)矩阵设函数y=f(x)=f(x1,...,xn)在点x0=(x10,...,xn0)的一个邻域内所有二阶偏导数连续,则称下列矩阵H为f(x)在x0点的海赛矩阵.显然海赛矩阵是对称的,从而它的所有特征根均为实数.3.极值存在的必要条件若x0是f(x)的极值点,如果存在,则进一步设在一个邻域内所有二阶导数连续,H为在点x0的海赛矩阵.则(1)x0是f(x)的极小点H≥0,即H 的特征根均为非负.(2)x0是f(x)的极大点H≤0,即H的特征根为非正.若在x0点有,则称x0是f(x)的临界点,f(x0)为临界值.4.极值存在的充分条件设f(x)在x0的一个邻域内所有二阶偏导数连续,且x0是f(x)的临界点(即),H为f(x)在x0点的海赛矩阵,则(1)H>0,即H为正定矩阵x0是f(x)的极小点.(2)H<0,即H为负定矩阵x0是f(x)的极大点.(3)H的特征根有正有负x0不是f(x)的极值点.(4)其余情况,则不能判定x0是或者不是f(x)的极值点.5.二元函数极值存在的充分条件作为4的特例。
heese矩阵多元函数极值点

heese矩阵多元函数极值点海塞矩阵(Hessian Matrix),又译作海森矩阵,是一个多元函数的二阶偏导数构成的方阵。
虽然它是一个具有悠久历史的数学成果。
可是在机器学习和图像处理(比如SIFT和SURF特征检測)中,我们也经常遇到它。
所以本文就来向读者道一道Hessian Matrix的来龙去脉。
本文的主要内容包括:多元函数极值问题回想一下我们是如何处理求一元函数极值的问题的。
比如。
f(x)=x2,我们会先求一阶导数,即f′(x)=2x,依据费马定理极值点处的一阶导数一定等于 0。
但这仅是一个必要条件。
而非充分条件。
对于f(x)=x2来说,函数的确在一阶导数为零的点取得了极值,可是对于f(x)=x3来说,显然只检查一阶导数是不足以下定论的。
这时我们须要再求一次导,假设二阶导数 f″<0,那么说明函数在该点取得局部极大值;假设二阶导数 f″>0,则说明函数在该点取得局部极小值;假设 f″=0。
则结果仍然是不确定的,我们就不得不再通过其它方式来确定函数的极值性。
假设我们要找一个多元函数中的极值点,方法也差不多。
作为一个演示样例。
最好还是用一个三元函数 f=f(x,y,z) 来作为演示样例。
首先要对函数中的每一个变量分别求偏导数,这会告诉我们该函数的极值点可能出如今哪里。
即∂f∂x=0∂f∂y=0∂f∂x=0下一个。
继续求二阶导数,包括混合偏导数在内有9种情况。
假设用矩阵形式表示,你会得到H=⎡⎡⎡⎡⎡⎡⎡⎡⎡∂2f∂x∂x∂2f∂y∂x∂2f∂z∂x∂2f ∂x∂y∂2f∂y∂y∂2f∂z∂y∂2f∂x∂z∂2f∂y∂z∂2f∂z ∂z⎡⎡⎡⎡⎡⎡⎡⎡⎡这个矩阵就称为Hessian矩阵。
当然上面所给出的不过一个三阶的Hessian矩阵。
稍作扩展。
我们能够对一个在定义域内二阶连续可导的实值多元函数 f(x1,x2,⋯,xn) 定义其Hessian矩阵H例如以下H=⎡⎡⎡⎡⎡⎡⎡⎡⎡⎡⎡∂2f∂x21∂2f∂x2∂x1⋮∂2f∂x n∂x1∂2f∂x1∂x2∂2f∂x22⋮∂2f∂xn∂x2⋯⋯⋱⋯∂2f∂x1∂xn∂2f∂x2∂xn⋮∂2f∂x2n⎡⎡⎡⎡⎡⎡⎡⎡⎡⎡⎡当一元函数的二阶导数等于 0 时,我们并不能确定函数在该点的极值性。
Hessian矩阵
引用海赛(Hesse)矩阵Hessian矩阵是多维变量函数的二阶偏导数矩阵,H(i,j)=d^2(f)/(d(xi)d(xj))它是对称的。
如果是正定的的可用导数=0的变量组确定它的极小值,负定的确定它的极大值,否则无法确定极值。
1.极值(极大值或极小值)的定义设有定义在区域D Rn上的函数 y=f(x)=f(x1,...,xn) . 对于区域D的一内点x0=(x10,...,xn0),若存在x0的一个邻域UD,使得f(x)≤f(x0) x∈U则称x0是f(x)的极大点,f(x0)称为f(x)的极大值.相反,如f(x)≥f(x0) x∈U则称x0是f(x)的极小点,f(x0)称为f(x)的极小值.2.海赛(Hessian)矩阵设函数y=f(x)=f(x1,...,xn)在点x0=(x10,...,xn0)的一个邻域内所有二阶偏导数连续,则称下列矩阵H为f(x)在x0点的海赛矩阵.显然海赛矩阵是对称的,从而它的所有特征根均为实数.3.极值存在的必要条件若x0是f(x)的极值点,如果存在,则进一步设在一个邻域内所有二阶导数连续,H为在点x0的海赛矩阵.则(1)x0是f(x)的极小点H≥0,即H 的特征根均为非负.(2)x0是f(x)的极大点H≤0,即H的特征根为非正.若在x0点有,则称x0是f(x)的临界点,f(x0)为临界值.4.极值存在的充分条件设f(x)在x0的一个邻域内所有二阶偏导数连续,且x0是f(x)的临界点(即),H为f(x)在x0点的海赛矩阵,则(1)H>0,即H为正定矩阵x0是f(x)的极小点.(2)H<0,即H为负定矩阵x0是f(x)的极大点.(3)H的特征根有正有负x0不是f(x)的极值点.(4)其余情况,则不能判定x0是或者不是f(x)的极值点.5.二元函数极值存在的充分条件作为4的特例。
观察二元函数极值存在的充分条件.设z=f(x,y)在(x0,y0)的一个邻域内所有二阶偏导数连续,且,记 .那么,海赛矩阵.(1)若A>0,detH=AC-B2>0,则H正定,从而(x0,y0)是f(x,y)的极小点.(2)若A<0,detH=AC-B2>0,则H负定,从而(x0,y0)是f(x,y)的极大点.(3)若detH=AC-B2<0,则H的特征根有正有负,从而(x0,y0)不是f(x,y)的极值点.(4)若detH=AC-B2=0,则不能判定(x0,y0)是否为f(x,y)的极值点.6.条件极值求函数 y=f(x)=f(x1,...,xn) x∈DRn (1),在约束条件:qk(x)=qk(x1,...,xn)=0,k=1,...,m,m<n (2),下的极值,称为条件极值问题.此处,假设雅可比矩阵的秩在D内处处为m,即保证m个约束条件是独立的.直接代入法从约束条件(2)中直接解出m个变量,代入到(1)中,将问题化为求n-m 个变量函数的直接极值问题.拉格朗日(Lagrange)乘数法引入拉格朗日函数:(3)其中λ1,...,λm称为拉格朗日乘子,是待定常数.条件极值问题(1)和(2)可化为求拉格朗日函数(3)的直接极值问题.(1) 若x0为(1)和(2)的条件极值点,则x0满足方程组满足上述方程组的点称为条件极值问题的临界点.显然极值点为临界点,而临界点未必一定是极值点.(2)若x0是临界点, HL为拉格朗日函数L在x0点的海赛矩阵, 则可按4中给出的极值存在的充分条件,由HL的正定、负定或不定,判断x0是极小点、极大点或不是极值点.。
