地大《高等数学(二)》离线作业二.doc1
中国地质大学远程与继续教育学院线性代数(专升本)阶段性作业2.docx

中国地质大学远程与继续教育学院线性代数(专升本)阶段性作业2单选题则下列运算没有意义的是.(6 分)(A): (?+(酬(B):(C):(D): AC:参考答案:D2.设.是「1矩阵-「,二是一「矩阵,则下列方阵.(6分)(A): AB(B): A r B r(C): B T A T(D):(硼参考答案:B3.设■' _都是〔阶方阵,则必有.(6分)(A):(B): AB = BA(C): |外1.设「是:1矩阵,二是」「矩阵,■是「矩阵,的运算结果是二阶(D):- --参考答案:C4. 下列命题中,正确的是_____ .(6分)(A):- -(B):若,则川W团(C):设「'是三角矩阵,则- 二也是三角矩阵(D)::-一:-一: _ 一参考答案:D5. 设「'都是匚阶矩阵,AB-^,则必有__________ .(6分)(A) -去-〔:(B) : .1 一(C) :同或昨°(D):参考答案:C6. __________________________________________ 设丄B都是"阶方阵,下列结论正确的是_______________________________________ .(6分)(A) :若二「均可逆,贝U…二可逆(B) :若-;-均可逆,则A 可逆(C) :若-;-可逆,贝U广;一打可逆(D) :若-;-可逆,贝U二「均可逆参考答案:B7•设"阶方阵满足关系式」BC = E ,则必有.(6分)(A) :二1」二二(B) : I 二二二二(C) :二一二二(D) :二'.1 二二参考答案:D8. _________________________________________________________________ 设』月C均为"阶方阵,若B二E + 1B , C-A+CA则B-C =____________________ .(6分)(A) :-(B) : _】(C) :…(D) : 一-:参考答案:A(a b眄A- b a b\9. __________________________________________________________ 设三阶矩阵e 0 口丿,若』的伴随矩阵的秩为i,则必有____________________________ .(6分)(A) 沁]勺或=(B) :二-或一亠「(C) : 一:「且一」■'(D) :一•-一且.■:■:':■仁.-.参考答案:B7•设"阶方阵满足关系式」BC = E ,则必有.(6分)参考答案:Cfl 210]3 -1 0 210. 矩阵1一1『一】-一二丿的秩为2,贝叮= ___ .(6分)(A) 3(B) 4(C) 5(D) 6参考答案:D11. 设二_都是•:阶非零矩阵,且贝U :-的秩_______ .(6分)(A) :必有一个等于零(B) :都小于(C) : 一个小于,一个等于(D) :都等于参考答案:B12. 下列矩阵中, _____ 不是初等矩阵.(6分)(0 0 1)0 10(A) : U °°(°冷(B) :b 0 0丿fl 0 0A』3 0(C) : 01,fl 0 0A0 10(D) : b 0 1 丿彷1处口13厂a2l兔、S 1 (fA =B =如氐 1 0 013.设Si乐禺丿1Sl +坷1 ^32给 + 如/1, 1(0 0 1?fl 0 0、PL Q i oJ ° 1丿,则必有________ .(6分)(A):(B) :(D) : ■■--参考答案:C14. 设…为3阶矩阵,将…的第2行加到第1行得Y ,再将匸的第1列的】倍加到第(11 0、P= 0 1 02列得C,记卩0 1丿,则_____________ .(6分)(A) :- 一(B) :(C) : - - -z(D) :-参考答案:B15. 设-为3阶矩阵,将…的第1列与第2列交换得匸,再将二的第2列加到第3列得C ,则满足丿0二c 的可逆矩阵0为 ________ .(6分)ro i o]1 o o(A) : I 】0 1 一(0 1 0: (1 0 1(B) : I 。
大学-高等数学(Ⅱ)试卷题(D)+答案

大学-高等数学(Ⅱ)试卷题(D )一、选择题:(每小题2分,共10分)1. 函数 ⎪⎩⎪⎨⎧=+≠++=0y x , 00y x , y x xy y x f 222222,),(则f(x,y)在(0,0)点 ( );A.连续但偏导数不存在;B.极限存在但不连续;C.偏导数存在但不连续;D.全微分存在.2.下列级数发散的是( )A .;(1)n nn n ∞=+- B.2(1)ln(1);1n n n n ∞=-++∑ C .222sin();n a π∞=+∑ D.1.1nn n ∞=+ 3.级数1sin (0) n nxx n ∞=≠∑!,则该级数( )。
A.是发散级数; B.是绝对收敛级数;C.是条件收敛级数;D. 仅在)1,0)(0,1(-内级数收敛,其他x 值时数发散。
4. 双曲抛物面22x y z p p-=.(p >0,q >0)与xOy 平面的交线是( ) A.双曲线 B.抛物线C.平行直线D.相交于原点的两条直线. 5.322(,)42,f x y x x xy y =-+-函数下列命题正确的是。
A.点(2,2)是f(x,y)的极小值点B. 点(0,0)是f(x,y)的极大值点C. 点(2,2)不是f(x,y)的驻 点D.f(0,0)不是 f(x,y)的极值.二、填空题:(每小题3分,共30分 )1.22yx 1x x y ln z --+-=)( ;2.曲面1-y x z 22+=在点(2 , 1, 4 )处的法线方程是 ;3.设yxarcsin1y x ) y ,f(x )(-+=,则=) 1 ,(x f x ; 4.已知D 是由直线y = 1,x = 2及x = y 所围成 ,则⎰⎰Dxyd σ= ;5.⎰⎰+-2212),(y ydx y x f dy 积分交换积分次序得 ;6.函数f(x,y)是以2为周期的周期函数,它在),[ππ-上的表达式为⎩⎨⎧<≤<≤=ππx 0 , e 0x - ,x )f(x x的和函数为S(x).则)(π25S = ; 7.若级数∑∞=1n n u 收敛,级数 ∑∞=1n n |u |发散,则级数∑∞=1n n u ;8.微分方程y / + P(x)y = Q(x)的的通解为_____________; 9.设y z x dz ==,则;10.设P(x,y)、Q(x,y)在曲线L 围成的单联通区域内具有一阶连续偏导数。
中国地质大学(北京)高数课后练习题

地大(北京)本科高数课后练习题第一章极限习题1.11.设x n=n1+1n (n=1,2,……),证明limn→∞x n=1,并填下表2.用“ε-N”方法证明下列各题(1)limn→∞1n2=0(2)limn→∞3n+12n+1=32(3)limn→∞(−1)n sinnn=0(4)limn→∞0.999…9(有n个9)=03.若limn→∞x n=a,证明limn→∞│x n│=│a│;反之是否成立?4.若数列{x n}有界,且limn→∞y n=0,证明limn→∞x n y n=05.对于数列{x n},若limn→∞x2n=a且limn→∞x2n+1=a,证明limn→∞x n=a9设limx→x0f(x)=A,limx→x0g(x)=B(1)若A>B,证明存在点x0的某个去心邻域,使得在此邻域内f(x)>g(x);(2)若在点x0的某个去心邻域内有f(x) ≧g(x),证明A≧B习题1.21.根据函数极限的定义证明(1)limx→3(3x−1)=8(2)limx→2(5x+2)=12(3)limx→−2x2−4x+2=-4(4)limx→−121−4x22x+1=22.当x→2时,y=x2→4,问δ等于多少,使得当│x-2│<δ时,恒有│y-4│<0.0013.设f(x)=f(x)={x 2,x<1x+1,x≥1(1)作f(x)的图形(2)根据图形写出极限limx→1−f(x)与limx→1+f(x)(3)当x→1时,f(x)有极限吗?4.求下列函数的极限:(1)limx→1+x │x│(2) limx→0+xx2+│x│(3)limx→0−xx2+│x│5. 根据函数极限的定义证明(1)limx→∞x2x+1=12(2)limx→√x=06. 下列极限是否存在?为什么?(1)limx→1x−1│x−1│(2)limx→∞arctanx(3) limx→∞e−x(4) limx→∞(1+e−x)7. 如果函数f(x)当x→x0时的极限存在,证明f(x)在点x0的某个去心邻域内有界。
《高等数学基础》形考任务2(2022春版本)
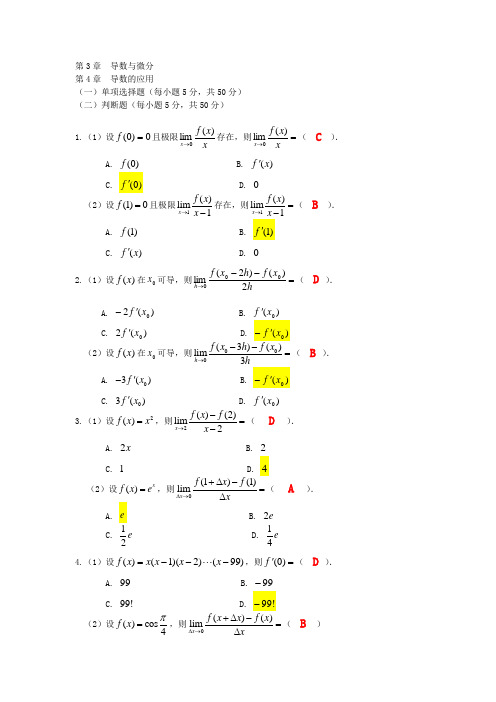
第3章 导数与微分第4章 导数的应用(一)单项选择题(每小题5分,共50分)(二)判断题(每小题5分,共50分)1.(1)设0)0(=f 且极限x x f x )(lim 0→存在,则=→xx f x )(lim 0( C ). A. )0(f B. )(x f 'C. )0(f 'D. 0(2)设(1)0f =且极限1()lim 1x f x x →-存在,则1()lim 1x f x x →=-( B ). A. (1)f B. (1)f 'C. ()f x 'D. 02.(1)设)(x f 在0x 可导,则=--→hx f h x f h 2)()2(lim 000( D ). A. )(20x f '- B. )(0x f 'C. )(20x f 'D. )(0x f '- (2)设)(x f 在0x 可导,则000(3)()lim 3h f x h f x h→--=( B ). A. 03()f x '- B. )(0x f '-C. 03()f x 'D. )(0x f '3.(1)设2()f x x =,则2()(2)lim 2x f x f x →-=-( D ). A. 2x B. 2C. 1D. 4 (2)设()xf x e =,则0(1)(1)lim x f x f x∆→+∆-=∆( A ). A. e B. 2eC. 12eD. 14e 4.(1)设)99()2)(1()(---=x x x x xf ,则=')0(f (D ). A. 99 B. 99- C. !99 D. !99-(2)设()cos 4f x π=,则0()()lim x f x x f x x∆→+∆-=∆( B )A. 2B. 0C. sin 4π- D. sin 4π5.(1)若函数()f x 在0x 处可导,则下列结论中错误的是( B )A. 函数)(x f 在点0x 处有定义B. ()0lim x x f x A →=,但()0A f x ≠ C. 函数)(x f 在点0x 处连续D. 函数)(x f 在点0x 处可微(2)下列结论中正确的是( C ).A. 若)(x f 在点0x 有极限,则在点0x 可导.B. 若)(x f 在点0x 连续,则在点0x 可导.C. 若)(x f 在点0x 可导,则在点0x 有极限.D. 若)(x f 在点0x 有极限,则在点0x 连续.6.(1)若函数)(x f 满足条件(D ),则存在),(b a ∈ξ,使得ab a f b f f --=)()()(ξ. A. 在),(b a 内连续B. 在),(b a 内可导C. 在),(b a 内连续且可导D. 在],[b a 内连续,在),(b a 内可导(2)若函数)(x f 满足条件( D ),且()()f a f b =,则存在),(b a ∈ξ,使得()0f ξ'=A. 在),(b a 内连续B. 在),(b a 内可导C. 在),(b a 内连续且可导D. 在],[b a 内连续,在),(b a 内可导7.(1)下列结论中( A )不正确.A. 若)(x f 在0x 处连续,则一定在0x 处可微.B. )(x f 在0x x =处不连续,则一定在0x 处不可导.C. 可导函数的极值点一定发生在其驻点上D. 若)(x f 在[],a b 内恒有()0f x '<,则)(x f 在[],a b 内是单调下降的(2)下列结论中( D )不正确.A. 若)(x f 在点0x 处可微,则一定在0x 处连续.B. 可导函数的极值点一定发生在其驻点上C. )(x f 在0x x =处不连续,则一定在0x 处不可导D. 函数的极值点一定发生在函数的不可导点8.(1)设)(x f 在),(b a 内有连续的二阶导数,),(0b a x ∈,若)(x f 满足( C ),则)(x f在0x 取到极小值.A. 0)(,0)(00=''>'x f x fB. 0)(,0)(00=''<'x f x fC. 0)(,0)(00>''='x f x fD. 0)(,0)(00<''='x f x f(2)设)(x f 在),(b a 内有连续的二阶导数,),(0b a x ∈,若)(x f 满足( D ),则)(x f在0x 取到极大值.A. 0)(,0)(00=''>'x f x fB. 0)(,0)(00=''<'x f x fC. 0)(,0)(00>''='x f x fD. 0)(,0)(00<''='x f x f9.(1)设)(x f 在),(b a 内有连续的二阶导数,且()0,()0f x f x '''<<,则)(x f 在此区间内是( A ).A. 单调减少且是凸的B. 单调减少且是凹的C. 单调增加且是凸的D. 单调增加且是凹的(2)设)(x f 在),(b a 内有连续的二阶导数,且()0,()0f x f x '''><,则)(x f 在此区间内是( B ).A. 单调减少且是凸的B. 单调减少且是凹的C. 单调增加且是凸的D. 单调增加且是凹的10.(1)设3ln y x x =,则dy =( )A. ()22ln x x xdx + B. ()223ln x x x dx + C. 23ln x xdx D. 223ln x x x +(2)设2ln y x x =,则dy =( )A. ()ln x x x dx +B. ()2ln x x x dx +C. 2ln x xdxD. 2ln x x x +(二)判断题(每小题5分,共50分)11.(1)若函数()f x 在[],a b 内恒有()0f x '<,则()f x 在[],a b 上的最小值为()f b . (对)(2)若函数()f x 在[],a b 内恒有()0f x '<,则()f x 在[],a b 上的最大值为()f b . (错)12.(1)设函数⎪⎩⎪⎨⎧=≠=0,00,1sin )(2x x x x x f ,则=')0(f 1 (错)(2)设函数31sin ,0()0,0x x f x x x ⎧≠⎪=⎨⎪=⎩,则=')0(f 0 (对)13. (1)设x x x f e 5e )e (2+=,则=x x f d )(ln d 2ln 5x x +. (对)(2)设函数2(3)65f x x x +=+-,则()214f x x '=- (错)14.(1)曲线()2x f x =在()1,2处的切线斜率是0 (错)(2)曲线()1f x =在()1,2处的切线斜率是2 (错)15. (1)曲线ln y x =在点()1,0处的切线方程是1y x =- (对)(2)曲线11y x =-在点()2,1处的切线方程是3y x =-+ (对)16.(1)设2sin x y x =,则2ln 2sin 2cos x x y x x '=⋅+ (对)(2)设1cos y x x =+,则21sin y x x '=-+ (错)17.(1)设ln y x x =,则1y x ''= (对)(2)设2ln y x x =,则2ln 2y x ''=+ (错)18. (1)设2()47f x x x =-+的极小值点为2x = (对)(2)函数()2()11f x x =++的极小值点为1x = (错)19.(1)若函数()f x 在点0x 可导,且0x 是()f x 的极值点,则()00f x '=(对) (2)满足()0f x '=的点一定是函数()y f x =的极值点 (错)20.(1)函数32()535f x x x x =-++的拐点的横坐标是35x =(错) (2)函数32()231214f x x x x =+-+的拐点的横坐标是2x = (错)7(1)下列结论中正确的是( B ? ).A. 若)(x f 在点0x 处连续,则一定在0x 处可微.B. )(x f 在x =处不连续,则一定在0处不可导.C. 可导函数的极值点一定发生在其驻点上D. 若)(x f 在[],a b 内恒有()0f x '<,则)(x f 在[],a b 内是单调下降的。
《高等数学(二)》 作业及参考答案

《高等数学(二)》作业一、填空题1.点A (2,3,-4)在第 卦限。
2.设22(,)sin,(,)yf x y x xy y f tx ty x=--=则 .3。
4.设25(,),ff x y x y y x y∂=-=∂则。
5.设共域D 由直线1,0x y y x ===和所围成,则将二重积分(,)Df x y d σ⎰⎰化为累次积分得 。
6.设L 为连接(1,0)和(0,1)两点的直线段,则对弧长的曲线积分()Lx y ds +⎰= 。
7.平面2250x y z -++=的法向量是 。
8.球面2229x y z ++=与平面1x y +=的交线在0x y 面上的投影方程为 。
9.设22,z u v ∂=-=∂z而u=x-y,v=x+y,则x。
10.函数z =的定义域为 。
11.设n 是曲面22z x y =+及平面z=1所围成的闭区域,化三重积为(,,)nf x y z dx dy dz ⎰⎰⎰为三次积分,得到 。
12.设L 是抛物线2y x =上从点(0,0)到(2,4)的一段弧,则22()Lx y dx -=⎰。
13.已知两点12(1,3,1)(2,1,3)M M 和。
向量1212M M M M =的模 ;向量12M M 的方向余弦cos α= ,cos β= ,cos γ= 。
14.点M (4,-3,5)到x 轴的距离为 。
15.设sin ,cos ,ln ,dzz uv t u t v t dt=+===而则全导数。
16.设积分区域D 是:222(0)x y a a +≤>,把二重积分(,)Df x y dx dy ⎰⎰表示为极坐标形式的二次积分,得 。
17.设D 是由直线0,01x y x y ==+=和所围成的闭区域,则二重积分Dx d σ⎰⎰= 。
18.设L 为XoY 面内直线x=a 上的一段直线,则(,)Lp x y dx ⎰= 。
19.过点0000(,,)p x y z 作平行于z 轴的直线,则直线方程为 。
地大《高等数学(一)》在线作业一-0007.33EF5BB9-057A-456A-B1D6-068436839ABE(总8页)

B:正确
答案:A
B:1
C:2
D:3
答案:B
函数y=
B:1
C:2
D:3
答案:B
y=x+arctanx的单调增区间为
A:(0,+∞)
B:(-∞,+∞)
C:(-∞,0)
D:(0,1)
答案:B
对一个函数先求不定积分再求微分,两者的作用抵消后只差一个常数。
A:错误
B:正确
答案:A
一元函数可导必连续,连续必可导。
地大《高等数学(一)》在线作业一-0007
∫(1/(√x (1+x))) dx
A:等于-2arccot√x+C
B:等于1/((2/3)x^(3/2)+(2/5)x^(5/2))+C
C:等于(1/2)arctan√x+C
D:等于2√xln(1+x)+C
答案:A
g(x)=1+x,x不等0时,f[g(x)]=(2-x)/x,则f‘(0)=( )
A:2
B:-2
C:1
D:-1
答案:B
∫{(e^x-1)/(e^x+1)}dx 等于( )
A:(e^x-1)/(e^x+1)+C
B:(e^x-x)ln(e^x+1)+C
C:x-2ln(e^x+1)+C
D:2ln(e^x+1)-x+C
答案:D
微分方程y'+y=x+1的一个特解是( )
A:x+y=0
B:x-y=0
A:错误
B:正确
答案:A
周期函数有无数个周期
地大《微积分(二)》在线作业二

C:arcsin2x
D:arcsin2x+c
答案:A
若∫_0^1[(2x+k)dx=2],则k=( )
A:0
B:-1
C:1
D:1/2
答案:C
当被积函数含有√(x^2-a^2 )时,可考虑令x=( )
A:asint
B:atant
C:asect
D:accost
答案:C
如果∫df(x)=∫dg(x),则必有( )。
A:f(x,y)=(√(x^2*y^2)与g(x,y)=(√xy)^2
B:f(x,y)=(√(x^2*y^2)与g(x,y)=|xy|
C:f(x,y)=ln(xy)^2与g(x,y)=2ln|xy|
D:f(x,y)=ln(xy)与g(x,y)=lnx+lny
答案:B,C
下列级数中,收敛的是( )。
A:∑1/(n^3)
地大《微积分(二)》在线作业二
设f(x+y,x-y)=x^2-y^2,则?f(x,y)/?x+?f(x,y)/?y=( )
A:2x-2y
B:2x+2y
C:x+y
D:x-y
答案:D
∫{(e^x-1)/(e^x+1)}dx =( )
A:(e^x-1)/(e^x+1)+C
B:(e^x-x)ln(e^x+1)+C
C:F(x)=ln(2+x)
D:F(x)=lnx/2
答案:D
设f(x)是连续函数,F(x)是f(x)的原函数,则( )
A:当f(x)是奇函数时,F(x)必是偶函数
B:当f(x)是偶函数时,F(x)必是奇函数
中国地质大学 管理数学(2)(高起专)阶段性作业1-4答案

管理数学(2)(高起专)阶段性作业11.点在下面的某个曲面上,该曲面是_______。
(10分)(A)(B)(C)(D)参考答案:A2.空间直角坐标系中表示______。
(10分)(A) 圆(B) 圆面(C) 圆柱面(D) 球面参考答案:C3.点关于平面的对称点是_______。
(10分)(A)(B)(C)(D)参考答案:B4.在球内部的点是_______。
(10分)(A)(B)(C)(D)参考答案:C5.两个向量与垂直的充要条件是_______。
(10分)(A)(B)(C)(D)参考答案:A6.设两平面方程分别为和,则两平面的夹角为______ _。
(10分)(A)(B)(C)(D)参考答案:B7.向量,则有_______。
(10分)(A) ∥(B) ⊥(C)(D)参考答案:B8.点P(-1、-2、1)到平面x+2y-2z-5=0的距离为_______。
(10分)(A) 2(B) 3(C) 4(D) 5参考答案:C9.点,的距离_______。
(10分)(A)(B)(C)(D)参考答案:C10.设a=i+2j-k,b=2j+3k,则a与b 的向量积为_______。
(10分)(A) i-j+2k(B) 8i-j+2k(C) 8i-3j+2k(D) 8i-3i+k参考答案:C管理数学(2)(高起专)阶段性作业21.函数z=xsiny在点(1,)处的两个偏导数分别为_______。
(10分)(A)(B)(C)(D)参考答案:A2.函数的定义域是_______。
(10分)(A)(B)(C)(D)参考答案:C3.二元函数的驻点是_______。
(10分)(A) (0,0)(B) (0,1)(C) (1,0)(D) (1,1)参考答案:D4.二元函数在(0,0)点处的极限是_______。
(10分)(A) 1(B) 0(C)(D) 不存在参考答案:B5.cosx的麦克劳林级数为_______。
(10分)(A)(B)(C)(D)参考答案:A6. 设可微,则下列结论正确的是_______。
