初三科学-简单机械综合专题
初中科学教案:简单机械 教案

初中科学精品教案:简单机械教案一、教学目标:1. 让学生了解和掌握简单机械的基本概念和分类。
2. 使学生能够运用杠杆、滑轮等简单机械的原理解决实际问题。
3. 培养学生的观察能力、动手能力和创新能力。
二、教学内容:1. 简单机械的定义和分类2. 杠杆的原理和分类3. 滑轮的原理和分类4. 实际问题分析与解决三、教学重点与难点:1. 教学重点:简单机械的基本概念、分类和原理;实际问题的解决。
2. 教学难点:杠杆和滑轮的原理在实际问题中的应用。
四、教学方法:1. 采用问题驱动法,引导学生主动探究简单机械的原理和应用。
2. 利用实验、观察、讨论等教学手段,培养学生的动手能力和观察能力。
3. 结合实际例子,让学生学会运用简单机械原理解决实际问题。
五、教学过程:1. 导入:通过展示生活中常见的简单机械,引发学生对简单机械的兴趣。
2. 新课:介绍简单机械的定义、分类和基本原理。
3. 实验与观察:让学生亲自动手进行实验,观察杠杆和滑轮的原理。
4. 实际问题分析:引导学生运用简单机械原理分析并解决实际问题。
6. 布置作业:让学生结合生活实际,运用所学知识解决相关问题。
六、教学评估:1. 课堂表现评估:观察学生在课堂上的参与程度、提问回答情况以及小组讨论的表现。
2. 实验操作评估:评价学生在实验过程中的操作技能、观察能力和问题解决能力。
3. 作业完成情况评估:检查学生作业的完成质量,特别是运用简单机械原理解决实际问题的能力。
4. 学生自评与互评:鼓励学生进行自我评价和同伴评价,以提高他们的自我认知和团队协作能力。
七、教学反思:1. 反思教学内容:检查教学内容是否符合学生的认知水平,是否需要调整或补充。
3. 反思教学效果:评估学生对简单机械原理的理解和应用能力,确定是否达到教学目标。
4. 学生反馈:听取学生的意见和建议,以便在后续教学中更好地满足他们的学习需求。
八、教学拓展:1. 开展简单机械设计比赛,让学生运用所学知识设计并制作实用的简单机械。
九年级科学上册简单机械简单机械 (1)

解题指导
【例题】 (2017·山东济宁)如图 3.42 所示为一个杠杆式 简易起吊机,它上面装了一个定滑轮可以改变拉绳的 方向,杠杆 OBA 可绕 O 点转动,重物通过绳子对杠杆 的拉力为阻力。图中能够正确表示动力臂的是 ( )
D. l4
【解析】 动力为促使杠杆转动的力,指直接作用在杠杆 上的力而不是经转换后的力,即动力作用在滑轮与杠杆之 间的拉绳上,所以 l2 为动力臂。 【答案】 B
反思
力臂是支点到力的作用线的距离,而不是支点到力的作用 点的距离;力必须是直接作用于杠杆上的力。
按时完成课后同步训练,全面提升自我!
单击此处进入课后同步训练
图 3.41
电子秤的工作原理如图 3.41 所示,当物体放在秤盘 上时,压力施给传感器,使传感器发生形变,从而使阻抗 发生变化,同时使激励电压发生变化,输出一个变化的模 拟信号。该信号经放大电路放大输出到模数转换器,转换 成便于处理的数字信号输出到 CPU 运算控制,CPU 根据 键盘命令以及程序将这种结果输出到显示器,直至显示这 种结果。电子秤是现代传感器技术、电子技术和计算机技 术一体化的电子称量装置,能满足并解决现实生活中提出 的“ 快速、准确、连续、自动” 的称量要求,同时有效地消 除人为误差,使之更符合法制计量管理和工业生产过程控 制的应用要求。
学习指要
知识要点
1.杠杆:一根硬棒在力的作用下能够绕固定点转动,这 根硬棒就叫做杠杆。
2.杠杆的五要素 (1)支点:使杠杆绕着转动的固定点 O。 (2)动力:使杠杆转动的力 F1。 (3)阻力:阻碍杠杆转动的力 F2。 (4)动力臂:从支点到动力作用线的距离 l1。 (5)阻力臂:从支点到阻力作用线的距离 l2。
重要提示
1.杠杆的形状可以是直的,也可以是弯的。 2.动力和阻力是作用在杠杆上的力,两个力的作用效果是使杠
简单机械第1课时(PPT课件(初中科学)40张)

l1 O
甲
l´ O
l1
乙
思考与讨论
如何使杠杆最省力?
提示:比较F沿不同 方向时力臂的大小。
沿F2方向用力时动力臂最大,所以F2最小。
如图所示,用撬棒向下撬石头,手握在撬
棒的末端B端,其中AO=0.1米,OB=1米,若
石头对A的压力为500牛,求在B端至少要用多
大的力才能撬起石头。
核桃钳就属于简单机械——杠杆,今天我们就来学习杠杆的知识。
一、杠杆
1.认识杠杆
我们每天都在使用机械,有简单的机械,也有 复杂的机械。
简单机械
较复杂的机械
这些能给我们提供方便的工具都称为机械。
• 任何复杂的机械都是由一些简单机械组合而成的。 • 杠杆就是一种非常简单的机械。
尝试使用下图各种工具,体验在使用过程中有什么 共同特征。Байду номын сангаас
第4节 简单机械
第1课时 杠杆
学习目标
能指出杠杆的支点、动力、阻力、动力臂和阻力臂。 会绘制杠杆的动力臂和阻力臂图示。 理解杠杆平衡原理,并能应用杠杆的平衡条件解决简单
的问题;会辨认生活中常见的省力杠杆、费力杠杆和等 臂杠杆。
情境导入
比一比:女生用核桃钳夹 核桃,男生用手捏核桃, 看谁先把核桃压碎。
画出下列杠杆的力臂
L2 L1
F2
O
L1 F1
L2 F2
2.人体上的杠杆
人体的杠杆系统,都有四个基本组成部分: 骨—— 一根硬棒; 肌肉收缩——动力的来源; 两根骨之间可以活动的关节——支点; 移动肢体或物体——阻力的来源。
寻找手臂上的杠杆
当手拿物体抬起时 找出相应的杠杆, 以及支点、动力、 阻力。
初中科学竞赛辅导《简单机械》经典计算20题(有解析)

初中科学竞赛辅导《简单机械》经典计算20题(温馨提示:题目的编排顺序遵循由易到难的原则,使用时可根据实际需要选择合适的题目进行训练;如有疑难问题,可与编者交流:QQ 16173689420)1、一保洁工人,要清洗一高楼的外墙,他使用了如图所示的装置进行升降,已知工人的质量为60kg,保洁器材的质量为20kg,人对绳的拉力为300N,吊篮在拉力的作用下1min匀速上升了10m,求:(1)此过程中的有用功(2)拉力F做功的功率;(3)滑轮组的机械效率(结果保留一位小数)。
解析:(1)提升工人和保洁器材做的功为有用功:W有=Gh=(60kg+20kg)×10N/kg×10m=8000J(2)将整个装置看作一个整体,那么三段绳子都受力,已知拉力为300N,则整个装置的总重为:F=3×300N=900N;拉力F做的功即为总功:W总=Fs=300N×30m=9000J;拉力做功功率:P= W/ t=9000/60s=150W(3)滑轮组的机械效率:η= W有/ W总=8000J/9000J≈88.9%答案:(1)此过程中的有用功为8000J;(2)拉力F做功的功率为150W;(3)滑轮组的机械效率为88.9%.2、随着城市的建设规划,衢州城内出现许多高层建筑,电梯是高层建筑的重要组成部分.某电梯公寓的电梯某次在竖直向上,运行的过程中,速度随时间变化的情况如图所示,忽略电梯受到的空气阻力和摩擦阻力,向上运行的动力只有竖直向上的电动机拉力,电梯箱和乘客的总质量为600kg,(g=10N/kg).求:(1)电梯在匀速运动阶段上升的高度h1是多少?拉力F1做了多少功?(2)电梯在前4秒作匀加速运动,如果匀加速阶段的平均速度等于该阶段速度的最大值和最小值的平均值,且在匀加速阶段,电动机的拉力F2做了11520J的功;求匀加速阶段电动机拉力F2的大小?(3)电梯开始向上运动后经过64s,电动机的拉力的平均功率是多大?解析:(1)电梯匀速阶段V1﹦0.8m/s,t1﹦60s,电梯在匀速运动阶段上升的高度h1=V1t1=0.8m/s×60s﹦48m;拉力F 1做功W 1=F 1h 1﹦6000N×48m﹦2.88×105J ;(2)匀加速阶段的平均速度v 2﹦(0.8m/s+0)/2﹦0.4m/s ; 匀加速阶段电动机拉力F 2﹦W 2/ S 2=11520J/0.4×4m﹦7200N ; (3)W=W 1+W 2=2.88×105J+11520J=299520J ;电动机的拉力的平均功率是P= W/ =299520J/64s=4680W ;答案:(1)电梯在匀速运动阶段上升的高度h1为48m ,拉力F 1 做了2.88×105J ;(2)匀加速阶段电动机拉力F 2的大小7200N ;(3)电动机的拉力的平均功率4680w 。
简单机械专题练习浙教版九年级上册科学

一.滑轮的计算常见例题掌握例1.如图所示的滑轮组将重10N的物体匀速提升0.1m,所用时间为2s,作用在绳子末端的拉力F为6N(不计绳重和绳与滑轮间的磨擦),下列计算结果正确的是()A、所做的有用功为1JB、动滑轮自重0.2NC、拉力F做功的功率为0.3WD、该滑轮组的机械效率为83.3%例2.利用如图所示的甲、乙两个滑轮组,在相同的时间内用大小相同的力F1和F2分别把质量相等的重物G1和G2提升到相同的高度,则()A、甲滑轮组的机械效率高B、乙滑轮组的机械效率高C、F2做功的功率大D、F1、F2做功的功率一样大例3.两滑轮组装置如图所示,已知每个滑轮重力都为G0,摩擦和绳重均不计,用它们分别匀速提起重为G=5G0的物体时,甲、乙两滑轮组的机械效率之比是()A、6:7B、7:6C、5:6D、5:7例4.如图所示,斜面长6m,高3m,用沿斜面向上、大小为100N的拉力F使物体在5s内沿斜面移动了2m,下列说法正确的是()A、滑轮组的机械效率是40%B、物体重300NC、拉力F做的功是600JD、拉力F的功率是40W例5.在不计摩擦和绳子质量的情况下,分别使用定滑轮、动滑轮、滑轮组(两个定滑轮和两个动滑轮)匀速提升同一物体到同一高度处,其机械效率分别为η定、η动、η组,则下列选项正确的是()A、η组<η动<η定B、η定<η动<η组C、η动<η定<η组D、η定<η组<η动例6.用如图所示的滑轮组提升重1500N的物体,拉力F的大小为400N,若将物体提升0.3m,则拉力做的功为_________ J,该装置的机械效率为_________ .例7.一个质量为70kg的工人,用如图所示的装置(包括滑轮组及装砖的托板)提升一堆砖.已知装砖的托板重200N,每块砖重100N.滑轮的摩擦和绳重均可忽略不计,当工人匀速提升10块砖时,此装置的机械效率为80%.那么,该人站在地面上用此装置提升这些砖的过程中,此装置的机械效率最高可达到_________ .(取g=10N/kg,结果保留1位小数)例8.如图12所示装置,物体B所受重力为G B,物体A在物体B的作用下在水平桌面上向右匀速运动.小明用一个水平向左的力拉物体A,使物体B以速度v匀速上升,此时滑轮组的机械效率为80%;若将物体B换成物体C后,小明用另一个水平向左的力拉物体A,使物体C以4v的速度匀速上升,此时滑轮组的机械效率为60%.不计绳重及滑轮组装置的摩擦,则第二次水平向左拉物体A时,拉力的功率是______.例9.如图所示装置,在水平拉力F的作用下,物体M沿水平地面做匀速直线运动,已知弹簧秤读数为10牛,物体M的运动速度为1米/秒(若不计滑轮与绳子质量、绳子与滑轮间的摩擦、滑轮与轴间的摩擦)。
浙教版科学九年级上册-3.4简单机械同步练习题
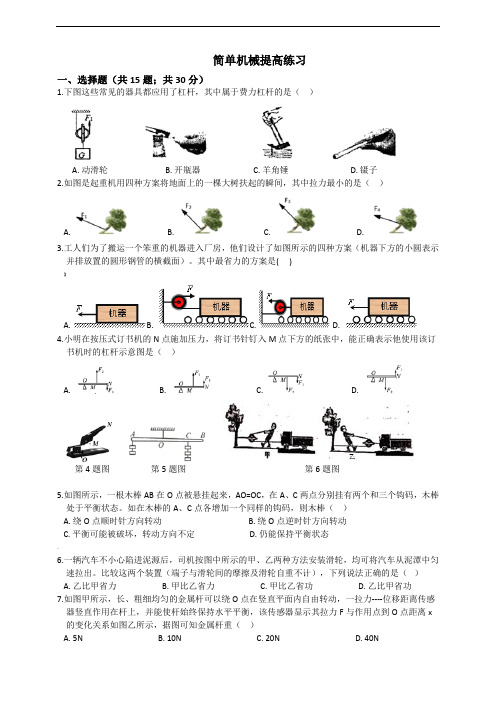
简单机械提高练习一、选择题(共15题;共30分)1.下图这些常见的器具都应用了杠杆,其中属于费力杠杆的是()A. 动滑轮B. 开瓶器C. 羊角锤D. 镊子2.如图是起重机用四种方案将地面上的一棵大树扶起的瞬间,其中拉力最小的是()A. B. C. D.3.工人们为了搬运一个笨重的机器进入厂房,他们设计了如图所示的四种方案(机器下方的小圆表示并排放置的圆形钢管的横截面)。
其中最省力的方案是( )】A. B. C. D.4.小明在按压式订书机的N点施加压力,将订书针钉入M点下方的纸张中,能正确表示他使用该订书机时的杠杆示意图是()A. B. C. D.第4题图第5题图第6题图5.如图所示,一根木棒AB在O点被悬挂起来,AO=OC,在A、C两点分别挂有两个和三个钩码,木棒处于平衡状态。
如在木棒的A、C点各增加一个同样的钩码,则木棒()A. 绕O点顺时针方向转动B. 绕O点逆时针方向转动C. 平衡可能被破坏,转动方向不定D. 仍能保持平衡状态。
6.一辆汽车不小心陷进泥源后,司机按图中所示的甲、乙两种方法安装滑轮,均可将汽车从泥潭中匀速拉出。
比较这两个装置(端子与滑轮间的摩擦及滑轮自重不计),下列说法正确的是()A. 乙比甲省力B. 甲比乙省力C. 甲比乙省功D. 乙比甲省功7.如图甲所示,长、粗细均匀的金属杆可以绕O点在竖直平面内自由转动,一拉力----位移距离传感器竖直作用在杆上,并能使杆始终保持水平平衡,该传感器显示其拉力F与作用点到O点距离x 的变化关系如图乙所示,据图可知金属杆重()A. 5NB. 10NC. 20ND. 40N第7题图第8题图8.图示滑轮组,在2s内将物重G为1000N的物体沿水平方向匀速移动,所用水平拉力F为300N,物体受到水平地面的摩擦力f为物重G的倍。
在此过程中,说法正确的是()】A. 绳子自由端沿水平方向移动的速度为/sB. 物体受到的拉力为600NC. 拉力F的功率为120WD. 滑轮组的机械效率为%9.如图,用刻度均匀的匀质杠杆进行“杠杆平衡条件”的实验(每个钩码重为牛),下列说法正确的是()A. 实验前出现图甲所示情况,应将杠杆的平衡螺母向左调B. 图乙,在AB处各增加一个钩码,杠杆仍然能保持平衡C. 图丙,弹簧测力计从a位置转到b位置,为保持杠杆在水平位置平衡,其示数将变大D. 图丁,用弹簧测力计在c点向上拉杠杆,为保持杠杆在水平位置平衡,其示数小于3牛10.育英学校高中部扩建,需要在新旧校址间建立一座桥梁。
新版浙教版初中科学九年级上册3.4简单机械精选汇总

浙教版初中科学
重点知识精选化学是一门非常有意思的学科,充满了新奇的实验!浙教版初中科学和你一起共同进步学业有成!
Little Tsinghua Education Tutorial Station 3.4 简单机械(第一课时)
A.两杠杆均为省力杠杆
B.两杠杆均为费力杠杆
C.ABC为省力杠杆
D.A′B′C′为省
力杠杆
②如右图,杠杆在水平方向平衡,若将测力计缓慢地自位置1移到位置2,并保持杠杆始终水平平衡,则测力计的读数变化是()
A.不断增大B.不断减小
C.先增大,然后减小
D.先减小,然后增大
③右图,OA=25cm,OB=20cm,OC=20cm,AC=15cm,杠杆水平平衡,测力计示数为()
A.36N B.45N
C.50N D.60N
作示意图,请在图中分别标出动力、阻力、动力臂、阻力臂。
Little Tsinghua Education Tutorial Station
承受的拉力为N,
米,则物体移动
受到地面的阻力= N
(不计绳重及滑轮转动摩擦)。
的重物,至少需要几个滑轮?画出简单机械滑轮组的组装图。
相信自己,就能走向成功的第一步
教师不光要传授知识,还要告诉学生学会生活。
数学思维可以让他们更理性
地看待人生。
专题十一 简单机械—2021届九年级科学中考总复习专题讲义(物理)

中考专题复习专题十一简单机械1、杠杆的五个要素(1)支点(O):杠杆绕着转动的固定点(2)动力(F1):作用在杠杆上,使杠杆转动的力(3)阻力(F2):作用在杠杆上,阻碍杠杆转动的力(4)动力臂(L1):支点到动力作用线的距离(5)阻力臂(L2):支点到阻力作用线的距离2、杠杆平衡(1)杠杆在动力和阻力的作用下,保持静止或匀速转动状态(杠杆平衡公式:动力X动力臂=阻力X阻力臂(F L= F L)力臂的关系力的关系特点举例省力杠杆L1 > L2 F1 < F2 省力费距离羊角锤费力杠杆L1 < L2 F1 > F2 费力省距离镊子等臂杠杆L1 = L2 F1 = F2 不省力不省距离改变力方向天平3定滑轮动滑轮拉力表达式F=G F=1G2绳移动距离h 2h物体移动距离h h省力状况不省力省一半实质等臂杠杆省力杠杆举例升旗起重机滑轮组:既省力又可改变力的方向4、机械效率:有用功跟总功的比值公式:ƞ=W有有/W有 * 100%(2)机械效率越高,表示机械对功的利用率越高一、单选题专题十一 简单机械1. 如图为吸盘式挂杆,将吸盘压在瓷砖上排尽其中的空气,挂杆就能被固定在瓷砖上。
挂有平底锅的挂钩沿光滑水平横杆从 P 点开始向吸盘 B 移动,若吸盘与横杆的重力、吸盘大小均忽略不计,设挂钩与吸盘 A 的距离为 l ,则吸盘 B 受到的摩擦力 F 的大小与 l 的关系图像为()A. B. C. D.2. 如图所示是汽车起重机,其中A ,B 组成滑轮组(结构A. 滑轮组中 A 滑轮用于改变力的方向B. 当 C 杆伸长时吊臂对 D 杆的压力将变大C. 当 D 杆伸长时力 F 的力臂将变小D. H 的作用是工作时以防翻车和避免轮胎受到的压力过大 3.(2017•嘉兴)如图是一种切甘蔗用的铡刀示意图。
下列有关说法正确的是( )A. 刀刃很薄可以增大压力B. 铡刀实质上是一种费力杠杆C. 甘蔗放在 a 点比 b 点更易被切断D. 手沿 F 1 方向用力比沿 F 2 方向更省力4.如图所示是使用简单机械匀速提升同一物体的四种方式(不计机械自重和摩擦),其中所需动力最小的是 ( )A.B. C. D.二、填空题5.(2016•金华)简单机械在我们的生活中应用广泛,请回答下列有关简单机械的问题:.(2)如图乙是一把剪刀,在使用过程中要达到相对省力的效果,则被剪物体应放在点(填字母“A ”或“6.(2016•湖州) 如图是三类不同用途的杠杆模型.这三类杠杆中,一定是省力杠杆的是第 类,钓鱼竿与第 类杠杆原理相同.7.图甲是一种壶口处配有自动开合小壶盖的电水壶。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
学员编号:年级:初三课时数:3学员姓名:辅导科目:科学学科教师:授课主题简单机械综合专题授课日期及时段教学内容一、专题检测1.如图所示,甲、乙两个物体的体积相等,甲的质量是乙质量的2倍,现杠杆处于水平平衡状态.若将甲、乙二物体同时浸没在水中,则杠杆将()AA.左端下沉B.右端下沉C.仍然保持水平状态D.无法确定2.如图所示,一根轻质木杆A端细线下所挂重为50N、底面积为2×10﹣2m2的重物静止在水平地面上.当在B点加竖直向下的力F=30N作用时,木杆能在水平位置处于平衡状态,此时细线竖直,已知OA=15cm,OB=5cm,则重物对水平地面的压强为2×103Pa;重物对杠杆的拉力为10N.3.在水平桌面上,放置一个重200N的物体,当匀速拉动物体时,物体与桌面的摩擦力为80N,如图所示.若忽略绳、滑轮的重力及绳与滑轮的摩擦,水平拉力F是40N,物体受到的摩擦力方向是水平向左.4.最近,中央电视台科教频道播出了在我市拍摄的“汽车落水后如何水下逃生”的纪录片.纪录片中,实验人员开着小车从高处落入滚滚的岷江,并在门窗紧闭的车中,尝试用不同的方法砸碎车窗玻璃逃生,惊心动魄.为了确保实验人员的安全,摄制组精心设计了紧急救援装置,用于当实验人员无法从车中逃生时迅速吊起汽车.现某课外活动小组,照此设计了如图所示的简单机械,模拟紧急救援落水汽车.实验中用实心圆柱体A代替小车,已知A的体积为0.12m3,质量为210kg.(g取10N/kg,设整个过程A均为匀速运动状态,忽略钢缆绳重及滑轮摩擦,不考虑风浪、水流等因素的影响.)(1)求A完全浸没在水中时受到的浮力是多大?(ρ水=1.0×103kg/m3)(2)若A完全浸没在水中时,滑轮组的机械效率为60%.那么A完全打捞出水面后,岸上钢绳的拉力F为多大?(3)若A完全打捞出水面后,以0.5m/s的速度被匀速提升,求岸上钢绳拉力F的功率.(4)从A上表面刚出水面到A完全离开水面的过程中,滑轮组机械效率如何变化?请简述理由.解:(1)F浮=ρ水gV排=1.0×103kg/m3)×10N/kg×0.12m3=1200N;(2)A的重力为:G物=m物g=210N×10N/kg=2100NA在水中时η=60%,则:W有=(G物﹣F浮)•h W总=(G物﹣F浮)•h+G动•h又∵η=60%∴=60% 即=60%解得:G动=600N由图知,滑轮组由5段绳子承担物重,∴A完全出水后,钢绳拉力F===540N;(3)物体上升速度为0.5m/s,所以绳端移动距离为v=5×0.5m/s=2.5m/s;则P===Fv=540N×2.5m/s=1350W(4)A从上表面刚出水面到A完全离开水面的过程中,A受到的浮力在减小,绳子对A的拉力在增大,滑轮组对A做的有用功在增加.在额外功一定的情况下,整个过程滑轮组的机械效率在变大.二、知识梳理1、问题:杠杆两侧分别悬挂密度为ρ1、ρ2的物体,杠杆平衡;当物体分别浸没到密度为ρ3、ρ4的液体中时,杠杆是否仍平衡?方法一:密度比密度比是指杠杆能否平衡决定于两侧所悬挂物体的密度与浸入的液体密度的比值的大小。
用数学方法证明如下:因为杠杆平衡,所以左边物体浸没在密度为ρ3的液体中时,右边物体浸没在密度为ρ4的液体中时,由①②③得:若时,密度为ρ1的物体端下沉;若时,密度为ρ2的物体端下沉;若时,杠杆仍平衡。
方法二:密度差密度差是指杠杆能否平衡决定于两侧所悬挂物体的密度与浸入的液体的密度差的大小。
若ρ1-ρ3>ρ2-ρ4时,密度为ρ1的物体端下沉;若ρ1-ρ3<ρ2-ρ4时,密度为ρ2的物体端下沉;若ρ1-ρ3=ρ2-ρ4时,杠杆仍平衡。
2、进行有关杠杆与密度、体积问题的计算,要使用公式ρ=m/v,这其中与杠杆的平衡条件中没有同类量,但这时应很容易想到重力与质量的关系,而重力与杠杆的平衡条件的力是同类量,所以,杠杆与密度问题的结合,要通过重力与质量的关系进行过渡。
3、进行有关杠杆、滑轮与压强问题的计算,要使用公式P=F/S,很显然,其中的压力与杠杆的平衡条件中的力是同类量,所以,杠杆与压强问题的结合,一定要通过这两个力的关系来实现。
三、题型突破1、杠杆平衡问题与浮力的综合1.如图,体积相同的铁块和铝块挂在杠杆的两端,杠杆处于平衡状态,现将铁块和铝块同时浸没到水中,杠杆将()A.左端下降B.右端下降C.杠杆仍然平衡D.条件不足,无法判断解答:因铝块、铁块体积相同,ρ>ρ铝,有m铁>m铝,G铁>G铝,由杠杆平衡条件,两侧力与力臂的乘积相同,铁但铝一侧的力臂大于铁一侧的力臂;浸没水中后,铁、铝受到的浮力相等,但铝一侧减小的力与力臂的乘积大,所以杠杆不再平衡,铁一侧将下降,即右端下降.故选B.2.质量相等的实心铁块和实心铜块(ρ铁<ρ铜),分别挂在杠杆的两端,杠杆处于平衡状态,若将铜块和铁块同时浸没在水中,则杠杆()A.仍保持平衡B.铁块一端下沉C.铜块一端下沉D.无法判断解答:由于两者质量相等,所以设铁块和铜块的质量为m,杠杆又处于平衡状态,根据杠杆的平衡条件可得:mgL1=mgL2,所以该杠杆是一个等臂杠杆,即L1=L2=L.铁块和铜块浸没在水中时,铁块受到的浮力:F铁=ρ水gV铁=ρg,同理铜块受到的浮力:F铜=ρ水g,由于ρ铁<ρ铜,所以ρg>ρ水g,即铁块受到的浮力大于铜块受到的浮力;此时作用在杠杆上的力是重力减去它们受到的浮力即:G﹣F浮.由此可知铁块产生的力矩(力臂和力的乘积):(mg﹣ρg)L,同理铜块产生的力矩:(mg﹣ρ水g),由于铜块受到的浮力小于铁块受到的浮力,所以:(mg﹣ρg)L<(mg﹣ρ水g)L,杠杆将向力矩大的一方,即铜块一侧倾斜,故铜块一端下沉.综上分析故选C.2、杠杆与浮力的综合计算1.如图所示,杠杆AOB处在水平位置平衡,OA:OB=1:2,浸入水中的铁球质量m=7.9kg,加在B端的力F=24.5N,ρ铁=7.9×103kg/m3,g=10N/kg.则空心体积是()A.1×10﹣3m3B.2×10﹣3m3C.3×10﹣3m3D.4×10﹣3m3解答:∵杠杆在水平位置平衡,∴F×OB=F A×OA,∴A端受到的拉力:F A===49N,对于铁球:∵F A+F浮=G球=m球g,∴铁求受到的浮力:F浮=m球g﹣F A=7.9kg×10N/kg﹣49N=30N,∵F浮=ρ水v排g,∴铁球排开水的体积(铁球的体积)v球=v排===3×10﹣3m3,7.9kg铁的体积:v铁===1×10﹣3m3,故空心部分体积:v空=v球﹣v铁=3×10﹣3m3﹣1×10﹣3m3=2×10﹣3m3.故选B.2.如图所示,某圆柱形容器内装有适量的水,底面积为20cm2.将物体B放入水中时,通过磅秤测得总质量为150g;使用一个杠杆提起物体B,发现当杠杆C端挂钩码A时,杠杆在水平位置恰好平衡,物体B刚好有一半体积露出水面.此时天平示数为50g,测得容器内液面下降了1cm.则物体B的密度为3×103kg/m3.(g取10N/kg)解答:第一次通过磅秤测得总质量150g:则G+G水+G B=m1g=0.15kg×10N/kg=1.5N…①容器B的体积:V=2Sh=2×20cm2×10﹣4×0.01m=4×10﹣5m3,第二次此时磅秤示数为50g:则G容器+G水+F浮=m2g=0.05×10N/kg=0.5N…②由①﹣②得,G B﹣F浮=1N…③,当B完全出水,液面将再下降1cm,圆柱形容器装有适量的水,底面积为20cm2,物体受到的浮力等于排开的水的重力,即浮力F浮=ρ水gV排=1.0×103kg/m3×10N/kg×4×10﹣5m3=0.4N将F浮=0.4N代入③,解得G B=1.2N,则m B===0.12kg=120g.则物体B的密度ρ===3g/cm3=3×103kg/m3.故答案为:3×103.3.如图所示轻质杠杆,把密度均为4.0×103kg/m3的甲、乙两个实心物体挂在A、B两端时,杠杆在水平位置平衡,若将甲物体浸没在水中,同时把支点从O移到O′时,杠杆又在新的位置平衡,若两次支点的距离O O′为OA的,求:甲、乙两个物体的质量之比.解答:(1)如图杠杆平衡,根据杠杆平衡条件得,G×OA=G乙×OB,整理可得:甲OB===;(2)甲浸没在水中,杠杆平衡,支点必须向右越大,增大甲的力臂,根据杠杆平衡条件得,(G甲﹣F浮)×O′A=G乙×O′B,(G甲﹣ρ水gV甲)×(OA+OA)=G乙×(OB﹣OA);(ρV甲g﹣ρ水gV甲)×OA=ρV乙g×(﹣OA)=ρV乙g×(﹣OA);整理可得:===因为甲乙密度相等,所以质量之比就等于体积之比,所以甲、乙两个物体的质量之比为2:1.答:甲、乙两个物体的质量之比为2:1.3、杠杆、滑轮与压强的综合计算1.把正方体甲放在水平地面上,对地面的压强是5.4×105Pa.AB是重力可忽略不计的杠杆,支点为0,且OA:0B=1:2.将正方体甲挂在杠杆的A端,在B端施40N竖直向下的拉力时,杠杆在水平位置平衡,如图所示,此时正方体甲对地面的压强变为1.8×105Pa.下列结果正确的是()A.当正方体甲对地面的压力刚好为零时,在杠杆B端应施加竖直向下的拉力是60NB.当正方体甲对地面的压力刚好为零时,在杠杆B端应施加竖直向下的拉力是20NC.正方体甲的重力是240ND.正方体甲的体积约是9.3×10﹣6m3解答:由题知:P1=5.4×105Pa;P2=1.8×105Pa;F1=40N;OA:0B=1:2,设正方体底面积为S;由杠杆平衡条件得:(P1S﹣P2S)•OA=F1•OB,化简得:3.6×105Pa•S=80N,即:S=;物体重力G=P1S=5.4×105Pa××10﹣3m2=120N.当正方体甲对地面的压力刚好为零时,G•OA=F1'•OBF1'=故选A.2.图是锅炉上的保险阀,当阀门受到的蒸气压强超过安全值时,阀门就会被顶开,让蒸气跑出一部分,使锅炉内的蒸气压强减小,阀门面积为3厘米2,杠杆重不计.(1)用毫米刻度尺从图上量出并记录杠杆的动力臂和阻力臂.(2)要保持锅炉内蒸气的压强为1.2×105帕,应在B处挂多重的物体?(3)锅炉用久了耐压能力会降低,怎样调节能使锅炉内蒸气的最大压强小于1.2×105帕?解答:(1)测量可得:动力臂OA=6.1mm,阻力臂OP=37.1mm.(2)气体产生的向上的动力:F=pS=1.2×105Pa×3×10﹣4m2=36N;根据杠杆的平衡条件可知:F1•OA=G•OP;所以物体的重力G==≈5.9N.(3)锅炉用久了耐压能力降低时动力的大小会减小;根据杠杆的平衡条件可知,F1•OA的值减小;要使保险阀起到保险作用,应减小G•OP数值的大小,即将重物向左移减小阻力臂或换成质量较小的物体减小阻力.答:(1)动力臂为OA=6.1mm,阻力臂为OB=37.1mm;(2)应在B处挂5.9N的物体;(3)将重物向左移或换成质量较小的物体.3.如图是小华利用杠杆提升浸没在水中的物体B的示意图.杠杆CD可绕支点O在竖直平面内转动,OC:OD=1:2,物体A为配重,其质量为200g.烧杯的底面积为75cm2,物体B的质量为320g,它的体积为40cm3.当物体B 浸没在水中时,水对杯底的压强为P1.当用力拉物体A,将物体B提出水面一部分以后,杠杆恰好在水平位置平衡,此时,竖直向下拉物体A的力为F,水对杯底的压强为P2.若p1与p2之差为40Pa,求拉力F的大小.(g取10N/kg,杠杆的质量、悬挂物体A和物体B的细绳的质量均忽略不计)解答:由P1、P2之差为40Pa.可求F′=△PS=40Pa×0.75×10﹣2m2=0.3N==0.3×10﹣4m3V排=0.4×10﹣4﹣0.3×10﹣4m3=0.1×10﹣4m3F浮=ρgV排=1.0×103kg/m3×10N/kg×0.1×10﹣4m3=0.1N由杠杆平衡条件得(F+GA)OC=(GB﹣F浮)×OD(F+2N)×OC=(3.2N﹣0.1N)×OD代入数值得F=4.2N答:拉力F为4.2N.4.如图所示,若滑轮重为4N,重物重为6N,OB=2•OA;要使轻质杠杆保持平衡,则F的大小为多少?(不计绳重和摩擦)解答:(1)不计绳重和摩擦,使用动滑轮的拉力:F拉=(G+G动)=(6N+4N)=5N.物体间力的作用是相互的,所以杠杆对动滑轮的拉力为:F'拉=F拉=5N.(2)根据杠杆平衡条件F1L1=F2L2得,F拉'×OA=F×OB,即:5N×OA=F×OB,所以,F=2.5N.答:F大小为2.5N.5.如图所示,AB是一杠杆,可绕支点O在竖直平面内转动,AO:OB=2:3,OD:DB=1:1,滑轮重为100N.当在B点施加大小为F的竖直向下的拉力时,杠杆在水平位置平衡,边长为0.2m的正方体M对水平地面的压强为7500Pa;当在D点施加大小为F的竖直向下的拉力时,杠杆在水平位置平衡,正方体M对水平地面的压强为15000Pa.(不计杠杆重、绳重和摩擦,图中各段绳子所受拉力均沿竖直方向)求:(1)正方体M的受到的重力;(2)拉力F的大小.解答:当F作用B点时,A点受拉力为F1.正方体M受拉力为f1,受重力为G,受支持力为N1 F1×2k=F×3kF1=1.5F f1=3F﹣100NN 1=P1S=7500Pa×0.04m2=300NN 1=G﹣(3F﹣100N)200N=G﹣3F ①当F作用D点时,A电受拉力为F2,正方体M受拉力为f2.受重力为G,受支持力为N2F2×2k=F×1.5k F2=0.75F f2+100N=1.5FN2=P2S=15000Pa×0.04m2=600N600N+f2=G,500N=G﹣1.5F ②由①②两式得F=200N G=800N答:(1)正方体M的受到的重力为800N;(2)拉力F的大小无为200N;4、滑轮与摩擦力的综合计算1.用如图所示的滑轮组拉动物体,当物体匀速移动时,绳端受到的拉力为30N;若物体重100N,不计滑轮重及摩擦,物体受到水平面的摩擦力大小是()A.30N B.60N C.90N D.100N解答:因为有3条绳子作用在动滑轮上,所以水平向左拉物体的拉力为F=3×30N=90N;又因为物体匀速运动,根据二力平衡条件可得,摩擦力的大小等于水平向左拉物体的拉力,大小为90N.故选C2.如图所示,物体A重80N,物体B重72N,物体A在物体B的作用下向右做匀速直线运动.如果在物体A上加一个水平向左的力,拉动物体A,使物体B以0.1m/s的速度匀速上升,则此时拉力F及3s内拉力F所做的功W分别是(已知动滑轮重18N,绳重以及绳与滑轮之间的摩擦不计)()A.F=90N;W=27J B.F=60N;W=54J C.F=30N;W=27J D.F=60N;W=18J解答:物体A在物体B的作用下向右做匀速直线运动时,f=F拉=(G+G动)=×(72N+18N)=30N.拉动A向左运动时,A受力如图,F=f+F拉=30N+30N=60N.h=vt=0.1m/s×3s=0.3m,S=3h=3×0.3m=0.9m,W=Fs=60N×0.9m=54J.故B说法正确.故选B.3.如图所示,体重为510N的人,用滑轮组拉重500N的物体A沿水平方向以0.02m/s的速度匀速运动.运动中物体A受到地面的摩擦阻力为200N,动滑轮重为20N.不计绳重和摩擦,地面上的定滑轮与物体A相连的绳子沿水平方向,地面上的定滑轮与动滑轮相连的绳子沿竖直方向,人对绳子的拉力与对地面的压力始终竖直向下且在同一直线上.则下列计算结果正确的是()A.绳子自由端受到拉力的大小是100N B.人对地面的压力是400NC.人对地面的压力为250N D.绳子自由端运动的速度是0.01m/s解答:A、由图知,n=2,不计绳重和摩擦,拉力F=(G轮+f地)=(20N+200N)=110N,故A错;BC、人对地面的压力F压=G﹣F=510N﹣110N=400N,故B正确、C错;D、绳子自由端运动速度v=2×0.02m/s=0.04m/s,故D错.故选B.5、滑轮与浮力的综合计算1.小雨的体重为660N,他使用如下图所示的滑轮组提升重物,已知动滑轮重100N.当匀速提升一个体积为0.02m3的重物(重物始终未出水面)时,他施加360N的力去提升重物,已知每只鞋底与地面的接触面积为2dm2.不计绳重和摩擦.求:(1)重物在水中受到的浮力;(2)此时他对地面的压强;(3)该物体的密度.解答:(1)F=ρ水gV排=1.0×103kg/m3×10N/kg×0.02m3=200N.浮(2)人站在水平地面上,受到竖直向下的重力、绳对人竖直向上的拉力和地面对人竖直向上的支持力,这三个力是平衡力,所以,G=F支+F拉,又因为他对地面的压力与支持力是一对相互作用力,所以,F压=F支=G人﹣F拉=660N﹣360N=300N,∴p===7.5×103Pa.(3)∵不计绳重和摩擦,使用滑轮组时的拉力F=(G物﹣F浮+G动),∴G=nF﹣G动+F浮=2×360N﹣100N+200N=820Nm===82kg则ρ===4.1×103kg/m3.答:(1)重物在水中受到的浮力为200N;(2)此时他对地面的压强为7.5×103Pa.(3)该物体的密度为4.1×103kg/m3.2.在一溶液池内有一个正方体的金属块沉在池底,小华利用滑轮组将其匀速提出液面,提升过程中,滑轮组绳端拉力F与金属块底部到池底的距离h的关系,如图27 所示.已知金属块被提出液面后,滑轮组的机械效率为75%.(假设溶液池足够大,金属块被提出液面前后液面高度不变,不计绳重及摩擦,g取10N/kg)求:(1)金属块浸没在液面下所受浮力;(2)金属块的密度;(3)金属块露出液面前,滑轮组的机械效率.解答:(1)根据题意及图象可得:金属块浸没时滑轮组绳端拉力F1=1200N,金属块离开液面时滑轮组绳端拉力F2=1600N,正方体边长L=0.5m,滑轮组绳子的股数n=3,因不计绳重及摩擦,则:F1=(G+G动﹣F浮)=(G+G动﹣F浮)﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣①F2=(G+G动)=(G+G动)﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣②②式﹣①式得:F浮=3×(F2﹣F1)=3×(1600N﹣1200N)=1200N.(2)当金属块被提出水面后则:η′==,∴G=nF2η′=3×1600N×75%=3600N;∴ρ====2880kg/m3.(3)将G=3600N,F2=1600N代入②式可得:G动=3F2﹣G=3×1600N﹣3600N=1200N;∴金属块被提出水面前机械效率为:η===≈66.7%.答:(1)金属块浸没在液面下所受浮力为1200N.(2)金属块的密度为2880kg/m3;(3)金属块露出液面前,滑轮组的机械效率为66.7%.四、专题过关1.如图所示,质量不计的不等臂杠杆两端分别挂上实心铁球A,B时,恰好能使杠杆在水平位置平衡.若将A和B 同时浸没在水中,则杠杆的状态是()A..右端下沉B.左端下沉C..仍然平衡D..不能判定解答:∵分别挂上实心铁球A,B时,恰好能使杠杆在水平位置平衡.根据杠杆的平衡条件:ρ铁V A g•OA=ρ铁V B g•OB,所以V A•OA=V B•OB若将A和B同时浸没在水中,则左端=(ρ铁V A g﹣ρ水V A g)•OA=ρ铁V A g•OA﹣ρ水V A g•OA右端=(ρ铁V B g﹣ρ水V B g)•OB=ρ铁V B g•OB﹣ρ水V B g•OB又V A•OA=V B•OB,所以ρ水V A g•OA=ρ水V B g•OB,所以ρ铁V A g•OA﹣ρ水V A g•OA=ρ铁V B g•OB﹣ρ水V B g•OB因此杠杆仍然平衡.故选C.2.如图所示,轻质等臂杠杆的A端挂实心铁块,B端挂实心铜块.两金属块都浸没在水中时,杠杆平衡.若将两个水杯撤去,则(已知ρ铁<ρ铜)()A.无法判断B.杠杆仍平衡C.A端上翘,B端下沉D.A端下沉,B端上翘解答:(1)铁块和铜块浸没在水中时,杠杆平衡,则:(G铁﹣F浮铁)L=(G铜﹣F浮铜)L,∴ρ铁gV铁﹣ρ水gV铁=ρ铜gV铜﹣ρ水gV铜,(ρ铁﹣ρ水)gV铁=(ρ铜﹣ρ水)gV铜,∵ρ铁<ρ铜,∴V铁>V铜,∵F浮=ρ水V排g=ρ水Vg,∴铁块和铜块受到的浮力:F浮铁>F浮铜,∴F浮铁L>F浮铜L,(2)当将两个水杯去掉,杠杆左端力和力臂的乘积为G铁L,杠杆右端力和力臂的乘积为G铜L,∵杠杆原来平衡,(G铁﹣F浮铁)L=(G铜﹣F浮铜)L,∴G铁L﹣F浮铁L=G铜L﹣F浮铜L,∴G铁L>G铜L,挂铁块的A端下沉,挂铜块的B端上翘.故选D.3.如图所示是乳牛喂水器,储水器中水面到阀门的深度为0.5m并保持不变,当浮球浸入水中一半时,阀门恰好关闭,杠杆水平,浮球浸入水中少于一半时阀门打开,浮球密度为0.8×103kg/m3,阀门截面积为2cm2,连杆、杠杆质量不计,求浮球的体积应为多少?(g取10N/kg)解答:已知:水深h=0.5m,浮球密度为ρ=0.8×103kg/m3,阀门截面积为S=2cm2=2×10﹣4m2,g=10N/kg球求:浮球的体积V=?解:阀门受到水的压强为:p=ρ水gh=1×103kg/m3×10N/kg×0.5m=5×103Pa,阀门受到水的压力为:F1=pS=5×103Pa×2×10﹣4m2=1N,则由杠杆的平衡条件得:杠杆右端受到的作用力:F2===0.4N,根据二力平衡条件可得,杠杆右端受到的作用力:F2=G﹣F浮,即F2=ρ球gV﹣ρ水g V,所以球的体积为:V==≈1.33×10﹣4m3.答:浮球的体积应为1.33×10﹣4m3.4.把正方体放在水平地面上,其对地面的压强为5.4×105Pa.AB是重力可忽略不计的杠杆,O为支点,且OA:OB=1:2.将正方体挂在杠杆的A端,在B端施加180N竖直向下的拉力时,杠杆在水平位置平衡,如图7所示,此时正方体对地面的压强变为1.8×105Pa.下列说法中正确的是()A.在杠杆B端施加270N竖直向下的拉力时,正方体对地面的压力刚好为零B.在杠杆B端施加1080N竖直向下的拉力时,正方体对地面的压力刚好为零C.正方体所受的重力为240ND.正方体的体积为10﹣3m3解答:由题知:P1=5.4×105Pa;P2=1.8×105Pa;F1=180N;OA:0B=1:2,设正方体底面积为S;由杠杆平衡条件得:(P1S﹣P2S)•OA=F1•OB,化简得:3.6×105Pa•S=360N,即:S=1×10﹣3m2;故其体积不可能为10﹣3m3,故D错误;物体重力G=P1S=5.4×105Pa×1×10﹣3m2=540N.故C错误;当正方体甲对地面的压力刚好为零时,G•OA=F2•OBF2===270N.故选A.5.如图所示,质量为8kg,边长为5cm的正方体物块A置于水平地面上,通过细绳系于轻质杠杆BOC的B端,杠杆可绕O点转动,且CO=3BO,在C端用F=20N的力竖直向下拉杠杆,使杠杆在水平位置平衡.(绳重不计,g取10N/kg)求:(1)物体A的重力G;(2)B端细绳的拉力F拉;(3)物体A对地面的压力F压;(4)物体A对地面的压强P.解答:(1)物体A的重力G=mg=8kg×10N/kg=80N;(2)由杠杆平衡条件得:F拉×OB=F×OC,则F拉===60N;(3)物体A对地面的压力F压=G﹣F拉=80N﹣60N=20N;(4)物体与地面的接触面积S=5cm×5cm=25cm2=2.5×10﹣3m2,物体对地面的压强P===8000Pa;答:(1)物体A的重力为80N.(2)B端细绳的拉力是60N.(3)物体A对地面的压力是20N.(4)物体A对地面的压强是8000Pa.6.如图所示的装置中,物体A的质量为100kg,其底面积为5×10﹣2m2,B、E是定滑轮,C、D是相同的动滑轮;杠杆MN可绕O点在竖直平面内转动,OM:ON=1:2.小文受到的重力为600N,他在N点施加竖直向下的拉力F T1时,杠杆在水平位置平衡,小文对地面的压力为F1,物体A受到的拉力为F A1,物体A对地面的压强p1为6×103Pa;当小文在N点施加竖直向下的拉力F T2时,杠杆仍在水平位置平衡,小文对地面的压力为F2,物体A受到的拉力为F A2,物体A对地面的压强p2为4×103Pa.杠杆MN和绳的质量、轴处的摩擦均忽略不计.g取10N/kg.求:(1)物体A受到的拉力F A1;(2)小文施加的拉力F T2;(3)小文对地面的压力之比F1:F2.解答:(1)以物体A为研究对象,受力分析如图所示.物体A始终处于静止状态:G A=N1+F A1,G A=N2+F A2;已知G A=1000N,∵p=,∴N1=p1S=6×103Pa×5×10﹣2m2=300N,N2=p2S=4×103Pa×5×10﹣2m2=200N,解得:F A1=700N;F A2=800N;(2)以人为研究对象,受力分析如图甲、乙所示.人始终处于静止状态:F1=G人﹣F T1,F2=G人﹣F T2,对杠杆进行受力分析如图丙、丁所示:根据杠杆平衡条件:F A1×OM=F T1×ON,F A2×OM=F T2×ON,已知OM:ON=1:2,F A1=700 N;F A2=800 N解得:F T1=350 N,F T2=400 N;(3)对地面的压力之比==;即压力之比为F1:F2=5:4;故答案为:(1)物体A受到的拉力F A1=700N;(2)小文施加的拉力F T2=400N;(3)小文对地面的压力之比F1:F2=5:4.7.如图所示,滑轮沿水平方向匀速拉动物体A,若拉力F=180N,则物体A与水平桌面的摩擦力为(滑轮重及轮和绳的摩擦不计)()A.180 N B.360 N C.90 N D.无法确定解答:如图所示,使用的是动滑轮,∵滑轮重、轮和绳的摩擦不计,∴f=F=×180N=90N.故选C.8.利用图中所示的装置,把质量为3Kg,密度为3×103Kg/m3的薄石块从水面下4m处拉出水面后,再提升10m.已知动滑轮重为10N(不计绳子与滑轮间的摩擦,设石块地两个上升过程都为匀速,g取10N/Kg).(1)石块的体积为多少?(2)石块浸没在水中时所受的浮力是多少?(3)石块离开水面后提升了10m所做的总功和有用功各是多少?(4)猜想石块地水中和离开水面后,这个滑轮组的机械效率是否相同?解答:(1)V===0.001m3;(2)∵石块浸没在水中,∴V排=V=0.001m3,F浮=ρ水V排g=1×103kg/m3×0.001m3×10N/kg=10N;(3)石块离开水面后:W有用=Gh=mgh=3kg×10N/kg×10m=300J,∵不计绳子与滑轮间的摩擦,∴F=(G物+G轮)=(30N+10N)=20N,s=2h=2×10m=20m,W总=Fs=20N×20m=400J;(4)石块在水中和离开水面后,滑轮组对物体的拉力增大,相当于利用滑轮组提升更重的物体,机械效率将变大.答:(1)石块的体积为0.001m3;(2)石块浸没在水中时所受的浮力是10N;(3)石块离开水面后提升了10m所做的总功和有用功各是400J和300J;(4)石块在水中和离开水面后,滑轮组的机械效率不相同.五、课后作业1.轻质杠杆两端分别挂重为G1和G2的两个实心金属球A和B,已知ρA>ρB,杠杆原来处于平衡状态,如果现在将它们同时浸没于酒精中,则杠杆还能平衡吗?解答:原来杠杆处于平衡状态,根据杠杆平衡条件可知:G1L1=G2L2球浸入酒精中后金属球受到的浮力为:F A=ρgV A=ρ酒g;F B=ρ酒gV B=ρ酒g,酒此时作用在杠杆上的力为球对杆的拉力等于球的重力减去球受到的浮力,即:F1=G1﹣ρ酒g;F2=G2﹣ρ酒g.左边力矩为:M A=(G1﹣ρ酒g)L1=G1(1﹣)L1=G1L1﹣G1L1;右边的力矩为:M B=(G2﹣ρ酒g)L2=G2(1﹣)L2=G2L2﹣G2L2;又因为ρA>ρB,所以:<.所以:G1L1﹣G1L1>G2L2﹣G2L2;因为两边的力距不相等,所以杠杆不会平衡,将向力矩大的左边倾斜.2.如图所示,顶面带有光滑凹槽的轻质杠杆AB可以绕支点O转动,杠杆的A端用细线沿竖直方向连接在地板上,OB=0.5m,在杠杆的B端悬挂一个密度为0.8×103kg/m3的圆柱体M.地板上有一个盛满水的容器.在圆柱体M体积的1/3浸入水中时,从容器内溢出0.4N的水,杠杆在水平位置平衡.此时让一个质量为200g的小球从B点沿凹槽向A端匀速运动,经过4s的时间,系在A端细线的拉力恰好等于0N.若整个过程中杠杆始终保持水平平衡,则小球的运动速度为m/s.(g取10N/kg)解答:圆柱体受到的浮力:F浮=G排=0.4N,∵F浮=ρ水V排g,∴圆柱体浸入水中的体积:V浸=V排===4×10﹣5m3,∴圆柱体的体积:V木=3V浸=3×4×10﹣5m3=1.2×10﹣4m3,圆柱体的质量:m=ρ木V木=0.8×103 kg/m3×1.2×10﹣4m3=0.096kg,圆柱体重:G=mg=0.096kg×10N/kg=0.96N,所以杠杆B端受到的拉力:F B=G﹣F浮=0.96N﹣0.4N=0.56N,∵杠杆平衡,∴F A×OA=F B×OB,小球的质量为:m球=200g=0.2kg,小球的重:G球=m球g=0.2kg×10N/kg=2N,设小球的运动速度为v,则小球滚动的距离s=vt,当A端的拉力为0时,杠杆再次平衡,此时小球到O点距离:s′=s﹣OB=vt﹣OB=v×4s﹣0.5m,∵杠杆平衡,∴G球×s′=F B×OB,即:2N×(v×4s﹣0.5m)=0.56N×0.5m,解得:v=0.16m/s.故答案为:0.16.3.(2010•门头沟区一模)如图所示小星沿杠杆GP水平向右匀速运动,通过对杠杆GP施加竖直向下的压力来提升物体A.其中B、C、E、F都是定滑轮,D是动滑轮,杠杆GP可绕O点在竖直平面内转动.正立方体A的边长为40cm,密度为5×103kg/m3.杠杆GP和细绳的质量均忽略不计,OG为10cm.当小星运动到H点,物体A对水平地面的压强为0Pa.此时通过细绳对动滑轮D的向下拉力F D=6000N.忽略细绳与滑轮的摩擦.g取10N/kg.求:(1)物体A的重力;(2)动滑轮D的重力;(3)若人的质量为40Kg,则OH的长度是多少?解答:(1)物体A的体积:V A=(0.4m)3=0.064m3,物体A的重力:G A=m A g=ρA GV A=5×103kg/m3×10N/kg×0.064m3=3200N;(2)以物体A为研究对象,受力分析如图1所示.F A=G A=3200N,以动滑轮为研究对象,受力分析如图2所示.2F A=F D+G动;2×3200N=6000N+G动,解得:G动=400N;(3)由于人对杠杆的压力等于人的重力,G人=m人g=40kg×10N/kg=400N,对杠杆进行受力分析如图3所示:根据杠杆平衡条件可得:F D×OG=G人×0H,6000N×0.1m=400N×0H,0H=1.5m.答:(1)物体A的重力为3200N;(2)动滑轮D的重力为400N;(3)若人的质量为40Kg,则OH的长度是1.5m.4.如图所示,重为2N的物体B恰能使重为30N的物体A匀速向右运动,则物体A受到水平桌面的摩擦阻力是N,若使物体A以0.2m/s的速度匀速向左运动,作用在A上水平向左的拉力的功率为W.(滑轮间的摩擦不计)解答:由对B物体受力分析可得,绳子对B的拉力等于B的重力,则B对绳子的拉力为2N;则绳子对动滑轮的拉力为2N,由滑轮组的特点可知动滑轮对A的拉力F=2×2N=4N;对A受力分析得:A在水平方向上受拉力及摩擦力而处于平衡状态,故摩擦力f=F=4N;要使物体向左匀速运动,则物体的摩擦力方向向右,则F'=f+F=4N+4N=8N;由功率公式P=Fv=8N×0.2m/s=1.6W.故答案为:4,1.6.5.如图是小刚利用现有设备设计的一个滑轮组来打捞落水铝锭的示意图.已知图中大小滑轮的质量之比为3:1,小刚身体的质量是65kg,铝锭的体积为0.06m3,铝锭出水前与完全出水后小刚对地面的压力之比为9:7,铝的密度为2.7×103kg/m3(若不计水的阻力、不计绳重和摩擦,g取10N/kg),求:(1)出水前铝锭受到的浮力是多少?(2)出水前此滑轮组的机械效率是多少?(3)出水后如果铝锭以0.06米/秒的速度匀速上升,小刚作用在绳子自由端拉力的功率是多少?解答:(1)出水前铝锭浸没在水中(V=V铝),所以,出水前铝锭受到的浮力是:排F浮=ρ水gV排=ρ水gV铝=1.0×103kg/m3×0.06m3×10N/kg=600N.(2)设小动滑轮的重力为G动,则大动滑轮的重力为3G动铝锭处于平衡状态,所以有:G人=mg=65kg×10N/kg=650NG铝=ρ铝gV铝=2.7×103kg/m3×0.06m3×10N/kg=1620NF拉=G铝﹣F浮=810N﹣300N=510N.以大动滑轮为研究对象:出水前小动滑轮对大动滑轮的拉力为F1,出水后小动滑轮对大动滑轮的拉力为F1’,受力分析如图(一)甲、乙所示.n=3出水前:。
