塑性变形计算题
《金属学原理》各章习题及解答(晶体的塑性变形)
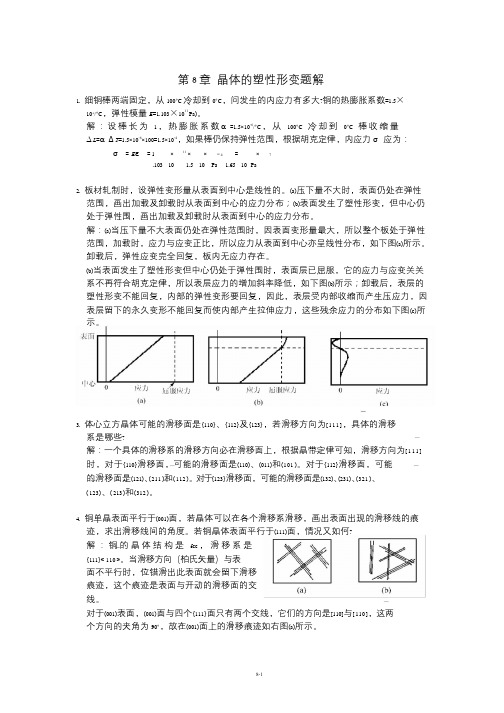
第8 章晶体的塑性形变题解1. 细铜棒两端固定,从100°C 冷却到0°C,问发生的内应力有多大?铜的热膨胀系数=1.5×10-6/°C,弹性模量E=1.103×1011 Pa)。
解:设棒长为 1 ,热膨胀系数α=1.5×10-6/°C ,从100°C 冷却到0°C 棒收缩量∆L=α∆T=1.5×10-6×100=1.5×10-4,如果棒仍保持弹性范围,根据胡克定律,内应力σ应为:σ=Eε=1 ×11 ××−4 =×7.103 10 1.5 10 Pa 1.65 10 Pa2. 板材轧制时,设弹性变形量从表面到中心是线性的。
(a)压下量不大时,表面仍处在弹性范围,画出加载及卸载时从表面到中心的应力分布;(b)表面发生了塑性形变,但中心仍处于弹性围,画出加载及卸载时从表面到中心的应力分布。
解:(a)当压下量不大表面仍处在弹性范围时,因表面变形量最大,所以整个板处于弹性范围,加载时,应力与应变正比,所以应力从表面到中心亦呈线性分布,如下图(a)所示。
卸载后,弹性应变完全回复,板内无应力存在。
(b)当表面发生了塑性形变但中心仍处于弹性围时,表面层已屈服,它的应力与应变关关系不再符合胡克定律,所以表层应力的增加斜率降低,如下图(b)所示;卸载后,表层的塑性形变不能回复,内部的弹性变形要回复,因此,表层受内部收缩而产生压应力,因表层留下的永久变形不能回复而使内部产生拉伸应力,这些残余应力的分布如下图(c)所示。
3. 体心立方晶体可能的滑移面是{110}、{112}及{123},若滑移方向为[111],具体的滑移系是哪些?解:一个具体的滑移系的滑移方向必在滑移面上,根据晶带定律可知,滑移方向为[111] 时,对于{110}滑移面,可能的滑移面是(110)、(011)和(101 )。
第五章塑性变形与回复再结晶--习题集

psi是一种压力单位,定义为英镑/平方英寸,145psi=1MpaPSI英文全称为Pounds per square inch。
P是磅pound,S是平方square,I 是英寸inch。
把所有的单位换成公制单位就可以算出:1bar≈14.5psi1 KSI = 1000 lb / in.2 = 1000 x 0.4536 x 9.8 N / (25.4 mm)2 = 6.89 N / mm2材料机械强度性能单位,要用到试验机来检测Density of Slip PlanesThe planar density of the (112) plane in BCC iron is 9.94 atoms/cm2. Calculate the planar density of the (110) plane and the interplanar spacings for both the (112) and the (110) planes. On which type of plane would slip normally occur?(112) planar density:The point of this problem is that slip generally occurs in high density directions and on high density planes. The high density directions are directions in which the Burgers' vector is short, and the high density planes are the "smoothest" for slip.It will help to visualize these two planes as we calculate the atom density.The (110) plane passes through the atom on the lattice point in the center of the unit cell. The plane is rectangular, with a height equal to the lattice parameter a0and a width equal to the diagonal of the cube face, which is 2 a0.Lattice parameter (height):Width:Thus, according to the geometry, the area of a (110) plane would beThere are two atoms in this area. We can determine that by counting the piece of atoms that lie within the circle (1 for the atom in the middle and 4 times 1/4 for the corners), or using atom coordinates as discussed in Chapter 3. Then the planar density isThe interplanar spacing for the (110) planes isFor the (112) plane, the planar density is not quite so easy to determine. Let us draw a larger array of four unit cells, showing the plane and the atoms it passes through.This plane is also rectangular, with a base width of √2 a0 (the diagonal of a cube face), and a height of √3 a0 (the body diagonal of a cube). It has four atoms at corners, which are counted as 1/4 for the portion inside the rectangle (4 x 1/4) and two atoms on the edges, counted as 1/2 for the portion inside the rectangle (2 x 1/2). This is a total of 2 atoms.Base width:Height:Hence, we can calculate the area and density as for the (110) plane.The planar density and interplanar spacing of the (110) plane are larger than that of the (112) plane, thus the (110) plane would be the preferred slip plane1.有一根长为5 m,直径为3mm的铝线,已知铝的弹性模量为70GPa,求在200N的拉力作用下,此线的总长度。
塑性力学考试题及答案

塑性力学考试题及答案一、选择题(每题2分,共20分)1. 塑性变形与弹性变形的主要区别是()。
A. 塑性变形是可逆的B. 弹性变形是可逆的C. 塑性变形是不可逆的D. 弹性变形是不可逆的2. 材料在塑性变形过程中,其应力-应变曲线上的哪一点标志着材料的屈服点?A. 最大应力点B. 最大应变点C. 应力-应变曲线上的转折点D. 应力-应变曲线的起始点3. 下列哪项不是塑性变形的特征?A. 材料形状的改变B. 材料体积的不变C. 材料内部结构的不可逆变化D. 材料的弹性恢复4. 塑性变形的三个基本假设中,不包括以下哪一项?A. 材料是连续的B. 材料是各向同性的C. 材料是不可压缩的D. 材料是完全弹性的5. 塑性变形的流动法则通常采用哪种形式来描述?A. 线性形式B. 非线性形式C. 指数形式D. 对数形式二、简答题(每题10分,共30分)6. 简述塑性变形的三个基本假设及其物理意义。
7. 解释什么是塑性屈服准则,并举例说明常用的屈服准则。
8. 描述塑性变形过程中的加载和卸载路径,并解释它们的区别。
三、计算题(每题25分,共50分)9. 给定一个材料的应力-应变曲线,如果材料在达到屈服点后继续加载,求出在某一特定应变下的材料应力。
10. 假设一个材料在单轴拉伸条件下发生塑性变形,已知材料的屈服应力和弹性模量,求出在塑性变形阶段的应变率。
答案一、选择题1. 答案:C2. 答案:C3. 答案:D4. 答案:D5. 答案:B二、简答题6. 塑性变形的三个基本假设包括:- 材料是连续的:假设材料没有空隙和裂缝,是连续的均匀介质。
- 材料是各向同性的:假设材料在所有方向上具有相同的物理性质。
- 材料是不可压缩的:假设在塑性变形过程中材料的体积保持不变。
7. 塑性屈服准则是判断材料是否开始发生塑性变形的条件。
常用的屈服准则包括:- Von Mises准则:适用于各向同性材料,当材料的等效应力达到某一临界值时,材料开始发生塑性变形。
弹塑性力学计算题终稿

1试根据下标记号法和求和约定展开下列各式(式中i 、j = x 、y 、z ):① ij ij σε ; ② j i x ';2在物体内某点,确定其应力状态的一组应力分量为:x σ= 0,y σ= 0,z σ=0,xy τ= 0,yz τ=3a ,zx τ=4a ,知0a >。
试求:1 该点应力状态的主应力1σ、2σ和3σ;2 主应力1σ的主方向;3主方向彼此正交;解:由式(2—19)知,各应力不变量为、,代入式(2—18)得:也即 (1)因式分解得:(2)则求得三个主应力分别为。
设主应力与xyz 三坐标轴夹角的方向余弦为、 、 。
将 及已知条件代入式(2—13)得:(3)由式(3)前两式分别得:(4)将式(4)代入式(3)最后一式,可得0=0的恒等式。
再由式(2—15)得:则知;(5)同理可求得主应力的方向余弦、、和主应力的方向余弦、、,并且考虑到同一个主应力方向可表示成两种形式,则得:主方向为:;(6)主方向为:;(7)主方向为:;(8)若取主方向的一组方向余弦为,主方向的一组方向余弦为,则由空间两直线垂直的条件知:(9)由此证得主方向与主方向彼此正交。
同理可证得任意两主应力方向一定彼此正交。
3一矩形横截面柱体,如图所示,在柱体右侧面上作用着均布切向面力q,在柱体顶面作用均布压力p。
试选取:3232ϕ=++++y Ax Bx Cx Dx Ex()做应力函数。
式中A、B、C、D、E为待定常数。
试求:(1)上述ϕ式是否能做应力函数;(2)若ϕ可作为应力函数,确定出系数A、B、C、D、E。
(3)写出应力分量表达式。
(不计柱体的体力)解:据结构的特点和受力情况,可以假定纵向纤维互不挤压,即:;由此可知应力函数可取为:(a)将式(a)代入,可得:(b)故有:; (c)则有:; (d)略去中的一次项和常数项后得:(e)相应的应力分量为:(f)边界条件:①处,,则; (g)②处,,则; (h) ③在y = 0处,,,即由此得:,再代入式(h)得:;由此得:(i)由于在y=0处,,积分得: (j ) ,积分得:(k )由方程(j ) (k)可求得:,投知各应力分量为:(l)据圣文南原理,在距处稍远处这一结果是适用的。
塑性变形计算题

五、计算题(共30分,每小题10分)1. 已知某点的应力状态⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=σ600000200200ij 。
(共18分)2. 1)求该点的主应力和主方向(10分);3. 2)通过计算判断该点是否处于平面应变状态(3分);4. 3)画出该点的应力莫尔圆和应变莫尔圆(5分)。
5. 如图所示,已知两端封闭且足够长的薄壁圆筒的半径为r ,壁厚为t ,屈服应力为s σ。
该圆筒受内压p 的作用而产生塑性变形,设材料各向同性且忽略其弹性变形,求:6. ⑴ 内压p 的大小;7. ⑵ 圆筒切向、轴向及径向应变增量的比值。
(12分)8. 已知半径为r ,壁厚为t 的薄壁圆筒,承受轴向拉伸和扭转联合作用而产生塑性变形,设加载过程中保持σ=τ2,且材料的屈服应力为s σ。
9. 1)求该圆筒屈服时的轴向载荷P 和扭矩M (6分);10. 2)设材料各向同性且忽略其弹性变形,求其切向、轴向及径向应变增量的比值(6分)。
(共12分)11. 已知薄壁管半径为r 壁厚为t ,在扭矩M 和轴向拉力P 的共同作用下产生塑性变形。
设材料的屈服应力为S σ(服从TRESCA 屈服准则),且在数值上P=M ,求:1)拉力P 的大小;2)该薄壁管上任意一点的三个主应力;3)该薄壁管上任意一点径向、轴向及环向应变增量的比值。
12. 已知薄壁球壳半径为r ,壁厚为t ,受内压p 作用。
求使用MISES 屈服准则时的内压p 的值,并求此时经向、纬向及径向应变增量的比值(15分)13. 如图所示,工件横截面尺寸为2a×h ,长度足够长,在上下模具之间进行平面应变镦粗,且工件和模具之间的摩擦满足常摩擦模型mK =τ。
试用主应力法确定工件与模具接触面上压应力的分布情况,以及变形力P 的大小。
14.如图所示,已知顶部被削平的楔体,承受均布载荷q的作用而产生塑性变形,若楔体夹角为a2δ,且,用滑移线法求均布载荷q的大小。
(8分)2=AB15.如下图所示,用滑移线法求光滑冲头压入两边为斜面的半无限体时单位压力q的大小。
塑性成形理论课后答案2修改

第一章1-10. 已知一点的应力状态10100015520⨯⎪⎪⎪⎭⎫ ⎝⎛--=ij σMPa ,试求该应力空间中122=+-z y x 的斜截面上的正应力n σ和切应力n τ为多少?解:若平面方程为Ax+By+Cz+D=0,则方向余弦为:222CB A A ++=l ,222CB A B ++=m ,222CB AC n ++=因此:312)(-211222=++=l ,322)(-212-222-=++=m ;322)(-212n 222=++= S x =σx l +τxy m +τxz n=3100325031200=⨯-⨯S y =τxy l +σy m +τzy n = 3350321503150=⨯+⨯S z =τxz l +τyz m +σz n=320032100-=⨯-11191000323200323350313100S S S -=-=⨯-⨯-⨯=++=n m l z y x σ125003200335031002222222=⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=++=z y x S S S S4.1391000125002=⎪⎭⎫⎝⎛-=τ1-11已知OXYZ 坐标系中,物体内某点的坐标为(4,3,-12),其应力张量为:⎪⎪⎪⎭⎫⎝⎛--=1030205040100 ij σ,求出主应力,应力偏量及球张量,八面体应力。
解:=1J z y x σσσ++=100+50-10=140=2J 222xy xz yz y x z x z y τττσσσσσσ---++=100×50+50×(-10)+100×(-10)-402-(-20)2-302=600=3J 321σσσ=2222xy z xz y yz x xz yz xy z y x τστστστττσσσ---+ =-192000019200060014023=-+-σσσσ1=122.2,σ2=31.7,σ3=49.5 σm=140/3=46.7;7.5630203.3403.53⎪⎪⎪⎭⎫ ⎝⎛--=' ij σ ;7.460007.4607.46m ⎪⎪⎪⎭⎫ ⎝⎛=i σσ8=σm =46.71.39)()()(312132322218=-+-+-±=σσσσσστ 1-12设物体内的应力场为3126x c xy x +-=σ,2223xy c y -=σ,y x c y c xy 2332--=τ,0===zx yz z ττσ,试求系数c 1,c 2,c 3。
《塑性变形与轧制技术》期末试卷含答案

《塑性变形与轧制技术》期末试卷姓名:班级:成绩一、填空题(每空1分,共20分)1. 金属压力加工的主要方法有:( )、( )、( )、( )和( )等。
2. 由钢锭或钢坯轧制成具有一定规格和性能的钢材的一系列加工工序的组合,称为( )工艺过程。
3. 由于加热不良可使原料造成( )、( )、( )、( )、( )、( )等缺陷。
4. 轧制制度的主要内容应包括( )、( )和( )等。
5. 按照适用范围,标准分为( )、( )和( )。
6. 生产车间各项设备、原材料、燃料、动力、定员以及资金等利用程度的指标称之为( )。
7. 依靠旋转方向相反的两个轧辊与轧件间的摩擦力,将轧件拖入轧辊辊缝中的现象,称为( )。
二、名词解释(每题3分,共30分)1、最小阻力定律2、简单轧制过程3、变形区概念4、前滑5、剩余摩擦力6、轧制压力7、塑性变形8、塑性加工9、工作应力10、热加工三、判断题(每题2分,共20分)1、咬入角是轧制时轧件与轧辊表面接触弧线所对的圆心角。
()2、其他条件不变,轧件宽度增大,宽展减小。
()3、总延伸系数等于各道次延伸系数之和。
()4、轧制前轧件的断面积与轧制后轧件的断面积之比等于延伸系数。
()5、轧件出口速度大于轧辊该处的线速度叫后滑。
()6、金属塑性加工中的工艺润滑的目的之一为减少二次氧化铁皮的产生。
()7、轧制是轧件由于摩擦力的作用而进入旋转的轧辊之间,被压缩而产生弹性变形的过程。
()8、高精度轧机生产的成品尺寸精度皆可达到±0.15mm。
()9、由于轧制过程有前滑、后滑现象,使轧制过程简单化。
()10、采利柯夫公式应用范围较为广泛,可用于冷轧,也可用于热轧;可用于厚板轧制,也可用于薄板轧制。
()四、计算题(每题15分,共30分)1、轧辊圆周速度v=3m/s,轧件入辊速度v H=2m/s,延伸系数μ=1.6,试求前滑值。
2、已知轧辊直径600mm,轧件轧前断面尺寸H×B=100mm×200mm,Δh=30mm,轧制温度t=1000℃,铸钢轧辊,轧制速度v=4m/s,轧件为低碳钢,用艾克隆得公式计算轧后轧件断面尺寸。
资料塑性变形力学计算
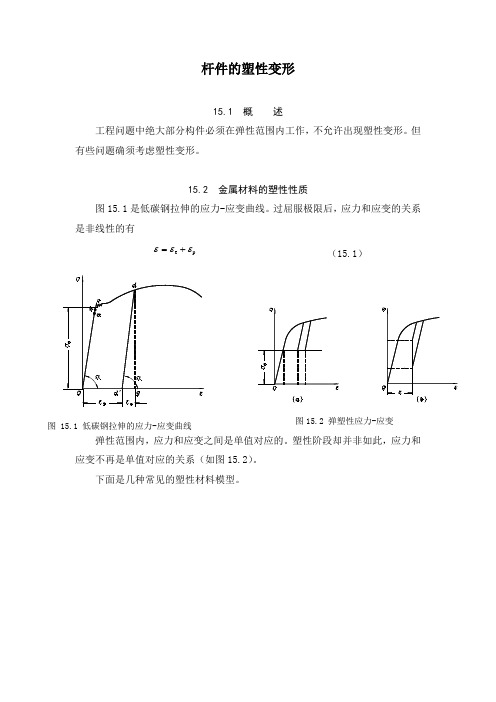
在二向应力状态下, ,以上条件变为
, , (b)
塑性条件(b)在 平面中是一个六角形,如图15.19所示。在三向应力的情况下,塑性条件(a)在应力空间中是六个平面。这就是特雷斯卡塑性条件的几何表示。如图15.20所示。柱面以内的点代表不发生塑性形变的应力状态,而柱面上的点代表进入塑性形变的应力状态。这样的柱面称为塑性曲面。
解:以 和 分别表 和 杆的轴力, 表 杆的轴力。令 , ,得
(e)
当载荷逐渐增加时, 杆的应力首先达到 ,这时的载荷即为 。由( )式的第二式得
由此解出
载荷继续增加,中间杆的轴力 保持为 ,两侧杆件仍然是弹性的。直至两侧的杆件的轴力 也达到 ,相应的载荷即为极限载荷 。这时由节点 的平衡方程知
加载过程中,载荷 与 点位移的关系已表示于图15.9 中。
式中m和 皆为常量。试导出实心圆轴扭转时应力和变形的计算公式。
解:根据圆轴扭转的平面假设,可以直接引用3.4中的( )式,求得横截ቤተ መጻሕፍቲ ባይዱ上任意点处的剪应变为
(d)
式中 是扭转角沿轴线的变化率, 为横截面上一点到圆心的距离, 即为该点剪应变。( )式表明,沿横截面半径,各点的剪应变是按直线规律变化的(图15.11 )。由( )、( )两式求出
例15.6在矩形截面梁形成塑性区后,将载荷卸尽,试求梁截面边缘处的应力。设材料是理想弹塑性的。
解:当矩形截面梁的横截面上出现塑性区时,应力分布表示于图15.14 。根据公式(15.7),截面上的弯矩为
这时梁内的最大应力为 。
卸载过程相当于把与上列弯矩数值相等、方向相反的另一弯矩加于梁上,且它引起的应力按线弹性公式计算,即最大应力为
按照第四强度理论,材料的塑性条件为公式(15.3),即
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
五、计算题(共30分,每小题10分)
1. 已知某点的应力状态⎥⎥⎥⎦
⎤⎢⎢⎢⎣⎡-=σ600000200200ij 。
(共18分)
1)求该点的主应力和主方向(10分);ﻫ2)通过计算判断该点是否处于平面应变状态(3分);ﻫ3)画出该点的应力莫尔圆和应变莫尔圆(5分)。
2. 如图所示,已知两端封闭且足够长的薄壁圆筒的半径为r ,壁厚为t,屈服应力为s σ。
该圆筒受内压p的作用而产生塑性变形,设材料各向同性且忽略其弹性变形,求:⑴ 内压p 的大小;⑵ 圆筒切向、轴向及径向应变增量的比值。
(12分
)
3. 已知半径为r ,壁厚为t 的薄壁圆筒,承受轴向拉伸和扭转联合作用而产生塑性变形,
设加载过程中保持σ=τ2,且材料的屈服应力为s σ。
1)求该圆筒屈服时的轴向载荷P 和扭矩M(6分);ﻫ2)设材料各向同性且忽略其弹性变形,求其切向、轴向及径向应变增量的比值(6分)。
(共12分)
4. 已知薄壁管半径为r 壁厚为t,在扭矩M和轴向拉力P 的共同作用下产生塑性变形。
设材料的屈服应力为S σ(服从TRE SCA 屈服准则),且在数值上P=M,求:
1)拉力P 的大小;
2)该薄壁管上任意一点的三个主应力;
3)该薄壁管上任意一点径向、轴向及环向应变增量的比值。
5. 已知薄壁球壳半径为r,壁厚为t ,受内压p 作用。
求使用MISES 屈服准则时的内
压p的值,并求此时经向、纬向及径向应变增量的比值(15分)
6. 如图所示,工件横截面尺寸为2a×h,长度足够长,在上下模具之间进行平面应变镦粗,
且工件和模具之间的摩擦满足常摩擦模型mK =τ。
试用主应力法确定工件与模具接触面上压应力的分布情况,以及变形力P 的大小。
7.如图所示,已知顶部被削平的楔体,承受均布载荷q的作用而产生塑性变形,若楔
体夹角为a2
δ,且,用滑移线法求均布载荷q的大小。
(8分)
2=
AB
8.如下图所示,用滑移线法求光滑冲头压入两边为斜面的半无限体时单位压力q的大
小。
9.如图所示,用上限法计算平冲头压入半无限体时所需的压力P。
假设冲头表面光滑,
无摩擦,冲头宽度为2b,长度(垂直于纸面方向的尺寸)足够长,图中的三个刚性块均为等边三角形。
10.下图为平面正挤压的刚性块变形模式,假设模壁光滑,试用上限法计算其上限载荷P。
(注:由于对称性,图中只画出了一半。
O区为死区,不流动。
)(8分)。
