九年级提优分层数学试卷
九年级数学提优试卷
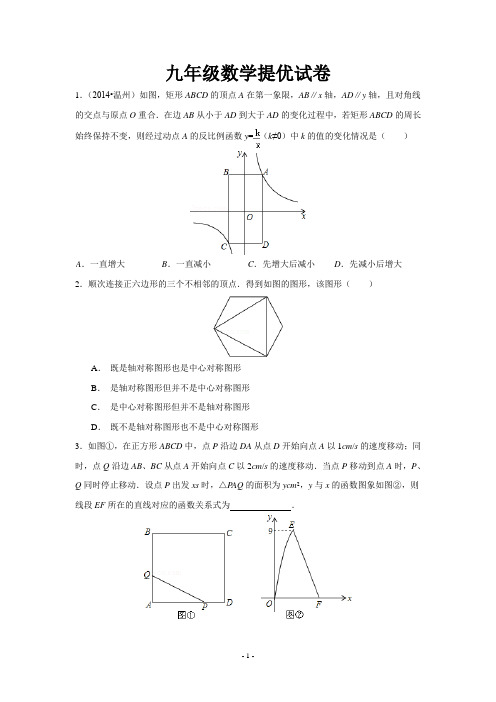
九年级数学提优试卷1.(2014•温州)如图,矩形ABCD的顶点A在第一象限,AB∥x轴,AD∥y轴,且对角线的交点与原点O重合.在边AB从小于AD到大于AD的变化过程中,若矩形ABCD的周长始终保持不变,则经过动点A的反比例函数y=(k≠0)中k的值的变化情况是()2.顺次连接正六边形的三个不相邻的顶点.得到如图的图形,该图形()A.既是轴对称图形也是中心对称图形B.是轴对称图形但并不是中心对称图形C.是中心对称图形但并不是轴对称图形D.既不是轴对称图形也不是中心对称图形3.如图①,在正方形ABCD中,点P沿边DA从点D开始向点A以1cm/s的速度移动;同时,点Q沿边AB、BC从点A开始向点C以2cm/s的速度移动.当点P移动到点A时,P、Q同时停止移动.设点P出发xs时,△P AQ的面积为ycm2,y与x的函数图象如图②,则线段EF所在的直线对应的函数关系式为.4.班级准备召开主题班会,现从由3名男生和2名女生所组成的班委中,随机选取两人担任主持人,求两名主持人恰为一男一女的概率.(请用“画树状图”或“列表”等方法写出过程)5.(2014•淮安)如图,在△ABC中,AC=BC,AB是⊙C的切线,切点为D,直线AC交⊙C 于点E、F,且CF=A C.(1)求∠ACB的度数;(2)若AC=8,求△ABF的面积.6.如图,点A(1,6)和点M(m,n)都在反比例函数y=(x>0)的图象上,(1)k的值为;(2)当m=3,求直线AM的解析式;(3)当m>1时,过点M作MP⊥x轴,垂足为P,过点A作AB⊥y轴,垂足为B,试判断直线BP与直线AM的位置关系,并说明理由.7.如图1,矩形OABC顶点B的坐标为(8,3),定点D的坐标为(12,0),动点P从点O出发,以每秒2个单位长度的速度沿x轴的正方向匀速运动,动点Q从点D出发,以每秒1个单位长度的速度沿x轴的负方向匀速运动,PQ两点同时运动,相遇时停止.在运动过程中,以PQ为斜边在x轴上方作等腰直角三角形PQR.设运动时间为t秒.(1)当t=1秒时,△PQR的边QR经过点B;(2)设△PQR和矩形OABC重叠部分的面积为S,求S关于t的函数关系式;(3)如图2,过定点E(5,0)作EF⊥BC,垂足为F,当△PQR的顶点R落在矩形OABC 的内部时,过点R作x轴、y轴的平行线,分别交EF、BC于点M、N,若∠MAN=45°,求t的值.8.如图,轮船从点A处出发,先航行至位于点A的南偏西15°且点A相距100km的点B处,再航行至位于点A的南偏东75°且与点B相距200km的点C处.(1)求点C与点A的距离(精确到1km);(2)确定点C相对于点A的方向.(参考数据:≈1.414,≈1.732)9.(2014年江苏徐州)如图,将透明三角形纸片P AB的直角顶点P落在第四象限,顶点A、B分别落在反比例函数y=图象的两支上,且PB⊥x于点C,P A⊥y于点D,AB分别与x 轴,y轴相交于点E、F.已知B(1,3).(1)k=3;(2)试说明AE=BF;(3)当四边形ABCD的面积为时,求点P的坐标.10.(2014年江苏徐州)如图,矩形ABCD的边AB=3cm,AD=4cm,点E从点A出发,沿射线AD移动,以CE为直径作圆O,点F为圆O与射线BD的公共点,连接EF、CF,过点E作EG⊥EF,EG与圆O相交于点G,连接CG.(1)试说明四边形EFCG是矩形;(2)当圆O与射线BD相切时,点E停止移动,在点E移动的过程中,①矩形EFCG的面积是否存在最大值或最小值?若存在,求出这个最大值或最小值;若不存在,说明理由;②求点G移动路线的长.。
九年级数学上册高分拔尖提优期末试题(青岛版)

九年级数学上册高分拔尖提优单元卷期末测试一、选择题(每小题3分,共36分)1.已知函数y=(m-2)25mx -是反比例函数,则m 的值为( ) A . 2B . -2C . 2或-2D . 任意实数 【答案】B【解析】∵函数()252m y m x -=-是反比例函数,∴22051m m -≠⎧⎨-=-⎩, 解得m=-2,故选B .2. 如图,在△ABC 中,点D 、E 分别在边AB 、AC 上,下列条件中不能判断△ABC ∽△AED 的是( )A . ∠AED=∠BB . ∠ADE=∠C C . AD AC AE AB = D . AD AE AB AC= 【答案】D 【解析】解:由题意得∠DAE=∠CAB ,A 、当∠AED=∠B 时,△ABC ∽△AED ,故本选项不符合题意;B 、当∠ADE=∠C 时,△ABC ∽△AED ,故本选项不符合题意;C 、当AD AE =AC AB时,△ABC ∽△AED ,故本选项不符合题意; D 、当AD AB =AE AC 时,不能推断△ABC ∽△AED ,故本选项符合题意; 故选D .3.如图,把矩形纸片ABCD 沿EF 翻折,点A 恰好落在BC 边的A ′处,若,∠EFA=60°,则四边形A′B′EF的周长是()A.B.C.D.【答案】D【解析】如图,过点E作EG⊥AD,∴∠AGE=∠FGE=90°∵矩形纸片ABCD,∴∠A=∠B=∠AGE=90°,∴四边形ABEG是矩形,∴BE=AG,EG=AB,在Rt△EFG中,∠EFG=60°,EG∴FG=1,EF=2,由折叠有,A'F=AF,A'B'=AB BE=B'E,∠A'FE=∠AFE=60°,∵BC∥AD,∴∠A'EF=∠AFE=60°,∴△A'EF是等边三角形,∴A'F=EF=2,∴AF=A'F=2,∴BE=AG=AF-FG=2-1=1∴B'E=1∴四边形A′B′EF的周长是A'B'+B'E+EF+A'F1+2+2=5故答案为D .4.若关于x 的一元二次方程kx 2﹣2x+1=0有两个不相等的实数根,则实数k 的取值范围是( ) A . k >1B . k <1C . k >1且k≠0D . k <1且k≠0【答案】D【解析】∵关于x 的一元二次方程kx 2﹣2x +1=0有两个不相等的实数根,∴k ≠0且△>0,即(﹣2)2﹣4×k ×1>0, 解得k <1且k ≠0.∴k 的取值范围为k <1且k ≠0.故选D .5.河堤横断面如图所示,堤高BC =6米,迎水坡AB 的坡比是1,则AC 的长是( )A . 米B . 12米C .D .【答案】D【解析】解:∵迎水坡AB 的坡比为1BC AC ∴= ∵堤高BC=6米,AC ∴==.故选D .6.点A 为反比例函数图象上一点,它到原点的距离为5,则x 轴的距离为3,若点A 第二象限内,则这个函数的解析式为( )A . y=12xB . y=﹣12xC . y=112xD . y=﹣112x 【答案】B【解析】设A 点坐标(x ,y ).∵A 点到x 轴的距离为3,∴|y |=3,y =±3. ∵A 点到原点的距离为5,∴x 2+y 2=52,解得x =±4, ∵点A 在第二象限,∴x =-4,y =3,∴点A 的坐标为(-4,3),设反比例函数的解析式为y =k x , ∴k =-4×3=-12, ∴反比例函数的解析式为y =12x, 故选B .7.如图是二次函数y =ax 2+bx+c 图象的一部分,图象过点A(﹣5,0),对称轴为直线x =﹣2,给出四个结论:①abc >0;②4a+b =0;③若点B(﹣3,y 1)、C(﹣4,y 2)为函数图象上的两点,则y 2<y 1;④a+b+c =0.其中,正确结论的个数是( )A . 1B . 2C . 3D . 4【答案】C 【解析】解:由图象可知:开口向下,故a <0,抛物线与y 轴交点在x 轴上方,故c >0,∵对称轴x =﹣2b a <0, ∴b <0,∴abc >0,故①正确;∵对称轴为x =﹣2, ∴﹣2b a=﹣2, ∴b =4a ,∴4a ﹣b =0,故②不正确;当x<﹣2时,此时y随x的增大而增大,∵﹣3>﹣4,∴y1>y2,故③正确;∵图象过点A(﹣5,0),对称轴为直线x=﹣2,∴点A关于x=﹣2对称点的坐标为:(1,0)令x=1代入y=ax2+bx+c,∴y=a+b+c=0,故④正确故选C.8.在同一直角坐标系中,函数y=kx-k与kyx=(k≠0)的图象大致是()A.B.C.D.【答案】D【解析】解:有两种情况,当k>0是时,一次函数y=kx-k的图象经过一、三、四象限,反比例函数kyx=(k≠0)的图象经过一、三象限;当k<0时,一次函数y=kx-k的图象经过一、二、四象限,反比例函数kyx=(k≠0)的图象经过二、四象限;根据选项可知,D选项满足条件.故选D.9.如图,⊙O是Rt△ABC外接圆,∠ACB=90°,∠A=25°,过点C作⊙O的切线,交AB的延长线于点D,则∠D的度数是()A.25°B.30°C.40°D.55°【答案】C【解析】连接OC,由圆周角定理可求得∠COD,由切线的性质可知∠OCD=90°,则可求得∠D.【详解】解:连接OC,则∠COD=2∠A=50°,∵CD为⊙O的切线,∴OC⊥CD,∴∠OCD=90°,∴∠D=90°-∠COD=40°,故选C.10. 如图,△ABC中,AB=5,BC=3,AC=4,以点C为圆心的圆与AB相切,则⊙C的半径为()A.2.3 B.2.4 C.2.5 D.2.6【答案】B【解析】在△ABC中,∵AB=5,BC=3,AC=4,∴AC2+BC2=32+42=52=AB2,∴∠C=90°,如图:设切点为D,连接CD,∵AB是⊙C的切线,∴CD⊥AB,∵S△ABC=12AC×BC=12AB×CD,∴AC×BC=AB×CD,即CD=AC BCAB⋅=345⨯=125,∴⊙C的半径为125,故选B.11.如图,在宽为20米、长为32米的矩形地面上修筑同样宽的道路(图中阴影部分),余下部分种植草坪.要使草坪的面积为540平方米,则道路的宽为()A.5米B.3米C.2米D.2米或5米【答案】C【解析】设道路的宽为x,根据题意得20x+32x-x2=20×32-540整理得(x-26)2=576开方得x-26=24或x-26=-24解得x=50(舍去)或x=2所以道路宽为2米.故选C.12.如图,平行四边形ABCD中,E为AD的中点,已知△DEF的面积为S,则四边形ABCE的面积为()A.8S B.9S C.10S D.11S【答案】B【解析】如图所示,∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC,∴△DEF ∽△BCF , ∴2:()DEF BCF DE S S BC=, 又∵E 是AD 中点,∴1122DE AD BC ==, ∴DE :BC =DF :BF =1:2, ∴:1:4DEF BCF SS =, ∴4BCF S S =,又∵DF :BF =1:2,∴2DCF SS =, ∴2()12.ABCD S DCF BCF S S S =+=∴四边形ABCE 的面积=9S ,故选B .二、填空题(本题满分18分,共有6道小题,每小题3分)13.方程x (2x -1)=x 的解是______.【解析】解:方程移项得:x (2x-1)-x=0,分解因式得:x (2x-1-1)=0,可得x=0或2x-2=0,解得:x 1=0,x 2=1.故答案为x 1=0,x 2=114.计算sin60°tan60°cos45°cos60°的结果为______.【解析】解:原式1=222⨯ 31=22- =115.如图,已知等边三角形ABC 的边长为6,以AB 为直径的⊙O 与边AC ,BC 分别交于D ,E 两点,则劣弧DE 的长为________.【解析】如图,连接OD 、OE ,∵△ABC 是等边三角形,∴∠A=∠B=∠C=60°,∵OA=OD ,OB=OE ,∴△AOD 、△BOE 是等边三角形,∴∠AOD=∠BOE=60°,∴∠DOE=60°,又∵OA=12AB=3, ∴DE 的长=603180ππ⨯=; 故答案为π.16.如图,过原点O 的直线与反比例函数1y ,2y 的图象在第一象限内分别交于点A ,B ,且A 为OB 的中点,若函数11y x=,则2y 与x 的函数表达式是_________.【解析】过A 作AC ⊥x 轴于C ,过B 作BD ⊥x 轴于D ,∵点A 在反比例函数11y x=上,∴设A (a ,1a ),∴OC=a,AC=1a,∵AC⊥x轴,BD⊥x轴,∴AC∥BD,∴△OAC∽△OBD,∴AC OC OABD OD OB==,∵A为OB的中点,∴12AC OC OABD OD OB===,∴BD=2AC=2a,OD=2OC=2a,∴B(2a,2a),设2kyx=,∴k=224aa⋅=,∴2y与x的函数表达式是:24yx=.故答案为24yx=.16.如图,将矩形沿图中虚线(其中x>y)剪成①②③④四块图形,用这四块图形恰能拼一个正方形.若y=2,则x的值等于________【解析】∵③所在的小直角三角形和③②构成的大直角三角形相似,∴x y xy x y -=+,∵y=2.∴x2-2x-4=0解得:x=1x1.1.17.如图,在矩形纸片ABCD中,AB=12,BC=5,点E在AB上,将△DAE沿DE折叠,使点A落在对角线BD上的点A′处,则AE的长为.【解析】:∵AB=12,BC=5,∴AD=5.∴BD 13=.根据折叠可得:AD=A′D=5,∴A′B=13-5=8.设AE=x ,则A′E=x ,BE=12-x ,在Rt △A′EB 中:()22212x x 8-=+,解得:10x 3=. 18.如图,在Rt △ABC 中,∠BAC=90°,AB=AC=16cm ,AD 为BC 边上高.动点P 从点A 出发,沿A→Dcm/s 的速度向点D 运动.设△ABP 的面积为S 1,矩形PDFE 的面积为S 2,运动时间为t 秒(0<t <8),则t= 秒时,S 1=2S 2.【解析】∵Rt △ABC 中,∠BAC=90°,AB=AC=16cm ,AD 为BC 边上的高,∴AD=BD=CD=.又∵,∴1118,22S AP BD t PD =⋅=⋅==. ∵PE ∥BC ,∴△APE ∽△ADC .∴PE AP DC AD =PE =⇒=. ∴PE=AP=.∴22S PD PE 16t 2t =⋅==-.∵S 1=2S 2,∴()28t 216t 2t =-,解得:t=6. 三、解答题(共6题;共46分)19.按要求解下列方程.(1)22340x x --=(配方法)(2)2(2)3(2)40x x ----=(自己喜欢的方法)【解析】解:(1)2322x x -=222333()2()244x x -+=+ 2341()416x -=344x -=±∴12x x ==(2)2(2)3(2)40x x ----=(21)(24)0x x -+--=(1)(6)0x x --=∴121,6x x ==20.已知:如图,在四边形ABCD 中,AB ∥CD ,E ,F 为对角线AC 上两点,且AE=CF ,DF ∥BE . 求证:四边形ABCD 为平行四边形.【解析】∵AB ∥CD ,∴∠DCA =∠BAC ,∵DF ∥BE ,∴∠DFA =∠BEC ,∴∠AEB =∠DFC ,在△AEB 和△CFD 中{DCF EABAE CF DFC AEB===∠∠∠∠,∴△AEB ≌△CFD (ASA ),∴AB=CD ,∵AB∥CD,∴四边形ABCD为平行四边形.21.如图,四边形ABCD是一个菱形绿地,其周长为40m,∠ABC=120°,在其内部有一个四边形花坛EFGH,其四个顶点恰好在菱形ABCD各边的中点,现在准备在花坛中种植茉莉花,其单价为10元/m2,请问需投资金多少元?(结果保留整数)【解析】连接BD,AC.∵菱形ABCD的周长为,∴菱形ABCD的边长为.∵∠ABC=120°,∴△ABD,△BCD是等边三角形.∴对角线BD=m,AC=m.∵E,F,G,H是菱形ABCD各边的中点,∴四边形EFGH是矩形,矩形的边长分别为m,.∴矩形EFGH的面积为(m2),即需投资金为10元).答:需投资金为866元.22.四边形ABCD是菱形,对角线AC=8cm,BD=6cm,DH⊥AB于H,求DH的长.【解析】解:∵四边形ABCD是菱形,AC=8cm,BD=6cm,∴AC ⊥BD ,OA =12 AC =4cm ,OB =12BD =3cm , ∴Rt △AOB 中,AB5,∵DH ⊥AB ,∵菱形ABCD 的面积S = 12AC •BD =AB •DH , 12×6×8=5DH , ∴DH =245. 23.如图,在平面直角坐标系中,直线AB 与x 轴、y 轴分别交于B 、A 两点,与反比例函数的图象交于点C ,连接CO ,过C 作CD ⊥x 轴于D ,已知tan ∠ABO =12,OB =4,OD =2.(1)求直线AB 和反比例函数的解析式;(2)在x 轴上有一点E ,使△CDE 与△COB 的面积相等,求点E 的坐标.【解析】解:(1)∵OB =4,OD =2∴DB =2+4=6∵CD ⊥x 轴, tan ∠ABO =12∴OA =2,CD =3∴A (0,2),B (4,0),C (-2,3)设直线AB 解析式为y =kx +b ,则 2,04b k b =⎧⎨=+⎩解得2,12b k =⎧⎪⎨=-⎪⎩∴直线AB解析式为122y x=-+设反比例函数解析式为myx =,得m=-2×3=-6∴反比例函数解析式为6 yx =-(2)∵△CDE与△COB的面积相等∴1122CD DE CD OB ⨯⨯=⨯⨯∴DE=OB=4∴点E的坐标为(-6,0)或(2,0)24.如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB =2∠PCB.(1)求证:PC是⊙O的切线;(2)求证:BC=12 AB;(3)点M是弧AB的中点,CM交AB于点N,若AB=8,求MN·MC的值.【解析】(1)证明:∵OA=OC,∴∠A=∠ACO又∵∠COB=2∠A,∠COB=2∠PCB,∴∠A=∠ACO=∠PCB.又∵AB 是⊙O 的直径∴∠ACO +∠OCB =90°.∴∠PCB +∠OCB =90°.即OC ⊥CP ,∵OC 是⊙O 的半径.∴PC 是⊙O 的切线.(2)证明:∵AC =PC ,∴∠A =∠P ,∴∠A =∠ACO =∠PCB =∠P .又∵∠COB =∠A +∠ACO ,∠CBO =∠P +∠PCB ,∴∠COB =∠CBO ,∴BC =OC .12BC AB =∴ (3)解:连接MB ,MA∵点M 是AB 的中点,∴∠ACM =∠BCM .∵∠ACM =∠ABM ,∴∠BCM =∠ABM .又∵∠BMN =∠CMB ,∴△MBN ∽△MCB . ∴MB MN MC MB= ∴2MB MN MC =⋅又∵AB 是⊙O 的直径,AM BM =∴∴∠AMB=90°,AM=BM . ∵AB =8,∴MB = ∴232MN MC MB ⋅==。
最新北师大版初中数学分层提优训练九年级上第6章《反比例函数》B卷(含详细答案及解析)

最新北师大版初中数学分层提优训练九年级上第6章《反比例函数》B卷(含详细答案及解析)一、选择题1. 一司机驾驶汽车从甲地去乙地,他以平均的速度用了到达乙地,当他按原路匀速返回时,汽车的速度与时间的函数关系是A. B. C. D.2. 下列函数中,不是的反比例函数的个数是;;;;.A. 个B. 个C. 个D. 个3. 如图,点是反比例函数的图象上的一点,过作平行四边形,使点在轴上,点在轴上,已知平行四边形的面积为,则的值为A. C.4. 将函数的图象沿轴向右平移个单位长度,得到的图象所相应的函数表达式是A. B. C. D.5. 如图,函数与的图象相交于点,则关于的不等式的解集是A. B. C. D.6. 函数的图象可能是A. B.C. D.7. 若点,,都是反比例函数图象上的点,并且,则下列各式中正确的是A. B. C. D.8. 反比例函数的图象与直线有两个交点,且两交点横坐标的积为负数,则的取值范围是A. B. C. D.9. 某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压是气体体积的反比例函数,其图象如图所示.当气球内的气压大于时,气球将爆炸.为了安全起见,气球的体积应A. 不小于B. 小于C. 不小于D. 小于10. 如图,和都是等腰直角三角形,,反比例函数在第一象限的图象经过点,则与的面积之差为A. B. C. D.二、填空题11. 把一个长、宽、高分别为的长方体铜块铸成一个圆柱体铜块,则该圆柱体铜块的底面积与高之间的函数关系式为.12. 反比例函数(为常数,)的图象是,它有两个分支且关于对称.13. 已知,两点都在反比例函数的图象上,且,则(填“”或“”).14. 已知一个函数的图象与的图象关于轴对称,则该函数的解析式为.15. 如图,直线过,两点,则的解集为.16. 如图,已知双曲线测与直线相交于,两点,过点作轴的垂线与过点作轴的垂线相交于点.若的面积为,则的值为.17. 请写出一个过点,且与轴无交点的函数解析式:.18. 如图,已知点,在反比例函数的图象上,点,在反比例函数的图象上,轴,,在轴的两侧,,,与的距离为,则的值是.19. 在平面直角坐标系中,直线与反比例函数的图象有唯一公共点,若直线与反比例函数的图象有个公共点,则的取值范围是.20. 如图,点为函数图象上一点,连接,交函数的图象于点,点是轴上一点,且,则的面积为.三、解答题21. 如图,反比例函数的图象与一次函数的图象在第一象限内相交于点,且点的横坐标为.(1)求点的坐标及一次函数的解析式;(2)若直线与反比例函数和一次函数的图象分别交于点,,求线段的长.22. 我们知道,蓄电池的电压为定值,使用此电源时,用电器的电流与电阻成反比例.已知电阻时,电流.(1)求确定与之间的函数关系式并说明此蓄电池的电压是多少;(2)若以此蓄电池为电源的用电器额定电流不能超过,则该电路中电阻的电阻值应满足什么条件?23. 如图,已知点是反比例函数的图象上一点,直线与反比例函数的图象在第四象限的交点为.(1)求直线的表达式;(2)动点在轴的正半轴上运动,当线段与线段之差达到最大时,求点的坐标.24. 已知反比例函数(为常数)的图象在第一、三象限内.(1)求的取值范围;(2)如图,若该反比例函数的图象经过平行四边形的顶点,点,的坐标分别为.①求出该反比例函数的表达式;②设点是该反比例函数图象上的一点,且在中,,求点的坐标.25. 解答题:(1)探究新知:如图,已知与的面积相等,试判断与的位置关系,并说明理由.(2)结论应用:①如图,点,在反比例函数的图象上,过点作轴,过点作轴,垂足分别为,.试证明:.②若①中的其他条件不变,只改变点,的位置如图所示,请判断与是否平行.26. 已知函数与函数交于点、两点(点在第一象限),(1)求,,的值;(2)函数与轴交于点,求的面积.27. 如图,在平面直角坐标系中,正方形的顶点与坐标原点重合,点的坐标为,点在轴的负半轴上,点,分别在边,上,且,,一次函数的图象过点和,反比例函数的图象经过点,与的交点为.(1)求反比例函数和一次函数的表达式;(2)若点在直线上,且使的面积与四边形的面积相等,求点的坐标.28. 已知函数.(1)若是的正比例函数,求的值.(2)若是的反比例函数,求的值.29. 如图,在平面直角坐标系中,已知点的坐标为(其中),射线与反比例函数的图象交于点,点,分别在函数的图象上,且轴,轴.(1)当点横坐标为时,求直线的表达式;(2)连接,当时,求点的坐标;(3)连接,,试猜想:的值是否随的变化而变化,如果不变,求出的值;如果变化,请说明理由.30. 如图,反比例函数的图象与一次函数的图象交于,两点,点的坐标为,点的坐标为.(1)求反比例函数与一次函数的表达式;(2)点为轴上的一个动点,若,求点的坐标.答案第一部分1. B2. C3. D4. B5. D6. C7. D 【解析】反比例函数的图象在第二、四象限,,所以它对应的;,对应的,都小于,且随的增大而增大,所以,即.8. B 【解析】将代入到反比例函数中,得:,整理,得:.因为反比例函数的图象与直线有两个交点,且两交点横坐标的积为负数,所以解得:.9. C 【解析】设球内气体的气压和气体体积的关系式为 .图象过点,.即在第一象限内,随的增大而减小,当时,.10. D【解析】设和的直角边长分别为、 .则点的坐标为.点在反比例函数的第一象限图象上,..第二部分11.12. 双曲线,原点13.【解析】因为,,所以反比例函数在第三象限内为减函数,所以.14.16.17. (答案不唯一)18.【解析】设点,到轴的距离分别为,,则由反比例函数的性质易得,所以,又与的距离为,所以,,则.19. 或【解析】解方程组得:,因为直线与反比例函数的图象有个公共点,所以方程有两个不相等的实数根,所以,所以或.20.【解析】设点的坐标为,点的坐标为 .点是轴上一点,且,点的坐标是 .设过点,的直线的解析式为: ..解得, .又点在上,,或(舍去)..第三部分21. (1)点在反比例函数的图象上,,,把代入一次函数,得,,一次函数的解析式为.(2)直线与反比例和一次函数的图象分别交于点,,当时,,.线段的长为.22. (1)根据题意,设,将,代入,得:,故,此蓄电池的电压是.(2)在中,当时,,,在第一象限内,随的增大而减小,如果要求以此蓄电池为电源的用电器额定电流不能超过时,则该电路中电阻的电阻值应不低于.23. (1)把代入,得.则.联立解得或则.设直线的表达式为,代入,两点坐标,得解得则直线的表达式为.(2)如图,直线交轴于点,当时,,得.则.因为(当,,三点在一条直线上时,“”成立),所以当点运动到点时,线段与之差达到最大,此时点的坐标为.24. (1)反比例函数(为常数)的图象在第一、三象限内,,解得.(2)①四边形为平行四边形,,,,,反比例函数的表达式为.②如图,以为圆心,长为半径作,与双曲线分别交于,,,四点,由对称性得,,.,,三点共线,故不能构成三角形.点坐标为和.25. (1) .理由如下:分别过点,,作, .垂足为,,则..与的面积相等,.四边形为平行四边形..(2)①连接,.设点的坐标为,点的坐标为.点,在反比例函数的图象上,,.轴,轴,,.,..由(1)中的结论可知:.②.26. (1)点,在上,解得,.把代入,.(2)根据题意得..27. (1)正方形的顶点,,,,,,把坐标代入得:,反比例解析式为,,,即,把与坐标代入中得:解得:,则直线解析式为;(2)把代入得:,,即,设,的面积与四边形的面积相等,,即,解得:,当时,,当时,,则坐标为或.28. (1)由题意,得解得.(2)由题意,得解得.29. (1)当时,,.设直线的表达式为,代入点,解得,直线的表达式为.(2)由轴,得点纵坐标为.当时,,,.,,即..(3)直线的表达式为,联立,解得.作,.当时,,即,当时,,即.,,,,,,.30. (1)把点代入,得..把点代入,得.点的坐标为.由直线过点,点得解得所求一次函数的表达式为.(2)如图设直线与轴的交点为,点的坐标为,连接,.则点的坐标为....,.点的坐标为或.。
初三数学提优测试卷

考试时间:120分钟满分:100分一、选择题(每题5分,共30分)1. 若实数a、b满足a + b = 2,则a^2 + b^2的最小值为:A. 2B. 4C. 6D. 82. 下列各数中,不是无理数的是:A. √3B. πC. 2.5D. √-13. 若x^2 - 4x + 4 = 0,则x的值为:A. 2B. -2C. 4D. -44. 在直角坐标系中,点P(3,4)关于x轴的对称点坐标为:A.(3,-4)B.(-3,4)C.(-3,-4)D.(3,-4)5. 若a、b、c是等差数列,且a + b + c = 15,则abc的最大值为:A. 15B. 20C. 25D. 30二、填空题(每题5分,共20分)6. 若sinα = 0.8,则cosα的值为______。
7. 二项式(x - 2)^5的展开式中,x^3的系数为______。
8. 若等腰三角形的底边长为8,腰长为10,则其面积为______。
9. 在△ABC中,∠A = 60°,∠B = 45°,则∠C的度数为______。
10. 若a、b、c、d是等比数列,且a + b + c + d = 16,则b的值为______。
三、解答题(每题15分,共45分)11. 解方程:2x^2 - 5x - 3 = 0。
12. 已知函数f(x) = x^2 - 4x + 3,求函数f(x)的对称轴和顶点坐标。
13. 在等腰三角形ABC中,AB = AC,∠B = 40°,求∠C的度数。
四、应用题(25分)14. 小明家准备装修客厅,客厅长为5米,宽为4米。
装修公司提供两种方案:方案一:铺满客厅的地面,每平方米需花费100元。
方案二:铺满客厅的地面,每平方米需花费80元,但需在四角各增加一个面积为1平方米的装饰区域。
(1)请计算两种方案的总花费。
(2)若小明家希望总花费不超过4000元,请问他应选择哪种方案?(3)请分析两种方案在美观和实用性方面的优缺点。
中考数学提优(含答案)

1、如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.(1)若△BPQ与△ABC相似,求t的值;(2)连接AQ,CP,若AQ⊥CP,求t的值;(3)试证明:PQ的中点在△ABC的一条中位线上2、(2013,盐城)如图①,若二次函数y=x2+bx+c的图象与x轴交于A(-2,0),B(3,0)两点,点A关于正比例函数y=x的图象的对称点为C.(1)求b、c的值;(2)证明:点C在所求的二次函数的图象上;(3)如图②,过点B作DB⊥x轴交正比例函数y=x的图象于点D,连结AC,交正比例函数y= x的图象于点E,连结AD、CD.如果动点P从点A沿线段AD方向以每秒2个单位的速度向点D运动,同时动点Q从点D沿线段DC方向以每秒1个单位的速度向点C运动.当其中一个点到达终点时,另一个点随之停止运动,连结PQ、QE、PE.设运动时间为t秒,是否存在某一时刻,使PE平分∠APQ,同时QE平分∠PQC?若存在,求出t的值;若不存在,请说明理由.3、如图,点O为矩形ABCD的对称中心,AB=10cm,BC=12cm.点E,F,G分别从A,B,C 三点同时出发,沿矩形的边按逆时针方向匀速运动,点E的运动速度为1cm/s,点F的运动速度为3cm/s,点G的运动速度为1.5cm/s.当点F到达点C(即点F与点C重合)时,三个点随之停止运动.在运动过程中,△EBF关于直线EF的对称图形是△EB'F,设点E,F,G运动的时间为t(单位:s).(1)当t=s时,四边形EBFB'为正方形;(2)若以点E,B,F为顶点的三角形与以点F,C,G为顶点的三角形相似,求t的值;(3)是否存在实数t,使得点B'与点O重合?若存在,求出t的值;若不存在,请说明理由.4、(2012 义乌市)在锐角△ABC中,AB=4,BC=5,∠ACB=45°,将△ABC绕点B按逆时针方向旋转,得到△A1BC1.(1)如图1,当点C1在线段CA的延长线上时,求∠CC1A1的度数;(2)如图2,连接AA1,CC1.若△ABA1的面积为4,求△CBC1的面积;(3)如图3,点E为线段AB中点,点P是线段AC上的动点,在△ABC绕点B按逆时针方向旋转过程中,点P的对应点是点P1,求线段EP1长度的最大值与最小值.5、(2014盐城)【问题情境】张老师给爱好学习的小军和小俊提出这样一个问题:如图1,在△ABC中,AB=AC,点P为边BC上的任一点,过点P作PD⊥AB,PE⊥AC,垂足分别为D、E,过点C作CF⊥AB,垂足为F.求证:PD+PE=CF.小军的证明思路是:如图2,连接AP,由△ABP与△ACP面积之和等于△ABC的面积可以证得:PD+PE=CF.小俊的证明思路是:如图2,过点P作PG⊥CF,垂足为G,可以证得:PD=GF,PE=CG,则PD+PE=CF.【变式探究】如图3,当点P在BC延长线上时,其余条件不变,求证:PD﹣PE=CF;请运用上述解答中所积累的经验和方法完成下列两题:【结论运用】如图4,将矩形ABCD沿EF折叠,使点D落在点B上,点C落在点C′处,点P为折痕EF上的任一点,过点P作PG⊥BE、PH⊥BC,垂足分别为G、H,若AD=8,CF=3,求PG+PH的值;【迁移拓展】图5是一个航模的截面示意图.在四边形ABCD中,E为AB边上的一点,ED⊥AD,EC⊥CB,垂足分别为D、C,且AD•CE=DE•BC,AB=2dm,AD=3dm,BD=dm.M、N 分别为AE、BE的中点,连接DM、CN,求△DEM与△CEN的周长之和.(注:可编辑下载,若有不当之处,请指正,谢谢!)。
初三提优试卷数学

一、选择题(每题5分,共25分)1. 下列各数中,有理数是()A. √16B. πC. √-1D. √2 - √32. 如果a > b,那么下列不等式中正确的是()A. a + 2 > b + 2B. a - 2 < b - 2C. 2a > 2bD. 2a < 2b3. 下列函数中,一次函数是()A. y = x^2 + 3x + 2B. y = 2x - 1C. y = √xD. y = 3/x4. 已知等腰三角形底边长为6,腰长为8,那么这个三角形的面积是()A. 24B. 32C. 36D. 485. 若等差数列{an}的前三项分别为2,5,8,那么这个数列的公差是()A. 1C. 3D. 4二、填空题(每题5分,共25分)6. 若x + 3 = 0,则x = ________。
7. (-2)^3 × (-1)^4 = ________。
8. 已知函数y = 3x - 2,当x = 2时,y = ________。
9. 在直角坐标系中,点P(3,4)关于x轴的对称点是_______。
10. 若等比数列{an}的第一项为a1,公比为q,则第四项a4 = ________。
三、解答题(共50分)11. (15分)解一元二次方程:x^2 - 5x + 6 = 0。
12. (15分)已知函数y = 2x - 3,求函数的图像与x轴的交点坐标。
13. (15分)已知等差数列{an}的前n项和为Sn,且S3 = 12,S5 = 30,求该数列的首项a1和公差d。
14. (15分)在直角坐标系中,点A(-2,3),B(4,-1),C(0,2)构成三角形ABC,求三角形ABC的周长。
答案:一、选择题1. C2. C3. B4. B5. B二、填空题7. -28. 19. (3,-4)10. a1q^3三、解答题11. 解:因式分解得:(x - 2)(x - 3) = 0,所以x = 2或x = 3。
最新北师大版初中数学分层提优训练九年级上第2章《一元二次方程》B卷(含详细答案及解析)

最新北师大版初中数学分层提优训练九年级上第2章《一元二次方程》B卷(含详细答案及解析)一、选择题1. 要组织一次篮球联赛,赛制为单循环形式(每两队之间都赛一场),计划安排场比赛,则参赛球队有A. 个B. 个C. 个D. 个2. 已知的值为,则代数式的值为A. B. C.3. 用配方法解一元二次方程时,下列变形正确的是A. B. C. D.4. 一台电视机的成本价为元,销售价比成本价增加 .因库存积压,所以就按销售价的出售,那么每台电视机的售价为A. 元B. 元C. 元D. 元5. 新年里,一个小组有若干人,若每人给小组的其他成员赠送一张贺年卡,则全组送贺卡共张,此小组人数为A. B. C. D.6. 关于的一元二次方程的一个根是,则的值为C. 或D.7. 设,是方程的两个实数根,则的值为A. B. C. D.8. 某种品牌的手机经过四、五月份连续两次降价,每部售价由元降到了元.则平均每月降价的百分率为A. B. C. D.9. 如图,,是半径为的上的两点,且.点从点出发,在上以每秒一个单位长度的速度匀速运动,回到点运动结束.设运动时间为(单位:),弦的长为,那么下列图象中可能表示与函数关系的是A. ①B. ③C. ②或④D. ①或③10. 一元二次方程的根的情况是A. 无实数根B. 有一正根一负根C. 有两个正根D. 有两个负根二、填空题11. 某商场销售一款童装,平均每天可售出件,每件盈利元.为了迎接“六一”儿童节,商场决定采取适当降价的措施.经调查,如果每件童装降价元,那么平均每天就可多售出件.要想平均每天销售这种童装盈利元,则每件童装应降价多少元?设每件童装应降价元,可列方程为.12. 已知关于的一元二次方程.方程两实数根分别为,,且满足,则的最后结果是.13. 如图是某种计算程序示意图,初始端输入后经式子处理后得到一个结果.若这个结果大于,则输出此结果;否则就将这一次得到的结果作为输入的再次运行程序,直到输出结果为止.()当初始端输入时,输出的结果是;()若该程序满足条件:存在实数,当初始端输入时,该程序的运算无法停止(即会一直循环运行),请写出一个符合条件的的值:.14. 一个容器盛满纯药液,第一次倒出若干升后,用水加满;第二次又倒出同样体积的溶液,这时容器里只剩下纯药液15. 方程的根是.16. 某校九年级学生毕业时,每个同学都将自己的相片向全班同学各送一张留作纪念,全班共送了张相片,如果全班有名学生,根据题意,列出方程为.17. 若两个连续奇数的积为,则这两个数为.18. 多项式加上一个单项式后,使它能成为一个整式的完全平方,那么加上的单项式可以是.(填上一个你认为正确的即可)19. 已知,,,是整数,且,若,,,满足方程,则.20. 在实数范围内定义一种运算“”,其规则为 .根据这个规则,方程的解为.三、解答题21. 解方程:.22. 解方程:.23. 已知关于的方程.(1)求证:方程总有两个不相等的实数根;(2)如果方程的两个实数根都是整数,求整数的值.24. 如图,一农户要建一个矩形猪舍,猪舍的一边利用长为的住房墙,另外三边用长的建筑材料围成,为方便进出,在垂直于住房墙的一边留一个宽的门,所围矩形猪舍的长、宽分别为多少时,猪舍面积为 ?25. 方法介绍:同学们,生活中的很多实际问题,我们往往抽象成数学问题,然后通过数形结合建立数学模型的方式来解决.例如:学校举办足球赛,共有五个球队参加比赛,每个队都要和其他各队比赛一场,问该学校一共要安排多少场比赛?这是一个实际问题,我们可以在平面内画出个点(任意个点都不在同一条直线上),如图①所示,其中每个点各代表一个足球队,两个队之间比赛一场就用一条线段把他们连起来,其中连接线段的条数就是安排比赛的场数.这样模型就建立起来了,如何解决这个模型呢?由于每个队都要与其他各队比赛一场,即每个点都要与另点连接一条线段,这样个点应该有条线段,而每两个点之间的线段都重复计算了一次,实际只有条线段,所以学校一共要安排场比赛.(1)学以致用:①根据图②回答:如果有个班级的足球队参加比赛,学校一共要安排场比赛;②根据规律,如果有个班级的足球队参加比赛,学校一共要安排场比赛.(2)问题解决:①小明今年参加了学校新组建的合唱队,老师让所有人每两人相互握手,认识彼此(每两人之间不重复握手).小明发现所有人握手次数总和为次,那么合唱队有多少人?②A,B,C,D,E五人参加一次会议,见面时他们相互握手问好,每两人之间不重复握手.已知A已经握了次,B已经握了次,C已经握了次,D已经握了次,请利用图③分析E已经和哪些人握手了.(3)问题拓展:根据上述模型的建立和问题的解决,请你提出一个问题,并进行解答.26. 已知关于的方程.(1)求证:方程总有两个不相等的实数根;(2)已知方程的一个根为,求代数式的值.27. 山西特产专卖店销售核桃,其进价为每千克元,按每千克元出售,平均每天可售出千克,后来经过市场调查发现,单价每降低元,则平均每天的销售可增加千克,若该专卖店销售这种核桃要想平均每天获利元,请回答:(1)每千克核桃应降价多少元?(2)在平均每天获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的几折出售?28. 已知关于的一元二次方程有两个不相等的实数根.(1)求的取值范围;(2)当时,求的值.29. 判断下列方程后面括号里的数是否为一元二次方程的根.(1))(2).(,)30. 已知关于的一元二次方程.(1)若方程有实数根,求实数的取值范围;(2)若方程两实数根分别为,,且满足,实数的值.答案第一部分1. C2. B3. D4. B5. C6. A7. B 【解析】,是方程的两个实数根,, ...8. C9. D10. C【解析】,,整理得:,则,,解得:,,故方程有两个正根.第二部分11.12.13. ,【解析】()当时,代数式;当时,,则输出的结果是.()根据题意得,解得,,取符合其中的一个数即可.14.15. ,16.17. 和或和【解析】设连续两个奇数分别为,,则根据题意得,解得,分别代入得这两个数为和或和18. 或或19.20. ,第三部分21. 将原方程化为一般形式,得这里,,.,,即22. 移项,得即则所以,.23. (1),是关于的一元二次方程..方程总有两个不相等的实数根.(2)由求根公式,得.,.方程的两个实数根都是整数,且是整数,或.24. 设矩形猪舍垂直于住房墙一边长为可以得出平行于墙的一边的长为,由题意得化简,得解得:当时,,当时,,答:所围矩形猪舍的长为、宽为25. (1)①;②【解析】①有个班级的足球队参加比赛,学校一共要安排比赛的场数是:.②个班级的足球队参加比赛,学校一共要安排场比赛.(2)①设合唱队有人,则整理得,解得,答:合唱队有人;②如图,E和 A,B握手了.(3)提出的问题:班级分组举办“两人三足”游戏,要求每个组的每个同学都要与组内其他同学组成一队,进行五十米折返跑,最后计算小组总时间来决定胜负.已知该游戏分为组,每组要折返跑次,那么这个班级一共有多少人?问题解答:设每组人数为人,有解得即每组有人,则班级总人数为(人),答:这个班级一共有人.26. (1),方程总有两个不相等的实数根.(2)是方程的一个根,把代入方程,得,.当方程的一个根为时,代数式的值是.27. (1)解:设每千克核桃应降价元.根据题意,得化简,得解得答:每千克核桃应降价元或元.(2)由(1)可知每千克核桃可降价元或元.因为要尽可能让利于顾客,所以每千克核桃应降价元.此时,售价为:(元),.答:该店应按原售价的九折出售.28. (1) \因为原方程有两个不相等的实数根,所以解得且.(2)..又且,..29. (1)当时,;当时,.都是方程的根.(2)当时,;当时,.所以不是方程的根,是方程的根.30. (1)根据题意可知,解得实数的取值范围是.(2)根据根与系数的关系可知,.,,即.,解得.又,不合题意舍去,.。
苏科版九年级下册数学提优训练(含答案)

九年级下数学提优训练1.如图,在矩形ABCD中,AB=8,BC=12,点E是BC的中点,连接AE,将△ABE沿AE折叠,点B 落在点F处,连接FC,则tan∠ECF=________2.如图,已知点E是矩形ABCD的对角线AC上的一动点,正方形EFGH的顶点G、H都在边AD上,若AB=3,BC=4,则tan∠AFE的值________3.如图,在等腰直角△ABC中,∠C=90°,点O是AB的中点,且AC=1,将一块直角三角板的直角顶点放在点O处,始终保持该直角三角板的两直角边分别与AC、BC相交,交点分别为D、E,则CD+CE =.4.如图,在Rt△ABC中,CM平分∠ACB交AB于点M,过点M作MN∥BC交AC于点N,且MN平分∠AMC,若AN=1,则BC的长为.5.如图,△AOB 为等腰三角形,顶点A 的坐标(2,5),底边OB 在x 轴上.将△AOB 绕点B 按顺时针方向旋转一定角度后得△A ′O ′B ,点A 的对应点A ′在x 轴上,则点O ′的坐标为 .6.如图,△ABC 的内心在y 轴上,点C 的坐标为(2,0),点B 的坐标是(0,2),直线AC 的解析式为,则tan A 的值是 .7.如图,直线x y 34=与双曲线x k y =(x >0)交于点A .将直线x y 34=向右平移29个单位后,与双曲线x k y =(x >0)交于点B ,与x 轴交于点C ,若2=BCAO ,则k = .8.若直线y =m (m 为常数)与函数()()⎪⎪⎩⎪⎪⎨⎧>≤=24222x xx x y 的图象恒有三个不同的交点,则常数m 的取值范围是 .9.如图,在Rt △ABC 中,∠C =90°,∠B =60°,点D 是BC 边上的点,CD =1,将△ABC 沿直线AD 翻折,使点C 落在AB 边上的点E 处,若点P 是直线AD 上的动点,则△PEB 的周长的最小值是 .10.如图,在△ABC 中,AB =AC ,DE 垂直平分AB .若BE ⊥AC ,AF ⊥BC ,垂足分别为点E ,F ,连接EF ,则∠EFC = .11.如图,在平行四边形OADB 中,对角线AB 、OD 相交于点C ,反比例函数xk y(k >0)在第一象限的图象经过A 、C 两点,若平行四边形OADB 面积为12,则k 的值为 .12.如图,矩形ABCD 中,AB =3,BC =4,EB ∥DF 且BE 与DF 之间的距离为3,则AE 的长是 .13.如图,在正方形ABCD中,AC为对角线,点E在AB边上,EF⊥AC于点F,连接EC,AF=3,△EFC 的周长为12,则EC的长为.14.如图,在菱形ABCD中,∠BAD=120°,点E、F分别在边AB、BC上,△BEF与△GEF关于直线EF对称,点B的对称点是点G,且点G在边AD上.若EG⊥AC,AB=26,则FG的长为.15.某工厂接受了20天内生产1200台GH型电子产品的总任务.已知每台GH型产品由4个G型装置和3个H型装置配套组成.工厂现有80名工人,每个工人每天能加工6个G型装置或3个H型装置.工厂将所有工人分成两组同时开始加工,每组分别加工一种装置,并要求每天加工的G、H型装置数量正好全部配套组成GH型产品.(1)按照这样的生产方式,工厂每天能配套组成多少套GH型电子产品?请列出二元一次方程组解答此问题.(2)为了在规定期限内完成总任务,工厂决定补充一些新工人,这些新工人只能独立进行G型装置的加工,且每人每天只能加工4个G型装置.1.设原来每天安排x名工人生产G型装置,后来补充m名新工人,求x的值(用含m的代数式表示)2.请问至少需要补充多少名新工人才能在规定期内完成总任务?16.如图1,已知△ABC中,AB=10cm,AC=8cm,BC=6cm,如果点P由B出发沿BA方向向点A匀速运动,同时点Q由A出发沿AC方向向点C匀速运动,它们的速度均为2cm/s,连接PQ,设运动的时间为t(单位:s)(0≤t≤4).解答下列问题:(1)当t为何值时,PQ∥BC.(2)设四边形BCQP的面积为S(单位:cm2),求s与t之间的函数关系式.(3)如图2把△APQ沿AP翻折,得到四边形AQPQ′那么是否存在某时刻t使四边形AQPQ′为菱形?若存在,求出此时菱形的面积;若不存在,请说明理由.17.如图,二次函数y=﹣ax2+2ax+c(a>0)的图象交x轴于A,B两点,交y轴于点C,过A的直线y=kx+2k(k≠0)与这个二次函数图象交于另一点F,与其对称轴交于点E,与y轴交于点D,且DE=EF.(1)求A点坐标;(2)若△BDF的面积为12,求此二次函数的表达式;(3)设二次函数图象顶点为P,连接PF,PC,若∠CPF=2∠DAB,求此二次函数的表达式.18.已知二次函数y =mx 2﹣5mx +1(m 为常数,m >0),设该函数图象与y 轴交于点A ,图象上一点B 与点A 关于该函数图象的对称轴对称.(1)求点A 、B 的坐标;(2)点O 为坐标原点,点M 为函数图象的对称轴上一动点,求当M 运动到何处时△MAO 的周长最小;(3)若该函数图象上存在点P 与点A 、B 构成一个等腰三角形,且△P AB 的面积为10,求m 的值.19.已知,如图,线段AB ,利用无刻度的直尺和圆规,作一个满足条件的△ABC :①△ABC 为直角三角形;②tan ∠A =31.(注:不要求写作法,但保留作图痕迹)20.“位似变化”是一种重要的几何变化,可以将图形放大或缩小,且与原图形相似.你能用位似变化解决下列问题吗?如图Rt△ABC中,∠C=90°,AC=12,BC=6,有矩形EFGH的一边EF在边AC上,点H在斜边AC 上,EF=2,HE=1.(1)请你用圆规和无刻度直尺在Rt△ABC内作一个最大的矩形且与矩形EFGH位似.(不要求写作法,但必须保留作图痕迹)(2)请证明你作图方法的正确性.(3)求最大矩形与矩形EFGH的面积之比.。
