对流扩散方程ppt课件
合集下载
第五章对流扩散问题(一维稳态对流扩散问题)
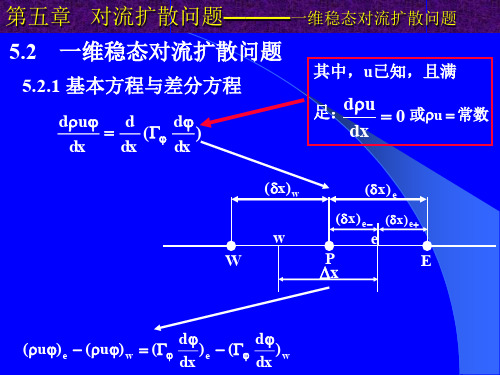
(u) e e P Fe ,0 E Fe ,0
(u) w w W Fw ,0 P Fw ,0
代入积分方程,并整理,即得:
a P P a E E a W W
其中
aE De Fe ,0
a W D w Fw ,0
a P De Fe ,0 D w Fw ,0 a E a W (Fe Fw )
du d u dx dx E W u ( x ) e ( x ) w E W u 2 x
所以,也可以说对流扩散问题的中心差分格式不满足正系数准则
第五章 对流扩散问题———一维稳态对流扩散问题
正系数准则的破坏会使差分方程不真实,从而引起不正确 的计算结果。如:
第五章 对流扩散问题———一维稳态对流扩散问题
很显然,对上风格式的差分方程,系数之和准则和正系 数准则都是满足的。为此,我们将它与中心差分格式做 一个比较如下: 上风格式 控制容积界面上 变量的选取 系数之和准则 正系数准则 中心差分格式
物理意义清晰, 仅具有数学意义, 合理 无物理考虑 满足 满足 满足 不满足
P<<-1
P=-1
P=0
P=1 P>>1
0
0 L/2 L
第五章 对流扩散问题———一维稳态对流扩散问题
说明
由图很容易看出,只有在贝克列数为零的极限条 件下,即对纯扩散问题或导热问题,变量在任意 两点之间的变化才是线性的。即在没有流动的情 况下,我们假定变量在任意两个节点之间的线性 分布才是可以接受的。 当贝克列数不为零时,即存在对流过程时,变量 在任意两点之间的变化是偏离线性的。贝克列数 的绝对值越大,这种偏离越严重。所以我们在用 控制容积法推导差分方程时,假定任意两个节点 之间变量呈线性变化显然是有问题的。
(u) w w W Fw ,0 P Fw ,0
代入积分方程,并整理,即得:
a P P a E E a W W
其中
aE De Fe ,0
a W D w Fw ,0
a P De Fe ,0 D w Fw ,0 a E a W (Fe Fw )
du d u dx dx E W u ( x ) e ( x ) w E W u 2 x
所以,也可以说对流扩散问题的中心差分格式不满足正系数准则
第五章 对流扩散问题———一维稳态对流扩散问题
正系数准则的破坏会使差分方程不真实,从而引起不正确 的计算结果。如:
第五章 对流扩散问题———一维稳态对流扩散问题
很显然,对上风格式的差分方程,系数之和准则和正系 数准则都是满足的。为此,我们将它与中心差分格式做 一个比较如下: 上风格式 控制容积界面上 变量的选取 系数之和准则 正系数准则 中心差分格式
物理意义清晰, 仅具有数学意义, 合理 无物理考虑 满足 满足 满足 不满足
P<<-1
P=-1
P=0
P=1 P>>1
0
0 L/2 L
第五章 对流扩散问题———一维稳态对流扩散问题
说明
由图很容易看出,只有在贝克列数为零的极限条 件下,即对纯扩散问题或导热问题,变量在任意 两点之间的变化才是线性的。即在没有流动的情 况下,我们假定变量在任意两个节点之间的线性 分布才是可以接受的。 当贝克列数不为零时,即存在对流过程时,变量 在任意两点之间的变化是偏离线性的。贝克列数 的绝对值越大,这种偏离越严重。所以我们在用 控制容积法推导差分方程时,假定任意两个节点 之间变量呈线性变化显然是有问题的。
第五章对流扩散问题(一维稳态对流扩散问题)

差分方程应 满足相邻系 数之和准则
第五章 对流扩散问题———一维稳态对流扩散问题
a P P a E E a W W
中心节点系数
相邻节点系数
aP aE , a W aP aE a W (Fe Fw )
考虑到连续方程
Fe-Fw=0
满足相邻系 数之和准则
a P aE a W
扩散项和以前的处理方法一样,即有:
(u) e e (u) w w e ( E P ) ( x ) e w ( P E ) ( x ) w
而控制容积界面上的变量值取其相应上风侧网格 节点上的值。即:
第五章 对流扩散问题———一维稳态对流扩散问题
第五章 对流扩散问题———一维稳态对流扩散问题 5.2 一维稳态对流扩散问题
5.2.1 基本方程与差分方程
du d d ( ) dx dx dx
(x)w
其中,u已知,且满
d u 足: 0 或u 常数 dx
( x ) e
( x ) e ( x ) e
w W
e P x
a P P a E E a W W
aE 1 4 1 2 4 aW 1 3 2 a P 1 3 4 4 2
2P E 3W
De Dw 1 Fe Fw 4
E 200, W 100
E 100 W 200
2 P 0.25E 1.75 W
De D w 1 Fe Fw 1.5
E 200, W 100
E 100 W 200
P 187.5
P 112.5
某问题 结果合理
第五章 对流扩散问题———一维稳态对流扩散问题
第五章 对流扩散问题———一维稳态对流扩散问题
a P P a E E a W W
中心节点系数
相邻节点系数
aP aE , a W aP aE a W (Fe Fw )
考虑到连续方程
Fe-Fw=0
满足相邻系 数之和准则
a P aE a W
扩散项和以前的处理方法一样,即有:
(u) e e (u) w w e ( E P ) ( x ) e w ( P E ) ( x ) w
而控制容积界面上的变量值取其相应上风侧网格 节点上的值。即:
第五章 对流扩散问题———一维稳态对流扩散问题
第五章 对流扩散问题———一维稳态对流扩散问题 5.2 一维稳态对流扩散问题
5.2.1 基本方程与差分方程
du d d ( ) dx dx dx
(x)w
其中,u已知,且满
d u 足: 0 或u 常数 dx
( x ) e
( x ) e ( x ) e
w W
e P x
a P P a E E a W W
aE 1 4 1 2 4 aW 1 3 2 a P 1 3 4 4 2
2P E 3W
De Dw 1 Fe Fw 4
E 200, W 100
E 100 W 200
2 P 0.25E 1.75 W
De D w 1 Fe Fw 1.5
E 200, W 100
E 100 W 200
P 187.5
P 112.5
某问题 结果合理
第五章 对流扩散问题———一维稳态对流扩散问题
热传导方程(扩散方程)ppt课件

( x ,t0) ( x )
波方程的Cauchy问题
由泛定方程和相应边界条件构成的定解问题称为 边值问题。
u0, (x,y),
u f (x, y).
Laplace方程的边值问题
由偏微分方程和相应的初始条件及边界条件构成 的定解问题称为混合问题。
uutt0a2(u(xxx,y,uzy)yuzz)0
kn|x0k(x) qnq0
u x
|xl
q0 k
u x |x0
q0 k
xl
若端点是绝热的,则
u u x|xl x x0 0
三、定解问题
定义1 在区域 G[0,) 上,由偏微分方程、初 始条件和边界条件中的其中之一组成的定解问题称为 初边值问题或混合问题。
u ut x,a 02 u xx (x 0),,
注 1、热传导方程不仅仅描述热传导现象,也可以
刻画分子、气体的扩散等,也称扩散方程;
2、上述边界条件形式上与波动方程的边界条件 一样,但表示的物理意义不一样;
3、热传导方程的初始条件只有一个,而波动方 程有两个初始条件。
4、除了三维热传导方程外,物理上,温度的分 布在同一个界面上是相同的,可得一维热传导方
gk1 k
u1.
注意第三边界条件的推导:
研究物体与周围介质在物体表面上的热交换问题
把一个温度变化规律为 u(x, y, z, t)的物体放入 空
气介质中,已知与物体表面接触处的空气介质温度
为 u1(x, y, z, t),它与物体表面的温度u(x, y, z, t)并不
相同。这给出了第三边界条件的提法。
或
u knk1(uu1).
即得到(1.10): ( u nu)|(x,y,z) g(x,y,z,t).
流体力学 扩散理论PPT课件

P 2 exp( S2 )
n
2N
令a表示分子运动速度,t为分子运动N次经历的时间;
N=at/l,Sl=x1
P 2l exp( x12 )
at 2lat
与
c(x1,t)
M exp(x12 )
4Dmt
4Dmt
比较,Dm=la/2=Nl2/(2t)
P l exp( x12 )
Dmt
4Dmt
2021/3/25
2021/3/25
授课:XXX
22
5
4
y2 (104 m2 )
3
2
1
2
y2 (102 m)
1
0
0.2 0.4 0.6 0.8 1.0
0.2 0.4 0.6 0.8 1.0 1.2
t(s)
t(s)
曲线验证了单个质点紊动扩散不同阶段的规律。当t>0.7s,线性关系良好。
Y2Y 1 2 .0 Y 0 2 .74 .3 8 2 .5 96 .0 1 4 0 m /s2 t 1 .00 .7 0 .3
D r(s 0 ,t) w i(s 0 ,t)w i(s 0 ,t)t A 1 t
s2 (s 0 ,t) s 0 2 w i(s 0 ,t)w i(s 0 ,t)t2 A 1 t2 d dts2s0 2(w i(s0,t)w i(s0,t))`1 2A 1
2021/3/25
授课:XXX
18
常数A1与s0的大小有关:
202而1/3按/25 t1/2增大,随后又按t-1/2授降课:低XXX
21
例:设在一均匀紊流内,在原点投入许多示踪质粒子,量测
不同时刻粒子的横向位移Y,Y2的统计值Y 2 及通过原点后的
第五章对流扩散问题(假扩散)
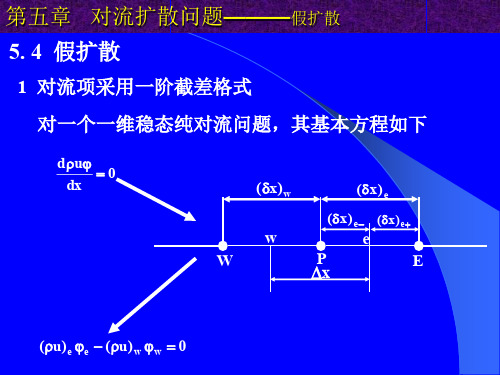
该问题的数值解如下:
1 n i
u t n u t n (1 ) i i 1 x x
MUD : du d ux d (( ) ) dx dx 2 dx
第五章 对流扩散问题———假扩散
由图可以看出,在区间 P 2 ,中心差分格式预报的 P 值优于迎风格式的预报值。对比这两种格式,其扩散项 的处理是完全相同的,所不同的仅仅是对流项的处理上 ,在中心差分格式中对流项的差分格式具有二阶精度, 而在迎风格式中对流项的差分格式只具有一阶精度。在 区间 P 2 ,两种格式预报 P值所表现出的差异性恰恰是 这两种格式精度不同的体现。观察上图,迎风格式所预 报的 P值具有该高不高和该低不低的特点,这一特点正 是由一阶精度迎风格式所引起的扩散系数为 ux / 2 的 假扩散项造成的。也反映了假扩散项的影响。
n n ux ut 2 n ( ) i u( ) i (1 )( 2 ) i O( x 2 , t 2 ) t x 2 x x
由此可以看出,我们前边得到的差分方程所逼近的是 一个非稳态对流扩散问题,而非原型问题所要求的非 稳态对流问题。
第五章 对流扩散问题———假扩散
1 n (1 P
ut n ut n ) P W x x
用编号法表示
1 n i
1 n , n 在点 (i, n) i i 1
u t n u t n (1 ) i i 1 x x
做Taylor展开
n n u 2 n 1 2 n ( ) i u( ) i ( 2 ) i x ( 2 ) i t O( x 2 , t 2 ) t x 2 x 2! t
第五章 对流扩散问题———假扩散
将 i 1 和 i 1 台劳 级数展开代入
对流扩散与相间传质讲解

2019/6/8
对流扩散与相间传质
2/27
JA
( D
DE
)
dcA dz
对流传质通量
在湍流主体中
DE D 在层流内层中
NA
DE RT
dpA dz
NA
D RT
dpA dz
D 较小
dpA dz
较大,DE
0
在缓冲层内
NA
D DE RT
dpA dz
溶
质p
A
在 气
pi
相
中
的
分
压
2019/6/8
气相主体
气膜 液膜
液
膜
边
液相主体
界
气
膜
边
界
相界面 传质方向
图32 2 双膜模型
对流扩散与相间传质
溶
质
A 在
液
相
ci
中 的
c
摩 尔
浓
度
6/27
双膜模型的理论要点是:
①在气-液两相接触面附近,分别存在着呈滞流流动的稳定气膜和液膜。 溶质连续稳定地通过两膜,膜的厚度随流体流动状态而变化; ②气-液两相在相界面上呈平衡状态,即相界面上不存在传质阻力。如以低浓度 气体溶解为例,则平衡关系服从Henry定律,即有 ci Hpi 或 c Hp ,其中H 为溶解度系数,单位随 c 和 p 的单位而定; ③膜层以外的气、液相主体,由于流体的充分湍动,分压或浓度均匀化,无分压 或浓度梯度。
溶质由气相主体 湍流扩散气膜边界 p 分子扩散相界面气侧 pi 无阻力溶解 相界面液侧 ci 分子扩散液膜边界 c 湍流扩散液相主体
对流扩散与相间传质 ppt课件
11.04.2020
NA
kG( pA
pAi)
pA pAi 1/ kG
NA
kL(cAi
cA)
cAi cA 1/ kL
气相对流传质k系 G 数R: D TGG pptBm 液相对流传质k系L 数DL: cLBctm
11.04.2020
对流扩散与相间传质
4
引入了有效膜模型后,使问题的描述形式得以简化,但问题并未最
终解决,G 或L 是一虚拟量,与 DE 一样,很难确定,这使得传质
第二十六讲 对流扩散与相间传质
一、对流扩散
(一)对流扩散过程 (二)对流扩散的有效膜模型
二、相间传质
(一)相间传质模型 1. 双膜模型 2. 溶质渗透模型 3. 表面更新模型
(二)相间传质速率方程 1. 双膜模型的数学描述 2. 相间传质速率方程 3. 传质速率方程的讨论
三、三种传递的类比
(一)普朗特的混合长理论 (二)三种传递的相似性 (三)三种传递的类比式
(一)对流传质过程
运动着的流体与壁面之间或两个有无限互溶的运动流体之间发生的传质,习惯称 之为对流传质。对流传质中既有分子传质,又有涡流传质。根据流体流动发生的 原因可分为自然对流传质和强制对流传质两类;根据流体的作用方式由可分为流 体与固体壁面间的传质及流体与流体之间的传质两类。工程上均采用强制湍流的 方式传质。
11.04.2020
对流扩散与相间传质
5
(一)相间传质模型
相际间的三种典型对流传质模型 双膜模型:稳定的气膜和液膜-在膜内为定态传质-Whitman-1923 溶质渗透模型:液相内为非定态-表面暴露时间相等-Higbie-1935 表面更新模型:液相内为非稳态-年龄分布函数-Danckwerts-1951 1. 双膜模型
第五章对流扩散方程
• 用四条线逼近准确解,十分接近指数格式 的结果,但计算量小得多
• 比混合格式复杂,计算量增加,但准确性 提高
• 稳定性:若用中心差分格式不能体现对流 项的物理本质,常会引起数值解的振荡
• 经济性:若用高阶格式,无数值振荡,但 格式复杂,求解相对困难,机时消耗较多
5.2 一维稳态对流扩散问题
d (u)
dx
d dx
d
dx
5.2.1 模型方程的精确解
d (u)
dx
d dx
d
dx
边界条件:
x 0, 0;x L, L
采用迎风思想:从来流上游方向找依赖区
在界面e上,若 ue 0,则e P ;若 ue 0,则e E ; 在界面w上,若 uw 0,则w W ;若 uw 0,则w P
界面流量
• 引入符号 • 对流:
a1, a2 max(a1, a2 )
(u)e Fee P Fe,0 E Fe,0 , (u)w Fww W Fw,0 P Fw,0
• 控制方程变为: dJ 0; 或 J const dx
J
F
0
0 L
exp(Pe) 1
界面上通量
Jw
Fw
W
W P
exp(Pw )
1Hale Waihona Puke JeFeP
P
exp(
E
Pe )
1
Fe exp( exp(Pe
Pe )
) 1
Fw exp(Pw )
1 P
Fe exp(Pe )
1E
Fw exp(Pw exp(Pw )
) 1
W
合并整理结果
aPP aEE aWW
• 系数
aE
• 比混合格式复杂,计算量增加,但准确性 提高
• 稳定性:若用中心差分格式不能体现对流 项的物理本质,常会引起数值解的振荡
• 经济性:若用高阶格式,无数值振荡,但 格式复杂,求解相对困难,机时消耗较多
5.2 一维稳态对流扩散问题
d (u)
dx
d dx
d
dx
5.2.1 模型方程的精确解
d (u)
dx
d dx
d
dx
边界条件:
x 0, 0;x L, L
采用迎风思想:从来流上游方向找依赖区
在界面e上,若 ue 0,则e P ;若 ue 0,则e E ; 在界面w上,若 uw 0,则w W ;若 uw 0,则w P
界面流量
• 引入符号 • 对流:
a1, a2 max(a1, a2 )
(u)e Fee P Fe,0 E Fe,0 , (u)w Fww W Fw,0 P Fw,0
• 控制方程变为: dJ 0; 或 J const dx
J
F
0
0 L
exp(Pe) 1
界面上通量
Jw
Fw
W
W P
exp(Pw )
1Hale Waihona Puke JeFeP
P
exp(
E
Pe )
1
Fe exp( exp(Pe
Pe )
) 1
Fw exp(Pw )
1 P
Fe exp(Pe )
1E
Fw exp(Pw exp(Pw )
) 1
W
合并整理结果
aPP aEE aWW
• 系数
aE
《对流扩散方程》课件
环境科学
描述污染物在大气、水体等环境 介质中的扩散、输移和归宿。
在环境科学中,对流扩散方程用 于模拟污染物在大气、水体等环 境介质中的扩散、输移和归宿过
程。
在环境保护、污染治理等领域, 对流扩散方程具有重要的应用价
值。
化学反应动力学
描述化学反应在流体或固定床 反应器中的传递和反应过程。
在化学反应动力学中,对流 扩散方程用于模拟化学反应 在流体或固定床反应器中的
初始条件
指定在求解开始时刻的解的性质,如 常数、函数等。
03 对流扩散方程的应用
流体动力学
01
描述流体在运动状态下的物质传递和扩散现象。
02
在流体动力学中,对流扩散方程用于模拟流体中的物质传递过
程,如温度、浓度、速度等。
在航空航天、船舶、汽车等领域的流体动力学分析中,对流扩
03
散方程被广泛应用。
应用于多尺度问题
研究对流扩散方程在多尺度问题中的应用,如 微纳尺度流动、大气污染扩散等。
探索新的应用领域
将该方程应用于其他领域,如生物医学、环境科学等。
与其他领域的交叉研究
与流体动力学结合
研究对流扩散方程与流体动力学之间的相互 作用和影响,探索更深入的物理机制。
与偏微分方程理论的交叉
将对流扩散方程的研究与偏微分方程理论相 结合,推动数学理论的发展。
02
03
有限体积法
将连续的求解域离散化为有限个小的 体积,在每个体积上近似函数,将微 分方程转化为代方程进行求解。
有限差分法
向前差分法
将微分方程中的导数项用前一步的函数值近似代替,得到向前差 分方程。
向后差分法
将微分方程中的导数项用后一步的函数值近似代替,得到向后差 分方程。
扩散(课件)PPT幻灯片课件
q Q - T
At
x
J dG D(c)
Adt
x
热通量——是单位时间,单位面 积传递的热量。
扩散通量——单位时间内通过单位横截面的粒
子数。用J表示,为矢量。
19
扩散具有方向性,且是各个方向的,故J 用矢量表示:
J iJ x jJ y kJ z D(i c j c k c )
有关,令c kP ,而且通常在金属膜两测
的气体压力容易测出。因此上述扩散过程 可方便地用通过金属膜的气体量F表示:
F
JxA
Dk(P2 l
P1) A
31
(二)不稳态扩散
非稳态扩散,求解菲克第二定律方程,可得c(x,t), 偏微分方程的解只能根据所讨论的初始条件和边 界条件而定,过程的条件不同,方程的解也不同。 一般情况下,D为常数时,解符合以下两种形式: (1)若扩散路程相对初始不均匀性的尺度来说 是短小的,则浓度分布作为路程和时间的函数, 可用误差函数很简单的表示出来。所谓短时解。 (2)扩散接近于完全均匀时,c(x,t)可用无穷三 角级数的第一项表示。所谓长时解。
即菲克第二定律。
26
菲克第一定律和菲克第二定律本质相同,均表明扩散的 结果是使不均匀达到均匀,非平衡逐渐达到平衡。
J D(c) x
C t
D
2C x 2
27
2.2.3 扩散方程的应用
对于扩散的实际问题,一般要求算出 穿过某一曲面(如平面、柱面、球面等)的 通量J,单位时间通过该面的物质量 dm/dt=AJ,以及浓度分布c(x,t),为此需要 分别求解菲克第一定律及菲克第二定律。
15
讨论:
根据迁移所需要的能量,在以上各种 扩散中: 1.易位扩散所需的活化能最大。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2 得到如下差分格式:
6
u n1 j
u
n j
a
u
n j 1
u
n j 1
2h
(
2
a
2)u
n j 1
2u
n j
h2
u
n j 1
稳 定 性 分 析 完 全 类 似 于中 心 差 分 格 式 , 显 然 有
h2
1(a )2
2h
1 2
7
4.3: 迎风差分格式
在 中心 显 式差 分 格式 的稳 定性 条 件中 , 当G
为了简单方便,设a>0,先对方程作扰动,得到另外一对流
扩散方程
u t
a u x
1
1 R
2u x 2
其中R 1 ha
2
对上面的方程构造迎风格式
12
u n1 j
u
n j
a
u
n j
u
n j 1
h
1
1 R
un j 1
2u
n j
h2
u
n j 1
称为逼近对流扩散方程的Samarskii格式.
n j
u n1 j
不 变 ,很 小 时 ,只 能 取 得 很 小 , 格 式 显得 不合适,当 0(极限情况)时,微分方 程
化 为对 流 方程 , 中 心显式 格式 转 化为 绝 对不
稳 定的 , 故 考虑 迎 风格式 :
u
n1 j
u
n j
a
u
n j
u
n j 1
h
u
n j 1
2u
n j
h2
u
n j 1
(a 0)
即:unj 1 (r )unj1 (1 r 2)unj unj1 ,(a 0)
u
n j
un j 1
2u
n j
h2
u
n j 1
n j
a
u
n j
u
n j 1
h
( 1 1 R
1)
un j 1
2u
n j
h2
u
n j 1
13
由Taylor公式可以得到
n j
(
u t
)
n j
(
2u x 2
)
n j
O(
h2 )
n j
a(
u x
)
n j
R 1
2
R
(
2u x 2
)
n j
O(h2 )
于是截断误差有 O( h2) 类似迎风格式的稳定性分析,可以得到
4:对流扩散方程
对流扩散方程的初值问题:
u t
a
u x
2u x 2
u( x,0) f ( x)
x , t 0
x , 0
1
4.1、中心显式差分格式
u n1 j
u
n j
a
un j 1
un j 1
un j 1
2u
n j
u
n j 1
2h
h2
其 截 断 误 差 为 :E O( h2 ), 而 且 当 0时 ,
un j 1
2h
(
ah
)
u
n j 1
2h
2u
n j
h2
u
n j 1
取
v
v
ah
,则变为中心格式,于是
2
2 a2
v, (1)
v
h2
1 , (2) 2
通过简单的推导,可以发现第一个稳定条件可以由第2个 条件推出,于是迎风格式的稳定条件就是(2).
11
4.4:Samarskii格式
Samarskii格式是具有迎风效应的关于空间的二阶格式,
将r1, r2代入,即得条件:
2
a2
,
h2 2
此两不等式为中心显式格式稳定的条件。
4
4.2: 修正中心差分格式
中
心
显格式的
截
断 误 差为
:
2
2u t 2
h2
4u x 4
假设对流 扩散方程的解充分光滑 ,对方程两 边
同 时 对t求 导 有 :
2u t 2
2
4u x 4
2a
3u x 3
a2
2u x 2
unj1 )
(u
n j1
2unj
u
n j 1
)
增长因子为:
G (r, ) 1 2(1 coswh) ir sin wh
G(r, ) 2 r2 sin2 wh 1 4 2 (1 cos wh)2 4r(1 cos wh)
1 (1 cos wh) 4 4 2 (1 cos wh) r2 (1 cos wh)
于 是 方程 的 截 断 误差 可以 改 写为 :
(
2
2
4u x 4
2a
3u x 3
a2
x2 u2 )
h2
4u x 4
2
a2
2u x 2
(
2
2
4u x 4
2a
x3 u3 )
h2
4u x 4
5
由此有当不趋近于0时,差分格式与下面的方程相容:
u t
a
u x
(
2
a
2) 2u x2
然 而 在 数 值 计 算 的 时 候是 一 不 为0的 固 定 常 数 ,
格 式 为 近 似 对 流 方 程 的无 条 件 不 稳 定 格 式 ; 当
a 0时 , 格 式 是 近 似 扩 散 方程 的 古 典 显 式 格 式 ,
只 有ar 1 时 , 格 式 才 稳 定 。 2
下面讨论稳定性:
设r a h , h2 ,格式改写成:
2
unj 1
u
n j
1 2
r ( u nj 1
8
其增长因子
G 1 (r 2)(1 cosh) ir sinh
G 2 r 2 sin2 h (1 (r 2)(1 cos h))2
1 (1 cos h) 2(r 2) 2r 2 (r 2 (r 2)2 )(1 cos h)
类 似 的 迎 风 格 式 稳 定 的充 要 条 件 是G 1, 相 当 于 要求:
于 是 导 致 了 扩 散 效 应 的损 失 , 特 别 在 a2 0
2 时 , 中 心 差 分 格 式 相 容对 于 流 方 程 , 而 此 时 中心
格 式 是 绝 对 不 稳 定 的 ,为 了 减 少 扩 散 效 应 的 损失 ,
在 相 应 的 扩 散 项 增 加 扩散 的 系 数 为 a2。 这 样
2(r 2 ) 2r 2 (r 2 (r 2 )2 )(1 cos h) 0
由 于 1 cos h 0,2, 条 件 化 为 :
2(r 2 ) 2r 2 0和 2(r 2 ) 2r 2 2(r 2 (r 2 )2) 0
9
而 2(r 2) 2r 2 2(r 2 (r 2)2 ) 2(r 2)(1 (r 2)) 0 1 (r 2) 0
只需验证 G 1,由于 1 cos wh 0,条件转化为:
4 4 2 (1 cos wh) r 2 (1 cos wh) 0
即 4 - 2r 2 (4 2 r 2 )(1 cos wh) 0
3
由于 1 cos wh 0,1,上述不等式转化为
2
4 2r 2 0, 4 2r 2 2(r 2 4 2 ) 0
即 r 2 1,此时有r 1,(r 2) r 2自然成立。
所 以 迎 风 格 式 的 稳 定 性条 件 是
h2 2 ah
当a 0时 , 情 况 类 似 , 稳 定 性条 件 是
h2 2 a h
10
也可以j
u
n j
a
un j 1
6
u n1 j
u
n j
a
u
n j 1
u
n j 1
2h
(
2
a
2)u
n j 1
2u
n j
h2
u
n j 1
稳 定 性 分 析 完 全 类 似 于中 心 差 分 格 式 , 显 然 有
h2
1(a )2
2h
1 2
7
4.3: 迎风差分格式
在 中心 显 式差 分 格式 的稳 定性 条 件中 , 当G
为了简单方便,设a>0,先对方程作扰动,得到另外一对流
扩散方程
u t
a u x
1
1 R
2u x 2
其中R 1 ha
2
对上面的方程构造迎风格式
12
u n1 j
u
n j
a
u
n j
u
n j 1
h
1
1 R
un j 1
2u
n j
h2
u
n j 1
称为逼近对流扩散方程的Samarskii格式.
n j
u n1 j
不 变 ,很 小 时 ,只 能 取 得 很 小 , 格 式 显得 不合适,当 0(极限情况)时,微分方 程
化 为对 流 方程 , 中 心显式 格式 转 化为 绝 对不
稳 定的 , 故 考虑 迎 风格式 :
u
n1 j
u
n j
a
u
n j
u
n j 1
h
u
n j 1
2u
n j
h2
u
n j 1
(a 0)
即:unj 1 (r )unj1 (1 r 2)unj unj1 ,(a 0)
u
n j
un j 1
2u
n j
h2
u
n j 1
n j
a
u
n j
u
n j 1
h
( 1 1 R
1)
un j 1
2u
n j
h2
u
n j 1
13
由Taylor公式可以得到
n j
(
u t
)
n j
(
2u x 2
)
n j
O(
h2 )
n j
a(
u x
)
n j
R 1
2
R
(
2u x 2
)
n j
O(h2 )
于是截断误差有 O( h2) 类似迎风格式的稳定性分析,可以得到
4:对流扩散方程
对流扩散方程的初值问题:
u t
a
u x
2u x 2
u( x,0) f ( x)
x , t 0
x , 0
1
4.1、中心显式差分格式
u n1 j
u
n j
a
un j 1
un j 1
un j 1
2u
n j
u
n j 1
2h
h2
其 截 断 误 差 为 :E O( h2 ), 而 且 当 0时 ,
un j 1
2h
(
ah
)
u
n j 1
2h
2u
n j
h2
u
n j 1
取
v
v
ah
,则变为中心格式,于是
2
2 a2
v, (1)
v
h2
1 , (2) 2
通过简单的推导,可以发现第一个稳定条件可以由第2个 条件推出,于是迎风格式的稳定条件就是(2).
11
4.4:Samarskii格式
Samarskii格式是具有迎风效应的关于空间的二阶格式,
将r1, r2代入,即得条件:
2
a2
,
h2 2
此两不等式为中心显式格式稳定的条件。
4
4.2: 修正中心差分格式
中
心
显格式的
截
断 误 差为
:
2
2u t 2
h2
4u x 4
假设对流 扩散方程的解充分光滑 ,对方程两 边
同 时 对t求 导 有 :
2u t 2
2
4u x 4
2a
3u x 3
a2
2u x 2
unj1 )
(u
n j1
2unj
u
n j 1
)
增长因子为:
G (r, ) 1 2(1 coswh) ir sin wh
G(r, ) 2 r2 sin2 wh 1 4 2 (1 cos wh)2 4r(1 cos wh)
1 (1 cos wh) 4 4 2 (1 cos wh) r2 (1 cos wh)
于 是 方程 的 截 断 误差 可以 改 写为 :
(
2
2
4u x 4
2a
3u x 3
a2
x2 u2 )
h2
4u x 4
2
a2
2u x 2
(
2
2
4u x 4
2a
x3 u3 )
h2
4u x 4
5
由此有当不趋近于0时,差分格式与下面的方程相容:
u t
a
u x
(
2
a
2) 2u x2
然 而 在 数 值 计 算 的 时 候是 一 不 为0的 固 定 常 数 ,
格 式 为 近 似 对 流 方 程 的无 条 件 不 稳 定 格 式 ; 当
a 0时 , 格 式 是 近 似 扩 散 方程 的 古 典 显 式 格 式 ,
只 有ar 1 时 , 格 式 才 稳 定 。 2
下面讨论稳定性:
设r a h , h2 ,格式改写成:
2
unj 1
u
n j
1 2
r ( u nj 1
8
其增长因子
G 1 (r 2)(1 cosh) ir sinh
G 2 r 2 sin2 h (1 (r 2)(1 cos h))2
1 (1 cos h) 2(r 2) 2r 2 (r 2 (r 2)2 )(1 cos h)
类 似 的 迎 风 格 式 稳 定 的充 要 条 件 是G 1, 相 当 于 要求:
于 是 导 致 了 扩 散 效 应 的损 失 , 特 别 在 a2 0
2 时 , 中 心 差 分 格 式 相 容对 于 流 方 程 , 而 此 时 中心
格 式 是 绝 对 不 稳 定 的 ,为 了 减 少 扩 散 效 应 的 损失 ,
在 相 应 的 扩 散 项 增 加 扩散 的 系 数 为 a2。 这 样
2(r 2 ) 2r 2 (r 2 (r 2 )2 )(1 cos h) 0
由 于 1 cos h 0,2, 条 件 化 为 :
2(r 2 ) 2r 2 0和 2(r 2 ) 2r 2 2(r 2 (r 2 )2) 0
9
而 2(r 2) 2r 2 2(r 2 (r 2)2 ) 2(r 2)(1 (r 2)) 0 1 (r 2) 0
只需验证 G 1,由于 1 cos wh 0,条件转化为:
4 4 2 (1 cos wh) r 2 (1 cos wh) 0
即 4 - 2r 2 (4 2 r 2 )(1 cos wh) 0
3
由于 1 cos wh 0,1,上述不等式转化为
2
4 2r 2 0, 4 2r 2 2(r 2 4 2 ) 0
即 r 2 1,此时有r 1,(r 2) r 2自然成立。
所 以 迎 风 格 式 的 稳 定 性条 件 是
h2 2 ah
当a 0时 , 情 况 类 似 , 稳 定 性条 件 是
h2 2 a h
10
也可以j
u
n j
a
un j 1
