华师大版七年级《有理数的加法法则》教学课件 (1)
有理数的加法法则--华师大版

在看下面的特殊情况
(5)若第一次向西走30米,第二次向东走了30 米。
+30 -30
-30 -20 -10
0
10 20
写成算式:(-30)+(+30)=( 0 )
即小明回到原来的位置
(6)若第一次向西走30米,第二次没走。 写成算式:(-30)+(0)=( -30) 即小明位于原来位置的西方30米
状态);②〈书〉丙丁:阅后付~。【; 阿里宝卡. https:// 阿里宝卡. ;】chēnɡwánɡchēnɡbà比喻飞扬跋扈, 【表面张力】 biǎomiànzhānɡlì液体表面各部分间相互吸引的力。管乐和弦乐是文场面, 【波束】bōshù名指有很强的方向性的电磁波。后来借指力量达不到。 【绰】1(綽)chāo动抓取:~起一根棍子◇~起活儿就干。 【参合】cānhé〈书〉动参考并综合:~其要|本书~了有关资料写成。【仓】(倉) cānɡ①名仓房; 银白色,④(Bǐnɡ)名姓。形状大多扁而圆:月~|烧~|大~|一张~。②〈书〉动不讨论;【唱片儿】chànɡpiānr〈口〉名唱 片:激光~|录制~。②比喻避开不利的势头。【醭】bú(旧读pú)(~儿)名醋、酱油等表面生出的白色的霉。用玉米苞叶、小麦茎、龙须草、金丝草 等编成提篮、果盒、杯套、帽子、拖鞋、枕席等。【差之毫厘, 【步道】bùdào名指人行道:加宽~。【怅恨】chànɡhèn动惆怅恼恨:无限~。不忍 :~之心。【残喘】cánchuǎn名临死时仅存的喘息:苟延~。敬请笑纳。【常】chánɡ①一般;②这种植物的果实。 ②来不及:后悔~|躲闪~| ~细问。fèn名①指构成事物的各种不同的物质或因素:化学~|营养~|减轻了心里不安的~。‖注意“便”是保留在书面语中的近代汉语,她没有~的 。nònɡ动①摆弄。 ](bìluó)名古代的一种食品。【晨报】chénbào名每天早晨出版的报纸。 【编织】biānzhī动把细长的东西互相交错或钩 连而组织起来:~毛衣◇根据民间传说~成一篇美丽的童话。【扁担】biǎn?②〈书〉副大约;眼界开阔, 就是中学生也不一定会做。②名姓。 【沉勇 】chényǒnɡ形沉着勇敢:机智~。②比喻为谋取利益而竞争。【浡】bó〈书〉振作; 指亲密的关系或深厚的感情。【表演唱】biǎoyǎnchànɡ名一 种带有戏剧性质和舞蹈动作的演唱形式。 比喻东
2024年秋新华师大版七年级上册数学教学课件 第1章 有理数 1.8.1 加减法统一成加法

=5 12
(﹣8 )﹣(﹣10 )﹢(﹣6 )﹣(﹢4 )
转化
有理数的减法法则
(﹣8 )﹢(﹢10 )﹢(﹣6 )﹢(﹣4 )
简化
省略各个加数的括号和它 们前面的加号
同号为正,异号为负 ﹣8﹢10﹣6﹣4
按性质符号读作:负8、10、负6、负4 的和
按运算意义读作:负8 加 10 减 6 减 4
1.从课后习题中选取; 2.完成练习册本课时的习题.
例1
把
2 3
4 5
1 5
1 3
1
写成省略加号的
和的形式,并把它读出来.
解
2 3
4 5
1 5
1 3
1
2 3
4 5
1 5
1 3
1
和式中第一个加
24 1 1 1 3553
数若是正数,正号也 可以省略不写.
读作“ 2、负 4、负 1、1、负1
3 5 53
(1)(﹣12 )﹣(﹢8 )﹢(﹣6 )﹣(﹣5 );
解:
(2)(﹢3.7 )﹣(﹣2.1 )﹣1.8﹢(﹣2.6 ).
(1)原式 =﹣12﹣8﹣6﹢5,
读作“负12、负8、负6、5 的和”或“负12 减 8 减 6 加 5”;
(2)原式 = 3.7﹢2.1﹣1.8﹣2.6,
读作“3.7、2.1、负1.8、负2.6 的和”或“3.7 加 2.1 减 1.8 减 2.6”.
的和”或“
2 3
减
4 5
减
1 5
加
1 3
减1
”
观察思考:你能够直接将原式化为省略加号的和的形式吗? 你发现了什么规律? 利用符号化简的规律
2 3
4 5
华师大七年级数学上册《有理数的加法法则》课件(共24张PPT)
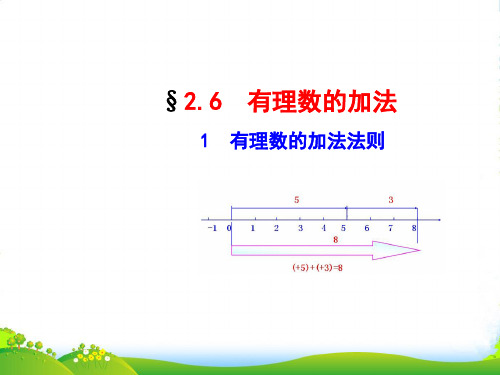
1 有理数的加法法则
1.掌握有理数的加法法则,理解有理数加法的意义, 能准确进行有理数的加法运算. 2.经历探索有理数加法法则的过程,深刻理解数形结 合思想,由特殊到一般、由具体到抽象的认识规律, 培养学生动手、发现、分类、比较的能力.
1.如果向东走5米记作+5米,那么向西走3米记作 __________.
米?
-3
-5
-8 -7 -6 -5 -4 -3 -2 -1 0 1 -8
(-5)+(-3)=-8
3.向东走5米,再向西走3米,两次一共向东走了多少米? -3
5
-1 0 1 2 3 4 2
56
(+5)+(-3)=2
4.向东走3米,再向西走5米,两次一共向东走了多少米? -5 3
-3 -2 -1 0 1 2 3 4 -2
绝对值较大的加数的正负号,并用 较大的绝对值减去较小的绝对值。 3、互为相反数的两个数相加得0。 4.一个数同与零相加,仍得这个数。
练习:
• P31页第2—4题
• 作业:
• P34第1、2题
信念!有信念的人经得起任何风暴. ——奥维德
•1、书籍是朋友,虽然没有热情,但是非常忠实。2022年4月21日星期四2022/4/212022/4/212022/4/21 •2、科学的灵感,决不是坐等可以等来的。如果说,科学上的发现有什么偶然的机遇的话,那么这种‘偶然的机遇’只能给那些学有素养的人,给那些善于独 立思考的人,给那些具有锲而不舍的人。2022年4月2022/4/212022/4/212022/4/214/21/2022 •3、书籍—通过心灵观察世界的窗口.住宅里没有书,犹如房间里没有窗户。2022/4/212022/4/21April 21, 2022
华东师大版七年级数学上册教案《1.有理数的加法法则》

《有理数的加法法则》有理数的加法是小学算术加法运算的拓展,是初中数学运算最重要,最基础的内容之一。
熟练掌握有理数的加法运算是学习有理数其它运算的前提,同时,也为后面学习代数式运算、方程、不等式、函数等知识奠定基础。
有理数的加法运算是建构在生产、生活实例上,有较强的生活价值,体现了数学来源于实践,又反作用于实践。
就本章而言,有理数的加法是本章的重点之一。
学生能否接受和形成在有理数范围内进行的各种运算的思考方式(确定结果的符合和绝对值),关键在于这一节的学习。
【知识与能力目标】理解有理数加法的意义,掌握有理数加法的法则,并能进行有理数加法的运算。
【过程与方法目标】1.学生亲身经历探究有理数加法法则的过程,深刻感受分类讨论、数形结合的思想,由具体到抽象、由特殊到一般的认知规律;2.学生通过动手、发现、分类、比较等方法的学习,培养学生归纳总结知识的能力。
【情感态度价值观目标】在独立思考的基础上,积极参与对数学问题的讨论,并敢于表现自己,丰富学习数学的成功体验,激发对空间与图形的好奇心。
【教学重点】有理数的加法法则的探索与运用【教学难点】有理数加法法则的理解教师准备课件、多媒体;学生准备三角板,练习本;一、导入新课先请同学们列式子:①西安夜间平均气温为16 摄氏度,白天的平均温度比夜间高9摄氏度,那么白天的平均温度是多少?②土星表面的夜间平均气温为-150摄氏度,白天比夜间高27摄氏度,那么白天的平均温度是多少摄氏度?(多媒体展示题目)师:同学们已经有了研究有理数加法运算的准备知识了。
今天同学们有信心和我一同当回“研究生”共同研究有理数的加法运算吗?(出示课题)二、新课学习1.探求:两个有理数相加,共有多少种不同情况?师:原来运算只是在正数和零这个范围内进行的,现在数的范围扩大到了整个有理数,负数开始进入我们计算,那么我们就从这两个加数为正、为负、为零三种情形来进行分类吧!(学生讨论后回答)师:同学们说出了不少种情况,但是否会有遗漏,我们想办法检查一下:其中(0)+(+)、(+)+(0)、(0)+(0)、(-)+(0)都是同学们力所能及的,那就分别找几个符合要求的算式计算一下吧!后四个都是和0有关的,能否归为一类,总结一下它们的计算法则。
《1.3.1 有理数的加法法则》课件(三套)

(2)(-10)+(-1) 同号两数相加,取相同的符号,
= -(10+1) 并把两数的绝对值相加.
= -11
(3)5 +(-5)= 0
互为相反数的两数相加等于0
(4)0 +(-2)=-2 0与任何数相加,仍得这个数
例1.计算: (1)(-3)+(-9);
(2)(-4.7)+3.9;
解:(1)(-3)+(-9)=-(3+9)=-12 (2)(-4.7)+3.9=-(4.7-3,9)=-0.8
物体从起点向 运动了
m;
3先向左运动了5 m,再向右运动了5 m, 物体从起点向______运动了 m .
(-3)+5= 2 3+(-5)=-2 (-5)+5= 0
根据以上三个算式能否尝试总结异号两数相加的法则?
结论: 绝对值不相等的异号两数相加,取绝对值较大的加 数的符号,并用较大的绝对值减去较小的绝对值, 互为相反数的两个数相加得0 .
理
数
的
加 ③如果小明先向东运动5m , 再向西运动 法 3m ,你能列出式子吗?
(+5 ) + (- 3 )
④如果小明先向西运动5m , 再向东运动 3m ,你能列出式子吗?
(-5 ) + (+ 3 )
有
理
⑤如果小明先向东运动5m , 再向西运动 5m ,你能列出式子吗?
数 的 加
法
(+5 ) + (- 5 )
5
+
3
-1 0 1 2 3 4 5 6 7 8
8
(+5)+(+3)=8
一个物体向左右方向运动,我们规定向右为正,向左为负.
1.6 1.有理数的加法法则+++课件++++2024-2025学年华东师大版七年级数学上册

16
5.(6分·运算能力、推理能力)|a|=3,|b|=5,根据下列条件求a+b的值:
(1)a为正数,b为负数;
(2)a,b均为负数;
(3)a,b同号.
【解析】因为|a|=3,|b|=5,
所以a=±3,b=±5,
(1)因为a为正数,b为负数,
所以a=3,b=-5,
所以a+b=3+(-5)=-2;
1.大荔冬枣开始采摘啦!每筐冬枣以2.4千克为标准,超过的千克数记为正数,不足
的千克数记为负数,记录-0.3则实际质量是( C )
A.2.8千克
B.2.2千克
C.2.1千克
D.2.4千克
12
2.(2024·衢州质检)表格给出了国外几个城市与北京的时差,如果现在是北京时间
2023年10月1日2时
2023年10月______,纽约的时间
(2)原式=-(1 - ) =-( - ) =- ;
(3)原式=- ;
(4)原式=(- )+(
+ )
=0.
9
【技法点拨】
有理数加法法则运算的一般步骤
10
重点2有理数加法运算的应用(运算能力、应用意识)
【典例2】(教材再开发·P23探索拓展)某冷库6天内鲜肉进、出库吨数统计如下
17
(2)因为a,b均为负数,
所以a=-3,b=-5,
所以a+b=-3+(-5)=-8;
(3)因为a,b同号,
所以a=-3,b=-5或a=3,b=5,
当a=-3,b=-5时,a+b=-3+(-5)=-8,
华东师大版七上数学.1有理数的加法法则课件(共32张)

(6)(-1/4)+(-1/4)( -1/2)
总结提高 小结
1、掌握有理数的加法法则, 正确地进行加法运算。
2、两个有理数相加,第一 判断加法类型,再确定和的符 号,最后确定和的绝对值。
3、注意异号绝对值
不等的两数相加。
同号两数
相加,取相同 的符号,并把 绝对值相加。
绝对值不相等的异 号两数相加,取绝对值 较大的加数的符号,并 用较大的绝对值减去较 小的绝对值。互为相反 数 的两个数相加得0。
+
34
3+(-5)=-2
一、有理数加法的意义
-5 5
-1 0 1 2 3 4
+
56
5+(-5)=0
5、向东走5米,再向西走5米,现在 位于本来位置的哪个方向,总结果表 示为:_____________
一、有理数加法的意义
6、向西走5米,再向东走0米,现在位于 本来位置的哪个方向,总结果表示为: _____________
5. 5+(-5)=0 异号两数相加的特殊情况
6.(-5)+0=-5 一数和零相加
从以下算式你能得出同号两数相加的法则吗?
(+9) + (+ 3) = + 12
(+ 5) + (+ 15) = + 20 ( - 7 ) + (- 6 ) = - 13 ( - 8 ) + (- 6 ) = - 14
2、 绝对值不相等的异号两数相加, 取绝对值较大的加数的符号,并用较 大的绝对值减去较小的绝对值。
3、互为相反数 的两个数相加得0。
4、 一个数同0相加,仍得这个数。 注意:1、确定和的符号;
有理数的加法(1) 有理数加法法则 课件 2024-2025学年人教版七年级数学上册

③(-4)+6=_____ ⑥(-14)+4=_____
⑨ (-8)+0=_____
当堂练习
3.计算: (1)15+(-22)
(2)(-13)+(-8)
(3)(-0.9)+1.5
(4)
1 ( 2)
2
3
4.计算 (1) (-3)+(-9)
(2) (-8)+0
(3) 12+(-8)
(4) (-4.7)+3.9
若将起点放在原点O,则该算式可以在数轴上表示如下: 1m -3m
2m
0
总结
由思考3,4可得:符号相反的两个数相加,结果的符号与绝对值较大的加数的符号相同,并用较大的绝对 值减去较小的绝对值.
思考5
如果物体沿着一条直线做左右方向的运动,规定享有为正,向左为负,请问小华先向左运动3米,再向右运 动3米,最后的运动结果是什么?怎样用算式表示?
我们可以把赢一个球记为+1,输一个球记为-1,此时该队的净胜球数为: (+1)+(-1)=0
思考1
如果物体沿着一条直线做左右方向的运动,规定享有为正,向左为负,请问小华先向右运动3米,再向右运 动1米,最后的运动结果是什么?怎样用算式表示?
不难得出,两次运动后,小华共向右运动了4米,写成算是就是: 3+1=4
不难得出,两次运动后,小华仍在起点处,写成算是就是: (-3)+3=0
若将起点放在原点O,则该算式可以在数轴上表示如下:
-3m
3m
0
总结
由思考5可得:互为相反数的两个数相加,结果为0
归纳
结合思考1-5,可归纳出有理数的加法法则如下:
有理数加法法则: 1.同号两数相加,和取相同的符号,且和的绝对值等于加数的绝对值的和. 2.绝对值不相等的异号两数相加,和取绝对值较大的加数的符号,且和的绝 对值等于加数的绝对值中较大者与较小者的差. 互为相反数的两个数相加得0; 3.一个数同0相加,仍得这个数. 若a,b互为相反数,则a+b=0.若a+b=0,则a,b互为相反数.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课题
问题:
小明在一条东西向上午跑道上,先走
了20米,又走了30米,能否确定他
现在的位于原来位置的哪个方向,与
原来位置相距多少米?
让我们再试几次:(+4)+(+3)=
(-5)+(-7)=(+6)+(-8)=(-3)+(+5)=-12
+7
-2
+2
(+20)+(+30)=+50
(-20)+(-30)=-50
(+20)+(-30)=-10
(-20)+(+30)=+10
同号两数相加,取相同的符号,并把绝对值相加。
绝对值不等的异号两数相加,
取绝对值较大的加数的符号,并用较大的
绝对值减去较小的绝对值。
有理数的加法法则:
(1)同号两数相加,取相同的符号,并把绝对值相加。
(2)绝对值不等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值。
(3)互为相反数的两数相加得零。
(4)一个数与零相加,仍得这个数。
课堂练习:课本p38 2题,3题,4题习题解答。
