数字信号处理chap9_第1讲
《数字信号处理基础》ppt课件信号分析与处理(bilingual).ppt

discrete- time signal 数值,而在其他时间没有定义。
信号按性质 分
确定性信号:用明确的数字关系来描述的信号。
determinative signal
随机信号: 不能精确地用明确的数字关系来描述。
random signal
系统(systems):互相之间有联系,有作用,共同完成目标的各 部分组合。(处理信号的设备或物理器件的集合。如:滤波 器filter、频谱仪spectrum meter等)
返回
小
结(CHAPTER SUMMARY)
1.an analog signal is defined at every point in time and may take any amplitude. A digital signal is defined only at sampling instants and may take only a finite number of amplitudes.
数字系统(digital system)优于模拟系统(analog system):
1)模拟系统是由元器件搭建而成的电路,元器件制造误差大, 会受温度影响,从而改变电路性能(circuit’s behavior)。
2)数字系统主要取决于软件(software),性能不受以上因素影
响。比模拟系统有更好的抗噪声性能;体积小、功耗低
零阶保持信号:zero order hold signal 平滑:smooth
采样周期:sampling period 频率分量:frequency elements
图像处理:image processing 传感器:sensor
电压:voltage
电流:current
数字信号处理ppt课件

三.自相关函数与 自协方差函数的性质
24
性质1 :相关函数与协方差函数的关系
Cxx m rxx m mx 2
Cxy m rxy m m*xmy
当 mx 0
Cxx m rxx m Cxy m rxy m
25
性质2:均方值、方差与相关函数和协方差函数
rxx
0
E
xn
2
Cxx 0 rxx 0 mx 2
五、功率谱密度
44
维纳——辛钦定理
1. 复频域
rxx
(m)
1
2
j
c Sxx (z)zm1dz,
Sxx
(z)
m
rxx
(m)z
m
C (Rx , Rx )
45
2. 频域
{ rxx(m)
1
2
Pxx (e j )e jm d
2
Pxx (e j ) rxx (m)e jm
m
46
3.性质
实平稳随机信号 rxx m rxx m
rxx m E x x n1 n1m
x1x2 p x1 , x2 ; m dx1dx2
18
自协方差函数
Cxx (m) E (xn1 mx )*(xn2 mx ) E (xn1 mx )*(xn1m mx )
rxx m mx 2
19
对于均值为零的随机过程 rxx m Cxx m
①偶函数
Pxx e j Pxx e j
②实函数
Pxx e j Pxx e j
③极点互为倒数出现
Sxx
z
Sxx
1 z
47
④功率谱在单位圆上的积分等于平均功率
E
x2
Chap9(系统初始化)

数据初始化
算法代码
• 与第二种方法不同的是:变量初值集中放在 一个数据段里,然后在初始化程序中把初值 表里的数据copy到相应的变量地址。 • 所谓拷贝法,就是将变量的初值-即初始化 数据单独存放在一个初始化数据段内(ROM)。 程序复位后,一段初始化程序将初始化数据 段内的变量初值拷贝到相应变量地址。 • 这种方法简省程序存储空间,也是C程序进 行初始化的方法。推荐使用。
算法代码
19
• 与拷贝法原理完全一样,不同点: • 编译器自动生成变量初值段 (.cinit) • 初始化程序由boot.c自动完成
20
C编译器产生的默认段
.cinit .const .text .bss .stack .sysmem .far 变量初值表 常量 代码 全局变量和静态变量 堆栈空间 用于存储器分配函数 Far变量
13
第一步:常量定义
伪指令.int,.short, .byte
14
第二步:变量定义
用于定义用户的未初始化数据段 回顾本讲第4页左右,用.sect声明变量是不妥的。
15
汇编器产生的三个默认段
汇编代码-ROM
数据常量-ROM 数据变量-RAM
变量也可以定义在默认段.bss内 .bss var, 2
-在应用程序前插入数据初始化程序段
m x b y
.sect "myData" .short 10 .short 5 .short 2 .short 0
MVK m, A0 MVKH m, A0 STH 10, *A0 . . .
缺点: 每个数据的初始化要用 三条指令,占用很大程序空间
7
人工初始化法原理
C H A P T E R
chap9(1)

25
高分子催化剂(Polymer Catalyst) 定义:由高分子母体 和催化基团A构成,基团不参加
反应,只起催化作用:
-A + 低分子反应物 —→ -A + 产物
制备措施: 化学结正当:将具有催化作用旳基团以化学结合形式接到 高分子上。 吸附法:利用正、负离子旳吸附作用,将催化基团吸附在 高分子载体上。 内包藏法:反应基团包在高分子载体内。
措施:将功能基团接到高分子母体上,作为化学试剂用。
24
高分子药物(Polymer Drug):
属高分子试 剂旳范围
高分子药物是将药物共价结合或络合在聚合物 上,或将带有药效基团旳单体聚合,就成了高分子药 物。在生物体内,基团经过体液水解或酶解,产生药 效,具有长期有效和副作用小旳优点。
缓释放或控制释放药剂:
变化,链构象亦变化,基团旳反应性会发生明显旳变化。
7
3)化学原因对基团活性旳影响
几率效应(Probability Effect)
高分子链上旳相邻基团进行无规成对反应时,中间 往往留有孤立基团,最高转化率受到几率旳限制,称为 几率效应。例PVC与Zn粉共热脱氯,按几率计算只能达 到86. 5%,与试验成果相符。
14
聚氯乙烯(PVC)旳氯化
PVC旳氯化能够水作介质在悬浮状态下50℃进 行,亚甲基氢被取代。
~~CH2C|H~~ + Cl2 Cl
~~CHCH~~ + HCl || Cl Cl
PVC是通用塑料,但其热变形温度低(约 80℃)。经氯化,使氯含量从原来旳56.8%提升到 62~68%,耐热性可提升10~40℃,溶解性能、耐候、 耐腐蚀、阻燃等性能也相应改善,所以CPVC可用 于热水管、涂料、化工设备等方面。
离散时间信号处理(英文版)chap9-第1讲

01
02
03
Discrete-time systems are mathematical models that describe the behavior of systems in which the input and output signals are functions of discrete time variables.
Periodic signals repeat at regular intervals, while aperiodic signals have no repeating pattern.
Classification of discrete-time signals
延时符
03
Operation of discrete-time signals
延时符
Contents
目录
Basic concepts of discrete-time systems Stability analysis of discrete-time systems
延时符
01signal processing is a branch of signal processing that deals with signals that vary over discrete time instants rather than continuously. It finds applications in various fields such as digital communication, audio processing, image processing, and more.
Background Introduction
Chap9-Oscillation
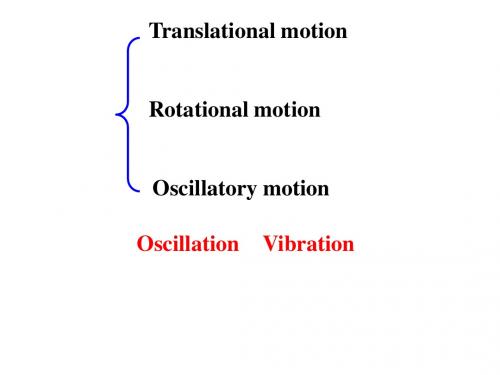
k Assuming: = ω 2 m
d x 2 +ω x = 0 2 dt
2
The dynamical equation of SHM简谐振动动力学方程
Solve the equation, we have:
x = C1 sin ωt + C 2 cos ωt
Generally:
x = A cos (ωt + φ )
x = A cos (ωt + φ )
Integral constant A: the maximum value of the position of the vibration in either the positive or negative x direction.
Amplitude: A
a. The motion of a pendulum单摆
b. The vibration of a stringed musical instrument
c. The molecules oscillating about their equilibrium positions
d. The electromagnetic waves
T=
2π
ω
m T= = 2π ω k
2π
k ω= m
1 1 f = = T 2π
k m
The period and the frequency depend only on the mass of the particle and the force constant. The period and the frequency depend only on the natural quantity of the system.
第九节矩阵位移法
(2 =1)
0
6EI l2 2EI l
0
6EI
l2 4EI
l
e
…(9-4)
F e k ee
…(9-5)
即为一般单元的刚度方程。其中 k e 称为局部坐标系中的单
元刚度矩阵。
2、一般单元刚度矩阵的性质
(1)单元刚度系数的意义
单元刚度矩阵中的每个元素称为单元刚度系数 kij ,其物理
意义表示由于单位杆端位移引起的杆端力。
( v1e
v2e
)
Fye1
6EI l2
(1e
2e )
12EI l3
( v1e
v2e )
Fye2
6EI l2
(1e
e 2
)
12 l
EI
3
( v1e
v2e
)
Fx1 M1
1
v1
Fy1
u1
…(9-2)
e
1
M2
Fx2
2 Fy2
v2
u2
2
式(9-1) 、(9-2)即为局部坐标系下平面刚架一般单元的单元刚度方
ke T Tk eT
F e kee
即为单元e在整体坐标中的单元刚度方程 其中 k e为整体坐标系的单元刚度矩阵,和 k e 同阶,且具有类似的性质。
§9-4 结构的整体刚度矩阵
作用在结构上的荷载与结构的结点位移, 也存在一一对应的关系,即为结构的整体刚 度方程。结构的整体刚度方程反映了结点荷 载和结构位移之间的关系,其实质就是位移 法的基本方程。求解方法一种是传统位移法, 另一种是直接刚度法。
l
Fxe1
EA l
u1e
EA l
u2e
chap9知识的学习
概念的结 构与分类 概念的获 得和运用
(略)
概念的学习
概念的获得实质上就是要理解一类事物共同的关键属性 概念同化就是利用学习者认知结构中原有的概念,以定义的方式直接给学习者提示概念的关键特征,从而使学习者获得概念的方式 奥苏贝尔把概念的同化分成了上位学习、下位学习和组合学习三种基本形式。 学习的方式 概念网络的形成 概念获得 学习方式 概念形成→规则-例子-规则 同 化→例子-规则-例子 概念关系图策略
隐性知念 命题和命题网络 知识的表征 ——指知
识在头脑中的标识形式 和组织结构
表象 图式 产生式 ——程序性知
识特有的表征方式
知识建构的基本机制
知识的学习可以分为知识的生成与 理解、知识的整合与深化、知识的 应用与迁移三个阶段。所有阶段的 知识学习都是双向建构的过程
Freekaoyan-紫此一家整理
Chap9 知识的学习
迁移及其分类
分类:内容领域、方向(顺向迁移&逆向迁移) 、效果(正迁移&负迁移) 、范围(特殊迁移&非特殊迁移) 、程度(近迁移&远迁移) 、 意识水平(即根据迁移的自动化程度分,高通路~&低通路~) 形式训练说 相同元素说——桑代克 早期 主张迁移要经过一个“形式训练的过程才能产生。认为通过一定的许梿,可以使心的各 种官能得到发展,从而转移到其他学习上去 只有在原先的学习情境与新的学习情境有相同要素时,原先的学习才有可能迁移到新的 学习中去,且迁移程度取决于相同要素的多寡 认为在经验中学到的原理原则是迁移发生的主要原因。 “水中打靶实验” 。根据迁移的概 概括化理论——贾德 括化理论,对原理了解概括得越好,对信情境中学习的迁移越好。但原则的概括有着较 大的年龄差异,年幼的学生要形成原则的概括就不容易。 三维迁移模型——奥斯古德 一般迁移与特殊迁移的新争论 专家-新手解决问题的研究 现代 元认知与迁移 基于空间假说的迁移理论 详见戴书 p289 这一争论归结起来还是一般能力与特殊能力、一般迁移与特殊迁移两者关系之争 两者解决新问题的共同特点是:把新问题划归某一特定问题类型;在头脑中形成有关问 题的直观表征;利用自己熟知的解决问题的线路解决 元认知是对认知过程和认知策略的认识;具有元认知能力的学习者能自动地掌握、控制 和监控自己的认知过程 强调两个方面:问题空间和解决问题的程序或技能
chap9[1]
第九章对外长期投资第一节对外投资的特点与原则对外投资对降低企业的经营风险,提高企业的收益具有重要的意义。
一、对外投资的目的 企业对外投资就是将资金投放于企业外部以分得投资收益。
企业对外投资主要出于以下目的。
(一)优化资源配置,提高资产利用效率 (二)优化投资组合,降低经营风险 (三)稳定与客户的关系,扩大市场占有率 (四)提高资产的流动性,增强企业的偿债能力 二、对外投资的特点 (一)对外投资的对象多样化,决策程序比较复杂 (二)对外投资的收益与风险差别较大 (三)对外投资的变现能力差别较大 (四)对外投资回收的时间和方式差别较大 三、对外投资的原则 (一)效益性原则 企业在进行对外投资时,必须考虑到该项投资的经济效益,以及对企业整体经济效益的影响。
(二)安全性原则 企业必须在投资报酬和风险之间权衡利弊。
所谓安全性原则就是投资能够按期收回本金和应得的投资收益。
(三)流动性原则 有的对外投资期限很长,一般不考虑在近期变现;有的对外投资,只是为了充分利用现有的闲置资金,这种投资就应当考虑其流动性,以便在将来需要现金时,能够及时变现。
(四)整体性原则 企业的对外投资活动是企业整体经营活动的一个重要组成部分,对外投资必须服从企业的整体经营活动,对外投资的目标应与企业总的经营目标相一致。
第二节对外直接投资 对外直接投资就是企业根据投资协议以货币资金、实物资产、无形资产对其他企业进行直接投资,以取得投资收益或者实现对被投资企业控股的目的。
对外直接投资是企业的一种重要的投资方式,它通常是一种长期的战略性投资,具有投资期限较长、耗资多、不经常发生、变现力较差等 特点。
一、对外直接投资应考虑的因素 (一)企业当前的财务状况 企业当前的财务状况是制约企业对外投资的一项重要因素。
(二)企业整体的经营目标 企业的对外投资必须服从企业整体的经营目标,对外投资的目标应与企业的整体经营目标相一致,或者有利于实现企业的整体经营目标。
数字信号处理课件第1章
例
[x,n]=stepseq(0,-3,4); stem(n,x)
0.8
0.7
0.6 0.5 0.4 0.3
0.2
0.1 0 -3 -2 -1 0 1 2 3 4
12
3. 矩形序列RN(n)
1, 0 n N 1 RN (n) = 0, 其它n
( 1.2.8)
上式中N称为矩形序列的长度。当N=4时,R4(n)的波 形如图所示。矩形序列可用单位阶跃序列表示,如下 式: RN(n)=u(n)-u(n-N ) (1.2.9)
2
各种各样的信号
a)声音波形; b)气温 c)地震波; d)金属表面粗糙度;
3
图像信号的表达
4
1.2
时域离散信号
对模拟信号xa(t)进行等间隔采样,采样间隔为T,得到
xa(t)
t=nT
= xa(nT),
(1.2.1)
这里n取整数。对于不同的n值, xa(nT)是一个有序的数 字序列:… xa(-T)、 xa(0)、 xa(T)…,该数字序列就是 时域离散信号。为简化,采样间隔可以不写,写成x(n) 信号,x(n)可以称为序列。对于具体信号,x(n)也代表 第n个序列值。这里n取整数,非整数时无定义,即
第1章 时域离散信号和时域离散系统
1.1 引言 1.2 时域离散信号 1.3 时域离散系统 1.4 时域离散系统的输入输出描述 法——线性常系数差分方程 1.5 模拟信号数字处理方法
1
1.1 引言
信号通常是一个自变量或几个自变量的函数。如果仅有 一个自变量,则称为一维信号;如果有两个以上的自变 量,则称为多维信号,如图像。 本门课程仅研究一维数字信号处理的理论与技术。关于 信号的自变量,有多种形式,可以是时间、距离、温 度、电压等,本课一般地把信号看作时间的函数,又称 序列。 本章作为本门课的基础,主要学习时域离散信号的表示 方法和典型信号、线性时不变系统的因果性和稳定性, 以及系统的输入输出描述法,线性常系数差分方程的解 法。最后介绍模拟信号数字处理方法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(ii) periodicity in n and k :
k ( n + rN ) ( k + rN ) n kn WN = WN = WN
(iii) 可约性:
mnk /m WNnk = WmN , WNnk = WNnk /m
k 2k W = W ( N/2 N )
X 3 [0]
X1[0]
X[0]
X 3 [1]
0 X 4 [0] WN
X1[1]
X[1]
X[2]
X [3]
X1[2]
X1[3]
0 X2[0] WN
x4 [1] = x1[3] = x[6]
x5 [0] = x2 [0] = x[1]
2 X 4 [1] WN
X 5 [0] X 5 [1]
N −1
+ j (Re{ x[ n ]} ⋅ Im{W Nnk } + Im{ x[ n ]} ⋅ Re{W Nnk })]
Complex Mul Complex Add Real Mul Real Add
one X[k] N-point DFT
N
N2
N-1 N(N-1)
4N
4N 2
2N+2(N-1) = 4N-2
当 N = 2v 时,共有 v = log2 N 级蝶形;每级都由N/2个蝶形运算组 成,每个蝶形有1次复乘、2次复加,因此每级运算需N/2次复乘 和N次复加。 v级运算总共需要 (N / 2)log2 N 复乘和 N log2 N 复加。
Comparison of the computation of DFT and DIT-FFT
(N =2v)
(i) The DIT-FFT N complex mul: log 2 N
Let
x[n]: 0 ≤ n ≤ N − 1, N = 2v
—— radix-2 FFT (i) Decompose x[n] into two sequences according n is even or odd ( N → N / 2)
⎧ x[2r ] = x1[r ] ⎨ ⎩ x[2r + 1] = x2 [r ] N r = 0,1,", − 1 2
0 N /2 − j (2π / N ) N /2 − jπ W = 1, W = e = e = −1, (iv) N N
( k + N / 2) k WN = −WN
FFT算法的基本思路
z
kn 利用 WN 的周期性、对称性、可约性,使DFT运 算中某些项合并
z
将长序列的DFT分解为若干短序列的DFT Decimation-In-Time FFT (DIT-FFT) Decimation-In-Frequency FFT (DIF-FFT)
A N-point DFT is decomposed into two N/2-point DFTs Butterfly Computation:
X1[k ]
X 2[k ]
k WN
X 1[k ] + WNk X 2 [k ]
−1
X 1[k ] − WNk X 2 [k ]
one complex multiplication + two complex addition
X 3 [0] = x3 [0] + W20 x3 [1] = x[0] + W20 x[4] = x [0] + W N0 x [4] X 3 [1] = x3 [0] + W21 x3 [1] = x[0] + W21 x[4] = x [0] − W N0 x [4]
0 ⎧ X 4 [0] = x[2] + WN x[6] ⎨ 0 X = x − W [1] [2] N x[6] ⎩ 4 0 ⎧ X 5 [0] = x[1] + WN x[5] ⎨ 0 X = x − W [1] [1] N x[5] ⎩ 5 0 ⎧ X 6 [0] = x[3] + WN x[7] ⎨ 0 X = x − W [1] [3] N x[7] ⎩ 6
X [4] X [5]
X [6] X [7]
1 X2[1] WN
2 X2[2] WN
3 X2[3] WN
Computation = two N/2-point DFTs + N/2 butterflies
complex mul: complex add:
N N N ⎞ N 2 ×⎛ + 1 × = + ⎜ ⎟ 2 ⎝ 2 ⎠ 2 2 2 ⎛ N ⎞⎛ N ⎞ ⎛N⎞ N 2 × ⎜ ⎟⎜ − 1⎟ +2 × ⎜ ⎟ = ⎝ 2 ⎠⎝ 2 ⎠ 2 ⎝2⎠
butterfly
So, the 8-point DIT-FFT:
x[0]
X [0]
0 WN 0 WN
0 WN
x[4]
X [1]
X [2]
x[2]
x[6]
2 WN
0 WN
X [3]
X [4]
X [5] X [6] X [7]
x[1]
x[5]
0 WN
1 WN
0 WN
x[3]
x[7]
0 WN
2 WN
3 WN
(iii) Further decomposition until 2-point DFTs are left e. g. N = 8 = 2 3
X3[k ] =
N / 4−1 1
∑
l =0
lk lk x3[l ]WN = x [ l ] W ∑ 3 N / 4 , k = 0,1 /4 l =0
2r +1) k
k 2rk 2rk = ∑x1[r] WN +WN x [ r ] W ∑2 N r =0 r =0
k rk = ∑ x1[r ]WNrk + W x [ r ] W N N∑ 2 2 2 r =0 r =0
= X 1[ k ] + WNk X 2 [ k ],
0 ≤ k ≤ N / 2 −1
z
For this reason, we are interested in computational procedures that reduce the number of multiplications and additions.
Approaches to reduce the computation of DFT by kn using the Properties of WN (i) complex conjugate symmetry:
2 WN
Computation of DIT-FFT
x[0]
X [0]
0 WN 0 WN 0 WN
x[4]
X [1]
X [2]
X [3]
0 WN
x[2]
x[6]
2 WN
x[1]
x[5]
0 WN 0 WN
0 WN
X [4] X [5]
X [6]
1 WN
x[3]
2 WN
3 WN
x[7]
2 WN
X [7]
9.0 Introduction
The Fast Fourier Transform (FFT) is not a new algorithm which is different from the DFT, but an efficient algorithm for fast computation of the DFT.
x3[0] = x1[0] = x[0]
x3[1] = x1[2] = x[4]
x4 [0] = x1[1] = x[2]
X 3 [0]
X 3 [1]
0 ≤ k ≤ N / 4 −1
X1[0]
X1[1]
0 X 4 [0] WN /2
X1[2]
X1[3]
x4 [1] = x1[3] = x[6]
1 X 4 [1] WN /2
Then,
nk X [k ] = ∑ x[n]WN = n =0
N −1 2
N −1
n even
N −1 2
∑
nk nk x[n] WN + ∑ x[n]WN n odd
N −1 2 N −1 2
( 2rk = ∑x[2r] WN + ∑x[2r +1] WN
r =0 r =0
N −1 2 N −1 2
2
2
计算量减少大约一半
(ii) The 2nd decomposition: N → N
2 4
⎧ x1[2l ] = x3[l ] ⎨ ⎩ x1[2l + 1] = x4 [l ]
N l = 0,1,", − 1 4
⎧ X 1[ k ] = X 3 [ k ] + W Nk / 2 X 4 [ k ] ⎨ k N + = − X [ k ] X [ k ] W N / 2 X 4 [k ] 3 ⎩ 1 4
Similarly,
⎧ x2 [2l ] = x5[l ] ⎨ ⎩ x2 [2l + 1] = x6 [l ] N l = 0,1,", − 1 4
⎧ X 2 [ k ] = X 5 [ k ] + W Nk / 2 X 6 [ k ] ⎨ k N + = − X [ k ] X [ k ] W N / 2 X 6 [k ] 5 ⎩ 2 4
9.3. Decimation-In-Time FFT algorithms
