围棋记录纸19路
围棋入门教程

围棋入门教程围棋是一种非常古老而精彩的棋类游戏,它源于中国,已经流传了几千年的历史。
围棋的规则相对简单,但是却有着无限的变化和策略。
下面是一个简明入门教程,帮助你快速入门围棋。
1. 棋盘和棋子:围棋的棋盘是一个19×19的方格,简称为19路棋盘。
棋子有黑白两色,分别放在棋盘上的交叉点上。
2. 下棋的目标:围棋的目标是以自己的棋子将更多的地盘,也就是棋盘上的交叉点围起来。
围住的地盘越多,就越有可能获胜。
3. 开局:围棋的开局是从空棋盘开始的。
黑棋先手,每次轮流在空棋盘上的任意一个交叉点上下棋。
棋子放下后,就不能再移动,也不能移动已经下过的棋子。
4. 气:棋子在棋盘上的交叉点上所拥有的空位叫做“气”。
一个棋子至少要有一个气,才能保持存活状态。
没有气的棋子会被对方吃掉,同时失去了控制地盘的能力。
5. 攻与守:围棋中的战略分为进攻和防守两种。
进攻是为了封堵对方的棋子,限制对方的发展空间;防守是为了保护自己的棋子,增加自己的气。
6. 活和死:一个或多个棋子被对方围起来,并没有足够的气了,就会被认定为死掉。
一个或多个棋子拥有足够的气,又可以进一步发展,就会被认定为活着。
7. 眼:眼是围棋中非常重要的概念。
眼是指一个或多个交叉点形成的空位,周围都是自己的棋子,对方无法进入。
一个棋子围成两个眼,就是安全的。
8. 结算:当双方都认为没有更好的着棋点了,或者协商一致结束时,游戏进入结算阶段。
此时,双方清点地盘上各自的领地,然后根据领地多少进行得分。
围棋是一种非常复杂而有趣的棋类游戏,在这500字的教程中,只能涉及到一些基本的规则和概念。
要真正掌握围棋,还需要大量的练习和实战经验。
希望这篇入门教程对你有所帮助,开始你的围棋之旅吧!。
地势均衡:围棋盘为什么是19路的?

地势均衡:围棋盘为什么是19路的?众所周知,围棋的棋盘是19路乘19路的,一共有361个交叉点。
可为什么是19这个数字呢?为什么棋盘的每条边是19条线,而不是17或21呢?大家往往能看到各种传说式的解释,比如围棋最早是古人研究天文的工具,棋盘上的361个点,代表着从天元代表的“一”演化出的360天。
这听起来固然很有道理,但其实从考古发掘出的古代棋盘来看,上古的棋盘曾经是15路以及17路的,19路棋盘的形成应该是公元后的事情,和上古一毛钱关系也没有。
其实,围棋盘之所以会从15路变成17路,又变成19路,是因为人们在下棋的过程中逐渐发现,19路棋盘的“地势均衡”比17路和15路更佳,更有利于围棋的发展。
那么,什么是“地势均衡”呢?我们得从围棋的基础规则说起。
图1. 一个终局的局面:标ⅹ的点是黑棋围住的地盘,标o的点是白棋围住的地盘围棋最基本的规则是“棋子气尽则亡”,但最终判断胜负的标准,却是看黑白哪方围住的地盘(也就是空)更大。
而根据气和吃子的基础规则,一块棋要想保证存活,至少要做出两只真眼。
所以,围住一块空并且守到终局,必须满足两个条件:1. 我方围住的空足够自己做出两只真眼;2. 敌方无法在我方的空里做出两只真眼。
如此说来,我们围空的大小要把握分寸。
不能太小,否则自身可能不活;也不能太大,否则别人进来一做活就没了。
那么,到底应该怎么围呢?围棋中指导如何围空的理论,最重要的两条就是“金角银边草肚皮”和“三四线理论”。
“金角银边草肚皮”,是指在角上围空效率最高,边次之,中腹(肚皮)最差。
所以角的价值最高,边其次,中腹最低。
图2. 分别在角上、边上和中腹做出两只真眼的黑棋图2是分别在角上、边上和中腹做活的最简便方式。
可以看出,想要在角上做活,用6个子就可以了;而想要在边上做活,至少需要8个子;在中腹做活最麻烦,起码需要10个子。
当然,在实际下棋的时候,我们不需要一上来就做眼,但也需要围住一块虚空,也就是“眼位”,就是保证自己有一块可以在将来做活的处女地。
围棋棋谱文字详解

围棋棋谱文字详解一、棋谱基本知识围棋棋谱是记录围棋棋局的工具,通常以黑白符号表示双方棋子在棋盘上的布局。
棋谱记录方式有多种,但最常用的是19×19的围棋棋盘,采用坐标系来定位棋子。
每个黑子用数字1表示,白子用数字2表示。
棋谱一般以数字和字母组合的方式记录每一手的落子位置、提子情况以及双方选手的交换情况。
二、棋子走法规则围棋的基本走法包括提子、交换、打劫和终局。
提子是指当双方任何一个子在棋盘上没有气(或称活子)时,会被对方提掉。
交换是指双方可以在规定时间内互换棋子,但只能换一颗。
打劫是指双方在可重复的情况下进行同样的局面,重新开始对局。
终局是指双方无法继续进行交换或打劫,判断胜负。
三、常用定式介绍定式是指在围棋开局阶段,双方在角部按照一定顺序摆放棋子的方法。
常用定式有星定式、小目定式、三三定式等。
这些定式都有各自的优缺点,根据不同局面选择合适的定式是围棋手必须掌握的技巧之一。
四、攻防策略技巧围棋中的攻防策略是决定胜负的关键之一。
在进攻时,要尽可能保持棋局的主动权,控制全局;在防守时,要尽可能保持棋局的平衡,不要出现漏洞。
一些常见的攻防策略技巧包括“飞”、“跳”、“镇”、“扭”等。
五、对杀与劫争处理对杀是指双方在同一条直线或斜线上紧挨着放置棋子,形成对杀局面。
劫争是指双方在对杀过程中轮流提子的情况。
正确处理对杀与劫争是围棋手必须掌握的技巧之一。
在对杀时,要尽可能减少对方的气数,增加自己的气数;在劫争时,要尽可能扩大劫材的数量和质量。
六、形势判断与决策形势判断是指围棋手根据棋局情况,对双方形势进行分析和评估,制定出合理的决策。
正确判断形势是围棋手必须掌握的技巧之一。
在判断形势时,要考虑双方提子的数量和质量、局面的主动权和平衡性等因素。
根据形势判断的结果,制定出合理的决策,包括选择合适的定式、攻防策略等。
七、棋局形势分析棋局形势分析是指对整个棋局进行全面、深入的分析和评估,找出双方的优劣势所在。
少儿围棋入门教程讲解

少儿围棋入门教程讲解围棋艺术,千变万化,具有经久不衰的魅力,这是它流传几千年至今受到人们喜爱的原因。
下面是有少儿围棋入门教程讲解,欢迎参阅。
少儿围棋入门教程讲解棋盘、棋子、计时钟。
在正规比赛中,这三样是不可缺少的,但一般的对局只需棋盘和棋子。
围棋棋盘:形状为正方形或略呈长方形的平面图,现在的棋盘为平面上画横竖各十九条平行线,构成三百六十一个交叉点。
为了便于判定棋盘上各点的位置,采用座标法进行编号,横线自上而下用汉字依次编为第一……十九路,竖线从左至右用阿拉伯数字编第1……19路。
记录、说明或教学的时候均以先竖后横的次序为准。
例如:图一中的A点:5.十路交叉点;B点:10.十一路……等等。
需要说明的是,在一般的棋盘上和正式比赛中的棋盘上都没有数字标记,图一中的数字只是在棋谱中为便于说明着子点或为方便易查而标明的。
棋盘上可分为九个部分,分别称为:左上角、左下角、右上角、右下角、上边、下边、左边、右边和中腹(见图二)。
棋盘上共有九个黑点称作“星”,棋心的黑点称作“天元”,“天元”并没有其他特殊意义。
棋盘上的九个部分只是大致的划分,并没有严格的界限,在这里只作笼统的说明。
棋子下在星位上或天元上与棋的内容和规则都没有直接关系。
“星座”与“天元”只是棋盘的标位。
棋盘的每条边线叫做第一线(或一路),紧靠第一线的那条线叫第二线,再向中腹移动依次称为第三线(三路)第四线(四路)等等。
一般简易的棋盘可用硬纸或塑料制成,但比赛用的正规棋盘都是木料制品。
围棋的棋子:围棋的棋子分黑白两种颜色,形状为圆形。
正式比赛的棋子黑方一百八十一枚,白方一百八十枚。
围棋的棋盘交叉点三百六十一处,两色的棋子相加应该等于这个数字。
棋盘与棋子的关系最为密切,这个问题较为复杂,在这里首先明确概念,以后再作说明。
一般用的棋子其数量并没有非常精确的数字规定,各色棋子一百六十枚到一百七十枚左右即够用,多点少点关系不大。
少儿围棋教学,对很多教棋者来说都是一个难题。
围棋棋盘多少条线

围棋棋盘多少条线围棋,是一种源远流长的策略游戏,也是中国文化瑰宝之一。
在围棋盘上,黑白两方玩家通过交替落子来争夺地盘,最终以占据更多领地的一方获胜。
而围棋棋盘上的线数,被认为是围棋的独特之处之一。
在一个标准的围棋棋盘上,也就是19×19的大小,究竟有多少条线呢?这是一个有趣的问题,同时也是一个数学问题。
首先,我们可以通过简单的计数来确定围棋棋盘上的线数。
在一个19×19的棋盘上,我们可以将其划分为横线和竖线两部分。
横线的数量为18条,因为我们需要从上方第二行开始数,到下方第19行结束。
同理,竖线的数量也为18条。
此外,我们还有斜线,也就是棋盘上的对角线。
围棋棋盘上的对角线可分为两类:主对角线和副对角线。
主对角线的数量为37条,因为棋盘上从左上角到右下角的对角线有19条,而从右上角到左下角的对角线也有18条,并且两者不重复。
副对角线的数量也为37条,方式与主对角线相似。
所以,主对角线和副对角线总共为74条。
综上所述,围棋棋盘上的总线数为:横线18条 + 竖线18条 + 主对角线37条 + 副对角线37条 = 110条。
然而,如果我们仅仅按照上述方法计算出的线数,我们并没有考虑到棋盘上的其他线条。
在围棋中,还有一种特殊情况,就是连接的线段。
连接一条线段需要两个交叉点,而一个棋盘格子上有四个交叉点(即四边),所以一个格子可以连接4条线段。
在19×19的围棋棋盘上,有361个格子,所以连接线段数为:361格子× 4线段 = 1444条线段。
然而,我们不能只计算连接线段的数量,还需要考虑连接线段与其他线条交叉的情况。
在一个标准的围棋棋盘上,每个交叉点都会与横线、竖线、主对角线和副对角线相交。
所以,每个交叉点会把横线、竖线、主对角线和副对角线分别分成两段。
另外,由于两条线相交会形成交叉点,所以每个交叉点还会形成一条新的线。
因此,每个交叉点会产生2段横线、2段竖线、2段主对角线、2段副对角线和1条新线。
围棋
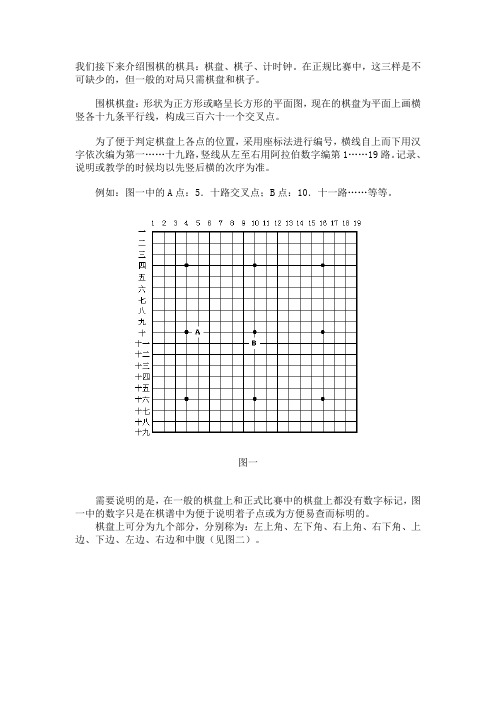
我们接下来介绍围棋的棋具:棋盘、棋子、计时钟。
在正规比赛中,这三样是不可缺少的,但一般的对局只需棋盘和棋子。
围棋棋盘:形状为正方形或略呈长方形的平面图,现在的棋盘为平面上画横竖各十九条平行线,构成三百六十一个交叉点。
为了便于判定棋盘上各点的位置,采用座标法进行编号,横线自上而下用汉字依次编为第一……十九路,竖线从左至右用阿拉伯数字编第1……19路。
记录、说明或教学的时候均以先竖后横的次序为准。
例如:图一中的A点:5.十路交叉点;B点:10.十一路……等等。
图一需要说明的是,在一般的棋盘上和正式比赛中的棋盘上都没有数字标记,图一中的数字只是在棋谱中为便于说明着子点或为方便易查而标明的。
棋盘上可分为九个部分,分别称为:左上角、左下角、右上角、右下角、上边、下边、左边、右边和中腹(见图二)。
图二棋盘上共有九个黑点称作“星”,棋心的黑点称作“天元”,“天元”并没有其他特殊意义。
棋盘上的九个部分只是大致的划分,并没有严格的界限,在这里只作笼统的说明。
棋子下在星位上或天元上与棋的内容和规则都没有直接关系。
“星座”与“天元”只是棋盘的标位。
棋盘的每条边线叫做第一线(或一路),紧靠第一线的那条线叫第二线,再向中腹移动依次称为第三线(三路)第四线(四路)等等。
一般简易的棋盘可用硬纸或塑料制成,但比赛用的正规棋盘都是木料制品。
围棋的棋子:围棋的棋子分黑白两种颜色,形状为圆形。
正式比赛的棋子黑方一百八十一枚,白方一百八十枚。
围棋的棋盘交叉点三百六十一处,两色的棋子相加应该等于这个数字。
棋盘与棋子的关系最为密切,这个问题较为复杂,在这里首先明确概念,以后再作说明。
一般用的棋子其数量并没有非常精确的数字规定,各色棋子一百六十枚到一百七十枚左右即够用,多点少点关系不大。
第二课行棋规则与胜负计算围棋的基本规则规定:对局者一方执黑子先行(让子棋除外),另一方执白子,双方轮流交替下一子到棋盘的交叉点上(已有棋子的交叉点不能下子,禁着点不能下子),棋子下定后不允许再挪动位置。
第5单元两位数乘两位数_笔算乘法例2_围棋的棋盘面由纵横各19道线交叉组成。

笔算两位数乘两位数的方法:
1、先用第二个因数个位上的数字去乘第 一个因数,积的末位要与个位对齐。
2、再用第二个因数十位上的数字去乘第 一个因数,积的末位要与十位对齐。
3、最后将两次乘得的积相加。
人教版三年级下册第5单元
棋盘上一共有多 少个交叉点?
围棋的棋盘面由纵横19道线交叉而成。
19 × 1 89
171 19
361
请你填一填:
21 ×1 4
84 21 294
32 ×3 4
128 96 108 8
93 ×21
93 1 86
1 95 3
「做一做」
23×34 54×13 17×28 39×27
34×41
22×74
44×59
15×21
53×27
86×13
19
×1 9
8
1 71 190 361
19×9的积
19×10的积 171+190的和
棋盘上一共有多 少个交叉点?
围棋的棋盘面由纵横19道线交叉而成。
19×19= 361(个)
答:棋盘上一共有361个交叉点。
围棋棋诀第一句就提到“棋之盘, 方十九,三百六十一叉点”。
21 × 24
84 42
504
19×19=
战国初期,有个叫弈实孩子特别聪明, 六岁,已经会计算棋盘的总交叉点数, 同学们,弈实六岁时就已经会计算棋盘
的总交叉点数,那大家会计算吗?
19×19=
想一想: 你是怎么计算的?
19×9=171 19×10=190 171+190=36
1
19≈20 19×19≈400
19×20=80 380-19=361
第十三讲棋盘中的数学(四)——棋盘格的计数问题

第十三讲棋盘中的数学(四)——棋盘格的计数问题与棋盘有关的另一大类数学问题是计数问题.我们只能就一些简单的例题进行解说,并随之介绍解题的思想方法.例1 如下左图,在中国象棋盘上,乙方一只边卒已经过河,它可以向前移一步到B,也可以横行一步到A,要使这个小卒沿最短路线走到对方帅所在的位置(假定前进路上没任何阻难),问有多少种不同的走法?解:为了解这个问题,可以从简单的情形开始,逐步进行.上右图中,小卒沿最短路线走到A、B、C、D、E、F、G、H的走法都只有一种,走到K,则有两种:先走到A再走到K,或者先走到B,再走到K.走到M,则有1+2=3种:先走到C再到M有一种,先走到K再到M有2种(因为走到K有2种走法).把走法的种数标在各点上,每个数等于它前面的两个数(下图中左方一个,下方一个)的和.走到帅的位置有70种不走法.说明:利用标数法可以很快求出从一个点到棋盘上另一点最短的不同路线数,这是一种很直观有用的计数方法.例2 围棋盘上横竖各有19条线(如下图),在棋盘上组成许多大小不同的正方形,问其中有多少个和图中右侧小正方形大小一样的正方形(小正解法1:我们把小正方形放在大正方形的左上角,则小正方形的右边线与大正方形的第10条竖线重合.将小正方形向右平行移动一格(如下图)则又可出现一个小正方形,顺次向右移动9次后,小正方形的右边线与大正方形的右边线重合.这样前后共得到10个小正方形.同样,将左上角小正方形再每次向下移动一格,也可得到10个小正方形.所以共有10×10=100个小正方形.解法2:将大正方形左上角的小正方形沿大正方形的对角线AC移动,第1次移动(如下图)可视为是右移一格和下移一格的合成,也可视为是下移一格和右移一格的合成.再加上初始位置的小正方形,这时就有1+3个小正方形.继续将小正方形沿对角线移动,共移动9次,小正方形就移动到大正方形的右下角.这时共包含小正方形(1+3+5…+19)个,我们可解法3:我们先在下右图小正方形中找一个代表点,例如右下角的代表点E,然后将小正方形按题意放在围棋盘上,仔细观察点E应在什么地方,通过观察,不难发现:①点E只能在棋盘右下角的正方形ABCD(包括边界)的格子点上.②反过来,右下角正方形ABCD中的每一个格子点都可以作为小正方形的点E,也只能作为一个小正方形的点E.这样一来,就将“小正方形的个数”化为“正方形ABCD中的格子点个数”了,很容易看出正方形ABCD中的格子点为10×10=100个.说明:以上三种解法都有一定代表性.其中解法3既巧妙又迅速,它利用了“一一对应就一样多”的配对原理.配对原理在计数中是非常重要的.例3 从8×8的方格棋盘(下图)中取出一个由三个小方格组成的“L”形(可旋转),问有多少种不同的取法?分析如果从2×2的方格中取“L”形,则有4种不同的取法,因此,我们只要知道从8×8的方格棋盘上总共可以取出多少个“田”字形就可以了,又由于每个“田”字形的中心点是棋盘内横线与竖线的交叉点(但不包括边界上的点),反过来每一个这样的交叉点都有一个以它为中心的“田”字形,于是问题就转化为求横线与竖线一共有多少个不在边界上的交叉点.解:设S是从棋盘上所能取出的所有“田”字形组成的集合,S′是棋盘内所有横线和竖线的交叉点(不包括边界上的点)组成的集合.由于每个“田”字形的中心点是棋盘内横线与竖线的一个交叉点且不在边界上,反过来,位于棋盘内横线与竖线交叉点四周的四个小方格恰好组成一个“田”字形,因此集合S与S′的元素能一一配对.由配对原理,这两个集合的元素一样多.而棋盘内横线与竖线的交叉点有:(9-2)×(9-2)=49(个).所以棋盘上可以取出“田”字形的个数为49个.又由于从一个“田”字形中可以取出4个“L”形,并且,从不同的“田”字形中取出的“L”形是不同的,所以可知,从棋盘上共可以取出49×4=196个“L”形,即题中“L”形的不同取法共196种.例4 如下图在5×5棋盘格中,共有多少个正方形?解:在5×5的棋盘格中包含 1×1的正方形共25个;包含 2×2的正方形共16个;包含3×3的正方形共9个;包含4×4的正方形共4个;包含5×5的正方形共1个;总计包含各种正方形共有:25+16+9+4+1=55个.说明:本题解法是先将正方形分成五类:1×1,2×2,3×3,4×4,5×5,对每一类都仿例3中第3种解法去解是非常迅速的.例5 下图中的正方形被分成9个相同的小正方形,它们一共有16个顶点(共同的顶点算一个),以其中不在一条直线上的三个点为顶点,可以构成三角形,在这些三角形中,与阴影三角形有同样大小面积的有多少个?分析解决这个问题,主要是运用两个结论:①同底等高的两个三角形的面积相等.②平行的两条直线间的距离处处相等.解:设原正方形的边长是3,则小正方形的边长是1,阴影三角形的面积是:所求的三角形可分两种情形:①三角形的一边长为2,这边上的高是3.这时,长为2的边只能在原正方形的边上.这样的三角形有:2×4×4=32(个).②三角形的一边长为3,这边上的高是2.这时,长为3的边是原正方形的一边或平行于一边的分割线(其中,与①重复的三角形不再算入).这样的三角形有:8×2=16(个).答:所求的三角形共48个(包括上页图中给出的三角形).说明:解本题,容易出现两种错误,一是“少”,如忽略了底是3,高是2的三角形,这样就少算了16个;二是“多”:在计算底是3,高是2的三角形时,没有考虑其中有16个在情形①中已经计算过了,于是会得出错误结果64个.棋盘格计数问题,本质上是一种数数问题.其一要注意会把对象分类.其二,在每类数数时要做到不重,不漏.这样才能得到正确的结果.习题十三1.下图是一个棋盘,将一个白子和一个黑子放在棋盘线交叉点上,但不能在同一条棋盘线上,问:共有多少种不同的放法?2.下图中的象棋盘上一只小卒过河后沿最短的路走到对方“帅”处,试问这小卒有多少种不同的走法?3.下图表示某城市的街道图,若从A走到B(只能由北往南,由西向东),问共有多少种不同的走法?4.下图是一个道路图,A处有一大群孩子,这群孩子向东或向北走,在从A开始的每个路口,都有一半人向北走,另一半人向东走,如果最后有60个孩子到过路口B,问:先后共有多少孩子到过路口C?5.如下图,在5×5的棋盘上放了二十枚棋子,问:以这些棋子为顶点的正方形共有多少个?。
