20世纪天才数学家Galois(伽罗瓦)临死前手稿
数学家伽罗瓦的传奇人生

数学家伽罗瓦的传奇人生伽罗瓦,这个名字在数学界闪耀着独特的光芒。
他的数学成就不仅为后世留下了重要的遗产,更是在他短暂而传奇的一生中,展现了不屈不挠的精神和对知识的追求。
让我们一起走进伽罗瓦的世界,探寻他的传奇人生。
伽罗瓦出生于法国一个中产阶级家庭,从小就展现出非凡的数学天赋。
他的数学才华在学校中得到了老师的赏识,但他的叛逆个性却常常让他陷入麻烦。
伽罗瓦对于学校的教育体系不满,他认为教育应该注重培养学生的创造力和思考能力,而不仅仅是灌输知识。
这种对教育的批判精神也成为他后来数学研究的动力。
伽罗瓦在数学领域的突破主要体现在代数领域。
他提出了伽罗瓦理论,这一理论对于代数方程的解法和群论的发展起到了重要的推动作用。
伽罗瓦理论的核心思想是将代数方程的解与其对应的群联系起来,通过研究群的性质来解决方程的求解问题。
这一理论的提出不仅拓宽了代数学的研究领域,也为后来的数学家提供了重要的工具和思路。
然而,伽罗瓦的数学成就并没有得到当时学术界的认可和赏识。
由于他的叛逆个性和政治立场的问题,他与一些权威数学家产生了矛盾。
这些矛盾最终导致了他的学术生涯的短暂和悲剧。
伽罗瓦在数学界的地位并没有得到应有的肯定,他的研究成果也因为他的早逝而没有得到充分的发展和推广。
然而,伽罗瓦的传奇并不仅仅在于他的数学成就,更在于他的人生态度和精神品质。
尽管他的短暂一生充满了挫折和困苦,但他从不放弃对知识的追求。
他坚信数学是一门纯粹而美丽的学科,他对于数学的热爱和执着让他在困境中找到了力量。
他用自己的短暂人生诠释了一种对于真理和智慧的追求,这种追求超越了个人的得失和荣辱,成为了他一生的信念和追求。
伽罗瓦的传奇人生也给我们带来了一些启示。
他的故事告诉我们,追求知识和真理并不容易,但只有坚持不懈、勇往直前,才能达到更高的境界。
他的故事也告诉我们,不要被外界的评价和困难所束缚,要相信自己的能力和价值,坚持自己的理想和信念。
伽罗瓦的传奇人生是数学界的一段佳话,他的数学成就和精神品质都值得我们学习和敬仰。
伽罗华最悲情的天才数学家

伽罗华:最悲情的天才数学家作者:姚兴航来源:《百科知识》2011年第09期他是一个天才少年,15岁学习数学,短短5年就创造出对后世影响深远的“群论”,带来数学的革命。
他也是一个悲情少年,两次升学未成,三次论文发表被拒,两次被捕入狱,20岁时就因与情敌对决而黯然离世。
他就是法国数学家伽罗华,其惊人才华的背后却是充满坎坷的悲剧人生。
2011年是伽罗华诞辰200周年,当我们再次追忆这段科学史上的传奇时,依然会为其成就赞叹,为其命运唏嘘。
令人惊叹的天才少年伽罗华1811年出生于法国巴黎,1826年,15岁的伽罗华开始选修初级数学的课程,从而使他的数学天赋被彻底激发。
伽罗华很快对数学教科书的内容感到无聊和厌倦,开始自学数学大师的巨著,如勒让德的《几何原理》、拉格朗日的《解析函数》等。
伽罗华有着炉火纯青的心算本领,可以凭借纯粹的心算完成最困难复杂的数学研究。
1828年伽罗华在法国一个专业数学杂志上,发表了他的第一篇论文——《周期连分数一个定理的证明》。
虽然此时的伽罗华还只是一个中学生,但已经能把大数学家的工作向着更完美的方向推进。
也正是这一年,17岁的伽罗华第一次参加升入巴黎综合理工学院的竞赛考试,这所学校被誉为法国科学界的最高学府。
但可能因为准备不足,伽罗华的考试失败了。
这次考试的失败让那些惊叹于他数学天赋的伙伴们感到吃惊。
许多人认为这次失败是一种不公正行为的结果,直至20多年后,这种争论仍未停息。
厄运不断的学术生涯早在1828年,17岁的伽罗华就开始研究方程论,他创造了“置换群”的概念和方法,解决了几百年来使人头痛的高次方程求解问题。
伽罗华最重要的成就,就是提出了“群”的概念,他用群论改变了整个数学的面貌。
1829年5月,伽罗华将其研究的初步结果提交给法国科学院。
负责审查这篇论文的是当时法国数学界的泰斗——柯西。
当时柯西意识到这篇论文的重要性,也曾提及要在科学院的会议上介绍这篇文章,但在随后的科学院会议上柯西并未提及伽罗华的工作。
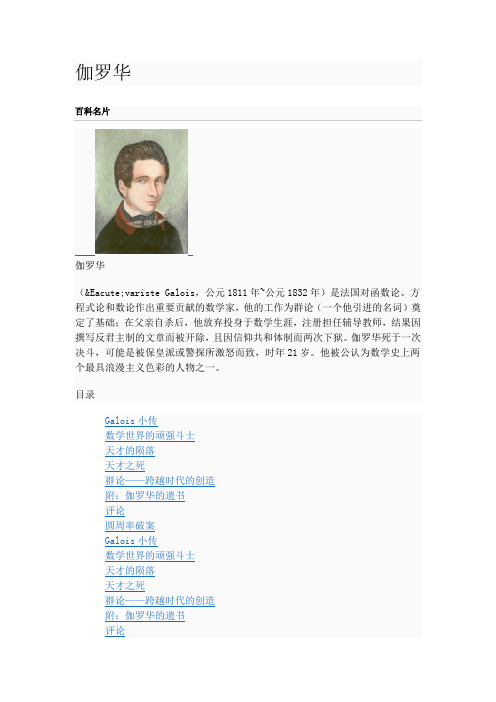
伽罗华

伽罗华(Évariste Galois,公元1811年~公元1832年)是法国对函数论、方程式论和数论作出重要贡献的数学家,他的工作为群论(一个他引进的名词)奠定了基础;所有这些进展都源自他尚在校就读时欲证明五次多项式方程根数解(Solution by Radicals)的不可能性(其实当时已为阿贝尔(Abel)所证明,只不过伽罗华并不知道),和描述任意多项式方程可解性的一般条件的打算。
虽然他已经发表了一些论文,但当他于1829年将论文送交法兰西科学院时,第一次所交论文却被柯西(Cauchy)遗失了,第二次则被傅立叶(Fourier)所遗失;他还与巴黎综合理工大学(école Polytechnique)的口试主考人发生顶撞而被拒绝给予一个职位。
在父亲自杀后,他放弃投身于数学生涯,注册担任辅导教师,结果因撰写反君主制的文章而被开除,且因信仰共和体制而两次下狱。
他第三次送交科学院的论文均被泊松(Poisson)所拒绝。
伽罗华死于一次决斗,可能是被保皇派或警探所激怒而致,时年21岁。
他被公认为数学史上两个最具浪漫主义色彩的人物之一。
Galois小传:1832年5月30日清晨,在巴黎的葛拉塞尔湖附近躺着一个昏迷的年轻人,过路的农民从枪伤判断他是决斗后受了重伤,就把这个不知名的青年抬到医院。
第二天早晨十点,这个可怜的年轻人离开了人世,数学史上最年轻、最富有创造性的头脑停止了思考。
后来的一些著名数学家们说,他的死使数学的发展被推迟了几十年,他就是伽罗华。
天才的童年1811年10月25日,伽罗华出生于法国巴黎郊区拉赖因堡伽罗瓦街的第54号房屋内。
现在这所房屋的正面有一块纪念牌,上面写着:“法国著名数学家埃瓦里斯特•伽罗瓦生于此,卒年20岁,1811~1832年”。
纪念牌是小镇的居民为了对全世界学者迄今公认的、曾有特殊功绩的、卓越的数学家——伽罗瓦表示敬意,于1909年6月设置的。
伽罗瓦的双亲都受过良好的教育。
中外数学家的数学小故事

中外数学家的数学小故事数学是一种理性的精神,使人类的思维得以运用到最完善的程度。
今天小编在这给大家整理了数学小故事大全,接下来随着小编一起来看看吧!数学小故事(一)1933年1月,希特勒一上台,就发布第一号法令,把犹太人比作“恶魔”,叫嚣着要粉碎“恶魔的权利”.不久,哥廷根大学接到命令,要学校辞退所有从事教育工作的纯犹太血统的人.在被驱赶的学者中,有一名妇女叫爱米·诺德(A.E.Noether 1882—1935),她是这所大学的教授,时年5l岁.她主持的讲座被迫停止,就连微薄的薪金也被取消.这位学术上很有造诣的女性,面对困境,却心地坦然,因为她一生都是在逆境中度过的.诺德生长在犹太籍数学教授的家庭里,从小就喜欢数学.1903年,21岁的诺德考进哥廷根大学,在那里,她听了克莱因、希尔伯特、闽可夫斯基等人的课,与数学解下了不解之缘.她学生时代就发表了几篇高质量的论文,25岁便成了世界上屈指可数的女数学博士.诺德在微分不等式、环和理想子群等的研究方面做出了杰出的贡献.但由于当时妇女地位低下,她连讲师都评不上,在大数学家希尔伯特的强烈支持下,诺德才由希尔伯特的“私人讲师”成为哥廷根大学第一名女讲师.接下来,由于她科研成果显着,又是在希尔伯特的推荐下,取得了“编外副教授”的资格,虽然她比起很多“教授”更有实力.诺德热爱数学教育事业,善于启发学生思考.她终生未婚,却有许许多多“孩子”.她与学生交往密切,和蔼可亲,人们亲切地把她周围的学生称为“诺德的孩子们”.我国代数学家曾炯之就是诺德“孩子”们中的一个.在希特勒的淫威下,诺德被迫离开哥廷根大学,去了美国工作.在美国,她同样受到学生们的尊敬和爱戴,同样有她的“孩子们”.1934年9月,美国设立了以诺德命名的博士后奖学金.不幸的是,诺德在美国工作不到两年,便死于外科手术,终年53岁.她的逝世,令很多数学同僚无限悲痛.爱因斯坦在《纽约时报》发表悼文说:“根据现在的权威数学家们的判断,诺德女士是自妇女受高等教育以来最重要的富于创造性数学天才.”数学小故事(二)八岁的高斯发现了数学定理。
伽罗瓦
伽罗华伽罗华(Évariste Galois,公元1811年~公元1832年)是法国对函数论、方程式论和数论作出重要贡献的数学家,他的工作为群论(一个他引进的名词)奠定了基础;在父亲自杀后,他放弃投身于数学生涯,注册担任辅导教师,结果因撰写反君主制的文章而被开除,且因信仰共和体制而两次下狱。
伽罗华死于一次决斗,可能是被保皇派或警探所激怒而致,时年21岁。
他被公认为数学史上两个最具浪漫主义色彩的人物之一。
目录Galois小传1832年5月30日清晨,在巴黎的葛拉塞尔湖附近躺着一个昏迷的年轻人,过路的农民从枪伤判断他是决斗后受了重伤,就把这个不知名的青年抬到医院。
第二天早晨十点,这个可怜的年轻人离开了人世,数学史上最年轻、最富有创造性的头脑停止了思考。
后来的一些著名数学家们说,他的死使数学的发展被推迟了几十年,他就是伽罗华。
少年1811年10月25日,伽罗华出生于法国巴黎郊区拉赖因堡伽罗华街的第54号房屋内。
现在这所房屋的正面有一块纪念牌,上面写着:“法国著名数学家埃瓦里斯特·伽罗华生于此,卒年20岁,1811~1832年”。
纪念牌是小镇的居民为了对全世界学者迄今公认的、曾有特殊功绩的、卓越的数学家——伽罗华表示敬意,于1909年6月设置的。
伽罗华的双亲都受过良好的教育。
在父母的熏陶下,伽罗华童年时代就表现出有才能、认真、热心等良好的品格。
其父尼古拉·加布里埃尔·伽罗华参与政界活动属自由党人,是拿破仑的积极支持者。
主持过供少年就学的学校,任该校校长。
又担任拉赖因堡15年常任市长,深受市民的拥戴。
伽罗华曾向同监的难友勒斯拜——法国著名的政治家、化学家和医生说过:“父亲是他的一切”。
可见父亲的政治态度和当时法国的革命热潮对伽罗华的成长和处事有较大的影响。
伽罗华的母亲玛利亚·阿代累达·伽罗华曾积极参与儿子的启蒙教育。
作为古代文化的热烈爱好者,她把从拉丁和希腊文学中汲取来的英勇典范介绍给她儿子。
数学家事迹1

数学家事迹1转载自喉哥满分网作者ilikesleep GuluckHi,everyone.自己是学数学的,而老爸也已是此行高手了,所以既有资料又难免有些偏爱,:),所以一同收集了一些数学家的事迹,大家看看,或许有用的。
11月考完到现在,对题库中的题目有些生疏了,不好乱说这些资料适用于哪个题目,靠大家自己斟酌了。
一些数学家的事迹。
伽罗华(Galois,1811-1832,法国)1829年5月,他写出了关于代数方程可解判断的论文,1830年2月修改。
由于审稿人去世,手稿竟被遗失。
1831年他再次修改了论文,但仍未得到公正的评价。
1832年他因为爱情之事与别人进行了决斗,在决斗前夕他整理了他的数学手稿,概括了他的主要成果。
他不幸死于决斗。
到1846年,他的部分文章才得以出版。
1870年,若当(Jordan,1838-1922)才全面的介绍了伽罗华的工作和思想。
伽罗华用群论彻底解决了根式求解高次方程的问题,并由此建立了关于群和域的理论--伽罗华理论,从而开辟了抽象代数的研究领域。
French mathematician who made valuable contributions to number theory algebra before being killed in a duel at the age of 21.康托尔(Cantor,1845-1918,法国)集合(set)论的创始者。
他的名言是:数学的本质在于思考的充分自由。
他的思想使得我们有可能研究超越了感觉想象到的高维和无限维的空间,使数学家可以建立起抽象的纯数学和种种特异的数学来,并且还将促使数学永无止境地向前发展。
但是康托尔的一生并不平坦,1884年他患了精神分裂症,并且以后34年间一直影响着他的生活。
他发病的一个重要原因是他的创见和思想不被当时的许多人(其中甚至包括一些数学界的领袖人物)所理解,反而受到了一些功击和不公正对待。
但是康托尔的集合论毕竟给数学这个乐园建立了一个坚实的基础,从而使现代数学成为了一门真正的独立科学。
浪漫的天才数学家伽罗瓦

64
数学通讯 ) 2012 年第 1 期 ( 下半月 )
#课外园地#
人在选举时恶意中伤而自杀. 父亲的冤死, 也导致他 的政治观与人生观的改变 , 思想走向极端. 在几天后 的升学口试中, 主考对伽罗瓦阐述的见解不理解, 并 加以嘲笑 , 失望之中的伽罗瓦被主考的/ 狂笑声所激 怒0 , 愤怒地把黑板擦砸到主考头上 , 结果可想而知 . 尽管他对父亲的去世无比悲痛 , 但他还是/ 沉着 而镇静0 地听从里夏尔的劝告 , 决定进巴黎高等师范 学校 . 这使他有可能继续深造 , 同时生活费用也有了 着落. 1829 年 10 月 25 日, 他被作为预备生 录取入 学. 进入师范学校后的第一年对伽罗瓦来说是最顺 利的一年 . 在这里, 他结识了一生中唯一亲近的朋友 ) ) ) 舍瓦利叶. 在数学大师著作的引领下 , 通过个人的努力, 使 其思想具有独创性和敏锐性, 许多数学难题被伽罗 瓦一个接一个的攻克, 终于登上了大师们建构的数 学高峰. 站在高峰上 , 伽罗瓦不光看到了数学王国里 旖旎的风光, 还发现了一座无人涉足的更高的山峰 , 即怎样判断哪些方程可以用根式求解, 哪些方程不 能用根式求解. 一元一 ( 二) 次方程的求解很早就被发现, 一元 三次方程解的公式( 卡当公式 ) 直到十六世纪初才由 意大利的数学家发现. 在费拉里给出一般的四次方 程解法后, 这就促使数学家们继续努力寻求五次及 以上的高次方程的解法. 这个问题持续了三个多世 纪都没有解决. 拉格朗日更是称这一问题是在/ 向人 类的智慧 挑战0 . 1770 年, 拉 格朗 日精心 分析了 二 次、 三次、 四次方程根式解的结构之后, 提出了方程 的预解式概念, 并且还进一步看出预解式和方程的 各个根在排列置换下的形式不变性 , 这时他认识到 求解一般五次方程的代数方法可能不存在. 此后, 挪 威数学家阿贝尔给出了高于四次的一般代数方程不 存在代数解的证明. 伽罗瓦从拉格朗日那里继承了问题转 化的思 想, 即把预解式的构成同置换群联系起来; 又改进拉 格朗日的思想, 即设法绕过拉氏预解式 , 并在阿贝尔 研究的基础上( 不可能用加、 减、 乘、 除、 开方运算和
盘点历史上英早逝的数学家

盘点历史上英早逝的数学家历史上有很多数学家,他们为数学的发展做出了许多巨大的贡献,在数学的舞台上绽放光芒,但是其中一部分数学家,来不及看到自己研究结果被肯定,就匆匆与这个世界告别。
实在令人遗憾。
今天来盘点一下历史上英年早逝的数学家们。
埃瓦里斯特·伽罗瓦伽罗瓦,1811年10月25日生,法国数学家。
现代数学中的分支学科群论的创立者。
用群论彻底解决了根式求解代数方程的问题,而且由此发展了一整套关于群和域的理论,人们称之为伽罗瓦群和伽罗瓦理论。
在世时在数学上研究成果的重要意义没被人们所认识,曾呈送科学院3篇学术论文,均被退回或遗失。
后转向政治,支持共和党,曾两次被捕。
21岁时死于一次决斗。
1830年七月革命发生,保皇势力出亡,高等师范校长将学生锁在高墙内,引起伽罗瓦强烈不满,12月伽罗瓦在校报上抨击校长的作法,因此被学校退学。
由于强烈支持共和主义,从1831年5月后,伽罗瓦两度因政治原因下狱,也曾企图自杀。
在监狱中,伽罗瓦仍然顽强地进行数学研究,一面修改他关于方程论的论文及其他数学工作,一面为将要出版的着作撰写序言。
伽罗瓦使用群论的想法去讨论方程式的可解性,整套想法现称为伽罗瓦理论,是当代代数与数论的基本支柱之一。
它直接推论的结果十分丰富:他系统化地阐释了为何五次以上之方程式没有公式解,而四次以下有公式解。
他漂亮地证明高斯的论断:正十七边形可做图。
他解决了古代三大作图问题中的两个:“不能任意三等分角”,“倍立方不可能”。
尼尔斯·亨利克·阿贝尔阿贝尔(1802年8月5日-1829年4月6日),挪威数学家,在很多数学领域做出了开创性的工作。
他最着名的一个结果是首次完整给出了高于四次的一般代数方程没有一般形式的代数解的证明。
这个问题是他那时最着名的未解决问题之一,悬疑达250多年。
他也是椭圆函数领域的开拓者,阿贝尔函数的发现者。
尽管阿贝尔成就极高,却在生前没有得到认可,他的生活非常贫困,死时只有27岁。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
This is a digital copy of a book that was preserved for generations on library shelves before it was carefully scanned by Google as part of a project to make the world’s books discoverable online.
It has survived long enough for the copyright to expire and the book to enter the public domain.A public domain book is one that was never subject to copyright or whose legal copyright term has expired.Whether a book is in the public domain may vary country to country.Public domain books are our gateways to the past,representing a wealth of history,culture and knowledge that’s often difficult to discover.
Marks,notations and other marginalia present in the original volume will appear in thisfile-a reminder of this book’s long journey from the publisher to a library andfinally to you.
Usage guidelines
Google is proud to partner with libraries to digitize public domain materials and make them widely accessible.Public domain books belong to the public and we are merely their custodians.Nevertheless,this work is expensive,so in order to keep providing this resource,we have taken steps to prevent abuse by commercial parties,including placing technical restrictions on automated querying.
We also ask that you:
+Make non-commercial use of thefiles We designed Google Book Search for use by individuals,and we request that you use thesefiles for personal,non-commercial purposes.
+Refrain from automated querying Do not send automated queries of any sort to Google’s system:If you are conducting research on machine translation,optical character recognition or other areas where access to a large amount of text is helpful,please contact us.We encourage the use of public domain materials for these purposes and may be able to help.
+Maintain attribution The Google“watermark”you see on eachfile is essential for informing people about this project and helping themfind additional materials through Google Book Search.Please do not remove it.
+Keep it legal Whatever your use,remember that you are responsible for ensuring that what you are doing is legal.Do not assume that just because we believe a book is in the public domain for users in the United States,that the work is also in the public domain for users in other countries.Whether a book is still in copyright varies from country to country,and we can’t offer guidance on whether any specific use of any specific book is allowed.Please do not assume that a book’s appearance in Google Book Search means it can be used in any manner anywhere in the world.Copyright infringement liability can be quite severe.
About Google Book Search
Google’s mission is to organize the world’s information and to make it universally accessible and useful.Google Book Search helps readers discover the world’s books while helping authors and publishers reach new audiences.You can search through the full text of this book on the web
at /。
