两种新的长方体重力异常正演公式及其理论推导
重力异常
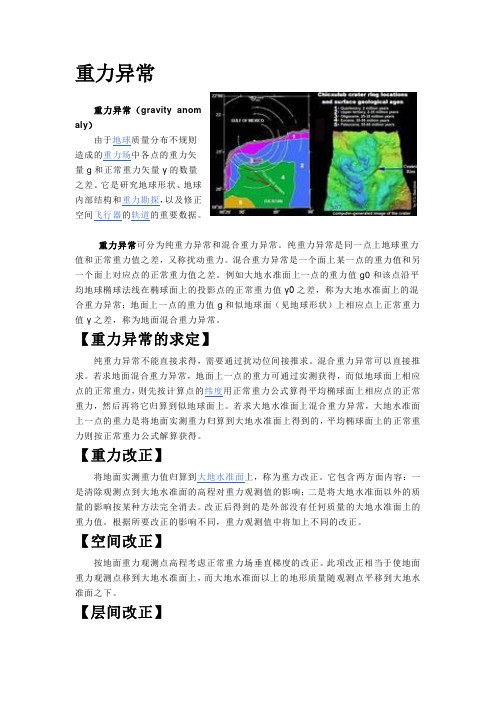
重力异常重力异常(gravity anomaly)由于地球质量分布不规则造成的重力场中各点的重力矢量g和正常重力矢量γ的数量之差。
它是研究地球形状、地球内部结构和重力勘探,以及修正空间飞行器的轨道的重要数据。
重力异常可分为纯重力异常和混合重力异常。
纯重力异常是同一点上地球重力值和正常重力值之差,又称扰动重力。
混合重力异常是一个面上某一点的重力值和另一个面上对应点的正常重力值之差。
例如大地水准面上一点的重力值g0和该点沿平均地球椭球法线在椭球面上的投影点的正常重力值γ0之差,称为大地水准面上的混合重力异常;地面上一点的重力值g和似地球面(见地球形状)上相应点上正常重力值γ之差,称为地面混合重力异常。
【重力异常的求定】纯重力异常不能直接求得,需要通过扰动位间接推求。
混合重力异常可以直接推求。
若求地面混合重力异常,地面上一点的重力可通过实测获得,而似地球面上相应点的正常重力,则先按计算点的纬度用正常重力公式算得平均椭球面上相应点的正常重力,然后再将它归算到似地球面上。
若求大地水准面上混合重力异常,大地水准面上一点的重力是将地面实测重力归算到大地水准面上得到的,平均椭球面上的正常重力则按正常重力公式解算获得。
【重力改正】将地面实测重力值归算到大地水准面上,称为重力改正。
它包含两方面内容:一是清除观测点到大地水准面的高程对重力观测值的影响;二是将大地水准面以外的质量的影响按某种方法完全消去。
改正后得到的是外部没有任何质量的大地水准面上的重力值。
根据所要改正的影响不同,重力观测值中将加上不同的改正。
【空间改正】按地面重力观测点高程考虑正常重力场垂直梯度的改正。
此项改正相当于使地面重力观测点移到大地水准面上,而大地水准面以上的地形质量随观测点平移到大地水准面之下。
【层间改正】消除过观测点的水平面同大地水准面之间的质量层对观测重力的影响而加的改正。
此项改正相当于把高出大地水准面的质量当作一个无限平面厚层全部移掉。
重力异常推断解释的方法

第三节 几种规则形状地质体正反问题的解法
五、无限水平板
(一)、正演公式
(二)、正演公式的两个实际应用
五、无限水平板
(二)、正演公式的两个实际应用
1、求正问题方面的应用 2、求反问题方面的应用
(二)、正演公式的两个实际应用 1、求正问题方面的应用
1) 、内容
2)、图例分析
3) 、实例分析
(二)、正演公式的两个实际应用 1、求正问题方面的应用 1) 、 内容 利用无限水平板重力异常公式能计算已知 闭合度的构造或其它已知顶底高差的任意 地质体可能产生的重力异常的最大值。
5、地质体形状和物性的简化
形状的简化:
把大致规则的地质体认为是规则的地质体, 把复杂的地质体视作若干简单形体的迭加。
物性的简化:
把密度大致均匀的地质体认作密度完全均匀 的地质体。
第四章 重力异常推断解释的方法
第一节 重力异常推断解释的一般方法
第二节 解正问题的基本公式 第三节 几种规则形状地质体正反问题的解法
一、均匀球体 1、 Δg正问题讨论
g max GM
D
2
x1/ n D
3
n 1
2
当M不变,D增大 A倍, Δgmax 减少1/A2倍, X1/n增大A倍。即 Δg 曲线变得越来越平缓。
一、均匀球体 1、 Δg正问题讨论
Δg球在剖面图和平面图上的表现形式:
第三节 几种规则形状地质体正反问题的解法 一、均匀球体 1、解正问题的基本公式 2、 Δg正问题讨论 3、Δg反问题讨论
2、均匀球体Δg反问题讨论 求解反问题是以相应的正问题为基础的 求球心埋深
x1
2
x1/ n D
3
n 1
试验二规则二度体重力异常正演计算

重力正演、反演

2)当σ>o时,极大值一侧对应着上升盘,极小 值一侧对应着下降盘,在极小值十分清晰且大 干极大值的绝对值时,属正断层类型,反之则 属逆断层类型。
二度铅垂柱体 对于沿水平方向延伸较长而横截面近于矩形的 矿脉,可以当成二度铅垂柱体来研究。在正演 它的异常时,坐标系及有关参数的选取见图,用 (x+α)与(x一α)分别代替铅垂台阶各公式中的 x,并将结果相减,即获得这一形体的重力异 常及各阶导数异常的公式:
当柱体的下底 H→+∞ 时,便可获得底部无限延 伸的铅垂脉的相应公式Δg→∞
( x − a) 2 + h 2 V xz = Gσ ln ( x + a) 2 + h 2 h h 2ah V zz = 2Gσ (tg −1 − tg −1 ) = 2Gσtg −1 2 x−a x+a x + h2 − a2 ⎡ ⎤ x+a x−a 2a ( a 2 + h 2 − x 2 ) V zzz = 2Gσ ⎢ = 2Gσ 2 − 2 2 2 2 ⎥ ( x + a) + h ⎦ ( x + a 2 + h 2 ) 2 − 4a 2 x 2 ⎣ ( x + a) + h
GM GMD = 2 2 nD ( x1 / n + D 2 ) 3 / 2
x 1/n = ± D n 2 / 3 − 1
取n=2,得x1/2=0.766D(X正半轴)和x’1/2=-0.766 D (X负半轴),说明异常半极值点的横坐标为球心 深的0.766倍
4、当D不变,使M加大m倍时,异常也同样加大
[( x + a ) 2 + H 2 ][( x − a ) 2 + h 2 ] V xz = Gσ ln [( x + a ) 2 + h 2 ][( x − a ) 2 + H 2 ] H h H h ) − tg −1 − tg −1 + tg −1 V zz = 2Gσ (tg −1 x+a x+a x−a x−a ⎡ ⎤ x+a x+a x−a x−a − + − V zzz = 2Gσ ⎢ ⎥ 2 2 ( x + a) 2 + H 2 ( x − a) 2 + h 2 ( x − a) 2 + H 2 ⎦ ⎣ ( x + a) + h
第八讲 重力异常反演课件

应用重力学第八讲重力异常反演d?解正问题是解反问题的基础,解反问题是目的。
仅从地质角度,解重力反演问题的目标9矿体类问题:寻找、研究或推断金属或非金属矿体;9构造类问题:研究地质构造,包括控矿构造,如含石油、天然气、煤的构造以及区域性的深部构造等。
从地球物理角度,解重力反演问题的目标9矿体类问题:确定地质体的几何和物性参数;9构造类问题:确定物性分界面的深度及起伏;9密度分布问题:确定密度的分布。
一、计算地质模型体的几何及物性参数(一)直接法直接利用由反演目标引起的局部异常,通过某种积分运算和函数关系,求得与异常分布有关地质体的某些参量。
(二)特征点法根据异常曲线上的一些点或特征点(如极大值点、零值点、拐点)的异常值及相应的坐标求取场源体的几何或物性参数;仅适用于剩余密度为常数的几何形体。
异常曲线形态分类第一类是单峰异常,零值点在无穷远处如球体的Δg曲线、台阶的Vxz曲线等;第二类是具有极大值、极小值和一个零值点如球体的Vxz曲线、台阶的Vzz、Vzzz曲线;第三类是具有一个极大值、两个极小值和两个零值点如球体、水平圆柱体的Vzz和Vzzz曲线;第四类是台阶的Δg曲线,一边高一边低的形态应用条件对异常作平滑处理,尽量准确确定原点的位置; 对异常曲线作分离处理,获得单纯由研究对象引起的异常;对剩余(局部)异常进行分类,判明该异常的场源体接近于何种可能的几何形体,然后选用相应的反演公式。
2223/2212()(GMDGMDg x D x D Δ=++)(6524.2/12/1x x ′−)(4811.03/13/1x x ′−)(4056.04/14/1x x ′−{{{ D1/2)nGD πμ=(三)选择法根据异常分布和变化特征,结合地质和其他地球物理和物性等资料,给出初始地质体模型;进行正演计算,将理论异常与实测异常对比; 若两者偏差较大,对模型进行修改,重算其理论异常计算,再次进行对比……;如此反复进行,直至两种异常的偏差达到事前要求的误差范围为止,则这最后的理论模型就可作为所求的解答了。
两种新的长方体重力异常正演公式及其理论推导

+(
z) arctan ( z)R | 2 | 2 | 2 ( x)( y) 1 1 1
g(x, y, z) = G ||| ( x) ln{( y) + R} + ( y) ln{( x) + R}
( z) arctan ( x)( y) | 2 | 2 | 2 ( z)R 1 1 1
g(x, y, z) = G ||| ( x) ln{( y) + R} + ( y) ln{( x) + R}
两种新的长方体重力异常正演公式及其理论推导
骆遥 1, 2
1 中国科学院地质与地球物理研究所,北京(100029) 2 中国科学院研究生院,北京(100049) E-mail:geo@
摘 要: 在前人推导长方体重力场、磁场正演理论表达式工作的基础上,重新对长方体重 力场正演理论表达式进行理论推导,提出了两种全新的长方体重力异常正演公式形式,并给 出了全部的理论推导过程,对比模型正演计算结果表明,新导出长方体重力场正演理论表达 式的正确。 关键词:长方体,重力场,正演,积分 中图分类号:P631
线数据单位为 g.u.
Fig2. The cubic model gravity contour map
5. 结论
综合前人对长方体重力场正演理论表达式的推导过程,并借鉴长方体磁场及其梯度场理 论表达式的推导,推导出了两种新的长方体重力场正演理论表达式(11)式和(13)式,对 比模型正演计算结果表明,新导出长方体重力场正演理论表达式是完全正确的。
似积分的推导[15~17],对 2 的推导有:
2= 2( 1
z)2 ( {(
y) {( x) +
R}2
重力正演计算PPT课件

2021/3/7
CHENLI
6
第二节 规则形状异常密度体的正演问题 第三章 重力异常的正演问题
3.2.1 密度均匀球体(点质量)
在实际工作中,一些近于等轴状的地质体,如矿巢、矿囊、岩株、穹窿构 造等,都可以近似当作球体来计算它们的重力异常。特别当地质体的水平尺寸小 于它的埋藏深度时,效果更好。对于均匀球体来说,它与将其全部剩余质量集中 在球心处的点质量所引起异常完全一样。
2021/3/7
CHENLI
5
第二节 规则形状异常密度体的正演问题 第三章 重力异常的正演问题
➢ 3.2.1 密度均匀球体(点质量) ➢ 3.2.2 密度均匀的水平圆柱体(水平物质线) ➢ 3.2.3 垂直台阶 ➢ 3.2.4 倾斜台阶 ➢ 3.2.5 二度长方体(铅垂柱体) ➢ 3.2.6 倾斜脉 ➢ 3.2.7 铅垂圆柱体 ➢ 3.2.8 直立长方体
3.2.1 密度均匀球体(点质量)
其它转换异常特征:
V xz
2V xz
g x
Dx
GM
[x 2
D
]2
5 2
V zz
2V z2
g z
2D 2 x2
GM
[x 2
D
]2
5 2
V zzz
3V z3
2 g z2
3 GM
2D 2 3x2
[x 2
Dபைடு நூலகம்
]2
7 2
2021/3/7
CHENLI
10
第二节 规则形状异常密度体的正演问题 第三章 重力异常的正演问题
2
mGal or *10g.u.
0.4
0.35
0.3
0.25
0.2
重力异常的计算

重力异常的计算
重力在我们生活中极其重要,它有着它独特的作用。
但是最近,有一个不寻常的现象发生了,而且科学家已经开始认真地研究它了重力异常。
重力异常是一种令人困惑的物理现象,它涉及一种令人难以置信的力量,甚至超出了现代物理学的认识范畴。
它比我们理解的重力更加复杂,更加不可思议,能够改变宇宙的样子。
重力异常的现象是由宇宙中的引力场引起的,它具有更大的吸引力,它可以影响物体的运动,甚至可以改变宇宙的形状。
如果我们发现重力异常,就能更深入地了解宇宙,以及宇宙中的精确规律,这也是科学家们一直在努力追求的。
为了更好地研究重力异常,科学家们通过计算机模拟的方法,建立起一个宏观的模型,来理解宇宙中的重力现象。
计算机可以模拟大量数据,找出和实际宇宙中的状况相似的模型。
另外,科学家还可以利用宇宙观测,从太阳系和星系的数据中,抽取出重力异常的信息,这些数据可以模拟出未来可能发生的重力现象,例如未来宇宙中可能发生的碰撞等。
此外,科学家还可以利用量子物理学的理论,研究重力在宇宙中的作用,以及它与其他种类的作用。
例如,它可以用来解释宇宙中大小两种不同的质量物质的结构,并用来解释它们如何形成和运动等。
通过对重力异常的研究,科学家们将能够更加深入地了解宇宙现象,帮助我们更好地了解宇宙是如何运作的,以及宇宙背后的物理原
理。
它将会加深我们对宇宙的认识,帮助我们更加深刻地了解这个宇宙,也许我们可以更好地把握宇宙未来的发展趋势。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
对长长方体重力场(3)式的积分求解,许多学者都进行了研究[7~12]。最早可能从 1830 年[11]开始,就不断有文献给出长方体重力场(3)式积分解的解析形式,到目前为止长方体 重力场理论表达式归纳起来有下面 4 种基本形式[7~12]:
g(x, y, z) = G ||| ( x) ln{( y) + R} + ( y) ln{( x) + R}
x)2 + ( z)2 + ( x)R}2 ( y)2 ( z)2
d
x)2 + ( z)2 + ( x)R}2
z) 2 d (( 1 1+ (
y)( y)2 (
z) /{( x)2 + ( z)2 + ( x)R}) z)2 /{( x)2 + ( z)2 + ( x)R}2
z) arctan (
( y)( z) x)2 + ( z)2 + (
1. 引 言
在地球物理勘探中,重力异常的正演计算在重磁异常的解释中有着重要的意义,它反映 场源与场分布特征之间的联系,是地质解释的基础。长方体是位场正演计算中最为常用的三 度体模型,可以用平行于直角坐标面的平面对任意形状的三维地质体进行分割,将三维复杂 地质形体重力异常的正演计算转化为一系列长方体体元重力异常的迭加;所以,长方体重力 异常的正演计算是重力勘探中最基本的问题。同时,随着高精度重磁资料处理解释工作的开 展,二维重磁反演已难以满足全方位确定地质构造精细展布的要求,重磁反演逐渐发展到三 维;重磁三维反演分为形态模型反演和物性模型反演,限于形态反演中存在的较大困难,近 年来物性反演成为三维重磁反演中的主要形式[1~6]。重磁三维物性反演中要将地质场源区域 离散化成离散的长方体单元,长方体重力异常的正演计算成为重磁三维物性反演中最为基本 的问题。因此,研究长方体重力异常的正演是一项基础性工作,具有重要的理论和实际意义。
1
11
(12)
按照与前面所述相类似的推过程对(12)式进行积分求解,可以得到 g 的另一种形式:
g(x, y, z) = G ||| ( +(
x) ln{( y) + R} + ( y) ln{(
z) arctan (
( x)( z) y)2 + ( z)2 + (
x) + R} | 2| 2| 2
y)R 1 1 1
(13)
其中, R = ( x)2 + ( y)2 + ( z)2 。其具体的推到过程十分类似不再进行重复。
对比现有的长方体重力场理论表达式(4)~(7)式,可以发现导出的长方体重力场理 论表达式(11)式和(13)式是一种全新的长方体重力场理论表达式形式。表达式(11)式 和(13)式均是长方体的长、宽边分别与 X、Y 坐标轴平行情况先重力场的正演计算公式, 通过坐标的旋转和平移变换[17~18]还可以计算任意倾斜情况下长方体所产生的重力场;因此, 表达式(4)~(7)式、(11)式和(13)式共同构成了长方体重力场正演计算的理论通式。
z) arctan (
( y)( z) x)2 + ( z)2 + (
x) + R} | 2| 2| 2
x)R 1 1 1
(11)
其中, R = ( x)2 + ( y)2 + ( z)2
如果求解(8)式时,先对 进行积分[13],则有
g(x, y, z) = G || 1 ln{( x) + R}d | 2 | 2
V R3 zdv
(2)
其中, R = {( x)2 + ( y)2 + ( z)2}1/2 。
于是,如图 1 所示的均匀密度长方体产生的重力场可以表示为:
g(x, y, z) = G
2 1
2 1
2 1
R3zd d d
(3)
其中 (x, y, z) 为观测点的坐标,( , , ) 为长方体场源点的坐标,其对应的积分限变化范围
+(
z) arctan ( z)R | 2 | 2 | 2 ( x)( y) 1 1 1
g(x, y, z) = G ||| ( x) ln{( y) + R} + ( y) ln{( x) + R}
( z) arctan ( x)( y) | 2 | 2 | 2 ( z)R 1 1 1
g(x, y, z) = G ||| ( x) ln{( y) + R} + ( y) ln{( x) + R}
+2(
z) arctan (
x) + ( y) + R | 2 | 2 | 2
( z)
111
g(x, y, z) = G ||| (x ) ln{( y ) + R} + ( y ) ln{(x ) + R}
(z ) arcsin ( y )2 + (z )2 + ( y )R | 2 | 2 | 2 {( y ) + R} ( y )2 + (z )2 1 1 1
(4) (5) (6) (7)
其中, R = ( x)2 + ( y)2 + ( z)2 。4 种长方体重力场理论表达式中主要不同在于
公式中的最后一项,公式(4)~(6)中最后一项均为反正切项,而公式(7)中最后一项为 反正弦项;值得指出的是公式(4)和(6)实际上是等价的,可以通过
arctan( ) = / 2 arctan(1/ ) 关系来进行证明[11]。
2. 长方体重力异常
位于空间中 P ' 点 ( , , ) 具有密度 的质量单元在 P 点 (x, y, z) 处产生的重力场为:
g =G
z R3
v,
(1)
式中 R 是点 P ' 到 P 的距离, v 质量单元的体积,G 是万有引力常数。通过对体积V 的积
分可得到均匀密度体的重力场:
g(x, y, z) = G
-4-
4. 新长方体重力场表达式模型计算验证
为了检验新导出的长方体重力场正演理论表达式的正确性,对表达式(4)~(6)式、 (11)式和(13)式分别取相同的长方体模型(模型顶面四个顶点在计算平面上的垂直投影 点与计算的网格点重合,并用黑点标出)进行正演计算比较,图 2 中 a、b 分别是应用原表 达式和新表达式正演所获得的长方体重力场等值线图。模型正演计算表明二者正演计算的重 力场数据(精确到六位小数点的情况下)完全一致,这充分说明新推导出的长方体重力场正 演计算理论表达式(11)式和(13)式是正确的。
z
y)} )2}R
d
=
2
1(
( x)2 x)2 + (
z)2 d
2 ( x)2 ( 1 {( x)2 + (
y) z)2
}R
d
=
2 {1
1
(
( z)2 x)2 + (
z)2
}d
2 1
R yd
+
2 ( z)2( 1 {( x)2 + (
y) z)2
}R
d
= ( 2 1) | ( z) arctan
x | 2 |( z1
x) + z)2
R}d
=
2 ( z)2( 1 {( x)2 + (
y) {( z)2 + (
x)2 / R + 2( x)R}2 + (
x) y)2
+ (
R} z
)2
d
-3-
=(
=( = |(
(
z) 2
1
z)( {(
1+ {(
y) {( x)2 / R + 2( x) + R}
为 ( 1 , 2 ) , ( 1 , 2 ) , ( 1 , 2 ) ; R = {( x)2 + ( y)2 + ( z)2}1/2 。
-1-
X
2 1
0 12
Y
1
2
Z
图 1.长方体模型 Fig1. The right rectangular prism model.
线数据单位为 g.u.
Fig2. The cubic model gravity contour map
5. 结论
综合前人对长方体重力场正演理论表达式的推导过程,并借鉴长方体磁场及其梯度场理 论表达式的推导,推导出了两种新的长方体重力场正演理论表达式(11)式和(13)式,对 比模型正演计算结果表明,新导出长方体重力场正演理论表达式是完全正确的。
||| ( x) ln{( y) + R} | 2 | 2 | 2 11 1
|| 2
(
x)2
d | 2| 2
1 {( y) + R}R 1 1
(10)
令
1=
2 ( x)2 d 1 {( y) + R}R
,根据 (
1 y)
+
R
=
(
R( x)2 + (
y) z)2 ,则有[14]:
1=
2( 1 {(
x)2{R ( x)2 + (
3. 新长方体重力场正演公式及其理论推导
长方体重力场 g(x, y, z) = G
2 1
2 1
2 1
R3zd d d
首先对
进行积分[13],有:
g(x, y, z) = G
再对(8)式中 进行积分[13],有:
| 2 2 1d d | 2
R 1
1
1
