第二章热力学性能4
物理化学 第二章-热力学第一定律-4

由于所有反应物及产物完全燃烧后都得到同样种类与数量的 CO2(g),H2O(l)及其它燃烧产物,所以我们可以构造以下循环:
始态 标准态下: 反应物+O2(g) H1
0 r H m
标准态下: 产物+O2(g) H2
末态 标准态下: CO2(g) ,H2O(l) 等燃烧产物
标准态下: 反应物+O2(g) H1
2H2(g)+O2(g) NH2COONH4)(s) C6H6(l)+7.5O2(g)
v
B(g)
-3 3 -1.5
v
B(g)
v
B(g)
§ 2.8 标准摩尔生成焓的计算
标准摩尔反应焓— 在某温度下,各自处在标准态下的反应物,
反应生成同样温度下各自处于标准态下的产物,该过程的摩尔
反应焓即为标准摩尔反应焓。 用公式表示:
标准摩尔反应焓等于HCl(g)的标准摩尔生成焓。
2. 标准摩尔燃烧焓
定义:一定温度下, 化学计量数为-1物质 B 与氧气进行完全燃
烧反应,生成规定燃烧产物时的标准摩尔反应焓变,称为B在该 温度下的标准摩尔燃烧焓。其符号为
c H m
在室温下,有机物的燃烧产物规定:
C 的燃烧产物为CO2(g), H 的燃烧产物为 H2O(l), N 的燃烧产物为 N2(g), S的燃烧产物一般为 SO2(g), Cl 的燃烧产物为一定组成的HCl(aq)。
四、绝热可逆过程: Qr=0 理想气体绝热可逆过程方程式:
P 1V1 P 2V2 K ' (a )
TV
( 1) 1 1
T2V2
( 1)
K ( b)
热力学第4定律

热力学第4定律
热力学第四定律是指熵的增加趋势。
在热力学中,熵是描述系统无序程度的物理量,也是一个衡量能量转化不可逆性的指标。
熵的增加意味着系统的无序程度增加,能量转化更难逆转,系统变得更加难以控制和预测。
在热力学的前三个定律中,我们学习了能量守恒定律、熵的不减定律和温度的零点定律。
这些定律告诉我们能量是守恒的,热量自然会向熵增加的方向流动,并且温度是有物理意义的。
然而,热力学第四定律则探讨了熵增加的趋势。
根据第四定律,自然界中系统的熵总是趋向于增加。
这可以理解为一个系统的无序程度总是增加的,热量总是朝着更高熵的方向传递。
为什么会有熵增加的趋势呢这是由于熵的定义和热力学过程的不可逆性。
熵的定义是系统的无序程度,而不可逆过程是指无法回到初始状态的过程。
热力学中的大部分过程都是不可逆的,例如摩擦、能量转化等。
由于不可逆过程的存在,能量的转化会导致系统的无序程度增加,即熵增加。
这是因为在能量转化过程中,有一部分能量会以废热的形式
散失,无法完全转化为有用的能量。
这就导致了熵的增加。
热力学第四定律的重要性在于提醒我们,自然界中系统总是朝着更高熵的方向发展。
这意味着无论我们如何努力,总会有一部分能量会以废热的形式散失,无法完全利用。
这也限制了热力学系统的能量转化效率。
总结起来,热力学第四定律是指熵的增加趋势,即系统的无序程度总是增加的。
这是由于不可逆过程导致能量转化的不完全性,部分能量以废热的形式散失。
熵的增加限制了能量转化的效率,也提醒我们能量守恒并不意味着能量利用的完全性。
热力学第二定律(4)
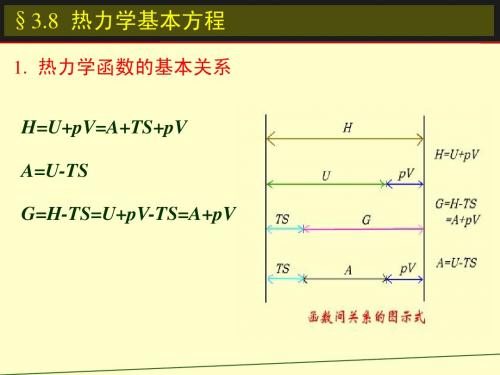
dH TdS Vdp
(3) dA SdT pdV (4)
A(T ,V )
G(T , p)
dG SdT Vdp
适用条件:(1)无相变化和化学变化(恒定组成)的均 相封闭系统发生单纯pVT变化的可逆或不可逆过程(2) 对于化学反应和相变化只适用于非体积功为零的可逆过程 即非体积功为零的恒定组成的封闭系统
解:对理想气体,
pV nRT
p nRT /V
p nR ( )V T V
p nR U ( )T T ( )V p T p 0 V T V
所以,理想气体的热力学能只是温度的函数。
§3.8 热力学基本方程
8、偏微分运算规则: z f ( x, y ) 循环关系式:
=
2U U V S SV V S T V S
S一定时对V 微分 U T ; S V
§3.8 热力学基本方程 (1) dU TdS pdV
§3.8 热力学基本方程 3、热力学方程的简单应用
例:试证明理想气体恒温过程ΔA=ΔG
dT 0 dA pdV A
V2 V1
dT 0 dG Vdp G Vdp nRT ln
p1 p2
V1 pdV nRT ln V2
p2 V nRT ln 1 p1 V2
H G / T 2 T T p
积分:
G2
G1
T2 G H d( ) 2 dT T1 T T
T2 H G2 G1 dT 2 T1 T T2 T1
§3.8 热力学基本方程
第4节 热力学第二定律 教学设计

第4节热力学第二定律[学习目标]1.知道传热、扩散现象、机械能与内能的转化等都具有方向性。
具有方向性的过程是不可逆的。
2.理解热力学第二定律的两种表述。
3.学会用热力学第二定律解释自然界中的能量转化、转移及方向性问题。
知识点1热力学第二定律1.热传导的方向性(1)热量可以自发地由高温物体传到低温物体。
(2)热量不能自发地由低温物体传到高温物体。
(3)热传导过程是有方向性的。
2.热力学第二定律的克劳修斯表述热量不能自发地从低温物体传到高温物体。
即热传导的过程具有方向性。
3.热力学第二定律的开尔文表述不可能从单一热库吸收热量,使之完全变成功,而不产生其他影响。
(该表述阐述了机械能与内能转化的方向性)[判一判]1.(1)热量不能由低温物体传给高温物体。
()(2)科技发达后,热机的效率可以达到100%。
()(3)机械能可以全部转化为内能,而内能不能自发地全部转化为机械能。
()提示:(1)×(2)×(3)√知识点2能源是有限的1.能量耗散能量在数量上虽然守恒,但其转移和转化却具有方向性。
在各种各样的活动中,其他形式的能最终都转化成内能流散到周围环境中,再也不能自动聚集起来驱动机械做功了,这种转化过程叫作能量耗散。
2.品质降低能量从高度有用的形式降级为不大可用的形式叫品质降低。
能量在利用过程中,总是由高品质的能量最终转化为低品质的能量。
能源的使用过程中虽然能的总量保持守恒,但能量的品质下降了。
[判一判]2.(1)能量耗散不遵循能量守恒定律。
()(2)能量耗散会导致能量品质的降低。
()(3)为了可持续发展,必须节约能源。
()提示:(1)×(2)√(3)√1.(对热力学第二定律的理解)关于热力学定律,下列说法中正确的是() A.在一定条件下物体的温度可以降到绝对零度B.第二类永动机和第一类永动机一样,都违背了能量守恒定律C.热机的效率可以达到100%D.在热传递中,热量不可能自发地从低温物体传给高温物体解析:选D。
无机非金属材料导论-第2章材料的热学性能_材料物理(1).

2. 比热容与摩尔热容
将1g质量的物体温度升高1K所需要增加的热量称 为物质的比热容,简称比热。 【J/K· g】 mol】 1mol物质的热容,称为摩尔热容。 【J/K·
3. 平均热容
物质从温度T1到T2所吸收的热量的平均值
C Q T2 T1
工程应用中应注意适用温度范围
4. 恒压热容与恒容热容
从原子间的相互作用力考虑:
r<r0时,曲线的斜率较大; 斥力随位移增大得很快。
r>r0时,曲线的斜率较小;
引力随位移的增大较慢。
两侧受力不对称,使得质点 振动的平衡位置右移,相邻 质点间距离增加,晶体膨胀。
从能量角度考虑: ara、 brb 为T1温度下质点振动的总能量
温度T1时,质点的振动位置在ra与 rb 之间变化,总能量在aAb间变化。
E (3NkT ) 3Nk 3R 25( J /( K m ol)) 热容:cv T v T v
模型过于简单,不能解释低温下热容减小的现象。
三、热容的其它理论
一个振子的平均能量
1.热容的量子理论
1摩尔固体的平均能量为
1.055 1034 J s
2.爱因斯坦热容理论
假设:每个原子皆为一个独立的振子,原子之间彼此无关, 并且i = 。 1摩尔固体的平均能量为 E 3 N
e kT 1
热容:
爱因斯坦比热函数
爱因斯坦温度
cv
E e 3Nk 3 Nkf e 2 T kT kT kT e 1
16.7 20.9
(2)化合物的热容定律(奈曼-考普( Neumann-Kopp )定律): 化合物的分子热容等于构成此化合物的各元素的原子热容 之和
第二章__热力学第一定律(4)
§2.8 化学计量数、反应进度和标准摩尔反应焓
引入反应进度的优点: 在反应进行到任意时刻,可以用任一反应物 或生成物来表示反应进行的程度,所得的值都是 相同的,即: d dnD dnE dnF dnG
H2O(g) 1000C,202.650kPa H2O(l) 1000C 恒温热源(100oC)
§2.7 相变化过程
(3)相变焓:恒温恒压,无非体积功 Qp=H
B() →
H()
B( )
H( )
(恒温恒压)
H H H
H H m n H h m
§2.8 化学计量数、反应进度和标准摩尔反应焓 1. 化学计量数
2H2 + O2 = 2H2O 写成: 0 = –2H2 – O2+ 2H2O aA + bB = yY + zZ 写成: 0 = – aA – bB + yY + zZ
0 BB
B
这里B为B组分化学计量数,而 A= – a , B= – b , Y= y, Z= z
1 H (g,p $ 2 2
)
1 Cl (g,p $ 2 2
) HCl(g,p )
$
$ 反应焓变为: r H m (298.15 K) 92.31 kJ mol-1
这就是HCl(g)的标准摩尔生成焓:
$ f H m (HCl, g) 92.31 kJ mol-1
§2.10 标准摩尔反应焓的计算
§2.8 化学计量数、反应进度和标准摩尔反应焓 2.反应进度
设某反应
0 = aA bB + yY + zZ
02章-热力学第一定律(4)

绝热过程功的计算
理想气体绝热可逆过程方程式:
对于理想气体,无体积功的绝热可逆过程:
∵ Q dU W dU pdV
Q 0
dU pdV ∴
C p / CV
又因理想气体:
dU
C C p / CV V
dT
所以: CV dT pdV
CV dT
pdV
nRT
dV V
(1)
Cp - CV = nR,令 C p / C称V 为热容比
知识链接:火力发电厂的能量利用
锅炉
汽轮机
发电机
冷却塔
200℃
R
Th TC Th
(473 300)K 36% 473 K
I < 20%
1度电/1000g 煤
高煤耗、高污染(S、N氧化物、粉尘和热污染)
火力发电厂的能量利用
400℃ 550℃
Th TC 673 300 55%
Th
卡诺循环(Carnot cycle)
整个循环:
U 0
Q2 是体系所吸的热,为正值,
Q Q2 Q1 Q1 是体系放出的热,为负值。
W W1 W3 (W2和W4对消)
即ABCD曲线所围面积为 热机所作的功。
Carnot 循环
整个循环过程中,系统作的总功W 与系统从环境 净吸热Q 之间有如下关系:
绝热过程功的求算
(1)理想气体绝热可逆过程的功
W V2 pdV V1
=
K V2 V V1
dV
=
K
(1
)
(V21 1
1 V1 1
)
(pV K )
因为 所以
p1V1 p2V2 K
W
=
p2V2
热力学第二定律(4)

定义: 熵
dS
Qrev
Tr
比熵 ds
qrev
Tr
于19世纪中叶首先克劳修斯 (R.Clausius)引入,式中S从1865年起称 为entropy,由清华大学刘仙洲教授译成 为“熵”。
熵的物理意义
定义:熵
dS
Qre
T
比熵 ds
qre
T
热源温度=工质温度
可逆时
dS 0 dS 0 dS 0
自发过程的方向性
摩擦生热
功量
100% 发电厂
热量
功量
40%
热量
放热
自发过程具有方向性、条件、限度
热力学第二定律的实质
自然界过程的方向性表现在不同的方面
能不能找出共同的规律性? 能不能找到一个判据?
热力学第二定律
热力学第二律的表述与实质
热二律的表述有 60-70 种
热功转换
1851年 开尔文-普朗克表述 热功转换的角度
Q
Q
p
2 b v
热力学第二定律的数学表达式
任意不可逆循环
Q Q 1 2 可得:
T1 T2
Q2 T2 1 1 Q1 T1
式中δQ2为绝对值: p a 2 b v
δQ2改用代数值:
Q1
T1
Q2
T2
0
1
克劳修斯不等式
热力学第二定律推论之一 卡诺定理给出热机的最高理想 热力学第二定律推论之二 克劳修斯不等式反映过程方向性 定义熵
∴ Q1
’-
Q1 = Q2 - Q2= 0
’
工质循环、冷热源均恢复原状, 外界无痕迹,只有可逆才行, 与原假定矛盾。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
排气温度问题:
机械温度问题:
(3) 排气量和供气量
– 排气量
? 单位时间内,排出气体换算为第1级进口状态时的容积
– 额定排气量(铭牌上)
? 排出的气量折算成特定的进口状态的容积流量。 ? 特定的进口状态:
p1 ? 0.1MPa ,T1 ? 20℃
qV ? qVd
pd Ts1 ps 1 Td
Z s1 Zd
(1) 吸、排气压力
?压缩机的吸、排气压力分别指第一级吸 入管道处和末级排出管道处的气体压力
?具有可变更性 ?名义吸、排气压力、额定排气压力
排气压力
? ? 压缩机最终排气压力 的大小由系统和管路的背压决定。 ?
压缩机排出压力 =系统压力 +管路阻力
p? ? pi ? p管
? 压缩机铭牌上压力为额定工况下的压力,即额定转速、 额定流量、设计系统压力及管路阻力下。
考虑补气、抽 气 考虑φ,抽气 洗涤,压缩因 子
考虑补气、抽 气
红王 院学工化学大业工古蒙内
2.2 往复式压缩机热力和动力性能
?2.2.1 压缩机的热力性能计算
?
?2.2.2 压缩机的动力性能计算
红王 院学工化学大业工古蒙内
2.2.1 压缩机的热力性能和计算
?1.排气压力和进排气系统 ?2.热力学参数 ?3.各种气量与参数的关系
1.排气压力和进排气系统
红王 院学工化学大业工古蒙内
? ? qVN ? qV
ps1 ? ? psa 1 T0
p0Ts 1
?标准状态:
m3 / m
p0 ? 1.013 ? 105 Pa ,T0 ? 0℃
?3.各种气量与参数的关系
理论容积流量 压缩机实际吸入量 压缩机实际排气量
排气量 供气量
吸气损失
泄露损失
换算到进口 压力温度下
换算到标态下干 气容积值
凝析系数λφ 凝析:
表示某级前因水蒸气凝析造成的气体体 积损失的程度。
??i ?
– 其中
Vsi Vd
(1状态下)?
p1 ? ? psa1
psi ? psai
psi p1
? psi:第i级进气压力,Pa; ? psai:第i级进气温度下的饱和蒸气压,Pa。 ? Φ:相对湿度
供气量
?将容积流量折算成标准状态下 时的干气容积值。
?
qV?
?
qVc
m3 / m
?qVd —末级排出气体量;
理想和实际 理论和实际
?qVφ—分离水分,折算为1状态,
qV?
?
qmW psa 1
? sa 1 p1
?qVc—中间抽加气的量,折算为1状态。
抽气系数 λc
? 表示某级前因抽、加气造成的气体体积损失的程 度
? ci
?
Vsi Vd
(1状态下)
?抽气: ? c ?1
? ?
例如:抽掉 20%, ? c=0.8
??加气: ? c ?1
?? 例如:加入 20%, ? c=1.2
凝析系数λφ 凝析:
表示某级前因水蒸气凝析造成的气体体 积损失的程度。
??i ?
– 其中
Vsi Vd
(1状态下)?
p1 ? ? psa1
psi ? psai
psi p1
? psi:第i级进气压力,Pa; ? psai:第i级进气温度下的饱和蒸气压,Pa。 ? Φ:相对湿度
红王 院学工化学大业工古蒙内
(2) 排气温度
压缩机的排气温度是指压缩机末级排 出气体的温度,在末级出气管处测量
压缩机其它各级的排气温度称为该级 的排气温度,从相应级的排气接管处 测得
? 2.排气温度
气体受压缩后,体积减少,但温度升高。温升与压力比有关。
排气温度计算:
n?1
T2
?
? T1 ??
?
p2 p1
?①吸气压力 —第1级吸入管道处。 ?②排气压力 —末级排出管道处。
自动阀
由进排气系统决定ps、pd
?③额定吸、排气压力—铭牌上压力
红王 院学工化学大业工古蒙内
2.热力学参数
?(1)压力 ?(2)排气温度 ?(3) 气量 ?(4)功率和效率 ?(5)抽气系数λc 、析水系数、泄露系数
红王 院学工化学大业工古蒙内
? ???
n
n?1
T
' d
?
? Ta ??
?
p
' 2
p
' 1
? ?? ?
n
每一级的排气温度限制见表2-1。
如: 空气压缩机:T2 < 160~180℃
石油气压缩机:T2 < 90~100 ℃
主要考虑介质的闪点温度,出现“积碳”、氧化爆炸等因素。
压缩机的温度控制一般较严格,温度是检测压缩机正常工作的敏 感参数,很多隐患可以从温度中得到。
