第六章6.1.3平方根教案
人教版数学七年级下册6.1.3《平方根》教案3

人教版数学七年级下册6.1.3《平方根》教案3一. 教材分析平方根是数学中的一个基本概念,它是指一个数乘以自身得到另一个数时,这个数就是原数的平方根。
平方根的引入可以帮助学生更好地理解有理数、无理数等概念,并且在实际问题中具有广泛的应用。
二. 学情分析学生在学习平方根之前,已经学习了有理数的乘法、平方等知识,对于乘法运算已经有了一定的理解。
但是,平方根的概念较为抽象,需要学生进行一定的思考和理解。
因此,在教学过程中,需要引导学生通过实际例子来理解平方根的概念,并通过练习来巩固所学知识。
三. 教学目标1.理解平方根的概念,掌握求一个数的平方根的方法。
2.能够应用平方根的概念解决实际问题。
3.培养学生的逻辑思维能力和解决问题的能力。
四. 教学重难点1.重点:平方根的概念和求一个数的平方根的方法。
2.难点:理解平方根的概念,能够应用平方根解决实际问题。
五. 教学方法采用问题驱动法、案例教学法、小组讨论法等教学方法,引导学生通过实际例子来理解平方根的概念,并通过练习来巩固所学知识。
六. 教学准备1.PPT课件2.教学视频或案例七. 教学过程1.导入(5分钟)通过一个实际例子来引入平方根的概念,例如:一个正方形的边长为4,求这个正方形的面积。
引导学生思考,如何求解这个问题。
2.呈现(15分钟)讲解平方根的概念,通过PPT课件或者板书,给出平方根的定义和性质。
同时,给出求一个数的平方根的方法。
让学生理解并掌握平方根的概念。
3.操练(10分钟)通过一些练习题,让学生运用平方根的概念来求解问题。
给予学生解答的指导,并纠正一些常见的错误。
4.巩固(10分钟)让学生通过一些实际问题,应用平方根的概念来解决问题。
让学生感受到平方根在实际问题中的应用价值。
5.拓展(10分钟)引导学生思考平方根的应用场景,例如:在物理学中,平方根的概念可以应用于振动频率的计算;在经济学中,平方根的概念可以应用于需求曲线的计算等。
让学生了解平方根在实际问题中的应用。
人教版数学七年级下册6.1.3《平方根》教学设计6

人教版数学七年级下册6.1.3《平方根》教学设计6一. 教材分析人教版数学七年级下册6.1.3《平方根》是学生在学习了有理数的乘方、平方差公式等知识的基础上,进一步研究平方根的概念和性质。
本节内容主要让学生掌握平方根的定义,了解平方根的性质,能熟练运用平方根解决实际问题。
教材通过引入平方根的概念,让学生感受数学与实际的联系,培养学生的数学应用能力。
二. 学情分析学生在学习本节内容时,已经具备了一定的数学基础,例如有理数的乘方、平方差公式等。
但平方根的概念和性质较为抽象,学生可能难以理解。
因此,在教学过程中,教师需要关注学生的认知水平,采取合适的教学策略,帮助学生掌握平方根的知识。
三. 教学目标1.知识与技能:让学生掌握平方根的定义和性质,能运用平方根解决实际问题。
2.过程与方法:通过观察、操作、探究等活动,培养学生的数学思维能力。
3.情感态度与价值观:激发学生学习数学的兴趣,感受数学与实际的联系。
四. 教学重难点1.重点:平方根的定义和性质。
2.难点:理解平方根的概念,能运用平方根解决实际问题。
五. 教学方法1.情境教学法:通过引入实际问题,激发学生的学习兴趣。
2.启发式教学法:引导学生主动探究,发现平方根的性质。
3.归纳总结法:在教学过程中,引导学生总结平方根的定义和性质。
六. 教学准备1.教学课件:制作平方根的相关课件,包括图片、动画等。
2.教学素材:准备一些实际问题,用于导入和巩固环节。
3.板书设计:设计简洁明了的板书,突出平方根的关键信息。
七. 教学过程1.导入(5分钟)利用课件展示一些实际问题,如面积、体积等,引导学生思考这些实际问题与数学的关系。
通过解答这些问题,引入平方根的概念。
2.呈现(10分钟)展示平方根的定义,让学生观察、思考,引导他们发现平方根的性质。
同时,通过举例说明平方根的实际应用,帮助学生理解平方根的概念。
3.操练(10分钟)让学生分组讨论,尝试解决一些关于平方根的实际问题。
人教版七年级数学下册6.1.3《平方根》教学设计

人教版七年级数学下册6.1.3《平方根》教学设计一. 教材分析平方根是初中数学的重要内容,是实数系统的基础概念之一。
人教版七年级数学下册6.1.3《平方根》一节,主要让学生了解平方根的定义,掌握求一个数的平方根的方法,以及了解平方根在实际生活中的应用。
二. 学情分析七年级的学生已经学习了有理数的乘方,对实数的概念有一定的了解。
但是,平方根的概念比较抽象,学生可能一时难以理解。
因此,在教学过程中,教师需要借助实例,引导学生从实际问题中发现平方根的概念,并通过大量的练习,让学生熟练掌握求一个数的平方根的方法。
三. 教学目标1.了解平方根的概念,掌握求一个数的平方根的方法。
2.能够运用平方根解决实际问题。
3.培养学生的数学思维能力,提高学生的数学素养。
四. 教学重难点1.重点:平方根的概念,求一个数的平方根的方法。
2.难点:平方根在实际生活中的应用。
五. 教学方法1.实例导入:通过实际问题,引导学生发现平方根的概念。
2.讲解演示:教师讲解平方根的定义,演示求一个数的平方根的方法。
3.练习巩固:学生进行大量的练习,巩固平方根的概念和方法。
4.拓展应用:引导学生运用平方根解决实际问题。
5.总结归纳:教师引导学生总结平方根的知识点。
六. 教学准备1.教学课件:制作平方根的教学课件,包括实例、讲解、练习等内容。
2.练习题:准备一些有关平方根的练习题,用于课堂练习和巩固。
3.教学工具:准备黑板、粉笔等教学工具。
七. 教学过程1.导入(5分钟)教师通过一个实际问题,引导学生发现平方根的概念。
例如:一块长方形的地毯,边长为6米,求这块地毯的面积。
学生可以很容易地得出答案,即36平方米。
教师进而引导学生思考:36平方米的面积,对应的长方形地毯的边长是多少?学生可以通过计算得出,边长是6米。
教师解释,6米就是36的平方根。
2.呈现(10分钟)教师讲解平方根的定义,演示求一个数的平方根的方法。
平方根的定义:如果一个非负数a的平方等于b,那么这个非负数a叫做b的平方根。
人教版七年级数学下册6.1.3平方根优秀教学案例

4.多种教学手段的运用:运用多媒体课件、实物模型等多种教学工具,以形象直观的方式展示平方根的概念和求解过程,增强了学生的直观感受和动手操作能力。
5.全面的教学评价:注重过程性评价与终结性评价相结合,全面了解学生对平方根知识的理解和掌握程度,同时也关注学生的情感态度和价值观的培养。
1.小组内讨论:让学生在小组内进行讨论,共同探究平方根的性质,以及如何求解一个数的平方根;
2.小组展示:鼓励小组代表进行成果展示,让学生在表达中加深对平方根知识的理解;
3.互相评价:组织学生进行互相评价,取长补短,共同提高。
(四)总结归纳
1.师生共同总结:教师引导学生一起总结本节课所学的平方根的概念、求解方法及性质;
在教学评价上,我注重过程性评价与终结性评价相结合,通过观察学生的课堂表现、作业完成情况、小组讨论参与度等方面,全面了解学生对平方根知识的理解和掌握程度。同时,我还设计了一道具有挑战性的拓展题,激发学生深入思考,提高学生的创新意识。
二、教学目标
(一)知识与技能
1.理解平方根的概念,掌握求一个数的平方根的方法;
(二)问题导向
1.设计问题链:通过一系列问题引导学生深入思考,如“什么是平方根?如何求一个数的平方根?平方根有哪些性质?”等问题;
2.引导学生自主探究:在解决问题的过程中,引导学生运用已有的知识与经验自主探究,培养学生的问题解决能力;
3.问题拓展:提出具有挑战性的问题,如“平方根在实际生活中有哪些应用?”等,激发学生的创新意识。
1.激发学生对数学的兴趣,树立学生自信心,培养积极的学习态度;
人教版七年级下数学6.1.3平方根教案
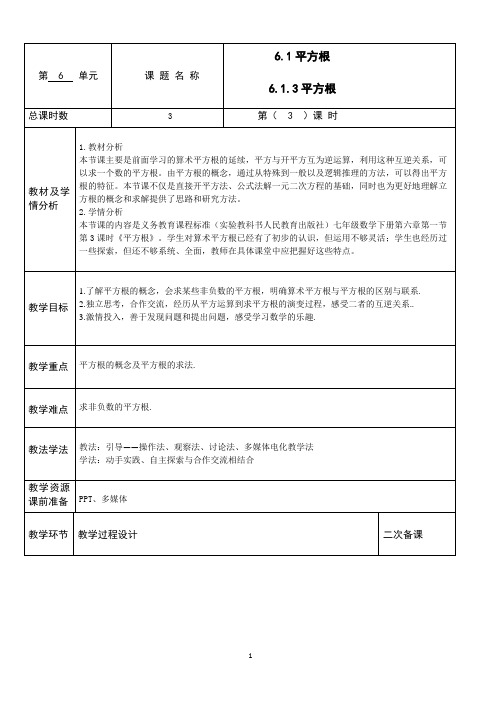
一、情境导入 填空:(1)3的平方等于9,那么9的算术平方根就是________; (2)25的平方等于425,那么425的算术平方根就是________; (3)展厅的地面为正方形,其面积49平方米,则边长为________米. 还有平方等于9,425,49的其他数吗? 二、合作探究 探究点1:平方根的定义及性质 填一填: (1)4的平方等于16,那么16的算术平方根就是________; (2)25的平方等于425,那么425的算术平方根就是_______; (3)展厅地面为正方形,其面积是49 m 2,则其边长为______m.. (4)写出左圈和右圈中的“?”表示的数: 问题1: 平方等于9的数有几个?是哪些数? 问题2: 如果a 是一个正数,平方等于a 的数有几个?怎样把它们表示出来?它们有什么关系? 问题3: 平方等于0的数有几个?有平方是负数的数吗? 问题4: 平方根与算术平方根有什么区别与联系? 要点归纳: 1.平方根的性质: (1)正数有两个平方根,两个平方根互为相反数. (2)0的平方根还是0. (3)负数没有平方根. 2.平方根与算术平方根的联系与区别:
联系:
(1)包含关系:平方根包含算术平方根,算术平方根是平方根的一种.
(2)只有非负数才有平方根和算术平方根.
(3)0的平方根是0,算术平方根也是0.
区别:
(1)个数不同:一个正数有两个平方根,但只有一个算术平方根.
a,而算术平方根表示为
一个正数的两个平方根分别是2a+1和
因为一个正数的平方根有两个,且它们互为相反数,
互为相反数,根据互为相反数的两个数的和为。
6.1.3平方根优秀教学设计

6. 1. 3平方根教学设计教学目标1. 掌握平方根的概念,明确平方根和算术平方根之间的联系和区别.2. 能用符号正确表示一个非负数的平方根,理解开平方运算和平方运算之间的互逆关系.二. 教学重难点重点:平方根的概念和求一个数的平方根难点:平方根和算术平方根三. 教学过程复习引入1. 什么是算术平方根?2. 算术平方根与被开方数均具有3. 填空(1) (2)(3) 思考:反过来,如果已知一个数的平方,怎样求这个数?二.新课讲授问题:如果一个数的平方等于9,这个数是多少? 由于(±3)2=9 ,所以这个数是3或-3. 想一想:3和-3有什么特征? 3和-3互为柑反数,会不会是巧合呢? 根据上而的研究过程填表:2 4如果我们把±1、±4、±6、±7、±护别叫做],】6,36,49,-的平方根,你能给出平方根 的概念吗?(一) 平方根的概念如果有一个数X,使得x2=a.那么我们把X 叫做a 的一个平方根,也叫作二次方根. 例如:(±1)2二1, 1的平方根为±1, (±3)2二9, 9的平方根为±3(二) 开平方求一个数a 的平方根的运算,叫做开平方注:平方与开平方是互逆的运算,平方的结果叫暮,而开平方的结果叫做平方根 举例:我们看到,±3的平方等于9. 9的平方根是±3,所以平方与开平方互 为逆运算.根摇这种互逆关系,可以求一个数的平方根.,(-3) 20. 82 =,(-0.8) 23 -> 9 9 3 因为七八!^'所临的平方根是切因为(±0.5) 2 = 0. 25,所以0.25的平方根是±0. 5.练习:⑷ ⑷冷 (5)-(-4/(6)749归纳: 1. 如果一个数为带分数,一般先将其化为假分数,再求其平方根:2•如果有乘方运算,先算出结果,再求其平方根; 3•如果这个正数a 不能写成有理数的平方的形式,那么可以将a 的平方根表示成+巫(四) 平方根性质思考:正数的平方根有什么特点?0的平方根是多少?负数有平方根吗?归纳:平方根性质:L 正数的平方根有两个,它们互为相反数,其中正的平方根就是这个数的算术平方根.2. 0的平方根是0.3. 负数没有平方根.(五) 平方根的表示方法正数a 的算术平方根可以用需 表示:正数a 的负的平方根,可以用符号 表示,正数a 的平方根可以用符号“±脳"表示,读作“正、负根号a".例如±爺=±3,±厉=±5(六)平方根•与算术平方根区别 说一说示±J7各表示什么意义?(三)典型例题例1求下列齐数的平方根:(1) 100:(3) 0. 25, 解:(1)因为(±10) 2 = lOOr 所以100的平方根是±10: (2) (3)(1) 表示7的负的平方根(2) 表示7的正的平方根(即算术平方根)(3) 表示7的平方根归纳:平方根打算术平方根的联系:(1) 具有包含关系:平方根包含算术平方根,算术平方根是平方根的一种;(2) 存在条件相同:只非负数才有平方根和算术平方根;(3) 0的平方根和算术平方根都是0.平方根与算术平方根的区别:(1) zk 义不同:如果一个数X 的平方等于a,那么这个数X 叫做a 的平方根,如果一个正 数X 的平方等于a,即x2 =a,那么这个正数x 叫做a 的算术平方根.(2) 个数不同:一个正数有两个平方根,而一个正数的算术平方根只有一个;(3)表示方法不同:正数a 的算术平方根表示为而正数a 的平方根表示为±(七)典型例题例2 求下列各式的值:(1) J36 (2) - Jo.81 : (3) ± ^5 —解:(1)因为62 = 36,所以辰=6:因为 6 92 二 0.81,所以-75^=-0.9L 讣算下列齐式的值(教材47页练习第3题)(1) A /9 (2) ⑶福 2.判断下列说法是否正确(教材47页复习巩固第4题) (1)5是25的算术平方根 (2) 525 7 是 —的一个平方根 0 Jo(-4) 2的平方根是-4 0的平方根丐算术平方根都是0 (3) (4) 例3求满足下列务•式的X 的值: (1) x2=361; (2)81x2・49=0; (3) (3x-l)^ = (-5)\ 解:(1) X = ±yf^ = ±19 (2) (3) 因为(严存5訂所以士—2 9 "3T 8 L Y-二49..49 .斗=—(2)81■一阿V81 93jf-l = ±5当3x-l二5时,% = 24 (3)当3%-1 = -51]寸,x=4 综上所述:x = 2^x = --三.课堂小结本节课学习了哪些知识?(1)(2)(3)(4) 平方根的概念平方根的性质平方根的表示方法求一个数的平方根。
6_1_3《平方根》教案

平方根第3课时课时安排:4课时课型:新授课教学目标【知识与技能】知道平方根的概念及一个数的平方根的表示,理解正数、负数、零的平方根的相关特点。
【过程与方法】通过案例,总结出平方根的概念,通过计算,真正理解解平方根的运算。
【情感态度】通过对平方根的学习,培养学生从多方面,多角度分析问题,解决问题的思想意识,养成全面分析问题的习惯.【教学重点】平方根的概念及其表示。
【教学难点】平方根和算术平方根的联系与区别.教学设计一、情境导入,初步理解问题假如一个数的平方等于9,这个数是多少?【教学分析】因为32=9,(-3)2=9,故平方等于9的数有两个:3和-3,把3和-3叫做9的平方根。
通过上述方法填写表格,当x2=1、16、36、49、425时,x=?师生共同总结:平方根定义:一般地,假如一个数的平方等于a,那么这个数叫做a的平方根或二次方根,即若x2=a,则x 为a的平方根,记为x=±a.二、思考探究,获取新知探究课本p45页图6.1-2总结出:把求一个数a 的平方根的运算,叫做开平方,而平方运算与开平方运算互为逆运算,根据这种关系,能够求一个数的平方根。
例1 求以下各数的平方根。
911100230254250164;.;;.();()()()()分析:可根据平方与开平方的互逆关系,通过平方运算求一个数的平方根.教学说明:一个正数的平方根有两个,不要丢掉其中负的平方根,算术平方根是其中的一个正平方根,不要弄错了符号。
求平方根时一定要把所求的数化成x 2的形式,同时注意正数有两个平方根。
例2 判断以下说法是否准确,并说明理由.(1)49的平方根是7; (2)2是4的一个平方根;(3)-5是25的一个平方根;(4)64的平方根是8 ;(5)-16的平方根是-4.三、使用新知,深化理解讲解课本p47第3、4题。
【教学说明】学生自主完成,教师巡视,然后集体订正.四、师生互动,课堂小结学完本节课请同学们谈谈自己的收获?五、课后作业布置作业:从教材“习题6.1”中选择.教学反思:。
人教版数学七年级下册6.1.3《平方根》教学设计2

人教版数学七年级下册6.1.3《平方根》教学设计2一. 教材分析平方根是初中数学中的重要概念,对于学生来说,掌握平方根的概念和求法是十分必要的。
本节课的内容包括平方根的定义、求法以及平方根的性质。
通过学习,学生能够理解平方根的概念,掌握求一个数的平方根的方法,以及了解平方根的性质。
二. 学情分析学生在之前的学习中已经掌握了有理数的概念,也了解了乘方的概念,这为本节课的学习提供了基础。
但是,对于平方根的概念和求法,学生可能还比较陌生,需要通过实例和练习来逐渐理解和掌握。
三. 教学目标1.知识与技能目标:理解平方根的概念,掌握求一个数的平方根的方法,了解平方根的性质。
2.过程与方法目标:通过观察、实验、探究等活动,培养学生的动手操作能力和抽象思维能力。
3.情感态度与价值观目标:激发学生学习数学的兴趣,培养学生的自主学习能力和团队合作精神。
四. 教学重难点1.重点:平方根的概念和求法,平方根的性质。
2.难点:平方根的性质的理解和应用。
五. 教学方法采用问题驱动法、案例分析法、小组合作法等教学方法,引导学生主动探究,培养学生的动手操作能力和抽象思维能力。
六. 教学准备1.准备平方根的实例和练习题。
2.准备教学课件和板书设计。
七. 教学过程1.导入(5分钟)通过一个实例,如“一个正方形的边长是a,求这个正方形的面积”,引出平方根的概念。
让学生思考,如何求一个数的平方根。
2.呈现(15分钟)介绍平方根的定义,通过PPT展示平方根的图像,让学生直观地理解平方根的概念。
然后,讲解如何求一个数的平方根,以及平方根的性质。
3.操练(10分钟)让学生分组进行练习,每组选择一个数,求出它的平方根,并观察平方根的性质。
教师巡回指导,解答学生的疑问。
4.巩固(10分钟)出示一些练习题,让学生独立完成,检验学生对平方根的概念和求法的掌握程度。
5.拓展(10分钟)引导学生思考,如何求一个数的算术平方根,以及算术平方根的性质。
让学生通过小组合作,共同探究这个问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
6.1.3平方根
凤台六中 孙长敏 【教学目标】 知识与技能
了解平方根的概念,会用根号表示正数的平方根; 了解开平方与平方互为逆运算,会用平方运算求某些非负数的平方根
过程与方法
通过学习平方根,进一步建立数感和符号感,发展抽象思维。
通过对正数平方根特点的探究,了解平方根与算术平方根的区别和联系,体验类比、化归等问题解决数学思想方法的运用,提高学生对问题的迁移能力。
情感、态度与价值观
通过对实际生活中问题的解决,让学生体验数学与生活实际是紧密联系着的。
通过探究活动培养动手能力和锻炼克服困难的意志,建立自信心,提高学习热情。
教学重点: 了解开方和乘方互为逆运算,弄懂平方根与算术平方根的区别和联系。
教学难点:平方根与算术平方根的区别和联系。
教学方法: 自主探究、启发引导、小组合作
教学过程
一、情境导入
如果一个数的平方等于9,这个数是多少?
讨论:这样的数有两个,它们是3和-3.注意()932
=-中括号的作用. 又如:25
42=x ,则x 等于多少呢? 二、探索归纳:
1、平方根的概念:如果一个数的平方等于a ,那么这个数就叫做a 的平方根.即:如果2x =a ,那么x 叫做a 的平方根.
求一个数的平方根的运算,叫做开平方.
例如:±3的平方等于9,9的平方根是±3,所以平方与开平方互为逆运算.
2、观察:课本P73的图14.1-2.
图14.1-2中的两个图描述了平方与开平方互为逆运算的运算过程,揭示了开平方运算的本质.并根据这个关系说出1,4,9的平方根.
例4 求下列各数的平方根。
(1) 100 (2) 16
9 (3) 0.25 3、按照平方根的概念,请同学们思考并讨论下列问题:
正数的平方根有什么特点?0的平方根是多少?负数有平方根吗?
一个是正数有两个平方根,即正数进行开平方运算有两个结果,一个是负数没有平方根,即负数不能进行开平方运算,符号:正数a 的算术平方根可用a 表示;正数a 的负的平方根可用-a 表示.
例5 求下列各式的值。
(1)144, (2)-81.0, (3)196121
± (4)256,()2
56 归纳:平方根和算术平方根两者既有区别又有联系.区别在于正数的平方根有两个,而它的算术平方根只有一个;联系在于正数的负平方根是它的算术平方根的相反数,根据它的算术平方根可以立即写出它的负平方根。
三、
课本P 46小练习1、2、3
四、小结:
1、什么叫做一个数的平方根?
2、正数、0、负数的平方根有什么规律?
3、怎样求出一个数的平方根?数a 的平方怎样表示?
五、作业
P 47-48习题6、1第4、7、8题。
教学反思。
