系统工程学第讲系统动力学
系统动力学方法

系统动力学的由来与发展
❖ 近年来SD正在成为一种新的系统工程方法 论和重要的模型方法,渗透到许多领域, 在国土规划、区域开发、环境治理和企业 战略研究等方面,正显示出它的重要作用。
❖ 尤其是随着国内外管理界对学习型组织的 关注,SD思想和方法的生命力更为强劲。
❖ 但目前应更加注重SD的方法论意义,并注 意其定量分析手段的应用场合及条件。
水准变量
(Level) 四个基本要素——状态、信息、决策、行动
两个基本变量——水准变量(L)、速率变量(R)
一个基本思想——反馈控制
因果关系分析
因果关系分析是构成系统动力学模型的基础,是社会系统内部关 系的真实写照。因果关系通过因果关系图来描述 因果箭 因果关系也称影响关系,可通过连接因果要素的“因果箭”表示。 因果关系的极性(正+,负-)表示因果的变化方向是否一致
❖ 计算机仿真实验 ❖ 结果分析 ❖ 模型修正 ❖ 比较与评价 ❖ 政策分析
认识 界定 要素及其因 建立结 建立数 仿真 比较与 政策 问题 系统 果关系分析 构模型 学模型 分析 评价 分析
(流图)(DYNAMOY方程)
SD结构模型化原理
(Rate)
决策
速率变量
信息
行动
信息
流 (行动)
系统 状态
SD的研究对象及其特点
❖ SD的研究对象主要是社会(经济)系统。 ❖ (1)社会系统中存在着决策环节 ❖ 社会系统的行为总是经过采集信息,并按照某个
政策进行信息加工处理作出决策后出现的,决定 是一个经过多次比较、反复选择、优化的过程。 ❖ 对于大规模复杂的社会系统来说,其决策环节所 需要的信息的信息量是十分庞大的。其中既有看 得见、摸得着的实体,又有看不见、摸不到的价 值、伦理、道德观念及个人、团体的偏见等因素。
系统动力学方法在工程系统优化中的应用研究

系统动力学方法在工程系统优化中的应用研究引言:工程系统的优化是一个复杂而关键的问题。
传统的优化方法往往只能考虑系统的局部因素,难以全面地分析和解决问题。
而系统动力学方法则提供了一种全面、综合的视角,能够更好地理解和优化工程系统。
本文将探讨系统动力学方法在工程系统优化中的应用研究。
一、系统动力学方法的基本原理系统动力学方法是一种以时间为基础的建模和分析方法,旨在研究系统内部结构和行为之间的关系。
其核心思想是将系统视为一系列相互作用的变量和因果关系的集合,通过建立动态方程来描述系统的演化过程。
系统动力学方法强调整体性思维,注重系统内部的反馈机制和延迟效应。
二、系统动力学方法在工程系统优化中的应用案例1. 供应链管理优化供应链是一个典型的工程系统,涉及到多个环节和参与方。
传统的供应链管理方法往往只考虑到局部的因素,难以全面地分析和优化供应链的整体性能。
而系统动力学方法可以通过建立供应链各环节之间的动态方程,考虑到延迟效应和反馈机制,从而更好地优化供应链的整体性能。
2. 城市交通优化城市交通是一个复杂而庞大的工程系统,涉及到交通流量、道路容量、交通信号等多个因素。
传统的交通优化方法往往只能考虑到局部的交通状况,难以全面地分析和优化城市交通系统。
而系统动力学方法可以通过建立城市交通各要素之间的动态方程,考虑到交通流量的延迟效应和反馈机制,从而更好地优化城市交通系统的整体性能。
三、系统动力学方法的优势和挑战1. 优势系统动力学方法具有较强的整体性和综合性,能够更好地理解和分析工程系统的复杂性。
它能够考虑到系统内部的反馈机制和延迟效应,从而更准确地预测系统的行为和性能。
此外,系统动力学方法还能够帮助决策者更好地制定策略和决策,提高系统的鲁棒性和适应性。
2. 挑战系统动力学方法在应用过程中也存在一些挑战。
首先,系统动力学方法需要大量的数据支持,对数据的质量和可靠性要求较高。
其次,系统动力学方法需要对系统的结构和行为有较深入的理解,需要专业的领域知识和建模经验。
系统工程学 第5讲系统动力学
p
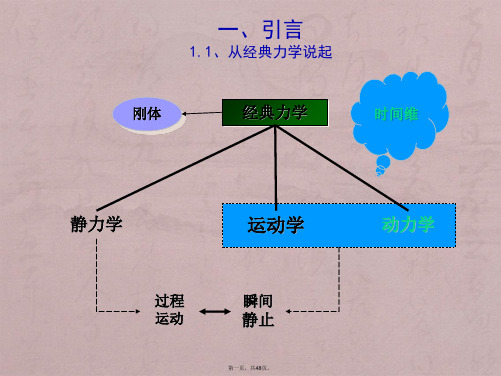
P 100 102 104.04 ┆
PR 2 2.04 2.0808
┆
100
0 一阶正反馈(简单 人口问题)系统输 出特性曲线
第二十三页,共48页。
3、一级负反馈回路
+
I
库存量
—
1000 R1
订货 量
R1
(—) +
L I•K=I•J+DT*R1•JK
库存 差额 D
期望库存Y
I
。。
Z
D
(订货调整时间,5)
+
明星位置空缺数量
+ 明星位置总数
现在明星数量
第四十四页,共48页。
4、讨论
毕业在即,同学们都在积极的寻找中意的单位,由于 背负着上学期间的贷款,大家都希望能把自己卖个好价钱 。
但现实是企业认为刚毕业的学生没有实际工作 经验,要花精力培养,而且培养后的人才很可能迅 速流失,因此企业不愿意给一个高价钱。
Forrester (MIT)
系统
动力学
系统
动态行为 结构
理论 基础
控制论 信息论 决策论
第六页,共48页。
系统动力学 模型
决策依据
2、系统动力学
2.2、研究对象:社会系统的基本特性
社会系统 SD的研究方法 非线性多重反馈系统
基本特征
决策环节
反馈
基本特性
自律性
1. 自主决策 2. 自我管理
3. 自我控制
L。1
。 A1
第十七页,共48页。
(初值) 。
(3)流图--流图举例
R1(利息1) L1
C1(利率)
R1(订货量)
库存量 I
6系统动力学
SD思想和方法的应用范围日益扩大。“Principles of Systems”(1968),“ Urban Dynamics”(1969)的出现.
70年代初至 80年代
90年代以来
1972年美国MIT的J.W.Forrester正式提出“Systems Dynamics”。 经历了两次关注。
SD成为一种重要的系统工程方法论和重要的建模方 法。尤其是随着国内外对复杂性理论的关注,SD思想 和方法的生命力更为强劲。
系统动力学在中国的发展
20世纪70年代末系统动力学引入中国,其中王其藩教授,许庆瑞 教授,以及陶在朴、胡玉奎等专家学者是先驱和积极倡导者。系 统动力学在中国的二十多年时间里,取得了飞跃发展,在八十年 代即已广泛传播,最多时有SD工作者有2000多人。 1986年成立了国内系统动力学学会筹委会。 1987年在上海成功举办了第5届国际系统动力学年会,这是我国 在此学术领域进入国际先进行列的标志。 1990年正式成立了国际系统动力学学会中国分会。 1993年正式成立了中国系统工程学会系统动力学专业委员会。 2005年11月4日-6日国际系统动力学学会中国分会等单位主办 “系统动力学与管理科学——2005亚太地区可持续发展国际会 议” 。 2007年第二届系统科学,管理科学与系统动力学国际会议在上海 召开,以后此类学术会议将每隔一年召开一次。
①因果关系(因果箭)
原因
结果
A
B
指一种现象发生的原因和可能引起的结果——一种思维方法
因果关系的意义:
1.描述问题
2.将复杂的问题以 简单且是系统化的 形式表示
3.可以说明系统的 边界和内部要素
鼠群模型的因果关系图
6.2.1 因果关系图
正因果关系
动力学系统

动力学系统动力学系统是一个非常重要的科学概念,是研究物理系统如何操作的一部分。
它涉及物体的方向性运动,是许多物理关系的基础。
本文将重点关注动力学系统的基本原理,例子和应用。
动力学是一门描述物体或物理系统在定义状态下的运动的学科。
这个定义状态包括:速度、加速度和位置。
动力学系统相对于其他物理系统而言,最大的特点在于它的运动是有序的,并且运动与定义状态之间有一一对应的关系。
在动力学中,物体的运动由受力而引起,并且运动受到重力影响。
动力学系统在物理学中被广泛应用,主要用于研究定义状态下物体的运动。
例如,在研究飞机飞行原理时,可以运用动力学系统来研究飞机的飞行轨迹。
动力学的原理也被用于研究城市规划,以及物体的旋转运动。
考虑粒子质量和物理环境,动力学系统可以描述物体的运动,用来模拟和研究物体的运动。
例如,研究一个物体在加速度下的运动,可以用此动力学系统来模拟,计算出一些定义状态下,物体在加速度下的运动轨迹。
动力学系统也可以用来分析和比较不同地区引起的摩擦和空气阻力。
例如,在研究风洞中的空气动力学时,可以使用动力学系统来分析和研究不同地区空气的摩擦和阻力。
在许多工程和科学领域,动力学系统是一种常见的模型,用于模拟各种现实系统。
例如,在自动控制工程中,我们可以使用动力学系统模型来模拟物体的控制规律,进而更好地操控机器的运动状态。
在建筑学中,动力学也被广泛应用,可以用来研究建筑物在不同情况下的运动特性。
例如,在研究桥梁受力情况时,可以利用动力学系统来模拟桥梁在不同状态下的受力情况,进而用来评估桥梁的稳定性。
以上就是动力学系统的基本概念,例子和应用。
动力学系统是一个重要的理论框架,用于描述物理系统在定义状态下的运动。
此外,动力学也被广泛应用于工程、科学和建筑学领域,为它们提供模型来研究物体的运动。
系统动力学模型

系统动力学模型系统动力学模型是指它是一种分析和模拟物理系统及其动力学过程的数学技术。
它可以用来研究运动学,控制系统,流体动力学,形式力学,电学,冲击学和弹性动力学等领域的数学模型,并可用于实际的工程问题的解决。
系统动力学模型基于物理系统的动力学处理和控制问题,用来研究物体的运动行为。
例如,系统动力学模型可以用来探讨汽车的运动性,即汽车在不同条件下的行驶特性,以确定汽车行驶性能的最佳状态。
此外,系统动力学模型还可以模拟任意静力学,力学,流体力学或热力学系统的运动模式。
系统动力学模型的建立要求具备完备的物理基础知识,形成一个系统模型的首要任务是了解物理系统的特性和行为,因此必须确定物理系统的运动方程和力学特征,物理量的表达式在构建模型时必须明确。
模式构建完成后,需要求解模型,并将模型运用到实际问题中,用以求解物理过程及其动力学运行状态。
为此,我们可以使用计算机模拟技术来求解模型,用以检验结果的正确性和准确性。
系统动力学模型在很多领域中都发挥着重要的作用,例如机械系统的设计,控制系统的调整,电子电气系统的设计,机器人的控制,航空航天技术,建筑工程设计等。
例如,在机器人技术中,系统动力学模型可以模拟机器人的运动特性,帮助机器人决定如何完成任务。
此外,系统动力学模型在工程设计中也有广泛应用,可用于分析和解决工程设计问题,以便改善工程性能。
例如,系统动力学模型可以帮助分析和解决结构物振动问题,提高结构物的稳定性和耐久性,以及改善系统的可靠性。
此外,系统动力学模型也可以帮助优化控制系统的性能,以提高系统的功率和可靠性。
综上所述,系统动力学模型是一个强大的工具,可以帮助我们研究和分析物理系统及其动力学过程,从而有效地改善工程性能。
它在机械,控制,电子,航空航天等各个领域都有广泛的应用,并被广泛用来分析和解决工程设计问题。
多体系统动力学基本理论

The orientation cosine matrix is A A1 A2 A3 (i j k i3 j3 k3 )
k 2 (k3 ) k (k1 )
j3
j2
1
i
j
k i1 k2 k k1 sin j2 cos k2 sin (sin i3 cos j3 ) cos k3 i1 i2 cos i3 sin j3 k2 k3
i1 j1 k1
cos sin 0 A1 sin cos 0 0 0 1
i
i1 (i2 ) i3
j
i1 j1 k1
i1 i2 j j 1 A2 2 , k1 k 2
(i1 )
i2 j2 k2
0 0 1 A2 0 cos sin 0 sin cos
i2 j2 k2
(k 2 )
i3 j3 k3
i2 i3 cos sin 0 j2 A3 j3 , A3 sin cos 0 k 2 k3 0 0 1 i i1 i2 i3 j j j j A1 1 A1 A2 2 A1 A2 A3 3 k k1 k 2 k3
Name DADS ADAMS Formulation method Newton Euler First Lagrange Results Time history Animation Time history Animation Frequency Response Time history
系统动力学建模步骤

系统动力学建模步骤一、引言系统动力学是一种研究复杂系统行为的方法,它通过建立数学模型来描述系统的结构和运动规律。
这种方法在工程、经济、社会科学等领域得到了广泛应用。
本文将介绍系统动力学建模的步骤。
二、确定研究对象和目标在进行系统动力学建模之前,首先需要明确研究对象和目标。
研究对象可以是一个生态系统、一个产业链、一个城市交通网络等等,而目标则是要解决什么问题或达到什么效果。
例如,我们可能想要了解某个生态系统中物种数量的变化规律,或者预测某个城市交通拥堵情况的发展趋势。
三、建立概念模型接下来,需要建立概念模型。
概念模型是对研究对象进行抽象和简化的过程,它用图形和符号表示出各个元素之间的关系。
例如,在研究生态系统时,我们可以将各物种看作节点,并用箭头表示它们之间的食物链关系。
四、确定变量及其关系在概念模型确定后,需要明确变量及其关系。
变量可以分为状态变量和流量变量。
状态变量是指系统中的某一状态,如生态系统中各物种的数量,而流量变量则是指这些状态之间的转移。
例如,在生态系统中,食物链上的物种数量就是状态变量,而它们之间的捕食关系就是流量变量。
五、建立数学模型建立数学模型是系统动力学建模的核心步骤。
在这一步骤中,需要将概念模型转化为数学方程组。
这些方程通常采用微分方程或差分方程来描述系统中各个元素之间的关系。
例如,在研究生态系统时,我们可以使用Lotka-Volterra模型来描述各物种之间的捕食关系。
六、进行仿真和验证建立好数学模型后,需要进行仿真和验证。
仿真可以通过计算机程序来实现,它可以帮助我们预测系统在不同条件下的行为。
验证则是通过与实际观测数据进行比较来检验模型的准确性。
如果模型与实际情况相符,则说明该模型具有很好的预测能力。
七、应用和优化最后一步是应用和优化模型。
应用包括将模型用于实际问题求解,并针对特定问题进行优化。
例如,在研究城市交通拥堵问题时,我们可以通过模拟不同的交通管理措施来找到最佳的解决方案。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、引言
1.1、从经典力学说起
刚体
经典力学
时间维
静力学
运动学
过程 运动
瞬间 静止
动力学
1、引言
1.2、从经典力学到系统动力学
经典动力学
刚体 (物理系统)
决策环节系统动力学 Nhomakorabea社会系统 (人机系统)
1、引言
1.3、再看系统结构
系统结构
静态结构 + 时、空维度
动态结构
系统结构模型
非线性
1. 原因与结果非线性 2. 时空分离性—滞后 3. 随机性
2、系统动力学
2.3、建模流程
明确目的
认识系统的结构、预测系统行为、 设计最佳参数、合理进行决策
确定系统边界
封闭的社会系统
因果关系分析
系统结构
建立SD模型
流程图、方程式
仿真实验
结果分析
模型修正
三、SD结构模型化原理
1 因果关系
因果箭 A
a. 水准(L)变量是积累变量,可定义在任何时点;而速率(R)变量只 在一个时段才有意义。
b. 决策者最为关注和需要输出的要素一般被处理成L变量。 c. 在反馈控制回路中,两个L变量或两个R变量不能直接相连 。 d. 为降低系统的阶次,应尽可能减少回路中L变量的个数。故在实际系
统描述中,辅助(A)变量在数量上一般是较多的。
因果关系图和流图 (4)
+
组织绩效
组织改善
( -)
+
-
组织缺陷
因果关系图和流图 (4)
+
组织绩效
组织改善
( -)
+
-
组织缺陷
多重反馈
+ +
人口 总数
-
+ -
出生 人数
+
死亡 人数
2 流图--流图符号
(1)常用要素 流 速率 水平变量 源与汇 参数
(2)流图符号
①流
实物流 信息流
R1
② 速率变量
R1
③ 水准变量
L1
④ 辅助变量
() 。
。
A1
⑤ 参数(量) ⑥ 源与汇 ⑦ 信息的取出
(常量) L。1
④ 辅助变量
。 A1
(初值) 。
(3)流图--流图举例
R1(利息1) L1
C1(利率)
R1(订货量) 库存量 I
(库存差额) D
Y(期望库存)
(出生人口) (人口总量) (死亡人口)
常量方程 (C方程) C C1=数值
赋初值方程(N方程) N L1=数值
或 “ L1=L10 , L10=数值”
2、一阶正反馈回路
人口 数
P
(+) +
L P•K=P•J+DT*PR•JK
N P=100
0
R PR•KL=C1*P•K
1 2
C C1=0.02
┆
年人口 增加
PR
P。
PR
。
C1(人口年自然增长率0.02)
p
P 100 102 104.04 ┆
PR 2 2.04 2.0808
┆
100
0 一阶正反馈(简单 人口问题)系统输 出特性曲线
3、一级负反馈回路
+
I
库存量
—
1000 R1
订货 量
R1
(—) +
L I•K=I•J+DT*R1•JK
库存 差额 D
期望库存Y
I
。。
Z
D
(订货调整时间,5)
D R1
I
。I 。Y(6000)
组织的艺术与实务,上海三联书店, 1998。
作者简介:1970年从斯坦福大学获工学学士后进入MIT攻读 管理硕士学位,在此期间被Forrester教授的SD整体动态搭 配的管理新理念所吸引。1978年获得博士学位后,一直和 MIT的工作伙伴及企业界人士一道,孜孜不倦地致力于将SD 与组织学习、创造原理、认知科学等融合,发展出一种人 类梦寐以求的组织蓝图—学习型组织。
R1
R2
P
C1(出生率)
C2(死亡率)
组织改善
。 组织 缺陷
组织 绩效
3 系统动力学原理
决策
(Rate) 源 速率变量
信息
行动
信息
流 反馈回路 (行动)
系统 状态
水准变量
(Level) 四个基本要素——状态、信息、决策、行动
两个基本变量——水准变量(L)、速率变量(R)
一个基本思想——反馈控制
5、 控制者
N I=1000 R R1•KL=D•K/Z
0 1000 5000 1000
A D•K=Y-I•K
1 2000 4000 800 1000
2、系统动力学
2.2、研究对象
Forrester (MIT)
系统 动力学
系统
动态行为 结构
理论 基础
控制论 信息论 决策论
系统动力学 模型
决策依据
2、系统动力学
2.2、研究对象:社会系统的基本特性
社会系统 SD的研究方法 非线性多重反馈系统
基本特征 决策环节
反馈
基本特性
自律性
1. 自主决策 2. 自我管理 3. 自我控制 4. 自我约束
+
-
B
A
B
A
B
因果链
B
D
+
++
A
C
B
D
-
-+
A
C
反馈回路
系统的 性质 行为
订货 速度
+
库存 差额
+
-
库存
-
量
因果关系图和流图 (1)
因果关系图和流图 (2)
库存量 +
-
订货量
( -)
库存差额
期望
库存
+
因果关系图和流图 (3)
出生 人口
+ (+)
+ (平均)出生率
+
- 人口
总量
()
死亡 人口
-
(平均)死亡率
(4)形成子结构及流图。
四、基本反馈回路的DYNAMO仿真分析
1、基本DYNAMO方程
水准方程(L方程) L L1·K=L1·J+DT*(RI·JK-RO·JK)
速率方程(R方程) R R1·KL=f ( L1·K,A1·K,…)
辅助方程(A方程)
A
A1·K=g(L1·K,A2·K,R1·JK,…)
ISM
系统动力学模型
二、系统动力学
2.1、产生与发展
Forrester (MIT)
工业动力学 20,50
工业系统
城市动力学 世界动力学
69、71
企业
更大的系统
> 城市 > 地区 > 国家 > 世界
学生
Meadows
系统动力学
增长的极限 1971
MIT世界模型
System Dynamics, SD/ J.W. Forrester(MIT) Industrial Dynamics (ID), 1959 Principles of Systems, 1968 Urban Dynamics (UD), 1969 World Dynamics (WD), 1971 SD, 1972 [美]彼得·圣吉(PeterM·Senge)著,第五项修炼—学习型
4、建模实例 水流系统
1、水塔 2、阀门 3、水箱
信息
4、阀门
源
速率 决策函数
决策
反馈 回路
实际 系统
信息
流(行动)
状态变量 水准
行动
5、流图-流图绘制程序和方法
(1)明确问题及其构成要素;
(2)绘制要素间相互作用关系的因果关系图。注意一定要 形成回路;
(3)确定变量类型(L变量、R变量和A变量)。将要素转化 为变量,是建模的关键一步。在此,应考虑以下几个具体原则:
