(完整版)交流电机坐标变换
交流电机坐标变换
a n 2 a 2 ( n 2 )
1
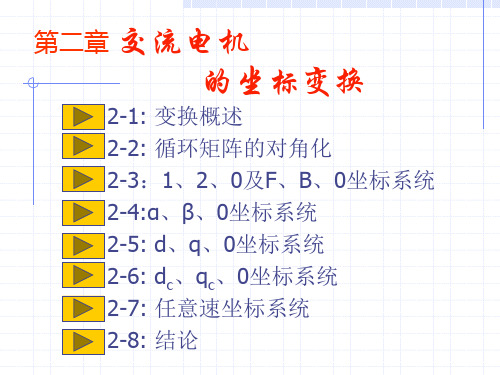
1 a a2 a n 1
1 1 1 1
这个变换矩阵将使置换矩阵π变成如下的对角矩阵:
a n 1 0 0 a n 2 D F 1πF 0 0 0 0
0 0 a 0
这时,变换矩阵满足条件
T1 (T* )T
既逆变换矩阵等于变换矩阵的共轭矩 阵的转置。
2-3.2 F、B、0坐标系统
如在变换矩阵的一般化中所述,变换矩阵也可以取为:
e j F a 2e j ae j
e j ae j a 2e j
1 1 1
如果上式中的θ就是转子的位置,则这个变换与120变换的 区别在于:120变换将坐标轴固定在定子轴线上,而FB0变 换则将坐标轴固定在转子上。
因此变换矩阵为:
2 F 2 2 2
3 1 3 1 3 3 1
为保证变换矩阵的可逆,上式中
2 / 3 2 / 3
2-3:1、2、0及F、B、0坐标系统
1、2、0坐标系统 F、B、0坐标系统
2-3.1: 1、2、0坐标系统
LS 0 L M S 0 M S0
M S0 LS 0 M S0
M S0 M S0 LS 0
它的特征根由一个单重根λ1和一个两重根λ2构成:
1 LS 0 2 M S 0 2 3 LS 0 M S 0
与这三个特征根对应的特征向量
3 1 2 X1 1 , X 2 2 , X 3 3 2 3 1 2 3
这样的矩阵称为循环矩阵。n阶循环矩阵只有n个不同的元素:
dq坐标变换数学原理解析

dq坐标变换数学原理解析
3.2 坐标变换和动态数学模型的简化
上节中虽已推导出异步电机的动态数 学模型,但是,要分析和求解这组非线性 方程显然是十分困难的。在实际应用中必 须设法予以简化,简化的基本方法是坐标 变换。
一、 坐标变换的基本思路
直流电机的数学模型比较简单: • 虽然电枢本身是旋转的,但其绕组通过换向器电 刷接到端接板上,因此,电枢磁动势的轴线始终被电 刷限定在 q 轴位置上,其效果好象一个在 q 轴上静止 的绕组一样。
由于进行坐标变换的是电流(代表磁动势) 的空间矢量,所以这样通过坐标变换实现的控 制系统就叫作矢量控制系统(Vector Control System)。
3.3.2 异步电动机在按转子磁场定向的 MT同步旋转坐标系中的数学模型
❖ 上述是矢量控制的基本思路,其中的矢 量变换包括三相/两相变换和同步旋转 变换。在进行两相同步旋转坐标变换时,
此方法也同样适用于电压和磁链的变换。
• 变换过程
3/2变换
C2s/2r
ABC坐标系
坐标系
dq坐标系
三、异步电动机在、静止坐标系上的
数学模型
把异步电机在三相
β
静 止 ABC 坐 标 系 上 的
Rs
数学模型变换到两相
Ls
Lm
坐标系上,由于两相
坐标轴互相垂直,两 相绕组之间没有磁的 耦合,仅此一点,就 会使数学模型简单了 许多。
在这里,不同电机模型彼此等效的原则 是:在不同坐标下所产生的磁动势完全一致。
(2)等效的两相交流电机绕组
两相静止绕组 和 ,它
们在空间互差90°,通以时间 上互差90°的两相平衡交流电 流,也产生旋转磁动势 F 。
永磁同步电动机(PMSM)三相坐标系的数学模型

永磁同步电动机(PMSM)三相坐标系的数学模型2 PMSM 三相坐标系的数学模型为方便分析起见,将三相永磁的同步电动机看作是理想的电机,也就是说它符合下列假设:(1) 转子上面没有阻尼绕组;定子中各个绕组的电枢电阻、电感值相等,三相定子的绕组按对称的星形分布;(2) 其气隙磁场服从正弦分布而且各次谐波忽略不计,感应电动势也服从正弦分布;(3) 永磁体的等效的励磁电流恒定不改变;电机中的涡流、趋肤效应、电机铁芯饱和和磁滞损耗的影响均忽略不计;温度与频率不影响电机的参数。
坐标系正方向的选取: (1) 转子逆时针方向旋转为正; (2) 正向电流生出正向磁链;(3) 电压,电流的正方向按照电动机的惯例。
则静止三相坐标系里PMSM 的定子侧电压方程3333s s s s u R i p ψ=⋅+ (4-1)静止三相坐标系里PMSM 的定子侧磁链方程3333()s s s f s L i F ψψθ=⋅+⋅ (4-2) 式中,3A s B C i i i i ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦,3000000s R R R R ⎛⎫ ⎪=⎪ ⎪⎝⎭,3A s B C ψψψψ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦ 3A s B C u u u u ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦,3sin ()sin(120)sin(120)s F θθθθ⎡⎤⎢⎥=-︒⎢⎥⎢⎥+︒⎣⎦3331cos120cos 240100cos1201cos120010cos 240cos1201001s m l L L L ︒︒⎛⎫⎛⎫⎪ ⎪=︒︒+ ⎪ ⎪ ⎪ ⎪︒︒⎝⎭⎝⎭电机统一理论和机电能量转换告诉我们,电机的电磁力矩[37]*I m ()s s e p T n i ψ=- (4-3) 式中,*代表取共轭复数,Im 代表取虚部。
3 PMSMdq 坐标系的数学模型三相交流电机是一个耦合强、非线性、阶次高的多变量系统,它在三相静止的坐标系里的数学模型相当复杂,应用传统的控制策略对其实现交流调速有很大的困难,所以对于一般的三相交流电机常常应用矢量控制的方法,采用坐标变换,把三相交流的绕组等效变换成两相互相垂直的交流绕组或者旋转的两相直流的绕组,等效变换以后其产生的磁动势相等,系统的变量之间得到了部分的解耦,它的数学模型得到了大大简化,使得对于系统的分析和控制也简化了很多,使得它的数学模型与比较简单的直流电机类似[52]。
(整理)坐标变换的原理和实现方法

由第二讲的内容可知,在三相静止坐标系中,异步电动机数学模型是一个多输入、多输出、非线性、强耦合的控制对象,为了实现转矩和磁链之间的解耦控制,以提高调速系统的动静态性能,必须对异步电动机的数学模型进行坐标变换。
3.1 变换矩阵的确定原则坐标变换的数学表达式可以用矩阵方程表示为y=ax (3-1)式(3-1)表示利用矩阵a将一组变量x变换为另一组变量y,其中系数矩阵a称为变换矩阵,例如,设x是交流电机三相轴系上的电流,经过矩阵a的变换得到y,可以认为y是另一轴系上的电流。
这时,a称为电流变换矩阵,类似的还有电压变换矩阵、阻抗变换矩阵等,进行坐标变换的原则如下:(1)确定电流变换矩时,应遵守变换前后所产生的旋转磁场等效的原则;(2)为了矩阵运算的简单、方便,要求电流变换矩阵应为正交矩阵;(3)确定电压变换矩阵和阻抗变换矩阵时,应遵守变换前后电机功率不变的原则,即变换前后功率不变。
假设电流坐标变换方程为:i=ci′ (3-2)式中,i′为新变量,i称为原变量,c为电流变换矩阵。
电压坐标变换方程为:u′=bu (3-3)式中,u′为新变量,u为原变量,b为电压变换矩阵。
根据功率不变原则,可以证明:b=ct (3-4)式中,ct为矩阵c的转置矩阵。
以上表明,当按照功率不变约束条件进行变换时,若已知电流变换矩阵就可以确定电压变换矩阵。
3.2 定子绕组轴系的变换(a-b-c<=>α-β)所谓相变换就是三相轴系到二相轴系或二相轴系到三相轴系的变换,简称3/2变换或2/3变换。
三相轴系和二相轴系之间的关系如图3-1所示,为了方便起见,令三相的a轴与两相的α轴重合。
假设磁势波形是按正弦分布,或只计其基波分量,当二者的旋转磁场完全等效时,合成磁势沿相同轴向的分量必定相等,即三相绕组和二相组绕的瞬时磁势沿α、β轴的投影应该相等,即:(3-5)式中,n3、n2分别为三相电机和两相电机每相定子绕组的有效匝数。
经计算并整理之后可得:(3-6)(3-7)图3-1 三相定子绕组和二相定子绕组中磁势的空间矢量位置关系用矩阵表示为:(3-8)如果规定三相电流为原电流i,两相电流为新电流i′,根据电流变换的定义式(3-2),式(3-8)具有i′=c-1i的形式,为了通过求逆得到c就要引进另一个独立于isα和isβ的新变量,记这个新变量为io,称之为零序电流,并定义为:(3-9)式中,k为待定系数。
三相永磁同步电机坐标变换推导

一、概述如今,在工业界中,三相永磁同步电机因其结构简单、运行稳定、效率高等特点成为了一种常见的电机类型。
而电机的控制则是保证电机能够稳定高效运行的关键。
掌握三相永磁同步电机的控制原理对于工程师来说至关重要。
在三相永磁同步电机的控制中,坐标变换技术是一种常用的数学方法,通过坐标变换可以将三相电机的控制问题转换为直流电机控制问题,从而简化了控制器的设计。
二、三相永磁同步电机的数学模型1. 三相永磁同步电机是一种特殊的同步电机,它的定子绕组被连接到一个三相交流电源上。
它的转子上装有永磁体,因此在没有机械负载情况下依然能够产生恒定的磁场,这使得电机具有较高的效率和响应速度。
2. 为了完成对三相永磁同步电机的控制,我们需要建立其数学模型。
假设电机有a、b、c三个定子绕组,每个绕组的电流分别为ia、ib、ic,电机的磁链为Ψ,电机的控制变量为u,那么电机的数学模型可以表示为:其中,Ld和Lq分别表示d轴和q轴上的电感,ψp是永磁体的磁通,M是电机的磁链,J是电机的转动惯量,B是电机的阻尼系数,Te为电机的电磁转矩。
三、坐标变换推导1. 在三相永磁同步电机的控制中,我们通常使用dq坐标系来描述电机的运动状态。
在dq坐标系中,d轴与永磁体的磁通方向一致,q轴与d轴垂直。
通过dq坐标变换可以将三相电机的控制问题转换为直流电机的控制问题。
2. 我们可以通过以下的数学推导来实现坐标变换:在直角坐标系下,电机的三相电流可以表示为:假设θ为电机的旋转角度,那么dq坐标系转换可以表示为:在dq轴上,电机的电流可以表示为:通过以上推导,我们可以得到电机在dq坐标系下的控制方程,从而可以实现对电机的控制。
四、结论通过以上的推导,我们可以看到坐标变换技三相永磁同步电机坐标变换推导是电机控制中的关键步骤。
坐标变换可以让我们更方便地对电机进行控制,简化了控制器的设计流程,并且使得控制更加高效和稳定。
在坐标变换的基础上,我们可以进一步推导出电机的控制方程,从而实现对电机的精确控制。
交流电机数学模型与坐标变换

磁链方程
d1 Ls q1 0 d2 Lm q2 0
Lm
0 Ls 0 Lm
Lm 0 Lr 0
0 id1 i Lm q1 0 id2 Lr iq2
0 1 L 1 Te pn I T I pn I T 2 2 Lr S
LSr I 0
10
2017/9/24
交流电机数学模型与坐标变换
浙江大学电气工程学院 代入 I ,
—交流电机调速理论与方法—
I T ,可得
Te = pnLm1[(iAia+iBib+iCic)sinθ+ (iAib+iBic+iCia)sin(θ+120˚)
d c uc ic R2 dt
U RI p
5 2017/9/24 交流电机数学模型与坐标变换
浙江大学电气工程学院
—交流电机调速理论与方法—
(2)磁链方程
A LAA B LBA C LCA a LaA L b bA LcA c
—交流电机调速理论与方法—
折算后的定转子匝数相等,磁阻相等 Laa=Lbb=Lcc=Lm1+Ll2
两相间互感: (a) 定子三相彼此之间,转子三相之间彼此间的位置固定,故为常值
(b) 定子任一相与转子任一相间位置总是变化,为θ的函数
(a)类:LAB=Lm1cos120˚=-Lm1/2 LAC=Lm1cos(-120˚)=-Lm1/2 故: LAB=LBC=LCA=LBA=LCB=LAC=-Lm1/2 Lab=Lbc=Lca=Lba=Lcb=Lac=-Lm1/2 (b)类: LAa=LaA=LBb=LbB=LCc=LcC=Lm1cosθ LAb=LbA=LBc=LcB=LCa=LaC=Lm1cos(θ+120˚) LAc=LcA=LBa=LaB=LCb=LbC=Lm1cos(θ-120˚)
三相坐标系和二相坐标系转换

交流电动机矢量控制变压变频调速系统(三)第三讲坐标变换的原理和实现方法收藏此信息打印该信息添加:李华德来源:未知由第二讲的内容可知,在三相静止坐标系中,异步电动机数学模型是一个多输入、多输出、非线性、强耦合的控制对象,为了实现转矩和磁链之间的解耦控制,以提高调速系统的动静态性能,必须对异步电动机的数学模型进行坐标变换。
3.1 变换矩阵的确定原则坐标变换的数学表达式可以用矩阵方程表示为y=ax (3-1)式(3-1)表示利用矩阵a将一组变量x变换为另一组变量y,其中系数矩阵a称为变换矩阵,例如,设x是交流电机三相轴系上的电流,经过矩阵a的变换得到y,可以认为y是另一轴系上的电流。
这时,a称为电流变换矩阵,类似的还有电压变换矩阵、阻抗变换矩阵等,进行坐标变换的原则如下:(1)确定电流变换矩时,应遵守变换前后所产生的旋转磁场等效的原则;(2)为了矩阵运算的简单、方便,要求电流变换矩阵应为正交矩阵;(3)确定电压变换矩阵和阻抗变换矩阵时,应遵守变换前后电机功率不变的原则,即变换前后功率不变。
假设电流坐标变换方程为:i=ci′ (3-2)式中,i′为新变量,i称为原变量,c为电流变换矩阵。
电压坐标变换方程为:u′=bu (3-3)式中,u′为新变量,u为原变量,b为电压变换矩阵。
根据功率不变原则,可以证明:b=ct (3-4)式中,ct为矩阵c的转置矩阵。
以上表明,当按照功率不变约束条件进行变换时,若已知电流变换矩阵就可以确定电压变换矩阵。
3.2 定子绕组轴系的变换(a-b-c<=>α-β)所谓相变换就是三相轴系到二相轴系或二相轴系到三相轴系的变换,简称3/2变换或2/3变换。
三相轴系和二相轴系之间的关系如图3-1所示,为了方便起见,令三相的a轴与两相的α轴重合。
假设磁势波形是按正弦分布,或只计其基波分量,当二者的旋转磁场完全等效时,合成磁势沿相同轴向的分量必定相等,即三相绕组和二相组绕的瞬时磁势沿α、β轴的投影应该相等,即:(3-5)式中,n3、n2分别为三相电机和两相电机每相定子绕组的有效匝数。
电机坐标变换的应用11

坐标变换的应用摘要:坐标变换理论从提出至今已经过去了将近一个世纪,其在电气工程领域被广泛应用,而且其不但在传统的电机矢量控制、瞬态分析领域被广泛采用,而且随着一些新的算法的产生,其在电机故障诊断、电网电能质量监测与控制领域也被采用。
由于其易于将复杂的、高阶的、非线性的、时变的问题得以简化,随着对其研究的深入,其应用范围与前景还将更加广阔。
关键词:坐标变换、矢量控制、瞬态分析、故障诊断、PQ问题一、坐标变换理论的提出坐标变换实质上是数学上的线性变换,电气工程领域的坐标变换理论的提出是有其背景的。
这种原理的基本出发点是:考虑到异步电机是一个多变量、强耦合、非线性的时变参数系统。
因此在20世纪20年代, Park 利用固定于转子上的参考坐标系上的量(如电压、电流、磁链等) 等效代替定子绕组中的量,从而消除了同步电机数学模型中的时变电感。
Park的这一思想一般被称为电机坐标变换理论,引起了电机分析方法的一场革命。
受此影响,Krause于1965 年将感应电机的定、转子绕组的变量同时变换到以任意速度旋转的参考坐标系中,建立了一般化无时变电感的感应电机数学模型【1】。
其实对电机进行分析时,所进行的坐标变换内容是十分丰富的,不但可将静止的坐标系变换到同一空间中另一个旋转的坐标系,或将实平面的坐标系变换到复平面的坐标系,还可以将坐标系统的空间扩展到N维,这都是对电机这种复杂的机电系统分析时所作的对策。
但这里需指出,既然是分析具体问题时提出的电机坐标变换理论,这里的坐标变换就是有约束的,一般有两种制约1)功率不变;2)气隙合成磁动势不变。
一般以第一种最为常用。
电机分析中常用的坐标变换有【2~3】:1)dq0系统及其派生的MT0系统dq0系统基于双反应理论,d轴与转子直轴重合,q轴超前d轴90度,坐标系与转子同向以同步速旋转;MT0左边系统又称磁场定向系统,M轴与电机合成磁场轴线一致,T轴超前M轴90度坐标系与转子同向以同步速旋转。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
若记 则
k
ej
2 n
k
,
k
0,1,2,
,n 1
a
ej
2 n
k ak
为求与特征根λk对应的特征向量,将之代入特
征方程,并令 x1 1/ ,n得
Xk
11 n
k
2k
n1 T k
按k=n-1,n-2,…,1,0的顺序,将各特征根代入上式就 得到n个特征向量。
或者 因此
πX X , X x1 x2 xn T
x2 x1 , x3 x2 ,
xn xn1 , x1 xn x1 xn 2 xn1 n1x2 n x1
这样,矩阵π的n个特征n个特征根:
A LA
Φ
B
M BA
N M NA
M AB LB M NB
M AN iA
M BN
iB
L
I
LN iN
假定存在一个非奇异矩阵T,将Φ变换成Φc,将I变换成Ic:
Φ T Φc , Φc 1 2 n I T Ic , Ic i1 i2 in
2-2.1 电感矩阵的特点
#由于互感的对等性,电感矩阵是对 称矩阵:
LA M AB M AC M AN
L
M AB M AC
M AN
LB M BC
M BN
M BC LC M CN
M BN M CN
LN
由于Mij=Mji, n阶对称矩阵中只有n(n+1)/2各不同 的元素。
#n相对称系统的电感矩阵是循环的
n相对称系统中各相自感相等,相同相对位置的两相 间的互感相等。即:
Li Lj , M i, j M i1, j1
这样的矩阵称为循环矩阵。n阶循环矩阵只有n个不同的元素:
LA M AB M AC M AN
L
M AN M AM
新的磁链φ1、 φ2、…、 φn称为实际磁链φA、 φB、…、 φN的分 量;同样i1、i2、…、in称为实际电流的分量。
利用这个变换,磁链方程变成:
TΦc L TI c
所以
Φc T1 L TI c
或者
Φc Lc Ic
其中
Lc T1 L T
如果变换T明显使得新的电感矩阵Lc较变换前的电感矩阵L 简单,这个变换才是有意义的。如果Lc变成一个对角矩阵, 那这个变换是最理想的:
1 L1 0
Φc
2
0
L2
n 0 0
0 i1 0i2 LcIc Ln in
2-2: 循环矩阵的对角化
1. 电感矩阵的特点 2. 循环矩阵的对角化 3. 电感矩阵的对角化 4. 变换矩阵的一般化 5. 三阶循环对称电感矩阵的变换
LA LA
M
a n 1
AB
M
an2
AB
LA M ABa
M
a 2 ( n 1)
AC
M a(n1)(n1) AN
M
a2(n2)
AC
M a(n1)(n2) AN
M ACa2
M
a ( n 1)
AN
LA M AB M AC M AN
0 0 0 0 1
1 0 0 0 0
不难证明,循环电感矩阵可以表示成
L
LA1 M ABπ M ACπ2
M
πn1
AN
根据矩阵理论,任何可以对角化矩阵π的变换T,也可以对 角化循环矩阵L。矩阵π称为置换矩阵。
2-2.2 循环矩阵的对角化
n阶置换矩阵π的n个特征根由下面特征方程给出:
2-2.4 变换矩阵的一般化
若在生成特征向量时,不是令x1=1,而是令其等于 一个模为1的复数,则
Xk e jk 1 k
2k
n1 T k
由此得到更加一般化的变换矩阵
e jn1
e jn2
e j1
Fg
n1 jn1
1 aa ee 2(n1) jn1 n
第二章 交流电机 的坐标变换
2-1: 变换概述 2-2: 循环矩阵的对角化 2-3:1、2、0及F、B、0坐标系统 2-4:α、β、0坐标系统 2-5: d、q、0坐标系统 2-6: dc、qc、0坐标系统 2-7: 任意速坐标系统 2-8: 结论
2-1: 变换概述
一个电机系统的磁链方程可以写成:
0 an2
0 0
0 0 0 0 a 0 0 1
2-2.3 电感矩阵的对角化
D F1πF π FDF 1
由此可以推导得
π2 {FDF 1}{FDF 1} FD 2F1
同样地
π3 FD 3F1 , ,πn1 FD F n1 1
M AB
LA M AN
M AC
M AB LA M AD
M AM M AL
LA
若n阶循环矩阵又是对称的,则根据n是奇数或偶数,其中只 有(n+1)/2或(n+2)/2个不同的元素。
#最简单的循环矩阵
0 1 0 0 0 0 0 1 0 0 π
这样
L F(LA1 M ABD M ACD2 M AN Dn1)F1
变换后的电感矩阵
LT F1LF LA1 M ABD M ACD2 M ANDn1
由于D,D2,…,Dn-1是对角矩阵,因此LT也是一个对角 矩阵:
LT
diag
n个特征向量构成了如下的变换矩阵:
1
F
1
an1 a2(n1)
n
a ( n 1)( n 1)
1
an2
a2(n2)
a (n1)(n2)
1 1 a 1 a2 1 an1 1
这个变换矩阵将使置换矩阵π变成如下的对角矩阵:
a n 1 0 D F1πF 0 0
