九年级上册一元二次方程易错题(Word版 含答案)
(易错题)初中数学九年级数学上册第一单元《一元二次方程》检测题(包含答案解析)
一、选择题1．一面足够长的墙，用总长为30米的木栅栏（图中的虚线）围一个矩形场地ABCD ，中间用栅栏隔成同样三块，若要围成的矩形面积为54平方米，设垂直于墙的边长为x 米，则x 的值为（ ）A ．3B ．4C ．3或5D ．3或4.5 2．用配方法解方程x 2﹣6x ﹣3＝0，此方程可变形为（ ） A ．（x ﹣3）2＝3B ．（x ﹣3）2＝6C ．（x+3）2＝12D ．（x ﹣3）2＝12 3．用配方法解方程x 2﹣4x ﹣7＝0，可变形为（ ） A ．（x+2）2＝3 B ．（x+2）2＝11 C ．（x ﹣2）2＝3 D ．（x ﹣2）2＝11 4．用直接开平方的方法解方程22(31)(25)x x +=-，做法正确的是（ ）A ．3125x x +=-B ．31(25)x x +=--C ．31(25)x x +=±-D ．3125x x +=±- 5．关于x 的一元二次方程()2230x a a x a +-+=的两个实数根互为倒数，则a 的值为（ ）A ．-3B ．0C ．1D ．-3或0 6．用配方法解方程2x 4x 70+-=，方程应变形为（ ） A ．2(2)3x += B ．2 (x+2)11= C ．2 (2)3?x -= D ．2()211x -= 7．新冠肺炎是一种传染性极强的疾病，如果有一人患病，经过两轮传染后有81人患病，设每轮传染中平均一个人传染了x 个人，下列列式正确是（ ）A ．(1)81x x x ++=B ．2181x x ++=C ．1(1)81x x x +++=D ．(1)81x x += 8．某中学举办篮球友谊赛，参赛的每两个队之间只比赛1场，共比赛10场，则参加此次比赛的球队数是（ ）A ．4B ．5C ．6D ．79．若方程()200++=≠ax bx c a 中，,,a b c 满足420a b c ++=和420a b c -+=，则方程的根是（ ）A ．1,0B ．1,0-C ．1,1-D ．2,2- 10．关于x 的一元二次方程（a －1）x²－x ＋a²－1＝0的一个根是0，则a 的值为（ ）A ．1B ．－1C ．1或－1D ．0 11．已知2x 2+x ﹣1＝0的两根为x 1、x 2，则x 1•x 2的值为（ ）A ．1B ．﹣1C ．12D ．12- 12．若()()2222230xy x y ++--=，则22x y +的值是（ ） A ．3 B ．-1 C ．3或1 D ．3或-1 二、填空题13．解方程：268x x +=-解：两边同时加_________，得26x x ++________8=-+________则方程可化为（_______）2=________两边直接开平方得_____________即_________或_____________所以1x =__________，2x =___________．14．当a =______，b =_______时，多项式22222425a ab b a b -+--+有最小值，这个最小值是_____．15．一元二次方程2210x x -+=的一次项系数为_________．16．一元二次方程22(1)210a x x a +++-=，有一个根为零，则a 的值为________． 17．对于任意实数a 、b ，定义：a ◆b ＝a 2+ab +b 2．若方程（x ◆2）﹣5＝0的两根记为m 、n ，则（m +2）（n +2）＝_____．18．若t 是一元二次方程()200++=≠ax bx c a 的根，则判别式24b ac =-△与完全平方式()22M at b =+的大小关系为___________19．若a ，b 是方程22430x x +-=的两根，则22a ab b +-=________．20．已知2x =是关于x 的方程220x x m ++=的一个根，则m =_________． 三、解答题21．解方程：2250x x +-=．22．（1）x 2﹣8x+1＝0；（2）2（x ﹣2）2＝x 2﹣4．23．若a 为方程2(16x =的一个正根，b 为方程22113y y -+=的一个负根，求+a b 的值．24．解方程：（1）x 2+6x ﹣2＝0．（2）（2x ﹣1）2＝x （3x +2）﹣7．25．用适当的方法解方程：（l ）2(3)26x x +=+（2）2810x x -+=．26．某地区2018年投入教育经费2000万元，2020年投入教育经费2420万元（1）求2018年至2020年该地区投入教育经费的年平均增长率；（2）按照义务教育法规定，教育经费的投入不低于国民生产总值的百分之四，结合该地区国民生产总值的增长情况，该地区到2022年需投入教育经费2900万元，如果按（1）中教育经费投入的增长率，到2022年该地区投入的教育经费是否能达到2900万元?请说明理由．【参考答案】***试卷处理标记，请不要删除一、选择题1．D解析：D【分析】设AD 长为x 米，四边形ABCD 是矩形，根据矩形的性质，即可求得AB 的长；根据题意可得方程x （30−4x ）＝54，解此方程即可求得x 的值．【详解】解：设与墙头垂直的边AD 长为x 米，四边形ABCD 是矩形，∴BC ＝MN ＝PQ ＝x 米，∴AB ＝30−AD−MN−PQ−BC ＝30−4x （米），根据题意得：x （30−4x ）＝54，解得：x ＝3或x ＝4.5，∴AD 的长为3或4.5米.故选：D ．【点睛】考查了一元二次方程的应用中的围墙问题，正确列出一元二次方程，并注意解要符合实际意义．2．D【分析】先移项，再把方程两边同时加上一次项系数一半的平方，最后配方即可得新答案．【详解】由原方程移项得：x 2﹣6x ＝3，方程两边同时加上一次项系数一半的平方得：x 2﹣6x+9＝12，配方得；（x ﹣3）2＝12．故选：D ．【点睛】此题主要考查配方法的运用，配方法的一般步骤为：移项、二次项系数化为1、两边同时加上一次项系数一半的平方、配方完成；熟练掌握配方法的步骤并熟记完全平方公式是解题关键．3．D解析：D【分析】方程常数项移到右边，两边加上4变形得到结果即可．【详解】解：x 2﹣4x ﹣7＝0，移项得：247x x -=配方得：24474x x -+=+ ，即2()211x -=故答案为：D ．【点睛】本题考查了解一元二次方程-配方法，熟练掌握完全平方公式是解题的关键．4．C解析：C【分析】一元二次方程22(31)(25)x x +=-，表示两个式子的平方相等，因而这两个数相等或互为相反数，据此即可把方程转化为两个一元一次方程，即可求解．【详解】解：22(31)(25)x x +=-开方得31(25)x x +=±-，故选：C ．【点睛】本题考查了解一元二次方程-直接开平方法，关键是将方程右侧看做一个非负已知数，根据法则：要把方程化为“左平方，右常数，先把系数化为1，再开平方取正负，分开求得方程解”来求解． 5．C解析：C根据方程两个实数根互为倒数，得到两根之积为1，利用根与系数的关系求出a 的值即可．【详解】解：∵关于x 的一元二次方程x 2+（a 2-3a ）x+a=0的两个实数根互为倒数，∴x 1•x 2=a=1．故选：C ．【点睛】本题考查了根与系数的关系，能熟记根与系数的关系的内容是解此题的关键，注意：已知一元二次方程ax 2+bx+c=0（a 、b 、c 为常数，a≠0，b 2-4ac≥0）的两根是x 1，x 2，那么x 1+x 2=-b a ，x 1•x 2=c a． 6．B解析：B【分析】根据配方法解一元二次方程的方法解答即可．【详解】解：用配方法解方程2470x x ，方程应变形为24411x x ++=，即()2211x +=． 故选：B ．【点睛】本题考查了一元二次方程的解法，熟练掌握配方的方法是解题的关键． 7．C解析：C【分析】平均一人传染了x 人，根据有一人患病，第一轮有（x+1）人患病，第二轮共有x+1+（x+1）x 人，即81人患病，由此列方程求解．【详解】解：设每轮传染中平均一个人传染了x 个人，根据题意得，x+1+（x+1）x=81故选：C ．【点睛】本题考查了一元二次方程的应用，关键是得到两轮传染数量关系，从而可列方程求解． 8．B解析：B【分析】根据球赛问题模型列出方程即可求解．【详解】解：设参加此次比赛的球队数为x 队，根据题意得：12x （x-1）=10， 化简，得x 2-x-20=0，解得x 1=5，x 2=-4（舍去），∴参加此次比赛的球队数是5队．故选：B ．【点睛】本题考查了一元二次方程的应用，解决本题的关键是掌握一元二次方程应用问题中的球赛问题．9．D解析：D【分析】联立420a b c ++=和420a b c -+=，前式减后式，可得0b =，前式加后式，可得4c a =-，将a 、c 代入原方程计算求出方程的根．【详解】∵根据题意可得：420420a b c a b c ++=⎧⎨-+=⎩①②， ①－②＝40b =，得0b =，①＋②＝820a c +=，∴解得：0b =，4c a =-．将a 、b 、c 代入原方程()200++=≠ax bx c a 可得， ∵240ax bx a +-=，240ax a -=24ax a =∴2x =±故选：D ．【点睛】本题考查解一元二次方程，联立关于a 、b 、c 的方程组，由方程组推出a 、b 、c 的数量关系是解题关键．10．B解析：B【分析】把0x =代入，求出a 的值即可．【详解】解：把0x =代入可得210a -=，解得1a =±，∵一元二次方程二次项系数不为0，∴1a ≠，∴1a =-，故选：B ．【点睛】本题考查一元二次方程的解，注意二次项系数不为0．11．D解析：D【分析】直接利用根与系数的关系解答．【详解】解：∵2x 2+x ﹣1＝0的两根为x 1、x 2，∴x 1•x 2＝12-＝﹣12． 故选：D ．【点睛】 此题主要考查了根与系数的关系，一元二次方程ax 2+bx+c=0（a≠0）的根与系数的关系为：x 1+x 2=-b a ，x 1•x 2=c a． 12．A解析：A【分析】用22a x y =+，解出关于a 的方程，取正值即为22x y +的值是．【详解】解：令22a x y =+，则(2)30a a --=，即2230a a --=，即(3)(1)0a a ，解得13a =，21a =-，又因为220a x y =+>，所以3a =故22x y +的值是3，故选：A ．【点睛】本题考查解一元二次方程，掌握换元思想可以使做题简单，但需注意220a x y =+>． 二、填空题13．999x+31x+3=±1x+3=1x+3=-1-2-4【分析】根据配方法求解即可【详解】解：两边同时加9得99则方程可化为1两边直接开平方得x+3=±1即x+3=1或x+3=-1所以-2-4故答案解析：9 9 9 x+3 1 x+3=±1 x+3=1 x+3=-1 -2 -4【分析】根据配方法求解即可．【详解】解：两边同时加9，得26x x ++98=-+9，则方程可化为()23x +=1，两边直接开平方得x+3=±1，即x+3=1或x+3=-1，所以1x =-2，2x =-4．故答案为：9；9；9；x+3；1；x+3=±1；x+3=1；x+3=-1；-2；-4．【点睛】本题考查了配方法的一般步骤：（1）把常数项移到等号的右边；（2）把二次项的系数化为1；（3）等式两边同时加上一次项系数一半的平方．选择用配方法解一元二次方程时，最好使方程的二次项的系数为1，一次项的系数是2的倍数． 14．4315【分析】利用配方法将多项式转化为然后利用非负数的性质进行解答【详解】解：===∴当a=4b=3时多项式有最小值15故答案为：4315【点睛】此题考查了配方法的应用以及非负数的性质熟练掌握完全解析：4 3 15【分析】利用配方法将多项式22222425a ab b a b -+--+转化为22(1)(3)15a b b --+-+，然后利用非负数的性质进行解答．【详解】解：22222425a ab b a b -+--+=22222691152b a a b b b a b --+-+++++=2222(1)(1)(3)15a a b b b -++-+++=22(1)(3)15a b b --+-+∴当a=4，b=3时，多项式22222425a ab b a b -+--+有最小值15．故答案为：4，3，15．【点睛】此题考查了配方法的应用，以及非负数的性质，熟练掌握完全平方公式是解本题的关键． 15．-2【分析】根据一元二次方程的一次项系数的定义即可求解【详解】解：一元二次方程x2－2x ＋1＝0一次项系数是：－2故答案为：－2【点睛】此题考查了一元二次方程的一般形式准确掌握一般式中的相关概念是解解析：-2【分析】根据一元二次方程的一次项系数的定义即可求解．【详解】解：一元二次方程x2－2x＋1＝0一次项系数是：－2．故答案为：－2．【点睛】此题考查了一元二次方程的一般形式，准确掌握一般式中的相关概念是解题的关键．16．1【分析】根据一元二次方程的解的定义把x=0代入（a+1）x2+2x+a2-1=0再解关于a的方程然后利用一元二次方程的定义确定a的值【详解】解：把x=0代入（a+1）x2+2x+a2-1=0得a2解析：1【分析】根据一元二次方程的解的定义，把x=0代入（a+1）x2+2x+a2-1=0，再解关于a的方程，然后利用一元二次方程的定义确定a的值．【详解】解：把x=0代入（a+1）x2+2x+a2-1=0得a2-1=0，解得a=1或a=-1，而a+1≠0，所以a的值为1．故答案为：1．【点睛】本题考查了一元二次方程的解：能使一元二次方程左右两边相等的未知数的值是一元二次方程的解．17．-1【分析】根据新定义可得出mn为方程x2＋2x−1＝0的两个根利用根与系数的关系可得出m＋n＝−2mn＝−1变形（m＋2）（n＋2）得到mn＋2（m＋n）＋4然后利用整体代入得方法进行计算【详解】解析：-1【分析】根据新定义可得出m、n为方程x2＋2x−1＝0的两个根，利用根与系数的关系可得出m＋n ＝−2、mn＝−1，变形（m＋2）（n＋2）得到mn＋2（m＋n）＋4然后利用整体代入得方法进行计算．【详解】解：∵（x◆2）﹣5＝x2+2x+4﹣5，∴m、n为方程x2+2x﹣1＝0的两个根，∴m+n＝﹣2，mn＝﹣1，∴（m+2）（n+2）＝mn+2（m+n）+4＝﹣1+2×（﹣2）+4＝﹣1．故答案为﹣1．【点睛】本题考查了一元二次方程ax 2＋bx ＋c ＝0（a≠0）的根与系数的关系：若方程两根为x 1，x 2，则x 1＋x 2＝b a -，x 1•x 2＝c a． 18．相等【分析】由t 是一元二次方程()的根利用公式法解一元二次方程即可得出t 的值将其代入完全平方式中即可得出M 的值由此即可得出结论【详解】∵t 是一元二次方程()的根∴或当时则；当时则；∴故答案为：相等【解析：相等【分析】由t 是一元二次方程20ax bx c ++=(0a ≠)的根利用公式法解一元二次方程即可得出t 的值，将其代入完全平方式()22M at b =+中即可得出M 的值，由此即可得出结论．【详解】∵t 是一元二次方程20ax bx c ++=(0a ≠)的根，∴t =t =当t =()224M b b b ac =-=-；当t =时，则()224M b b b ac =-=-； ∴24b ac M =-=．故答案为：相等．【点睛】本题考查了根的判别式、完全平方式以及利用公式法解一元二次方程，利用公式法解一元二次方程求出t 值是解题的关键．19．4【分析】根据根与系数的关系得出a+b=-2ab=-再变形后代入即可求出答案【详解】解：∵是方程的两根∴故答案为：4【点睛】本题考查了根与系数的关系能够整体代入是解此题的关键解析：4【分析】根据根与系数的关系得出a+b=-2，ab=-32，再变形后代入，即可求出答案． 【详解】解：∵a ，b 是方程22430x x +-=的两根， ∴42232a b ab ⎧+=-=-⎪⎪⎨⎪=-⎪⎩，()()()222222224a ab b a a b b a b a b +-=+-=--=-+=-⨯-=．故答案为：4．【点睛】本题考查了根与系数的关系，能够整体代入是解此题的关键．20．－8【分析】利用方程的根的性质把x=2代入方程得到关于m 的方程解这个方程即可【详解】已知是关于x 的方程的一个根故答案为：-8【点睛】本题考查一元二次方程的根问题掌握方程的根的性质会用方程的解代入构造 解析：－8【分析】利用方程的根的性质把x=2代入方程得到关于m 的方程，解这个方程即可【详解】已知2x =是关于x 的方程220x x m ++=的一个根，22220m +⨯+=8m =-故答案为：-8【点睛】本题考查一元二次方程的根问题，掌握方程的根的性质，会用方程的解代入构造参数方程是解题关键三、解答题21．1211x x =-=-【分析】利用配方法解方程．【详解】2250x x +-=225x x +=2(1)6x +=1x =-±∴1211x x =-=-【点睛】此题考查解一元二次方程的方法—配方法，将等式变形为平方形式是解题的关键．22．（1）x 1＝x 2＝42）x 1＝2，x 2＝6．【分析】（1）先配方、然后运用直接开平方求解即可；（2）先将等式右边因式分解，然后移项，最后用因式分解法求解即可．【详解】解：（1）x 2﹣8x+1＝0，x 2﹣8x ＝﹣1，x 2﹣8x+16＝﹣1+16，（x ﹣4）2＝15，∴x ﹣4＝∴x1＝x 2＝4（2）∵2（x ﹣2）2＝x 2﹣4，∴2（x ﹣2）2﹣（x+2）（x ﹣2）＝0，则（x ﹣2）（x ﹣6）＝0，∴x ﹣2＝0或x ﹣6＝0．解得x 1＝2，x 2＝6．【点睛】本题主要考查了一元二次方程的解法，掌握配方法、直接开平方法和因式分解法是解答本题的关键．23．a+b= 5【分析】先求出2(16x =的根4x ，由a 为方程2(16x =的一个正根，得4a =+，再求22113y y -+=的根=1y ±b 为方程22113y y -+=的一个负根，得1b =+a b 即可．【详解】2(16x -=，4x -=±，4x ，a 为方程2(16x =的一个正根，4a =+，22113y y -+=，()2113y -=，1y -==1y ±b 为方程22113y y -+=的一个负根，1b =415a b +=+=．【点睛】本题考查一元二次方程的解法，会比较方程根的正负与大小，掌握一元二次方程的解法是24．（1）x 1＝﹣，x 2＝﹣3；（2）x 1＝2，x 2＝4．【分析】（1）方程利用配方法求出解即可；（2）方程整理后，利用分解因式分解法求出解即可．【详解】解：（1）方程整理得：x 2+6x ＝2，配方得：x 2+6x +9＝11，即（x +3）2＝11，开方得：x +3＝，解得：x 1＝﹣，x 2＝﹣3（2）方程整理得：x 2﹣6x +8＝0，分解因式得：（x ﹣2）（x ﹣4）＝0，可得x ﹣2＝0或x ﹣4＝0，解得：x 1＝2，x 2＝4．【点睛】此题考查了解一元二次方程-配方法，以及因式分解法，熟练掌握各自的解法是解本题的关键．25．（1）13x =-，21x =-；（2）1x =，24x =【分析】（1）用因式分解法求解可得；（2）用配方法求解即可．【详解】解：（1）∵（x+3）2-2（x+3）=0，∴（x+3）（x+1）=0，∴x+3=0或x+1=0，解得：x=-3或x=-1；（2）2810x x -+=281x x -=-28+1615x x -=2(4)15x -=4x -=∴1x =，24x =【点睛】本题主要考查解一元二次方程的能力，熟练掌握解一元二次方程的几种常用方法：直接开平方法、因式分解法、公式法、配方法，结合方程的特点选择合适、简便的方法是解题的关键．26．（1）10%；（2）可以，理由见解析（1）设年平均增长率是x ，列式()2200012420x +=，求出结果；（2）利用（1）中算出的增长率算出2022年的教育经费，看是否超过2900万元．【详解】解：（1）设年平均增长率是x ， ()2200012420x +=1 1.1x +=±10.1x =，2 2.1x =-（舍去），答：年平均增长率是10%；（2）2022年的教育经费是()2242010.12928.2⨯+=（万元）， 2928.22900>，答：教育经费可以达到2900万元．【点睛】本题考查一元二次方程的应用，解题的关键是掌握增长率问题的列式方法．。
人教版九年级上册数学期中试卷易错题(Word版 含答案)
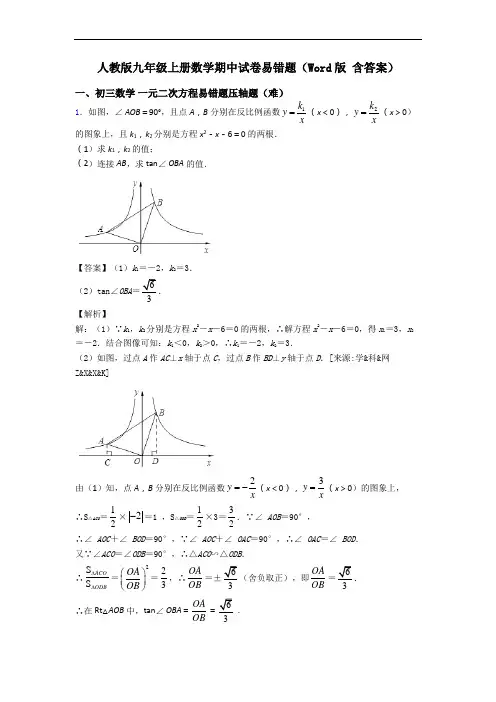
人教版九年级上册数学期中试卷易错题（Word 版 含答案）一、初三数学 一元二次方程易错题压轴题（难） 1．如图，∠ AOB ＝90°，且点A ，B 分别在反比例函数1k y x =（x ＜0），2k y x=（x ＞0）的图象上，且k 1，k 2分别是方程x 2－x －6＝0的两根．（1）求k 1，k 2的值；（2）连接AB ，求tan ∠ OBA 的值．【答案】（1）k 1＝－2，k 2＝3．（2）tan∠OBA ＝6． 【解析】 解：（1）∵k 1，k 2分别是方程x 2－x －6＝0的两根，∴解方程x 2－x －6＝0，得x 1＝3，x 2＝－2．结合图像可知：k 1＜0，k 2＞0，∴k 1＝－2，k 2＝3．（2）如图，过点A 作AC ⊥x 轴于点C ，过点B 作BD ⊥y 轴于点D ．[来源:学&科&网Z&X&X&K]由（1）知，点A ，B 分别在反比例函数2y x =-（x ＜0），3y x =（x ＞0）的图象上， ∴S △ACO ＝12×2-＝1 ，S △ODB ＝12×3＝32．∵∠ AOB ＝90°， ∴∠ AOC ＋∠ BOD ＝90°，∵∠ AOC ＋∠ OAC ＝90°，∴∠ OAC ＝∠ BOD ．又∵∠ACO ＝∠ODB ＝90°，∴△ACO ∽△ODB ．∴S S ACO ODB ∆∆＝2OA OB ⎛⎫ ⎪⎝⎭＝23，∴OA OB ＝±63（舍负取正），即OA OB ＝63． ∴在Rt △AOB 中，tan ∠ OBA ＝OA OB 6．2．已知关于x的一元二次方程（x﹣3）（x﹣4）﹣m2=0．（1）求证：对任意实数m，方程总有2个不相等的实数根；（2）若方程的一个根是2，求m的值及方程的另一个根．【答案】（1）证明见解析；（2）m的值为±2，方程的另一个根是5．【解析】【分析】（1）先把方程化为一般式，利用根的判别式△=b2-4ac证明判断即可；（2）根据方程的根，利用代入法即可求解m的值，然后还原方程求出另一个解即可.【详解】（1）证明：∵（x﹣3）（x﹣4）﹣m2=0，∴x2﹣7x+12﹣m2=0，∴△=（﹣7）2﹣4（12﹣m2）=1+4m2，∵m2≥0，∴△＞0，∴对任意实数m，方程总有2个不相等的实数根；（2）解：∵方程的一个根是2，∴4﹣14+12﹣m2=0，解得m=±，∴原方程为x2﹣7x+10=0，解得x=2或x=5，即m的值为±，方程的另一个根是5．【点睛】此题主要考查了一元二次方程根的判别式，熟练掌握一元二次方程的根的判别式与根的关系是关键.当△=b2-4ac＞0时，方程有两个不相等的实数根；当△=b2-4ac=0时，方程有两个相等的实数根；当△=b2-4ac＜0时，方程没有实数根.3．计算题（1）先化简，再求值：21xx-÷（1+211x-），其中x=2017．（2）已知方程x2﹣2x+m﹣3=0有两个相等的实数根，求m的值．【答案】（1）2018；（2）m=4【解析】分析：（1）根据分式的运算法则和运算顺序，先算括号里面的，再算除法，注意因式分解的作用；（2）根据一元二次方程的根的判别式求解即可.详解：（1）21xx-÷（1+211x-）=2221111x x x x -+÷-- =()()22111x x x x x+-⋅- =x+1，当x=2017时，原式=2017+1=2018（2）解：∵方程x 2﹣2x+m ﹣3=0有两个相等的实数根，∴△=（﹣2）2﹣4×1×（m ﹣3）=0，解得，m=4点睛：此题主要考查了分式的混合运算和一元二次方程的根的判别式，关键是熟记分式方程的运算顺序和法则，注意通分约分的作用.4．如图，平面直角坐标系中，直线l 分别交x 轴、y 轴于A 、B 两点（OA ＜OB ）且OA 、OB 的长分别是一元二次方程()2x 31x 30-++=的两个根，点C 在x 轴负半轴上， 且AB ：AC=1：2（1）求A 、C 两点的坐标；（2）若点M 从C 点出发，以每秒1个单位的速度沿射线CB 运动，连接AM ，设△ABM 的面积为S ，点M 的运动时间为t ，写出S 关于t 的函数关系式，并写出自变量的取值范围；（3）点P 是y 轴上的点，在坐标平面内是否存在点Q ，使以 A 、B 、P 、Q 为顶点的四边形是菱形？若存在，请直接写出Q 点的坐标；若不存在，请说明理由．【答案】解：（1）解)2x 31x 30-+=得（x 3x ﹣1）=0， 解得x 13，x 2=1。
九年级数学上册 一元二次方程易错题(Word版 含答案)
九年级数学上册 一元二次方程易错题（Word 版 含答案）一、初三数学 一元二次方程易错题压轴题（难）1．如图，在矩形ABCD 中，6AB cm =，8AD cm =，点P 从点A 出发沿AD 向点D 匀速运动，速度是1/cm s ，过点P 作PE AC ∥交DC 于点E ，同时，点Q 从点C 出发沿CB 方向，在射线CB 上匀速运动，速度是2/cm s ，连接PQ 、QE ，PQ 与AC 交与点F ，设运动时间为()(08)<<t s t ．（1）当t 为何值时，四边形PFCE 是平行四边形；（2）设PQE 的面积为2()s cm ，求s 与t 的函数关系式；（3）是否存在某一时刻t ，使得PQE 的面积为矩形ABCD 面积的932； （4）是否存在某一时刻t ，使得点E 在线段PQ 的垂直平分线上．【答案】（1）83t =；（2）S =299(08)8t t t -+<<；（3）当2t s =或6s 时，PQE 的面积为矩形ABCD 面积的932；（4）当573256=t 时，点E 在线段PQ 的垂直平分线上 【解析】 【分析】（1）由四边形PFCE 是平行四边形，可得,PF CE ∥由PD QC 得四边形CDPQ 为平行四边形，即PD CQ =，列式82t t -=，计算可解. （2）由PE AC ∥，得=DP DE DA DC ，代入时间t ，得886-=t DE 解得364=-DE t ，34CE t =再通过S S =梯形CDPQ PDE CEQ S S --△△构建联系，可列函数式299(08)8S t t t =-+<<.（3）由PQE 的面积为矩形ABCD 面积的932得299986832S t t =-+=⨯⨯，可解当2t s =或6s 时，PQE 的面积为矩形ABCD 面积的932． （4）当点E 在线段PQ 的垂直平分线上时，=EQ PE ，得22=EQ PE ，由Rt CEQ 与△Rt PDE 可得，222+=CE CQ EQ ，222PD DE PE +=，即2222+=+CE CQ PD DE ，代入364=-DE t ，34CE t =，2CQ t =，8PD t =-可得222233(2)(8)644⎛⎫⎛⎫+=-+- ⎪ ⎪⎝⎭⎝⎭t t t t ，计算验证可解.【详解】（1）当四边形PFCE 是平行四边形时，∥PF CE ， 又∵PD QC ，∴四边形CDPQ 为平行四边形， ∴PD CQ =， 即82t t -=， ∴83t =（2）∵PE AC ∥，∴=DP DEDA DC ， 即886-=t DE， ∴364=-DE t ， ∴336644=-+=CE t t ，∴21133(8)66242248⎛⎫=⋅=--=-+ ⎪⎝⎭△PDE S PD DE t t t t ， 2113322244=⋅=⨯⨯=△CEQ S CE CQ t t t ，S 梯形11()(28)632422=+⋅=+-⋅=+CDPQ QC PD CD t t t ，∴S S =梯形299(08)8--=-+<<△△CDPQ PDE CEQ S S t t t（3）由题意，299986832-+=⨯⨯t t 解得12t =，26t =所以当2t s =或6s 时，PQE 的面积为矩形ABCD 面积的932．（4）当点E 在线段PQ 的垂直平分线上时，=EQ PE ， ∴22=EQ PE ，在Rt CEQ 中，222+=CE CQ EQ ， 在△Rt PDE 中，222PD DE PE +=， ∴2222+=+CE CQ PD DE ，即222233(2)(8)644⎛⎫⎛⎫+=-+- ⎪ ⎪⎝⎭⎝⎭t t t t 解得1573256-=t ，2573256+=-t （舍）所以当57325-=t 时，点E 在线段PQ 的垂直平分线上． 【点睛】本题考查的是一次函数与几何图形的实际应用，勾股定理，平行线的性质，解一元二次方程，需要注意的是在解一元二次方程的实际应用中经常会涉及到解的验证，不可忽略.2．如图，在长方形ABCD 中，边AB 、BC 的长（AB ＜BC ）是方程x 2-7x +12=0的两个根．点P 从点A 出发，以每秒1个单位的速度沿△ABC 边 A →B →C →A 的方向运动，运动时间为t （秒）．（1）求AB 与BC 的长；（2）当点P 运动到边BC 上时，试求出使AP 长为10时运动时间t 的值；（3）当点P 运动到边AC 上时，是否存在点P ，使△CDP 是等腰三角形？若存在，请求出运动时间t 的值；若不存在，请说明理由．【答案】(1) AB ＝3，BC ＝4;(2) t ＝4;(3) t 为10秒或9.5秒或535秒时，△CDP 是等腰三角形. 【解析】试题分析：（1）解一元二次方程即可求得边长； （2）结合图形，利用勾股定理求解即可；（3）根据题意，分为：PC ＝PD ，PD ＝PC ，PD ＝CD ，三种情况分别可求解. 试题解析：(1)∵x 2－7x ＋12＝(x －3)(x －4)＝0 ∴1x ＝3或2x ＝4 . 则AB ＝3，BC ＝4(2)由题意得()223t-310?+=（） ∴14t =，22t =(舍去) 则t ＝4时，AP ＝10.(3)存在点P ，使△CDP 是等腰三角形. ①当PC ＝PD ＝3时， t ＝3431++ ＝10(秒). ②当PD ＝PC(即P 为对角线AC 中点)时，AB ＝3，BC ＝4. ∴AC＝2234+ ＝5，CP 1＝ 12AC ＝2.5 ∴t＝34 2.51++ ＝9.5(秒) ③当PD ＝CD ＝3时，作DQ⊥AC 于Q. 1341221552DQ ⨯⨯==⨯，22129355PQ ⎛⎫=-= ⎪⎝⎭ ∴PC＝2PQ ＝185∴183453515t ++==(秒) 可知当t 为10秒或9.5秒或535秒时，△CDP 是等腰三角形.3．已知:在平面直角坐标系xoy 中,直线k y x b =+分别交x 、y 轴于点A 、B 两点,OA=5,∠OAB=60°.(1)如图1,求直线AB 的解析式；(2)如图2,点P 为直线AB 上一点，连接OP ,点D 在OA 延长线上，分别过点P 、D 作OA 、OP 的平行线,两平行线交于点C ，连接AC,设AD=m,△ABC 的面积为S,求S 与m 的函数关系式; (3)如图3,在(2)的条件下,在PA 上取点E ,使PE=AD, 连接EC,DE,若∠ECD=60°,四边形ADCE 的周长等于22，求S 的值.【答案】(1)直线解析式为353y x =-+53253+；(3)203S =.【解析】 【分析】(1)先求出点B 坐标，设AB 解析式为y kx b =+，把点A(5，0)，B(0，分别代入，利用待定系数法进行求解即可；(2)由题意可得四边形ODCP 是平行四边形，∠OAB=∠APC=60°，则有PC=OD=5+m ，∠PCH=30°，过点C 作CH ⊥AB ，在Rt △PCH 中 利用勾股定理可求得)5m +，再由S=12AB •CH 代入相关数据进行整理即可得； (3) 先求得∠PEC=∠ADC ，设∠OPA=α，则∠OPC= ∠ADC= ∠PEC=60°+α，在BA 延长线上截取AK=AD ，连接OK ，DK ，DE ，证明△ADK 是等边三角形，继而证明△PEC ≌△DKO ，通过推导可得到OP=OK=CE=CD ，再证明△CDE 是等边三角形，可得CE=CD=DE ，连接OE ，证明△OPE ≌△EDA ，继而可得△OAE 是等边三角形，得到OA=AE=5 ，根据四边形ADCE 的周长等于22，可得ED=172m -，过点E 作EN ⊥OD 于点N ，则DN=52m +，由勾股定理得222EN DN DE +=， 可得关于m 的方程，解方程求得m 的值后即可求得答案.【详解】(1)在Rt △ABO 中OA=5，∠OAB=60°， ∴∠OBA=30°，AB=10 ， 由勾股定理可得OB=， ∴B(0，，设AB 解析式为y kx b =+，把点A(5，0)，B(0，)分别代入，得05k bb=+⎧⎪⎨=⎪⎩，∴k b ⎧=⎪⎨=⎪⎩，∴直线解析式为y =+ (2)∵CP//OD ，OP//CD ，∴四边形ODCP 是平行四边形，∠OAB=∠APC=60°， ∴PC=OD=5+m ，∠PCH=30°， 过点C 作CH ⊥AB ，在Rt △PCH 中 PH=52m +，由勾股定理得)5m +， ∴S=12AB •CH=110(5)2222m m ⨯⨯+=+；(3) ∵∠ECD=∠OAB=60°，∴∠EAD+∠ECD=180°，∠CEA+∠ADC=180°， ∴∠PEC=∠ADC ，设∠OPA=α，则∠OPC= ∠ADC= ∠PEC=60°+α， 在BA 延长线上截取AK=AD ，连接OK ，DK ，DE ， ∵∠DAK=60°， ∴△ADK 是等边三角形， ∴AD=DK=PE ，∠ODK=∠APC ， ∵PC=OD ， ∴△PEC ≌△DKO ，∴OK=CE ，∠OKD=∠PEC=∠OPC=60°+α， ∠AKD= ∠APC=60° ， ∴∠OPK= ∠OKB ， ∴OP=OK=CE=CD ， 又∵∠ECD=60°， ∴△CDE 是等边三角形， ∴CE=CD=DE ，连接OE ，∵ ∠ADE=∠APO ，DE=CD=OP ， ∴△OPE ≌△EDA ， ∴AE=OE ， ∠OAE=60°， ∴△OAE 是等边三角形， ∴OA=AE=5 ，∵四边形ADCE 的周长等于22， ∴AD+2DE=17， ∴ED=172m-， 过点E 作EN ⊥OD 于点N ，则DN=52m +， 由勾股定理得222EN DN DE +=，即22253517()()()222m m -++=， 解得13m =，221m =-(舍去)， ∴S=15325322+=203.【点睛】本题考查的四边形综合题，涉及了待定系数法，平行四边形的判定与性质，勾股定理，全等三角形的判定与性质，等边三角形的判定与性质，解一元二次方程等，综合性较强，有一定的难度，正确添加辅助线，熟练掌握和灵活运用相关知识是解题的关键.4．如图，在平面直角坐标系中，O 为原点，点A （0，8），点B （m ，0），且m ＞0.把△AOB 绕点A 逆时针旋转90°，得△ACD ，点O ，B 旋转后的对应点为C ，D ， （1）点C 的坐标为 ；（2）①设△BCD 的面积为S ，用含m 的式子表示S ，并写出m 的取值范围； ②当S=6时，求点B 的坐标（直接写出结果即可）.【答案】（1）C （8，8）；（2）①S=0.5m 2﹣4m （m ＞8），或S=﹣0.5m 2+4m （0＜m ＜8）；②点B 的坐标为（7，0）或（2，0）或（6，0）. 【解析】 【分析】（1）由旋转的性质得出AC ＝AO ＝8，∠OAC ＝90°，得出C （8，8）即可；（2）①由旋转的性质得出DC ＝OB ＝m ，∠ACD ＝∠AOB ＝90°，∠OAC ＝90°，得出∠ACE ＝90°，证出四边形OACE 是矩形，得出DE ⊥x 轴，OE ＝AC ＝8，分三种情况：a、当点B在线段OE的延长线上时，得出BE＝OB−OE＝m−8，由三角形的面积公式得出S ＝0.5m2−4m（m＞8）即可；b、当点B在线段OE上（点B不与O，E重合）时，BE＝OE−OB＝8−m，由三角形的面积公式得出S＝−0.5m2＋4m（0＜m＜8）即可；c、当点B与E重合时，即m＝8，△BCD不存在；②当S＝6，m＞8时，得出0.5m2−4m＝6，解方程求出m即可；当S＝6，0＜m＜8时，得出−0.5m2＋4m＝6，解方程求出m即可．【详解】（1）∵点A（0，8），∴AO=8，∵△AOB绕点A逆时针旋转90°得△ACD，∴AC=AO=8，∠OAC=90°，∴C（8，8），故答案为（8，8）；（2）①延长DC交x轴于点E，∵点B（m，0），∴OB=m，∵△AOB绕点A逆时针旋转90°得△ACD，∴DC=OB=m，∠ACD=∠AOB=90°，∠OAC=90°，∴∠ACE=90°，∴四边形OACE是矩形，∴DE⊥x轴，OE=AC=8，分三种情况：a、当点B在线段OE的延长线上时，如图1所示：则BE=OB﹣OE=m﹣8，∴S=0.5DC•BE=0.5m（m﹣8），即S=0.5m2﹣4m（m＞8）；b、当点B在线段OE上（点B不与O，E重合）时，如图2所示：则BE=OE﹣OB=8﹣m，∴S=0.5DC•BE=0.5m（8﹣m），即S=﹣0.5m2+4m（0＜m＜8）；c、当点B与E重合时，即m=8，△BCD不存在；综上所述，S=0.5m2﹣4m（m＞8），或S=﹣0.5m2+4m（0＜m＜8）；②当S=6，m＞8时，0.5m2﹣4m=6，解得：m=4±27（负值舍去），∴m=4+27；当S=6，0＜m＜8时，﹣0.5m2+4m=6，解得：m=2或m=6，∴点B的坐标为（4+27，0）或（2，0）或（6，0）.【点睛】本题是三角形综合题目，考查了坐标与图形性质、旋转的性质、矩形的判定与性质、三角形面积公式、一元二次方程的解法等知识；本题综合性强，有一定难度．5．已知二次函数y＝9x2﹣6ax+a2﹣b，当b＝﹣3时，二次函数的图象经过点（﹣1，4）①求a的值；②求当a ≤x ≤b 时，一次函数y ＝ax +b 的最大值及最小值； 【答案】①a 的值是﹣2或﹣4；②最大值＝13，最小值＝9 【解析】 【分析】①根据题意解一元二次方程即可得到a 的值；②根据a ≤x ≤b ，b ＝﹣3求得a=-4，由此得到一次函数为y ＝﹣4x ﹣3，根据函数的性质当x ＝﹣4时，函数取得最大值，x ＝﹣3时，函数取得最小值，分别计算即可.【详解】解：①∵y ＝9x 2﹣6ax +a 2﹣b ，当b ＝﹣3时，二次函数的图象经过点（﹣1，4） ∴4＝9×（﹣1）2﹣6a ×（﹣1）+a 2+3， 解得，a 1＝﹣2，a 2＝﹣4， ∴a 的值是﹣2或﹣4； ②∵a ≤x ≤b ，b ＝﹣3 ∴a ＝﹣2舍去， ∴a ＝﹣4， ∴﹣4≤x ≤﹣3， ∴一次函数y ＝﹣4x ﹣3，∵一次函数y ＝﹣4x ﹣3为单调递减函数，∴当x ＝﹣4时，函数取得最大值，y ＝﹣4×（﹣4）﹣3＝13 x ＝﹣3时，函数取得最小值，y ＝﹣4×（﹣3）﹣3＝9. 【点睛】此题考查解一元二次方程，一次函数的性质，（2）是难点，正确理解a 、b 的关系得到函数解析式是解题的关键.6．某连锁超市派遣调查小组在春节期间调查某种商品的销售情况，下面是调查后小张与其 他两位成员交流的情况．小张：“该商品的进价为 24元/件．”成员甲：“当定价为 40元/件时，每天可售出 480件．”成员乙：“若单价每涨 1元，则每天少售出 20件；若单价每降 1元，则每天多售出 40件．” 根据他们的对话，请你求出要使该商品每天获利 7680元，应该怎样合理定价？ 【答案】要使该商品每天获利7680元，应定价为36元/件、40元/件或48元/件 【解析】 【分析】设每件商品定价为x 元，则在每件40元的基础上涨价时每天的销售量是[]48020(40)x --件，每件商品的利润是(24)x -元，在每件40元的基础上降价时每天的销量是[]48040(40)x +-件，每件的利润是(24)x -元，从而可以得到答案．【详解】解：设每件商品定价为x 元．①当40x ≥时，[](24)48020(40)7680x x ---= ， 解得：1240,48;x x ==②当40x <时，[](24)48040(40)7680x x -+-=， 解得：1236,40x x ==（舍去），.答：要使该商品每天获利7680元，应定价为36元/件、40元/件或48元/件． 【点睛】本题考查的是一元二次方程中的升降价对销售量产生影响方面的应用，用含有未知数的代数式表示销售量是这一类题的关键．7．阅读下列材料 计算：（1﹣﹣）×（+）﹣（1﹣﹣）（+），令+＝t ，则：原式＝（1﹣t ）（t +）﹣（1﹣t ﹣）t ＝t +﹣t 2﹣+t 2＝在上面的问题中，用一个字母代表式子中的某一部分，能达到简化计算的目的，这种思想方法叫做“换元法”，请用“换元法”解决下列问题： （1）计算：（1﹣﹣）×（+）﹣（1﹣﹣）×（+）（2）因式分解：（a 2﹣5a +3）（a 2﹣5a +7）+4 （3）解方程：（x 2+4x +1）（x 2+4x +3）＝3 【答案】（1）；（2）（a 2﹣5a +5）2；（3）x 1＝0，x 2＝﹣4，x 3＝x 4＝﹣2【解析】 【分析】（1）仿照材料内容，令+＝t 代入原式计算．（2）观察式子找相同部分进行换元，令a 2﹣5a ＝t 代入原式进行因式分解，最后要记得把t 换为a ．（3）观察式子找相同部分进行换元，令x 2+4x ＝t 代入原方程，即得到关于t 的一元二次方程，得到t 的两个解后要代回去求出4个x 的解． 【详解】 （1）令+＝t ，则： 原式＝（1﹣t ）（t +）﹣（1﹣t ﹣）t ＝t +﹣t 2﹣﹣t +t 2+＝（2）令a 2﹣5a ＝t ，则：原式＝（t +3）（t +7）+4＝t 2+7t +3t +21+4＝t 2+10t +25＝（t +5）2＝（a 2﹣5a +5）2 （3）令x 2+4x ＝t ，则原方程转化为：（t +1）（t +3）＝3t 2+4t +3＝3t （t +4）＝0∴t 1＝0，t 2＝﹣4 当x 2+4x ＝0时，x （x +4）＝0解得：x 1＝0，x 2＝﹣4当x 2+4x ＝﹣4时，x 2+4x +4＝0（x +2）2＝0解得：x 3＝x 4＝﹣2【点睛】本题考查用换元法进行整式的运算，因式分解，解一元二次方程．利用换元法一般可达到降次效果，从而简便运算．8．如图，已知AB 是⊙O 的弦，半径OA=2，OA 和AB 的长度是关于x 的一元二次方程x 2﹣4x+a=0的两个实数根．（1）求弦AB 的长度；（2）计算S △AOB ；（3）⊙O 上一动点P 从A 点出发，沿逆时针方向运动一周，当S △POA =S △AOB 时，求P 点所经过的弧长（不考虑点P 与点B 重合的情形）．【答案】（1）AB=2；（2）S △AOB 33）当S △POA =S △AOB 时，P 点所经过的弧长分别是43π、83π、103π． 【解析】试题分析：（1）OA 和AB 的长度是一元二次方程的根，所以利用一元二次方程的根与系数的关系即可求出AB 的长度；（2）作出△AOB 的高OC ，然后求出OC 的长度即可求出面积；（3）由题意知：两三角形有公共的底边，要面积相等，即高要相等．试题解析：（1）由题意知：OA 和AB 的长度是x 2﹣4x+a=0的两个实数根，∴OA+AB=﹣41-=4，∵OA=2，∴AB=2；（2）过点C作OC⊥AB于点C，∵OA=AB=OB=2，∴△AOB是等边三角形，∴AC=12AB=1，在Rt△ACO中，由勾股定理可得：OC=3，∴S△AOB=12AB﹒OC=12×2×3=3；（3）延长AO交⊙O于点D，由于△AOB与△POA有公共边OA，当S△POA=S△AOB时，∴△AOB与△POA高相等，由（2）可知：等边△AOB的高为3，∴点P到直线OA的距离为3，这样点共有3个①过点B作BP1∥OA交⊙O于点P1，∴∠BOP1=60°，∴此时点P经过的弧长为：1202180π⨯=43π，②作点P2，使得P1与P2关于直线OA对称，∴∠P2OD=60°，∴此时点P经过的弧长为：2402180π⨯=83π，③作点P3，使得B与P3关于直线OA对称，∴∠P3OP2=60°，∴此时P经过的弧长为：3002180π⨯=103π，综上所述：当S△POA=S△AOB时，P点所经过的弧长分别是43π、83π、103π．【点睛】本题主要考查了一元二次方程与圆的综合知识．涉及等边三角形性质，圆的对称性等知识，能综合运用所学知识，选择恰当的方法进行解题是关键．9．在等腰三角形△ABC中，三边分别为a、b、c，其中ɑ＝4，若b、c是关于x的方程x2﹣（2k+1）x+4（k﹣12）＝0的两个实数根，求△ABC的周长．【答案】△ABC的周长为10．【解析】【分析】分a为腰长及底边长两种情况考虑：当a=4为腰长时，将x=4代入原方程可求出k值，将k值代入原方程可求出底边长，再利用三角形的周长公式可求出△ABC的周长；当a=4为底边长时，由根的判别式△=0可求出k值，将其代入原方程利用根与系数的关系可求出b+c的值，由b+c=a 可得出此种情况不存在．综上即可得出结论． 【详解】当a ＝4为腰长时，将x ＝4代入原方程，得：()214421402k k ⎛⎫-++-= ⎪⎝⎭解得：52k =当52k =时，原方程为x 2﹣6x +8＝0， 解得：x 1＝2，x 2＝4，∴此时△ABC 的周长为4+4+2＝10；当a ＝4为底长时，△＝[﹣（2k +1）]2﹣4×1×4（k ﹣12）＝（2k ﹣3）2＝0， 解得：k ＝32， ∴b +c ＝2k +1＝4．∵b +c ＝4＝a ，∴此时，边长为a ，b ，c 的三条线段不能围成三角形．∴△ABC 的周长为10．【点睛】本题考查了根的判别式、根与系数的关系、一元二次方程的解、等腰三角形的性质以及三角形的三边关系，分a 为腰长及底边长两种情况考虑是解题的关键．10．如图，某农家拟用已有的长为8m 的墙或墙的一部分为一边，其它三边用篱笆围成一个面积为12m 2的矩形园子．设园子中平行于墙面的篱笆长为ym （其中y ≥4），另两边的篱笆长分别为xm ．（1）求y 关于x 的函数表达式，并求x 的取值范围．（2）若仅用现有的11m 长的篱笆，且恰好用完，请你帮助设计围制方案．【答案】（1）y ＝；1.5≤x ≤3；（2）长为8m ，宽为1.5m ．【解析】【分析】（1）由矩形的面积公式可得出y 关于x 的函数表达式，结合4≤y ≤8可求出x 的取值范围； （2）由篱笆的长可得出y ＝（11﹣2x ）m ，利用矩形的面积公式结合矩形园子的面积，即可得出关于x 的一元二次方程，解之取其较小值即可得出结论．【详解】（1）∵矩形的面积为12m2，∴y＝．∵4≤y≤8，∴1.5≤x≤3．（2）∵篱笆长11m，∴y＝（11﹣2x）m．依题意，得：xy＝12，即x（11﹣2x）＝12，解得：x1＝1.5，x2＝4（舍去），∴y＝11﹣2x＝8．答：矩形园子的长为8m，宽为1.5m．【点睛】本题考查了一元二次方程的应用以及反比例函数的应用，解题的关键是：（1）利用矩形的面积公式，找出y关于x的函数表达式；（2）找准等量关系，正确列出一元二次方程．。
一元二次方程易错题(Word版 含答案)
试题解析：(1)∵x2－7x＋12＝(x－3)(x－4)＝0
∴ ＝3或 ＝4 .
则AB＝3，BC＝4
(2)由题意得
∴ ， (舍去)
则t＝4时，AP＝ .
(3)存在点P，使△CDP是等腰三角形.
①当PC＝PD＝3时， t＝ ＝10(秒).
（1）求2008年底至2010年底该市汽车拥有量的年平均增长率；
（2）为了保护城市环境，缓解汽车拥堵状况，该市交通部门拟控制汽车总量，要求到2012
年底全市汽车拥有量不超过125.48万辆；另据统计，从2011年初起，该市此后每年报废的
汽车数量是上年底汽车拥有量的10%假设每年新增汽车数量相同，请你估算出该市从2011
根据勾股定理得PQ= ,
P，Q两点的距离为2 cm.
（3）点Q从C点移动到B点所花的时间为16÷2=8s，
当点P在AO上时，S△POQ＝ ＝ ＝12，
解得t＝4．
当点P在OC上时，S△POQ＝ ＝ ＝12，
解得t＝6或﹣ （舍弃）．
当点P在CB上时，S△POQ＝ ＝ ＝12，
解得t＝18＞8（不符合长率为x．
根据题意，得75（1+x）2=108，则1+x=±1.2
解得x1=0.2=20%，x2=﹣2.2（不合题意，舍去）．
答：该市汽车拥有量的年平均增长率为20%．
（2）设全市每年新增汽车数量为y万辆，则2010年底全市的汽车拥有量为（108×90%+y）万辆，2011年底全市的汽车拥有量为[（108×90%+y）×90%+y]万辆．
综上所述，经过4s或6s时，△POQ的面积为12cm2．
一元二次方程易错题(Word版 含答案)
一元二次方程易错题（Word 版 含答案）一、初三数学 一元二次方程易错题压轴题（难）1．如图1，平面直角坐标系xOy 中，等腰ABC ∆的底边BC 在x 轴上，8BC =，顶点A在y 的正半轴上，2OA =，一动点E 从(3,0)出发，以每秒1个单位的速度沿CB 向左运动，到达OB 的中点停止．另一动点F 从点C 出发，以相同的速度沿CB 向左运动，到达点O 停止．已知点E 、F 同时出发，以EF 为边作正方形EFGH ，使正方形EFGH 和ABC ∆在BC 的同侧．设运动的时间为t 秒（0t ≥）．（1）当点H 落在AC 边上时，求t 的值；（2）设正方形EFGH 与ABC ∆重叠面积为S ，请问是存在t 值，使得9136S =？若存在，求出t 值；若不存在，请说明理由；（3）如图2，取AC 的中点D ，连结OD ，当点E 、F 开始运动时，点M 从点O 出发，以每秒25OD DC CD DO ---运动，到达点O 停止运动．请问在点E 的整个运动过程中，点M 可能在正方形EFGH 内（含边界）吗？如果可能，求出点M 在正方形EFGH 内（含边界）的时长；若不可能，请说明理由．【答案】（1）t=1；（2）存在，143t =，理由见解析；（3）可能，3455t ≤≤或4533t ≤≤或35t ≤≤理由见解析 【解析】 【分析】（1）用待定系数法求出直线AC 的解析式，根据题意用t 表示出点H 的坐标，代入求解即可；（2）根据已知，当点F 运动到点O 停止运动前，重叠最大面积是边长为1的正方形的面积，即不存在t ，使重叠面积为9136S =，故t ﹥4,用待定系数法求出直线AB 的解析式，求出点H 落在BC 边上时的t 值，求出此时重叠面积为169﹤9136，进一步求出重叠面积关于t 的表达式，代入解t 的方程即可解得t 值；（3）由已知求得点D （2，1），AC=结合图形分情况讨论即可得出符合条件的时长． 【详解】（1）由题意，A(0，2)，B(-4，0)，C(4，0)， 设直线AC 的函数解析式为y=kx+b ， 将点A 、C 坐标代入，得：402k b b +=⎧⎨=⎩，解得：122k b ⎧=-⎪⎨⎪=⎩， ∴直线AC 的函数解析式为122y x =-+， 当点H 落在AC 边上时，点E(3-t ，0)，点H （3-t ，1）， 将点H 代入122y x =-+，得： 11(3)22t =--+，解得：t=1；（2）存在，143t =，使得9136S =． 根据已知，当点F 运动到点O 停止运动前，重叠最大面积是边长为1的正方形的面积，即不存在t ，使重叠面积为9136S =，故t ﹥4， 设直线AB 的函数解析式为y=mx+n ， 将点A 、B 坐标代入，得：402m n n -+=⎧⎨=⎩，解得：122m n ⎧=⎪⎨⎪=⎩， ∴直线AC 的函数解析式为122y x =+， 当t ﹥4时，点E （3-t ，0）点H （3-t ，t-3），G(0，t-3)， 当点H 落在AB 边上时，将点H 代入122y x =+，得： 13(3)22t t -=-+，解得：133t =；此时重叠的面积为221316(3)(3)39t -=-=， ∵169﹤9136，∴133﹤t ﹤5， 如图1，设GH 交AB 于S ，EH 交AB 于T,将y=t-3代入122y x =+得：1322t x -=+， 解得：x=2t-10， ∴点S(2t-10，t-3)，将x=3-t 代入122y x =+得：11(3)2(7)22y t t =-+=-， ∴点T 1(3,(7))2t t --， ∴AG=5-t ，SG=10-2t ，BE=7-t ，ET=1(7)2t -， 211(7)24BET S BE ET t ∆==-, 21(5)2ASGS AG SG t ∆==- 所以重叠面积S=AOB BET ASG S S S ∆∆∆--=4-21(7)4t --2(5)t -=2527133424t t -+-， 由2527133424t t -+-=9136得：1143t =，29215t =﹥5(舍去)， ∴143t =；（3）可能，35≤t≤1或t=4． ∵点D 为AC 的中点，且OA=2,OC=4， ∴点D （2，1），AC=255 易知M 点在水平方向以每秒是4个单位的速度运动； 当0﹤t ﹤12时，M 在线段OD 上，H 未到达D 点，所以M 与正方形不相遇； 当12﹤t ﹤1时， 12+12÷（1+4）=35秒， ∴t =35时M 与正方形相遇，经过1÷（1+4）=15秒后，M 点不在正方行内部，则3455t ≤≤； 当t=1时，由（1）知，点F 运动到原E 点处，M 点到达C 处； 当1≤t≤2时，当t=1+1÷（4-1）=43秒时，点M 追上G 点，经过1÷（4-1）=13秒，点M 都在正方形EFGH 内（含边界），4533t ≤≤ 当t=2时，点M 运动返回到点O 处停止运动，当 t=3时，点E 运动返回到点O 处, 当 t=4时，点F 运动返回到点O 处, 当35t ≤≤时，点M 都在正方形EFGH 内（含边界）， 综上，当3455t ≤≤或4533t ≤≤或35t ≤≤时，点M 可能在正方形EFGH 内（含边界）．【点睛】本题考查了一次函数与几何图形的综合，涉及求一次函数的解析式、正方形的性质、直角三角形的性质、不规则图形的面积、解一元二次方程等知识，解答的关键是认真审题，提取相关信息，利用待定系数法、数形结合法等解题方法确定解题思路，进而推理、探究、发现和计算．2．如图，在矩形ABCD 中，6AB cm =，8AD cm =，点P 从点A 出发沿AD 向点D 匀速运动，速度是1/cm s ，过点P 作PE AC ∥交DC 于点E ，同时，点Q 从点C 出发沿CB 方向，在射线CB 上匀速运动，速度是2/cm s ，连接PQ 、QE ，PQ 与AC 交与点F ，设运动时间为()(08)<<t s t ．（1）当t 为何值时，四边形PFCE 是平行四边形；（2）设PQE 的面积为2()s cm ，求s 与t 的函数关系式；（3）是否存在某一时刻t ，使得PQE 的面积为矩形ABCD 面积的932； （4）是否存在某一时刻t ，使得点E 在线段PQ 的垂直平分线上．【答案】（1）83t =；（2）S =299(08)8t t t -+<<；（3）当2t s =或6s 时，PQE 的面积为矩形ABCD 面积的932；（4）当57325-=t 时，点E 在线段PQ 的垂直平分线上 【解析】 【分析】（1）由四边形PFCE 是平行四边形，可得,PF CE ∥由PD QC 得四边形CDPQ 为平行四边形，即PD CQ =，列式82t t -=，计算可解. （2）由PE AC ∥，得=DP DE DA DC ，代入时间t ，得886-=t DE 解得364=-DE t ，34CE t =再通过S S =梯形CDPQ PDE CEQ S S --△△构建联系，可列函数式299(08)8S t t t =-+<<.（3）由PQE 的面积为矩形ABCD 面积的932得299986832S t t =-+=⨯⨯，可解 当2t s =或6s 时，PQE 的面积为矩形ABCD 面积的932． （4）当点E 在线段PQ 的垂直平分线上时，=EQ PE ，得22=EQ PE ，由Rt CEQ 与△Rt PDE 可得，222+=CE CQ EQ ，222PD DE PE +=，即2222+=+CE CQ PD DE ，代入364=-DE t ，34CE t =，2CQ t =，8PD t =-可得222233(2)(8)644⎛⎫⎛⎫+=-+- ⎪ ⎪⎝⎭⎝⎭t t t t ，计算验证可解.【详解】（1）当四边形PFCE 是平行四边形时，∥PF CE ， 又∵PD QC ，∴四边形CDPQ 为平行四边形， ∴PD CQ =，即82t t -=， ∴83t =（2）∵PE AC ∥，∴=DP DEDA DC ， 即886-=t DE， ∴364=-DE t ，∴336644=-+=CE t t ， ∴21133(8)66242248⎛⎫=⋅=--=-+ ⎪⎝⎭△PDE S PD DE t t t t ， 2113322244=⋅=⨯⨯=△CEQ S CE CQ t t t ，S 梯形11()(28)632422=+⋅=+-⋅=+CDPQ QC PD CD t t t ，∴S S =梯形299(08)8--=-+<<△△CDPQ PDE CEQ S S t t t （3）由题意，299986832-+=⨯⨯t t 解得12t =，26t =所以当2t s =或6s 时，PQE 的面积为矩形ABCD 面积的932． （4）当点E 在线段PQ 的垂直平分线上时，=EQ PE ， ∴22=EQ PE ，在Rt CEQ 中，222+=CE CQ EQ ，在△Rt PDE 中，222PD DE PE +=， ∴2222+=+CE CQ PD DE ，即222233(2)(8)644⎛⎫⎛⎫+=-+- ⎪ ⎪⎝⎭⎝⎭t t t t解得1256-=t ，2256+=-t （舍）所以当256-=t 时，点E 在线段PQ 的垂直平分线上． 【点睛】本题考查的是一次函数与几何图形的实际应用，勾股定理，平行线的性质，解一元二次方程，需要注意的是在解一元二次方程的实际应用中经常会涉及到解的验证，不可忽略.3．随着人们经济收入的不断提高及汽车产业的快速发展，汽车已越来越多地进入普通家庭．据某市交通部门统计，2008年底该市汽车拥有量为75万辆，而截止到2010年底，该市的汽车拥有量已达108万辆．（1）求2008年底至2010年底该市汽车拥有量的年平均增长率；（2）为了保护城市环境，缓解汽车拥堵状况，该市交通部门拟控制汽车总量，要求到2012年底全市汽车拥有量不超过125.48万辆；另据统计，从2011年初起，该市此后每年报废的汽车数量是上年底汽车拥有量的10%假设每年新增汽车数量相同，请你估算出该市从2011年初起每年新增汽车数量最多不超过多少万辆．【答案】解：（1）2008年底至2010年底该市汽车拥有量的年平均增长率是20%（2）从2011年初起每年新增汽车数量最多不超过20万辆【解析】【分析】（1）设年平均增长率x，根据等量关系“2008年底汽车拥有量×（1+年平均增长率）×（1+年平均增长率）”列出一元二次方程求得．（2）设从2011年初起每年新增汽车的数量y，根据已知得出2011年报废的车辆是2010年底拥有量×10%，推出2011年底汽车拥有量是2010年底拥有量-2011年报废的车辆=2010年拥有量×（1-10%），得出等量关系是： 2010年拥有量×（1-10%）+新增汽车数量]×（1-10%）+新增汽车数量”，列出一元一次不等式求得．【详解】解：（1）设该市汽车拥有量的年平均增长率为x．根据题意，得75（1+x）2=108，则1+x=±1.2解得x1=0.2=20%，x2=﹣2.2（不合题意，舍去）．答：该市汽车拥有量的年平均增长率为20%．（2）设全市每年新增汽车数量为y万辆，则2010年底全市的汽车拥有量为（108×90%+y）万辆，2011年底全市的汽车拥有量为[（108×90%+y）×90%+y]万辆．根据题意得（108×90%+y）×90%+y≤125.48，解得y≤20．答：该市每年新增汽车数量最多不能超过20万辆．4．如图，在△ABC 中，∠B=90°，AB=12 cm，BC=16 cm．点 P从点 A 开始沿 AB 边向点 B 以1 cm/s的速度移动，点 Q从点 B开始沿 BC 边向点 C以 2 cm/s的速度移动．如果 P、 Q分别从 A、B同时出发，当一个点到达终点时，另一个点也随之停止运动．设运动的时间为 t 秒．（1）当 t 为何值时，△PBQ的面积等于 35cm2？（2）当 t 为何值时，PQ的长度等82cm？（3）若点 P，Q的速度保持不变，点 P在到达点 B后返回点 A，点 Q在到达点 C后返回点B，一个点停止，另一个点也随之停止．问：当 t为何值时，△PCQ的面积等于 32cm2？【答案】（1）t为5或7；（2）t为45或4；（3）t为4或16【解析】【分析】（1）分别用含t的代数式表示PB，BQ的长，利用面积公式列方程求解即可．（2）分别用含t的代数式表示PB，BQ的长，利用勾股定理列方程求解即可．（3）分段要清楚，，P，Q都没有返回，表示好PB，CQ的长，用面积公式列方程，，P不返回，Q返回，表示好PB，CQ的长，用面积公式列方程，，两点都返回，表示好PB，CQ的长，用面积公式列方程即可得到答案．【详解】解：（1），.根据三角形的面积公式，得，即，整理，得，解得，.故当为5或7时，的面积等于35.（2）根据勾股定理，得，整理，得，解得，.故当为或4时，的长度等于.（3）①当时，，，由题意，得，解得：，（舍去）.②当时，，，由题意，得，次方程无解.③当时，，， 由题意，得，解得：（舍去），.综上所述，当为4或16时，的面积等于.【点睛】本题考查的是在运动过程中应用一元二次方程解决实际问题，建立正确情境下的几何模型是解决问题的关键，特别是最后一问，关键是弄懂分段的时间界点，才能正确的表示PB ，CQ 的长．5．已知关于x 的一元二次方程()222130x k x k --+-=有两个实数根．()1求k 的取值范围；()2设方程两实数根分别为1x ，2x ，且满足221223x x +=，求k 的值．【答案】（1）134k ≤；（2）2k =-． 【解析】 【分析】()1根据方程有实数根得出()()22[2k 1]41k 38k 50=---⨯⨯-=-+≥，解之可得．()2利用根与系数的关系可用k 表示出12x x +和12x x 的值，根据条件可得到关于k 的方程，可求得k 的值，注意利用根的判别式进行取舍． 【详解】 解：()1关于x 的一元二次方程()222130x k x k --+-=有两个实数根，0∴≥，即()()22[21]4134130k k k ---⨯⨯-=-+≥，解得134k ≤． ()2由根与系数的关系可得1221x x k +=-，2123x x k =-，()222222121212()2(21)23247x x x x x x k k k k ∴+=+-=---=-+， 221223x x +=，224723k k ∴-+=，解得4k =，或2k =-，134k ≤， 4k ∴=舍去， 2k ∴=-． 【点睛】本题考查了一元二次方程2ax bx c 0(a 0,++=≠a ，b ，c 为常数)根的判别式.当0>，方程有两个不相等的实数根；当0=，方程有两个相等的实数根；当0<，方程没有实数根.以及根与系数的关系．6．计算题（1）先化简，再求值：21x x -÷（1+211x -），其中x=2017．（2）已知方程x 2﹣2x+m ﹣3=0有两个相等的实数根，求m 的值． 【答案】（1）2018；（2）m=4 【解析】分析：（1）根据分式的运算法则和运算顺序，先算括号里面的，再算除法，注意因式分解的作用；（2）根据一元二次方程的根的判别式求解即可.详解：（1）21x x -÷（1+211x -）=2221111x x x x -+÷-- =()()22111x x x x x +-⋅- =x+1，当x=2017时，原式=2017+1=2018（2）解：∵方程x 2﹣2x+m ﹣3=0有两个相等的实数根， ∴△=（﹣2）2﹣4×1×（m ﹣3）=0， 解得，m=4点睛：此题主要考查了分式的混合运算和一元二次方程的根的判别式，关键是熟记分式方程的运算顺序和法则，注意通分约分的作用.7．图1是李晨在一次课外活动中所做的问题研究：他用硬纸片做了两个三角形，分别为△ABC 和△DEF ，其中∠B=90°，∠A=45°，BC=，∠F=90°，∠EDF=30°， EF=2．将△DEF的斜边DE 与△ABC 的斜边AC 重合在一起，并将△DEF 沿AC 方向移动．在移动过程中，D 、E 两点始终在AC 边上(移动开始时点D 与点A 重合)． （1）请回答李晨的问题：若CD=10，则AD= ；（2）如图2，李晨同学连接FC ，编制了如下问题，请你回答：①∠FCD的最大度数为；②当FC∥AB时，AD= ；③当以线段AD、FC、BC的长度为三边长的三角形是直角三角形，且FC为斜边时，AD= ;④△FCD的面积s的取值范围是 .【答案】（1）2；（2）① 60°；②；③；④.【解析】试题分析：（1）根据等腰直角三角形的性质，求出AC的长，即可得到AD的长.（2）①当点E与点C重合时，∠FCD的角度最大，据此求解即可.②过点F作FH⊥AC于点H，应用等腰直角三角形的判定和性质，含30度角直角三角形的性质求解即可.③过点F作FH⊥AC于点H，AD=x，应用含30度角直角三角形的性质把FC用x来表示，根据勾股定理列式求解.④设AD=x，把△FCD的面积s表示为x的函数，根据x的取值范围来确定s的取值范围.试题解析：（1）∵∠B=90°，∠A=45°，BC=，∴AC=12.∵CD=10，∴AD=2.（2）①∵∠F=90°，∠EDF=30°，∴∠DEF=60°.∵当点E与点C重合时，∠FCD的角度最大，∴∠FCD的最大度数=∠DEF="60°."② 如图，过点F作FH⊥AC于点H，∵∠EDF=30°， EF=2，∴DF=. ∴DH=3，FH=.∵FC∥AB，∠A=45°，∴∠FCH="45°." ∴HC=. ∴DC=DH+HC=.∵AC=12，∴AD=.③如图，过点F作FH⊥AC于点H，设AD=x，由②知DH=3，FH=，则HC=.在Rt△CFH中，根据勾股定理，得.∵以线段AD、FC、BC的长度为三边长的三角形是直角三角形，且FC为斜边，∴，即，解得.④设AD=x，易知，即.而，当时，；当时，.∴△FCD的面积s的取值范围是.考点：1.面动平移问题；2.等腰直角三角形的判定和性质；3.平行的性质；4.含30度角直角三角形的性质；5.勾股定理；6.由实际问题列函数关系式；7.求函数值.8．如图直线y＝kx+k交x轴负半轴于点A，交y轴正半轴于点B，且AB＝2（1）求k的值；（2）点P从A出发，以每秒1个单位的速度沿射线AB运动，过点P作直线AB的垂线交x轴于点Q，连接OP，设△PQO的面积为S，点P运动时间为t，求S与t的函数关系式，并直接写出t的取值范围；（3）在（2）的条件下，当P在AB的延长线上，若OQ+AB＝7（BQ﹣OP），求此时直线PQ的解析式．【答案】（1）k32）当0＜t＜12时，S＝12•OQ•P y＝12（1﹣2t3＝﹣323．当t ＞12时，S ＝12OQ •P y ＝12（2t ﹣1）•32t ＝32t 2﹣34t ．（3）直线PQ 的解析式为y ＝﹣3x +53． 【解析】 【分析】（1）求出点B 的坐标即可解决问题；（2）分两种情形①当0＜t ＜12时，②当t ＞12时，根据S ＝12OQ •P y ，分别求解即可；（3）根据已知条件构建方程求出t ，推出点P ，Q 的坐标即可解决问题． 【详解】解：（1）对于直线y ＝kx +k ，令y ＝0，可得x ＝﹣1， ∴A （﹣1，0）， ∴OA ＝1，∵AB ＝2， ∴OB ＝223AB OA -=∴k ＝3． （2）如图，∵tan ∠BAO ＝3OBOA= ∴∠BAO ＝60°， ∵PQ ⊥AB ， ∴∠APQ ＝90°， ∴∠AQP ＝30°， ∴AQ ＝2AP ＝2t ， 当0＜t ＜12时，S ＝12•OQ •P y ＝12（1﹣2t 3323． 当t ＞12时，S ＝12OQ •P y ＝12（2t ﹣1）•32t ＝32t 2﹣34t ． （3）∵OQ +AB 7（BQ ﹣OP ），∴2t ﹣1+2∴2t +121t t -+∴4t 2+4t +1＝7t 2﹣7t +7， ∴3t 2﹣11t +6＝0， 解得t ＝3或23（舍弃）， ∴P （12Q （5，0）， 设直线PQ 的解析式为y ＝kx +b ，则有1250k b k b ⎧+=⎪⎨⎪+=⎩解得k b ⎧=⎪⎪⎨⎪=⎪⎩，∴直线PQ的解析式为33y x =-+． 【点睛】本题属于一次函数综合题，考查了一次函数的性质，三角形的面积，无理方程等知识，解题的关键是学会利用参数构建方程解决问题．9．使得函数值为零的自变量的值称为函数的零点．例如，对于函数1y x =-，令y=0，可得x=1，我们就说1是函数1y x =-的零点． 己知函数222(3)y x mx m =--+(m m 为常数)．（1）当m =0时，求该函数的零点；（2）证明：无论m 取何值，该函数总有两个零点； （3）设函数的两个零点分别为1x 和2x ，且121114x x +=-，此时函数图象与x 轴的交点分 别为A 、B(点A 在点B 左侧)，点M 在直线10y x =-上，当MA+MB 最小时，求直线AM 的函数解析式．【答案】（1）当m =0和 （2）见解析,（3）AM 的解析式为112y x =--． 【解析】 【分析】（1）根据题中给出的函数的零点的定义，将m=0代入y=x 2-2mx-2（m+3），然后令y=0即可解得函数的零点；（2）令y=0，函数变为一元二次方程，要想证明方程有两个解，只需证明△＞0即可； （3）根据题中条件求出函数解析式进而求得A 、B 两点坐标，个、作点B 关于直线y=x-10的对称点B′，连接AB′，求出点B′的坐标即可求得当MA+MB 最小时，直线AM 的函数解析式 【详解】（1）当m =0时，该函数的零点为6和6-．（2）令y=0，得△=∴无论m 取何值，方程总有两个不相等的实数根．即无论m 取何值，该函数总有两个零点． （3）依题意有，由解得．∴函数的解析式为．令y=0，解得∴A()，B(4,0)作点B 关于直线10y x =-的对称点B’，连结AB’， 则AB’与直线10y x =-的交点就是满足条件的M 点．易求得直线10y x =-与x 轴、y 轴的交点分别为C （10,0），D （0,10）． 连结CB’，则∠BCD=45° ∴BC=CB’=6，∠B’CD=∠BCD=45° ∴∠BCB’=90° 即B’（106-，）设直线AB’的解析式为y kx b =+，则20{106k b k b -+=+=-，解得112k b =-=-， ∴直线AB’的解析式为112y x =--， 即AM 的解析式为112y x =--．10．在等腰三角形△ABC 中，三边分别为a 、b 、c ，其中ɑ＝4，若b 、c 是关于x 的方程x 2﹣（2k +1）x +4（k ﹣12）＝0的两个实数根，求△ABC 的周长． 【答案】△ABC 的周长为10． 【解析】 【分析】分a 为腰长及底边长两种情况考虑：当a=4为腰长时，将x=4代入原方程可求出k 值，将k 值代入原方程可求出底边长，再利用三角形的周长公式可求出△ABC 的周长；当a=4为底边长时，由根的判别式△=0可求出k 值，将其代入原方程利用根与系数的关系可求出b+c 的值，由b+c=a 可得出此种情况不存在．综上即可得出结论． 【详解】当a ＝4为腰长时，将x ＝4代入原方程，得：()214421402k k ⎛⎫-++-= ⎪⎝⎭解得：52k = 当52k =时，原方程为x 2﹣6x +8＝0， 解得：x 1＝2，x 2＝4，∴此时△ABC 的周长为4+4+2＝10；当a ＝4为底长时，△＝[﹣（2k +1）]2﹣4×1×4（k ﹣12）＝（2k ﹣3）2＝0， 解得：k ＝32， ∴b +c ＝2k +1＝4． ∵b +c ＝4＝a ，∴此时，边长为a ，b ，c 的三条线段不能围成三角形． ∴△ABC 的周长为10． 【点睛】本题考查了根的判别式、根与系数的关系、一元二次方程的解、等腰三角形的性质以及三角形的三边关系，分a 为腰长及底边长两种情况考虑是解题的关键．。
一元二次方程单元试卷(word版含答案)
一元二次方程单元试卷（word 版含答案）一、初三数学 一元二次方程易错题压轴题（难）1．如图，在长方形ABCD 中，边AB 、BC 的长（AB ＜BC ）是方程x 2-7x +12=0的两个根．点P 从点A 出发，以每秒1个单位的速度沿△ABC 边 A →B →C →A 的方向运动，运动时间为t （秒）．（1）求AB 与BC 的长；（2）当点P 运动到边BC 上时，试求出使AP 长为10时运动时间t 的值；（3）当点P 运动到边AC 上时，是否存在点P ，使△CDP 是等腰三角形？若存在，请求出运动时间t 的值；若不存在，请说明理由．【答案】(1) AB ＝3，BC ＝4;(2) t ＝4;(3) t 为10秒或9.5秒或535秒时，△CDP 是等腰三角形. 【解析】试题分析：（1）解一元二次方程即可求得边长； （2）结合图形，利用勾股定理求解即可；（3）根据题意，分为：PC ＝PD ，PD ＝PC ，PD ＝CD ，三种情况分别可求解. 试题解析：(1)∵x 2－7x ＋12＝(x －3)(x －4)＝0 ∴1x ＝3或2x ＝4 . 则AB ＝3，BC ＝4(2)由题意得()223t-310?+=（） ∴14t =，22t =(舍去) 则t ＝4时，AP 10.(3)存在点P ，使△CDP 是等腰三角形. ①当PC ＝PD ＝3时， t ＝3431++ ＝10(秒). ②当PD ＝PC(即P 为对角线AC 中点)时，AB ＝3，BC ＝4. 2234+＝5，CP 1＝ 12AC ＝2.5 ∴t＝34 2.51++ ＝9.5(秒)③当PD＝CD＝3时，作DQ⊥AC于Q.1341221552DQ⨯⨯==⨯，22129355PQ⎛⎫=-=⎪⎝⎭∴PC＝2PQ＝18 5∴183453515t++==(秒)可知当t为10秒或9.5秒或535秒时，△CDP是等腰三角形.2．（1）课本情境:如图，已知矩形AOBC，AB＝6cm，BC＝16cm，动点P从点A出发，以3cm/s的速度向点O运动，直到点O为止；动点Q同时从点C出发，以2cm/s的速度向点B运动，与点P同时结束运动，出发时，点P和点Q之间的距离是10cm；（2）逆向发散:当运动时间为2s时，P，Q两点的距离为多少？当运动时间为4s时，P，Q 两点的距离为多少？（3）拓展应用：若点P沿着AO→OC→CB移动，点P，Q分别从A，C同时出发，点Q从点C移动到点B停止时，点P随点Q的停止而停止移动，求经过多长时间△POQ的面积为12cm2？【答案】（1）85s或245s（2）62cm；213cm（3）4s或6s【解析】【分析】(1)过点P作PE⊥BC于E，得到AP＝3t，CQ＝2t，PE＝6，EQ＝16﹣3t﹣2t＝16﹣5t，利用勾股定理得到方程，故可求解；（2）根据运动时间求出EQ、PE，利用勾股定理即可求解；(3) 分当点P在AO上时，当点P在OC上时和当点P在CB上时，根据三角形的面积公式列出方程即可求解．【详解】解：（1）设运动时间为t秒时，如图，过点P作PE⊥BC于E，由运动知，AP＝3t，CQ＝2t，PE＝6，EQ＝16﹣3t﹣2t＝16﹣5t，∵点P 和点Q 之间的距离是10 cm ， ∴62+（16﹣5t ）2＝100， 解得t 1=85，t 2=245， ∴t ＝85s 或245s . 故答案为85s 或245s（2）t=2时，由运动知AP ＝3×2＝6 cm ，CQ ＝2×2＝4 cm ， ∴四边形APEB 是矩形， ∴PE ＝AB ＝6，BE ＝6，∴EQ ＝BC ﹣BE ﹣CQ ＝16﹣6﹣4＝6， 根据勾股定理得PQ=2262PE EQ +=, ∴当t ＝2 s 时，P ，Q 两点的距离为62 cm ；当t ＝4 s 时，由运动知AP ＝3×4＝12 cm ，CQ ＝2×4＝8cm ， ∴四边形APEB 是矩形， ∴PE ＝AB ＝6，BQ ＝8，CE=OP=4 ∴EQ ＝BC ﹣CE ﹣BQ ＝16﹣4﹣8＝4， 根据勾股定理得PQ=22213PE EQ +=, P ，Q 两点的距离为213cm .（3）点Q 从C 点移动到B 点所花的时间为16÷2=8s ， 当点P 在AO 上时，S △POQ ＝2PO CO ⋅＝(163)62t -⋅＝12， 解得t ＝4．当点P 在OC 上时，S △POQ ＝2PO CQ ⋅＝(316)22t t-⋅＝12， 解得t ＝6或﹣23（舍弃）． 当点P 在CB 上时，S △POQ ＝2PQ CO ⋅＝(2223)62t t +-⨯＝12， 解得t ＝18＞8（不符合题意舍弃），综上所述，经过4 s 或6 s 时，△POQ 的面积为12 cm 2． 【点睛】此题主要考查勾股定理的应用、一元二次方程与动点问题，解题的关键是熟知勾股定理的应用，根据三角形的面积公式找到等量关系列出方程求解．3．如图，在平面直角坐标系中，O 为原点，点A （0，8），点B （m ，0），且m ＞0.把△AOB 绕点A 逆时针旋转90°，得△ACD ，点O ，B 旋转后的对应点为C ，D ， （1）点C 的坐标为 ；（2）①设△BCD 的面积为S ，用含m 的式子表示S ，并写出m 的取值范围； ②当S=6时，求点B 的坐标（直接写出结果即可）.【答案】（1）C （8，8）；（2）①S=0.5m 2﹣4m （m ＞8），或S=﹣0.5m 2+4m （0＜m ＜8）；②点B 的坐标为（7，0）或（2，0）或（6，0）. 【解析】 【分析】（1）由旋转的性质得出AC ＝AO ＝8，∠OAC ＝90°，得出C （8，8）即可；（2）①由旋转的性质得出DC ＝OB ＝m ，∠ACD ＝∠AOB ＝90°，∠OAC ＝90°，得出∠ACE ＝90°，证出四边形OACE 是矩形，得出DE ⊥x 轴，OE ＝AC ＝8，分三种情况：a 、当点B 在线段OE 的延长线上时，得出BE ＝OB−OE ＝m−8，由三角形的面积公式得出S ＝0.5m 2−4m （m ＞8）即可；b 、当点B 在线段OE 上（点B 不与O ，E 重合）时，BE ＝OE−OB ＝8−m ，由三角形的面积公式得出S ＝−0.5m 2＋4m （0＜m ＜8）即可；c 、当点B 与E 重合时，即m ＝8，△BCD 不存在；②当S ＝6，m ＞8时，得出0.5m 2−4m ＝6，解方程求出m 即可； 当S ＝6，0＜m ＜8时，得出−0.5m 2＋4m ＝6，解方程求出m 即可． 【详解】（1）∵点A（0，8），∴AO=8，∵△AOB绕点A逆时针旋转90°得△ACD，∴AC=AO=8，∠OAC=90°，∴C（8，8），故答案为（8，8）；（2）①延长DC交x轴于点E，∵点B（m，0），∴OB=m，∵△AOB绕点A逆时针旋转90°得△ACD，∴DC=OB=m，∠ACD=∠AOB=90°，∠OAC=90°，∴∠ACE=90°，∴四边形OACE是矩形，∴DE⊥x轴，OE=AC=8，分三种情况：a、当点B在线段OE的延长线上时，如图1所示：则BE=OB﹣OE=m﹣8，∴S=0.5DC•BE=0.5m（m﹣8），即S=0.5m2﹣4m（m＞8）；b、当点B在线段OE上（点B不与O，E重合）时，如图2所示：则BE=OE﹣OB=8﹣m，∴S=0.5DC•BE=0.5m（8﹣m），即S=﹣0.5m2+4m（0＜m＜8）；c、当点B与E重合时，即m=8，△BCD不存在；综上所述，S=0.5m2﹣4m（m＞8），或S=﹣0.5m2+4m（0＜m＜8）；②当S=6，m＞8时，0.5m2﹣4m=6，解得：m=4±27（负值舍去），∴m=4+27；当S=6，0＜m＜8时，﹣0.5m2+4m=6，解得：m=2或m=6，∴点B的坐标为（4+27，0）或（2，0）或（6，0）.【点睛】本题是三角形综合题目，考查了坐标与图形性质、旋转的性质、矩形的判定与性质、三角形面积公式、一元二次方程的解法等知识；本题综合性强，有一定难度．4．如图，在△ABC 中，∠B=90°，AB=12 cm，BC=16 cm．点 P从点 A 开始沿 AB 边向点 B 以1 cm/s的速度移动，点 Q从点 B开始沿 BC 边向点 C以 2 cm/s的速度移动．如果 P、 Q分别从 A、B同时出发，当一个点到达终点时，另一个点也随之停止运动．设运动的时间为 t 秒．（1）当 t 为何值时，△PBQ的面积等于 35cm2？（2）当 t 为何值时，PQ的长度等82cm？（3）若点 P，Q的速度保持不变，点 P在到达点 B后返回点 A，点 Q在到达点 C后返回点B，一个点停止，另一个点也随之停止．问：当 t为何值时，△PCQ的面积等于 32cm2？【答案】（1）t为5或7；（2）t为45或4；（3）t为4或16【解析】【分析】（1）分别用含t的代数式表示PB，BQ的长，利用面积公式列方程求解即可．（2）分别用含t的代数式表示PB，BQ的长，利用勾股定理列方程求解即可．（3）分段要清楚，，P，Q都没有返回，表示好PB，CQ的长，用面积公式列方程，，P不返回，Q返回，表示好PB，CQ的长，用面积公式列方程，，两点都返回，表示好PB，CQ的长，用面积公式列方程即可得到答案．【详解】解：（1），.根据三角形的面积公式，得，即，整理，得，解得，.故当为5或7时，的面积等于35.（2）根据勾股定理，得，整理，得，解得，.故当为或4时，的长度等于.（3）①当时，，，由题意，得，解得：，（舍去）.②当时，，，由题意，得，次方程无解.③当时，，，由题意，得，解得：（舍去），.综上所述，当为4或16时，的面积等于.【点睛】本题考查的是在运动过程中应用一元二次方程解决实际问题，建立正确情境下的几何模型是解决问题的关键，特别是最后一问，关键是弄懂分段的时间界点，才能正确的表示PB ，CQ 的长．5．某连锁超市派遣调查小组在春节期间调查某种商品的销售情况，下面是调查后小张与其 他两位成员交流的情况．小张：“该商品的进价为 24元/件．”成员甲：“当定价为 40元/件时，每天可售出 480件．”成员乙：“若单价每涨 1元，则每天少售出 20件；若单价每降 1元，则每天多售出 40件．” 根据他们的对话，请你求出要使该商品每天获利 7680元，应该怎样合理定价？ 【答案】要使该商品每天获利7680元，应定价为36元/件、40元/件或48元/件 【解析】 【分析】设每件商品定价为x 元，则在每件40元的基础上涨价时每天的销售量是[]48020(40)x --件，每件商品的利润是(24)x -元，在每件40元的基础上降价时每天的销量是[]48040(40)x +-件，每件的利润是(24)x -元，从而可以得到答案．【详解】解：设每件商品定价为x 元．①当40x ≥时，[](24)48020(40)7680x x ---= ， 解得：1240,48;x x ==②当40x <时，[](24)48040(40)7680x x -+-=， 解得：1236,40x x ==（舍去），.答：要使该商品每天获利7680元，应定价为36元/件、40元/件或48元/件． 【点睛】本题考查的是一元二次方程中的升降价对销售量产生影响方面的应用，用含有未知数的代数式表示销售量是这一类题的关键．6．机械加工需用油进行润滑以减小摩擦，某企业加工一台设备润滑用油量为90kg ，用油的重复利用率为60%，按此计算，加工一台设备的实际耗油量为36kg ，为了倡导低碳，减少油耗，该企业的甲、乙两个车间都组织了人员为减少实际油耗量进行攻关． （1）甲车间通过技术革新后，加工一台设备润滑油用油量下降到70kg ，用油的重复利用率仍然为60%，问甲车间技术革新后，加工一台设备的实际油耗量是多少千克？（2）乙车间通过技术革新后，不仅降低了润滑油用油量，同时也提高了用油的重复利用率，并且发现在技术革新前的基础上，润滑用油量每减少1kg ，用油的重复利用率将增加1.6%，例如润滑用油量为89kg 时，用油的重复利用率为61.6%． ①润滑用油量为80kg ，用油量的重复利用率为多少？②已知乙车间技术革新后实际耗油量下降到12kg ，问加工一台设备的润滑用油量是多少千克？用油的重复利用率是多少？ 【答案】（1）28（2）①76%②75，84% 【解析】试题分析：（1）直接利用加工一台设备润滑油用油量下降到70kg ，用油的重复利用率仍然为60%，进而得出答案；（2）①利用润滑用油量每减少1kg ，用油的重复利用率将增加1.6%，进而求出答案； ②首先表示出用油的重复利用率，进而利用乙车间技术革新后实际耗油量下降到12kg ，得出等式求出答案．试题解析：（1）根据题意可得：70×（1﹣60%）=28（kg ）； （2）①60%+1.6%（90﹣80）=76%； ②设润滑用油量是x 千克，则 x{1﹣[60%+1.6%（90﹣x ）]}=12， 整理得：x 2﹣65x ﹣750=0， （x ﹣75）（x+10）=0， 解得：x 1=75，x 2=﹣10（舍去）， 60%+1.6%（90﹣x ）=84%，答：设备的润滑用油量是75千克，用油的重复利用率是84%． 考点：一元二次方程的应用7．已知关于x 的一元二次方程()222130x k x k --+-=有两个实数根．()1求k 的取值范围；()2设方程两实数根分别为1x ，2x ，且满足221223x x +=，求k 的值．【答案】（1）134k ≤；（2）2k =-． 【解析】 【分析】()1根据方程有实数根得出()()22[2k 1]41k 38k 50=---⨯⨯-=-+≥，解之可得．()2利用根与系数的关系可用k 表示出12x x +和12x x 的值，根据条件可得到关于k 的方程，可求得k 的值，注意利用根的判别式进行取舍． 【详解】 解：()1关于x 的一元二次方程()222130x k x k --+-=有两个实数根，0∴≥，即()()22[21]4134130k k k ---⨯⨯-=-+≥，解得134k ≤． ()2由根与系数的关系可得1221x x k +=-，2123x x k =-，()222222121212()2(21)23247x x x x x x k k k k ∴+=+-=---=-+， 221223x x +=，224723k k ∴-+=，解得4k =，或2k =-，134k ≤， 4k ∴=舍去， 2k ∴=-． 【点睛】本题考查了一元二次方程2ax bx c 0(a 0,++=≠a ，b ，c 为常数)根的判别式.当0>，方程有两个不相等的实数根；当0=，方程有两个相等的实数根；当0<，方程没有实数根.以及根与系数的关系．8．已知关于x 的二次函数22(21)1y x k x k =--++的图象与x 轴有2个交点.（1）求k 的取值范围；（2）若图象与x 轴交点的横坐标为12,x x ，且它们的倒数之和是32-，求k 的值. 【答案】（1）k ＜-34；（2）k=﹣1 【解析】试题分析：（1）根据交点得个数，让y=0判断出两个不相等的实数根，然后根据判别式△= b 2-4ac 的范围可求解出k 的值；（2）利用y=0时的方程，根据一元二次方程的根与系数的关系，可直接列式求解可得到k 的值.试题解析：（1）∵二次函数y=x 2-（2k-1）x+k 2+1的图象与x 轴有两交点， ∴当y=0时，x 2-（2k-1）x+k 2+1=0有两个不相等的实数根． ∴△=b 2-4ac=[-（2k-1）]2-4×1×（k 2+1）＞0． 解得k ＜-34； （2）当y=0时，x 2-（2k-1）x+k 2+1=0． 则x 1+x 2=2k-1，x 1•x 2=k 2+1， ∵=== 32-，解得：k=-1或k= 13-（舍去）， ∴k=﹣19．已知关于x 的一元二次方程x 2﹣x +a ﹣1=0． （1）当a=﹣11时，解这个方程；（2）若这个方程有两个实数根x 1，x 2，求a 的取值范围；（3）若方程两个实数根x 1，x 2满足[2+x 1（1﹣x 1）][2+x 2（1﹣x 2）]=9，求a 的值． 【答案】（1）123,4x x =-=（2）54a ≤（3）-4 【解析】 【分析】（1）根据一元二次方程的解法即可求出答案； （2）根据判别式即可求出a 的范围； （3）根据根与系数的关系即可求出答案． 【详解】（1）把a =﹣11代入方程，得x 2﹣x ﹣12=0， （x +3）（x ﹣4）=0， x +3=0或x ﹣4=0， ∴x 1=﹣3，x 2=4；（2）∵方程有两个实数根12x x ，， ∴△≥0，即（﹣1）2﹣4×1×（a ﹣1）≥0， 解得54a ≤：； （3）∵12x x ，是方程的两个实数根，222211221122101011x x a x x a x x a x x a -+-=-+-=∴-=--=-，，，． ∵[2+x 1（1﹣x 1）][2+x 2（1﹣x 2）]=9，∴221122229x x x x ⎡⎤⎡⎤+-+-=⎣⎦⎣⎦， 把22112211x x a x x a -=--=-，代入，得：[2+a ﹣1][2+a ﹣1]=9，即（1+a ）2=9， 解得：a =﹣4，a =2（舍去）， 所以a 的值为﹣4．点睛：本题考查了一元二次方程，解题的关键是熟练运用判别式以及根与系数的关系．10．如图直线y ＝kx +k 交x 轴负半轴于点A ，交y 轴正半轴于点B ，且AB ＝2 （1）求k 的值；（2）点P 从A 出发，以每秒1个单位的速度沿射线AB 运动，过点P 作直线AB 的垂线交x 轴于点Q ，连接OP ，设△PQO 的面积为S ，点P 运动时间为t ，求S 与t 的函数关系式，并直接写出t的取值范围；（3）在（2）的条件下，当P在AB的延长线上，若OQ+AB＝7（BQ﹣OP），求此时直线PQ的解析式．【答案】（1）k32）当0＜t＜12时，S＝12•OQ•P y＝12（1﹣2t3＝﹣323．当t＞12时，S＝12OQ•P y＝12（2t﹣1）•32t＝32t2﹣34t．（3）直线PQ的解析式为y 353．【解析】【分析】（1）求出点B的坐标即可解决问题；（2）分两种情形①当0＜t＜12时，②当t＞12时，根据S＝12OQ•P y，分别求解即可；（3）根据已知条件构建方程求出t，推出点P，Q的坐标即可解决问题．【详解】解：（1）对于直线y＝kx+k，令y＝0，可得x＝﹣1，∴A（﹣1，0），∴OA＝1，∵AB＝2，∴OB223AB OA-=∴k3（2）如图，∵tan ∠BAO ＝3OB OA= ∴∠BAO ＝60°，∵PQ ⊥AB ，∴∠APQ ＝90°，∴∠AQP ＝30°，∴AQ ＝2AP ＝2t ， 当0＜t ＜12时，S ＝12•OQ •P y ＝12（1﹣2t 3323． 当t ＞12时，S ＝12OQ •P y ＝12（2t ﹣1）•32t ＝32t 2﹣34t ． （3）∵OQ +AB 7（BQ ﹣OP ），∴2t ﹣1+22221373(21)(1)24t t t +--+ ∴2t +1271t t -+∴4t 2+4t +1＝7t 2﹣7t +7，∴3t 2﹣11t +6＝0，解得t ＝3或23（舍弃）， ∴P （1233Q （5，0）， 设直线PQ 的解析式为y ＝kx +b ，则有133250k b k b ⎧+=⎪⎨⎪+=⎩解得353k b ⎧=⎪⎪⎨⎪=⎪⎩，∴直线PQ 的解析式为33y x =-+． 【点睛】 本题属于一次函数综合题，考查了一次函数的性质，三角形的面积，无理方程等知识，解题的关键是学会利用参数构建方程解决问题．。
九年级一元二次方程易错题(Word版 含答案)
九年级一元二次方程易错题（Word版含答案）一、初三数学一元二次方程易错题压轴题（难）1．阅读与应用：阅读1：a，b为实数，且a＞0，b＞0，因为()2≥0，所以a﹣2+b≥0，从而a+b≥2(当a＝b时取等号)．阅读2：若函数y＝x+(m＞0，x＞0，m为常数)，由阅读1结论可知：x+≥2，所以当x＝，即x＝时，函数y＝x+的最小值为2．阅读理解上述内容，解答下列问题：问题1：已知一个矩形的面积为4，其中一边长为x，则另一边长为，周长为2(x+)，求当x＝时，周长的最小值为；问题2：汽车的经济时速是汽车最省油的行驶速度，某种汽车在每小时70～110公里之间行驶时(含70公里和110公里)，每公里耗油()L．若该汽车以每小时x公里的速度匀速行驶，1h的耗油量为yL．(1)求y关于x的函数关系式(写出自变量x的取值范围)；(2)求该汽车的经济时速及经济时速的百公里耗油量．【答案】问题1：2，8；问题2：(1)y=；(2)10.【解析】【分析】（1）利用题中的不等式得到x+=4，从而得到x=2时，周长的最小值为8；（2）根据耗油总量=每公里的耗油量×行驶的速度列出函数关系式即可，经济时速就是耗油量最小的形式速度．【详解】(1)∵x+≥2＝4，∴当x＝时，2(x+)有最小值8．即x＝2时，周长的最小值为8；故答案是：2；8；问题2：，当且仅当，即x＝90时，“＝”成立，所以，当x＝90时，函数取得最小值9，此时，百公里耗油量为，所以，该汽车的经济时速为每小时90公里，经济时速的百公里耗油量为10L．【点睛】本题考查了配方法及反比例函数的应用，最值问题，解题的关键是读懂题目提供的材料，易错点是了解“耗油总量=每公里的耗油量×行驶的速度”，难度中等偏上．2．随着人们经济收入的不断提高及汽车产业的快速发展，汽车已越来越多地进入普通家庭．据某市交通部门统计，2008年底该市汽车拥有量为75万辆，而截止到2010年底，该市的汽车拥有量已达108万辆．（1）求2008年底至2010年底该市汽车拥有量的年平均增长率；（2）为了保护城市环境，缓解汽车拥堵状况，该市交通部门拟控制汽车总量，要求到2012年底全市汽车拥有量不超过125.48万辆；另据统计，从2011年初起，该市此后每年报废的汽车数量是上年底汽车拥有量的10%假设每年新增汽车数量相同，请你估算出该市从2011年初起每年新增汽车数量最多不超过多少万辆．【答案】解：（1）2008年底至2010年底该市汽车拥有量的年平均增长率是20%（2）从2011年初起每年新增汽车数量最多不超过20万辆【解析】【分析】（1）设年平均增长率x，根据等量关系“2008年底汽车拥有量×（1+年平均增长率）×（1+年平均增长率）”列出一元二次方程求得．（2）设从2011年初起每年新增汽车的数量y，根据已知得出2011年报废的车辆是2010年底拥有量×10%，推出2011年底汽车拥有量是2010年底拥有量-2011年报废的车辆=2010年拥有量×（1-10%），得出等量关系是： 2010年拥有量×（1-10%）+新增汽车数量]×（1-10%）+新增汽车数量”，列出一元一次不等式求得．【详解】解：（1）设该市汽车拥有量的年平均增长率为x．根据题意，得75（1+x）2=108，则1+x=±1.2解得x1=0.2=20%，x2=﹣2.2（不合题意，舍去）．答：该市汽车拥有量的年平均增长率为20%．（2）设全市每年新增汽车数量为y万辆，则2010年底全市的汽车拥有量为（108×90%+y）万辆，2011年底全市的汽车拥有量为[（108×90%+y）×90%+y]万辆．根据题意得（108×90%+y）×90%+y≤125.48，解得y≤20．答：该市每年新增汽车数量最多不能超过20万辆．3．已知关于x 的方程24832x nx n --=和()223220x n x n -+-+=，是否存在这样的n 值，使第一个方程的两个实数根的差的平方等于第二个方程的一整数根？若存在，请求出这样的n 值；若不存在，请说明理由？【答案】存在，n=0. 【解析】 【分析】在方程①中，由一元二次方程的根与系数的关系，用含n 的式子表示出两个实数根的差的平方，把方程②分解因式，建立方程求n ，要注意n 的值要使方程②的根是整数. 【详解】 若存在n 满足题意.设x1，x2是方程①的两个根，则x 1+x 2=2n ，x 1x 2=324n +-，所以(x 1-x 2)2=4n 2+3n+2， 由方程②得，(x+n-1)[x-2(n+1)]=0， ①若4n 2+3n+2=-n+1，解得n=-12，但1-n=32不是整数，舍. ②若4n 2+3n+2=2(n+2)，解得n=0或n=-14(舍)， 综上所述，n=0.4．如图，∠ AOB ＝90°，且点A ，B 分别在反比例函数1k y x =（x ＜0），2ky x=（x ＞0）的图象上，且k 1，k 2分别是方程x 2－x －6＝0的两根． （1）求k 1，k 2的值；（2）连接AB ，求tan ∠ OBA 的值．【答案】（1）k 1＝－2，k 2＝3． （2）tan∠OBA 6． 【解析】解：（1）∵k 1，k 2分别是方程x 2－x －6＝0的两根，∴解方程x 2－x －6＝0，得x 1＝3，x 2＝－2．结合图像可知：k 1＜0，k 2＞0，∴k 1＝－2，k 2＝3．（2）如图，过点A 作AC ⊥x 轴于点C ，过点B 作BD ⊥y 轴于点D ．[来源:学&科&网Z&X&X&K]由（1）知，点A，B分别在反比例函数2yx=-（x＜0），3yx=（x＞0）的图象上，∴S△ACO＝12×2-＝1 ，S△ODB＝12×3＝32．∵∠AOB＝90°，∴∠ AOC＋∠ BOD＝90°，∵∠ AOC＋∠ OAC＝90°，∴∠ OAC＝∠ BOD．又∵∠ACO＝∠ODB＝90°，∴△ACO∽△ODB．∴SSACOODB∆∆＝2OAOB⎛⎫⎪⎝⎭＝23，∴OAOB＝±6（舍负取正），即OAOB＝6．∴在Rt△AOB中，tan∠OBA＝OAOB＝6．5．如图，A、B、C、D为矩形的4个顶点，AB＝16cm，BC＝6cm，动点P、Q分别以3cm/s、2cm/s的速度从点A、C同时出发，点Q从点C向点D移动．(1)若点P从点A移动到点B停止，点P、Q分别从点A、C同时出发，问经过2s时P、Q 两点之间的距离是多少cm？(2)若点P从点A移动到点B停止，点Q随点P的停止而停止移动，点P、Q分别从点A、C 同时出发，问经过多长时间P、Q两点之间的距离是10cm？(3)若点P沿着AB→BC→CD移动，点P、Q分别从点A、C同时出发，点Q从点C移动到点D停止时，点P随点Q的停止而停止移动，试探求经过多长时间△PBQ的面积为12cm2？【答案】（1）2cm；（2）85s或245s；（3）经过4秒或6秒△PBQ的面积为12cm2．【解析】试题分析：（1）作PE⊥CD于E，表示出PQ的长度，利用PE2+EQ2=PQ2列出方程求解即可；（2）设x秒后，点P和点Q的距离是10cm．在Rt△PEQ中，根据勾股定理列出关于x的方程（16-5x）2=64，通过解方程即可求得x的值；（3）分类讨论：①当点P在AB上时；②当点P在BC边上；③当点P在CD边上时．试题解析：（1）过点P作PE⊥CD于E．则根据题意，得EQ=16-2×3-2×2=6（cm），PE=AD=6cm；在Rt△PEQ中，根据勾股定理，得PE2+EQ2=PQ2，即36+36=PQ2，∴2cm；∴经过2s时P、Q两点之间的距离是2；（2）设x秒后，点P和点Q的距离是10cm．（16-2x-3x）2+62=102，即（16-5x）2=64，∴16-5x=±8，∴x1=85，x2=245；∴经过85s或245sP、Q两点之间的距离是10cm；（3）连接BQ．设经过ys后△PBQ的面积为12cm2．①当0≤y≤163时，则PB=16-3y，∴12PB•BC=12，即12×（16-3y）×6=12，解得y=4；②当163＜x≤223时，BP=3y-AB=3y-16，QC=2y，则1 2BP•CQ=12（3y-16）×2y=12，解得y1=6，y2=-23（舍去）；③223＜x≤8时，QP=CQ-PQ=22-y，则1 2QP•CB=12（22-y）×6=12，解得y=18（舍去）．综上所述，经过4秒或6秒△PBQ的面积为 12cm2．考点：一元二次方程的应用．6．如图，在平面直角坐标系中，正方形ABCD的顶点A在y轴正半轴上，顶点B在x轴正半轴上，OA、OB的长分别是一元二次方程x2﹣7x+12=0的两个根（OA＞OB）．（1）求点D的坐标．（2）求直线BC的解析式．（3）在直线BC上是否存在点P，使△PCD为等腰三角形？若存在，请直接写出点P的坐标；若不存在，说明理由．【答案】（1）D（4，7）（2）y=3944x （3）详见解析【解析】试题分析：（1）解一元二次方程求出OA、OB的长度，过点D作DE⊥y于点E，根据正方形的性质可得AD=AB，∠DAB=90°，然后求出∠ABO=∠DAE，然后利用“角角边”证明△DAE 和△ABO全等，根据全等三角形对应边相等可得DE=OA，AE=OB，再求出OE，然后写出点D的坐标即可；（2）过点C作CM⊥x轴于点M，同理求出点C的坐标，设直线BC的解析式为y=kx+b （k≠0，k、b为常数），然后利用待定系数法求一次函数解析式解答；（3）根据正方形的性质，点P与点B重合时，△PCD为等腰三角形；点P为点B关于点C 的对称点时，△PCD为等腰三角形，然后求解即可．试题解析：（1）x2﹣7x+12=0，解得x1=3，x2=4，∵OA＞OB，∴OA=4，OB=3，过D作DE⊥y于点E，∵正方形ABCD，∴AD=AB，∠DAB=90°，∠DAE+∠OAB=90°，∠ABO+∠OAB=90°，∴∠ABO=∠DAE，∵DE⊥AE，∴∠AED=90°=∠AOB，∵DE⊥AE∴∠AED=90°=∠AOB，∴△DAE≌△ABO（AAS），∴DE=OA=4，AE=OB=3，∴OE=7，∴D（4，7）；（2）过点C作CM⊥x轴于点M，同上可证得△BCM≌△ABO，∴CM=OB=3，BM=OA=4，∴OM=7，∴C（7，3），设直线BC的解析式为y=kx+b（k≠0，k、b为常数），代入B（3，0），C（7，3）得，，解得，∴y=x﹣；（3）存在．点P与点B重合时，P1（3，0），点P与点B关于点C对称时，P2（11，6）．考点：1、解一元二次方程；2、正方形的性质；3、全等三角形的判定与性质；4、一次函数7．在等腰三角形△ABC 中，三边分别为a 、b 、c ，其中ɑ＝4，若b 、c 是关于x 的方程x 2﹣（2k +1）x +4（k ﹣12）＝0的两个实数根，求△ABC 的周长． 【答案】△ABC 的周长为10． 【解析】 【分析】分a 为腰长及底边长两种情况考虑：当a=4为腰长时，将x=4代入原方程可求出k 值，将k 值代入原方程可求出底边长，再利用三角形的周长公式可求出△ABC 的周长；当a=4为底边长时，由根的判别式△=0可求出k 值，将其代入原方程利用根与系数的关系可求出b+c 的值，由b+c=a 可得出此种情况不存在．综上即可得出结论． 【详解】当a ＝4为腰长时，将x ＝4代入原方程，得：()214421402k k ⎛⎫-++-= ⎪⎝⎭解得：52k = 当52k =时，原方程为x 2﹣6x +8＝0， 解得：x 1＝2，x 2＝4，∴此时△ABC 的周长为4+4+2＝10；当a ＝4为底长时，△＝[﹣（2k +1）]2﹣4×1×4（k ﹣12）＝（2k ﹣3）2＝0， 解得：k ＝32， ∴b +c ＝2k +1＝4． ∵b +c ＝4＝a ，∴此时，边长为a ，b ，c 的三条线段不能围成三角形． ∴△ABC 的周长为10． 【点睛】本题考查了根的判别式、根与系数的关系、一元二次方程的解、等腰三角形的性质以及三角形的三边关系，分a 为腰长及底边长两种情况考虑是解题的关键．8．已知：如图，在平面直角坐标系中，矩形AOBC 的顶点C 的坐标是（6，4），动点P 从点A 出发，以每秒1个单位的速度沿线段AC 运动，同时动点Q 从点B 出发，以每秒2个单位的速度沿线段BO 运动，当Q 到达O 点时，P ，Q 同时停止运动，运动时间是t 秒（t ＞0）．（1）如图1，当时间t ＝ 秒时，四边形APQO 是矩形；（2）如图2，在P ，Q 运动过程中，当PQ ＝5时，时间t 等于 秒；（3）如图3，当P ，Q 运动到图中位置时，将矩形沿PQ 折叠，点A ，O 的对应点分别是D ，E ，连接OP ，OE ，此时∠POE ＝45°，连接PE ，求直线OE 的函数表达式．【答案】（1）t ＝2；（2）1或3；（3）y ＝12x ． 【解析】 【分析】先根据题意用t 表示AP 、BQ 、PC 、OQ 的长．（1）由四边形APQO 是矩形可得AP ＝OQ ，列得方程即可求出t ．（2）过点P 作x 轴的垂线PH ，构造直角△PQH ，求得HQ 的值．由点H 、Q 位置不同分两种情况讨论用t 表示HQ ，即列得方程求出t ．根据t 的取值范围考虑t 的合理性． （3）由轴对称性质，对称轴PQ 垂直平分对应点连线OC ，得OP ＝PE ，QE ＝OQ ．由∠POE ＝45°可得△OPE 是等腰直角三角形，∠OPE ＝90°，即点E 在矩形AOBC 内部，无须分类讨论．要求点E 坐标故过点E 作x 轴垂线MN ，易证△MPE ≌△AOP ，由对应边相等可用t 表示EN ，QN ．在直角△ENQ 中利用勾股定理为等量关系列方程即求出t ． 【详解】∵矩形AOBC 中，C （6，4） ∴OB ＝AC ＝6，BC ＝OA ＝4依题意得：AP ＝t ，BQ ＝2t （0＜t≤3） ∴PC ＝AC ﹣AP ＝6﹣t ，OQ ＝OB ﹣BQ ＝6﹣2t （1）∵四边形APQO 是矩形 ∴AP ＝OQ ∴t ＝6﹣2t 解得：t ＝2 故答案为2．（2）过点P 作PH ⊥x 轴于点H ∴四边形APHO 是矩形∴PH ＝OA ＝4，OH ＝AP ＝t ，∠PHQ ＝90° ∵PQ ＝5∴HQ 22PQ PH 3-=①如图1，若点H 在点Q 左侧，则HQ ＝OQ ﹣OH ＝6﹣3t ∴6﹣3t ＝3 解得：t ＝1②如图2，若点H 在点Q 右侧，则HQ ＝OH ﹣OQ ＝3t ﹣6 ∴3t ﹣6＝3解得：t＝3故答案为1或3．（3）过点E作MN⊥x轴于点N，交AC于点M∴四边形AMNO是矩形∴MN＝OA＝4，ON＝AM∵矩形沿PQ折叠，点A，O的对应点分别是D，E∴PQ垂直平分OE∴EQ＝OQ＝6﹣2t，PO＝PE∵∠POE＝45°∴∠PEO＝∠POE＝45°∴∠OPE＝90°，点E在矩形AOBC内部∴∠APO+∠MPE＝∠APO+∠AOP＝90°∴∠MPE＝∠AOP在△MPE与△AOP中PME OAP90MPE AOPPE0P︒⎧∠=∠=⎪∠=∠⎨⎪=⎩∴△MPE≌△AOP（AAS）∴PM＝OA＝4，ME＝AP＝t∴ON＝AM＝AP+PM＝t+4，EN＝MN﹣ME＝4﹣t∴QN＝ON﹣OQ＝t+4﹣（6﹣2t）＝3t﹣2∵在Rt△ENQ中，EN2+QN2＝EQ2∴（4﹣t）2+（3t﹣2）2＝（6﹣2t）2解得：t1＝﹣2（舍去），t2＝43∴AM＝43+4＝163，EN＝4﹣43＝83∴点E坐标为（163，83）∴直线OE的函数表达式为y＝12x．【点睛】本题考查了矩形的判定和性质，勾股定理，轴对称的性质，全等三角形的判定和性质，解一元一次和一元二次方程．在动点题中要求运动时间t的值，常规做法是用t表示相关线段，再利用线段相等或勾股定理作为等量关系列方程求值．要注意根据t 的取值范围考虑方程的解的合理性．9．已知关于x 的方程230x x a ++=①的两个实数根的倒数和等于3，且关于x 的方程2(1)320k x x a -+-=②有实数根，又k 为正整数，求代数式2216k k k -+-的值． 【答案】0.【解析】【分析】 由于关于x 的方程x 2+3x +a =0的两个实数根的倒数和等于3，利用根与系数的关系可以得到关于a 的方程求出a ，又由于关于x 的方程（k -1）x 2+3x -2a =0有实数根，分两种情况讨论，该方程可能是一次方程、有可能是一元二次方程，又k 为正整数，利用判别式可以求出k ，最后代入所求代数式计算即可求解．【详解】解：设方程①的两个实数根分别为x 1、x 2则12123940x x x x a a +-⎧⎪⎨⎪-≥⎩＝＝＝ ， 由条件，知12121211x x x x x x ++==3， 即33a -=，且94a ≤， 故a ＝－1，则方程②为(k -1)x 2+3x +2=0，Ⅰ.当k -1=0时，k =1,x =23-，则22106k k k -=+-. Ⅱ.当k -1≠0时，∆=9-8（k -1）=17-6-8k ≥0，则178k ≤， 又k 是正整数，且k ≠1，则k =2，但使2216k k k -+-无意义. 综上，代数式2216k k k -+-的值为0 【点睛】本题综合考查了根的判别式和根与系数的关系，在解方程时一定要注意所求k 的值与方程判别式的关系．要注意该方程可能是一次方程、有可能是一元二次方程，10．定南县某楼盘准备以每平方米4000元的均价对外销售，由于国务院有关房地产的新政策出台后，购房者持币观望，房地产开发商为了加快资金周转，对价格经过两次下调后，决定以每平方米3240元的均价开盘销售．（1）求平均每次下调的百分率；（2）某人准备以开盘价均价购买一套100平方米的住房，开发商给予以下两种优惠方案以供选择：①打9．8折销售；②不打折，一次性送装修费每平方米80元，试问哪种方案更优惠？【答案】（1）10%；（2）方案②【解析】试题分析：首先设下调的百分率为x，根据题意列出方程进行求解，得出答案；分别求出两种方案所需要花费的钱数，然后进行比较．试题解析：（1）设平均每次下调的百分率是x，依题意得，4000（1-x）2=3240解之得：x=0．1=10%或x=1．9（不合题意，舍去）答：平均每次下调的百分率是10%．（2）方案①实际花费=100×3240×98%=317520元方案②实际花费=100×3240-100×80=316000元∵317520＞316000 ∴方案②更优惠考点：一元二次方程的应用。
九年级上册数学 一元二次方程易错题(Word版 含答案)
6．如图，已知 AB 是⊙O 的弦，半径 OA=2，OA 和 AB 的长度是关于 x 的一元二次方程 x2﹣ 4x+a=0 的两个实数根． （1）求弦 AB 的长度； （2）计算 S△AOB； （3）⊙O 上一动点 P 从 A 点出发，沿逆时针方向运动一周，当 S =S △POA △AOB 时，求 P 点所经 过的弧长（不考虑点 P 与点 B 重合的情形）．
（1）当 t 为何值时，△PBQ 的面积等于 35cm2？
（2）当 t 为何值时，PQ 的长度等 8 2 cm？
（3）若点 P，Q 的速度保持不变，点 P 在到达点 B 后返回点 A，点 Q 在到达点 C 后返回点 B，一个点停止，另一个点也随之停止．问：当 t 为何值时，△PCQ 的面积等于 32cm2？
【答案】（1）AB=2；（2）S△AOB= 3 ；（3）当 S =S △POA △AOB 时，P 点所经过的弧长分别是
4 、 8 、 10 ． 33 3
【解析】
试题分析：（1）OA 和 AB 的长度是一元二次方程的根，所以利用一元二次方程的根与系数
的关系即可求出 AB 的长度；
（2）作出△AOB 的高 OC，然后求出 OC 的长度即可求出面积；
（3）由题意知：两三角形有公共的底边，要面积相等，即高要相等． 试题解析：（1）由题意知：OA 和 AB 的长度是 x2﹣4x+a=0 的两个实数根，
(易错题)初中数学九年级数学上册第一单元《一元二次方程》检测题(有答案解析)
一、选择题1．下列方程中，没有实数根的是（ ） A ．2670x x ++= B ．25260x x --= C ．22270x x -=D ．2220x x -+-=2．已知一元二次方程2210x x --＝的两个根分别是1x ，2x ，则2112x x x -+的值为（ ）． A ．-1 B ．0 C ．2 D ．3 3．x=－2是关于x 的一元二次方程2x 2+3ax －2a 2=0的一个根，则a 的值为（ ） A ．1或4B ．－1或－4C ．－1或4D ．1或－44．下列方程中是一元二次方程的是（ ） A ．210x +=B ．220x -=C ．21x y +=D ．211x x+= 5．方程22x x =的解是（ ） A ．0x = B ．2x =C ．10x =，22x =D ．10x =，22x =6．若m 是方程220x x c --=的一个根，设2(1)p m =-，2q c =+，则p 与q 的大小关系为（ ） A ．p ＜qB ．p ＝qC ．p ＞qD ．与c 的取值有关7．下列一元二次方程中，有两个不相等实数根的是（ ） A ．2104x x -+= B ．2390x x ++= C ．2250x x -+= D ．25130x x -=8．若关于x 的一元二次方程260x x c -+=有两个相等的实数根，则常数c 的值为（ ） A ．3B ．6C ．8D ．99．在一幅长80cm ，宽50cm 的矩形风景画的四周镶一条金色纸边，制成一幅矩形挂图，如图所示，如果要使整个挂图的面积是5400cm 2，设金色纸边的宽为xcm ，那么x 满足的方程是（ ）A ．x 2+65x-350=0B ．x 2+130x-1400=0C ．x 2-130x-1400=0D ．x 2-65x-350=0 10．下列关于x 的一元二次方程中，有两个不相等的实数根的方程是（ ）A ．290x +=B ．24410x x -+=C ．210x x ++=D ．210x x +-=11．已知a 、b 、m 、n 为互不相等的实数，且(a +m )( a +n )＝2，(b +m )( b +n )＝2，则ab ﹣mn的值为（ ） A ．4 B ．1 C ．﹣2 D ．﹣1 12．已知m 是方程2210x x --=的一个根，则代数式2242020m m -+的值为（ ）A ．2022B ．2021C ．2020D ．2019二、填空题13．已知关于x 的一元二次方程230x mx +=+的一个根为1，则方程的另一个根为________．14．设a ，b 是方程220190x x +-=的两个实数根，则11a b+=_____． 15．一元二次方程22(1)210a x x a +++-=，有一个根为零，则a 的值为________． 16．设m 、n 是一元二次方程x 2+2x ﹣7＝0的两个根，则m+n ＝_____．17．已知关于x 的一元二次方程2230ax x +-=有两个不相等的实数根，则a 的取值范围是______．18．已知x ＝2是关于x 一元二次方程x 2+kx ﹣6＝0的一个根，则另一根是_____． 19．若t 是一元二次方程()200++=≠ax bx c a 的根，则判别式24b ac =-△与完全平方式()22M at b =+的大小关系为___________20．参加足球联赛的每两队之间都进行两场比赛，共要比赛90场，共有________个队参加比赛．三、解答题21．如图，有一道长为10m 的墙，计划用总长为54m 的篱笆，靠墙围成由六个小长方形组成的矩形花圃ABCD ．若花圃ABCD 面积为272m ，求AB 的长．22．解方程：（1）26160x x +-=． （2）22430x x --=．23．设,a b 是一个直角三角形的两条直角边的长，且()()2222112a b ab +++=，求这个直角三角形的斜边长c 的值．24．（1）用配方法解：221470x x --=； （2）用因式分解法解：()()222332x x -=-． 25．解下列方程（1）2210x x ++= （2）233x x26．解下列方程： （1）x （x －1）＝1－x （2）(x-3) 2 = (2x-1) (x +3)【参考答案】***试卷处理标记，请不要删除一、选择题 1．D 解析：D 【分析】根据判别式的意义对各选项进行判断． 【详解】A 、224641780b ac =-=-⨯⨯=>，则方程有两个不相等的实数根，所以A 选项不符合题意；B 、()()224541261290b ac =-=--⨯⨯-=>，则方程有两个不相等的实数根，所以B 选项不符合题意；C 、()224274207290b ac =-=--⨯⨯=>，则方程有两个不相等的实数根，所以C 选项不符合题意；D 、()()224241240b ac =-=-⨯-⨯-=-<，则方程没有实数根，所以D 选项符合题意． 故选：D ． 【点睛】本题考查了根的判别式：一元二次方程20ax bx c ++=(0a ≠)的根与24b ac =-有如下关系：当△＞0时，方程有两个不相等的实数根；当△=0时，方程有两个相等的实数根；当△＜0时，方程无实数根．2．D解析：D 【分析】分别根据一元二次方程的根的意义和一元二次方程根与系数的关系分别得到21112210,2x x x x --=+=，变形代入求值即可得到答案．【详解】解：由题意得21112210,2x x x x --=+=，即21121x x -=，∴原式211122123x x x x =-++=+=． 故选：D ．【点睛】此题主要考查了一元二次方程的解的根与系数的关系，灵活运用根与系数的关系是解答此题的关键．3．D解析：D 【分析】根据一元二次方程的解的定义知，x=－2满足关于x 的一元二次方程2x 2+3ax －2a 2=0，可得出关于a 的方程，通过解方程即可求得a 的值． 【详解】解：将x=－2代入一元二次方程2x 2+3ax －2a 2=0， 得：()()222-23-2-20a a ⨯+⋅=， 化简得：2+340a a -=， 解得：a=1或a=-4． 故选：D ． 【点睛】本题考查了一元二次方程的解的定义．一元二次方程ax 2+bx+c=0（a≠0）的所有解都满足该一元二次方程的关系式．4．B解析：B 【分析】直接利用一元二次方程的定义分析得出答案． 【详解】解：A.210x +=，是一元一次方程，故本选项不符合题意． B.220x -=，是一元二次方程，故本选项符合题意． C.21x y +=，是二元二次方程，故本选项不符合题意．D.211x x+=，该方程分式方程，故本选项不符合题意． 故选B ． 【点睛】此题主要考查了一元二次方程的定义，正确把握定义是解题关键．5．C解析：C 【分析】移项并因式分解，得到两个关于x 的一元一次方程，即可求解． 【详解】解：移项，得220x x -=， 因式分解，得()20x x -=，∴0x =或20x -=， 解得10x =，22x =，故选：C ． 【点睛】本题考查解一元二次方程，掌握因式分解法是解题的关键．6．A解析：A 【分析】结合m 是方程220x x c --=的一个根，计算p-q 的值即可解决问题． 【详解】解：∵m 是方程220x x c --=的一个根， ∴220m m c --= ∵2(1)p m =-，2q c =+，∴222(1)(2)212211p q m c m m c m m c -=--+=-+--=---=-， ∴p ＜q 故选：A ． 【点睛】此题主要考查了一元二次方程的解以及整式的运算，熟练掌握一元二次方程的解的应用是解答此题的关键．7．D解析：D 【分析】先把各方程化为一般式，再分别计算方程根的判别式，然后根据判别式的意义对各选项进行判断． 【详解】A 、()221414104b ac =-=--⨯⨯=，方程有两个相等的两个实数根； B 、2243419270b ac =-=-⨯⨯=-<，方程没有实数根； C 、()2242415160b ac =-=--⨯⨯=-<，方程没有实数根；D 、()224134501690b ac =-=--⨯⨯=>，方程有两个不相等的两个实数根； 故选：D ． 【点睛】本题考查了根的判别式：一元二次方程20ax bx c ++=(0a ≠)的根与24b ac =-有如下关系：当△＞0时，方程有两个不相等的两个实数根；当△=0时，方程有两个相等的两个实数根；当△＜0时，方程无实数根．8．D解析：D 【分析】根据方程有两个相等的实数根结合根的判别式即可得出关于c 的一元一次方程，解方程即可得出结论． 【详解】 解：260x x c -+=有两个相等的实根，2(6)40c ∴∆=--=，解得：9c = 故选：D ． 【点睛】本题考查了根的判别式以及解一元一次方程，由方程有两个相等的实数根结合根的判别式得出关于c 的一元一次方程是解题的关键．9．A解析：A 【分析】本题可设长为（80+2x ），宽为（50+2x ），再根据面积公式列出方程，化简即可． 【详解】解：依题意得：（80+2x ）（50+2x ）=5400， 即4000+260x+4x 2=5400， 化简为：4x 2+260x-1400=0， 即x 2+65x-350=0． 故选：A ． 【点睛】本题考查的是一元二次方程的应用，解此类题目要注意运用面积的公式列出等式再进行化简．10．D解析：D 【分析】分别求出每个方程的根的判别式即可得到方程的根的情况. 【详解】A 选项：2049360∆=-⨯=-<，∴该方程没有实数根，故A 错误；B 选项：()244410∆=--⨯⨯=，∴该方程有两个相等的实数根，故B 错误； C 选项：2141130∆=-⨯⨯=-<，∴该方程没有实数根，故C 错误；D 选项：()2141150∆=-⨯⨯-=>，∴方程有两个不相等的实数根，故D 正确；故选：D. 【点睛】此题考查一元二次方程的根的情况，正确求根的判别式的值，掌握一元二次方程的根的三种情况是解题的关键.11．C解析：C 【分析】先把已知条件变形得到a 2+ (m +n ) a +mn ﹣2＝0，b 2+( m +n ) b +mn ﹣2＝0，则可把a 、b 看作方程x 2+( m +n ) x +mn ﹣2＝0的两实数根，利用根与系数的关系得到ab ＝mn ﹣2，从而得到ab ﹣mn 的值． 【详解】解：∵(a +m )( a +n )＝2，(b +m )( b +n )＝2， ∴a 2+( m +n )a +mn ﹣2＝0，b 2+( m +n )b +mn ﹣2＝0， 而a 、b 、m 、n 为互不相等的实数，∴可以把a 、b 看作方程x 2+（m +n ）x +mn ﹣2＝0的两个实数根， ∴ab ＝mn ﹣2， ∴ab ﹣mn ＝﹣2． 故选：C ． 【点睛】本题考查一元二次方程根与系数的关系及整式的乘法，理解代数思想，把“a 、b 看作方程x 2+（m +n ）x +mn ﹣2＝0的两实数根”是解题关键．12．A解析：A 【分析】把x m =代入方程2210x x --=求出221m m -=，把2242020m m -+化成()2222020m m -+，再整体代入求出即可．【详解】∵把x m =代入方程2210x x --=得：2210m m --=， ∴221m m -=，∴()222420202220202120202022m m m m -+=-+=⨯+=， 故选：A ． 【点睛】本题考查了一元二次方程的解，采用了整体代入的方法．注意：能使一元二次方程左右两边相等的未知数的值是一元二次方程的解．二、填空题13．3【分析】先将x=1代入求得m 的值然后解一元二次方程即可求出另一根【详解】解：∵一元二次方程的一个根为1∴1+m+3=0即m=-4∴（x-1）（x-3）=0x-1=0x-3=0∴x=1或x=3即该方解析：3【分析】先将x=1代入求得m 的值，然后解一元二次方程即可求出另一根． 【详解】解：∵一元二次方程230x mx +=+的一个根为1 ∴1+m+3=0，即m=-4 ∴2430x x -+= （x-1）（x-3）=0 x-1=0，x-3=0∴x=1或x=3，即该方程的另一根为3． 故答案为3． 【点睛】本题主要考查了一元二次方程的解和解一元二次方程，关于x 的一元二次方程230x mx +=+的一个根为1求得m 的值成为解答本题的关键．14．【分析】根据根与系数关系即可得出a+b 和ab 的值再对代数式变形整体代入即可【详解】解：∵ab 是方程的两个实数根∴∴故答案为：【点睛】本题考查根与系数关系熟记根与系数关系的公式是解题关键 解析：22019【分析】根据根与系数关系即可得出a+b 和ab 的值，再对代数式11a b+变形整体代入即可． 【详解】解：∵a ，b 是方程2220190+-=x x 的两个实数根， ∴2a b +=-，2019ab =-，∴112220192019a b a b ab +-+===-． 故答案为：22019．【点睛】本题考查根与系数关系．熟记根与系数关系的公式是解题关键．15．1【分析】根据一元二次方程的解的定义把x=0代入（a+1）x2+2x+a2-1=0再解关于a 的方程然后利用一元二次方程的定义确定a 的值【详解】解：把x=0代入（a+1）x2+2x+a2-1=0得a2解析：1 【分析】根据一元二次方程的解的定义，把x=0代入（a+1）x 2+2x+a 2-1=0，再解关于a 的方程，然后利用一元二次方程的定义确定a 的值． 【详解】解：把x=0代入（a+1）x 2+2x+a 2-1=0得a 2-1=0， 解得a=1或a=-1， 而a+1≠0， 所以a 的值为1． 故答案为：1． 【点睛】本题考查了一元二次方程的解：能使一元二次方程左右两边相等的未知数的值是一元二次方程的解．16．﹣2【分析】直接根据根与系数的关系求解即【详解】解：∵mn 是一元二次方程x2+2x ﹣7＝0的两个根∴m+n ＝﹣2故答案为﹣2【点睛】本题考查一元二次方程根与系数的关系是重要考点难度较易掌握相关知识是解析：﹣2． 【分析】直接根据根与系数的关系求解，即b m n a+=-． 【详解】解：∵m 、n 是一元二次方程x 2+2x ﹣7＝0的两个根， ∴m+n ＝﹣2． 故答案为﹣2． 【点睛】本题考查一元二次方程根与系数的关系，是重要考点，难度较易，掌握相关知识是解题关键．17．且【分析】根据题意一元二次方程有两个不相等的实数根可知根的判别式据此解一元一次不等式即可解题注意二次项系数不为零【详解】关于x 的一元二次方程有两个不相等的实数根即且故答案为：且【点睛】本题考查一元二解析：13a >-且0a ≠． 【分析】根据题意，一元二次方程2230ax x +-=有两个不相等的实数根，可知根的判别式2=40b ac ∆->，据此解一元一次不等式即可解题，注意二次项系数不为零．【详解】关于x 的一元二次方程2230ax x +-=有两个不相等的实数根，2=40b ac ∴∆->即224(3)0a -⨯->4120a +>13a ∴>-且0a ≠故答案为：13a >-且0a ≠． 【点睛】本题考查一元二次方程根的判别式、一元一次不等式、一元二次方程的定义等知识，是重要考点，难度较易，掌握相关知识是解题关键．18．-3【分析】设方程的另一个根为x2根据两根之积列出关于x2的方程解之可得答案【详解】解：设方程的另一个根为x2则2x2＝﹣6解得x2＝﹣3故答案为：﹣3【点睛】本题考查了一元二次方程ax2+bx+c解析：-3． 【分析】设方程的另一个根为x 2，根据两根之积列出关于x 2的方程，解之可得答案． 【详解】解：设方程的另一个根为x 2， 则2x 2＝﹣6， 解得x 2＝﹣3， 故答案为：﹣3． 【点睛】本题考查了一元二次方程ax 2+bx +c =0（a ≠0）根与系数的关系，若x 1，x 2为方程的两个根，则x 1，x 2与系数的关系式：12bx x a +=-，12c x x a⋅=． 19．相等【分析】由t 是一元二次方程()的根利用公式法解一元二次方程即可得出t 的值将其代入完全平方式中即可得出M 的值由此即可得出结论【详解】∵t 是一元二次方程()的根∴或当时则；当时则；∴故答案为：相等【解析：相等 【分析】由t 是一元二次方程20ax bx c ++=(0a ≠)的根利用公式法解一元二次方程即可得出t 的值，将其代入完全平方式()22M at b =+中即可得出M 的值，由此即可得出结论． 【详解】∵t 是一元二次方程20ax bx c ++=(0a ≠)的根，∴2b t a -+=或2b t a--=，当2b t a -+=时，则()224M b bb ac =-=-；当2b t a-=时，则()224M b bb ac =-=-；∴24b ac M =-=．故答案为：相等．本题考查了根的判别式、完全平方式以及利用公式法解一元二次方程，利用公式法解一元二次方程求出t 值是解题的关键．20．10【分析】设共有x 个队参加比赛根据每两队之间都进行两场比赛结合共比了90场即可得出关于x 的一元二次方程解之即可得出结论【详解】解：设共有x 个队参加比赛根据题意得：2×x （x-1）=90整理得：x2解析：10．【分析】设共有x 个队参加比赛，根据每两队之间都进行两场比赛结合共比了90场即可得出关于x 的一元二次方程，解之即可得出结论．【详解】解：设共有x 个队参加比赛，根据题意得：2×12x （x-1）=90， 整理得：x 2-x-90=0，解得：x=10或x=-9（舍去）．故答案为：10．【点睛】本题考查了一元二次方程的应用，根据每两队之间都进行两场比赛结合共比了90场列出关于x 的一元二次方程是解题的关键．三、解答题21．AB 的长是12m【分析】设AB 的长是x m ，则BC 的长是（18-x ）m ，根据题意得方程，解方程即可得到结论．【详解】解：设AB 的长是x m ，则BC 的长是()18x -m ．根据题意，得()1872-=x x ．解这个方程，得16x =，212x =．当6x =时，181210-=>x （不合题意，舍去）．当12x =时，186-=x 符合题意．答：AB 的长是12m ．【点睛】本题考查了一元二次方程的应用，同时也利用了矩形的性质，解题时首先正确了解题意，然后根据题意列出方程即可解决问题．22．（1）18x =-，22x =；（2）1x =，2x =．（1）运用因式分解法求解即可；（2）运用公式法求解即可．【详解】解：（1）26160x x +-=()()820x x +-=解得18x =-，22x =．（2）22430x x --=，∵2a =，4b =-，3c =-，∴224(4)42(3)162440b ac -=--⨯⨯-=+=，x ===∴1x =，2x =． 【点睛】本题考查了解一元二次方程，在解答中注意计算的正确性．23【分析】对题目中所给的条件进行变形，利用整体思想求解出22a b +的值，从而结合勾股定理求解斜边长即可．【详解】由题意得()()22222120a b a b +++-=， ()()2222340a b a b +∴+-+=223a b ∴+=或224a b +=-(不合题意，舍去）则2223c a b =+=c ∴=负舍）．【点睛】本题考查解一元二次方程及勾股定理的应用，能够准确从条件中求解出直角边的平方和是解题关键．24．（1）1x =2x =；（2）x 1=1，x 2=-1． 【分析】（1）先移项，把二次项系数化为1，再把方程两边同时加上一次项系数一半的平方，进而开平方解方程即可得答案；（2）先根据完全平方公式把方程两边展开，再移项整理成一元二次方程的一般形式，再利用因式分解法解方程即可得答案．【详解】（1）221470x x --=移项得：2x 2-14x=7，二次项系数化为1得：x 2-7x=72， 配方得：x 2-7x+27()2=72+27()2，即（x-72）2=634，开平方得：x-72=，解得：1x =2x =． （2）()()222332x x -=-展开得：4x 2-12x+9=9x 2-12x+4移项、合并得：5x 2-5=0，分解因式得（x+1）(x-1)=0，解得：x 1=1，x 2=-1．【点睛】本题考查配方法及因式分解法解一元二次方程，熟练掌握解方程的步骤是解题关键． 25．（1）121x x ==-；（2）123,4x x ==．【分析】（1）利用配方法解一元二次方程即可得；（2）利用因式分解法解一元二次方程即可得．【详解】（1）2210x x ++=，2(1)0x +=，解得121x x ==-；（2）233x x ，2330x x ， 3310x x ，即()()340x x --=，30x -=或40x -=，3x =或4x =，即123,4x x ==．【点睛】本题考查了解一元二次方程，主要解法包括：直接开平方法、配方法、因式分解法、公式法、换元法等，熟练掌握各解法是解题关键． 26．（1）12x 1x -1==，；（2）12x 12x 1=-=，．【分析】（1）根据因式分解法，可得答案； （2）根据因式分解法，可得答案．【详解】解：（1）x （x －1）＝1－x方程整理，得，x （x ﹣1）+（x ﹣1）＝0， 因式分解，得，（x ﹣1）（x +1）＝0 于是，得，x ﹣1＝0或x +1＝0，解得x 1＝1，x 2＝﹣1；（2）(x-3) 2 = (2x-1) (x +3)方程整理，得，x 2+11x ﹣12＝0因式分解，得，（x +12）（x ﹣1）＝0 于是，得，x +12＝0或x ﹣1＝0，解得x 1＝﹣12，x 2＝1．【点睛】本题考查了解一元二次方程，因式分解是解题关键．。
九年级上册数学 一元二次方程易错题(Word版 含答案)
程，
，P 不返回，Q 返回，表示好 PB，CQ 的长，用面积公式列方程，
，两点都返回，表示好 PB，CQ 的长，用面积公式列方程即可得到答案．
【详解】
解：（1）
，
.
根据三角形的面积公式，得
，
即
，
整理，得
，
解得
，
.
故当 为 5 或 7 时，
的面积等于 35 .
（2）根据勾股定理，得
，
整理，得
，
解得
，
平方，把方程②分解因式，建立方程求 n，要注意 n 的值要使方程②的根是整数.
【详解】
若存在 n 满足题意.
设 x1，x2 是方程①的两个根，则 x1+x2=2n，x1x2= 3n 2 ，所以(x1-x2)2=4n2+3n+2， 4
由方程②得，(x+n-1)[x-2(n+1)]=0，
①若 4n2+3n+2=-n+1，解得 n=- 1 ，但 1-n= 3 不是整数，舍.
九年级上册数学 一元二次方程易错题（Word 版 含答案）
一、初三数学 一元二次方程易错题压轴题（难）
1．如图，在△ABC 中，∠B=90°，AB=12 cm，BC=16 cm．点 P 从点 A 开始沿 AB 边向点 B 以 1 cm/s 的速度移动，点 Q 从点 B 开始沿 BC 边向点 C 以 2 cm/s 的速度移动．如果 P、 Q 分 别从 A、B 同时出发，当一个点到达终点时，另一个点也随之停止运动．设运动的时间为 t 秒．
①当 x≥40 时， (x 24)480 20(x 40) 7680 ，
解得： x1 40, x2 48;
②当 x 40 时， (x 24)480 40(40 x) 7680，
中考一元二次方程组易错题50题含答案
中考一元二次方程组易错题50题含答案解析一、单选题1．将一元二次方程2314x x -=-化成一般形式后，常数项为1，则二次项系数和一次项系数分别是（ ） A ．3、-4B ．3-、-4C ．3、4D ．3-、42．用配方法解一元二次方程3x 2+8x ﹣3＝0时，原方程可变形为（ ）A ．242539x ⎛⎫+= ⎪⎝⎭B ．24733x ⎛⎫+= ⎪⎝⎭C ．289139x ⎛⎫+= ⎪⎝⎭D ．2433x ⎛⎫+= ⎪⎝⎭ 3．根据关于x 的一元二次方程20x px q ++=，可列表如下：则方程20x px q ++=的一个根的范围是（ ）A ．1.2 1.3x << B ．1.1 1.2x <<C ．0.51x <<D ．00.5x <<4．若1x ，2x 是一元二次方程2560x x -+=的两个根，则12x x +，12x x 的值分别是（ ） A ．1和6B ．5和6-C ．5-和6D ．5和65．下列方程是一元二次方程的是（ ） A ．21x = B ．212x xy +=C ．213x x+=D ．21xy =6．若m 是方程的根,则式子的值为（ ）A ．2007B ．2008C ．2009D ．20107．已知ABC 的三边长分别为a ，b ，c ，且关于x 的一元二次方程2()20c b x ax c b +-+-=有两个相等的实数根，若2|5|(5)0a b -+-=，则ABC 的形状为（ ） A ．等腰三角形 B ．等边三角形C ．直角三角形D ．等腰直角三角形8．某小区原有一块长为50米，宽为40米的矩形健身场地，现计划在场内沿四周铺一圈宽度相等的小路，使小路所占的面积是原面积的110，设这条小路的宽度为x 米，则所列方程正确的是（ ）A ．12(5040)504010x x +=⨯⨯B ．1(50)(40)5040110x x ⎛⎫--=⨯⨯- ⎪⎝⎭C ．1(502)(402)5040110x x ⎛⎫++=⨯⨯+ ⎪⎝⎭D ．1(502)(402)5040110x x ⎛⎫--=⨯⨯- ⎪⎝⎭9．已知关于x 的一元二次方程：220x x m -+=有两个不相等的实数根1x ，2x ，则（ ） A ．120x x +<B ．120x x <C ．121x x >-D ．121x x <10．有1人患了流感，经过两轮传染后共有81人患了流感，设每轮传染中每人传染x 人，其中20%的人因自身抵抗力强而未患流感，则根据题意可列方程为（ ） A ．0.2（1+x ）2＝81 B ．（1+0.2x ）2＝81 C ．0.8（1+x ）2＝81D ．（1+0.8x ）2＝8111．若方程290x mx -+=的左边是一个完全平方式，则m 等于（ ） A ．3B ．6C ．3±D ．6±12．若一元二次方程x （kx +1）﹣x 2+3＝0无实数根，则k 的最小整数值是（ ） A ．2B ．1C ．0D ．﹣113．随着国内新冠疫情逐步得到控制，人们的口罩储备逐渐充足，市场的口罩需求量在逐渐减少，某口罩厂六月份的口罩产量为100万只，由于市场需求量减少，八月份的产量减少到64万只，则该厂七八月份的口罩产量的月平均减少率为（ ） A ．18%B ．20%C ．36%D ．40%14．下列命题正确的是（ ） A ．方程210x +=没有实数根 B ．方程2410mx x -+=是一元二次方程 C ．方程2212x x+=是一元二次方程 D ．方程()10x x -=的根为115．如果2||-2-x-6x x =0，则x 等于( ) A ．±2 B ．-2 C ．2D ．316．若关于x 的一元二次方程2500＝（）ax bx a ++≠的一个解是=1x -，则2013a b -+的值是（ ）A ．2012B ．2014C ．2016D ．201817．如果一元二次方程x 2+（m+1）x+m=0的两个根是互为相反数，那么有（ ） A ．m=0 B ．m=﹣1C ．m=1D ．以上结论都不对18．若方程x 2﹣3x ﹣1=0的两根也是方程x 4+ax 2+bx +c =0的根，则a +b ﹣2c 的值为（ ） A ．﹣13B ．﹣9C ．6D ．019．某工厂一月份利润1万元，二月份、三月份平均每月增长10%，那么第一季度的总利润是______万元. A ．()2110%+ B ．()3110%+C ．()()2110%110%⎡⎤+++⎣⎦D ．()()21110%110%⎡⎤++++⎣⎦20．下列方程一定有实数根的是（ ） A ．2x 10+=B ．(2x+1)2+3=0C ．(x-1)2=0D ．21(x a)a 2-=二、填空题21．一元二次方程230x x +=的二次项系数是______. 22．方程2832x x -=-的一般形式为________．23．若m 是方程22310x x -+=的根，则2692019m m ++-的值为__________． 24．关于x 的方程220x mx n ++＝的两个根是﹣2和1，则nm 的值为_____． 25．一元二次方程220x x +-=的解是1x =________，2x =________．26．若关于x 的一元二次方程()211x k +=有实数根，则实数k 的取值范围是______． 27．2019年12月6日，某市举行了2020年商品订货交流会，参加会议的每两家公司之间都签订了一份合同，所有参会公司共签订了28份合同，则共有_____家公司参加了这次会议．28．一个三角形的两边长分别为4cm 和7cm ，第三边长是一元二次方程x 2﹣10x+21=0的实数根，则三角形的周长是____cm ．29．方程(5)(21)3x x --=的根的判别式24b ac -= ____30．已知3是关于x 的方程x 2﹣2x ﹣n ＝0的一个根，则n 的值为_____．31．某种植物主干长出若干数目的分支，每个分支长出相同数目的小分支，若主干、分支、小分支的总数为31，则每个分支长出小分支的数目为 _____．32．在实数范围内定义一种运算“＊”，其规则为a ＊b ＝a 2－b 2，根据这个规则，方程（x ＋2）＊3＝0的解为__________33．已知关于x 的方程230x x m --=的一个根是1，则m =___________．34．若关于x 的一元二次方程()22141102a x a x ⎛⎫+--+= ⎪⎝⎭的一次项系数为0，则a 的值为_____．35．如图是一张长8cm ，宽7cm 的矩形铁皮，将其剪去两个全等的正方形和两个全等的矩形（阴影部分)，剩余部分可制成底面积是15cm 2的有盖的长方体铁盒．设剪去的正方形的边长为x cm ． 则列出的方程是____________36．新世纪百货大楼“宝乐”牌童装平均每天可售出20件，每件盈利40元．为了迎接“六一”儿童节，商场决定采取适当的降价措施．经调查，如果每件童装降价1元，那么平均每天就可多售出2件．要想平均每天销售这种童装盈利1200元，则每件童装应降价多少元？设每件童装应降价x 元，可列方程为__________．37．已知1x ，2x 是一元二次方程240x x m -+=的两根，若11x =，则1212x x x x +-=______．38．已知关于x 的方程210ax bx ++=的两根为1和2，则方程()2(1)110a xb x -+-+=的两根分别______．39．在实数范围内分解因式：2345x x --=_____________________40．已知在长方形纸片ABCD 中，6AB =，5AD =，现将两个边长分别为a 和b 的正方形纸片按图1、图2两种方式放置（图1、图2中两张正方形纸片中均有部分重叠），长方形中未被这两张正方形纸片覆盖的部分用阴影表示，设图1中阴影部分的面积为1S ，图2中阴影部分的面积为2S ；若213-=S S 时，则b =_________；若再在边长为a 大正方形的左上角摆放一个边长为b 的小正方形（如图3），当18S =时，则图3中阴影部分的面积3S =_________．三、解答题 41．按要求作答（1）解方程2320x x --+=；（2）计算)(111． 42．解方程： (1)260x x +-= (2)()32142x x x +=+ 43．解方程： (1)232x x -=- (2)2610x x +-=44．某农户要利用一面25m 长的墙建一个长方形的养鸡场，一边靠墙，另三边用木栅栏围成，木栅栏长40m ．(1)鸡场的面积能达到2200m 吗？如果能，求出与墙平行的边的长； (2)鸡场的面积能达到2210m 吗？为什么？ 45．解方程：()213123x -=． 46．2(1)69x x +=-；(2) 3x2+6x-4=047．江苏是全国首个自然村“村村通宽带”省份．我市某村为了将当地农产品外销，建立了淘宝网店．该网店于今年7月底以每袋25元的成本价收购一批农产品．当商品售价为每袋40元时，8月份销售256袋．9、10月该商品十分畅销．销售量持续走高．在售价不变的基础上，10月份的销售量达到400袋．设9、10这两个月月平均增长率不变．（1）求9、10这两个月的月平均增长率；（2）为迎接双“十一”，11月份起，该网店采用降价促销的方式回馈顾客，经调查发现，该农产品每降价1元/每袋，销售量就增加5袋，当农产品每袋降价多少元时，该淘宝网店11月份获利4250元？ 48．用适当的方法解下列方程： （1）（2x+1）2=（x ﹣1）2 （2）．49．已知函数24)1(2m m y m x +-++=是关于x 的二次函数． （1）满足条件的m 的值；（2）m 为何值时，抛物线有最低点？求出这个最低点，这时当x 为何值时，y 随x 的增大而增大？（3）m 为何值时，函数有最大值？最大值是多少？这时当x 为何值时，y 随x 的增大而减小？50．如图，矩形ABCD 的边BC 在x 轴上，AD 与y 轴交于点E ，线段OB 、OC 的长是方程28150x x -+=的两根()OC OB <且tan 2EBO ∠=．(1)求点A 的坐标；(2)直线BE 从点B 出发，以每秒一个单位长度的速度沿x 轴正方向平移，设移动时间为()08t t ≤≤秒，直线BE 扫过四边形EBCD 的面积为S ，求S 关于t 的函数解析式； (3)平面内是否存在点P ，使得以B 、E 、C 、P 为顶点的四边形为平行四边形？若存在，请直接写出P 点坐标，若不存在，请说明理由．参考答案：1．B【分析】先化为一般形式，再解答．【详解】解：∵一元二次方程2314x x -=-化成一般形式后，常数项为1，则：23410x x --+=，∵二次项系数和一次项系数分别为3-、-4， 故选B ．【点睛】此题考查了一元二次方程的一般形式，一元二次方程的一般形式为ax 2+bx +c =0（a ≠0）．其中a 是二次项系数，b 是一次项系数，c 是常数项，解题关键是掌握一元二次方程的一般形式． 2．A【分析】根据完全平方公式,配方即可. 【详解】解：3x 2+8x ﹣3＝0， x 2+83x ﹣1＝0，x 2+83x +（43）2＝1+（43）2242539x ⎛⎫+= ⎪⎝⎭．故选：A ．【点睛】此题考查的是解一元二次方程:配方法,掌握完全平方公式的特征是解决此题的关键. 3．B【分析】根据二次函数的增减性可得答案．【详解】由x=1.1时,x 2+px+q−1=−0.59；x=1.2时,x 2+px+q−1=0.84， 由函数的增减性，得x 2+px+q=1的正数解满足1.1 1.2x <<， 故选B.【点睛】本题考查估算一元二次方程的近似解，解题的关键是掌握估算一元二次方程的近似解的方法. 4．D【分析】根据一元二次方程根与系数的关系求解即可．【详解】解：∵1x ，2x 是一元二次方程2560x x -+=的两个根， ∵x 1+x 2=5，x 1x 2=6， 故选：D ．【点睛】本题考查了一元二次方程ax 2+bx +c =0（a ≠0）的根与系数的关系：若方程两个为x 1，x 2，则x 1+x 2=-b a ，x 1•x 2=ca．5．A【分析】根据一元二次方程的定义逐个判断即可．【详解】解：A ．21x =是一元二次方程，故此选项符合题意；B ．212x xy +=是二元二次方程，不是一元二次方程，故此选项不符合题意；C ．213x x+=是分式方程，不是整式方程，不是一元二次方程，故此选项不符合题意； D ．21xy =是二元二次方程，不是一元二次方程，故此选项不符合题意． 故选：A ．【点睛】本题考查一元二次方程的定义．只含有一个未知数，并且所含末知数的项的最高次数是2的整式方程，叫一元二次方程．理解和掌握一元二次方程的定义是解题的关键． 6．C【详解】试题分析：把m 代入x 2+x ﹣1=0得到m 2+m ﹣1=0,即m 2+m=1,把m 2+m=1代入式子,再将式子变形为23()2006m m ++的形式,即可求出式子的值为2009．故选C ．考点：一元二次方程的解． 7．D【分析】先根据根的判别式以及勾股定理的逆定理求得ABC 为直角三角形；由2|5|(5)0a b -+-=得55a b ==，，从而可得ABC 为等腰直角三角形．【详解】解：∵一元二次方程2()20c b x ax c b +-+-=有两个相等的实数根，∵2(2)4()()0a c b c b ∆=--+-=，即222+=a b c ， ∵ABC 为直角三角形， 又2|5|(5)0a b -+-=， ∵55a b ==，，∵ABC 为等腰直角三角形， 故选：D ．【点睛】本题考查了根的判别式：一元二次方程20(0)ax bx c a ++=≠的根与24b ac ∆=-有如下关系：当0∆>时，方程有两个不相等的两个实数根；当Δ0=时，方程有两个相等的两个实数根；当Δ0<时，方程无实数根．也考查了勾股定理的逆定理及等腰三角形的判定、非负数的应用． 8．D【分析】由小路的宽度可得出小路围起来的部分是长为（50－2x ）米、宽为（40－2x ）米的矩形，再利用矩形的面积计算公式，即可得出关于x 的一元二次方程，此题得解． 【详解】解：∵这条小路的宽度为x 米，∵小路围起来的部分是长为（50－2x ）米、宽为（40－2x ）米的矩形． 依题意得：（50－2x ）（40－2x ）＝50×40×（1110-）． 故选：D ．【点睛】本题考查了由实际问题抽象出一元二次方程，找准等量关系，正确列出一元二次方程是解题的关键． 9．D【分析】根据题意及一元二次方程根的判别式可得440m ->，然后再根据一元二次方程根与系数的关系可进行求解．【详解】解：∵关于x 的一元二次方程：220x x m -+=有两个不相等的实数根1x ，2x ， ∵440m ->，解得：1m <， ∵由韦达定理可得：121220,1b cx x x x m a a+=-=>==<， ∵只有D 选项正确； 故选D ．【点睛】本题主要考查一元二次方程根的判别式及根与系数的关系，熟练掌握一元二次方程根的判别式及根与系数的关系是解题的关键． 10．D【分析】由于每轮传染中平均一个人传染的人数是x 人，其中20%的人因自身抵抗力强而未患流感，那么经过第一轮后有（1＋0.8x ）人患了流感，经过第二轮后有（1＋0.8x ）2人患了流感，再根据经过两轮传染后共有81人患了流感即可列出方程．【详解】解：依题意得（1+0.8x ）2＝81， 故选：D ．【点睛】本题考查了一元二次方程的运用，解此类题关键是根据题意分别列出不同阶段患了流感的人数． 11．D【分析】根据配方法计算即可；【详解】∵方程290x mx -+=的左边是一个完全平方式， ∵()22293x mx x mx -+=-+±，∵()236m =⨯±=±， 故答案选D ．【点睛】本题主要考查了配方法的应用，准确计算是解题的关键． 12．A【分析】由根的判别式与方程根的情况，可得△＜0，从而求出k 的取值范围，再确定k 的最小整数，同时要保证二次项系数不为0．【详解】∵一元二次方程x （kx +1）﹣x 2+3＝0，即（k ﹣1）x 2+x +3＝0无实数根， ∵∵＝b 2﹣4ac ＝1﹣4×（k ﹣1）×3＜0且k ﹣1≠0， 解得k ＞1312． ∵k 的最小整数值是2． 故选：A ．【点睛】本题主要考查了一元二次方程的概念和根的判别式，熟练掌握根据一元二次方程根的情况列出不等式是解题的关键． 13．B【分析】设该厂七八月份的口罩产量的月平均减少率为x ，利用等量关系：八月份的产量=六月份的产量×（1-产量的月平均减少率2），即可得出关于x 的一元二次方程，解方程取其合适的值即可得出结论．【详解】解：设该厂七八月份的口罩产量的月平均减少率为x ， 依题意得：2100(1)64x -=，解得：10.220%==x ，2 1.8x =（不符合题意，舍去），∵该厂七八月份的口罩产量的月平均减少率为20%．故选：B ．【点睛】本题考查了一元二次方程的应用，理解题意，找准等量关系，正确列出一元二次方程是解题的关键．14．A【分析】根据一元二次方程的判别式、一元二次方程的定义和一元二次方程的解，对选项一一进行分析，即可得出答案．【详解】解：A 、对方程210x +=，∵40∆=-<，∵方程没有实数根，故原说法正确； B 、对方程2410mx x -+=，当0m =时，是一元一次方程，故原说法错误；C 、方程2212x x+=是分式方程，故原说法错误； D 、方程()10x x -=的根为0或1，故原说法错误．故选：A【点睛】本题考查了一元二次方程的判别式、一元二次方程的定义和一元二次方程的解，解本题的关键在熟练掌握相关一元二次方程的知识点．15．C【分析】根据“当分式的分子为0，且分母不为0时，分式的值为0”得到|x|-2=0，且x 2-x-6≠0，解之即可得到答案．【详解】解：由题意可得22060x x x ⎧-=⎨--≠⎩解得x=2故选C ．【点睛】本题考查了分式的值为0的条件．当分式的分子为0，且分母不为0时，分式的值为0．16．D【分析】将=1x -代入2500＝（）ax bx a ++≠可得5a b -=-，然后将所求式子变形，再将a b -的值代入，即可解答本题．【详解】解：∵关于x 的一元二次方程2500＝（）ax bx a ++≠的一个解是=1x -，∵50a b -+=，∵5a b -=-，∵()()20132013201352018a b a b -+=--=--=．故选D ．【点睛】本题考查一元二次方程的解和代数式求值，解题的关键是明确一元二次方程的解的含义．17．B【详解】试题解析：设该一元二次方程的两个根分别是12x x 、，则根据题意知()1210x x m +=-+=， 即10m +=，解得， 1.m =-故选B ．点睛：一元二次方程20ax bx c ++=的两根分别是12,.x x 则1212,.b c x x x x a a+=-⋅= 18．A【分析】设m 是方程x 2﹣3x ﹣1=0的一个根．根据方程解的意义知，m 既满足方程x 2﹣3x ﹣1=0，也满足方程x 4+ax 2+bx +c =0，将m 代入这两个方程，并整理，得（9+a ）m 2+（6+b ）m +c +1=0．从而可知：方程x 2﹣3x ﹣1=0的两根也是方程（9+a ）x 2+（6+b ）x +c +1=0的根，这两个方程实质上应该是同一个一元二次方程，然后根据同一个一元二次方程的定义找出相对应的系数间的关系即可．【详解】解：设m 是方程x 2﹣3x ﹣1=0的一个根，则m 2﹣3m ﹣1=0，所以m 2=3m +1．由题意，m 也是方程x 4+ax 2+bx +c =0的根，∵m 4+am 2+bm +c =0，把m 2=3m +1代入此式，得：（3m +1）2+am 2+bm +c =0，整理得：（9+a ）m 2+（6+b ）m +c +1=0．∵方程x 2﹣3x ﹣1=0的两根也是方程（9+a ）x 2+（6+b ）x +c +1=0的根，这两个方程实质上应该是同一个一元二次方程，从而有（9+a ）x 2+（6+b ）x +c +1=k （x 2﹣3x ﹣1）（其中k 为常数），∵b =﹣3a ﹣33，c =﹣a ﹣10．∵a +b ﹣2c =a +（﹣3a ﹣33）﹣2（﹣a ﹣10）=﹣13．故选A ．【点睛】本题主要考查了一元二次方程的解．该题难度比较大，在解题时，采用了“转化法”，即将所求转化为求（9+a ）x 2+（6+b ）x +c +1=k （x 2﹣3x ﹣1）（其中k 为常数）的相应的系数间的关系．19．D【分析】首先表示出二月份的利润：一月份的利润()110%⨯+，再表示三月份的利润：二月份的利润()110%⨯+，即三月份的利润=一月份的利润()2110%⨯+，最后第一季度的总利润为前三个月份的利润相加起来即可. 【详解】解：一月份的利润为1万元∴二月份的利润为()1110%⨯+万元，即()110%+万元三月份的利润为()21110%⨯+万元，即()2110%+万元，∴第一季度的总利润为()()21110%110%⎡⎤++++⎣⎦万元 故选择D.【点睛】此题主要考查了一元二次方程的应用——增长率问题，若设变化前的量为a ，变化后的量为b ，平均变化率为x ，则经过两次变化后的数量关系为()21a x b +=，得到前三月份的量总和的等量关系是解决本题的关键．20．C【分析】根据非负数的性质可判断A 、B 中的方程没有实数解，方程D 中只有a≥0时，方程有实数解．【详解】A. 2x =−1 ，方程没有实数解，所以 A 选项错误；B. 将方程移项得：2(2x 1)3+=-，该方程没有实数解，故B 选项错误；C. x−1=0, 则 1x =2x =1 ，所以 C 选项正确；D. 当 a<0 时，方程没有实数解，所以 D 选项错误．故选C.【点睛】本题主要考查用配方法解一元二次方程，熟悉掌握是关键.21．1【分析】根据一元二次方程的一般形式直接填空即可．【详解】一元二次方程230x x +=，二次项系数为1．故答案为1．【点睛】一元二次方程的一般形式是：ax 2+bx +c =0（a ，b ，c 是常数且a ≠0）特别要注意a ≠0的条件．这是在做题过程中容易忽视的知识点．在一般形式中ax 2叫二次项，bx 叫一次项，c 是常数项．其中a ，b ，c 分别叫二次项系数，一次项系数，常数项．22．23820x x +-=【分析】一元二次方程的一般形式是：ax 2+bx+c=0（a ，b ，c 是常数且a≠0）特别要注意a≠0的条件，根据一元二次方程的一般形式将2832x x -=-变形为23820x x +-=即可得到答案．【详解】根据一元二次方程的一般形式将2832x x -=-变形为23820x x +-=，则答案为23820x x +-=.【点睛】本题考查一元二次方程的一般形式，解题的关键是掌握一元二次方程的一般形式．23．2022【分析】根据一元二次方程的解的定义即可求出答案．【详解】由题意可知：2m 2−3m+1＝0，∵2m 2−3m ＝-1∵原式＝-3（2m 2−3m ）＋2019＝2022．故答案为：2022．【点睛】本题考查一元二次方程的解，解题的关键是正确理解一元二次方程的解的定义，本题属于基础题型．24．﹣8【分析】由方程的两根结合根与系数的关系可求出m 、n 的值，将其代入nm 中即可求出结论．【详解】解：∵关于x 的方程220x mx n ++＝的两个根是﹣2和1， ∵1,222m n -=-=-， ∵m ＝2，n ＝﹣4，∵()428nm ⨯＝﹣＝﹣． 故答案为：﹣8．【点睛】本题主要考查一元二次方程根与系数的关系，熟练掌握根与系数的关系是解题的关键．25． 1 -2【分析】根据因式分解法进行求解一元二次方程即可．【详解】解：220x x +-=()()120x x -+=∵10x -=或20x +=解得：121,2x x ==-；故答案为1；-2．【点睛】本题主要考查一元二次方程的解法，熟练掌握一元二次方程的解法是解题的关键．26．0k ≥##0k ≤【分析】根据平方的非负性可得结果．【详解】解：∵关于x 的一元二次方程()211x k +=有实数根，而()2110x +≥，∵0k ≥．故答案为：0k ≥．【点睛】本题考查了一元二次方程的解，掌握平方的非负性是解决此题的关键． 27．8【分析】每家公司都与其他公司鉴定了一份合同，设有x 家公司参加，则每个公司要签()1x -份合同，签订合同共有()112x x -份． 【详解】设共有x 家公司参加了这次会议， 根据题意，得：12x (x ﹣1)=28， 整理，得： x 2﹣x ﹣56=0，解得：x 1=8，x 2=﹣7(不合题意，舍去) ，答：共有8家公司参加了这次会议．故答案是：8．【点睛】考查了一元二次方程的应用，甲乙之间互签合同，只能算一份，本题属于不重复记数问题，类似于若干个人，每两个人之间都握手，握手总次数．解答中注意舍去不符合题意的解．28．18．【详解】试题分析：由方程x2﹣10x+21=0，利用分解因式得：（x﹣3）（x﹣7）=0，解得：x=3或x=7，当x=3时，三角形三边分别为3cm，4cm，7cm，3+4=7，不合题意，舍去；当x=7时，三角形三边为4cm，7cm，7cm，此时周长为4+7+7=18cm，考点：1、解一元二次方程-因式分解法；2、三角形三边关系29．105【详解】解：方程（x-5）（2x-1）=3化为一元二次方程的一般形式为：2x2-11x+2=0，∵∵=b2-4ac=（-11）2-4×2×2=105．故答案为：105．30．3【分析】根据一元二次方程的定义，把x＝3代入x2﹣2x﹣n＝0中得到关于n的方程，然后关于n的方程即可．【详解】解：把x＝3代入x2﹣2x﹣n＝0得9﹣6﹣n＝0，解得n＝3．故答案为3【点睛】本题考查了一元二次方程的解：能使一元二次方程左右两边相等的未知数的值是一元二次方程的解．31．5【分析】先设每个分支长出小分支的数目为x，再根据题意列出一元二次方程进行求解即可．【详解】解：设每个分支长出小分支的数目为x，依题意得：2++=，x x131整理得：2300+-=，x x解得：1x ＝5，2x ＝﹣6（不合题意，舍去）．故答案为：5．【点睛】本题考查了一元二次方程的实际应用，解决本题的关键是列出正确的方程进行求解．32．1或-5【详解】直接根据定义的这种运算的规则求解．解：∵a ﹡b=a 2-b 2，∵（x+2）﹡3=（x+2）2-32，解方程（x+2）2-32=0，（x+2+3）（x+2-3）=0，∵x 1=1，x 2=-5．33．2-【分析】已知1x =是方程的根，把1x =代入原方程即可得到关于m 的方程，即可求得m 的值．【详解】解：∵关于x 的方程230x x m --=的一个根是1，∵21310m -⨯-=，解得 2m =-．故答案为：2-．【点睛】本题主要考查了一元二次方程的解的定义，把方程的解代回原方程是解决本题的关键．34．12【分析】利用一元二次方程定义进行计算即可．【详解】解：由题意得：-（4a 2-1）=0，且a+12≠0，解得：a=12， 故答案为：12．【点睛】此题主要考查了一元二次方程，关键是掌握只含有一个未知数，并且未知数的最高次数是2的整式方程叫一元二次方程．35．(4-x )(7-2x )=15【分析】根据矩形铁皮的长与宽，以及底面面积列出三组等式解方程组,整理即可得出结果．【详解】设长方体铁盒底面长为acm ，宽为bcm正方形边长为xcm由题意得:2()82715x b a x ab +=⎧⎪+=⎨⎪=⎩①②③ 由②得72a x =-，由①得4b x =-，代入③中得：()()47215x x --=故答案为：()()47215x x --=【点睛】本题考查一元二次方程的应用，三元方程组解法，关键在于设多个未知数，利用代数表示列出方程．36．（40﹣x ）（20+2x ）=1200．【详解】试题分析：设每件童装应降价x 元，可列方程为：（40﹣x ）（20+2x ）=1200．故答案为（40﹣x ）（20+2x ）=1200．考点：1．由实际问题抽象出一元二次方程；2．销售问题．37．1【分析】将11x =代入240x x m -+=求得一元二次方程的一般式，再利用根与系数的关系求解即可．【详解】解：将11x =代入240x x m -+=中21410m -⋅+=解得：3m =∵2430x x -+=∵12x x ，是一元二次方程2430x x -+=的两根，∵124x x +=，123x x =，∵1212431x x x x +-=-=．故答案为：1．【点睛】本题考查了一元二次方程的根与系数的关系，若12x x 、是方程20ax bx c ++=(0a ≠)的两根，则12b x x a+=-，12c x x a =，掌握相关知识是解题的关键．38．2、3【分析】观察给出的两个方程，得到1、2也是关于()x 1-的方程()2a(x 1)b x 110-+-+=的两个根，求出x 即可．【详解】两个方程的系数、结构相同，所以1、2也是关于()x 1-的方程()2a(x 1)b x 110-+-+=的两个根，x 11∴-=或x 12-=，x 2∴=或x 3=．故答案为2、3．【点睛】本题考查了一元二次方程的根的意义.解决本题的关键是：根据给出的方程特点，得到给出的两个方程的解相同．39．3x x ⎛ ⎝⎭⎝⎭【分析】令23450x x --=，求出方程的两个解，再写成因式分解性质即可.【详解】令23450x x --=解方程得：12x x ==∵2345x x --=3(x x故答案为3x x ⎛ ⎝⎭⎝⎭【点睛】本题考查实属范围内的因式分解，利用一元二次方程求解可以很容易解决此类问题，熟练掌握一元二次方程求解是解题关键.40． 3 6.5##132【分析】先将1S ，2S ，3S 用用a ，b 表示，再分别根据213-=S S 与18S =，211S =计算即可．【详解】解：在图1中，根据题意得：1ABCD S S S S S =--+长方形小正方形大正方形大小正方形重叠部分，∵()2122656630a b a b b a ab S b =⨯--++-=-+-+，同理在图2中，2ABCD S S S S S =--+长方形小正方形大正方形大小正方形重叠部分，∵()2222655530a b a b b a ab S b =⨯--++-=-+-+∵()()2221530630S a ab b a ab b S b -=-+-+--+-+=， 又∵213-=S S ，∵3b =．又∵18S =，即26308a ab b -+-+=，将3b =代入方程26308a ab b -+-+=中得：2363308a a -+-⨯+=解得：124,1a a ==-（舍去），∵4a =．在图3中，3S S S S S =+--小正方形大正方形左上空白大直角三角形右下空白小直角三角形 ∵()2222232211111111134343222222222a b a b b a a b ab S =+-+-=+-=⨯+⨯-⨯⨯= 故答案为：3；132． 【点睛】本题考查列代数式，整式的混合运算，解一元二次方程，掌握相关知识和技巧是解题的关键．本题难度较大，所列式子较复杂，需要较强的阅读理解能力和对数学思想的运用能力．41．(1) 12x x ==(2) 3 【分析】(1)本题是一元二次方程，解答该方程可选择直接用公式法解答.(2)本题为实数的运算，首先把两个乘法先运算出来，第一个乘法式可以由平方差公式计算，第二个乘法可先把根式化为最简根式再进行约分，最后加减时，注意合并同类根式.【详解】(1)解：原方程中a=-1，b=-3，c=2首先用根的判别式24b ac =-△判断该二元一次方程是否有解得：224(3)4(1)2170b ac =-=--⨯-⨯=>，所以该方程有解由公式x =可得：x =即解得12x x ==(2)原式=211-511=-3=故答案为(1) 12x x == (2) 3 【点睛】本题考查了一元二次方程的解法和实数的混合运算，需要注意的是一元二次方程解答直接首先用根的判别式判断是否有解，在实数运算过程中，先算乘除与乘方后算加减，有括号的先算括号里面的.涉及到根式运算时，务必要化简根式与合并同类根式 42．(1)13x =-，22x =； (2)123x =，212x =-．【分析】（1）利用因式分解法求解即可；（2）移项，利用因式分解法求解即可．【详解】（1）解：260x x +-=则()()320x x +-=解得13x =-，22x =（2）解：()32142x x x +=+()()3212210x x x +-+=，即()()32210x x -+=， 解得123x =，212x =-． 【点睛】此题考查了一元二次方程的求解，解题的关键是掌握一元二次方程的求解方法． 43．(1)11x =，22x =(2)13x =-23x =-【分析】（1）根据因式分解法解一元二次方程；（2）根据配方法解一元二次方程即可求解．【详解】（1）解：232x x -=-，移项得，2320x x -+=，即(1)(2)0x x --=，∵10x -=或20x -=，解得：11x =，22x =；（2）解：2610x x +-=，移项得，261x x +=，配方得，26910x x ++=，即2(3)10x +=，∵3x +=，解得：13x =-23x =-【点睛】本题考查了解一元二次方程，掌握解一元二次方程的方法是解题的关键． 44．(1)面积能达到2200m ，此时与墙平行的边的长是20米(2)不能，理由见解析【分析】(1) 设鸡场的一边为x m ，另外两边均为402x -m ，根据矩形的面积公式建立方程求出其解即可；(2)根据题意得出方程， 求出其解的情况就可以得出结论；(1)设与墙平行的边的长是x 米，则()402200x x -÷=，整理得x 2-40x +400=0，解得：x 1=x 2=20，解得2025x =<，即面积能达到2200m ，此时与墙平行的边的长是20米．(2)由()402210x x -÷=得2404200x x -+=，此时Δ0<，所以面积不能达到2210m ．【点睛】本题考查了运用矩形的面积公式建立一元二次方程求解的运用，一元二次方程根的判别式的运用，解答时根据矩形的面积公式建立一元二次方程是关键．45．129,3x x ==-【分析】先去分母，然后利用直接开平方法进行求解即可． 【详解】解：()213123x -= ()2336x -=，36x -=±，解得：129,3x x ==-．【点睛】本题主要考查直接开平方法，熟练掌握一元二次方程的解法是解题的关键．46．（1）123x x ==-；（2）12x x ==【详解】试题分析：（1）移项后把方程的左边分解因式得到即(x +3)2=0，求出方程的解即可；（2）首先求出b2-4ac 的值，代入公式 试题解析：(1)2 69x x +=-，移项得：2x 690x ++=，即(x +3)2=0，解得：x 1=x 2=-3，∵原方程的解是123x x ==-.（2）2=b 43648840ac ∆-=+=>，所以方程有两个不相等的实数根，x =所以12x x == 47．(1)、25%；(2)、5元.【分析】(1)设9、10这两个月的月平均增长率为x，根据题意列出方程，从而求出x的值得出答案；(2)设当每袋降价m元时，根据题意列出方程，求出m的值得出答案.【详解】(1)设9、10这两个月的月平均增长率为x，根据题意可得：256（1+x）2=400，解得：x1=14，x2=-94（不合题意舍去）．答：9、10这两个月的月平均增长率为25%；(2)设当每袋降价m元时，根据题意可得：（40-25-m）（400+5m）=4250，解得：m1=5，m2=-70（不合题意舍去）．答：当每袋降价5元时，获利4250元考点：一元二次方程的应用48．（1）x1=0，x2=2；（2）x1=﹣10，x2=8【详解】试题分析：（1）先移项得到（2x+1）2﹣（x﹣1）2=0，然后利用因式分解法解方程；（2）先把方程化为整式方程x2+2x﹣80=0，再解整式方程，然后进行检验确定原方程的解．解：（1）（2x+1）2﹣（x﹣1）2=0，（2x+1+x﹣1）（2x+1﹣x+1）=0，2x+1+x﹣1=0或2x+1﹣x+1=0，所以x1=0，x2=2；（2）去分母得120（x+2）﹣120x=3x（x+2），整理得x2+2x﹣80=0，（x+10）（x﹣8）=0，解得x1=﹣10，x2=8，检验：当x=﹣10，x（x+2）≠0；当x=8，x（x+2）≠0，则x1=﹣10，x2=8是原方程的解，所以原方程的解为x1=﹣10，x2=8．考点：解一元二次方程-因式分解法；解分式方程．49．（1）m1=2，m2=﹣3；（2）当m=2时，抛物线有最低点，最低点为：（0，1），当x＞0时，y随x的增大而增大；（3）当m=﹣3时，函数有最大值，最大值为1，当x＞0时，y 随x的增大而减小【分析】（1）利用二次函数的定义得出关于m的等式，解方程即可得出答案；。
人教版九年级上册数学一元二次方程易错题(Word版含答案)
人教版九年级上册数学一元二次方程易错题（Word版含答案）一、初三数学一元二次方程易错题压轴题（难）1 . RIAABC中，£ACB=90。
，AC=BC=6.动点P从点A出发，在线段AC上以每秒1个单位长度的速度向点C作匀速运动，到达点C停止运动.设运动时间为t秒图1（1）如图1，过点P作PDL4C,交A8于D,若4PBC与△PAD的而积和是△ABC的而积7的土，求t的值；9（2）点Q在射线PC上，且PQ = 2AP,以线段PQ为边向上作正方形PQNM.在运动过程中，若设正方形PQNM与△ABC重叠部分的面积为8,求t的值.【答案】（1）打=2,弓=4：（2）t的值为:J7或2方时，重叠面积为8.【解析】【分析】（1）先求出△ ABC的面积，然后根据题意可得AP=t, CP=6 - t,然后再APBC与△ PAD7的面积和是AABC的面积的亏，列出方程、解方程即可解答：（2）根据不同时间段分三种情况进行解答即可.【详解】（1）•/ RtA AB C 中，匕AC8=90°, AC=8C=6,1S M8C=— X6x6=18,2.. AP=t, CP=6 ・ t,・..△「8（：与^ PAD的面枳和=-f2+-x6x （6・t）,2 27•・• △ PBC与八PAD的面积和是△ ABC的面积的1,1 72 29解之,得ti=2, tz = 4：(2)・.・"=t, PQ=2AP...PQ=2t,i 7①如图1,当0《怀2时，S= （2t） 2・：产=5产=8,解得：代=抑,t2=・§J7 （不合题意，舍去），7 711] 2②如图2,当2<t<3 时，S=-x6x6 - -t2 - - （6 - 2t）2=12t- -^ = 8,2 2 2 54解得：h=4 （不合题意，舍去），t2=-（不合题意，舍去），③如图3,当3《仁6时，S=；X 6x6 -：户=8,解得：tC，tz=.2,（不合题意，舍去），【点睛】本题考查了三角形和矩形上的动点问题，根据题意列出方程和分情况讨论是解答本题的关键.2.阅读与应用：阅读1:。
(易错题)初中数学九年级数学上册第一单元《一元二次方程》测试题(答案解析)
一、选择题1．下列方程是关于x 的一元二次方程的是（ ）A ．20ax bx c ++=B ．210x y -+=C ．2120x x +-=D ．(1)(2)1x x x -+=-2．用直接开平方的方法解方程22(31)(25)x x +=-，做法正确的是（ ）A ．3125x x +=-B ．31(25)x x +=--C ．31(25)x x +=±-D ．3125x x +=±- 3．用配方法解下列方程时，配方错误的是（ ）A ．x 2﹣2x ﹣99＝0化为（x ﹣1）2＝100B ．x 2+8x+9＝0化为（x+4）2＝25C ．2x 2﹣7x ﹣4＝0化为（x ﹣74）2＝8116 D ．3x 2﹣4x ﹣2＝0化为（x ﹣23）2＝109 4．如图，若将上图正方形剪成四块，恰能拼成下图的矩形，设1a =，则b =（ ）A 51-B 51+C 53+D 21 5．一元二次方程2610x x +-=配方后可变形为（ ） A ．()2310x += B ．()238x += C ．()2310x -= D ．()238x -= 6．由于疫情得到缓和，餐饮行业逐渐回暖，某地一家餐厅重新开张，开业第一天收入约为5000元，之后两天的收入按相同的增长率增长，第3天收入约为6050元，若设每天的增长率为x ，则x 满足的方程是（ ）A ．5000（1+x ）＝6050B ．5000（1+2x ）＝6050C ．5000（1﹣x ）2＝6050D ．5000（1+x ）2＝60507．已知a ，b ，c 分别是三角形的三边长，则关于x 的方程()()220a b x cx a b ++++=根的情况是（ ）A ．有两个不相等的实数根B ．有两个相等的实数根C ．有且只有一个实数根D ．没有实数根8．方程29180x x -+=的两个根是等腰三角形的底和腰，则这个等腰三角形的周长为（ ）A ．12B ．15C ．12或15D ．18 9．一元二次方程20x x -=的根是（ ）A ．10x =，21x =B ．11x =，21x =-C ．10x =，21x =-D ．121x x == 10．已知关于x 的一元二次方程()22210x m x m -+＝-有实数根，则m 的取值范围是（ ）A ．0m ≠B ．14mC ．14m <D ．14m > 11．一元二次方程x 2=4x 的解是（ ）A ．x=4B ．x=0C ．x=0或-4D ．x=0或4第II 卷（非选择题）请点击修改第II 卷的文字说明参考答案12．已知方程2202030x x +-=的根分别为a 和b ，则代数式2a a 2020a b ++的值为（ ）A ．0B ．2020C ．1D ．-2020二、填空题13．已知12,x x 是一元二次方程21402x mx m -+-=的两个实数根且12111x x +=，则m 的值为______．14．一元二次方程 x ( x +3)＝0的根是__________________．15．一元二次方程（x +2）（x ﹣3）＝0的解是：_____．16．用配方法解方程x 2+4x+1＝0，则方程可变形为（x+2）2＝_____．17．如图，要设计一幅宽20cm ，长30cm 的图案，其中有两横彩条、一竖彩条，横、竖彩条的宽度比为1:3，如果要使彩条所占面积是图案面积的19%，竖彩条的宽度为________．18．已知实数a ，b 是方程210x x --=的两根，则11a b+的值为______．19．一件商品原价300元，连续两次降价后，现售价是243元，若每次降价的百分率相同，那么这个百分率为______．20．若关于x 的一元二次方程x 2+2x ﹣m 2﹣m ＝0（m ＞0），当m ＝1、2、3、…2020时，相应的一元二次方程的两个根分别记为α1、β1，α2、β2，…，α2020、β2020，则112220202020111111αβαβαβ++++++的值为_____．三、解答题21．解下列方程：（1）2x 2﹣4x ＋1＝0；（2）（2x ﹣1）2＝（3﹣x ）2．22．解下列方程（1）22(4)216x x +=-；（2）22x x =+．23．我们知道20x ≥，2()0a b ±≥，这一性质在数学中有着广泛的应用，比如，探究多项式2245x x +-的最小值时，我们可以这样处理：解：原式()2225x x =+- ()22222115x x =++-- 222(1)15x ⎡⎤=+--⎣⎦22(1)25x =+--22(1)7x =+-因为()210x +≥，所以()221707x +-≥-，即()22177x +-≥-所以()2217x +-的最小值是7-，即224 5x x +-的最小值是7-．请根据上面的探究思路，解答下列问题：（1）多项式()2531x -+的最小值是_________；（2）求多项式24163x x -+的最小值（写过程）．24．用配方法解方程：22450x x +-=．25．请回答下列各题： （1）先化简，再求值：2319369x x x xx x x +--⎛⎫-÷ ⎪--+⎝⎭，其中x = （2）已知关于x 的方程2320x x m +-=没有实数根，求实数m 的取值范围． 26．解方程：（1）2237x x +=；（2）x(2x+5)=2x+5．【参考答案】***试卷处理标记，请不要删除一、选择题1．D解析：D【分析】利用一元二次方程定义进行解答即可．【详解】A 、当a ＝0时，不是一元二次方程，故此选项不合题意；B 、含有两个未知数，不是一元二次方程，故此选项不合题意；C 、不是整式方程，故此选项不合题意；D 、是一元二次方程，故此选项符合题意；故选：D ．【点睛】此题主要考查了一元二次方程定义，关键是掌握判断一个方程是否是一元二次方程应注意抓住5个方面：“化简后”；“一个未知数”；“未知数的最高次数是2”；“二次项的系数不等于0”；“整式方程”．2．C解析：C【分析】一元二次方程22(31)(25)x x +=-，表示两个式子的平方相等，因而这两个数相等或互为相反数，据此即可把方程转化为两个一元一次方程，即可求解．【详解】解：22(31)(25)x x +=-开方得31(25)x x +=±-，故选：C ．【点睛】本题考查了解一元二次方程-直接开平方法，关键是将方程右侧看做一个非负已知数，根据法则：要把方程化为“左平方，右常数，先把系数化为1，再开平方取正负，分开求得方程解”来求解． 3．B解析：B【分析】将常数项移到方程的右边，然后将二次项系数化为1，继而两边都加上一次项系数一半的平方配成完全平方式后即可得出答案．【详解】解：A 、由x 2﹣2x ﹣99＝0得x 2﹣2x=99，则x 2﹣2x+1=100，即（x ﹣1）2＝100，故本选项正确，不符合题意；B 、由x 2+8x+9＝0得x 2+8x=-9，则x 2+8x+16=-9+16即（x+4）2＝7此选项错误，符合题意；C 、由2x 2﹣7x ﹣4＝0得2x 2﹣7x=4，则x 2﹣72x ＝2，∴x 2﹣72x+4916＝2+4916，即274x ⎛⎫- ⎪⎝⎭＝8116，故本选项正确，不符合题意； D 、由3x 2﹣4x ﹣2＝0，得3x 2﹣4x=2，则x 2﹣43x ＝23，∴故x 2﹣43x+49＝23+49，即（x ﹣23）2＝109，故本选项正确，不符合题意； 故选：B ．【点睛】本题主要考查解一元二次方程−配方法，用配方法解一元二次方程的步骤：①把原方程化为a 2x ＋bx ＋c ＝0（a≠0）的形式；②方程两边同除以二次项系数，使二次项系数为1，并把常数项移到方程右边； ③方程两边同时加上一次项系数一半的平方；④把左边配成一个完全平方式，右边化为一个常数；⑤如果右边是非负数，就可以进一步通过直接开平方法来求出它的解，如果右边是一个负数，则判定此方程无实数解．4．B解析：B【分析】根据上图可知正方形的边长为a+b ，下图长方形的长为a+b+b ，宽为b ，并且它们的面积相等，由此可列出（a+b ）2=b(a+b+b)，解方程即可求得结论．【详解】解：根据题意得：正方形的边长为a+b ，长方形的长为a+b+b ，宽为b ，则（a+b ）2=b(a+b+b)，即a 2﹣b 2+ab=0， ∴2)10a a b b +-=（，解得：a b =， ∵a b ＞0，∴a b =，∴当a=1时，12b ==，故选：B ．【点睛】本题考查了图形的拼接、解一元二次方程、正方形的面积、长方形的面积，正确理解题意，找到隐含的数量关系列出方程是解答的关键．5．A解析：A【分析】方程常数项移到右边，两边加上一次项系数一半的平方即可得到结果．【详解】解：∵x 2+6x-1=0，∴x 2+6x=1，∴x 2+6x+9=10，∴(x+3)²=10，故选：A ．【点睛】本题考查了解一元二次方程-配方法，熟练掌握完全平方公式是解题的关键．6．D解析：D【分析】根据开业第一天收入约为5000元，之后两天的收入按相同的增长率增长，第3天收入约为6050元列方程即可得到结论．【详解】解：设每天的增长率为x ，依题意，得：5000（1+x ）2＝6050．故选：D ．【点睛】本题考查了由实际问题抽象出一元二次方程，找准等量关系，正确列出一元二次方程是解题的关键．7．D解析：D【分析】由于这个方程是一个一元二次方程，所以利用根的判别式可以判断其根的情况．而()()2(2)4c a b a b =-++，根据三角形的三边关系即可判断．【详解】∵a ，b ，c 分别是三角形的三边，∴a+b ＞c ．∴c+a+b ＞0，c-a-b ＜0，∴()()2(2)4c a b a b =-++22=-+c a b44()()()=++--<，40c a b c a b∴方程没有实数根．故选：D．【点睛】本题主要考查了三角形三边关系、一元二次方程的根的判别式等知识点．重点是对22-+进行因式分解．c a b44()8．B解析：B【分析】首先求出方程的根，再根据三角形三边关系定理列出不等式，确定是否符合题意．【详解】解：解方程x2-9x+18=0，得x1=3，x2=6，当3为腰，6为底时，不能构成等腰三角形；当6为腰，3为底时，能构成等腰三角形，周长为6+6+3=15．故选：B．【点睛】本题考查了解一元二次方程，从边的方面考查三角形，涉及分类讨论的思想方法．求三角形的周长，不能盲目地将三边长相加起来，而应养成检验三边长能否组成三角形的好习惯，把不符合题意的舍去．9．A解析：A【分析】方程左边分解因式后，利用两数相乘积为0，两因式中至少有一个为0转化为两个一元一次方程来求解．【详解】解：∵x2-x=0，∴x（x-1）=0，则x=0或x-1=0，解得：x1=0，x2=1，故选：A．【点睛】此题考查了解一元二次方程-因式分解法，熟练掌握因式分解的方法是解本题的关键．10．B解析：B【分析】由方程有实数根即△＝b2﹣4ac≥0，从而得出关于m的不等式，解之可得．【详解】解：根据题意得，△＝b 2﹣4ac ＝[﹣（2m ﹣1）]2﹣4m 2＝﹣4m +1≥0， 解得：14m， 故选：B ．【点睛】本题主要考查根的判别式，熟练掌握一元二次方程的根与判别式间的关系是解题的关键． 11．D解析：D【分析】先移项，利用因式分解法解一元二次方程.【详解】解：x 2=4xx 2-4x=0x （x-4）=0x=0或x=4，故选：D.【点睛】此题考查解一元二次方程，直接开平方法，配方法，公式法，因式分解法，根据一元二次方程的特点选择恰当的解法是解题的关键.12．A解析：A【分析】将a 代入方程，可得2202030a a +-=，即220302a a =-，代入要求的式子，即可得到3+ab ，而a 、b 是方程的两个根，根据韦达定理，可求出ab 的值，即可求出答案．【详解】解：∵方程2202030x x +-=的根分别为a 和b∴2202030a a +-=，即220302a a =-∴2a a 2020a b ++=32020a -+ab+2020a=3+ab∵ab=-3∴2a a 2020a b ++=32020a -+ab+2020a=3+ab=3-3=0故选：A ．【点睛】本题主要考查一元二次方程的解以及韦达定理，熟练解代入方程以及观察式子特点，抵消部分式子是解决本题的关键．二、填空题13．-8【分析】先利用根与系数的关系得到再把变形为从而代入得到方程解之即可【详解】解：∵是一元二次方程的两个实数根∴∵∴即解得：m=-8故答案为：-8【点睛】本题考查了根与系数的关系根据根与系数的关系找解析：-8【分析】先利用根与系数的关系得到12x x m +=，12142x x m ⋅=-，再把12111x x +=变形为1212x x x x +=，从而代入得到方程，解之即可．【详解】解：∵12,x x 是一元二次方程21402x mx m -+-=的两个实数根， ∴12x x m +=，12142x x m ⋅=-， ∵12111x x +=， ∴1212x x x x +=，即142m m =-， 解得：m=-8，故答案为：-8．【点睛】 本题考查了根与系数的关系，根据根与系数的关系，找出12x x m +=，12142x x m ⋅=-是解题的关键． 14．【分析】用因式分解法解方程即可【详解】解：x(x+3)＝0x ＝0或x+3＝0；故答案为：【点睛】本题考查了一元二次方程的解法掌握两个数的积为0这两个数至少有一个为0是解题关键解析：12x 0x -3==，【分析】用因式分解法解方程即可．【详解】解：x ( x +3)＝0，x ＝0或 x +3＝0，12x 0x -3==，；故答案为：12x 0x -3==，．【点睛】本题考查了一元二次方程的解法，掌握两个数的积为0，这两个数至少有一个为0是解题关键．15．x1＝﹣2x2＝3【分析】利用因式分解法把原方程化为x+2＝0或x ﹣3＝0然后解两个一次方程即可【详解】（x+2）（x ﹣3）＝0x+2＝0或x ﹣3＝0所以x1＝﹣2x2＝3故答案为x1＝﹣2x2＝3解析：x 1＝﹣2，x 2＝3【分析】利用因式分解法把原方程化为x+2＝0或x ﹣3＝0，然后解两个一次方程即可．【详解】（x +2）（x ﹣3）＝0，x +2＝0或x ﹣3＝0，所以x 1＝﹣2，x 2＝3．故答案为x 1＝﹣2，x 2＝3．【点睛】本题考查了解一元二次方程−因式分解法：先把方程的右边化为0，再把左边通过因式分解化为两个一次因式的积的形式，那么这两个因式的值就都有可能为0，这就能得到两个一元一次方程的解，这样也就把原方程进行了降次，把解一元二次方程转化为解一元一次方程的问题了（数学转化思想）．16．3【分析】先移项再两边配上4写成完全平方公式即可【详解】解：∵∴即故答案为：3【点睛】本题考查了用配方法解一元二次方程掌握用配方法解一元二次方程的步骤即可解析：3【分析】先移项，再两边配上4，写成完全平方公式即可．【详解】解：∵241x x +=-，∴24414x x ++=-+，即()223x +=，故答案为：3．【点睛】本题考查了用配方法解一元二次方程，掌握用配方法解一元二次方程的步骤即可． 17．3cm 【分析】设横彩条的宽度是xcm 竖彩条的宽度是3xcm 根据如果要使彩条所占面积是图案面积的19可列方程求解【详解】解：设横彩条的宽度是xcm 竖彩条的宽度是3xcm 则（30-3x ）（20-2x ）=解析：3cm【分析】设横彩条的宽度是xcm ，竖彩条的宽度是3xcm ，根据“如果要使彩条所占面积是图案面积的19%”，可列方程求解．【详解】解：设横彩条的宽度是xcm ，竖彩条的宽度是3xcm ，则（30-3x ）（20-2x ）=20×30×（1-19%），解得x 1=1，x 2=19（舍去）．所以3x=3．答：竖彩条的宽度是3cm．故答案为：3cm【点睛】本题考查一元二次方程的应用，解题的关键是理解题意，学会正确寻找等量关系，构建方程解决问题．18．-1【分析】利用根与系数的关系得到a+b=1ab=-1再根据异分母分式加减法法则进行计算代入求值【详解】∵是方程的两根∴a+b=1ab=-1∴===-1故答案为：-1【点睛】此题考查一元二次方程根与解析：-1【分析】利用根与系数的关系得到a+b=1，ab=-1，再根据异分母分式加减法法则进行计算代入求值.【详解】∵a，b是方程210x x--=的两根，∴a+b=1，ab=-1，∴11a b+=a b ab +=1 1-=-1，故答案为：-1.【点睛】此题考查一元二次方程根与系数的关系式，异分母分式的加减法计算法则.19．10【分析】设这个百分率为x然后根据题意列出一元二次方程最后求解即可【详解】解：设这个百分率为x由题意得：300（1-x）2=243解得x=10或x=190（舍）故答案为10【点睛】本题主要考查了一解析：10%【分析】设这个百分率为x%，然后根据题意列出一元二次方程，最后求解即可．【详解】解：设这个百分率为x%，由题意得：300（1-x%）2=243，解得x=10或x=190（舍）．故答案为10%．【点睛】本题主要考查了一元二次方程的应用—百分率问题，弄清题意、设出未知数、列出一元二次方程成为解答本题的关键．20．【分析】由一元二次方程根与系数的关系解题即【详解】解：∵x2+2x﹣m2﹣m ＝0m ＝123…2020∴由根与系数的关系得：α1+β1＝﹣2α1β1＝﹣1×2；α2+β2＝﹣2α2β2＝﹣2×3；…α 解析：40402021【分析】 由一元二次方程根与系数的关系解题，即+=-b c a a αβαβ=，． 【详解】解：∵x 2+2x ﹣m 2﹣m ＝0，m ＝1，2，3， (2020)∴由根与系数的关系得：α1+β1＝﹣2，α1β1＝﹣1×2；α2+β2＝﹣2，α2β2＝﹣2×3；…α2020+β2020＝﹣2，α2020β2021＝﹣2020×2021；∴原式＝3320202020112211223320202020++++++++αβαβαβαβαβαβαβαβ 2222=++++12233420202021⨯⨯⨯⨯ 1111111=2(1)2233420202021⨯-+-+-++- 1=2(1)2021⨯-4040=2021故答案为：40402021． 【点睛】本题考查一元二次方程根与系数的关系，是重要考点，难度较易，掌握相关知识是解题关键．三、解答题21．（1）x 1＝1＋2，x 2＝1﹣2；（2）x 1＝﹣2，x 2＝43 【分析】（1）利用配方法解一元二次方程；（2）利用因式分解法解方程．【详解】（1）解：2x 2﹣4x ＋1＝0，x 2﹣2x ＝﹣12， x 2﹣2x ＋1＝﹣12＋1，即（x ﹣1）2＝12，∴x ﹣1＝±2，∴x 1＝1＋2，x 2＝1﹣2； （2）解：（2x ﹣1）2＝（3﹣x ）2．（2x ﹣1）2﹣（3﹣x ）2＝0，[（2x ﹣1）＋（3﹣x ）][（2x ﹣1）﹣（3﹣x ）]＝0，∴x ＋2＝0或3x ﹣4＝0，∴x 1＝﹣2，x 2＝43． 【点睛】本题考查一元二次方程的解法，熟练掌握配方法、因式分解法、公式法，并熟练运用是关键．22．（1）124,3x x ==-；（2）121,2x x =-=【分析】（1）化成一般式以后利用因式分解法解即可；（2）化成一般式以后利用因式分解法解即可；【详解】解：（1）28-x+4=x 2x -x-12=0(x+3)(x-4)=0∴124,3x x ==-（2） 220x x --=(2)(1)0x x -+=121,2x x ∴=-=【分析】本题主要考查解一元二次方程的能力，熟练掌握解一元二次方程的几种常用方法：直接开平方法、因式分解法、公式法、配方法，结合方程的特点选择合适、简便的方法是解题的关键．23．（1）1；（2）13-．【分析】（1）根据偶次方的非负性得到2(3)0x -，得到答案；（2）根据完全平方公式把原式变形，根据偶次方的非负性解答．【详解】解：（1）∵2(3)0x -≥，∴25(3)11x -+≥，∴多项式25(3)1x -+的最小值是1．故答案为：1；（2）24163x x -+()2443x x =-+ ()22244223x x =-+-+ 24(2)43x ⎡⎤=--+⎣⎦24(2)163x =--+24(2)13x =--∵2(2)0x -≥，∴24(2)1313x --≥-，∴多项式24163x x -+的最小值为13-．【点睛】本题考查的是配方法的应用，掌握完全平方公式、偶次方的非负性是解题的关键．24．121122x x =-+=-- 【分析】 利用完全平方公式进行配方解一元二次方程即可得．【详解】22450x x +-=，2245x x +=，2522x x +=， 252112x x ++=+， ()2712x +=，12x +=±，12x =-±，即121,122x x =-+=--． 【点睛】 本题考查了利用配方法解一元二次方程，熟练掌握配方法是解题关键．25．（1）12）13m <-． 【分析】 （1）根据分式的加减乘除混合运算法则计算即可，求值时注意分母有理化.（2）根据方程没有实数根，可知∆<0，进而求得m 得取值范围.【详解】（1）由题意得：原式23193(3)x x x xx x +--⎛⎫=-÷ ⎪--⎝⎭ 2(3)(3)(1)(3)(3)9x x x x x x x x ⎡⎤+----=⨯⎢⎥--⎣⎦ 2229(3)(3)9x x x x x x x --+-=⨯-- 29(3)(3)9x x x x x --=⨯-- 29(3)(3)9x x x x x --=⨯--3x x-=．3x =，∴原式1===． （2）该方程没有实数根，2242430b ac m ∴∆=-=+⨯⨯<，故4120m +<，解得13m <-． 【点睛】本题考查分式的混合运算以及一元二次方程根的判别，熟练掌握分式运算法则以及根的判别公式是解题关键.26．（1）112x =，23x =；（2）11x =，252x =- 【分析】（1）先把方程化为一般式，然后利用因式分解法解方程；（2）利用因式分解法求解．【详解】解：（1）2x 2-7x+3=0，（2x-1）（x-3）=0，2x-1=0或x-3=0，所以x 1=12，x 2=3； （3）移项得，x （2x+5）-（2x+5）=0，因式分解得，（2x+5）（x-1）=0，∴x-1=0，2x+5=0，∴11x=，25 2x=-；【点睛】本题考查了解一元二次方程的能力，熟练掌握解一元二次方程的几种常用方法：直接开平方法、因式分解法、公式法、配方法，结合方程的特点选择合适、简便的方法是解题的关键．。
完整word版-初三上学期数学错题集(一二)及答案
初三上学期数学错题集（一元二次方程）（一） 2012.09.09已打印1、若方程（m-2）x㎡-2+mx2=7是关于x的一元二次方程，则m的值为。
2、根据题意，列出方程：（不必求解，写出一般形式）学校图书馆去年年底有图书5万册，预计到明年年底增加到7.2万册，求这两年的平均增长率。
3、方程x2=0的实数根有（）A．0个B．1个C．2个D．1个或2个4、下列二次三项式中，是完全平方式的是（填序号）。
①9x2-12xy+4y2；②4y2-4y-1；③x2-25x+5；④2x2-4x+1；5、写出一个一元二次方程，使它的两根：一根是正数，另一根在-2与-1之间。
6、方程（x-2）(x+3)=6的解是（）A．x1=-4,x2=3 B．x1=2,x2=3C．x1=2,x2=-3 D．x1=4,x2=-37、用因式分解法解方程5（x+3)-2x（x+3)=0，可把它化为两个一元一次方程、求解。
初三上学期数学错题集（一元二次方程）（二）2012.09.15已打印1、解方程：（1）3y(y-1)2=2-2y （2）7 x2=21x （3）（x2+1）2-3(x2+1)-28=02、若△ABC的边长都是方程x2-10x+21=0的根，求△ABC的周长。
3、若△ABC 的边长都是方程x 2-7x+12=0的根，求△ABC 的周长。
4、已知P=157m-1,Q= m 2-158m(m 为任意实数)，则P 、Q 的大小关系为 （ ） A ．P<Q B. P=Q C. P>Q D.不能确定 5、关于x 的方程（k+1）x 2+2(k+1) x+k=0无实数根，则k 的取值范围是 。
6、已知a 是整数，满足⎩⎨⎧>->+023013a a 试解关于x 的一元二次方程x 2-4=x(ax-3).7、k 为何值时，关于x 的方程（k-1）x 2-(2k+1) x+k+1 = 0（1）有一解？（2）有两个不相等的实数根？8、已知△ABC 的两边AB 、AC 的长是关于x 的一元二次方程x 2-(2k+1) x+k(k+1) = 0的两个实数根，第三边BC 的长为5.（1）k 为何值时，△ABC 是以BC 为斜边的直角三角形？（2）k 为何值时，△ABC 是等腰三角形？并求△ABC 的边长。
中考一元二次方程组易错题50题含答案解析
中考一元二次方程组易错题50题含答案解析一、单选题1．方程2560x x --=的两根之和为（ ） A ．6-B ．5C ．5-D ．12．已知2是关于x 的方程230x mx m +-=的一个根，则这个方程的另一个根为（ ） A ．6-B ．6C ．3-D ．33．以﹣2和3为两根的一元二次方程是（ ） A ．x 2+x ﹣6=0 B ．x 2﹣x ﹣6=0 C ．x 2+6x ﹣1=0D ．x 2﹣6x+1=04．关于x 的一元二次方程2(2)10a x x -+-=，则a 的条件是（ ） A ．4a ≠B ．3a ≠C ．2a ≠D ．1a ≠5．下列一元二次方程中,没有实数根的是（ ） A ．2210x x -+= B ．2210x x -+= C ．2210x x --=D ．220x x -=6．下列方程中，属于一元二次方程是 ( ) A ．2x 2﹣y ﹣1＝0B ．x 2＝1C ．x 2﹣x （x+7）＝0D ．211x = 7．一元二次方程220x px +-=的一个根为2，则p 的值以及另一个根为（ ） A ．1，－1B ．1，1C ．－1，－1D ．－1，18．从正方形的铁皮上，截去2cm 宽的一条长方形，余下的面积是248cm ，则原来的正方形铁皮的面积是（ ） A ．28cmB ．29cmC ．264cmD ．268cm9．观察下列两个多项式相乘的运算过程：根据你发现的规律，若（x ＋m ）（x ＋n ） ＝x 2－5x ＋4，则m ＋n 的值为（ ）A ．－5B ．5C ．－4D ．410．关于x 的一元二次方程x 2+mx+m 2﹣7＝0的一个根是﹣2，则m 的值可以是（ ）A ．﹣1B ．3C ．﹣1或3D ．﹣3或111．下列各式中是一元二次方程的是（ ） A ．x 2+1＝1xB ．x （x+1）＝x 2﹣3C ．2x 2+3x ﹣1D ．﹣x 2+3x ﹣1＝12．若方程()23630m x x --+=有解，则m 的取值范围是（ ）A ．6m <B ．6m ≤C ．6m ≤且3m ≠D ．6m <且3m ≠13．某商品原价300元，连续两次降价a%后售价为260元，下面所列方程正确的是（ ）A ．300（1+a%）2＝260B ．300（1﹣a 2%）＝260C ．300（1﹣2a%）＝260D ．300（1﹣a%）2＝26014．方程x 2+x ﹣6＝0的两个根为（ ） A ．x 1＝﹣3，x 2＝﹣2 B ．x 1＝﹣3，x 2＝2 C ．x 1＝﹣2，x 2＝3D ．x 1＝2，x 2＝3 15．下列方程中是一元二次方程的是（ ）①ax 2+bx +c ＝0；①231223x x --=；①（x ﹣2）（2x ﹣1）＝0；①2120x x --=；①21y =；①x 2＝8．A ．①①①①B ．①C ．①①①①①①D ．①①①16．若关于x 的一元二次方程2(2)40x a x --+=有两个相等的实数根，则实数a 的值为（ ） A ．2B ．-2C ．-2或6D ．-6或217．下列方程中是一元二次方程的有（ ）①2320ax x -+= ①(1)(1)y y x x -=+ ① 2244x x = ①22226x y y x -+=+A ．①①B ．①①C ．①D ．①①①18．若关于x 的一元二次方程x 2﹣4x+c=0有两个相等的实数根，则常数c 的值为（ ） A ．±4B ．4C ．±16D ．1619．已知方程22610x x +-=的两个实数根为12,x x ，则1211+x x 的值为（ ） A ．-3B ．3C ．6D ．-6二、填空题20．已知x ＝1是一元二次方程x 2﹣mx+1＝0的一个解，则m 的值是_____． 21．方程22021x x =的解是 _____．22．已知m 是一元二次方程2250x x --=的一个根，则223-+=m m _________； 23．一元二次方程210x 的解__________．24．2017年生产1吨某种商品的成本是3000元，由于原料价格上涨，两年后，2019年生产1吨该商品的成本是5000元，求该种商品成本的年平均增长率．设年平均增长率为x ，则所列的方程应为_______（不增加其它未知数）． 25．请写出一个以1、2为根的一元二次方程________26-3为根，且二次项系数为1的一元二次方程为_______． 27．一元二次方程223x +=中，=a _______，b =________，c =________． 28．若m 是方程2310x x -+=的一个根，则2262021m m -+的值为_____．29．今年“国庆节”和“中秋节”双节期间，某微信群规定，群内的每个人都要发一个红包，并保证群内其他人都能抢到且自己不能抢自己发的红包，若此次抢红包活动，群内所有人共收到90个红包，则该群一共有_____人．30．方程22430x x +-=和2230x x -+=的所有的根的和等于____．31．若1x ，2x 是方程2x x 20160--=的两个实数根，则312x 2017x 2016+-=______. 32．在等腰ABC 中，顶角36A =︒，点D 在一腰AC 上，连接BD ，线段BD 与底边BC 的长相等．若6BC =．则AD =________；若6AB =，则AD =________．33．如果关于x 的方程x 2-5x + a = 0有两个相等的实数根，那么a=_____. 34．如果关于x 的方程22393042x kx k k ++-+=的两个实数根分别为x 1，x 2，那么2017120182x x 的值为________________． 35．已知等腰三角形的每条边长都是一元二次方程27100x x -+=的根，则这个三角形的周长为_______________；36．下面这首诗生动的刻画出了周瑜的一生： 大江东去浪淘尽，千古风流数人物； 而立之年督东吴，早逝英年两位数；十位恰小个位三，个位平方与寿符．(注：而立之年表示人到了30岁) 聪明的同学，你一定能算得出周瑜去世时的年龄是__________岁． 37．已知一元二次方程22510x x --=的两根为1x ,2x ，则12x x +=___38．已知关于x 的方程mx 2＋2x ＋5m ＝0有两个不相等的实数根12,x x ，且122x x <<，则实数m 的取值范围为________．39．如果a 、b 、c 为互不相等的实数，且满足关系式b 2+c 2＝2a 2+16a+14与bc ＝a 2﹣4a ﹣5，那么a 的取值范围是_____．三、解答题40．随着国内新能源汽车的普及，为了适应社会的需求，全国各地都在加快公共充电桩的建设，某省2018年公共充电桩的数量为2万个，2020年公共充电桩的数量为2.88万个．（1）求2018年至2020年该省公共充电桩数量的年平均增长率；（2）按照这样的增长速度，预计2021年该省将新增多少万个公共充电桩？41．解下列方程：2104x --=． 42．据统计，某市2018年某种品牌汽车的年产量为64万辆，到2020年，该品牌汽车的年产量达到100万辆．若该品牌汽车年产量的年平均增长率从2018年开始五年内保持不变．（1）求年平均增长率；（2）求该品牌汽车2021年的年产量为多少万辆？43．如图，利用一面墙（墙长20米），用总长度43米的篱笆（图中实线部分）围成一个矩形鸡舍ABCD ，且中间共留两个1米的小门，设篱笆BC 长为x 米．(1)AB=________米（用含x 的代数式表示）；(2)若矩形鸡舍ABCD 面积为150平方米，求篱笆BC 的长；(3)矩形鸡舍ABCD 面积是否有可能达到210平方米？若有可能，求出相应x 的值；若不可能，则说明理由． 44．解分式方程21211x x x -=++ 45．关于x 的一元二次方程2220x x m ++=有两个不相等的实数根． （1）求m 的取值范围；（2）若1x ，2x 是一元二次方程2220x x m ++=的两个根，且22128x x +=，求m 的值．46．材料阅读：材料1：符号“1212a ab b ”称为二阶行列式，规定它的运算法则为12122112a a a b a b b b =-．如525(4)2(3)1434=⨯--⨯-=---．材料2：我们已经学习过求解一元一次方程、二元一次方程组、分式方程等方程的解法，虽然各类方程的解法不尽相同，但是蕴含了相同的基本数学思想——转化，把未知转化为已知．用“转化”的数学思想，还可以解一些新的方程．例如，求解部分一元二次方程20(0)ax bx c a ++=≠时，我们可以利用因式分解把它转化为一元一次方程来求解．如解方程：2320x x ++=．①232(1)(2)x x x x ++=++①(1)(2)0x x ++=．故10x +=或20x +=．因此原方程的解是11x =-，22x =-．根据材料回答以下问题： （1）二阶行列式3642=___________；二阶行列式3321x x =中x 的值为__________． （2）求解241214x x x -=+中x 的值．（3）结合材料，若31x x m x-=，618x n -=，且0m n -<，求x 的取值范围．47．某地特产槟榔芋深受欢迎，某商场以7元/千克收购了3 000千克优质槟榔芋，若现在马上出售，每千克可获得利润3元．根据市场调查发现，近段时间内槟榔芋的售价每天上涨0.2元/千克，为了获得更大利润，商家决定先贮藏一段时间后再出售．根据以往经验，这批槟榔芋的贮藏时间不宜超过100天，在贮藏过程中平均每天损耗约10千克．（1）若商家将这批槟榔芋贮藏x 天后一次性出售，请完成下列表格：（2）将这批槟榔芋贮藏多少天后一次性出售最终可获得总利润29 000元？ 48．综合与探究如图，抛物线2y ax x c =++与x 轴交于A ，()4,0B 两点（点A 在点B 的左侧）．与y 轴交于点()0,4C ，直线BC 经过B ，C 两点，点Р是第一象限内抛物线上的一个动点，连接PB ，PC ．(1)求抛物线的函数表达式；(2)设点P 的横坐标为n ，四边形OBPC 的面积为S ，求S 的最大值并求出此时点P 的坐标；(3)在（2）的条件下，当S 取最大值时，在PC 的垂直平分线上是否存在一点M ，使BPM △是等腰三角形？若存在，请直接写出点M 的坐标；若不存在，请说明理由．49．已知：如图，△ABC 是边长为4cm 的等边三角形，动点P 、Q 同时从A 、B 两点出发，分别沿AB 、BC 方向匀速移动，它们的速度都是1cm /s ，当点P 到达点B 时，P 、Q 两点停止运动，设点P 的运动时间t (s )，解答下列各问题： （1）求ABC ∆的面积;（2）当t 为何值是，△PBQ 是直角三角形？（3）探究：是否存在某一时刻t ，使四边形APQC 的面积是ABC ∆面积的八分之五？如果存在，求出t 的值；不存在请说明理由.参考答案：1．B【分析】根据一元二次方程根与系数的关系求解． 【详解】解：由一元二次方程根与系数的关系可得： 一元二次方程的两根之和为：551--=， 故选B ．【点睛】本题考查一元二次方程的应用，熟练掌握一元二次方程根与系数的关系是解题关键． 2．A【分析】把2x =代入方程230x mx m +-=中，得出22230m m +-=，解得4m =，再解一元二次方程即可．【详解】解：把2x =代入方程230x mx m +-=中， 得出：22230m m +-=， 解得：4m =，①关于x 的方程为：24120x x +-=， ①12x =，26x =-，①这个方程的另一个根为6-， 故选：A ．【点睛】此题考查了一元二次方程的解，因式分解法解一元二次方程，得出该方程是解题的关键． 3．B【分析】由一元二次方程根与系数关系,设该方程一般形式中a=1,1x +2x =1=-b;1x 2x = -6 = c,即可得出答案.【详解】解:将1x =2, 2x =-3代入公式,可得到x 2-(2-3)x+2⨯(-3)=0,即x 2﹣x ﹣6=0, 所以B 选项是正确的.【点睛】本题考查了根与系数的关系.解题时熟记一元二次方程的根与系数的关系: 1x +2x =ba-，1x 2x =c a.4．C【分析】根据一元二次方程的定义求解即可．【详解】解：①2(2)10a x x -+-=是关于x 的一元二次方程， ①20a -≠， 即2a ≠， 故选：C ．【点睛】本题考查了一元二次方程的定义，方程的两边都是整式，只含有一个未知数，并且整理后未知数的最高次数都是2，象这样的方程叫做一元二次方程． 5．A【分析】根据一元二次方程根的判别式24b ac ∆=- 逐个求解即可．【详解】A ､224(1)42170b ac ∆=-=--⨯⨯=-<,没有实数根,故A 正确; B ､224(2)4110b ac ∆=-=--⨯⨯=,有两个相等的实数根,故B 不正确;C ､224(1)42(1)90b ac ∆=-=--⨯⨯-=>,有两个不相等的实数根,故C 不正确;D ､224(2)41040b ac ∆=-=--⨯⨯=>,有两个不相等的实数根,故D 不正确． 故选:A ．【点睛】本题主要考查了一元二次方程根的判别式24b ac ∆=-,解题的关键是熟练运用一元二次方程根的判别式判断一元二次方程根的情况． 6．B【分析】本题根据一元二次方程的定义解答．一元二次方程必须满足四个条件：（1）未知数的最高次数是2；（2）二次项系数不为0；（3）是整式方程；（4）含有一个未知数．由这四个条件对四个选项进行验证，满足这四个条件者为正确答案．【详解】解：A 、含有2个未知数，故选项错误；B 、含有1个未知数，并且未知数的最高次数是2，是一元二次方程，故选项正确；C 、化简后未知数的最高次数是1，故选项错误；D 、是分式方程，故选项错误． 故选B ．【点睛】本题考查了一元二次方程的概念，判断一个方程是否是一元二次方程，首先要看是否是整式方程，然后看化简后是否是只含有一个未知数且未知数的最高次数是2．7．C【分析】先设方程的另一个根为t ，再由根与系数的关系得出关于t 、p 的方程组，求解即可得到答案．【详解】设方程的另一个根为t ，由题意得 222t p t +=-⎧⎨=-⎩ 解得11t p =-⎧⎨=-⎩ ∴ p 的值以及另一个根分别为－1，1．故选：C ．【点睛】本题考查了一元二次方程根与系数的关系，即设一元二次方程20(0)ax bx c a ++=≠ 的两个实数根为12,x x ，则1212·b x x ac x x a ⎧+=-⎪⎪⎨⎪=⎪⎩，熟练掌握知识点是解题的关键． 8．C【分析】设原来的正方形铁皮的边长为cm x ，则截去2cm 宽的一条长方形的长为()2cm x -，根据长方形面积公式列方程求出正方形的边长，再用正方形面积公式求解．【详解】解：原来的正方形铁皮的边长为cm x ，则截去2cm 宽的一条长方形的长为()2cm x -，根据题意，得()2=48x x -，解得：18x =，26x =-(不符合题意，舍去)，①原来的正方形铁皮的面积()222864cm x ===，故选：C ．【点睛】本题考查一元二次方程的应用，理解题意，设恰当未知数，找等量关系，列出方程是解是的关键． 9．A【分析】从题例两个多项式相乘的运算过程中发现规律，利用规律求出m 、n 的值再求和．【详解】解：根据题意得，m+n=-5，mn =4故选：A．【点睛】本题考查多项式乘以多项式，理解例题中的运算过程并发现规律是解题关键．10．C【分析】先把x＝﹣2代入方程x2+mx+m2﹣7＝0得4﹣2m+m2﹣7＝0，然后解关于m的方程即可．【详解】解：把x＝﹣2代入方程x2+mx+m2﹣7＝0得4﹣2m+m2﹣7＝0，解得m＝﹣1或3．故选：C．【点睛】本题主要考查一元一次方程的解及根与系数的关系，解题关键是熟练掌握计算法则.11．D【详解】只含有一个未知数并且未知数的最高次数是2的整式方程为一元二次方程，根据这一定义可以对各选项作出相应的判断.A选项：该方程中含有1x，不是整式方程，故A选项不符合题意.B选项：该方程整理后为x=-3. 整理后的方程为一元一次方程，故B选项不符合题意.C选项：因为本选项的式子不是等式，所以该式子不是方程. 故C选项不符合题意.D选项：在该方程中，等号两侧均为整式，只有x一个未知数且x的最高次数为2，符合一元二次方程的定义，故D选项符合题意.故本题应选D.点睛：本题考查了一元二次方程的相关概念. 在判断一个方程是否是一元二次方程的时候，首先应该判断该方程是否是整式方程，如果不是整式方程，则一定不是一元二次方程. 如果原方程是整式方程，则应对原方程进行必要的整理，利用整理后的方程进行判断. 另外，方程是含有未知数的等式. 不是等式的式子一定不是方程，也不可能是一元二次方程.12．B【分析】直接分方程为一次方程和二次方程时分别讨论即可．【详解】当方程为一次方程时，30m-=，解得3m=，当方程为二次方程时，此时30m -≠，即3m =，①方程()23630m x x --+=有解，①()264330m ∆=--⨯≥，解得6m ≤，①6m ≤且3m =，综上所述，m 的取值范围是6m ≤，故选B ．【点睛】本题考查了根的判别式，解题时注意不要忘记方程为一次方程的情况． 13．D【分析】根据降价后的价格＝原价（1﹣降低的百分率），本题可先表示第一次降价后商品的售价，再根据题意表示第二次降价后的售价，即可列出方程．【详解】解：当商品第一次降价a%时，其售价为300（1﹣a%），当商品第二次降价a%后，其售价为300（1﹣a%）2．故所列方程为：300（1﹣a%）2＝260，故选：D ．【点睛】本题主要考查一元二次方程的应用，找出合适的等量关系是解题的关键． 14．B【分析】利用因式解法即可求解．【详解】原方程因式分解得：()()320x x +-=，①1232x x =-=，．故选：B ．【点睛】本题考查了解一元二次方程－因式分解法，熟练掌握一元二次方程的解法是解题的关键．15．D【分析】分析:根据一元二次方程的定义（含有一个未知数，并且含有未知数的项的最高次数是2的整式方程叫一元二次方程）进行判断即可．【详解】解：①当a ＝0时，ax 2+bx +c ＝0不是一元二次方程； ①231223x x --=是一元二次方程；①（x ﹣2）（2x ﹣1）＝0是一元二次方程； ①2120x x--=是分式方程；①21y =不是一元二次方程；①x 2＝8是一元二次方程．①是一元二次方程的是①①①．故选：D ．【点睛】本题考查了一元二次方程的定义，解题时，要注意两个方面：1、一元二次方程包括三点：①是整式方程，①只含有一个未知数，①所含未知数的项的最高次数是2；2、一元二次方程的一般形式是ax 2+bx +c =0（a ≠0）．16．C【分析】根据一元二次方程有两个相等的实数根，得到根的判别式等于0，求出a 的值即可． 【详解】关于x 的一元二次方程2(2)40x a x --+=有两个相等的实数根，∴∆2(2)160a =--=，即2(2)16a -=，开方得：24a -=或24a ，解得：6a =或2-．故选：C ．【点睛】此题考查了根的判别式，熟练掌握一元二次方程根的判别式的意义是解本题的关键．17．C【分析】根据一元二次方程满足的条件：一个未知数、未知数的最高次数为2、二次项系数不为0、整式方程对每小题分析判断即可求解．【详解】①、当a≠0时是一元二次方程，当a=0时是一元一次方程，不符合题意； ①、有两个未知数，不是一元二次方程，不符合题意；①、是分式方程，不是整式方程，不符合题意①、整理方程为：2260y y -=+，是一元二次方程，符合题意，只有①是一元二次方程，故选：C ．【点睛】本题考查了一元二次方程的概念，熟知一元二次方程满足的条件是解答的关键，对于一般式20(0)ax bx c a ++=≠，特别要注意a≠0这一条件，这是做题过程中容易忽视的知识点．18．B【分析】根据方程有两个相等的实数根结合根的判别式即可得出关于c 的一元一次方程，解方程即可得出结论．【详解】①方程x 2-4x+c=0有两个相等的实数根，①①=（-4）2-4×1×c=16-4c=0，解得：c=4．故选B ．【点睛】本题考查了根的判别式以及解一元一次方程，由方程有两个相等的实数根结合根的判别式得出关于c 的一元一次方程是解题的关键．19．C【分析】根据一元二次方程根与系数关系得出123x x +=-，1212x x =-，将1211+x x 通分，代入数值即可求解．【详解】①方程2610x x +-=的两个实数根为12,x x ，①123x x +=-，1212x x =-，①121212113612x x x x x x +-+===-， 故选：C ．【点睛】本题考查了一元二次方程根与系数关系、分式的化简求值，熟练掌握根与系数关系是解答的关键．20．2【分析】把x ＝1代入一元二次方程x 2﹣mx+1＝0，可得110,m -+=再解方程可得答案．【详解】解： x ＝1是一元二次方程x 2﹣mx+1＝0的一个解，110,m ∴-+=2.m ∴=故答案为：2.【点睛】本题考查的是一元二次方程的解，掌握方程的解的含义是解题的关键． 21．1202021x x ==，【分析】根据因式分解法解该一元二次方程即可．【详解】解：22021x x =220210x x -=(20021)x x -=①0x =或20210x -=①1202021x x ==，故答案为：1202021x x ==，．【点睛】本题考查解一元二次方程，掌握因式分解法解一元二次方程的步骤是解题关键． 22．8【分析】把x m =代入原方程可得：225,m m -= 从而可得答案. 【详解】解： m 是一元二次方程2250x x --=的一个根，2250,m m ∴--=225,m m ∴-=2238.m m ∴-+=故答案为：8.【点睛】本题考查的是一元二次方程的解的含义，求代数式的值，掌握方程的解使方程的左右两边相等是解题的关键.23．1x =±【分析】利用直接开平方法求解可得．【详解】解：①x 2-1=0，①x 2=1，则x=±1.故答案为x=±1．【点睛】本题主要考查解一元二次方程的能力，熟练掌握解一元二次方程的几种常用方法：直接开平方法、因式分解法、公式法、配方法，结合方程的特点选择合适、简便的方法是解题的关键．24．()2300015000x +=．【分析】设这种商品的年平均增长率为x ，根据题意列方程即可．【详解】解：设这种商品的年平均增长率为x ，由题意得：()2300015000x +=，故答案为：()2300015000x +=．【点睛】本题考查增长率问题，解题的关键是明确题意，根据等量关系列出方程． 25．2320x x --=【详解】试题分析：以1、2为根的一元二次方程是(1)(2)0x x --=，即2320x x --=. 考点：一元二次方程的解26．(230x x +--3的和与积，然后根据根与系数的关系求出满足条件的一元二次方程．【详解】解：①33，3--①以-31的一元二次方程为(230x x +-．故答案为：(230x x +-．【点睛】本题考查了一元二次方程根与系数的关系，熟记两根之和与两根之积是解题的关键．27． 2 -3【分析】先移项把一元二次方程化为一般形式，然后进行求解即可【详解】解：①223x +=，①2230x -=，①2a =，b =3c =-，故答案为：23-．【点睛】本题主要考查了一元二次方程的一般形式，解题的关键在于能够熟练掌握一元二次方程的一般形式为()200ax bx c a ++=≠．【分析】由已知可得2310m m -+=，即有231m m -=-，整体代入易求得2262021m m -+的值．【详解】①m 是方程2310x x -+=的一个根，①2310m m -+=，即231m m -=-，①222620212(3)20212(1)20212019m m m m -+=-+=⨯-+=，故答案为：2019．【点睛】本题考查了一元二次方程的解，求代数式的值，用整体思想求值更简便． 29．10【分析】设该群一共有x 人，则每人收到（x ﹣1）个红包，根据群内所有人共收到90个红包，即可得出关于x 的一元二次方程，解之取其正值即可得出结论．【详解】解：设该群一共有x 人，则每人收到（x ﹣1）个红包，依题意，得：x （x ﹣1）＝90，解得：x 1＝10，x 2＝﹣9（舍去）．故答案为10．【点睛】此题考查了一元二次方程的应用，解题关键是要读懂题目的意思，根据题目给出的条件，找出合适的等量关系，列出方程，再求解．30．-2．【分析】先利用根的判别式求出根的情况，再利用两根和的公式计算即可得到答案.【详解】在方程22430x x +-=中2442(3)400∆=-⨯⨯-=>，①方程22430x x +-=有两个不相等的实数根；在方程2230x x -+=中2(2)41380∆=--⨯⨯=-<，①方程2230x x -+=没有实数根．设方程22430x x +-=的两个实数根分别为m 、n ，则有422m n +=-=-． 故答案为：-2【点睛】此题考查一元二次方程根的判别式公式，根与系数的关系公式，正确掌握计算公式是解题的关键.【分析】先根据一元二次方程的解的定义得到x12=x1+2016，再计算x13=x12+2016x1=2017x1+2016，则原式可化简为2017（x1+x2），然后利用根与系数的关系求解．【详解】①x1是方程x2-x-2016=0的两实数根，①x12=x1+2016，①x13=x12+2016x1=x1+2016+2016x1=2017x1+2016，①原式=2017x1+2016+2017x2-2016=2017（x1+x2），①x1，x2是方程x2-x-2016=0的两实数根，①x1+x2=1，①原式=2017．故答案为2017．【点睛】本题主要考查了根与系数的关系，根据已知将原式化简，利用根与系数的关系是解答此题的关键．32．63-+【分析】根据等边对等角和外角的性质证明①ABD=①A，得到AD=BD=BC=6；设AD=x，再证明①ABC①①BDC，得到AB BCBD DC=，解之即可．【详解】解：①①A=36°，AB=AC，①①ABC=①C=（180°-36°）÷2=72°，①BD=BC，①①BDC=①C=72°，①①BDC=①A+①ABD，①①ABD=72°-36°=36°，①①ABD=①A，①AD=BD，①BD=BC=6，①AD=6；若AB=AC=6，设AD=x，则BD=BC=x，①①BDC =①ABC =72°，①C =①C ，①①ABC ①①BDC ， ①AB BC BD DC=，即66x x x =-，解得：x =3-+或3--（负值舍去），经检验：x =3-+①AD =3-+，故答案为：6，3-+【点睛】本题考查了等腰三角形的判定和性质，相似三角形的判定和性质，外角的性质，解分式方程和一元二次方程，解题的关键是灵活运用等边对等角，从而证明三角形相似． 33．254【分析】若一元二次方程有两个相等的实数根，则方程的根的判别式等于0，由此可列出关于a 的等式，求出a 的值．【详解】①关于x 的方程x 2-5x+a=0有两个相等的实数根，①①=25-4a=0，即a=254． 故答案为：254. 【点睛】一元二次方程根的情况与判别式△的关系：（1）△＞0⇔方程有两个不相等的实数根；（2）△=0⇔方程有两个相等的实数根；（3）△＜0⇔方程没有实数根．34．23- 【分析】由方程有两个实数根，得到根的判别式的值大于等于0，列出关于k 的不等式，利用非负数的性质得到k 的值，确定出方程，求出方程的解，代入所求式子中计算即可求出值．【详解】①方程x 2+kx+239342k k -+＝0有两个实数根， ①b 2-4ac=k 2-4（34k 2-3k+92）=-2k 2+12k-18=-2（k-3）2≥0， ①k=3， 代入方程得：x 2+3x+94=（x+32）2=0， 解得：x 1=x 2=-32， 则2017120182x x =-23． 故答案为-23．【点睛】此题考查了根的判别式，非负数的性质，以及配方法的应用，求出k 的值是本题的突破点．35．6或12或15【分析】先利用因式分解的方法解方程得到x 1=2，x 2=5，根据题意讨论：当腰为2，底边为5时；当腰为5，底边为2时，然后分别计算出等腰三角形的周长．【详解】①x 2-7x +10=0，①（x -2）（x -5）=0，①x -2=0或x -5=0，①x 1=2，x 2=5，当腰为2，底边为5时，2+2=4<5，不能构成三角形；当腰为5，底边为2时，等腰三角形的周长为2+5+5=12；当腰为2，底边为2时，等腰三角形的周长为2+2+2=6，当腰为5，底边为5时，等腰三角形的周长为5+5+5=15．故答案为6或12或15．【点睛】本题考查了解一元二次方程-因式分解法：就是先把方程的右边化为0，再把左边通过因式分解化为两个一次因式的积的形式，那么这两个因式的值就都有可能为0，这就能得到两个一元一次方程的解，这样也就把原方程进行了降次，把解一元二次方程转化为解一元一次方程的问题了（数学转化思想）．也考查了三角形三边的关系．36．36【分析】这是一道数字问题的应用题，等量关系隐于诗词中，及周瑜去世时年龄为两位数，十位数字比个位数字小3，个位数字的平方等于这两个数，于是可以设个位数字为x ，列出一元二次方程求解．【详解】设周瑜去世时的年龄的个位数字为x ，则十位数字为x －3，由题意，得 x 2＝10(x －3)＋x ，即x 2－11x ＋30＝0，解得x 1＝5，x 2＝6，当x ＝5时，周瑜的年龄25岁，非而立之年，不合题意，舍去；当x ＝6时，周瑜的年龄36岁，符合题意，故答案为36.【点睛】本题考查了一元二次方程的应用，判断所求的解是否符合题意，舍去不合题意的解．找到关键描述语，找到等量关系准确的列出方程是解决问题的关键．37．52【详解】根据韦达定理，可得，12x x +=5238．−49＜m ＜0 【分析】根据关于x 的方程mx 2＋2x ＋5m ＝0有两个不相等的实数根x 1，x 2，可以得到m 的取值范围，再根据x 1＜2＜x 2和一元二次方程和二次函数的关系，可以利用分类讨论的方法求出m 的取值范围，本题得以解决．【详解】解：①关于x 的方程mx 2＋2x ＋5m ＝0有两个不相等的实数根x 1，x 2，①2024?50m m m ≠⎧⎨-⎩＞，解得，m ＜0或0＜m ①x 1＜2＜x 2，①当m ＜0时，m ×22＋2×2＋5m ＞0， 解得−49＜m ＜0；当0＜m m ×22＋2×2＋5m ＜0， 解得m 无解；故答案为：−49＜m ＜0． 【点睛】本题考查抛物线与x 轴的交点、根的判别式、一元二次方程与二次函数的关系，解答本题的关键是明确题意，利用二次函数的性质和一元二次方程的知识解答．39．a ＞﹣1且a≠﹣56且a≠﹣78 【详解】试题解析：222221614,45b c a a bc a a +=++=--，22222()216142(45)4844(1)b c a a a a a a a ∴+=+++--=++=+，即有2(1).b c a +=±+又245bc a a =--，所以b ,c 可作为一元二次方程222(1)450x a x a a ±++--=①的两个不相等实数根，故224(1)4(45)24240a a a a =+---=+>，解得a >−1.若当a =b 时，那么a 也是方程①的解，222(1)450a a a a a ∴±++--=，即24250a a --=或650a --=，解得,a =或5.6a =- 当a =b =c 时，16140450a a +=--=，， 解得75,84a a =-=- (舍去)，所以a 的取值范围为1a >-且56a ≠-且a ≠7.8a ≠-故答案为1a >-且56a ≠- 且a ≠7.8a ≠- 40．（1）2018年至2020年该省公共充电桩数量的年平均增长率为20%．（2）预计2021年该省将新增0.576万个公共充电桩．【分析】（1）设2018年至2020年该省公共充电桩数量的年平均增长率为x ，根据该省2018年及2020年公共充电桩，即可得出关于x 的一元二次方程，解之取其正值即可得出结论；（2）根据该省2021年公共充电桩数量=该省2020年公共充电桩数量×增长率，即可求出结论．【详解】解：（1）设2018年至2020年该省公共充电桩数量的年平均增长率为x ， 依题意得：2（1+x ）2=2.88，解得：x 1=0.2=20%，x 2=-2.2（不合题意，舍去）．答：2018年至2020年该省公共充电桩数量的年平均增长率为20%．（2）2.88×20%=0.576（万个）．答：预计2021年该省将新增0.576万个公共充电桩．【点睛】本题考查了一元二次方程的应用，找准等量关系，正确列出一元二次方程是解题的关键．41．11x =，21x =- 【分析】利用公式法解一元二次方程，注意解题规范．【详解】解：1a =，b =14c =-. (221Δ441404b ac ⎛⎫=-=-⨯⨯-=> ⎪⎝⎭， 方程有两个不相等的实数根，(21x -===⨯即11x =+，21x =. 【点睛】本题考查公式法解一元二次方程，是重要考点，难度较易，掌握相关知识是解题关键．42．（1）25%；（2）125万辆．【分析】（1）设年平均增长率为x ，根据“该品牌汽车2018年和2020年的产量”列出关于x 的一元二次方程，最后求解即可；（2）根据“该品牌汽车2021年的年产量＝2020年的年产量×（1＋增长率）”计算即可．【详解】解：（1）设年平均增长率为x ，依题意，得：64（1＋x ）2＝100，解得：x 1＝0.25＝25%，x 2＝﹣2.25（不合题意，舍去）．答：年平均增长率为25%；（2）100×（1＋25%）＝125（万辆）．答：该品牌汽车2021年的年产量为125万辆．【点睛】本题主要考查了一元二次方程的应用，审清题意、找准等量关系、列出关于x的一元二次方程成为解答本题的关键．43．(1)（45−3x）(2)篱笆BC的长为10米(3)不可能，理由见解析【分析】（1）设篱笆BC长为x米，根据篱笆的全长结合中间共留2个1米的小门，即可用含x的代数式表示出AB的长；（2）根据矩形鸡舍ABCD面积为150平方米，即可得出关于x的一元二次方程，解之取其较大值即可得出结论；（3）根据矩形鸡舍ABCD面积为210平方米，即可得出关于x的一元二次方程，由根的判别式Δ=-55＜0，可得出该方程没有实数根，进而可得出矩形鸡舍ABCD面积不可能达到210平方米．【详解】（1）解：设篱笆BC长为x米，①篱笆的全长为43米，且中间共留两个1米的小门，①AB=43+2−3x=45−3x（米）．故答案为：（45−3x）．（2）解：依题意，得：（45−3x）x=150，整理，得：x2−15x+50=0，解得：x1=5，x2=10．当x=5时，AB=45−3x=30＞20，不合题意，舍去；当x=10时，AB=45−3x=15，符合题意．答：篱笆BC的长为10米．（3）解：不可能，理由如下：依题意，得：（45−3x）x=210，整理得：x2−15x+70=0，①Δ=（−15）2−4×1×70=−55＜0，①方程没有实数根，。
(易错题)初中数学九年级数学上册第一单元《一元二次方程》测试(含答案解析)
一、选择题1．用配方法解方程x 2﹣6x ﹣3＝0，此方程可变形为（ ）A ．（x ﹣3）2＝3B ．（x ﹣3）2＝6C ．（x+3）2＝12D ．（x ﹣3）2＝12 2．若关于x 的方程kx²+4x-1=0有实数根，则k 的取值范围是（ ） A ．k-4且k≠0 B ．k≥-4C ．k>-4且k≠0D ．k>-4 3．关于x 的一元二次方程()25410a x x ---＝有实数根，则a 满足（ ）． A ．5a ≠B ．1a ≥且5a ≠C ．1a ≥D ．1a <且5a ≠ 4．关于x 的一元二次方程2210kx x +-=有两个不相等的实数根，则k 的取值范围是（ ）A ．1k >-B ．1k ≥-C ．0k ≠D ．1k >-且0k ≠ 5．下列一元二次方程中，没有实数根的是（ ） A ．(2)(2)0x x -+= B ．220x -=C ．2(1)0x -=D ．2(1)20x ++=6．若整数a 使得关于x 的一元二次方程()2210a x -+=有两个实数根，并且使得关于y 的分式 方程32133ay y y y -+=--有整数解，则符合条件的整数a 的个数为（ ） A ．2B ．3C ．4D ．5 7．方程29180x x -+=的两个根是等腰三角形的底和腰，则这个等腰三角形的周长为（ ）A ．12B ．15C ．12或15D ．18 8．当分式2369x x x --+的值为0时，则x 等于（ ） A ．3 B ．0 C ．3± D ．-39．《代数学》中记载，形如2833x x +=的方程，求正数解的几何方法是：“如图1，先构造一个面积为2x 的正方形，再以正方形的边长为一边向外构造四个面积为2x 的矩形，得到大正方形的面积为331649+=，则该方程的正数解为743-=．”小聪按此方法解关于x 的方程2100x x m ++=时，构造出如图2所示的图形，已知阴影部分的面积为50，则该方程的正数解为（ ）．A．6 B．3 532-C．532-D．535-10．关于x的一元二次方程（m-2）x2+3x-1＝0有实数根，那么m的取值范围是（）A．m≤14B．m≥14-且m≠2C．m≤14-且m≠﹣2 D．m≥14-11．如图，是一个简单的数值运算程序，则输入x的值为（）A31B．31C31或31D．无法确定12．已知一元二次方程x2﹣6x+c＝0有一个根为2，则另一根及c的值分别为（）A．2，8 B．3，4 C．4，3 D．4，8二、填空题13．一元二次方程（x＋1）（x﹣3）＝3x＋4化为一般形式可得_________．14．某校八年级举行足球比赛，每个班级都要和其他班级比赛一次，结果一共进行了6场比赛，则八年级共有_____个班级．15．关于x的方程222(1)0x m x m m+-+-=有两个实数根α，β，且2212αβ+=，那么m的值为________．16．若关于x的一元二次方程()23x c-=有实根，则c的值可以是_________________．(写出一个即可)17．关于x的方程2880kx x-+=有两个实数根，则k的取值范围______________．18．已知x1和x2是方程2x2-5x+1=0的两个根，则1212x xx x+的值为_____．19．已知a、b、c满足227a b+=，221b c-=-，2617c a-=-，则a b c++=_______．20．当x=______时，−4x2−4x+1有最大值．三、解答题21．5月10日，重庆正式启动“加快发展直播带货行动计划”，以推动直播带货和“网红经济”发展，已知云阳桃片糕每盒12元，仙女山红茶每盒50元，第一次直播期间，共卖出云阳桃片糕和仙女山红茶共计2000盒．（1）若卖出桃片糕和红茶的总销售额不低于54400元，则至少卖出仙女山红茶多少盒？ （2）第一次直播结束，为了回馈顾客，在第二次直播期向，桃片糕每盒降价10%3a ，红茶每盒降价4a %，桃片糕数量在（1）问最多的数量下增加6a %，红茶数量在（1）问最少的数量下增加4a %，最终第二次直播总销售额比第一次直播的最低销售额54400元少80a 元，求a 的值．22．先阅读理解下面的例题，再按要求解答下面的问题：例题：说明代数式m 2+2m+4的值一定是正数．解：m 2+2m+4＝m 2+2m+1+3＝（m+1）2+3．∵（m+1）2≥0，∴（m+1）2+3≥3，∴m 2+2m+4的值一定是正数．（1）说明代数式﹣a 2+6a ﹣10的值一定是负数．（2）设正方形面积为S 1，长方形的面积为S 2，正方形的边长为a ，如果长方形的一边长比正方形的边长少3，另一边长为4，请你比较S 1与S 2的大小关系，并说明理由． 23．若关于x 的一元二次方程x 2-6x +m +1=0的两根是x 1，x 2，且x 12+x 22=24，求m 的值． 24．用一块边长为70cm 的正方形薄钢片制作一个长方体盒子．（1）如果要做成一个没有盖的长方体盒子，可先在薄钢片的四个角上截去四个相同的小正方形（如图①），然后把四边折合起来（如图②）．当做成的盒子的底面积为2900cm 时，求该盒子的容积；（2）如果要做成一个有盖的长方体盒子，制作方案要求同时符合下列两个条件： ①必须在薄钢片的四个角上截去一个四边形（如图③阴影部分），②沿虚线折合后薄钢片即无空隙又不重叠地围成各盒面，求当底面积为2800cm 时，该盒子的高．25．阅读下列材料，解答问题．222(25)(37)(52)x x x -++=+．解：设25,37m x n x =-=+，则52m n x +=+， 原方程可化为222()m n m n +=+，0mn ，即(25)(37)0x x -+=．250x ∴-=或370x +=，解得1257,23x x ==-． 请利用上述方法解方程：222(45)(32)(3)x x x -+-=-．26．解下列方程（1）2280x x +-=；（2）（2y ＋1）2－25＝0；（3）24430t t --=；（4）2（m ＋3）＝m 2－9 ．【参考答案】***试卷处理标记，请不要删除一、选择题1．D解析：D【分析】先移项，再把方程两边同时加上一次项系数一半的平方，最后配方即可得新答案．【详解】由原方程移项得：x 2﹣6x ＝3，方程两边同时加上一次项系数一半的平方得：x 2﹣6x+9＝12，配方得；（x ﹣3）2＝12．故选：D ．【点睛】此题主要考查配方法的运用，配方法的一般步骤为：移项、二次项系数化为1、两边同时加上一次项系数一半的平方、配方完成；熟练掌握配方法的步骤并熟记完全平方公式是解题关键．2．B解析：B【分析】分k=0和k≠0两种情况考虑，当k=0时可以找出方程有一个实数根；当k≠0时，根据方程有实数根结合根的判别式可得出关于m 的一元一次不等式，解不等式即可得出k 的取值范围．结合上面两者情况即可得出结论．【详解】解：当k=0时，原方程为-4x+1=0，解得：x=14， ∴k=0符合题意；当k≠0时，∵方程kx 2-4x-1=0有实数根，∴△=（-4）2+4k≥0，解得：k≥-4且k≠0．综上可知：k 的取值范围是k≥-4．故选：B ．【点睛】本题考查了根的判别式，总结：一元二次方程根的情况与判别式△的关系：（1）△＞0⇔方程有两个不相等的实数根；（2）△=0⇔方程有两个相等的实数根；（3）△＜0⇔方程没有实数根．3．B解析：B【分析】由方程有实数根可知根的判别式b 2-4ac≥0，结合二次项的系数非零，可得出关于a 一元一次不等式组，解不等式组即可得出结论．【详解】解：由已知得：()()()25044510a a -≠⎧⎪⎨--⨯-⨯-≥⎪⎩， 解得：a≥1且a≠5．故选：B ．【点睛】本题考查了根的判别式，解题的关键是得出关于a 的一元一次不等式组．本题属于基础题，难度不大，解决该题型题目时，由根的判别式结合二次项系数非零得出不等式组是关键．4．D解析：D【分析】根据一元二次方程根的判别式得到关于k 的不等式，然后求解不等式即可.【详解】是一元二次方程，0k ∴≠．有两个不相等的实数根，则Δ0>，2Δ24(1)0k =-⨯-⨯>，解得1k >-．1k ∴>-且0k ≠．故选D【点睛】本题考查一元二次方程ax 2+bx +c =0(a ≠0)根的判别式：（1）当△=b 2﹣4ac ＞0时，方程有两个不相等的实数根；（2）当△=b 2﹣4ac =0时，方程有有两个相等的实数根；（3）当△=b 2﹣4ac ＜0时，方程没有实数根.5．D解析：D【分析】分别利用因式分解法和直接开平方法解一元二次方程、一元二次方程的根的判别式即可得．【详解】A 、由因式分解法得：122,2x x ==-，此项不符题意；B 、由直接开平方法得：120x x ==，此项不符题意；C 、由直接开平方法得：121x x ==，此项不符题意；D 、方程2(1)20x ++=可变形为2230x x ++=，此方程的根的判别式2241380∆=-⨯⨯=-<，则此方程没有实数根，此项符合题意； 故选：D ．【点睛】本题考查了解一元二次方程，熟练掌握各解法是解题关键．6．B解析：B【分析】对于关于x 的一元二次方程()2210a x -+=有两个实数根，利用判别式的意义得到a-2≠0且2a+3≥0且△=2-4（a-2）≥0，解不等式组得到整数a 为：-1，0，1，3，4，5；接着解分式方程得到y=61a -，而y≠3，则61a -≠3，解得a≠3，从而得到当a=-1，0，4时，分式方程有整数解，然后求符合条件的所有a 的个数．【详解】解：∵整数a 使得关于x 的一元二次方程()2210a x -+=有两个实数根， ∴a-2≠0且2a+3≥0且△=2-4（a-2）≥0， ∴31122a -≤≤且a≠2， ∴整数a 为：-1，0，1，3，4，5；去分母得3-ay+3-y=-2y ，解得y=61a -， 而y≠3，则61a -≠3，解得a≠3， 当a=-1，0，4时，分式方程有整数解，∴符合条件的所有a 的个数是3．故选：B ．【点睛】本题考查了根的判别式：一元二次方程ax 2+bx+c=0（a≠0）的根与△=b 2-4ac 有如下关系：当△＞0时，方程有两个不相等的实数根；当△=0时，方程有两个相等的实数根；当△＜0时，方程无实数根．7．B解析：B【分析】首先求出方程的根，再根据三角形三边关系定理列出不等式，确定是否符合题意．【详解】解：解方程x 2-9x+18=0，得x 1=3，x 2=6，当3为腰，6为底时，不能构成等腰三角形；当6为腰，3为底时，能构成等腰三角形，周长为6+6+3=15．故选：B ．【点睛】本题考查了解一元二次方程，从边的方面考查三角形，涉及分类讨论的思想方法．求三角形的周长，不能盲目地将三边长相加起来，而应养成检验三边长能否组成三角形的好习惯，把不符合题意的舍去．8．D解析：D【分析】先根据分式的值为0的条件列出关于x 的不等式组，求出x 的值即可．【详解】 依题意得：230690x x x ⎧-⎨-+≠⎩＝，解得x ＝−3．故选：D【点睛】本题考查的是分式的值为0的条件，熟知分式值为零的条件是分子等于零且分母不等于零是解答此题的关键．9．D解析：D【分析】 仿照题目中的做法可得空白部分小正方形的边长为52，先计算出大正方形的面积=阴影部分的面积+4个小正方形的面积，从而可得大正方形的边长，再用其减去两个空白正方形的边长即可．【详解】解：如图2，先构造一个面积为2x 的正方形，再以正方形的边长为一边向外构造四个面积为52x 的矩形，得到大正方形的面积为255045025752⎛⎫+⨯=+= ⎪⎝⎭， ∴5252⨯=． 故选：D ．【点睛】本题考查了一元二次方程的几何解法，读懂题意并数形结合是解题的关键．10．B解析：B【分析】关于x 的一元二次方程（m-2）x 2+3x-1＝0有实数根，由于二次项系数有字母，要考虑二次项系数不为0，再由一元二次方程（m-2）x 2+3x-1＝0有实数根，满足△≥0，取它们的公共部分即可．【详解】关于x 的一元二次方程（m-2）x 2+3x-1＝0有实数根，m-2≠0,m≠2,△=9-4×(-1)×(m-2)≥0, m 1-4≥, 关于x 的一元二次方程（m-2）x 2+3x-1＝0有实数根，m 的取值范围是m 1-4≥且m≠2． 故选：B ．【点睛】本题考查关于x 的一元二次方程（m-2）x 2+3x-1＝0有实数根的问题，关键掌握方程的定义，二次项系数不为0，含x 的最高次项的次数为2，而且是整式的方程，注意判别式使用条件，前提是一元二次方程，还要求一般形式．11．C解析：C【分析】先根据数值运算程序可得一个关于x 的一元二次方程，再利用直接开平方法解方程即可得．【详解】由题意得：()2319x --=-， ()213x -=，1-=x ，1x =±即1x =或1x =，故选：C ．【点睛】本题考查了解一元二次方程，根据数值运算程序正确建立方程是解题关键．12．D解析：D【分析】设方程的另一个根为t ，根据根与系数的关系得到t +2＝6，2t ＝c ，然后先求出t ，再计算c 的值．【详解】解：设方程的另一个根为t ，根据题意得t +2＝6，2t ＝c ，解得t ＝4，c ＝8．故选：D ．【点睛】本题考查了根与系数的关系：若x 1，x 2是一元二次方程ax 2+bx+c=0（a≠0）的两根时，x 1+x 2=-b a ，x 1x 2=c a． 二、填空题13．x2﹣5x ﹣7＝0【分析】利用多项式乘多项式的法则展开再利用等式的性质进行移项合并进行计算【详解】（x ＋1）（x ﹣3）＝3x ＋4x2﹣2x ﹣3＝3x ＋4x2﹣5x ﹣7＝0故答案是：x2﹣5x ﹣7＝0解析：x 2﹣5x ﹣7＝0 ．【分析】利用多项式乘多项式的法则展开，再利用等式的性质进行移项、合并，进行计算．【详解】（x ＋1）（x ﹣3）＝3x ＋4，x 2﹣2x ﹣3＝3x ＋4，x 2﹣5x ﹣7＝0．故答案是：x 2﹣5x ﹣7＝0．【点睛】本题考查一元二次方程的变形，属于基础题型．14．3【分析】设共有个班级参加比赛根据共有45场比赛列出方程求出方程的解即可得到结果【详解】解：设共有个班级参加比赛根据题意得：整理得：即解得：或（舍去）则共有3个班级球队参加比赛故答案为：3【点睛】此解析：3．【分析】设共有x 个班级参加比赛，根据共有45场比赛列出方程，求出方程的解即可得到结果．【详解】解：设共有x 个班级参加比赛， 根据题意得：(1)62x x -=， 整理得：260x x --=，即(3)(2)0x x -+=， 解得：3x =或2x =-（舍去）．则共有3个班级球队参加比赛．故答案为：3．【点睛】此题考查了一元二次方程的应用，解题的关键是找出等量关系“需安排6场比赛”． 15．-1【分析】根据方程的根的判别式得出m 的取值范围然后根据根与系数的关系可得α+β=-2（m-1）α•β=m2-m 结合α2+β2=12即可得出关于m 的一元二次方程解之即可得出结论【详解】解：∵关于x 的解析：-1【分析】根据方程的根的判别式，得出m 的取值范围，然后根据根与系数的关系可得α+β=-2（m-1），α•β=m 2-m ，结合α2+β2=12即可得出关于m 的一元二次方程，解之即可得出结论．【详解】解：∵关于x 的方程x 2+2（m-1）x+m 2-m=0有两个实数根，∴△=[2（m-1）]2-4×1×（m 2-m ）=-4m+4≥0，解得：m≤1．∵关于x 的方程x 2+2（m-1）x+m 2-m=0有两个实数根α，β，∴α+β=-2（m-1），α•β=m 2-m ，∴α2+β2=（α+β）2-2α•β=[-2（m-1）]2-2（m 2-m ）=12，即m 2-3m-4=0，解得：m=-1或m=4（舍去）．故答案为：-1．【点睛】本题考查了根与系数的关系、根的判别式以及解一元二次方程，解题的关键是：（1）牢记“当△≥0时，方程有两个实数根”；（2）根据根与系数的关系得出关于m 的一元二次方程．16．1（答案不唯一）【分析】根据非负数的性质可得于是只要使c 的值非负即可【详解】解：若关于的一元二次方程有实根则所以的值可以是1（答案不唯一）故答案为：1（答案不唯一）【点睛】本题考查了一元二次方程的解 解析：1（答案不唯一）【分析】根据非负数的性质可得0c ≥，于是只要使c 的值非负即可．【详解】解：若关于x 的一元二次方程()23x c -=有实根，则0c ≥，所以c 的值可以是1（答案不唯一）．故答案为：1（答案不唯一）．【点睛】本题考查了一元二次方程的解法，正确理解题意、掌握非负数的性质是关键． 17．且【分析】利用根的判别式b2-4ac 由于原方程有实数根那么判别式大于或等于零【详解】解：∵关于x 的方程有两个实数根且解得：且故答案为且【点睛】关于x 的方程有两个实数根（1）说明这是一个一元二次方程故解析：k 2≤且0k ≠【分析】利用根的判别式b 2-4ac .由于原方程有实数根，那么判别式大于或等于零.【详解】解：∵关于x 的方程2880kx x -+=有两个实数根，2(8)480k ∆=--⋅⋅≥，且0k ≠，解得：k 2≤且0k ≠，故答案为k 2≤且0k ≠，．【点睛】关于x 的方程有两个实数根，（1）说明这是一个一元二次方程，故“二次项系数不能为0”；（2）“根的判别式△的值要大于或等于0”；这两个条件要同时满足，解题时不要忽略了第一个条件.18．5【分析】直接根据根与系数的关系求出再代入求值即可【详解】解：∵x1x2是方程2x2-5x+1=0的两个根∴x1+x2=-∴故答案为：5【点睛】本题考查了根与系数的关系：若x1x2是一元二次方程ax解析：5【分析】直接根据根与系数的关系，求出12x x +，12x x 再代入求值即可．【详解】解：∵x 1，x 2是方程2x 2-5x+1=0的两个根，∴x 1+x 2=--55-=22，121=2x x ． ∴121252==512x x x x + 故答案为：5．【点睛】本题考查了根与系数的关系：若x 1，x 2是一元二次方程ax 2+bx+c=0（a≠0）的两根时，x 1+x 2=b a -，x 1x 2=c a． 19．3【分析】题中三个等式左右两边分别相加后再移项可以通过配方法得到三个平方数的和为0然后根据非负数的性质可以得到abc 的值从而求得a+b+c 的值【详解】解：题中三个等式左右两边分别相加可得：即∴∴a=解析：3【分析】题中三个等式左右两边分别相加后再移项，可以通过配方法得到三个平方数的和为0.然后根据非负数的性质可以得到a 、b 、c 的值，从而求得a+b+c 的值．【详解】解：题中三个等式左右两边分别相加可得：2222267117a b b c c a ++-+-=--，即222226110a b b c c a ++-+-+=，∴()()()2223110a b c -+++-=， ∴a=3,b=-1,c=1，∴a+b+c=3-1+1=3，故答案为3．【点睛】本题考查配方法的应用，熟练掌握配方法的方法和步骤并灵活运用是解题关键． 20．【分析】先根据完全平方公式将原式配方进而利用非负数的性质求出即可【详解】解：∵-4x2-4x+1=-(4x2+4x-1)=-(2x+1)2+2-(2x+1)2≤0∴当x=-时4x2-4x+1有最大值 解析：12- 【分析】先根据完全平方公式将原式配方，进而利用非负数的性质求出即可．【详解】解：∵-4x 2-4x+1=-(4x 2+4x-1)=-(2x+1)2+2，-(2x+1)2≤0，∴当x=-12时，4x 2-4x+1有最大值是2． 故答案为：-12． 【点睛】此题主要考查了配方法的应用以及非负数的性质，正确配方得出是解题关键．三、解答题21．（1）至少卖出仙女山红茶800盒；（2）a的值为5．【分析】（1）设卖出仙女山红茶x盒，则卖出桃片糕（2000-x）盒，由题意得关于x的不等式，求解即可；（2）根据（1）的结果得出桃片糕最多卖出的盒数，根据题意得出关于x的方程，解方程即可．【详解】解：（1）设卖出仙女山红茶x盒，则卖出桃片糕（2000-x）盒，由题意得：50x+12（2000-x）≥54400，解得：x≥800，∴x的最小值是800，∴至少卖出仙女山红茶800盒；（2）∵（1）中最少卖出仙女山红茶800盒，∴桃片糕最多卖出的盒数为：2000-800=1200（盒）．由题意得：12×（110%3a）×1200×（1+6a%）+50（1-4a%）×800×（1+4a%）=54400-80a，解得：a1=0（舍去），a2=5．∴a的值为5．【点睛】本题考查了一元一次不等式和一元二次方程在实际问题中的应用，理清题中的数量关系并正确列式是解题的关键．22．（1）见解析；（2）S1＞S2，见解析【分析】（1）利用配方法，将原式化成含平方代数式形式﹣（a﹣3）2﹣1，可判断其值为负数；（2）用a分别表示出S1与S2，再作差比较即可．【详解】解：（1）﹣a2+6a﹣10＝﹣（a2﹣6a+9）﹣1＝﹣（a﹣3）2﹣1，∵（a﹣3）2≥0，∴﹣（a﹣3）2≤0，∴﹣（a﹣3）2﹣1＜0，∴代数式﹣a2+6a﹣10的值一定是负数；（2）S1＞S2，理由是：∵S1＝a2，S2＝4（a﹣3），∴S1﹣S2＝a2﹣4（a﹣3）＝a2﹣4a+12＝a 2﹣4a+4+8＝（a ﹣2）2+8，∵（a ﹣2）2≥0，∴（a ﹣2）2+8≥8，∴S 1﹣S 2＞0，∴S 1＞S 2．【点睛】本题主要考查配方法的应用，掌握配方法是解题的关键，注意两数比较大小时可用作差法．23．m =5．【分析】先根据根与系数的关系求得x 1+x 2=6、x 1x 2=m +1，再对x 12+x 22=24变形，然后将x 1+x 2=6、x 1x 2=m +1代入得到关于m 的方程，最后求解即可．【详解】解：∵x 1，x 2是关于x 的一元二次方程x 2-6x +m +1=0的两根，∴x 1+x 2=6，x 1x 2=m +1，∴x 12+x 22=（x 1+x 2）2-2x 1x 2=24，∴62-2（m +1）=24，解得：m=5．【点睛】本题主要考查了一元二次方程根与系数的关系和完全平方公式的应用，正确应用完全平方公式成为解答本题的关键．24．（1）18000cm 3；（2）15cm【分析】（1）根据图中给出的信息，设四个相同的小正方形边长为x ，先表示出盒子的正方形底面的边长，然后根据底面积=900即可得到方程，求解即可；（2）该盒子的高为y ，根据底面积为800列出方程，解之即可．【详解】解：（1）设四个相同的小正方形边长为x ，由题意可得：（70-2x ）2=900，解得：x 1=20，x 2=50（舍），∴该盒子的容积为900×20=18000cm 3；（2）设该盒子的高为y ， 根据题意得：()7027028002y y -⨯-=， 解得：y 1=15，y 2=55（舍）， 因此当底面积是800平方厘米时，盒子的高是15厘米．【点睛】本题主要考查了一元二次方程的实际运用，只要搞清楚盒子底面各边的长和盒子的高的关系即可作出正确解答．25．x1=54，x2=23【分析】设m＝4x-5，n＝3x-2，则m-n＝（4x-5）-（3x-2）＝x-3，代入后求出mn＝0，即可得出（4x-5）（3x-2）＝0，求出即可．【详解】解：（4x-5）2+（3x-2）2＝（x-3）2，设m＝4x-5，n＝3x-2，则m-n＝（4x-5）-（3x-2）＝x-3，原方程化为：m2+n2＝（m-n）2，整理得：mn＝0，即（4x-5）（3x-2）＝0，∴4x-5＝0，3x-2＝0，∴x1=54，x2=23．【点睛】本题考查了解一元二次方程，能把一元二次方程转化成（4x-5）（3x-2）＝0是解此题的关键．26．（1）x1＝－4，x2＝2；（2）y1＝2，y2＝－3；（3）t1＝32，t2＝12-；（4）m1＝－3，m2＝5【分析】（1）根据因式分解法即可求解；（2）可以变形为：（2y＋1）2＝25，直接开方求解（3）常数项移到右边，两边加上一次项系数一半的平方，开方即可求出解；（4）先移项，使方程右边为零，然后将方程左边进行因式分解，使分解后的两个一次因式分别为零，即可解答．【详解】（1）x2+2x-8＝0，（x+4）（x-2）＝0，则x+4＝0或x-2＝0，解得x＝-4或x＝2(2) （2y＋1）2－25＝0；(2y+1)2=25，∴2y+1=±5，∴y1=2,y2=-3；(3)24430t t--=；4t2−4t=3，4t2−4t+1=3+1，(2t−1)2=4，∴2t−1=±2，∴t1=32 ,t2=12（4）2（m＋3）＝m2－92（m＋3）-（m＋3）（m-3）＝0（m＋3）(2-m+3)=0∴m+3=0或5−m=0，∴m1=-3,m2=5．【点睛】此题考查解一元二次方程-直接开平方法，解一元二次方程-配方法，解一元二次方程-因式分解法，解题关键在于掌握运算法则．。
九年级数学一元二次方程易错题(Word版 含答案)
九年级数学一元二次方程易错题（Word 版 含答案）一、初三数学 一元二次方程易错题压轴题（难）1．如图，在四边形ABCD 中，9054ABC BCD AB BC cm CD cm ∠=∠=︒===，，点P 从点C 出发以1/cm s 的速度沿CB 向点B 匀速移动，点M 从点A 出发以15/cm s 的速度沿AB 向点B 匀速移动，点N 从点D 出发以/acm s 的速度沿DC 向点C 匀速移动．点P M N 、、同时出发，当其中一个点到达终点时，其他两个点也随之停止运动，设移动时间为ts ．（1）如图①，①当a 为何值时，点P B M 、、为顶点的三角形与PCN △全等?并求出相应的t 的值； ②连接AP BD 、交于点E ，当AP BD ⊥时，求出t 的值；（2）如图②，连接AN MD 、交于点F ．当3883a t ==，时，证明：ADF CDF S S ∆∆=．【答案】（1）① 2.5t =， 1.1a =或2t =，0.5a =；②1t =；（2）见解析【解析】【分析】（1）①当PBM PCN ≅△△时或当MBP PCN ≅△△时，分别列出方程即可解决问题； ②当AP BD ⊥时，由ABP BCD ≅△△，推出BP CD =，列出方程即可解决问题； （2）如图②中，连接AC 交MD 于O 只要证明AOM COD ≅△△，推出OA OC =，可得ADO CDO S S ∆∆=，AFO CFO S S ∆∆=，推出ADO AFO CDO CFO S S S S ∆∆∆∆-=-，即ADF CDF S S ∆∆=；【详解】解：（1）①90ABC BCD ∠=∠=︒，∴当PBM PCN ≅△△时，有BM NC =，即5t t -=①5 1.54t at -=-②由①②可得 1.1a =， 2.5t =．当MBP PCN ≅△△时，有BM PC =，BP NC =，即5 1.5t t -=③54t at -=-④，由③④可得0.5a =，2t =．综上所述，当 1.1a =， 2.5t =或0.5a =，2t =时，以P 、B 、M 为顶点的三角形与PCN △全等；②AP BD ⊥，90BEP ∴∠=︒，90APB CBD ∴∠+∠=︒，90ABC ∠=︒，90APB BAP ∴∠+∠=︒，BAP CBD ∴∠=∠，在ABP △和BCD 中，BAP CBD AB BCABC BCD ∠=∠⎧⎪=⎨⎪∠=∠⎩， ()ABP BCD ASA ∴≅△△，BP CD ∴=，即54t -=，1t ∴=；（2）当38a =，83t =时，1DN at ==，而4CD =， DN CD ∴<，∴点N 在点C 、D 之间，1.54AM t ==，4CD =，AM CD ∴=，如图②中，连接AC 交MD 于O ，90ABC BCD ∠=∠=︒，180ABC BCD ∴∠+∠=︒，//AB BC ∴，AMD CDM ∴∠=∠，BAC DCA ∠=∠，在AOM 和COD △中，AMD CDM AM CDBAC DCA ∠=∠⎧⎪=⎨⎪∠=∠⎩， ()AOM COD ASA ∴≅△△，OA OC ∴=，ADO CDO S S ∆∆∴=，AFO CFO S S ∆∆=，ADO AFO CDO CFO S S S S ∆∆∆∆∴-=-，ADF CDF S S ∆∆∴=．【点睛】本题考查三角形综合题、全等三角形的判定和性质、等高模型等知识，解题的关键是灵活运用所学知识解决问题，学会用分类讨论的思想思考问题，属于中考压轴题．2．某中心城市有一楼盘，开发商准备以每平方米7000元价格出售，由于国家出台了有关调控房地产的政策，开发商经过两次下调销售价格后，决定以每平方米5670元的价格销售．（1）求平均每次下调的百分率；（2）房产销售经理向开发商建议：先公布下调5%，再下调15%，这样更有吸引力，请问房产销售经理的方案对购房者是否更优惠？为什么？【答案】（1）平均每次下调的百分率为10%．（2）房产销售经理的方案对购房者更优惠．【解析】【分析】（1）根据利用一元二次方程解决增长率问题的要求，设出未知数，然后列方程求解即可；（2）分别求出两种方式的增长率，然后比较即可.【详解】（1）设平均每次下调x%，则7000（1﹣x）2=5670，解得：x1=10%，x2=190%（不合题意，舍去）；答：平均每次下调的百分率为10%．（2）（1﹣5%）×（1﹣15%）=95%×85%=80.75%，（1﹣x）2=（1﹣10%）2=81%．∵80.75%＜81%，∴房产销售经理的方案对购房者更优惠．3．（1）课本情境:如图，已知矩形AOBC，AB＝6cm，BC＝16cm，动点P从点A出发，以3cm/s的速度向点O运动，直到点O为止；动点Q同时从点C出发，以2cm/s的速度向点B运动，与点P同时结束运动，出发时，点P和点Q之间的距离是10cm；（2）逆向发散:当运动时间为2s时，P，Q两点的距离为多少？当运动时间为4s时，P，Q 两点的距离为多少？（3）拓展应用：若点P沿着AO→OC→CB移动，点P，Q分别从A，C同时出发，点Q从点C移动到点B停止时，点P随点Q的停止而停止移动，求经过多长时间△POQ的面积为12cm2？【答案】（1）85s或245s（2）62cm；213cm（3）4s或6s【解析】【分析】(1)过点P作PE⊥BC于E，得到AP＝3t，CQ＝2t，PE＝6，EQ＝16﹣3t﹣2t＝16﹣5t，利用勾股定理得到方程，故可求解；（2）根据运动时间求出EQ、PE，利用勾股定理即可求解；(3) 分当点P在AO上时，当点P在OC上时和当点P在CB上时，根据三角形的面积公式列出方程即可求解．【详解】解：（1）设运动时间为t秒时，如图，过点P作PE⊥BC于E，由运动知，AP＝3t，CQ＝2t，PE＝6，EQ＝16﹣3t﹣2t＝16﹣5t，∵点P和点Q之间的距离是10 cm，∴62+（16﹣5t）2＝100，解得t1=85，t2=245，∴t＝85s或245s.故答案为85s或245s（2）t=2时，由运动知AP＝3×2＝6 cm，CQ＝2×2＝4 cm，∴四边形APEB是矩形，∴PE＝AB＝6，BE＝6，∴EQ＝BC﹣BE﹣CQ＝16﹣6﹣4＝6，根据勾股定理得PQ=2262PE EQ +=,∴当t ＝2 s 时，P ，Q 两点的距离为62 cm ；当t ＝4 s 时，由运动知AP ＝3×4＝12 cm ，CQ ＝2×4＝8cm ， ∴四边形APEB 是矩形，∴PE ＝AB ＝6，BQ ＝8，CE=OP=4∴EQ ＝BC ﹣CE ﹣BQ ＝16﹣4﹣8＝4，根据勾股定理得PQ=22213PE EQ +=,P ，Q 两点的距离为213cm .（3）点Q 从C 点移动到B 点所花的时间为16÷2=8s ，当点P 在AO 上时，S △POQ ＝2PO CO ⋅＝(163)62t -⋅＝12， 解得t ＝4．当点P 在OC 上时，S △POQ ＝2PO CQ ⋅＝(316)22t t -⋅＝12， 解得t ＝6或﹣23（舍弃）． 当点P 在CB 上时，S △POQ ＝2PQ CO ⋅＝(2223)62t t +-⨯＝12， 解得t ＝18＞8（不符合题意舍弃），综上所述，经过4 s 或6 s 时，△POQ 的面积为12 cm 2．【点睛】此题主要考查勾股定理的应用、一元二次方程与动点问题，解题的关键是熟知勾股定理的应用，根据三角形的面积公式找到等量关系列出方程求解．4．阅读以下材料，并解决相应问题：材料一：换元法是数学中的重要方法，利用换元法可以从形式上简化式子，在求解某些特殊方程时，利用换元法常常可以达到转化的目的，例如在求解一元四次方程42210x x -+=，就可以令21x =，则原方程就被换元成2210t t -+=，解得 t = 1，即21x =，从而得到原方程的解是 x = ±1材料二：杨辉三角形是中国数学上一个伟大成就，在中国南宋数学家杨辉 1261 年所著的《详解九章算法》一书中出现，它呈现了某些特定系数在三角形中的一种有规律的几何排列，下图为杨辉三角形：……………………………………（1）利用换元法解方程：()()222312313+-++-=x x x x（2）在杨辉三角形中，按照自上而下、从左往右的顺序观察， an 表示第 n 行第 2 个数（其中 n≥4），bn 表示第 n 行第 3 个数，n c 表示第(n )1-行第 3 个数，请用换元法因式分解：()41-⋅+n n n b a c【答案】（1）3172x -+=或3172x -= 或x=-1或x=-2；（2）()41-⋅+n n n b a c =（n 2-5n+5）2【解析】【分析】（1）设t=x 2+3x-1，则原方程可化为：t 2+2t=3，求得t 的值再代回可求得方程的解； （2）根据杨辉三角形的特点得出a n ，b n ，c n ，然后代入4（b n -a n ）•c n +1再因式分解即可．【详解】（1）解：令t=x 2+3x-1则原方程为：t 2+2t=3解得：t=1 或者 t=-3当t=1时，x 2+3x-1=1 解得：3172x -+= 或3172x -= 当t=-3时，x 2+3x-1=-3解得：x=-1或x=-2 ∴方程的解为：3172x -+= 或3172x -= 或x=-1或x=-2 （2）解：根据杨辉三角形的特点得出：a n =n-1(1)(2)2n n n b --= (2)(3)2n n n c --= ∴4（b n -a n ）•c n +1=（n-1）（n-4）（n-2）（n-3）+1=（n 2-5n+4）（n 2-5n+6）+1=（n2-5n+4）2+2（n2-5n+4）+1=（n2-5n+5）2【点睛】本题主要考查因式分解的应用．解一些复杂的因式分解问题，常用到换元法，即对结构比较复杂的多项式，若把其中某些部分看成一个整体，用新字母代替（即换元），则能使复杂的问题简单化，明朗化，在减少多项式项数，降低多项式结构复杂程度等方面有独到作用．5．随着经济收入的不断提高以及汽车业的快速发展，家用汽车已越来越多地进入普通家庭，汽车消费成为新亮点．抽样调查显示，截止2008年底全市汽车拥有量为14.4万辆．已知2006年底全市汽车拥有量为10万辆．（1）求2006年底至2008年底我市汽车拥有量的年平均增长率；（2）为保护城市环境，要求我市到2010年底汽车拥有量不超过15.464万辆，据估计从2008年底起，此后每年报废的汽车数量是上年底汽车拥有量的10%，那么每年新增汽车数量最多不超过多少辆？（假定每年新增汽车数量相同）【答案】详见解析【解析】试题分析：（1）主要考查增长率问题，一般用增长后的量=增长前的量×（1+增长率）解决问题；（2）参照增长率问题的一般规律，表示出2010年的汽车拥有量，然后根据关键语列出不等式来判断正确的解．试题解析：（1）设年平均增长率为x，根据题意得：10（1+x）2=14.4，解得x=﹣2.2（不合题意舍去）x=0.2，答：年平均增长率为20%；（2）设每年新增汽车数量最多不超过y万辆，根据题意得：2009年底汽车数量为14.4×90%+y，2010年底汽车数量为（14.4×90%+y）×90%+y，∴（14.4×90%+y）×90%+y≤15.464，∴y≤2．答：每年新增汽车数量最多不超过2万辆．考点：一元二次方程—增长率的问题6．机械加工需用油进行润滑以减小摩擦，某企业加工一台设备润滑用油量为90kg，用油的重复利用率为60%，按此计算，加工一台设备的实际耗油量为36kg，为了倡导低碳，减少油耗，该企业的甲、乙两个车间都组织了人员为减少实际油耗量进行攻关．（1）甲车间通过技术革新后，加工一台设备润滑油用油量下降到70kg，用油的重复利用率仍然为60%，问甲车间技术革新后，加工一台设备的实际油耗量是多少千克？（2）乙车间通过技术革新后，不仅降低了润滑油用油量，同时也提高了用油的重复利用率，并且发现在技术革新前的基础上，润滑用油量每减少1kg，用油的重复利用率将增加1.6%，例如润滑用油量为89kg 时，用油的重复利用率为61.6%．①润滑用油量为80kg ，用油量的重复利用率为多少？②已知乙车间技术革新后实际耗油量下降到12kg ，问加工一台设备的润滑用油量是多少千克？用油的重复利用率是多少？【答案】（1）28（2）①76%②75，84%【解析】试题分析：（1）直接利用加工一台设备润滑油用油量下降到70kg ，用油的重复利用率仍然为60%，进而得出答案；（2）①利用润滑用油量每减少1kg ，用油的重复利用率将增加1.6%，进而求出答案； ②首先表示出用油的重复利用率，进而利用乙车间技术革新后实际耗油量下降到12kg ，得出等式求出答案．试题解析：（1）根据题意可得：70×（1﹣60%）=28（kg ）；（2）①60%+1.6%（90﹣80）=76%；②设润滑用油量是x 千克，则x{1﹣[60%+1.6%（90﹣x ）]}=12，整理得：x 2﹣65x ﹣750=0，（x ﹣75）（x+10）=0，解得：x 1=75，x 2=﹣10（舍去），60%+1.6%（90﹣x ）=84%，答：设备的润滑用油量是75千克，用油的重复利用率是84%．考点：一元二次方程的应用7．已知关于x 的二次函数22(21)1y x k x k =--++的图象与x 轴有2个交点.（1）求k 的取值范围；（2）若图象与x 轴交点的横坐标为12,x x ，且它们的倒数之和是32-，求k 的值. 【答案】（1）k ＜-34 ；（2）k=﹣1 【解析】试题分析：（1）根据交点得个数，让y=0判断出两个不相等的实数根，然后根据判别式△= b 2-4ac 的范围可求解出k 的值；（2）利用y=0时的方程，根据一元二次方程的根与系数的关系，可直接列式求解可得到k 的值.试题解析：（1）∵二次函数y=x 2-（2k-1）x+k 2+1的图象与x 轴有两交点，∴当y=0时，x 2-（2k-1）x+k 2+1=0有两个不相等的实数根．∴△=b 2-4ac=[-（2k-1）]2-4×1×（k 2+1）＞0．解得k ＜-34； （2）当y=0时，x 2-（2k-1）x+k 2+1=0．则x 1+x 2=2k-1，x 1•x 2=k 2+1，∵=== 32-， 解得：k=-1或k= 13-（舍去），∴k=﹣18．已知关于x 的一元二次方程x 2﹣x +a ﹣1=0．（1）当a=﹣11时，解这个方程；（2）若这个方程有两个实数根x 1，x 2，求a 的取值范围；（3）若方程两个实数根x 1，x 2满足[2+x 1（1﹣x 1）][2+x 2（1﹣x 2）]=9，求a 的值．【答案】（1）123,4x x =-=（2）54a ≤（3）-4 【解析】【分析】（1）根据一元二次方程的解法即可求出答案；（2）根据判别式即可求出a 的范围；（3）根据根与系数的关系即可求出答案．【详解】（1）把a =﹣11代入方程，得x 2﹣x ﹣12=0，（x +3）（x ﹣4）=0，x +3=0或x ﹣4=0，∴x 1=﹣3，x 2=4；（2）∵方程有两个实数根12x x ，，∴△≥0，即（﹣1）2﹣4×1×（a ﹣1）≥0，解得54a ≤：； （3）∵12x x ，是方程的两个实数根，222211221122101011x x a x x a x x a x x a -+-=-+-=∴-=--=-，，，． ∵[2+x 1（1﹣x 1）][2+x 2（1﹣x 2）]=9，∴221122229x x x x ⎡⎤⎡⎤+-+-=⎣⎦⎣⎦，把22112211x x a x x a -=--=-，代入，得：[2+a ﹣1][2+a ﹣1]=9，即（1+a ）2=9，解得：a =﹣4，a =2（舍去），所以a 的值为﹣4．点睛：本题考查了一元二次方程，解题的关键是熟练运用判别式以及根与系数的关系．9．如图，抛物线y=ax 2+bx+c 与x 轴交于点A 和点B （1，0），与y 轴交于点C （0，3），其对称轴l为x=﹣1．（1）求抛物线的解析式并写出其顶点坐标；（2）若动点P在第二象限内的抛物线上，动点N在对称轴l上．①当PA⊥NA，且PA=NA时，求此时点P的坐标；②当四边形PABC的面积最大时，求四边形PABC面积的最大值及此时点P的坐标．【答案】（1）y=﹣（x+1）2+4，顶点坐标为（﹣1，4）；（2）①点P2﹣1，2）；②P（﹣32，154）【解析】试题分析：（1）将B、C的坐标代入已知的抛物线的解析式，由对称轴为1x=-即可得到抛物线的解析式；（2）①首先求得抛物线与x轴的交点坐标，然后根据已知条件得到PD=OA，从而得到方程求得x的值即可求得点P的坐标；②ΔOBCΔAPDABCP C=PDOS S S S++四边形梯形，表示出来得到二次函数，求得最值即可．试题解析：（1）∵抛物线2y ax bx c=++与x轴交于点A和点B（1，0），与y轴交于点C（0，3），其对称轴l为1x=-，∴{312a b ccba++==-=-，解得：1{23abc=-=-=，∴二次函数的解析式为223y x x=--+=2(1)4x-++，∴顶点坐标为（﹣1，4）；（2）令2230y x x=--+=，解得3x=-或1x=，∴点A（﹣3，0），B（1，0），作PD⊥x轴于点D，∵点P在223y x x=--+上，∴设点P（x，223x x--+），①∵PA⊥NA，且PA=NA，∴△PAD≌△AND，∴OA=PD，即2232y x x=--+=，解得21（舍去）或x=21-，∴点P（21-，2）；②设P(x，y)，则223y x x=--+，∵ΔOBCΔAPDABCP C=PDOS S S S++四边形梯形=12OB•OC+12AD•PD+12(PD+OC)•OD=11131+(3)(3)()222x y y x⨯⨯⨯+++-=333222x y-+=2333(23)222x x x -+--+=239622x x --+=23375()228x -++， ∴当x=32-时，ABCP S 四边形最大值=758，当x=32-时，223y x x =--+=154，此时P （32-，154）．考点：1．二次函数综合题；2．二次函数的最值；3．最值问题；4．压轴题．10．已知：如图，在平面直角坐标系中，矩形AOBC 的顶点C 的坐标是（6，4），动点P 从点A 出发，以每秒1个单位的速度沿线段AC 运动，同时动点Q 从点B 出发，以每秒2个单位的速度沿线段BO 运动，当Q 到达O 点时，P ，Q 同时停止运动，运动时间是t 秒（t ＞0）．（1）如图1，当时间t ＝ 秒时，四边形APQO 是矩形；（2）如图2，在P ，Q 运动过程中，当PQ ＝5时，时间t 等于 秒；（3）如图3，当P ，Q 运动到图中位置时，将矩形沿PQ 折叠，点A ，O 的对应点分别是D ，E ，连接OP ，OE ，此时∠POE ＝45°，连接PE ，求直线OE 的函数表达式．【答案】（1）t ＝2；（2）1或3；（3）y ＝12x ． 【解析】【分析】 先根据题意用t 表示AP 、BQ 、PC 、OQ 的长．（1）由四边形APQO 是矩形可得AP ＝OQ ，列得方程即可求出t ．（2）过点P 作x 轴的垂线PH ，构造直角△PQH ，求得HQ 的值．由点H 、Q 位置不同分两种情况讨论用t 表示HQ ，即列得方程求出t ．根据t 的取值范围考虑t 的合理性． （3）由轴对称性质，对称轴PQ 垂直平分对应点连线OC ，得OP ＝PE ，QE ＝OQ ．由∠POE ＝45°可得△OPE 是等腰直角三角形，∠OPE ＝90°，即点E 在矩形AOBC 内部，无须分类讨论．要求点E坐标故过点E作x轴垂线MN，易证△MPE≌△AOP，由对应边相等可用t表示EN，QN．在直角△ENQ中利用勾股定理为等量关系列方程即求出t．【详解】∵矩形AOBC中，C（6，4）∴OB＝AC＝6，BC＝OA＝4依题意得：AP＝t，BQ＝2t（0＜t≤3）∴PC＝AC﹣AP＝6﹣t，OQ＝OB﹣BQ＝6﹣2t（1）∵四边形APQO是矩形∴AP＝OQ∴t＝6﹣2t解得：t＝2故答案为2．（2）过点P作PH⊥x轴于点H∴四边形APHO是矩形∴PH＝OA＝4，OH＝AP＝t，∠PHQ＝90°∵PQ＝5=∴HQ3①如图1，若点H在点Q左侧，则HQ＝OQ﹣OH＝6﹣3t∴6﹣3t＝3解得：t＝1②如图2，若点H在点Q右侧，则HQ＝OH﹣OQ＝3t﹣6∴3t﹣6＝3解得：t＝3故答案为1或3．（3）过点E作MN⊥x轴于点N，交AC于点M∴四边形AMNO是矩形∴MN＝OA＝4，ON＝AM∵矩形沿PQ折叠，点A，O的对应点分别是D，E∴PQ垂直平分OE∴EQ＝OQ＝6﹣2t，PO＝PE∵∠POE＝45°∴∠PEO＝∠POE＝45°∴∠OPE＝90°，点E在矩形AOBC内部∴∠APO+∠MPE＝∠APO+∠AOP＝90°∴∠MPE＝∠AOP在△MPE与△AOP中PME OAP90 MPE AOPPE0P︒⎧∠=∠=⎪∠=∠⎨⎪=⎩∴△MPE≌△AOP（AAS）∴PM＝OA＝4，ME＝AP＝t∴ON＝AM＝AP+PM＝t+4，EN＝MN﹣ME＝4﹣t∴QN＝ON﹣OQ＝t+4﹣（6﹣2t）＝3t﹣2∵在Rt△ENQ中，EN2+QN2＝EQ2∴（4﹣t）2+（3t﹣2）2＝（6﹣2t）2解得：t1＝﹣2（舍去），t2＝43∴AM＝43+4＝163，EN＝4﹣43＝83∴点E坐标为（163，83）∴直线OE的函数表达式为y＝12x．【点睛】本题考查了矩形的判定和性质，勾股定理，轴对称的性质，全等三角形的判定和性质，解一元一次和一元二次方程．在动点题中要求运动时间t的值，常规做法是用t表示相关线段，再利用线段相等或勾股定理作为等量关系列方程求值．要注意根据t的取值范围考虑方程的解的合理性．。
人教版九年级上册数学 一元二次方程易错题(Word版 含答案)
人教版九年级上册数学一元二次方程易错题（Word版含答案）一、初三数学一元二次方程易错题压轴题（难）1．Rt△ABC中，∠ACB＝90°，AC＝BC＝6，动点P从点A出发，在线段AC上以每秒1个单位长度的速度向点C作匀速运动，到达点C停止运动．设运动时间为t秒（1）如图1，过点P作PD⊥AC，交AB于D，若△PBC与△PAD的面积和是△ABC的面积的79，求t的值；（2）点Q在射线PC上，且PQ＝2AP，以线段PQ为边向上作正方形PQNM．在运动过程中，若设正方形PQNM与△ABC重叠部分的面积为8，求t的值．【答案】（1）t1＝2，t2＝4；（2）t 47758．【解析】【分析】（1）先求出△ABC的面积，然后根据题意可得AP＝t，CP＝6﹣t，然后再△PBC与△PAD的面积和是△ABC的面积的79，列出方程、解方程即可解答；（2）根据不同时间段分三种情况进行解答即可.【详解】（1）∵Rt△ABC中，∠ACB＝90°，AC＝BC＝6，∴S△ABC＝12×6×6＝18，∵AP＝t，CP＝6﹣t，∴△PBC与△PAD的面积和＝12t2+12×6×（6﹣t），∵△PBC与△PAD的面积和是△ABC的面积的79，∴12t2+12×6×（6﹣t）＝18×79，解之，得t1＝2，t2＝4；（2）∵AP＝t，PQ＝2AP，∴PQ＝2t，①如图1，当0≤t≤2时，S＝（2t）2﹣12t2＝72t2＝8，解得：t1＝477，t2＝﹣477（不合题意，舍去），②如图2，当2≤t≤3时，S＝12×6×6﹣12t2﹣12（6﹣2t）2＝12t﹣25t2＝8，解得：t1＝4（不合题意，舍去），t2＝45（不合题意，舍去），③如图3，当3≤t≤6时，S＝126×6﹣12t2＝8，解得：t1＝25，t2＝﹣25（不合题意，舍去），综上，t的值为477或25时，重叠面积为8．【点睛】本题考查了三角形和矩形上的动点问题，根据题意列出方程和分情况讨论是解答本题的关键.2．阅读与应用：阅读1：a，b为实数，且a＞0，b＞0，因为()2≥0，所以a﹣2+b≥0，从而a+b≥2(当a＝b时取等号)．阅读2：若函数y＝x+(m＞0，x＞0，m为常数)，由阅读1结论可知：x+≥2，所以当x＝，即x＝时，函数y＝x+的最小值为2．阅读理解上述内容，解答下列问题：问题1：已知一个矩形的面积为4，其中一边长为x，则另一边长为，周长为2(x+)，求当x＝时，周长的最小值为；问题2：汽车的经济时速是汽车最省油的行驶速度，某种汽车在每小时70～110公里之间行驶时(含70公里和110公里)，每公里耗油()L ．若该汽车以每小时x 公里的速度匀速行驶，1h 的耗油量为yL ．(1)求y 关于x 的函数关系式(写出自变量x 的取值范围)； (2)求该汽车的经济时速及经济时速的百公里耗油量． 【答案】问题1：2，8；问题2：(1)y=；(2)10.【解析】 【分析】（1）利用题中的不等式得到x+=4，从而得到x=2时，周长的最小值为8；（2）根据耗油总量=每公里的耗油量×行驶的速度列出函数关系式即可，经济时速就是耗油量最小的形式速度． 【详解】 (1)∵x +≥2＝4，∴当x ＝ 时，2(x +)有最小值8． 即x ＝2时，周长的最小值为8； 故答案是：2；8； 问题2：，当且仅当，即x ＝90时，“＝”成立，所以，当x ＝90时，函数取得最小值9， 此时，百公里耗油量为，所以，该汽车的经济时速为每小时90公里，经济时速的百公里耗油量为10L ． 【点睛】本题考查了配方法及反比例函数的应用，最值问题，解题的关键是读懂题目提供的材料，易错点是了解“耗油总量=每公里的耗油量×行驶的速度”，难度中等偏上．3．问题提出：（1）如图1，在四边形ABCD 中，已知：AD BC ∥，90D ∠=︒，4BC =，ABC 的面积为8，求BC 边上的高． 问题探究（2）如图2在（1）的条件下，点E 是CD 边上一点，且2CE =，EAB CBA =∠∠，连接BE ，求ABE △的面积 问题解决（3）如图3，在（1）的条件下，点E 是CD 边上任意一点，连接AE 、BE ，若EAB CBA =∠∠，ABE △的面积是否存在最小值；若存在，求出最小值；若不存在；请说明理由．【答案】（1）4；（2）203；（3）存在，最小值为16216- 【解析】 【分析】（1）作BC 边上的高AM ，利用三角形面积公式即可求解；（2）延长DA ，过B 点作BF ⊥DA 于点F ，作BH ⊥AE 于点H ，易得四边形BCDF 为矩形，在（1）的条件下BC=CD=4，则BCDF 为正方形，由EAB CBA =∠∠，结合∠FAB=∠CBA 可得∠FAB=∠EAB ，从而推出BF=BH=4，易证Rt △BCE ≌Rt △BHE ，所以EH=CE=2，设AD ＝a ，则AF=AH=4-a ，在Rt △ADE 中利用勾股定理建立方程可求出a ，最后根据S △ABE =1AE BH 2即可求解； （3）辅助线同（2），设AD=a ，CE=m ，则DE=4-m ，同（2）可得出m 与a 的关系式，设△ABE 的面积为y ，由y=1AE BH 2得到m 与y 的关系式，再求y 的最小值即可． 【详解】（1）如图所示，作BC 边上的高AM ，∵S △ABC =1BC AM=82∴82AM==44⨯ 即BC 边上的高为4；（2）如图所示，延长DA ，过B 点作BF ⊥DA 于点F ，作BH ⊥AE 于点H ，∵AD BC ∥，90D ∠=︒ ∴∠BCD=∠D=90°=∠F ∴四边形BCDF 为矩形， 又∵BC=CD=4∴四边形BCDF 为正方形， ∴DF=BF=BC=4， 又∵AD ∥BC ∴∠FAB=∠CBA 又∵∠EAB=∠CBA ∴∠FAB=∠EAB ∵BF ⊥AF ，BH ⊥AE ∴BH=BF=4，在Rt △BCE 和Rt △BHE 中， ∵BE=BE ，BH=BC=4 ∴Rt △BCE ≌Rt △BHE （HL ） ∴EH=CE=2同理可证Rt △BAF ≌Rt △BAH （HL ） ∴AF=AH设AD=a ，则AF=AH=4-a在Rt △ADE 中，AD=a ，DE=2，AE=AH+EH=4-a+2=6-a 由勾股定理得AD 2+DE 2=AE 2，即()22226+=-a a解得8=3a∴AE=6-a=103S △ABE =111020AE BH=4=2233⨯⨯ （3）存在，如图所示，延长DA ，过B 点作BF ⊥DA 于点F ，作BH ⊥AE 于点H ，同（2）可得CE=EH ，AF=AH ，设AD=a ，CE=EH=m ，则DE=4-m ，AF=AH=4-a在Rt △ADE 中，AD 2+DE 2=AE 2，即()()22244+-=-+a m a m 整理得8=4+ma m ∴AE=AH+HE=2816444+-+=++m m m m m设△ABE 的面积为y ，则y=()222161116AE BH=42244++=++m m m m ∴()()24216+=+y m m整理得：223240++-=m ym y ∵方程必有实数根∴()2=423240∆-⨯⨯-≥y y整理得2322560+-≥y y∴()()16216162160⎡⎤⎡⎤-----≥⎣⎦⎣⎦y y （注：利用求根公式进行因式分解）又∵面积y ≥0 ∴16216≥-y即△ABE 的面积最小值为16216-． 【点睛】本题考查四边形综合问题，正确作出辅助线，得出AB 平分∠FAC ，利用角平分线的性质定理得到BF=BH ，结合勾股定理求出AE 是解决（2）题的关键，（3）题中利用一元二次方程的判别式求最值是解题的关键．4．阅读下列材料 计算：（1﹣﹣）×（+）﹣（1﹣﹣）（+），令+＝t ，则：原式＝（1﹣t）（t+）﹣（1﹣t﹣）t＝t+﹣t2﹣+t2＝在上面的问题中，用一个字母代表式子中的某一部分，能达到简化计算的目的，这种思想方法叫做“换元法”，请用“换元法”解决下列问题：（1）计算：（1﹣﹣）×（+）﹣（1﹣﹣）×（+）（2）因式分解：（a2﹣5a+3）（a2﹣5a+7）+4（3）解方程：（x2+4x+1）（x2+4x+3）＝3【答案】（1）；（2）（a2﹣5a+5）2；（3）x1＝0，x2＝﹣4，x3＝x4＝﹣2【解析】【分析】（1）仿照材料内容，令+＝t代入原式计算．（2）观察式子找相同部分进行换元，令a2﹣5a＝t代入原式进行因式分解，最后要记得把t换为a．（3）观察式子找相同部分进行换元，令x2+4x＝t代入原方程，即得到关于t的一元二次方程，得到t的两个解后要代回去求出4个x的解．【详解】（1）令+＝t，则：原式＝（1﹣t）（t+）﹣（1﹣t﹣）t＝t+﹣t2﹣﹣t+t2+＝（2）令a2﹣5a＝t，则：原式＝（t+3）（t+7）+4＝t2+7t+3t+21+4＝t2+10t+25＝（t+5）2＝（a2﹣5a+5）2（3）令x2+4x＝t，则原方程转化为：（t+1）（t+3）＝3t2+4t+3＝3t（t+4）＝0∴t1＝0，t2＝﹣4当x2+4x＝0时，x（x+4）＝0解得：x1＝0，x2＝﹣4当x2+4x＝﹣4时，x2+4x+4＝0（x+2）2＝0解得：x3＝x4＝﹣2【点睛】本题考查用换元法进行整式的运算，因式分解，解一元二次方程．利用换元法一般可达到降次效果，从而简便运算．5．已知关于x的一元二次方程（x﹣3）（x﹣4）﹣m2=0．（1）求证：对任意实数m，方程总有2个不相等的实数根；（2）若方程的一个根是2，求m的值及方程的另一个根．【答案】（1）证明见解析；（2）m的值为±2，方程的另一个根是5．【解析】【分析】（1）先把方程化为一般式，利用根的判别式△=b2-4ac证明判断即可；（2）根据方程的根，利用代入法即可求解m的值，然后还原方程求出另一个解即可.【详解】（1）证明：∵（x﹣3）（x﹣4）﹣m2=0，∴x2﹣7x+12﹣m2=0，∴△=（﹣7）2﹣4（12﹣m2）=1+4m2，∵m2≥0，∴△＞0，∴对任意实数m，方程总有2个不相等的实数根；（2）解：∵方程的一个根是2，∴4﹣14+12﹣m2=0，解得m=±，∴原方程为x2﹣7x+10=0，解得x=2或x=5，即m的值为±，方程的另一个根是5．【点睛】此题主要考查了一元二次方程根的判别式，熟练掌握一元二次方程的根的判别式与根的关系是关键.当△=b2-4ac＞0时，方程有两个不相等的实数根；当△=b2-4ac=0时，方程有两个相等的实数根；当△=b2-4ac＜0时，方程没有实数根.6．如图，已知AB是⊙O的弦，半径OA=2，OA和AB的长度是关于x的一元二次方程x2﹣4x+a=0的两个实数根．（1）求弦AB的长度；（2）计算S△AOB；（3）⊙O上一动点P从A点出发，沿逆时针方向运动一周，当S△POA=S△AOB时，求P点所经过的弧长（不考虑点P与点B重合的情形）．【答案】（1）AB=2；（2）S △AOB 33）当S △POA =S △AOB 时，P 点所经过的弧长分别是43π、83π、103π． 【解析】试题分析：（1）OA 和AB 的长度是一元二次方程的根，所以利用一元二次方程的根与系数的关系即可求出AB 的长度；（2）作出△AOB 的高OC ，然后求出OC 的长度即可求出面积； （3）由题意知：两三角形有公共的底边，要面积相等，即高要相等． 试题解析：（1）由题意知：OA 和AB 的长度是x 2﹣4x+a=0的两个实数根， ∴OA+AB=﹣41-=4， ∵OA=2， ∴AB=2；（2）过点C 作OC⊥AB 于点C ，∵OA=AB=OB=2，∴△AOB 是等边三角形，∴AC=12AB=1， 在Rt△ACO 中，由勾股定理可得：3△AOB =12AB ﹒OC=1233； （3）延长AO 交⊙O 于点D ，由于△AOB 与△POA 有公共边OA ， 当S △POA =S △AOB 时，∴△AOB 与△POA 高相等，由（2）可知：等边△AOB 3P 到直线OA 3，这样点共有3个 ①过点B 作BP 1∥OA 交⊙O 于点P 1，∴∠BOP 1=60°， ∴此时点P 经过的弧长为：1202180π⨯=43π， ②作点P 2，使得P 1与P 2关于直线OA 对称，∴∠P 2OD=60°， ∴此时点P 经过的弧长为：2402180π⨯=83π， ③作点P 3，使得B 与P 3关于直线OA 对称，∴∠P 3OP 2=60°， ∴此时P 经过的弧长为：3002180π⨯ =103π， 综上所述：当S △POA =S △AOB 时，P 点所经过的弧长分别是43π、83π、103π．【点睛】本题主要考查了一元二次方程与圆的综合知识．涉及等边三角形性质，圆的对称性等知识，能综合运用所学知识，选择恰当的方法进行解题是关键．7．图1是李晨在一次课外活动中所做的问题研究：他用硬纸片做了两个三角形，分别为△ABC和△DEF，其中∠B=90°，∠A=45°，BC=，∠F=90°，∠EDF=30°， EF=2．将△DEF 的斜边DE与△ABC的斜边AC重合在一起，并将△DEF沿AC方向移动．在移动过程中，D、E两点始终在AC边上(移动开始时点D与点A重合)．（1）请回答李晨的问题：若CD=10，则AD= ；（2）如图2，李晨同学连接FC，编制了如下问题，请你回答：①∠FCD的最大度数为；②当FC∥AB时，AD= ；③当以线段AD、FC、BC的长度为三边长的三角形是直角三角形，且FC为斜边时，AD= ;④△FCD的面积s的取值范围是 .【答案】（1）2；（2）① 60°；②；③；④.【解析】试题分析：（1）根据等腰直角三角形的性质，求出AC的长，即可得到AD的长.（2）①当点E与点C重合时，∠FCD的角度最大，据此求解即可.②过点F作FH⊥AC于点H，应用等腰直角三角形的判定和性质，含30度角直角三角形的性质求解即可.③过点F作FH⊥AC于点H，AD=x，应用含30度角直角三角形的性质把FC用x来表示，根据勾股定理列式求解.④设AD=x，把△FCD的面积s表示为x的函数，根据x的取值范围来确定s的取值范围.试题解析：（1）∵∠B=90°，∠A=45°，BC=，∴AC=12.∵CD=10，∴AD=2.（2）①∵∠F=90°，∠EDF=30°，∴∠DEF=60°.∵当点E与点C重合时，∠FCD的角度最大，∴∠FCD的最大度数=∠DEF="60°."② 如图，过点F作FH⊥AC于点H，∵∠EDF=30°， EF=2，∴DF=. ∴DH=3，FH=.∵FC∥AB，∠A=45°，∴∠FCH="45°." ∴HC=. ∴DC=DH+HC=.∵AC=12，∴AD=.③如图，过点F作FH⊥AC于点H，设AD=x，由②知DH=3，FH=，则HC=.在Rt△CFH中，根据勾股定理，得.∵以线段AD、FC、BC的长度为三边长的三角形是直角三角形，且FC为斜边，∴，即，解得.④设AD=x，易知，即.而，当时，；当时，.∴△FCD的面积s的取值范围是.考点：1.面动平移问题；2.等腰直角三角形的判定和性质；3.平行的性质；4.含30度角直角三角形的性质；5.勾股定理；6.由实际问题列函数关系式；7.求函数值.8．如图，正方形ABCD的四个顶点分别在正方形EFGH的四条边上，我们称正方形EFGH 是正方形ABCD的外接正方形．探究一：已知边长为1的正方形ABCD，是否存在一个外接正方形EFGH，它的面积是正方形ABCD面积的2倍？如图，假设存在正方形EFGH，它的面积是正方形ABCD的2倍．因为正方形ABCD的面积为1，则正方形EFGH的面积为2，所以EF＝FG＝GH＝HE2EB＝x，则BF2﹣x，∵Rt△AEB≌Rt△BFC∴BF＝AE2﹣x在Rt△AEB中，由勾股定理，得x2+2﹣x）2＝12解得，x1＝x2＝2 2∴BE＝BF，即点B是EF的中点．同理，点C，D，A分别是FG，GH，HE的中点．所以，存在一个外接正方形EFGH，它的面积是正方形ABCD面积的2倍探究二：已知边长为1的正方形ABCD，是否存在一个外接正方形EFGH，它的面积是正方形ABCD面积的3倍？（仿照上述方法，完成探究过程）探究三：已知边长为1的正方形ABCD，一个外接正方形EFGH，它的面积是正方形ABCD面积的4倍？（填“存在”或“不存在”）探究四：已知边长为1的正方形ABCD，是否存在一个外接正方形EFGH，它的面积是正方形ABCD面积的n倍？（n＞2）（仿照上述方法，完成探究过程）【答案】不存在，详见解析【解析】【分析】探究二，根据探究一的解答过程、运用一元二次方程计算即可；探究三，根据探究一的解答过程、运用一元二次方程根的判别式解答；探究四，根据探究一的解答过程、运用一元二次方程根的判别式解答．【详解】探究二：因为正方形ABCD的面积为1，则正方形EFGH的面积为3，所以EF=FG=GH=HE3，设EB=x，则BF3x，∵Rt△AEB≌Rt△BFC，∴BF=AE3﹣x，在Rt△AEB中，由勾股定理，得，x 2+x ）2=12，整理得x 2x +1=0，b 2﹣4ac =3﹣4＜0，此方程无解，不存在一个外接正方形EFGH ，它的面积是正方形ABCD 面积的3倍；探究三：因为正方形ABCD 的面积为1，则正方形EFGH 的面积为4，所以EF =FG =GH =HE =2，设EB =x ，则BF =2﹣x ，∵Rt △AEB ≌Rt △BFC ，∴BF =AE =2﹣x ，在Rt △AEB 中，由勾股定理，得，x 2+（2﹣x ）2=12，整理得2x 2﹣4x +3=0，b 2﹣4ac =16﹣24＜0，此方程无解，不存在一个外接正方形EFGH ，它的面积是正方形ABCD 面积的3倍，故答案为不存在；探究四：因为正方形ABCD 的面积为1，则正方形EFGH 的面积为n ，所以EF =FG =GH =HE ，设EB =x ，则BF ﹣x ，∵Rt △AEB ≌Rt △BFC ，∴BF =AE ﹣x ，在Rt △AEB 中，由勾股定理，得，x 2+﹣x ）2=12，整理得2x 2﹣+n ﹣1=0，b 2﹣4ac =8﹣4n ＜0，此方程无解，不存在一个外接正方形EFGH ，它的面积是正方形ABCD 面积的n 倍．【点睛】本题考查了正方形的性质、全等三角形的判定和性质、一元二次方程的解法等知识.读懂探究一的解答过程、正确运用一元二次方程根的判别式是解题的关键．9．已知关于x 的方程230x x a ++=①的两个实数根的倒数和等于3，且关于x 的方程2(1)320k x x a -+-=②有实数根，又k 为正整数，求代数式2216k k k -+-的值． 【答案】0.【解析】【分析】 由于关于x 的方程x 2+3x +a =0的两个实数根的倒数和等于3，利用根与系数的关系可以得到关于a 的方程求出a ，又由于关于x 的方程（k -1）x 2+3x -2a =0有实数根，分两种情况讨论，该方程可能是一次方程、有可能是一元二次方程，又k 为正整数，利用判别式可以求出k ，最后代入所求代数式计算即可求解．【详解】解：设方程①的两个实数根分别为x 1、x 2则12123940x x x x a a +-⎧⎪⎨⎪-≥⎩＝＝＝ ， 由条件，知12121211x x x x x x ++==3， 即33a -=，且94a ≤， 故a ＝－1，则方程②为(k -1)x 2+3x +2=0，Ⅰ.当k -1=0时，k =1,x =23-，则22106k k k -=+-. Ⅱ.当k -1≠0时，∆=9-8（k -1）=17-6-8k ≥0，则178k ≤， 又k 是正整数，且k ≠1，则k =2，但使2216k k k -+-无意义. 综上，代数式2216k k k -+-的值为0 【点睛】本题综合考查了根的判别式和根与系数的关系，在解方程时一定要注意所求k 的值与方程判别式的关系．要注意该方程可能是一次方程、有可能是一元二次方程，10．如图1，已知△ABC 中，AB=10cm,AC=8cm,BC=6 cm ,如果点P 由B 出发沿BA 方向向点A 匀速运动，同时点Q 由A 出发沿AC 方向向点C 匀速运动，它们的速度均为2cm /s ，连接PQ ，设运动的时间为t （单位：s ）（0≤t≤4）.解答下列问题：（1）当t 为何值时，PQ∥BC．（2）是否存在某时刻t ，使线段PQ 恰好把△ABC 的面积平分？若存在求出此时t 的值；若不存在，请说明理由.（3）如图2，把△APQ 沿AP 翻折，得到四边形AQPQ′.那么是否存在某时刻t 使四边形AQPQ′为菱形？若存在，求出此时菱形的面积；若不存在，请说明理由.【答案】（1）当BF PC⊥s时，PQ∥BC．（2）不存在某时刻t，使线段PQ恰好把△ABC 的面积平分．（3）存在时刻t，使四边形AQPQ′为菱形，此时菱形的面积为137-cm2．【解析】（1）证△APQ∽△ABC，推出APAB=AQAC，代入得出10210t-=28t，求出方程的解即可；（2）假设存在某时刻t，使线段PQ恰好把△ABC的面积平分，得出方程-5 6t2+6t=12×12×8×6，求出此方程无解，即可得出答案.（3）首先根据菱形的性质及相似三角形比例线段关系，求得PQ、OD、和PD的长度；然后在Rt△PQD中，根据勾股定理列出方程（8-185t）2-（6-65t）2=（2t）2，求得时间t的值；最后根据菱形的面积等于△AQP的面积的2倍，进行计算即可.解：（1）BP=2t，则AP=10﹣2t．∵PQ∥BC，∴△APQ∽△ABC，∴APAB=AQAC，即10210t-=28t，解得：t=20 9,∴当t=209时，PQ∥BC.（2）如答图1所示，过P点作PD⊥AC于点D．∴PD∥BC，∴F ，即B ，解得6PD 6-5t =． 216625S PD AQ t t =⨯=-， 假设存在某时刻t ，使线段PQ 恰好把△ABC 的面积平分，则有S △AQP = C S △ABC ，而S △ABC =12AC•BC=24，∴此时S △AQP =12． 而S △AQP 2665t t =-， ∴266125t t -=，化简得：t 2﹣5t+10=0， ∵△=（﹣5）2﹣4×1×10=﹣15＜0，此方程无解，∴不存在某时刻t ，使线段PQ 恰好把△ABC 的面积平分．（3）假设存在时刻t ，使四边形AQPQ′为菱形，则有AQ=PQ=BP=2t ．如答图2所示，过P 点作PD⊥AC 于点D ，则有PD∥BC，∴D ，即COD ∆，解得：OC ，h ，∴QD=AD﹣AQ=t ．在Rt△PQD 中，由勾股定理得：QD 2+PD 2=PQ 2，即h ，化简得：13t 2﹣90t+125=0，解得：t 1=5，t 2=t ，∵t=5s 时，AQ=10cm ＞AC ，不符合题意，舍去，∴t=52． 由（2）可知，S △AQP =54∴S 菱形AQPQ′=2S △AQP =2×258=3372+cm 2． 所以存在时刻t ，使四边形137-cm 2． “点睛”本题考查了三角形的面积，勾股定理的逆定理，相似三角形的性质和判定的应用，主要考查学生综合运用进行推理和计算的能力.解决问题的关键是作辅助线构造相似三角形以及直角三角形，根据相似三角形的对应边成比例以及勾股定理进行列式求解.。
数学九年级上册 一元二次方程易错题(Word版 含答案)
数学九年级上册 一元二次方程易错题（Word 版 含答案）一、初三数学 一元二次方程易错题压轴题（难）1．已知:在平面直角坐标系xoy 中,直线k y x b =+分别交x 、y 轴于点A 、B 两点,OA=5,∠OAB=60°.(1)如图1,求直线AB 的解析式；(2)如图2,点P 为直线AB 上一点，连接OP ,点D 在OA 延长线上，分别过点P 、D 作OA 、OP 的平行线,两平行线交于点C ，连接AC,设AD=m,△ABC 的面积为S,求S 与m 的函数关系式; (3)如图3,在(2)的条件下,在PA 上取点E ,使PE=AD, 连接EC,DE,若∠ECD=60°,四边形ADCE 的周长等于22，求S 的值.【答案】(1)直线解析式为353y x =-+(2)S=5325322m +；(3)203S =. 【解析】 【分析】(1)先求出点B 坐标，设AB 解析式为y kx b =+，把点A(5，0)，B(0，3分别代入，利用待定系数法进行求解即可；(2)由题意可得四边形ODCP 是平行四边形，∠OAB=∠APC=60°，则有PC=OD=5+m ，∠PCH=30°，过点C 作CH ⊥AB ，在Rt △PCH 中 利用勾股定理可求得CH=)352m +，再由S=12AB •CH 代入相关数据进行整理即可得； (3) 先求得∠PEC=∠ADC ，设∠OPA=α，则∠OPC= ∠ADC= ∠PEC=60°+α，在BA 延长线上截取AK=AD ，连接OK ，DK ，DE ，证明△ADK 是等边三角形，继而证明△PEC ≌△DKO ，通过推导可得到OP=OK=CE=CD ，再证明△CDE 是等边三角形，可得CE=CD=DE ，连接OE ，证明△OPE ≌△EDA ，继而可得△OAE 是等边三角形，得到OA=AE=5 ，根据四边形ADCE 的周长等于22，可得ED=172m -，过点E 作EN ⊥OD 于点N ，则DN=52m +，由勾股定理得222EN DN DE +=， 可得关于m 的方程，解方程求得m 的值后即可求得答案.【详解】(1)在Rt △ABO 中OA=5，∠OAB=60°， ∴∠OBA=30°，AB=10 ， 由勾股定理可得OB=53，∴B(0，53)，设AB解析式为y kx b=+，把点A(5，0)，B(0，53)分别代入，得0553k bb=+⎧⎪⎨=⎪⎩，∴353kb⎧=-⎪⎨=⎪⎩，∴直线解析式为353y x=-+；(2)∵CP//OD，OP//CD，∴四边形ODCP是平行四边形，∠OAB=∠APC=60°，∴PC=OD=5+m，∠PCH=30°，过点C作CH⊥AB，在Rt△PCH中 PH=52m+，由勾股定理得CH=()35m+，∴S=12AB•CH=135325310(5)2m m⨯⨯+=+；(3) ∵∠ECD=∠OAB=60°，∴∠EAD+∠ECD=180°，∠CEA+∠ADC=180°，∴∠PEC=∠ADC，设∠OPA=α，则∠OPC= ∠ADC= ∠PEC=60°+α，在BA延长线上截取AK=AD，连接OK，DK，DE，∵∠DAK=60°，∴△ADK是等边三角形，∴AD=DK=PE，∠ODK=∠APC，∵PC=OD，∴△PEC≌△DKO，∴OK=CE，∠OKD=∠PEC=∠OPC=60°+α，∠AKD= ∠APC=60°，∴∠OPK= ∠OKB，∴OP=OK=CE=CD，又∵∠ECD=60°，∴△CDE是等边三角形，∴CE=CD=DE ，连接OE ，∵ ∠ADE=∠APO ，DE=CD=OP ， ∴△OPE ≌△EDA ， ∴AE=OE ， ∠OAE=60°， ∴△OAE 是等边三角形， ∴OA=AE=5 ，∵四边形ADCE 的周长等于22， ∴AD+2DE=17， ∴ED=172m-， 过点E 作EN ⊥OD 于点N ，则DN=52m +， 由勾股定理得222EN DN DE +=， 即22253517()()()22m m -++=， 解得13m =，221m =-(舍去)， ∴S=153253+=203.【点睛】本题考查的四边形综合题，涉及了待定系数法，平行四边形的判定与性质，勾股定理，全等三角形的判定与性质，等边三角形的判定与性质，解一元二次方程等，综合性较强，有一定的难度，正确添加辅助线，熟练掌握和灵活运用相关知识是解题的关键.2．已知关于x 的方程x 2﹣（2k +1）x +k 2+1＝0． （1）若方程有两个不相等的实数根，求k 的取值范围；（2）若方程的两根恰好是一个矩形两邻边的长，且k ＝2，求该矩形的对角线L 的长． 【答案】（1）k ＞34；（215【解析】 【分析】（1）根据关于x 的方程x 2－(2k ＋1)x ＋k 2＋1＝0有两个不相等的实数根，得出△＞0，再解不等式即可；（2）当k=2时，原方程x 2-5x+5=0，设方程的两根是m 、n ，则矩形两邻边的长是m 、n ，利用根与系数的关系得出m+n=5，mn=5，，利用完全平方公式进行变形即可求得答案. 【详解】解：（1）∵方程x 2－(2k ＋1)x ＋k 2＋1＝0有两个不相等的实数根， ∴Δ＝[－(2k ＋1)]2－4×1×(k 2＋1)＝4k －3＞0， ∴k ＞34； (2)当k ＝2时，原方程为x 2－5x ＋5＝0， 设方程的两个根为m ，n ， ∴m ＋n ＝5，mn ＝5，==.【点睛】本题考查了根的判别式、根与系数的关系、矩形的性质等，一元二次方程根的情况与判别式△的关系：（1）△＞0时，方程有两个不相等的实数根；（2）△=0时，方程有两个相等的实数根；（3）△＜0时，方程没有实数根．3．我市茶叶专卖店销售某品牌茶叶，其进价为每千克 240 元，按每千克 400 元出售，平均每周可售出 200 千克，后来经过市场调查发现，单价每降低 10 元，则平均每周的销售量可增加 40 千克，若该专卖店销售这种品牌茶叶要想平均每周获利 41600 元，请回答： （1）每千克茶叶应降价多少元？（2）在平均每周获利不变的情况下，为尽可能让利于顾客，赢得市场，该店应按原售价的 几折出售？【答案】（1）每千克茶叶应降价30元或80元；（2）该店应按原售价的8折出售． 【解析】 【分析】（1）设每千克茶叶应降价x 元，利用销售量×每件利润=41600元列出方程求解即可； （2）为了让利于顾客因此应下降价80元，求出此时的销售单价即可确定几折． 【详解】（1）设每千克茶叶应降价x 元．根据题意，得： （400﹣x ﹣240）（200+10x×40）=41600． 化简，得：x 2﹣10x +240=0．解得：x1=30，x2=80．答：每千克茶叶应降价30元或80元．（2）由（1）可知每千克茶叶可降价30元或80元．因为要尽可能让利于顾客，所以每千克茶叶某应降价80元．此时，售价为：400﹣80=320（元），320100%80% 400⨯=．答：该店应按原售价的8折出售．【点睛】本题考查了一元二次方程的应用，解题的关键是根据题目中的等量关系列出方程．4．如图，在△ABC 中，∠B=90°，AB=12 cm，BC=16 cm．点 P从点 A 开始沿 AB 边向点 B 以1 cm/s的速度移动，点 Q从点 B开始沿 BC 边向点 C以 2 cm/s的速度移动．如果 P、 Q分别从 A、B同时出发，当一个点到达终点时，另一个点也随之停止运动．设运动的时间为 t 秒．（1）当 t 为何值时，△PBQ的面积等于 35cm2？（2）当 t 为何值时，PQ的长度等82cm？（3）若点 P，Q的速度保持不变，点 P在到达点 B后返回点 A，点 Q在到达点 C后返回点B，一个点停止，另一个点也随之停止．问：当 t为何值时，△PCQ的面积等于 32cm2？【答案】（1）t为5或7；（2）t为45或4；（3）t为4或16【解析】【分析】（1）分别用含t的代数式表示PB，BQ的长，利用面积公式列方程求解即可．（2）分别用含t的代数式表示PB，BQ的长，利用勾股定理列方程求解即可．（3）分段要清楚，，P，Q都没有返回，表示好PB，CQ的长，用面积公式列方程，，P不返回，Q返回，表示好PB，CQ的长，用面积公式列方程，，两点都返回，表示好PB，CQ的长，用面积公式列方程即可得到答案．【详解】解：（1），.根据三角形的面积公式，得，即，整理，得， 解得，.故当为5或7时，的面积等于35.（2）根据勾股定理，得，整理，得，解得，.故当为或4时，的长度等于.（3）①当时，，，由题意，得，解得：，（舍去）.②当时，，，由题意，得，次方程无解.③当时，，， 由题意，得，解得：（舍去），.综上所述，当为4或16时，的面积等于. 【点睛】本题考查的是在运动过程中应用一元二次方程解决实际问题，建立正确情境下的几何模型是解决问题的关键，特别是最后一问，关键是弄懂分段的时间界点，才能正确的表示PB ，CQ 的长．5．已知关于x 的方程24832x nx n --=和()223220x n x n -+-+=，是否存在这样的n 值，使第一个方程的两个实数根的差的平方等于第二个方程的一整数根？若存在，请求出这样的n 值；若不存在，请说明理由？【答案】存在，n=0. 【解析】 【分析】在方程①中，由一元二次方程的根与系数的关系，用含n 的式子表示出两个实数根的差的平方，把方程②分解因式，建立方程求n ，要注意n 的值要使方程②的根是整数. 【详解】若存在n满足题意.设x1，x2是方程①的两个根，则x1+x2=2n，x1x2=324n+-，所以(x1-x2)2=4n2+3n+2，由方程②得，(x+n-1)[x-2(n+1)]=0，①若4n2+3n+2=-n+1，解得n=-12，但1-n=32不是整数，舍.②若4n2+3n+2=2(n+2)，解得n=0或n=-14 (舍)，综上所述，n=0.6．已知关于x的一元二次方程（x﹣3）（x﹣4）﹣m2=0．（1）求证：对任意实数m，方程总有2个不相等的实数根；（2）若方程的一个根是2，求m的值及方程的另一个根．【答案】（1）证明见解析；（2）m的值为±2，方程的另一个根是5．【解析】【分析】（1）先把方程化为一般式，利用根的判别式△=b2-4ac证明判断即可；（2）根据方程的根，利用代入法即可求解m的值，然后还原方程求出另一个解即可.【详解】（1）证明：∵（x﹣3）（x﹣4）﹣m2=0，∴x2﹣7x+12﹣m2=0，∴△=（﹣7）2﹣4（12﹣m2）=1+4m2，∵m2≥0，∴△＞0，∴对任意实数m，方程总有2个不相等的实数根；（2）解：∵方程的一个根是2，∴4﹣14+12﹣m2=0，解得m=±，∴原方程为x2﹣7x+10=0，解得x=2或x=5，即m的值为±，方程的另一个根是5．【点睛】此题主要考查了一元二次方程根的判别式，熟练掌握一元二次方程的根的判别式与根的关系是关键.当△=b2-4ac＞0时，方程有两个不相等的实数根；当△=b2-4ac=0时，方程有两个相等的实数根；当△=b2-4ac＜0时，方程没有实数根.7．（本题满分10分）如图，在平面直角坐标系中，直线AB与x轴、y轴分别交于点A、B，直线CD与x轴、y轴分别交于点C、D，AB与CD相交于点E，线段OA、OC的长是一元二次方程－18x+72=0的两根（OA＞OC），BE=5，tan∠ABO=．（1）求点A，C的坐标；（2）若反比例函数y=的图象经过点E，求k的值；（3）若点P在坐标轴上，在平面内是否存在一点Q，使以点C，E，P，Q为顶点的四边形是矩形？若存在，请写出满足条件的点Q的个数，并直接写出位于x轴下方的点Q的坐标；若不存在，请说明理由．【答案】(1)、A（12，0），C（﹣6，0）；(2)、k=36；(3)、6个；Q1（10，﹣12），Q2（﹣3，6﹣3）.【解析】试题分析：(1)、首先求出方程的解，根据OA＞OC求出两点的坐标；(2)、根据∠ABO的正切值求出OB的长度，根据Rt△AOB得出AB的长度，作EM⊥x轴，根据三角形相似得出点E的坐标，然后求出k的值；(3)、分别以CE为矩形的边，在点C、E处设计直角，垂线与两坐标轴相交，得到点P，进而得到点Q；以CE为矩形对角线，则以CE的中点为圆心做圆，与两坐标轴相交，得到点P，再得点Q.试题解析：（1）由题意，解方程得：x1=6，x2=12．∵OA＞OC，∴OA=12，OC=6．∴A（12，0），C（﹣6，0）；（2）∵tan∠ABO=，∠AOB=90°∴∴OB=16．在Rt△AOB中，由勾股定理，得AB=20∵BE=5，∴AE=15．如图1，作EM⊥x轴于点M，∴EM∥OB．∴△AEM∽△ABO，∴，即：∴EM=12，AM=9，∴OM=12﹣9=3．∴E（3，12）．∴k=36；（3）满足条件的点Q的个数是6，x轴的下方的Q1（10，﹣12），Q2（﹣3，6﹣3）；方法：如下图①分别以CE为矩形的边，在点C、E处设计直角，垂线与两坐标轴相交，得到点P，进而得到点Q；（有三种）②以CE为矩形对角线，则以CE的中点为圆心做圆，与两坐标轴相交，得到点P，再得点Q；（有三种）如图①∵E（3，12），C（﹣6，0），∴CG=9，EG=12，∴EG2=CG•G P，∴GP=16，∵△CPE与△PCQ是中心对称，∴CH=GP=16，QH=FG=12，∵OC=6，∴OH=10，∴Q（10，﹣12），如图②作MN∥x轴，交EG于点N，EH⊥y轴于点H ∵E（3，12），C（﹣6，0），∴CG=9，EG=12，∴CE=15，∵MN=CG=，可以求得PH=3﹣6，同时可得PH=QR ，HE=CR ∴Q （﹣3，6﹣3），考点：三角形相似的应用、三角函数、一元二次方程.8．某建材销售公司在2019年第一季度销售,A B 两种品牌的建材共126件，A 种品牌的建材售价为每件6000元，B 种品牌的建材售价为每件9000元.（1）若该销售公司在第一季度售完两种建材后总销售额不低于96.6万元，求至多销售A 种品牌的建材多少件？（2）该销售公司决定在2019年第二季度调整价格，将A 种品牌的建材在上一个季度的基础上下调%a ，B 种品牌的建材在上一个季度的基础上上涨%a ；同时，与（1）问中最低销售额的销售量相比，A 种品牌的建材的销售量增加了1%2a ，B 种品牌的建材的销售量减少了2%5a ，结果2019年第二季度的销售额比（1）问中最低销售额增加2%23a ，求a 的值.【答案】（1）至多销售A 品牌的建材56件;(2)a 的值是30. 【解析】 【分析】（1）设销售A 品牌的建材x 件，根据售完两种建材后总销售额不低于96.6万元，列不等式求解；（2）根据题意列出方程求解即可. 【详解】（1）设销售A 品牌的建材x 件.根据题意，得()60009000126966000x x +-≥， 解这个不等式，得56x ≤， 答：至多销售A 品牌的建材56件.（2）在（1）中销售额最低时，B 品牌的建材70件， 根据题意，得()()()12260001%561%90001%701%6000569000701%2523a a a a a ⎛⎫⎛⎫⎛⎫-⨯+++⨯-=⨯+⨯+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，令%a y =，整理这个方程，得21030y y -=，解这个方程，得1230,10y y ==， ∴10a =（舍去），230a =， 即a 的值是30. 【点睛】本题考查了一元二次方程和一元一次不等式的应用，解答本题的关键是读懂题意，设出未知数，找出合适的等量关系和不等关系，列方程组和不等式求解．9．如图，某农家拟用已有的长为8m的墙或墙的一部分为一边，其它三边用篱笆围成一个面积为12m2的矩形园子．设园子中平行于墙面的篱笆长为ym（其中y≥4），另两边的篱笆长分别为xm．（1）求y关于x的函数表达式，并求x的取值范围．（2）若仅用现有的11m长的篱笆，且恰好用完，请你帮助设计围制方案．【答案】（1）y＝；1.5≤x≤3；（2）长为8m，宽为1.5m．【解析】【分析】（1）由矩形的面积公式可得出y关于x的函数表达式，结合4≤y≤8可求出x的取值范围；（2）由篱笆的长可得出y＝（11﹣2x）m，利用矩形的面积公式结合矩形园子的面积，即可得出关于x的一元二次方程，解之取其较小值即可得出结论．【详解】（1）∵矩形的面积为12m2，∴y＝．∵4≤y≤8，∴1.5≤x≤3．（2）∵篱笆长11m，∴y＝（11﹣2x）m．依题意，得：xy＝12，即x（11﹣2x）＝12，解得：x1＝1.5，x2＝4（舍去），∴y＝11﹣2x＝8．答：矩形园子的长为8m，宽为1.5m．【点睛】本题考查了一元二次方程的应用以及反比例函数的应用，解题的关键是：（1）利用矩形的面积公式，找出y关于x的函数表达式；（2）找准等量关系，正确列出一元二次方程．10．如图1，已知△ABC中，AB=10cm,AC=8cm,BC=6 cm ,如果点P由B出发沿BA方向向点A匀速运动，同时点Q由A出发沿AC方向向点C匀速运动，它们的速度均为2cm /s，连接PQ，设运动的时间为t（单位：s）（0≤t≤4）.解答下列问题：（1）当t为何值时，PQ∥BC．（2）是否存在某时刻t，使线段PQ恰好把△ABC的面积平分？若存在求出此时t的值；若不存在，请说明理由.（3）如图2，把△APQ沿AP翻折，得到四边形AQPQ′.那么是否存在某时刻t使四边形AQPQ′为菱形？若存在，求出此时菱形的面积；若不存在，请说明理由.【答案】（1）当BF PC ⊥s 时，PQ∥BC．（2）不存在某时刻t ，使线段PQ 恰好把△ABC 的面积平分．（3）存在时刻t ，使四边形AQPQ′为菱形，此时菱形的面积为1372-cm 2． 【解析】（1）证△APQ∽△ABC，推出AP AB =AQ AC ，代入得出10210t -=28t ，求出方程的解即可；（2）假设存在某时刻t ，使线段PQ 恰好把△ABC 的面积平分，得出方程-56t 2+6t=12×12×8×6，求出此方程无解，即可得出答案. （3）首先根据菱形的性质及相似三角形比例线段关系，求得PQ 、OD 、和PD 的长度；然后在Rt△PQD 中，根据勾股定理列出方程（8-185t ）2-（6-65t ）2=（2t ）2，求得时间t 的值；最后根据菱形的面积等于△AQP 的面积的2倍，进行计算即可.解：（1）BP=2t ，则AP=10﹣2t ． ∵PQ∥BC，∴△APQ∽△ABC， ∴AP AB =AQ AC ， 即10210t -=28t ， 解得：t=209, ∴当t=209时，PQ∥BC. （2）如答图1所示，过P 点作PD⊥AC 于点D ．∴PD∥BC，∴F ，即B ，解得6PD 6-5t =． 216625S PD AQ t t =⨯=-， 假设存在某时刻t ，使线段PQ 恰好把△ABC 的面积平分，则有S △AQP = C S △ABC ，而S △ABC =12AC•BC=24，∴此时S △AQP =12． 而S △AQP 2665t t =-， ∴266125t t -=，化简得：t 2﹣5t+10=0， ∵△=（﹣5）2﹣4×1×10=﹣15＜0，此方程无解，∴不存在某时刻t ，使线段PQ 恰好把△ABC 的面积平分．（3）假设存在时刻t ，使四边形AQPQ′为菱形，则有AQ=PQ=BP=2t ．如答图2所示，过P 点作PD⊥AC 于点D ，则有PD∥BC，∴D ，即COD ∆，解得：OC ，h ，∴QD=AD﹣AQ=t ．在Rt△PQD 中，由勾股定理得：QD 2+PD 2=PQ 2，即h ，化简得：13t 2﹣90t+125=0，解得：t 1=5，t 2=t ，∵t=5s 时，AQ=10cm ＞AC ，不符合题意，舍去，∴t=52． 由（2）可知，S △AQP =54∴S 菱形AQPQ′=2S △AQP =2×258=32+cm 2．所以存在时刻t ，使四边形cm 2． “点睛”本题考查了三角形的面积，勾股定理的逆定理，相似三角形的性质和判定的应用，主要考查学生综合运用进行推理和计算的能力.解决问题的关键是作辅助线构造相似三角形以及直角三角形，根据相似三角形的对应边成比例以及勾股定理进行列式求解.。
一元二次方程单元复习练习(Word版 含答案)
∴S△ACO＝ × ＝1 ，S△ODB＝ ×3＝ ．∵∠AOB＝90°，
∴∠AOC＋∠BOD＝90°，∵∠AOC＋∠OAC＝90°，∴∠OAC＝∠BOD．
又∵∠ACO＝∠ODB＝90°，∴△ACO∽△ODB．
∴ ＝ ＝ ，∴ ＝± （舍负取正），即 ＝ ．
（2）①利用润滑用油量每减少1kg，用油的重复利用率将增加1.6%，进而求出答案；
②首先表示出用油的重复利用率，进而利用乙车间技术革新后实际耗油量下降到12kg，得出等式求出答案．
试题解析：（1）根据题意可得：70×（1﹣60%）=28（kg）；
（2）①60%+1.6%（90﹣80）=76%；
②设润滑用油量是x千克，则
∴在Rt△AOB中，tan∠OBA＝ ＝ ．
4．已知关于x的一元二次方程 有两个实数根．
求k的取值范围；
设方程两实数根分别为 ， ，且满足 ，求k的值．
【答案】（1） ；（2） ．
【解析】
【分析】
根据方程有实数根得出 ，解之可得．
利用根与系数的关系可用k表示出 和 的值，根据条件可得到关于k的方程，可求得k的值，注意利用根的判别式进行取舍．
2009年底汽车数量为14.4×90%+y，
2010年底汽车数量为（14.4×90%+y）×90%+y，
∴（14.4×90%+y）×90%+y≤15.464，
∴y≤2．
答：每年新增汽车数量最多不超过2万辆．
考点：一元二次方程—增长率的问题
2．机械加工需用油进行润滑以减小摩擦，某企业加工一台设备润滑用油量为90kg，用油的重复利用率为60%，按此计算，加工一台设备的实际耗油量为36kg，为了倡导低碳，减少油耗，该企业的甲、乙两个车间都组织了人员为减少实际油耗量进行攻关．
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
九年级上册一元二次方程易错题（Word 版 含答案）一、初三数学 一元二次方程易错题压轴题（难）1．如图，在矩形ABCD 中，6AB cm =，8AD cm =，点P 从点A 出发沿AD 向点D 匀速运动，速度是1/cm s ，过点P 作PE AC ∥交DC 于点E ，同时，点Q 从点C 出发沿CB 方向，在射线CB 上匀速运动，速度是2/cm s ，连接PQ 、QE ，PQ 与AC 交与点F ，设运动时间为()(08)<<t s t ．（1）当t 为何值时，四边形PFCE 是平行四边形；（2）设PQE 的面积为2()s cm ，求s 与t 的函数关系式；（3）是否存在某一时刻t ，使得PQE 的面积为矩形ABCD 面积的932； （4）是否存在某一时刻t ，使得点E 在线段PQ 的垂直平分线上．【答案】（1）83t =；（2）S =299(08)8t t t -+<<；（3）当2t s =或6s 时，PQE 的面积为矩形ABCD 面积的932；（4）当573256=t 时，点E 在线段PQ 的垂直平分线上【解析】【分析】（1）由四边形PFCE 是平行四边形，可得,PF CE ∥由PD QC 得四边形CDPQ 为平行四边形，即PD CQ =，列式82t t -=，计算可解.（2）由PE AC ∥，得=DP DE DA DC ，代入时间t ，得886-=t DE 解得364=-DE t ，34CE t = 再通过S S =梯形CDPQ PDE CEQ S S --△△构建联系，可列函数式299(08)8S t t t =-+<<. （3）由PQE 的面积为矩形ABCD 面积的932得299986832S t t =-+=⨯⨯，可解当2t s =或6s 时，PQE 的面积为矩形ABCD 面积的932． （4）当点E 在线段PQ 的垂直平分线上时，=EQ PE ，得22=EQ PE ，由Rt CEQ 与△Rt PDE 可得，222+=CE CQ EQ ，222PD DE PE +=，即2222+=+CE CQ PD DE ，代入364=-DE t ，34CE t =，2CQ t =，8PD t =- 可得222233(2)(8)644⎛⎫⎛⎫+=-+- ⎪ ⎪⎝⎭⎝⎭t t t t ，计算验证可解. 【详解】（1）当四边形PFCE 是平行四边形时，∥PF CE ，又∵PD QC ，∴四边形CDPQ 为平行四边形，∴PD CQ =，即82t t -=， ∴83t = （2）∵PE AC ∥， ∴=DP DE DA DC， 即886-=t DE ， ∴364=-DE t ， ∴336644=-+=CE t t ， ∴21133(8)66242248⎛⎫=⋅=--=-+ ⎪⎝⎭△PDE S PD DE t t t t ， 2113322244=⋅=⨯⨯=△CEQ S CE CQ t t t ， S 梯形11()(28)632422=+⋅=+-⋅=+CDPQ QC PD CD t t t ， ∴S S =梯形299(08)8--=-+<<△△CDPQ PDE CEQ S S t t t （3）由题意，299986832-+=⨯⨯t t 解得12t =，26t =所以当2t s =或6s 时，PQE 的面积为矩形ABCD 面积的932．（4）当点E 在线段PQ 的垂直平分线上时，=EQ PE ，∴22=EQ PE ， 在Rt CEQ 中，222+=CE CQ EQ ，在△Rt PDE 中，222PD DE PE +=，∴2222+=+CE CQ PD DE ， 即222233(2)(8)644⎛⎫⎛⎫+=-+- ⎪ ⎪⎝⎭⎝⎭t t t t 解得1573256-=t ，2573256+=-t （舍） 所以当57325-=t 时，点E 在线段PQ 的垂直平分线上． 【点睛】本题考查的是一次函数与几何图形的实际应用，勾股定理，平行线的性质，解一元二次方程，需要注意的是在解一元二次方程的实际应用中经常会涉及到解的验证，不可忽略.2．已知:在平面直角坐标系xoy 中,直线k y x b =+分别交x 、y 轴于点A 、B 两点,OA=5,∠OAB=60°.(1)如图1,求直线AB 的解析式；(2)如图2,点P 为直线AB 上一点，连接OP ,点D 在OA 延长线上，分别过点P 、D 作OA 、OP 的平行线,两平行线交于点C ，连接AC,设AD=m,△ABC 的面积为S,求S 与m 的函数关系式;(3)如图3,在(2)的条件下,在PA 上取点E ,使PE=AD, 连接EC,DE,若∠ECD=60°,四边形ADCE 的周长等于22，求S 的值.【答案】(1)直线解析式为353y x =-+53253+；(3)203S =. 【解析】【分析】 (1)先求出点B 坐标，设AB 解析式为y kx b =+，把点A(5，0)，B(0，3分别代入，利用待定系数法进行求解即可；(2)由题意可得四边形ODCP 是平行四边形，∠OAB=∠APC=60°，则有PC=OD=5+m ，∠PCH=30°，过点C 作CH ⊥AB ，在Rt △PCH 中 利用勾股定理可求得CH=)52m +，再由S=12AB •CH 代入相关数据进行整理即可得； (3) 先求得∠PEC=∠ADC ，设∠OPA=α，则∠OPC= ∠ADC= ∠PEC=60°+α，在BA 延长线上截取AK=AD ，连接OK ，DK ，DE ，证明△ADK 是等边三角形，继而证明△PEC ≌△DKO ，通过推导可得到OP=OK=CE=CD ，再证明△CDE 是等边三角形，可得CE=CD=DE ，连接OE ，证明△OPE ≌△EDA ，继而可得△OAE 是等边三角形，得到OA=AE=5 ，根据四边形ADCE 的周长等于22，可得ED=172m -，过点E 作EN ⊥OD 于点N ，则DN=52m +，由勾股定理得222EN DN DE +=， 可得关于m 的方程，解方程求得m 的值后即可求得答案.【详解】(1)在Rt △ABO 中OA=5，∠OAB=60°，∴∠OBA=30°，AB=10 ，由勾股定理可得OB=，∴B(0，，设AB 解析式为y kx b =+，把点A(5，0)，B(0，)分别代入，得05k b b=+⎧⎪⎨=⎪⎩，∴k b ⎧=⎪⎨=⎪⎩，∴直线解析式为y =+(2)∵CP//OD ，OP//CD ，∴四边形ODCP 是平行四边形，∠OAB=∠APC=60°，∴PC=OD=5+m ，∠PCH=30°，过点C 作CH ⊥AB ，在Rt △PCH 中 PH=52m +，由勾股定理得CH=()52m +， ∴S=12AB •CH=110)2m ⨯+=+；(3) ∵∠ECD=∠OAB=60°，∴∠EAD+∠ECD=180°，∠CEA+∠ADC=180°，∴∠PEC=∠ADC ，设∠OPA=α，则∠OPC= ∠ADC= ∠PEC=60°+α，在BA 延长线上截取AK=AD ，连接OK ，DK ，DE ，∵∠DAK=60°，∴△ADK 是等边三角形，∴AD=DK=PE ，∠ODK=∠APC ，∵PC=OD ，∴△PEC ≌△DKO ，∴OK=CE ，∠OKD=∠PEC=∠OPC=60°+α， ∠AKD= ∠APC=60° ，∴∠OPK= ∠OKB ，∴OP=OK=CE=CD ，又∵∠ECD=60°，∴△CDE 是等边三角形，∴CE=CD=DE ，连接OE ，∵ ∠ADE=∠APO ，DE=CD=OP ，∴△OPE ≌△EDA ，∴AE=OE ， ∠OAE=60°，∴△OAE 是等边三角形，∴OA=AE=5 ，∵四边形ADCE 的周长等于22，∴AD+2DE=17， ∴ED=172m -， 过点E 作EN ⊥OD 于点N ，则DN=52m +， 由勾股定理得222EN DN DE +=，即22253517()()()222m m -++=， 解得13m =，221m =-(舍去)，∴S=15325322+=203.【点睛】本题考查的四边形综合题，涉及了待定系数法，平行四边形的判定与性质，勾股定理，全等三角形的判定与性质，等边三角形的判定与性质，解一元二次方程等，综合性较强，有一定的难度，正确添加辅助线，熟练掌握和灵活运用相关知识是解题的关键.3．（1）课本情境:如图，已知矩形AOBC ，AB ＝6cm ，BC ＝16cm ，动点P 从点A 出发，以3cm/s 的速度向点O 运动，直到点O 为止；动点Q 同时从点C 出发，以2cm/s 的速度向点B 运动，与点P 同时结束运动，出发 时，点P 和点Q 之间的距离是10cm ；（2）逆向发散:当运动时间为2s 时，P ，Q 两点的距离为多少？当运动时间为4s 时，P ，Q 两点的距离为多少？（3）拓展应用：若点P 沿着AO→OC→CB 移动，点P ，Q 分别从A ，C 同时出发，点Q 从点C 移动到点B 停止时，点P 随点Q 的停止而停止移动，求经过多长时间△POQ 的面积为12cm 2？【答案】（1）85s 或245s （2）62cm ；213cm （3）4s 或6s 【解析】【分析】(1)过点P 作PE ⊥BC 于E ，得到AP ＝3t ，CQ ＝2t ，PE ＝6，EQ ＝16﹣3t ﹣2t ＝16﹣5t ，利用勾股定理得到方程，故可求解；（2）根据运动时间求出EQ 、PE ，利用勾股定理即可求解；(3) 分当点P 在AO 上时，当点P 在OC 上时和当点P 在CB 上时，根据三角形的面积公式列出方程即可求解．【详解】解：（1）设运动时间为t 秒时，如图，过点P 作PE ⊥BC 于E ，由运动知，AP ＝3t ，CQ ＝2t ，PE ＝6，EQ ＝16﹣3t ﹣2t ＝16﹣5t ，∵点P 和点Q 之间的距离是10 cm ，∴62+（16﹣5t ）2＝100，解得t 1=85，t 2=245， ∴t ＝85s 或245s . 故答案为85s 或245s（2）t=2时，由运动知AP ＝3×2＝6 cm ，CQ ＝2×2＝4 cm ，∴四边形APEB 是矩形，∴PE ＝AB ＝6，BE ＝6，∴EQ ＝BC ﹣BE ﹣CQ ＝16﹣6﹣4＝6，根据勾股定理得2262PE EQ +=∴当t ＝2 s 时，P ，Q 两点的距离为2 cm ；当t ＝4 s 时，由运动知AP ＝3×4＝12 cm ，CQ ＝2×4＝8cm ，∴四边形APEB 是矩形，∴PE ＝AB ＝6，BQ ＝8，CE=OP=4∴EQ ＝BC ﹣CE ﹣BQ ＝16﹣4﹣8＝4，根据勾股定理得22213PE EQ +=,P ，Q 两点的距离为13.（3）点Q 从C 点移动到B 点所花的时间为16÷2=8s ，当点P 在AO 上时，S △POQ ＝2PO CO ⋅＝(163)62t -⋅＝12， 解得t ＝4．当点P 在OC 上时，S △POQ ＝2PO CQ ⋅＝(316)22t t -⋅＝12， 解得t ＝6或﹣23（舍弃）． 当点P 在CB 上时，S △POQ ＝2PQ CO ⋅＝(2223)62t t +-⨯＝12， 解得t ＝18＞8（不符合题意舍弃），综上所述，经过4 s 或6 s 时，△POQ 的面积为12 cm 2．【点睛】此题主要考查勾股定理的应用、一元二次方程与动点问题，解题的关键是熟知勾股定理的应用，根据三角形的面积公式找到等量关系列出方程求解．4．如图，在平面直角坐标系中，O 为原点，点A （0，8），点B （m ，0），且m ＞0.把△AOB 绕点A 逆时针旋转90°，得△ACD ，点O ，B 旋转后的对应点为C ，D ，（1）点C 的坐标为 ；（2）①设△BCD 的面积为S ，用含m 的式子表示S ，并写出m 的取值范围；②当S=6时，求点B 的坐标（直接写出结果即可）.【答案】（1）C （8，8）；（2）①S=0.5m 2﹣4m （m ＞8），或S=﹣0.5m 2+4m （0＜m ＜8）；②点B 的坐标为（7，0）或（2，0）或（6，0）.【解析】【分析】（1）由旋转的性质得出AC＝AO＝8，∠OAC＝90°，得出C（8，8）即可；（2）①由旋转的性质得出DC＝OB＝m，∠ACD＝∠AOB＝90°，∠OAC＝90°，得出∠ACE＝90°，证出四边形OACE是矩形，得出DE⊥x轴，OE＝AC＝8，分三种情况：a、当点B在线段OE的延长线上时，得出BE＝OB−OE＝m−8，由三角形的面积公式得出S ＝0.5m2−4m（m＞8）即可；b、当点B在线段OE上（点B不与O，E重合）时，BE＝OE−OB＝8−m，由三角形的面积公式得出S＝−0.5m2＋4m（0＜m＜8）即可；c、当点B与E重合时，即m＝8，△BCD不存在；②当S＝6，m＞8时，得出0.5m2−4m＝6，解方程求出m即可；当S＝6，0＜m＜8时，得出−0.5m2＋4m＝6，解方程求出m即可．【详解】（1）∵点A（0，8），∴AO=8，∵△AOB绕点A逆时针旋转90°得△ACD，∴AC=AO=8，∠OAC=90°，∴C（8，8），故答案为（8，8）；（2）①延长DC交x轴于点E，∵点B（m，0），∴OB=m，∵△AOB绕点A逆时针旋转90°得△ACD，∴DC=OB=m，∠ACD=∠AOB=90°，∠OAC=90°，∴∠ACE=90°，∴四边形OACE是矩形，∴DE⊥x轴，OE=AC=8，分三种情况：a、当点B在线段OE的延长线上时，如图1所示：则BE=OB﹣OE=m﹣8，∴S=0.5DC•BE=0.5m（m﹣8），即S=0.5m2﹣4m（m＞8）；b、当点B在线段OE上（点B不与O，E重合）时，如图2所示：则BE=OE﹣OB=8﹣m，∴S=0.5DC•BE=0.5m（8﹣m），即S=﹣0.5m2+4m（0＜m＜8）；c、当点B与E重合时，即m=8，△BCD不存在；综上所述，S=0.5m2﹣4m（m＞8），或S=﹣0.5m2+4m（0＜m＜8）；②当S=6，m＞8时，0.5m2﹣4m=6，解得：m=4±27（负值舍去），∴m=4+27；当S=6，0＜m＜8时，﹣0.5m2+4m=6，解得：m=2或m=6，∴点B的坐标为（4+27，0）或（2，0）或（6，0）.【点睛】本题是三角形综合题目，考查了坐标与图形性质、旋转的性质、矩形的判定与性质、三角形面积公式、一元二次方程的解法等知识；本题综合性强，有一定难度．5．阅读以下材料，并解决相应问题：材料一：换元法是数学中的重要方法，利用换元法可以从形式上简化式子，在求解某些特殊方程时，利用换元法常常可以达到转化的目的，例如在求解一元四次方程42210x x -+=，就可以令21x =，则原方程就被换元成2210t t -+=，解得 t = 1，即21x =，从而得到原方程的解是 x = ±1材料二：杨辉三角形是中国数学上一个伟大成就，在中国南宋数学家杨辉 1261 年所著的《详解九章算法》一书中出现，它呈现了某些特定系数在三角形中的一种有规律的几何排列，下图为杨辉三角形：……………………………………（1）利用换元法解方程：()()222312313+-++-=x x x x（2）在杨辉三角形中，按照自上而下、从左往右的顺序观察， an 表示第 n 行第 2 个数（其中 n≥4），bn 表示第 n 行第 3 个数，n c 表示第(n )1-行第 3 个数，请用换元法因式分解：()41-⋅+n n n b a c【答案】（1）317x -+=或317x --= 或x=-1或x=-2；（2）()41-⋅+n n n b a c =（n 2-5n+5）2【解析】【分析】（1）设t=x 2+3x-1，则原方程可化为：t 2+2t=3，求得t 的值再代回可求得方程的解； （2）根据杨辉三角形的特点得出a n ，b n ，c n ，然后代入4（b n -a n ）•c n +1再因式分解即可．【详解】（1）解：令t=x 2+3x-1则原方程为：t 2+2t=3解得：t=1 或者 t=-3当t=1时，x 2+3x-1=1 解得：317x -+=或317x --=当t=-3时，x 2+3x-1=-3解得：x=-1或x=-2∴方程的解为：317x -+=或317x --=或x=-1或x=-2（2）解：根据杨辉三角形的特点得出： a n =n-1(1)(2)2n n n b --= (2)(3)2n n n c --=∴4（b n -a n ）•c n +1=（n-1）（n-4）（n-2）（n-3）+1=（n 2-5n+4）（n 2-5n+6）+1 =（n 2-5n+4）2+2（n 2-5n+4）+1=（n 2-5n+5）2 【点睛】本题主要考查因式分解的应用．解一些复杂的因式分解问题，常用到换元法，即对结构比较复杂的多项式，若把其中某些部分看成一个整体，用新字母代替（即换元），则能使复杂的问题简单化，明朗化，在减少多项式项数，降低多项式结构复杂程度等方面有独到作用．6．如图，在△ABC 中，∠B=90°，AB=12 cm ，BC=16 cm ．点 P 从点 A 开始沿 AB 边向点 B 以 1 cm/s 的速度移动，点 Q 从点 B 开始沿 BC 边向点 C 以 2 cm/s 的速度移动．如果 P 、 Q 分别从 A 、B 同时出发，当一个点到达终点时，另一个点也随之停止运动．设运动的时间为 t 秒．（1）当 t 为何值时，△PBQ 的面积等于 35cm2？ （2）当 t 为何值时，PQ 的长度等82cm ？（3）若点 P ，Q 的速度保持不变，点 P 在到达点 B 后返回点 A ，点 Q 在到达点 C 后返回点 B ，一个点停止，另一个点也随之停止．问：当 t 为何值时，△PCQ 的面积等于 32cm 2？ 【答案】（1）t 为5或7；（2）t 为45或4；（3）t 为4或16 【解析】 【分析】（1）分别用含t 的代数式表示PB ，BQ 的长，利用面积公式列方程求解即可． （2）分别用含t 的代数式表示PB ，BQ 的长，利用勾股定理列方程求解即可． （3）分段要清楚，，P ，Q 都没有返回，表示好PB ，CQ 的长，用面积公式列方程，，P 不返回，Q 返回，表示好PB ，CQ 的长，用面积公式列方程，，两点都返回，表示好PB ，CQ 的长，用面积公式列方程即可得到答案．【详解】解：（1），.根据三角形的面积公式，得，即，整理，得，解得，. 故当为5或7时，的面积等于35.（2）根据勾股定理，得，整理，得，解得，.故当为或4时，的长度等于.（3）①当时，，，由题意，得，解得：，（舍去）.②当时，，，由题意，得，次方程无解. ③当时，，，由题意，得， 解得：（舍去），.综上所述，当为4或16时，的面积等于. 【点睛】本题考查的是在运动过程中应用一元二次方程解决实际问题，建立正确情境下的几何模型是解决问题的关键，特别是最后一问，关键是弄懂分段的时间界点，才能正确的表示PB ，CQ 的长．7．已知关于x 的方程24832x nx n --=和()223220x n x n -+-+=，是否存在这样的n 值，使第一个方程的两个实数根的差的平方等于第二个方程的一整数根？若存在，请求出这样的n 值；若不存在，请说明理由？【答案】存在，n=0. 【解析】【分析】在方程①中，由一元二次方程的根与系数的关系，用含n的式子表示出两个实数根的差的平方，把方程②分解因式，建立方程求n，要注意n的值要使方程②的根是整数.【详解】若存在n满足题意.设x1，x2是方程①的两个根，则x1+x2=2n，x1x2=324n+-，所以(x1-x2)2=4n2+3n+2，由方程②得，(x+n-1)[x-2(n+1)]=0，①若4n2+3n+2=-n+1，解得n=-12，但1-n=32不是整数，舍.②若4n2+3n+2=2(n+2)，解得n=0或n=-14 (舍)，综上所述，n=0.8．（本题满分10分）如图，在平面直角坐标系中，直线AB与x轴、y轴分别交于点A、B，直线CD与x轴、y轴分别交于点C、D，AB与CD相交于点E，线段OA、OC的长是一元二次方程－18x+72=0的两根（OA＞OC），BE=5，tan∠ABO=．（1）求点A，C的坐标；（2）若反比例函数y=的图象经过点E，求k的值；（3）若点P在坐标轴上，在平面内是否存在一点Q，使以点C，E，P，Q为顶点的四边形是矩形？若存在，请写出满足条件的点Q的个数，并直接写出位于x轴下方的点Q的坐标；若不存在，请说明理由．【答案】(1)、A（12，0），C（﹣6，0）；(2)、k=36；(3)、6个；Q1（10，﹣12），Q2（﹣3，6﹣3）.【解析】试题分析：(1)、首先求出方程的解，根据OA＞OC求出两点的坐标；(2)、根据∠ABO的正切值求出OB的长度，根据Rt△AOB得出AB的长度，作EM⊥x轴，根据三角形相似得出点E的坐标，然后求出k的值；(3)、分别以CE为矩形的边，在点C、E处设计直角，垂线与两坐标轴相交，得到点P，进而得到点Q；以CE为矩形对角线，则以CE的中点为圆心做圆，与两坐标轴相交，得到点P，再得点Q.试题解析：（1）由题意，解方程得：x1=6，x2=12．∵OA＞OC，∴OA=12，OC=6．∴A（12，0），C（﹣6，0）；（2）∵tan∠ABO=，∠AOB=90°∴∴OB=16．在Rt△AOB中，由勾股定理，得AB=20∵BE=5，∴AE=15．如图1，作EM⊥x轴于点M，∴EM∥OB．∴△AEM∽△ABO，∴，即：∴EM=12，AM=9，∴OM=12﹣9=3．∴E（3，12）．∴k=36；（3）满足条件的点Q的个数是6，x轴的下方的Q1（10，﹣12），Q2（﹣3，6﹣3）；方法：如下图①分别以CE为矩形的边，在点C、E处设计直角，垂线与两坐标轴相交，得到点P，进而得到点Q；（有三种）②以CE为矩形对角线，则以CE的中点为圆心做圆，与两坐标轴相交，得到点P，再得点Q；（有三种）如图①∵E（3，12），C（﹣6，0），∴CG=9，EG=12，∴EG2=CG•GP，∴GP=16，∵△CPE与△PCQ是中心对称，∴CH=GP=16，QH=FG=12，∵OC=6，∴OH=10，∴Q（10，﹣12），如图②作MN∥x轴，交EG于点N，EH⊥y轴于点H ∵E（3，12），C（﹣6，0），∴CG=9，EG=12，∴CE=15，∵MN=CG=，可以求得PH=3﹣6，同时可得PH=QR，HE=CR ∴Q（﹣3，6﹣3），考点：三角形相似的应用、三角函数、一元二次方程.9．如图，正方形ABCD的四个顶点分别在正方形EFGH的四条边上，我们称正方形EFGH 是正方形ABCD的外接正方形．探究一：已知边长为1的正方形ABCD，是否存在一个外接正方形EFGH，它的面积是正方形ABCD面积的2倍？如图，假设存在正方形EFGH，它的面积是正方形ABCD的2倍．因为正方形ABCD的面积为1，则正方形EFGH的面积为2，所以EF＝FG＝GH＝HE2EB＝x，则BF2﹣x，∵Rt△AEB≌Rt△BFC∴BF＝AE2﹣x在Rt△AEB中，由勾股定理，得x2+2﹣x）2＝12解得，x1＝x2＝2∴BE＝BF，即点B是EF的中点．同理，点C，D，A分别是FG，GH，HE的中点．所以，存在一个外接正方形EFGH，它的面积是正方形ABCD面积的2倍探究二：已知边长为1的正方形ABCD，是否存在一个外接正方形EFGH，它的面积是正方形ABCD面积的3倍？（仿照上述方法，完成探究过程）探究三：已知边长为1的正方形ABCD，一个外接正方形EFGH，它的面积是正方形ABCD面积的4倍？（填“存在”或“不存在”）探究四：已知边长为1的正方形ABCD，是否存在一个外接正方形EFGH，它的面积是正方形ABCD面积的n倍？（n＞2）（仿照上述方法，完成探究过程）【答案】不存在，详见解析【解析】【分析】探究二，根据探究一的解答过程、运用一元二次方程计算即可；探究三，根据探究一的解答过程、运用一元二次方程根的判别式解答；探究四，根据探究一的解答过程、运用一元二次方程根的判别式解答．【详解】探究二：因为正方形ABCD的面积为1，则正方形EFGH的面积为3，所以EF=FG=GH=HE，设EB=x，则BF x，∵Rt△AEB≌Rt△BFC，∴BF=AE﹣x，在Rt△AEB中，由勾股定理，得，x2+x）2=12，整理得x2x+1=0，b2﹣4ac=3﹣4＜0，此方程无解，不存在一个外接正方形EFGH，它的面积是正方形ABCD面积的3倍；探究三：因为正方形ABCD的面积为1，则正方形EFGH的面积为4，所以EF=FG=GH=HE=2，设EB=x，则BF=2﹣x，∵Rt△AEB≌Rt△BFC，∴BF=AE=2﹣x，在Rt△AEB中，由勾股定理，得，x2+（2﹣x）2=12，整理得2x2﹣4x+3=0，b2﹣4ac=16﹣24＜0，此方程无解，不存在一个外接正方形EFGH，它的面积是正方形ABCD面积的3倍，故答案为不存在；探究四：因为正方形ABCD 的面积为1，则正方形EFGH 的面积为n ， 所以EF =FG =GH =HE =n ，设EB =x ，则BF =n ﹣x ， ∵Rt △AEB ≌Rt △BFC ， ∴BF =AE =n ﹣x ，在Rt △AEB 中，由勾股定理，得， x 2+（n ﹣x ）2=12， 整理得2x 2﹣2n x +n ﹣1=0， b 2﹣4ac =8﹣4n ＜0， 此方程无解，不存在一个外接正方形EFGH ，它的面积是正方形ABCD 面积的n 倍． 【点睛】本题考查了正方形的性质、全等三角形的判定和性质、一元二次方程的解法等知识.读懂探究一的解答过程、正确运用一元二次方程根的判别式是解题的关键．10．如图1，已知△ABC 中，AB=10cm,AC=8cm,BC=6 cm ,如果点P 由B 出发沿BA 方向向点A 匀速运动，同时点Q 由A 出发沿AC 方向向点C 匀速运动，它们的速度均为2cm /s ，连接PQ ，设运动的时间为t （单位：s ）（0≤t≤4）.解答下列问题： （1）当t 为何值时，PQ∥BC．（2）是否存在某时刻t ，使线段PQ 恰好把△ABC 的面积平分？若存在求出此时t 的值；若不存在，请说明理由.（3）如图2，把△APQ 沿AP 翻折，得到四边形AQPQ′.那么是否存在某时刻t 使四边形AQPQ′为菱形？若存在，求出此时菱形的面积；若不存在，请说明理由.【答案】（1）当BF PC ⊥s 时，PQ∥BC．（2）不存在某时刻t ，使线段PQ 恰好把△ABC 的面积平分．（3）存在时刻t ，使四边形AQPQ′为菱形，此时菱形的面积为1372-cm 2． 【解析】（1）证△APQ∽△ABC，推出AP AB =AQ AC ，代入得出10210t -=28t，求出方程的解即可；（2）假设存在某时刻t ，使线段PQ 恰好把△ABC 的面积平分，得出方程-56t 2+6t=12×12×8×6，求出此方程无解，即可得出答案. （3）首先根据菱形的性质及相似三角形比例线段关系，求得PQ 、OD 、和PD 的长度；然后在Rt△PQD 中，根据勾股定理列出方程（8-185t ）2-（6-65t ）2=（2t ）2，求得时间t 的值；最后根据菱形的面积等于△AQ P 的面积的2倍，进行计算即可. 解：（1）BP=2t ，则AP=10﹣2t ． ∵PQ∥BC，∴△APQ∽△ABC， ∴AP AB =AQ AC， 即10210t -=28t， 解得：t=209, ∴当t=209时，PQ∥BC. （2）如答图1所示，过P 点作PD⊥AC 于点D ．∴PD∥BC，∴F ，即B ，解得6PD 6-5t =．216625S PD AQ t t =⨯=-， 假设存在某时刻t ，使线段PQ 恰好把△ABC 的面积平分， 则有S △AQP = C S △ABC ，而S △ABC =12AC•BC=24，∴此时S △AQP =12． 而S △AQP 2665t t =-， ∴266125t t -=，化简得：t 2﹣5t+10=0， ∵△=（﹣5）2﹣4×1×10=﹣15＜0，此方程无解， ∴不存在某时刻t ，使线段PQ 恰好把△ABC 的面积平分．（3）假设存在时刻t ，使四边形AQPQ′为菱形，则有AQ=PQ=BP=2t ． 如答图2所示，过P 点作PD⊥AC 于点D ，则有PD∥BC，∴D，即COD∆，解得：OC，h，∴QD=AD﹣AQ=t．在Rt△PQD中，由勾股定理得：QD2+PD2=PQ2，即h，化简得：13t2﹣90t+125=0，解得：t1=5，t2=t，∵t=5s时，AQ=10cm＞AC，不符合题意，舍去，∴t=52．由（2）可知，S△AQP=5 4∴S菱形AQPQ′=2S△AQP=2×258337+cm2．所以存在时刻t，使四边形137-cm2．“点睛”本题考查了三角形的面积，勾股定理的逆定理，相似三角形的性质和判定的应用，主要考查学生综合运用进行推理和计算的能力.解决问题的关键是作辅助线构造相似三角形以及直角三角形，根据相似三角形的对应边成比例以及勾股定理进行列式求解.。