几何证明的好方法截长补短
几何证明的好方法——截长补短有一类几何题其命题主要是证明三条线段长度的“和”或“差”及其比例关系。
这一类题目一般可以采取“截长”或“补短”的方法来进行求解。
所谓“截长”，就是将三者中最长的那条线段一分为二，使其中的一条线段与已知线段相等，然后证明其中的另一段与已知的另一段的大小关系。
所谓“补短”，就是将一个已知的较短的线段延长至与另一个已知的较短的长度相等。
然后求出延长后的线段与最长的已知线段的关系。
有的是采取截长补短后，使之构成某种特定的三角形进行求解。
截长法：（1）过某一点作长边的垂线（2）在长边上截取一条与某一短边相同的线段，再证剩下的线段与另一短边相等。
……补短法（1）延长短边。
（2）通过旋转等方式使两短边拼合到一起。
……几种截长补短解题法类型我们大致可把截长补短分为下面几种类型；类型①a±b=c类型②a±b=kc类型③±a b c类型④c²=a·b对于类型①，可采取直接截长或补短，绕后进行证明。
或者化为类型②证明。
对于②，可以将a±b与c构建在一个三角形中，然后证明这个三角形为特殊三角形，如等边三角形，等腰直角三角形，或一个角为30°的直角三角形等。
对于类型③，一般将截长或补短后的a±b与c构建在一个三角形中，与类型②相同。
实际上是求类型②中的k值。
对于类型④，将c²=a·b化为ca=bc的形式，然后通过相似三角形的比例关系进行证明。
在证明相似三角形的过程中，可能会用到截长或补短的方法。
例：B A在正方形ABCD中，DE=DF，DG⊥CE，交CA于G，GH⊥AF，交AD于P，交CE延长线于H，请问三条粗线DG，GH，CH的数量关系方法一（好想不好证）B A方法二（好证不好想）B AM例题不详解。
（第2页题目答案见第3、4页）E（1）正方形ABCD中，点E在CD上，点F在BC上，∠EAF=45o。
求证：EF=DE+BF（1）变形a正方形ABCD中，点E在CD延长线上，点F在BC延长线上，∠EAF=45o。
请问现在EF、DE、BF又有什么数量关系？（1）变形b正方形ABCD中，点E在DC延长线上，点F在CB延长线上，∠EAF=45o。
请问现在EF、DE、BF又有什么数量关系？（1）变形cD正三角形ABC 中，E 在AB 上，F 在AC 上∠EDF=45o 。
DB=DC ，∠BDC=120o 。
请问现在EF 、BE 、CF 又有什么数量关系？（1）变形dFE正方形ABCD 中，点E 在CD 上，点F 在BC 上，∠EAD=15o ，∠FAB=30o 。
AD=3 求∆AEF 的面积（1）解：（简单思路）FE延长CD 到点G ，使得DG=BF ，连接AG 。
由四边形ABCD 是正方形得∠ADG=∠ABF=90oAD=AB又DG=BF所以∆ADG≅∆ABF（SAS）∠GAD=∠FABAG=AF由四边形ABCD是正方形得∠DAB=90o=∠DAF+∠FAB=∠DAF+∠GAD=∠GAF所以∠GAE=∠GAF-∠EAF=90o-45o=45o∠GAE=∠FAE=45o又AG=AFAE=AE所以∆EAG≅∆EAF（SAS）EF=GE=GD+DE=BF+DE变形a解：（简单思路）EF= BF-DE在BC上截取BG，使得BG=DF，连接AG。
由四边形ABCD是正方形得∠ADE=∠ABG=90oAD=AB又DE=BG所以∆ADE≅∆ABG（SAS）∠EAD=∠GABAE=AG由四边形ABCD是正方形得∠DAB=90o=∠DAG+∠GAB=∠DAG+∠EAD=∠GAE所以∠GAF=∠GAE-∠EAF=90o-45o=45o∠GAF=∠EAF=45o又AG=AEAF=AF所以∆EAF≅∆GAF（SAS）EF=GF=BF-BG=BF-DE变形b解：（简单思路）GEF=DE-BF在DC上截取DG，使得DG=BF，连接AG。
由四边形ABCD是正方形得∠ADG=∠ABF=90oAD=AB又DG=BF所以∆ADG≅∆ABF（SAS）∠GAD=∠FABAG=AF由四边形ABCD是正方形得∠DAB=90o=∠DAG+∠GAB=∠BAF+∠GAB=∠GAF所以∠GAE=∠GAF-∠EAF=90o-45o=45o∠GAE=∠FAE=45o又AG=AFAE=AE所以∆EAG≅∆EAF（SAS）EF=EG=ED-GD=DE-BF变形c解：（简单思路）GDEF=BE+FC延长AC到点G，使得CG=BE，连接DG。
由∆ABC是正三角形得∠ABC=∠ACB=60o又DB=DC，∠BDC=120o所以∠DBC=∠DCB=30o∠DBE=∠ABC+∠DBC=60o+30o=90o∠ACD=∠ACB+∠DCB=60o+30o=90o所以∠GCD=180o-∠ACD=90o∠DBE=∠DCG=90o又DB=DC，BE=CG所以∆DBE≅∆DCG（SAS）∠EDB=∠GDCDE=DG又∠DBC=120o=∠EDB+∠EDC=∠GDC+∠EDC=∠EDG所以∠GDF=∠EDG-∠EDF=120o-60o=60o∠GDF=∠EDF=60o又DG=DEDF=DF所以∆GDF≅∆EDF（SAS）EF=GF=CG+FC=BE+FC变形d解：（简单思路）延长CD到点G，使得DG=BF，连接AG。
过E作EH⊥AG.前面如（1）所证，∆ADG≅∆ABF，∆EAG≅∆EAF∠GAD=∠FAB=30o，S∆EAG=S∆EAF在Rt∆ADG中，∠GAD=30o，AD=3∠AGD=60o，AG=2设EH=x在Rt∆EGH中和Rt∆EHA中∠AGD=60o，∠HAE=45oHG=33x，AH=xAG=2=HG+AH=33x+x,EH=x=3-3S∆EAF=S∆EAG=EH⨯AG÷2=3-3.（第5页题目答案见第6页）（2）O E正方形ABCD中，对角线AC与BD交于O，点E在BD上，AE平分∠DAC。
求证：AC/2=AD-EO（2）加强版M CA正方形ABCD中，M在CD上，N在DA延长线上，CM=AN，点E在BD上，NE平分∠DNM。
请问MN、AD、EF有什么数量关系？（2）解：（简单思路）过E作EG⊥AD于G因为四边形ABCD是正方形∠ADC=90o，BD平分∠ADC，AC⊥BD所以∠ADB=∠ADC/2=45o因为AE平分∠DAC，EO⊥AC，EG⊥AD所以∠EAO=∠EAG，∠DGE=∠AOE=∠AGE=90o又AE=AE，所以∆AEO≅∆AEG（AAS）所以AG=AO，EO=EG又∠ADB=45o，∠DGE=90o所以∆DGE为等腰直角三角形DG=EG=EOAD-DG=AD-EO=AG=AO=AC/2（2）加强版解：（简单思路）M CAMN/2=AD-EF过E作EG⊥AD于G，作EQ⊥AB于Q，过B做BP⊥MN于P按照（2）的解法，可求证，∆GNE≅∆FNE（AAS）∆DGE为等腰直角三角形AG=AD-DG=AD-EF，因为四边形ABCD为正方形，∠ABC=∠GAQ=∠BCM=90oBD平分∠ABC，BC=BA∠ABD=∠ABC/2=45o，又∠EQB=90o ∆EQB为等腰Rt三角形，∠BEQ=45o因为∠GAQ=∠EGA=∠EQA=90o所以四边形AGEQ为矩形，EQ=AG=AD-EF，EQ//AG∠QEN=∠ENG又∠ENG=∠ENF，所以∠QEN=∠ENF由BC=BA，∠BCM=∠BAN=90o，CM=AN，所以∆BCM≅∆BAN（SAS）BM=BN，∠CBM=∠ABN∠ABC=90o=∠ABM+∠CBM=∠ABM+∠ABN=∠MBN，又BM=BN所以∆MBN为等腰Rt三角形，又BP⊥斜边MN于P，所以∆NPB为等腰Rt三角形。
BP=MN/2，∠PNB=45o。
∠BNE=∠ENF+∠PNB∠BEN=∠QEN+∠QEB又∠QEN=∠ENF，∠PNB=∠QEB=45o所以∠BNE=∠BENBN=BE，又∠PNB=∠QEB=45o=∠NBP=∠EBQ所以∆BEQ≅∆BNP（SAS）EQ=BP因为EQ=AG=AD-EF，BP=MN/2所以AD-EF=MN/2。
综合题体中的截长补短1、如图，在⊙O中，C是AB的中点，直线CD⊥AB于点E，AB＝BE，PB、PA组成的⊙O的一条折弦，C是劣弧AB的中点，直线CD⊥PA于点E，则AE ＝PE+PB，请证明你的结论。
分析：本题要证明AE＝PE+PB，可以将AE分为两段，使其中一段长度等于PE，然后另一段长度关于PB。
反之亦。
证明△AHC≌△BPC。
然后再证明PB ＝PE，那么AE＝PE+PB。
证明：在AE上截取AH＝PB，连接AC、CH、BC、CP。
∵C是AB的中点∴AC＝BC∴AC＝BC∵CP＝CP∴∠A＝∠B∴在△CAH与△CBP中CA=CB∠A=∠BAH=BP∴△CAH≌△CBP (SAS)∴CH＝CP∵CE⊥HP∴ PE ＝EH ∴ AE ＝PE+PB2、 如图，⊙O 为△ABC 的外接圆，弦CP 平分△ABC 的外角∠BCQ ，∠ACB＝120°， 求BC AC PC-的值。
分析：要求BC AC PC-的值，可用截长的方法来做，即可在AB 上截取BE ＝AC ，使△PBE ≌△PAC 。
即可求出BC AC PC-的值。
解：连接PA 、PB ，在BC 上截取BE ，使BE ＝AC ，连接PE 。
∵∠QCP+∠PCA ＝180° 又∵∠PCA+∠PBA ＝120° ∴∠QCP ＝∠PBA ∵PB ＝PB ∴∠PCB ＝∠PAB 又∵∠QCP ＝∠PBA ∴∠PBA ＝∠PAB ∴PA ＝PB ，PB ＝PA 在△PBE 与△PAC 中∴△PBE ≌△PAC （SAS ） ∴PC ＝PE∴∠PEC ＝∠BCP ＝30°∴CEPC＝3 ∴BC AC PC-＝3PB=PA ∠PBC=∠QAP BE=AC3、如图，⊙O为△ABC的外接圆，弦CP平分△ABC的外角∠ACQ，∠ACB＝90°，求证：①PA＝PB②AC－BC＝2PC分析：要证明AC－BC＝2PC，可使用截长的方法，即在AC上截取AH＝BC，HC＝AC-BC，然后将HC与PC构建一个等腰直角三角形，且HC为斜边，PC为直角边。
通过求解△APH≌△CBP。
即可证明AC－BC＝2PC。
证明：连接PA、PB，在AC上截取AH＝BC。
∵CP平分∠ACQ, ∠ACQ＝90°∴∠PCA＝∠QCP＝45°∵四边形APCB为圆的内接四边形∴∠PAB+∠PCB＝180°＝∠PCQ＝∠PCB∴PA＝PB∴PA＝PB∵PC＝PC∴∠CBP＝∠PAC在△APH与△CBP中AH=CB∠CBP=∠PACAP=BP∴△APH≌△CBP∴PH＝PC∵∠PCH＝45°又∵△PHC为等腰直角三角形∴AC－AH＝A C－CB＝HC＝2PC∴AC－BC＝2PC4、 如图，⊙O 为△ABC 的外接圆，弦CD 平分∠ACB ，∠ACB ＝120°，求CA CBCD+的值。
全等三角形-截长补短法
全等三角形-截长补短法全等三角形截长补短法在初中数学的几何学习中，全等三角形是一个重要的知识点，而解决全等三角形相关问题时，截长补短法是一种非常实用且巧妙的方法。
首先，咱们来聊聊什么是截长补短法。
简单来说，截长补短就是通过在图形中截取或者延长某条线段，使得图形中的线段关系发生变化，从而构造出全等三角形，帮助我们解决问题。
比如说，有一个三角形 ABC，其中∠B ＝ 2∠C，要证明 AB ＝ AC ＋ CD。
这时候，我们就可以考虑使用截长补短法。
如果使用截长的思路，就在 AB 上截取 AE ＝ AC，然后连接 DE。
这样一来，因为 AE ＝AC，再加上公共边 AD，以及已知的∠CAD ＝∠EAD，就可以证明△ACD 和△AED 全等。
然后通过一系列的角度推导，就能得出结论。
要是用补短的方法呢，就是延长 AC 至 E，使 CE ＝ CD，连接 DE。
通过角度关系证明∠E ＝∠CDE，进而得出∠B ＝∠BDE，再证明△ABD 和△AED 全等。
接下来，咱们通过几个具体的例子来更深入地理解截长补短法。
例 1：在△ABC 中，AB ＞ AC，AD 平分∠BAC，P 为 AD 上一点。
求证：AB AC ＞ PB PC。
我们来用截长的方法解决。
在 AB 上截取 AE ＝ AC，连接 PE。
因为 AD 平分∠BAC，所以∠BAD ＝∠CAD。
又因为 AE ＝ AC，AP 是公共边，所以△APE ≌△APC。
那么 PC ＝ PE。
在△PBE 中，根据三角形两边之差小于第三边，有 PB PE ＜ BE。
而 BE ＝ AB AE ＝ AB AC，所以 AB AC ＞ PB PC。
例 2：已知在正方形 ABCD 中，∠MAN ＝ 45°，∠MAN 绕点 A 顺时针旋转，它的两边分别交 CB、DC 于点 M、N。
求证：BM ＋ DN ＝MN。
这道题我们用补短的方法。
延长 CB 至 E，使 BE ＝ DN，连接 AE。
八年级上册数学截长补短法
八年级上册数学截长补短法一、截长补短法的概念。
1. 定义。
- 截长补短法是几何证明题中一种常用的辅助线添加方法。
“截长”就是将一条较长的线段截成两段或几段，使得其中的一段或几段与已知线段相等；“补短”就是将一条较短的线段延长，使得延长后的线段与已知的较长线段相等。
- 例如，在三角形ABC中，要证明AB = AC+CD（假设AB>AC），“截长”的做法可以是在AB上截取AE = AC，然后去证明BE=CD；“补短”的做法可以是延长AC到F，使CF = CD，然后去证明AB = AF。
2. 适用情况。
- 当题目中出现证明两条线段之和等于第三条线段或者两条线段之差等于第三条线段等类型的问题时，常常考虑使用截长补短法。
- 比如在四边形或者三角形的边的关系证明中经常用到。
如在等腰三角形的相关证明中，如果要证明等腰三角形腰长与底边一部分线段的关系时，可能就需要用到这种方法。
二、截长补短法的解题步骤。
1. 截长法解题步骤。
- 第一步：观察图形和已知条件，确定要截的线段。
一般选择较长的那条线段进行截取。
- 第二步：根据已知条件截取合适的长度，使得截取后的线段与其他已知线段有一定的联系。
例如，在三角形中，如果有角平分线的条件，可能会截取与角平分线到角两边距离相等的线段。
- 第三步：连接截取点与其他点，构造全等三角形或者其他特殊的几何关系。
- 第四步：利用全等三角形的性质或者其他几何定理进行推理，得出要证明的结论。
- 例如：在三角形ABC中，AD是∠BAC的角平分线，∠C = 2∠B，求证：AB = AC+CD。
- 证明（截长法）：在AB上截取AE = AC，连接DE。
- 因为AD是角平分线，所以∠EAD = ∠CAD。
- 在△AED和△ACD中，AE = AC，∠EAD = ∠CAD，AD = AD，根据SAS（边角边）定理，△AED≌△ACD。
- 所以∠AED = ∠C，CD = ED。
- 又因为∠C = 2∠B，∠AED = ∠B + ∠EDB，所以∠B = ∠EDB。
《截长补短法》课件
04
截长补短法的实例
实例一：几何图形
总结词
通过图形直观展示
详细描述
在PPT中，我们可以使用几何图形来展示截长补短法的应用。例如，在平面几何中，我们可以通过将一个不规则 图形切割成几个规则图形，然后进行补充，从而得到一个新的规则图形。这种方法可以帮助学生更好地理解几何 图形的性质和特点。
实例二：数据可视化
原理的数学解释
截长补短法是一种基于几何和代数知识 的解题方法，其原理可以通过数学公式
和定理进行解释。
在几何学中，截长补短法可以用于证明 一些线段或角度的性质和关系，例如通 过截取线段来证明两个三角形相似或通 过补全角度来证明一个四边形是平行四
边形。
在代数中，截长补短法可以用于解决一 些方程和不等式问题，例如通过将一个 复杂的多项式方程进行截取和补全，来
索其在其他领域的应用。
拓展应用范围
尝试将截长补短法与其他几何 作图方法结合，拓展其应用范 围，解决更多复杂的几何问题 。
提高教学水平
在数学教学中，加强对截长补 短法的介绍和讲解，帮助学生 更好地理解和掌握该方法。
激发学习兴趣
通过引导学生运用截长补短法 解决实际问题，激发他们对数
学学习的兴趣和热情。
THANKS
简单、更易于解决的小问题。
补全短线段
补全短线段是指在解题过程中，将一些较短的线段或步骤进行补充和整合，使其形 成一个完整的解决方案。
通过补全短线段，可以将零散的信息和步骤整合起来，形成一个完整的知识体系或 解决方案。
在数学问题中，补全短线段通常用于将一些分散的条件和信息整合起来，形成一个 完整的证明或解题过程。
找到满足条件的解。
03
截长补短法的步骤
几何辅助线之截长补短 总结+例题
截长补短专题知识导航“截长补短”是几何证明题中十分重要的方法，通常用来证明几条线段的数量关系，即若题目条件或结论中含有“c b a =+”的条件，需要添加辅助线时可以考虑“截长补短”的方法。
截长法：在较长的线段上截取一条线段等于较短线段，再设法证明较长线段的剩余线段等于另外的较短线段。
补短法：①延长较短线段中的一条，使延长出来的线段等于另外的较短线段，然后证明两线段之和等于较长线段。
即延长a ，得到b ，证：c b a =+。
②延长较短线段中的一条，使延长后的线段等于较长线段，然后证明延长出来的部分等于另一条较短线段。
即延长a ，得到c ，证：a c b -=。
【核心考点1】角平分线相关截长补短1. 如图，BP 平分ABC ∠，D 为BP 上一点，E ，F 分别在BA ，BC 上，且满足DE DF =，若140BED ∠=︒，则BFD ∠的度数是( )A ．40︒B ．50︒C ．60︒D ．70︒【分析】作DG AB ⊥于G ，DH BC ⊥于H ，根据角平分线的性质得到DH DG =，证明Rt DEG Rt DFH ∆≅∆，得到DEG DFH ∠=∠，根据互为邻补角的性质得到答案．【解答】解：作DG AB ⊥于G ，DH BC ⊥于H ，D 是ABC ∠平分线上一点，DG AB ⊥，DH BC ⊥， DH DG ∴=，在Rt DEG ∆和Rt DFH ∆中， DG DHDE DF=⎧⎨=⎩， ()Rt DEG Rt DFH HL ∴∆≅∆，DEG DFH ∴∠=∠，又180DEG BED ∠+∠=︒， 180BFD BED ∴∠+∠=︒，BFD ∴∠的度数18014040=︒-︒=︒，故选：A ．2. 已知，如图，ABC ∆中，2C B ∠=∠，12∠=∠，求证：AB AC CD =+．【分析】在AB 上截取AE AC =，由“SAS ”可证ADE ADC ∆≅∆，可证DE DC =，C AED ∠=∠，可证B BDE ∠=∠，可得BE DE DC ==，即结论可得． 【解答】证明：如图，在AB 上截取AE AC =，AE AC =，12∠=∠，AD AD =()ADE ADC SAS ∴∆≅∆DE DC ∴=，C AED ∠=∠， 2C B ∠=∠，AED B BDE ∠=∠+∠，B BDE ∴∠=∠ BE DE DC ∴==，AB AE BE =+， AB AC DC ∴=+。
“截长补短法”在一类几何证明题中的运用
“截长补短法”在一类几何证明题中的运用探究线段的和、差、倍、分是平面几何中常见的问题，“截长补短法”是解决这一类问题的一种常用的特殊方法，“截长”就是将题中的某条线段截成题中的几条线段之和；“补短”就是将题中某条线段延长（补上某线段），然后，证明它与题中某条线段相等。
例1 已知：△ABC是⊙O的内接等边三角形，点P为弧BC上一动点，求证：PA=PB+PC。
分析：直接证明PA=PB+PC，困难较大。
可用截长法：在PA上截取PD=PB，再证明PC=DA即可（或用补短法：在BP或CP上各补上与CP或BP相等的线段，再证明PA与这条线段相等）。
证明（截长法）：在PA上截取PD=PB，连接BD，∵△ABC是圆O的内接等边三角形，∴ BA=BC，∠ABC=∠ACB=60°。
∵∠BPA=∠BCA，∴∠BPA=60°。
∴△BPD是等边三角形。
∴ BD=BP，∠DBP=60°。
∴∠ABD=∠CBP。
∴△ABD≌△CBP。
∴ PC=DA。
又∵ PA=PD+DA，∴ PA=PB+PC。
证明（补短法）：延长BP到D使PD=PC，连接CD，∵△ABC是圆内接等边三角形，∴ AC=BC，∠ABC=∠ACB=60°。
∵∠BPA=∠BCA，∠ABC=∠APC，∴∠BPA=60°=∠APC。
∴∠CPD=60°。
∴△CPD是等边三角形。
∴ CD=CP ∠DCP=60°。
∴∠ACP=∠BCD。
∴△ACP≌△BCD。
∴ PA=BA。
又∵ BD=PD+BP，∴ PA=PB+PC。
例2 已知：四边形ABCD是☉O的内接正方形，点P为弧BC上一动点，求证：PA=PC+■PB。
分析一：要证明PA=PC+■PB，我们可以在PA上取AD=PC，连接BD，再想办法证明PD=■PB，问题可以解决。
证明：在AP上截取AE=PC，连接BE。
∵四边形ABCD是圆内接正方形，∴ AB=CB，∠BPA=45°。
一题多解｜截长补短问题6种证明方法
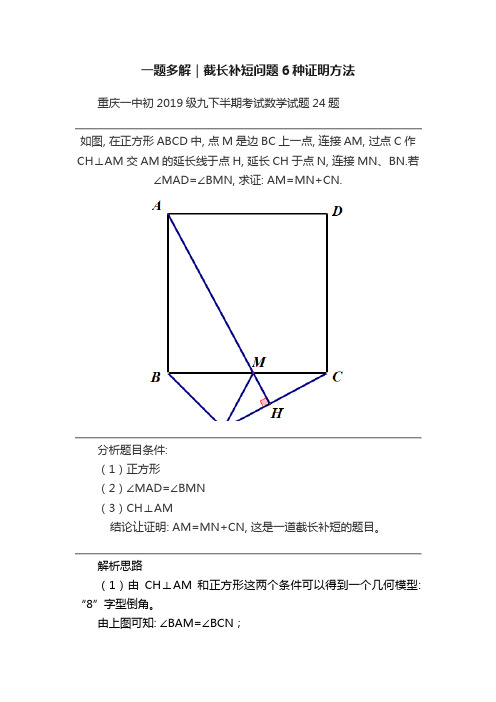
一题多解｜截长补短问题6种证明方法重庆一中初2019级九下半期考试数学试题24题如图, 在正方形ABCD中, 点M是边BC上一点, 连接AM, 过点C作CH⊥AM交AM的延长线于点H, 延长CH于点N, 连接MN、BN.若∠MAD=∠BMN, 求证: AM=MN+CN.分析题目条件:（1）正方形（2）∠MAD=∠BMN（3）CH⊥AM结论让证明: AM=MN+CN, 这是一道截长补短的题目。
解析思路（1）由CH⊥AM和正方形这两个条件可以得到一个几何模型: “8”字型倒角。
由上图可知: ∠BAM=∠BCN；（2）由∠MAD=∠BMN和正方形这两个条件, 可以得到：∠MAD=∠BMN=∠AMB；方法1: 在AM上截取MN'=MN, 连接CN'（1）首先证明△BMN≌△BMN', 得到BN=BN', ∠MBN=∠MBN'；（2）再次证明△BCN≌△BCN', 得到CN=CN', ∠BCN=∠BCN'=∠BAM；（3）其次∠BAC=∠BAM+∠CAM=45°, ∠BCA=∠BCN'+∠ACN'=45°;所以∠CAM=∠ACN', 所以AN'=CN'（4）最后, 通过边之间的关系可以得到：AN'=CN'=CN, 所以AM=MN+CN方法2: 延长MN与AB相交于点G, 连接CG（1）首先∠AMB=∠GMB, MB⊥AG, 由“三线合一”知: MA=MG；（2）结合分析和第一步证明可知: ∠1=∠2=∠3（3）同理: ∠BGC=∠BGM+∠CGM=45°, ∠BCG=∠BCN+∠GCN=45°;所以∠NCG=∠NGC, 所以NG=NC; （4）最后, 通过边之间的关系可以得到：AM=MN+CN；方法3: 连接BD交AH于点E, 连接EC；（1）首先证明△ABE≌△CBE, 得到AE=CE；（2）再次证明△ECM≌△NCM, 得到EM=MN;（3）最后, 通过边之间的关系可以得到：AM=MN+CN；方法4: 在AB上截取BG=BM, 连接CG交AM于点P（1）首先证明△ABM≌△CBG, 得到∠BAM=∠BCG=∠BCN, AG=CM；（2）再次证明△APG≌△CPM, 得到AP=CP;（3）然后证明△PCM≌△NCM, 得到CN=CP=AP;（4）最后, 通过边之间的关系可以得到：AM=MN+CN；方法5: 延长AB与MN相交与点G, 延长CN与BG交于点Q（1）首先∠AMB=∠GMB, MB⊥AG, 由“三线合一”知: MA=MG；（2）△GBM≌△CBQ, 所以边之间的关系可以得到QG=CM；（3）△GNQ≌△CNM, 所以NG=NC, NQ=NM；（4）最后, 通过边之间的关系可以得到：AM=MN+CN；方法6: 延长AB与CN交于点G, 连接MG；（1）首先证明△ABM≌△CBG, 所以∠AMB=∠NMB=∠CGB；（2）同时△BGM为等腰RT△；（3）所以∠NGM=∠CGB-45°；∠NMG=∠BMN-45°；所以∠NGM=∠NMG；所以NG=NM；（4）最后, 通过边之间的关系可以得到：AM=MN+CN；。
谈谈“截长补短”在几何证明中的运用
谈谈“截长补短”在几何证明中的运用作者：冯军来源：《新一代》2009年第09期摘要:几何证明题是数学试题中必不可少的题型,其数量成千上万,但不少题目之间还是存在一定的方法和技巧可以运用的,其中“截长补短”就是一种非常重要的几何证明手段。
关键词:几何证明;截长补短中图分类号:G622 文献标识码:A文章编号: 1003-2851(2009)09-0066-01几何证明题是数学试题中必不可少的题型,其数量成千上万,但不少题目之间还是存在一定的方法和技巧可以运用的,其中“截长补短”就是一种非常重要的几何证明手段。
例1:如图,已知:AP是△ABC的∠BAC的平分线,AB+BP=AC.求证:∠B=2∠C.分析一:在条件AB+BP=AC中,AC被称为长线段,可在AC上截取AD=AB,这就叫做截长,截长后可以得到两组相等线段,AD=AB和PB=DC,它们可作为条件使用。
证明:在AC上截取AD=AB则PB=DC.∵AP平分∠BAC , ∴∠BAP=∠DAP.又∵AB=AD, AP公用,∴△ABP≌△ADP. ∴PB=PD. ∠B=∠ADP=∠DPC+∠C.∴PD=DC.∴∠DPC=∠C.∴∠B=2∠C.分析二:在条件AB+BP=AC中,AB和BP被称为短线段可以拼接在一起,延长AB到E使BE=BP,这就叫补短,补短后可得两组相等的线段,BE=BP和AE=AC,可以作为条件使用。
证明:延长AB使BE=BP.则可得:AE=AB+BE=AB+BP=AC和∠E=∠BPE.∵AP平分∠BAC,∴∠EAP=∠CAP, AP公用, ∴△EAP≌△CAP.∴∠E=∠C. 而∠ABC=∠E+∠BPE, ∴∠ABC=2∠E=2∠C.互换上题中的条件AB+BP=AC和结论∠B=2∠C得一条新题。
例2:如图,已知:AP是△ABC的∠BAC的平分线,∠B=2∠C.求证:AB+BP=AC.分析一:在AC上截取AD=AB,截长后得AD=AB,可以作为条件使用,由于AB+BP=AC是需要证明的结论,所以还需要证到BP=DC,可以先证明△ABP≌△ADP得∠ADP=∠B和BP=DP,再用∠B=2∠C和∠ADP=∠C+∠DPC,得∠C+∠DPC=2∠C,得∠DPC=∠C,再得DP =DC,从而证到AB+BP=AC,证明略。
13.13专题13：截长补短法-角平分线
13.13专题13：截长补短法-角平分线一．【知识要点】1.截长补短（截长法，补短法）是证明线段和差问题的基本方法:有一类几何题其命题主要是证明三条线段长度的“和”或“差”及其比例关系。
这一类题目一般可以采取“截长”或“补短”的方法来进行求解。
所谓“截长”，就是将三者中最长的那条线段一分为二，使其中的一条线段与已知线段相等，然后证明其中的另一段与已知的另一段的大小关系。
所谓“补短”，就是将一个已知的较短的线段延长至与另一个已知的较短的长度相等。
然后求出延长后的线段与最长的已知线段的关系。
有的是采取截长补短后，使之构成某种特定的三角形进行求解。
二．【经典例题】1．如图，已知AD∥BC，∠PAB的平分线与∠CBA的平分线相交于E，CE的连线交AP于D．求证：AD+BC=AB．2.如图，∠A=60°，BE平分∠ABC，CD平分∠ACB，求证：BD+CE=BC3.如图,△ABC中,AB>AC,AD是∠BAC的平分线，点P是线段AD上异于A，D的任意一点,则AB+PC与AC+PB的大小关系是( )A. AB+PC>AC+PBB. AB+PC<AC+PBC.AB+PC=AC+PBD.不确定4.如图,在等腰Rt△ABC中,AC=BC,∠ACB=90°,点D、E分别在CA的延长线和AC 的延长线上,AD=CE,F为BA延长线上的一点,且∠CFA=∠DFA,求证:DF十BE=CF.5.如图,△ABC中,∠BAC、∠BCA的平分线相交于点P,若∠CBA=40°,BC=AP+AC.（1）求∠PBC的度数;（2）求∠BCA的度数.6.（8分）如图,在△ABC中,AD、CE分别平分△BAC、△ACB, AD、CE交于O.(1)探究△AOC的度数与△B的数量关系;(2)若△ABC=60°, 求证:AC=AE+CD.7．如图，△ABC中，AB＝AC，∠A＝100°，BD平分∠ABC．（1）求∠ADB的度数．（2）求证：BC＝BD+AD．三．【题库】【A】1.已知：AD∥BC，EA,EB分别平分∠DAB,∠CBA，CD过点E，求证：AB＝AD+BC。
几何证明的好方法——截长补短
几何证明的好方法——截长补短有一类几何题其命题主要是证明三条线段长度的“和”或“差”及其比例关系。
这一类题目一般可以采取“截长"或“补短”的方法来进行求解.所谓“截长”，就是将三者中最长的那条线段一分为二，使其中的一条线段与已知线段相等,然后证明其中的另一段与已知的另一段的大小关系.所谓“补短”，就是将一个已知的较短的线段延长至与另一个已知的较短的长度相等。
然后求出延长后的线段与最长的已知线段的关系。
有的是采取截长补短后，使之构成某种特定的三角形进行求解.截长法:(1）过某一点作长边的垂线(2）在长边上截取一条与某一短边相同的线段，再证剩下的线段与另一短边相等。
……补短法(1)延长短边.（2)通过旋转等方式使两短边拼合到一起。
……几种截长补短解题法类型我们大致可把截长补短分为下面几种类型；类型①a±b=c类型②a±b=kc类型③±a b c类型④c²=a·b对于类型①，可采取直接截长或补短,绕后进行证明。
或者化为类型②证明.对于②,可以将a±b与c构建在一个三角形中，然后证明这个三角形为特殊三角形，如等边三角形，等腰直角三角形，或一个角为30°的直角三角形等。
对于类型③,一般将截长或补短后的a±b与c构建在一个三角形中,与类型②相同。
实际上是求类型②中的k值。
对于类型④，将c²=a·b化为ca=bc的形式，然后通过相似三角形的比例关系进行证明。
在证明相似三角形的过程中，可能会用到截长或补短的方法。
例:B A在正方形ABCD中，DE=DF，DG⊥CE，交CA于G，GH⊥AF，交AD于P,交CE延长线于H，请问三条粗线DG，GH，CH的数量关系方法一（好想不好证）B A方法二（好证不好想)B AM例题不详解.（第2页题目答案见第3、4页）E(1)正方形ABCD中，点E在CD上,点F在BC上，∠EAF=45o.求证：EF=DE+BF（1）变形a正方形ABCD中,点E在CD延长线上,点F在BC延长线上,∠EAF=45o。
专题 全等三角形模型——截长补短与倍长中线(解析版)
全等三角形模型——截长补短与倍长中线截长补短截长：即在一条较长的线段上截取一段较短的线段在线段AB 上截取AD AC=补短：即在较短的线段上补一段线段使其和较长的线段相等延长AC ，使得AD AB =1.ABC D 中，AD 是BAC Ð的平分线，且AB AC CD =+．若60BCA Ð=°，则ABC Ð的大小为( )A ．30°B ．60°C ．80°D ．100°【分析】可在AB 上取AC AC ¢=，则由题中条件可得BC C D ¢=¢，即2C AC D B Ð=Т=Ð，再由三角形的外角性质即可求得B Ð的大小．【解答】解：如图，在AB 上取AC AC ¢=，AD Q 是角平分线，DAC DAC ¢\Ð=Ð，ACD \D @△()AC D SAS ¢，CD C D ¢\=，又AB AC CD =+Q ，AB AC C B ¢¢=+，BC C D \¢=¢，DCBAAB CD260C AC D B ¢\Ð=Ð=Ð=°，30B \Ð=°．故选：A ．2.阅读：探究线段的和．差．倍．分关系是几何中常见的问题，解决此类问题通常会用截长法或补短法，具体做法是在某条线段上截取一条线段与特定线段相等，或是将某条线段延长，使之与特定线段相等，再利用三角形全等的有关性质加以说明．（1）请完成下题的证明过程：如图1，在ABC D 中，2B C Ð=Ð，AD 平分BAC Ð．求证：AB BD AC +=．证明：在AC 上截取AE AB =，连接DE（2）如图2，//AD BC ，EA ，EB 分别平分DAB Ð，CBA Ð，CD 过点E ，求证：AB AD BC =+．【分析】（1）在AC 上截取AE AB =，连接DE ，证明ABD AED D @D ，得到B AED Ð=Ð，再证明ED EC =即可；（2）由等腰三角形的性质知AE FE =，再证明ADE FCE D @D 即可解决本题．【解答】证明：在AC 上截取AE AB =，连接DE ，如图1:AD Q 平分BAC Ð，BAD DAC \Ð=Ð，在ABD D 和AED D 中，AE AB BAD DAC AD AD =ìïÐ=Ðíï=î，()ABD AED SAS \D @D ，B AED \Ð=Ð，BD DE =，又2BC Ð=Ð，2AED C \Ð=Ð，而2AED C EDC C Ð=Ð+Ð=Ð，C EDC \Ð=Ð，DE CE \=，AB BD AE CE AC \+=+=；（2）延长AE 、BC 交于F ，AB BF =Q ，BE 平分ABF Ð，AE EF \=，在ADE D 和FCE D 中，DAE F AE EFAED CEF Ð=Ðìï=íïÐ=Ðî，()ADE FCE ASA \D @D ，AD CF \=，AB BF BC CF BC AD \==+=+．3.如图，在ABC D 中，AD 平分BAC Ð交BC 于D ，在AB 上截取AE AC =．（1）求证：ADE ADC D @D ；（2）若6AB =，5BC =，4AC =，求BDE D的周长．【分析】（1）根据SAS 证明ADE ADC D @D 即可；（2）根据全等三角形的性质和线段之间的关系进行解答即可．【解答】证明：（1）AD Q 平分BAC Ð，EAD CDA \Ð=Ð，在ADE D 与ADC D 中，AE AC EAD CDA AD AD =ìïÐ=Ðíï=î，()ADE ADC SAS \D @D ，（2）ADE ADC D @D Q ，ED DC \=，BDE \D 的周长6457BE BD DE AB AE BC DC DC AB AC BC DC DC AB AC BC =++=-+-+=-+-+=-+=-+=4.（2020秋•武昌区期中）如图，ABC D 中，60ABC Ð=°，AD 、CE 分别平分BAC Ð、ACB Ð，AD 、CE 相交于点P（1）求CPD Ð的度数；（2）若3AE =，7CD =，求线段AC 的长．【分析】（1）利用60ABC Ð=°，AD 、CE 分别平分BAC Ð，ACB Ð，即可得出答案；（2）由题中条件可得APE APF D @D ，进而得出APE APF Ð=Ð，通过角之间的转化可得出CPF CPD D @D ，进而可得出线段之间的关系，即可得出结论．【解答】解：（1）60ABC Ð=°Q ，AD 、CE 分别平分BAC Ð，ACB Ð，120BAC BCA \Ð+Ð=°，1()602PAC PCA BAC BCA Ð+Ð=Ð+Ð=°，120APC \Ð=°，60CPD \Ð=°．（2）如图，在AC 上截取AF AE =，连接PF ．AD Q 平分BAC Ð，BAD CAD \Ð=Ð，在APE D 和APF D 中AE AF EAP FAP AP AP =ìïÐ=Ðíï=î，()APE APF SAS \D @D ，APE APF \Ð=Ð，120APC Ð=°Q ，60APE \Ð=°，60APF CPD CPF \Ð=Ð=°=Ð，在CPF D 和CPD D 中，FPC DPC CP CPFCP DCP Ð=Ðìï=íïÐ=Ðî，()CPF CPD ASA \D @D CF CD \=，3710AC AF CF AE CD \=+=+=+=．5.如图，在ABC D 中，60BAC Ð=°，AD 是BAC Ð的平分线，且AC AB BD =+，求ABC Ð的度数．【分析】在AC上截取AE AB=，根据角平分线的定义可得BAD CADÐ=Ð，然后利用“边角边”证明ABDD和AEDD全等，根据全等三角形对应边相等可得BD DE=，全等三角形对应角相等可得B AEDÐ=Ð，再求出CE BD=，从而得到CE DE=，根据等边对等角可得C CDEÐ=Ð，根据三角形的一个外角等于与它不相邻的两个内角的和可得2AED CÐ=Ð，然后根据三角形的内角和定理列方程求出CÐ，即可得解．【解答】解：如图，在AC上截取AE AB=，ADQ平分BACÐ，BAD CAD\Ð=Ð，在ABDD和AEDD中，AE ABBAD CAD AD AD=ìïÐ=Ðíï=î，()ABD AED SAS\D@D，BD DE\=，B AEDÐ=Ð，AC AE CE=+Q，AC AB BD=+，CE BD\=，CE DE\=，C CDE\Ð=Ð，即2B CÐ=Ð，在ABCD中，180BAC B CÐ+Ð+Ð=°，602180C C\°+Ð+Ð=°，解得40CÐ=°，24080ABC\Ð=´°=°．6.如图，五边形ABCDE 中，AB AE =，BC DE CD +=，120BAE BCD Ð=Ð=°，180ABC AED Ð+Ð=°，连接AD ．求证：AD 平分CDE Ð．【分析】连接AC ，将ABC D 绕A 点旋转120°到AEF D ，由AB AE =，120BAE Ð=°，得到AB 与AE 重合，并且AC AF =，又由180ABC AED Ð+Ð=°，得到180AEF AED Ð+Ð=°，即D ，E ，F 在一条直线上，而BC DE CD +=，得CD DF =，则易证ACD AFD D @D ，于是ADC ADF Ð=Ð．【解答】证明：如图，连接AC ，将ABC D 绕A 点旋转120°到AEF D ，AB AE =Q ，120BAE Ð=°，AB \与AE 重合，并且AC AF =，又180ABC AED Ð+Ð=°Q ，而ABC AEF Ð=Ð，180AEF AED Ð+Ð=°Q ，D \，E ，F 在一条直线上，而BC EF =，BC DE CD +=，CD DF \=，又AC AF =Q ，ACD AFD \D @D ，ADC ADF \Ð=Ð，即AD 平分CDE Ð．7.已知：如图，在ABC D 中，D 是BA 延长线上一点，AE 是DAC Ð的平分线，P 是AE 上的一点（点P 不与点A 重合），连接PB ，PC ．通过观察，测量，猜想PB PC +与AB AC +之间的大小关系，并加以证明．【分析】根据全等三角形的判定与性质，可得FP CP =，根据三角形的两边之和大于第三边，可得答案．【解答】解：PB PC AB AC +>+，理由如下：在BA 的延长线上截取AF AC =，连接PF ，在FAP D 和CAP D 中，AF AC FAP CAP AP AP =ìïÐ=Ðíï=î，()FAP CAP SAS \D @D ，FP CP \=．在FPB D 中，FP BP FA AB +>+，即PB PC AB AC +>+．8.已知ABC D 中，AB AC =，BE 平分ABC Ð交边AC 于E ．（1）如图（1），当108BAC Ð=°时，证明：BC AB CE =+；（2）如图（2），当100BAC Ð=°时，（1）中的结论还成立吗？若不成立，是否有其他两条线段之和等于BC，若有请写出结论并完成证明．【分析】（1）如图1中，在BC 上截取BD BA =．只要证明BEA BED D @D ，CE CD =即可解决问题；（2）结论：BC BE AE =+．如图2中，在BA 、BC 上分别截取BF BE =，BH BE =．则EBH EBF D @D ，再证明EA EH EF CF ===即可解决问题；【解答】解：（1）如图1中，在BC 上截取BD BA =．BA BD =Q ，EBA EBD Ð=Ð，BE BE =，BEA BED \D @D ，BA BD \=，108A BDE Ð=Ð=°，AB AC =Q ，36C ABC \Ð=Ð=°，72EDC Ð=°，72CED \Ð=°，CE CD \=，BC BD CD AB CE \=+=+．（2）结论：BC BE AE =+．理由：如图2中，在BA 、BC 上分别截取BF BE =，BH BE =．则EBH EBF D @D ，EF EH \=，100BAC Ð=°Q ，AB AC =，40ABC C \Ð=Ð=°，20EBA EBC \Ð=Ð=°，80BFE H EAH \Ð=Ð=Ð=°，AE EH \=，BFE C FEC Ð=Ð+ÐQ ，40CEF C \Ð=Ð=°，EF CF \=，BC BF CF BE AE \=+=+．9.（2020秋•建华区期末）阅读下面文字并填空：数学习题课上李老师出了这样一道题：“如图1，在ABC D 中，AD 平分BAC Ð，2B C Ð=Ð．求证：AB BD AC +=．”李老师给出了如下简要分析：要证AB BD AC +=，就是要证线段的和差问题，所以有两个方法：方法一：“截长法”．如图2，在AC 上截取AE AB =，连接DE ，只要证BD = EC 即可，这就将证明线段和差问题 为证明线段相等问题，只要证出△ @△ ，得出B AED Ð=Ð及BD = ，再证出Ð = ，进而得出ED EC =，则结论成立．此种证法的基础是“已知AD 平分BAC Ð，将ABD D 沿直线AD 对折，使点B 落在AC 边上的点E 处”成为可能．方法二：“补短法”．如图3，延长AB 至点F ，使BF BD =．只要证AF AC =即可，此时先证Ð C =Ð，再证出△ @△ ，则结论成立．“截长补短法”是我们今后证明线段或角的“和差倍分”问题常用的方法．【分析】方法一、如图2，在AC 上截取AE AB =，由“SAS ”可证ABD AED D @D ，可得B AED Ð=Ð，BD DE =，由角的数量关系可求DE CE =，即可求解；方法二、如图3，延长AB 至点F ，使BF BD =，由“AAS ”可证AFD ACD D @D ，可得AC AF =，可得结论．【解答】解：方法一、在AC 上截取AE AB =，连接DE ，如图2:AD Q 平分BAC Ð，BAD DAC \Ð=Ð，在ABD D 和AED D 中，AE AB BAD DAC AD AD =ìïÐ=Ðíï=î，()ABD AED SAS \D @D ，B AED \Ð=Ð，BD DE =，又2B C Ð=ÐQ ，2AED C \Ð=Ð，而2AED C EDC C Ð=Ð+Ð=Ð，C EDC \Ð=Ð，DE CE \=，AB BD AE CE AC \+=+=，故答案为：EC ，转化，ABD ，AED ，DE ，EDC ，C Ð；方法二、如图3，延长AB 至点F ，使BF BD =，F BDF \Ð=Ð，2ABD F BDF F \Ð=Ð+Ð=Ð，2ABD C Ð=ÐQ ，F C \Ð=Ð，在AFD D 和ACD D 中，FAD CAD F CAD AD Ð=ÐìïÐ=Ðíï=î，()AFD ACD AAS \D @D ，AC AF \=，AC AB BF AB BD \=+=+，故答案为F ，AFD ，ACD ．倍长中线倍长中线：即延长三角形的中线，使得延长后的线段是原中线的两倍．其目的是构造一对对顶的全等三角形；其本质是转移边和角．其中BD CD =，延长AD 使得DE AD =，则BDE CDA △≌△．10.三角形ABC 中，AD 是中线，且4AB =，6AC =，求AD 的取值范围是 ．【分析】延长AD 到E ，使AD DE =，连接BE ，证ADC EDB D @D ，推出8AC BE ==，在ABE D 中，根据三角形三边关系定理得出AB BE AE AB BE -<<+，代入求出即可．【解答】解：延长AD 到E ，使AD DE =，连接BE ，AD Q 是BC 边上的中线，BD CD \=，在ADC D 和EDB D 中，Q AD DE ADC EDB DC BD =ìïÐ=Ðíï=î，()ADC EDB SAS \D @D ，4AC BE \==，在ABE D 中，AB BE AE AB BE -<<+，64264AD \-<<+，15AD \<<，故答案为：15AD <<．11.（2021春•碑林区校级期中）问题背景：课外兴趣小组活动时，老师提出了如下问题：如图1，ABCD 中，若4AB =，3AC =，求BC 边上的中线AD 的取值范围．小明在组内经过合作交流，得到了如下ED ABC的解决方法：延长AD 到点E ，使DE AD =，则得到ADC EDB D @D ，小明证明BED CAD D @D 用到的判定定理是： （用字母表示）；问题解决：小明发现：解题时，条件中若出现“中点”“中线”字样，可以考虑延长中线构造全等三角形，把分散的已知条件和所求证的结论集合到同一个三角形中．请写出小明解决问题的完整过程；拓展应用：以ABC D 的边AB ，AC 为边向外作ABE D 和ACD D ，AB AE =，AC AD =，90BAE CAD Ð=Ð=°，M 是BC 中点，连接AM ，DE ．当3AM =时，求DE 的长．【分析】问题背景：先判断出BD CD =，由对顶角相等BDE CDA Ð=Ð，进而得出()ADC EDB SAS D @D ；问题解决：先证明()ADC EDB SAS D @D ，得出3BE AC ==，最后用三角形三边关系即可得出结论；拓展应用：如图2，延长AM 到N ，使得MN AM =，连接BN ，同（1）的方法得出()BMN CMA SAS D @D ，则BN AC =，进而判断出ABN EAD Ð=Ð，进而判断出ABN EAD D @D ，得出AN ED =，即可求解．【解答】解：问题背景：如图1，延长AD 到点E ，使DE AD =，连接BE ，AD Q 是ABC D 的中线，BD CD \=，在ADC D 和EDB D 中，AD ED CDA BDE CD BD =ìïÐ=Ðíï=î，()ADC EDB SAS \D @D ，故答案为：SAS；问题解决：如图1，延长AD 到点E ，使DE AD =，连接BE ，AD Q 是ABC D 的中线，BD CD \=，在ADC EDB D @D 中，AD ED CDA BDE CD BD =ìïÐ=Ðíï=î，()ADC EDB SAS \D @D ，BE AC \=，在ABE D 中，AB BE AE AB BE -<<+，4AB =Q ，3AC =，4343AE \-<<+，即17AE <<，DE AD =Q ，12AD AE \=，\1722AD <<；拓展应用：如图2，延长AM 到N ，使得MN AM =，连接BN ，由问题背景知，()BMN CMA SAS D @D ，BN AC \=，CAM BNM Ð=Ð，AC AD =Q ，//AC BN ，BN AD \=，//AC BN Q ，180BAC ABN \Ð+Ð=°，90BAE CAD Ð=Ð=°Q ，180BAC EAD \Ð+Ð=°，ABN EAD \Ð=Ð，在ABN D 和EAD D 中，AB EA ABN EAD BN AD =ìïÐ=Ðíï=î，()ABN EAD SAS \D @D ，AN DE \=，MN AM =Q ，2DE AN AM \==，3AM =Q ，6DE \=．12.如图，ABC D 中，D 为BC 的中点．（1）求证：2AB AC AD +>；（2）若5AB =，3AC =，求AD 的取值范围．【分析】（1）再延长AD 至E ，使DE AD =，构造ADC EDB D @D ，再根据三角形的三边关系可得2AB AC AD +>；（2）直接利用三角形的三边关系：三角形两边之和大于第三边，三角形的两边差小于第三边可得53253AD -<<+，再计算即可．【解答】（1）证明：由BD CD =，再延长AD 至E ，使DE AD =，D Q 为BC 的中点，DB CD \=，在ADC D 和EDB D 中AD DE ADC BDE DB CD =ìïÐ=Ðíï=î，BE AC \=，在ABE D 中，AB BE AE +>Q ，2AB AC AD \+>；（2）5AB =Q ，3AC =，53253AD \-<<+，14AD \<<．13.如图，平面直角坐标系中，A 为y 轴正半轴上一点，B 、C 分别为x 轴负半轴，x 轴正半轴上的点，AB AD =，AC AE =，90BAD CAE Ð=Ð=°，连DE ．如图，F 为BC 的中点，求证：2DE AF =．【分析】延长AF 至点N ，使FN AF =，连接BN ，证明BFN CFA D @D ，根据全等三角形的性质得到BN AC =，FBN FCA Ð=Ð，证明ABN DAE D @D ，根据全等三角形的性质证明；【解答】证明：延长AF 至点N ，使FN AF =，连接BN ，在BFN D 和CFA D 中，FB FC BFN CFA FN AF =ìïÐ=Ðíï=î，BN AC \=，FBN FCA Ð=Ð，BN AE \=，ABN DAE Ð=Ð，在ABN D 和DAE D 中，AB AD ABN DAE BN AE =ìïÐ=Ðíï=î，()ABN DAE SAS \D @D ，AN DE \=，2DE AF \=．14.如图，AD 是ABC D 的边BC 上的中线，CD AB =，AE 是ABD D 的边BD 上的中线．求证：2AC AE =．【分析】延长AE 至点F ，使EF AE =，连接DF ，由SAS 证得ABE FDE D @D ，得出DF AB CD ==，EDF B Ð=Ð，易证AB BD =，得出ADB BAD Ð=Ð，证明ADC ADF Ð=Ð，由SAS 证得ADF ADC D @D ，即可得出结论．【解答】证明：延长AE 至点F ，使EF AE =，连接DF ，如图所示：AE Q 是ABD D 的边BD 上的中线，BE DE \=，在ABE D 与FDE D 中，AE EF AEB FED BE DE =ìïÐ=Ðíï=î，()ABE FDE SAS \D @D ，DF AB CD \==，EDF B Ð=Ð，AD Q 是ABC D 的边BC 上的中线，CD AB =，AB BD \=，ADB BAD \Ð=Ð，ADC B BAD BDA EDF ADF \Ð=Ð+Ð=Ð+Ð=Ð，在ADF D 与ADC D 中，AD AD ADF ADC DF DC =ìïÐ=Ðíï=î，()ADF ADC SAS \D @D ，2AC AF AE \==．15.如图，在ABC D 中，D ，E 是AB 边上的两点，AD EB =，CF 是AB 边上的中线，则求证AC BC CD CE +>+．【分析】如图，延长CF 至H ，使FH CF =，连接AH ，DH ，延长CD 交AH 于点G ，通过证明AFH BFC D @D ，BCE AHD D @D ，可得BC AH =，CE DH =，利用三角形的三边关系可求解．【解答】证明：如图，延长CF 至H ，使FH CF =，连接AH ，DH ，延长CD 交AH 于点G，Q是AB边上的中线，CF\=，且CFB AFHAF BF=，Ð=Ð，CF FH()\D@DAFH BFC SAS=，Ð=Ð，且AD BE\=，CBE HADBC AH\D@D()BCE AHD SAS\=，CE DH在AGC+>+，D中，AC AG DC DG在GDH+>，D中，DG GH DHAC AG DG GH DC DG DH\+++>++，\+>+，AC AH DC DH\+>+．AC BC CD CE16.如图1，ABCÐ=Ð．D中，CD为ABCD的中线，点E在CD上，且AED BCD（1）求证：AE BC=．（2）如图2，连接BE，若2CBEÐ的度数为 （直接写出结果），Ð=°，则ACDAB AC DE==，14【分析】（1）如图1，延长CD到F，使DF CDD@D，可得=，连接AF，由“SAS”可证ADF BDCAF BC=，F BCDÐ=Ð，由等腰三角形的性质可得结论；（2）由等腰三角形的性质可得DEB DBEÐ=Ð，可得14DCB DEBÐ=Ð-°，14ACB ABC DEBÐ=Ð=Ð+°，即可求解．【解答】证明：（1）如图1，延长CD到F，使DF CD=，连接AF，CDQ为ABCD的中线，AD BD\=，且ADF BDCÐ=Ð，且CD DF=，()ADF BDC SAS\D@D，AF BC\=，F BCDÐ=Ð，AED BCDÐ=ÐQ，AED F\Ð=Ð，AE AF\=，AE BC\=；（2）12DE AB=Q，CD为ABCD的中线，DE AD DB\==，DEB DBE\Ð=Ð，14 ABC DBE CBE DEB\Ð=Ð+Ð=Ð+°，DEB DCB CBEÐ=Ð+ÐQ，14DCB DEB\Ð=Ð-°，AC AB=Q，14ACB ABC DEB\Ð=Ð=Ð+°28ACD ACB DCB\=Ð-Ð=°，故答案为：28°．17.如图，ABC D 中，点D 是BC 中点，连接AD 并延长到点E ，连接BE ．（1）若要使ACD EBD D @D ，应添上条件： ；（2）证明上题：（3）在ABC D 中，若5AB =．3AC =，可以求得BC 边上的中线AD 的取值范围4AD <．请看解题过程：由ACD EBD D @D 得：AD ED =，3BE AC ==，因此AE AB BE <+，即8AE <，而12AD AE =，则4AD <请参考上述解题方法，可求得AD m >，则m 的值为 ．（4）证明：直角三角形斜边上的中线等于斜边的一半．（提示：画出图形，写出已知，求证，并加以证明）【分析】（1）根据“边角边”求证三角形全等的方法可以添加条件AD DE =；（2）易证BD CD =，根据“边角边”求证三角形全等的方法即可解题；（3）根据三角形三边关系即可解题；（4）已知RT ABC D 中90BAC Ð=°，AD 是斜边中线，求证12AD BC =；证明：延长AD 到点E 使得DE AD =，连接BE ，易证ACD EBD D @D ，可得C DBE Ð=Ð，AC BE =，即可证明BAC ABE D @D ，可得BC AE =，即可解题．【解答】解：（1）应添上条件：AD DE =，故答案为AD DE =；（2）Q 点D 是BC 中点，BD CD \=，Q 在ACD D 和EBD D 中，BD CD ADC BDE AD DE =ìïÐ=Ðíï=î，()ACD EBD SAS \D @D ；（3）Q 三角形两边之差小于第三边，AE AB BE \>-，即2AE >，12AD AE =Q ，1AD \>，故答案为 1；（4）已知RT ABC D 中90BAC Ð=°，AD 是斜边中线，求证12AD BC =，证明：延长AD 到点E 使得DE AD =，连接BE ，Q 点D 是BC 中点，BD CD \=，Q 在ACD D 和EBD D 中，BD CD ADC BDE AD DE =ìïÐ=Ðíï=î，()ACD EBD SAS \D @D ；C DBE \Ð=Ð，AC BE =，90ABC C Ð+Ð=°Q ，90ABC DBE \Ð+Ð=°，即90ABE Ð=°，Q 在BAC D 和ABE D 中，90AB BA ABE BAC AC BE =ìïÐ=Ð=°íï=î，()BAC ABE SAS \D @D ；BC AE \=，12AD BC \=．。