算法初步高考题赏析
算法初步高考题赏析课件PPT

的程序,则输出i的值为
A.3
B.4
C.5
D.6
6
一、输出结果
3、求输入信息
程序框图如右,若 输出y的值是9, 则输入的实数x的 值可以为( )
A.3 B.-3 C.-2 D.2
7
二、填写框图内容
(2010浙江理)某程序 框图如图所示,若输出的 S=57,则判断框内为 (A) k>4? (B)k>5? (C) k>6? (D)k>7?
后,若输出的S的值等于16,那 么在程序框图中的判断框内应
填写的条件是(
)
A.i>5?
B.i>6?
C.i>7?
D.i>8?
13
三、练习
(2009天津文)阅读右面的程 序框图,则输出的S= A、 14 B、 20 C、 30 D、 55
14
三、练习
(2010辽宁文)如果执行 右面的程序框图,输入n=6, m=4,那么输出的p等于 (A)720 (B) 360 (C) 240 (D) 120
15
三、练习
开始
(2009山东)执行右边
的程序框图,输出的 S=0,T=0,n=0
T=
. T>S
否
S=S+5
n=n+2
T=T+n
是
输出T 结束
16
三、练习 右图给出的是计算
111 1 2 4 6 20
的值的一个程序框图, 其中判断框内应填入 的条件是( ) (A)i>10(B)i ≤ 10 (C)i>20(D)i<20
②处应填写 y log2 x 。
10
三、练习
一个算法的程序框图如图所示, 如 果 输 入 的 x 值 是 - 20 , 则 输 出的结果是________.
高考历年真题分类解析之第十四章 算法初步(理)

第十四章算法初步1.(2018全国Ⅱ,7)为计算S=1−12+13−14+⋯+199−1100,设计了下面的程序框图,则在空白框中应填入( )A.S=S+1B.S=S+2C.S=S+3D.S=S+41.B 由S=1−12+13−14+⋯+199−1100得程序框图先对奇数项累加,偶数项累加,最后再相减.因此在空白框中应填入S=S+2,选B.2.(2018天津,3)阅读如图所示的程序框图,运行相应的程序,若输入S的值为20,则输出S的值为( )A.1 B.2 C.3 D.42.B 结合流程图运行程序如下:首先初始化数据:S=20,S=2,S=0,SS =202=10,结果为整数,执行S=S+1=1,S=S+1=3,此时不满足S≥5;SS =203,结果不为整数,执行S=S+1=4,此时不满足S≥5;SS =204=5,结果为整数,执行S=S+1=2,S=S+1=5,此时满足S≥5;跳出循环,输出S=2. 3.(2018北京,3)执行如图所示的程序框图,输出的s值为( )A.12 B.56C.76 D.7123.B 初始化数值S=1,S=1,循环结果执行如下:第一次:S=1+(−1)1⋅12=12,S=2,S=2≥3不成立;第二次:S=12+(−1)2⋅13=56,S=3,S=3≥3成立,循环结束,输出S=56,故选B.4.(2017•新课标Ⅰ,8)如图程序框图是为了求出满足3n﹣2n>1000的最小偶数n,那么在和两个空白框中,可以分别填入()A.A>1000和n=n+1B.A>1000和n=n+2C.A≤1000和n=n+1D.A≤1000和n=n+24.D 因为要求A>1000时输出,且框图中在“否”时输出,所以“ ”内不能输入“A>1000”,又要求n为偶数,且n的初始值为0,所以“ ”中n依次加2可保证其为偶数,所以D选项满足要求,故选D.5.(2017•新课标Ⅱ,8)执行如图的程序框图,如果输入的a=﹣1,则输出的S=()A.2B.3C.4D.55. B 执行程序框图,有S=0,k=1,a=﹣1,代入循环,第一次满足循环,S=﹣1,a=1,k=2;满足条件,第二次满足循环,S=1,a=﹣1,k=3;满足条件,第三次满足循环,S=﹣2,a=1,k=4;满足条件,第四次满足循环,S=2,a=﹣1,k=5;满足条件,第五次满足循环,S=﹣3,a=1,k=6;满足条件,第六次满足循环,S=3,a=﹣1,k=7;7≤6不成立,退出循环输出,S=3;故选B.6.(2017•新课标Ⅲ,7)执行如图的程序框图,为使输出S的值小于91,则输入的正整数N的最小值为()A.5B.4C.3D.26. D 由题可知初始值t=1,M=100,S=0,要使输出S的值小于91,应满足“t≤N”,则进入循环体,从而S=100,M=﹣10,t=2,要使输出S的值小于91,应接着满足“t≤N”,则进入循环体,从而S=90,M=1,t=3,若此时输出S,则S的值小于91,故t=3应不满足“t≤N”,跳出循环体,所以输入的N的最小值为2,故选D.7.(2017•山东,6)执行两次如图所示的程序框图,若第一次输入的x值为7,第二次输入的x值为9,则第一次,第二次输出的a值分别为()A.0,0B.1,1C.0,1D.1,07. D 当输入的x值为7时,第一次,不满足b2>x,也不满足x能被b整数,故b=3;第二次,满足b2>x,故输出a=1;当输入的x值为9时,第一次,不满足b2>x,也不满足x能被b整数,故b=3;第二次,不满足b2>x,但满足x能被b整数,故输出a=0故选D.8.(2017·天津,3)阅读右面的程序框图,运行相应的程序,若输入N的值为24,则输出N的值为()A.0B.1C.2D.38. C 第一次N=24,能被3整除,N= ≤3不成立,第二次N=8,8不能被3整除,N=8﹣1=7,N=7≤3不成立,第三次N=7,不能被3整除,N=7﹣1=6,N= =2≤3成立,输出N=2,故选C.9.(2017•北京,3)执行如图所示的程序框图,输出的S值为()A.2B.C.D.9. C 当k=0时,满足进行循环的条件,执行完循环体后,k=1,S=2,当k=1时,满足进行循环的条件,执行完循环体后,k=2,S= ,当k=2时,满足进行循环的条件,执行完循环体后,k=3,S= ,当k=3时,不满足进行循环的条件,故输出结果为.10.(2016·全国Ⅰ,9)执行如图所示的程序框图,如果输入的x=0,y=1,n=1,则输出x,y的值满足( )A.y=2xB.y=3xC.y=4xD.y=5x10.C [执行题中的程序框图,知第一次进入循环体:x=0+1-12=0,y=1×1=1,x2+y2<36;第二次执行循环体:n=1+1=2,x=0+2-12=12,y=2×1=2,x2+y2<36;第三次执行循环体:n=2+1=3,x=12+3-12=32,y=3×2=6,x2+y2>36,满足x2+y2≥36,故退出循环,输出x=32,y=6,满足y=4x,故选C.]11.(2016·全国Ⅱ,8)中国古代有计算多项式值的秦九韶算法,如图是实现该算法的程序框图.执行该程序框图,若输入的x=2,n=2,依次输入的a为2,2,5,则输出的s=( )A.7B.12C.17D.3411.C [由框图可知,输入x=2,n=2,a=2,s=2,k=1,不满足条件;a=2,s=4+2=6,k=2,不满足条件;a=5,s=12+5=17,k=3,满足条件输出s=17,故选C.]12.(2016·全国Ⅲ,7)执行如图的程序框图,如果输入的a=4,b=6,那么输出的n=( )A.3B.4C.5D.612.B [第一次循环a =6-4=2,b =6-2=4,a =4+2=6,i =6,n =1; 第二次循环a =-6+4=-2,b =4-(-2)=6,a =6-2=4,i =10,n =2; 第三次循环a =6-4=2,b =6-2=4,a =4+2=6,i =16,n =3;第四次循环a =4-6=-2,b =4-(-2)=6,a =6-2=4,i =20,n =4,满足题意,结束循环.]13.(2015·四川,3)执行如图所示的程序框图,输出S 的值为( )A. -32B. 32C.-12D.1213.D [每次循环的结果依次为:k =2,k =3,k =4,k =5>4,∴S =sin 5π6=12.选D.]14.(2015·天津,3)阅读如图所示的程序框图,运行相应的程序,则输出S 的值为( )A.-10B.6C.14D.1814.B [运行相应的程序,第一次循环:i=2,S=20-2=18;第二次循环:i=4,S=18-4=14;第三次循环:i=8,S=14-8=6;8>5,终止循环,输出S=6,故选B.]15.(2015·重庆,7)执行如图所示的程序框图,输出的结果为( )A.(-2,2)B.(-4,0)C.(-4,-4)D.(0,-8)15.B [第一次循环:S=1-1=0,t=1+1=2;x=0,y=2,k=1;第二次循环:S=0-2=-2,t=0+2=2,x=-2,y=2,k=2;第三次循环:S=-2-2=-4,t=-2+2=0,x=-4,y=0,k=3.输出(-4,0).]16.(2015·福建,6)阅读如图所示的程序框图,运行相应的程序,则输出的结果为( )A.2B.1C.0D.-116.C [当i =1,S =0进入循环体运算时,S =0,i =2;S =0+(-1)=-1,i =3;S =-1+0=-1,i =4;∴S =-1+1=0,i =5;S =0+0=0,i =6>5,故选C.]17.(2015·北京,3)执行如图所示的程序框图,若输出k 的值为8,则判断框内可填入的条件是( )A.s ≤34B.s ≤56C.s ≤1112D.s ≤252417.C [由程序框图,k 的值依次为0,2,4,6,8,因此s =12+14+16=1112(此时k =6)还必须计算一次,因此可填s ≤1112,选C.]18.(2015·新课标全国Ⅱ,8)下边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b分别为14,18,则输出的a=( )A.0B.2C.4D.1418.B [由题知,若输入a=14,b=18,则第一次执行循环结构时,由a<b知,a=14,b=b-a=18-14=4;第二次执行循环结构时,由a>b知,a=a-b=14-4=10,b=4;第三次执行循环结构时,由a>b知,a=a-b=10-4=6,b=4;第四次执行循环结构时,由a>b知,a=a-b=6-4=2,b=4;第五次执行循环结构时,由a<b知,a=2,b=b-a=4-2=2;第六次执行循环结构时,由a=b知,输出a=2,结束,故选B.]19.(2014·天津,3)阅读下边的程序框图,运行相应的程序,输出S的值为( )A.15B.105C.245D.94519.B [S =1,i =1;S =3,i =2;S =15,i =3;S =105,i =4,结束循环,输出S =105.]20.(2014·安徽,3)如图所示程序框图(算法流程图)的输出结果是( )A.34B.55C.78D.8920.B[⎩⎨⎧x =1,y =1,z =2,⎩⎨⎧x =1,y =2,z =3,⎩⎨⎧x =2,y =3,z =5,⎩⎨⎧x =3,y =5,z =8,⎩⎨⎧x =5,y =8,z =13,⎩⎨⎧x =8,y =13,z =21,⎩⎨⎧x =13,y =21,z =34,⎩⎨⎧x =21,y =34,z =55≥50,退出循环,输出z =55.选B.]21.(2014·陕西,4)根据下边框图,对大于2的整数N ,输出的数列的通项公式是( )A.a n =2nB.a n =2(n -1)C.a n =2nD.a n =2n -121.C[⎩⎨⎧S =1,i =1,a 1=2×1=2,⎩⎨⎧S =2,i =2,a 2=2×2=4,⎩⎨⎧S =4,i =3,a 3=2×4=8,⎩⎨⎧S =8,i =4,a 4=2×8=16,输出a 1=2,a 2=22,a 3=23,a 4=24,排除A 、B 、D.选C.]22.(2014·北京,4)当m =7,n =3时,执行如图所示的程序框图,输出的S 值为( )A.7B.42C.210D.84022.C [⎩⎨⎧m =7,n =3,k =7,S =1,m -n +1=5;⎩⎨⎧S =7,k =6,m -n +1=5;⎩⎨⎧S =42,k =5,m -n +1=5;⎩⎨⎧S =210,k =4<m -n +1. 输出S =210.故选C.]23.(2014·福建,5)阅读如图所示的程序框图,运行相应的程序,输出的S 的值等于( )A.18B.20C.21D.4023.B [程序运行如下:S =0,n =1;S =0+21+1=3,n =2,S <15;S =3+22+2=9,n =3,S <15;S =9+23+3=20,满足条件,输出S =20,故选B.]24.(2014·四川,5)执行如图的程序框图,如果输入的x ,y ∈R ,那么输出的S 的最大值为( )A.0B.1C.2D.324.C[在约束条件⎩⎨⎧x ≥0,y ≥0,x +y ≤1下,S =2x +y的最大值应在点(1,0)处取得,即S max =2×1+0=2,显然2>1,故选C.]25.(2014·重庆,5)执行如图所示的程序框图,若输出k 的值为6,则判断框内可填入的条件是( )A.s>12B.s>35C.s>710D.s>4525.C [程序框图的执行过程如下:s=1,k=9,s=910,k=8;s=910×89=810,k=7;s=810×78=710,k=6,循环结束.故可填入的条件为s>710.故选C.]26.(2014·湖南,6)执行如图所示的程序框图,如果输入的t∈[-2,2],则输出的S属于( )A.[-6,-2]B.[-5,-1]C.[-4,5]D.[-3,6]26.D [当0≤t≤2时,S=t-3∈[-3,-1].当-2≤t<0时,2t2+1∈(1,9],则S∈(-2,6].综上,S∈[-3,6],故选D.] 27.(2014·新课标全国Ⅰ,7)执行下面的程序框图,若输入的a,b,k分别为1,2,3,则输出的M=( )A.203B.72C.165D.15827.D [第一次循环:M =32,a =2,b =32,n =2;第二次循环:M =83,a =32,b =83,n =3;第三次循环:M =158,a =83,b =158,n =4,退出循环,输出M 为158,故选D.]28.(2014·新课标全国Ⅱ,7)执行如图的程序框图,如果输入的x ,t 均为2,则输出的S =( )A.4B.5C.6D.728.D [k =1,M =11×2=2,S =2+3=5;k =2,M =22×2=2,S =2+5=7;k =3,3>t ,∴输出S =7,故选D.]29.(2014·江西,7)阅读如下程序框图,运行相应的程序,则程序运行后输出的结果为( )A.7B.9C.10D.1129.B [执行程序框图,第一次循环:i=1,S=lg 13<-1,否;执行第二次循环:i=3,S=lg 13+lg35=lg15<-1,否;执行第三次循环:i=5,S=lg 15+lg57=lg17<-1,否;执行第四次循环:i=7,S=lg 17+lg79=lg19<-1,否;执行第五次循环:i=9,S=lg 19+lg911=lg111<-1,是,结束循环,输出i为9,故选B.]30.(2018江苏,4)一个算法的伪代码如图所示,执行此算法,最后输出的S 的值为________.30.8 由伪代码可得I=3,S=2;I=5,S=4;I=7,S=8,因为7>6,所以结束循环,输出S=8.点睛:本题考查伪代码,考查考生的读图能力,难度较小.31.(2017•江苏,4)如图是一个算法流程图:若输入x的值为,则输出y 的值是________.31.-2 初始值x= ,不满足x≥1,所以y=2+log 2 =2﹣=﹣2,故答案为:﹣2.32.(2015·山东,13)执行如图所示的程序框图,输出的T 的值为________.32.116 [当n =1时,T =1+∫10x 1d x =1+⎪⎪⎪12x 210=1+12=32; 当n =2时,T =32+∫10x 2d x =32+⎪⎪⎪13x 310=32+13=116; 当n =3时,结束循环,输出T =116.]33.(2014·江苏,3)如图是一个算法流程图,则输出的n 的值是________.33.5 [n=1,21<20,N;n=2,22<20,N;n=3,23<20,N;n=4,24<20,N;n =5,25>20,Y,故输出n=5.]34.(2014·山东,11)执行如图所示的程序框图,若输入的x的值为1,则输出的n的值为________.34.3[x=1,n=0→1-4+3=0→x=2,n=1→22-4×2+3=-1<0→x=3,n=2→32-4×3+3=0→x=4,n=3→42-4×4+3>0→输出n=3.]35.(2014·浙江,11)若某程序框图如图所示,当输入50时,则该程序运行后输出的结果是________.35.6 [第一次循环,S=1,i=2;第二次循环,S=2+2=4,i=3;第三次循环,S=8+3=11,i=4;第四次循环,S=22+4=26,i=5;第五次循环,S=52+5=57,i=6,57>50,退出循环,故输出的结果为6.]。
高考数学精品资料—算法知识点分析 试题

算法初步算法的含义、程序框图〔一〕理解算法的含义,理解算法的思想。
〔二〕理解程序框图的三种根本逻辑构造:顺序构造、条件构造和循环构造。
算法不仅是数学及其应用的重要组成局部,也是计算机科学的重要根底。
算法初步虽然是新课标增加的内容,但与前面的知识有着亲密的联络,并且与实际问题的联络也非常亲密。
因此,在高考中算法初步知识将与函数、数列、三角、概率、实际问题等知识点进展整合,是高考试题命制的新“靓〞点。
这样试题就遵循了“在知识网络交汇处设计试题〞的命制原那么,既符合高考命题“才能立意〞的宗旨,又突出了数学的学科特点。
这样做,可以从学科的整体高度和思维价值的高度考虑问题,可以提醒数学各知识之间得到的内在联络,可以使考察到达必要的深度。
考察形式与特点是:〔1〕选择题、填空题主要考察算法的含义、流程图、根本算法语句等内容,一般在每份试卷中有1~2题,多为中档题出现。
(2)在解答题中可通过让学生读程序框图去解决其它问题,此类试题往往是与数列题结合在一起,具有一定的综合性,可以考察学生的识图才能及对数列知识的掌握情况.第1课时 算法的含义1.算法的概念:对一类问题的机械的、统一的求解方法称为算法。
2.算法的特性:〔1〕有限性〔2〕确定性例1.给出求1+2+3+4+5的一个算法。
解:算法1第一步:计算1+2,得到3第二步:将第一步中的运算结果3与3相加,得到6第三步:将第二步中的运算结果6与4相加,得到10第四步:将第三步中的运算结果10与5相加,得到15算法2第一步:取n=5第二步:计算第三步:输出运算结果变式训练1.典型例题根底过关知识网络高考导航21n n )(写出求111123100++++的一个算法.解:第一步:使1S =,;第二步:使2I =;第三步:使1n I=;第四步:使S S n =+;第五步:使1I I =+;第六步:假如100I ≤,那么返回第三步,否那么输出S .例2. 给出一个判断点P ),(00y x 是否在直线y=x-1上的一个算法。
《算法初步》高考题型例析
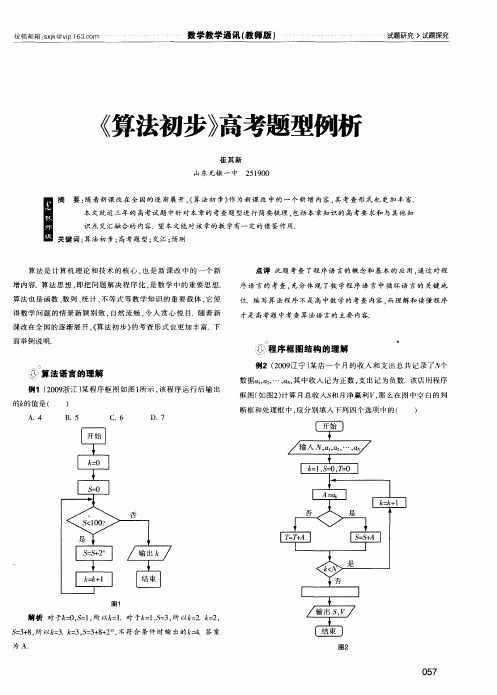
增 内容 . 法 思 想 , 算 即把 问 题 解 决程 序化 , 数 学 中的 重 要 思想 . 是 点 评 此 题 考 查 了程 序 语 言 的概 念 和 基 本 的 应 用 . 通过 对 程
序 语 言 的 考 查 , 分 体 现 了数 学 程 序 语 言 中循 环 语 言 的 关 键 地 充 位.编 写算 法程 序 不 是 高 中数 学的 考 查 内容 . 而理 解和 读 懂程 序
倒3(0 9 20 广东 ) 随机抽取某产品r , t 测得其长度分别为a, 件 。
啦, , 则 图3 示的 程序 框 图输 出的s … %, 所 =
本 的数 字特 征是
.
图4
解 析 当x l , 一 ; ≤1 ,= 所 以有 分段 函 数, > 时 y 2当 时 y , , =
才是 高考 题 中考 查 算 法语 言 的主 要 内容.
算 法也 是 函数 、 数列 、 计 、 等式 等 数 学 知 识 的 重要 载 体 , 使 统 不 它
得 数学 问题 的 情 景 新颖 别 致 . 自然 流 畅 + 人 赏 心 悦 目.随着 新 令
课 改在 全 国 的逐 渐展 开 ,算 法初 步 》 考 查形 式 也 更 加 丰富.下 《 的
面举 例说 明.
、
程序框 图结构 的理 解
、
例2 (0 9 宁 ) 店一 个 月 的收 入 和 支 出总 共 记 录 了Ⅳ个 20辽 某
数 据o , … , , 中收 入 记 为正 数 , 出 记 为负 数.该 店用 程 序 。 啦, 其 支
算法 语言 的理解
例 1 (0 9 20 浙江 ) 某程 序 框 图 如 图 l 所示 , 程 序 运行 后 输 出 该
高考试题中的《算法初步》

高考试题中的《算法初步》高考过后,我们的新课程刚好上到必修三,第一章便是算法初步。
在边学边教的过程中我发现:算法初步虽然是新课标增加的内容,但与前面的知识有着密切的联系,并且与实际问题的联系也非常密切。
例如,这一部分里面的条件结构最易和分段函数相结合;循环结构常用来求数列的和或积,而此时的循环体关键语句就与此数列的通项公式有紧密联系。
在暑假期间,我仔细研究了2010年高考试题中的算法初步相关题目。
在高考中算法初步知识与函数、数列、三角、概率、实际问题等知识点进行了整合,是高考命题的新“靓”点,不仅从学科的整体高度和思维价值的高度考虑问题,而且可以揭示数学各知识之间的内在联系,还可以使考查达到必要的深度。
考查形式与特点是:形式:选择题、填空题。
主要考查算法的含义、流程图、基本算法语句等内容,一般在每份试卷中有1~2题,多为中档题出现。
特点:几乎全部以程序框图为考察对象,有时需要读程序框图,得相应结果;有时要通过结果,填写框图中的内容。
这也告诉我们框图是算法的核心,能画好框图就说明已经分析设计好了算法,也就能将他翻译成程序语句,这也指导我们在教学中这一章要以程序框图为重点。
以下是2010年高考中的算法试题汇编,按选择和填空分别整理,可以从试题中看出教学方向,指导我们的教学。
(一)选择题(共9题)的i值等于A.2 B..5输入正整数n,m,满足n≥m,那么输出的P等于(A)1mnC-(B)1mnA-(C)mnC-------------------------------------输入6,4n m==,那么输出的p等于(A)C)240 (D)120 框图,输入N=5,则输出的数等于(A)54(B)45(C)65-------------------------------------x 1,x2,…x10平均数x的程序框图,图中空白框中应填入的内容为( )nx n(C) S=S+ n (D) S=S+1nx1,x2,…,x10的乘积S的程序框图,图中空白框中应填入的内容为( )(A)S=S*(n+1) (B )S=S*xn+1------------------------------------若输出s 的值为-7,则判断框内可填写( )(A)i <3? (B )i <4?(C )i <运行相应的程序,则输出s 的值为( )------------------------------------S=57,则判断框内位( )(B )k >5?(C ) k >6? (D )k >7?(二)填空题(共11题)值________。
年高考数学试题分项版—算法初步(解析版)

2017年高考数学试题分项版—算法初步(解析版)一、选择题1.(2017·全国Ⅰ文,10)如图所示的程序框图是为了求出满足3n-2n>1000的最小偶数n,那么在错误!未定义书签。
和错误!两个空白框中,可以分别填入()A.A>1000和n=n+1B.A>1 000和n=n+2C.A≤1 000和n=n+1D.A≤1 000和n=n+21.【答案】D【解析】因为题目要求的是“满足3n-2n>1 000的最小偶数n”,所以n的叠加值为2,所以错误!未定义书签。
内填入“n=n+2”.由程序框图知,当错误!内的条件不满足时,输出n,所以错误!内填入“A≤1 000”.故选D.2.(2017·全国Ⅲ文,8)执行下面的程序框图,为使输出S的值小于91,则输入的正整数N 的最小值为( )A.5 B.4C.3D.22.【答案】D【解析】假设N=2,程序执行过程如下:t=1,M=100,S=0,1≤2,S=0+100=100,M=-错误!未定义书签。
=-10,t=2,2≤2,S=100-10=90,M=-错误!=1,t=3,3>2,输出S=90<91.符合题意.∴N=2成立.显然2是N的最小值.故选D.3.(2017·北京文,3)执行如图所示的程序框图,输出的s值为( )A.2 B.错误!未定义书签。
C.错误!未定义书签。
ﻩD.8 53.【答案】C【解析】开始:k=0,s=1;第一次循环:k=1,s=2;第二次循环:k=2,s=\f(3,2);第三次循环:k=3,s=错误!未定义书签。
,此时不满足循环条件,输出s,故输出的s值为错误!未定义书签。
.故选C.4.(2017·天津文,4)阅读右面的程序框图,运行相应的程序,若输入N的值为19,则输出N的值为()A.0B.1C.2D.34.【答案】C【解析】输入N=19,第一次循环,19不能被3整除,N=19-1=18,18>3;第二次循环,18能被3整除,N=错误!未定义书签。
2021-2022年高考数学总复习专题12.1算法初步试题含解析

2021年高考数学总复习专题12.1算法初步试题含解析【三年高考】1.【xx江苏,4】右图是一个算法流程图,若输入的值为,则输出的的值是▲ .【答案】【考点】循环结构流程图【名师点睛】算法与流程图的考查,侧重于对流程图循环结构的考查.先明晰算法及流程图的相关概念,包括选择结构、循环结构、伪代码,其次要重视循环起点条件、循环次数、循环终止条件,更要通过循环规律,明确流程图研究的数学问题,是求和还是求项.2. 【xx高考江苏】右图是一个算法的流程图,则输出的a的值是 .【答案】9【解析】试题分析:第一次循环:,第二次循环:,此时,循环结束,输出的a的值是9,故答案应填:9【考点】循环结构流程图【名师点睛】算法与流程图的考查,侧重于对流程图循环结构的考查.先明晰算法及流程图的相关概念,包括选择结构、循环结构、伪代码,其次要重视循环起始条件、循环次数、循环终止条件,更要通过循环规律,明确流程图研究的数学问题,是求和还是求项. 3.【xx江苏高考,4】根据如图所示的伪代码,可知输出的结果S为________.【答案】7【解析】第一次循环:;第二次循环:;第三次循环:;结束循环,输出【考点定位】循环结构流程图4.【xx课标3,理7】执行右图的程序框图,为使输出S的值小于91,则输入的正整数N的最小值为A.5 B.4 C.3 D.2【答案】D【考点】流程图【名师点睛】利用循环结构表示算法,一定要先确定是用当型循环结构,还是用直到型循环结构;当型循环结构的特点是先判断再循环,直到型循环结构的特点是先执行一次循环体,再判断;注意输入框、处理框、判断框的功能,不可混用;赋值语句赋值号左边只能是变量,不能是表达式,右边的表达式可以是一个常量、变量或含变量的运算式.5.【xx课标II,理8】执行右面的程序框图,如果输入的,则输出的()A.2 B.3 C.4 D.5【答案】B【解析】试题分析:阅读流程图,初始化数值循环结果执行如下:第一次: ;第二次:121,1,3S a k =-+==-= ;第三次: ;第四次:242,1,5S a k =-+==-= ;第五次: ;第六次:363,1,7S a k =-+==-= ;结束循环,输出 。
2019年高考真题和模拟题分项汇编专题11算法初步(解析版)

专题 11算法初步1.【 2019 年高考天津卷理数】阅读下面的程序框图,运转相应的程序,输出S 的值为A . 5B .8C. 24 D. 29【答案】 B【剖析】依据程序框图,逐渐写出运算结果即可.【分析】 S 1,i 2 ; j 1, S 1 2 21 5, i 3 ; S 8,i 4 ,结束循环,输出S 8.应选B.【名师点睛】解答此题要注意要明确循环体停止的条件是什么,会判断什么时候停止循环体.2.【 2019 年高考北京卷理数】履行如下图的程序框图,输出的s 值为A . 1B .2 C. 3 D. 4 【答案】 B【剖析】依据程序框图中的条件逐次运算即可.【分析】初始:s 1 ,k 1 ,运转第一次,运转第二次,2 122 ,s12 ,k3 22 2 23,s22 ,k3 2运转第三次,2 2 2s22 ,结束循环,3 2输出 s 2 ,应选B.【名师点睛】此题考察程序框图,属于简单题,侧重基础知识、基本运算能力的考察.13.【 2019 年高考全国Ⅰ卷理数】如图是求2 1 的程序框图,图中空白框中应填入2 12A .A1B .A1 A22 AC.A1D.A12 A11 2A【答案】 A【剖析】此题主要考察算法中的程序框图,浸透阅读、剖析与解决问题等修养,仔细剖析式子构造特色1, k 111 , k k1=2;【分析】初始: A2,由于第一次应当计算 1 = 22 2 A21 k2 21 1 k k 1履行第 2 次, ,由于第二次应当计算21=2 A=3,,22结束循环,故循环体为 A1 ,应选 A .2 A1【秒杀速解】仔细察看计算式子的构造特色,可知循环体为A.2 A4.【 2019 年高考全国Ⅲ卷理数】履行下面的程序框图,假如输入的为 0. 01,则输出 s 的值等于A . 211 24B . 225 C . 21 126D . 227【答案】 C【剖析】依据程序框图,联合循环关系进行运算,可得结果. 【分析】输入的为,x 1,s 0 1, x1 0.01? 不知足条件;2s 0 1 1, x 1 0.01? 不知足条件;2 4S 01 11 , x 1 0.0078125 0.01? 知足条件,结束循环;2 26 128 输出 S 1 11 2 (1 11 22 6 2 7 ) 22 6,应选 C .【名师点睛】解答此题重点是利用循环运算,依据计算精准度确立数据剖析.5.【 2019 年高考江苏卷】下列图是一个算法流程图,则输出的 S 的值是 ______________.【答案】 5【剖析】联合所给的流程图运转程序确立输出的值即可. 【分析】履行第一次,S Sx 1 , x 1 4 不建立,持续循环,x x 1 2 ;2 2履行第二次, SS x 3, x2 2 履行第三次, SSx3, x 2履行第四次, SSx5, x 22 4 不建立,持续循环, x x 1 3;3 4 不建立,持续循环, x x 1 4 ; 4 4 建立,输出 S 5. 【名师点睛】辨别、运转程序框图和完美程序框图的思路:(1)要明确程序框图的次序构造、条件构造和循环构造;(2)要辨别、运转程序框图,理解框图所解决的实质问题;( 3)依据题目的要求达成解答并考证.6.【天津市和平区2018-2019 学年度第二学期高三年级第三次质量检查】在如下图的计算1 5 9 L 2017 的程序框图中,判断框内应填入的条件是A . i 2017?B . i 2017?【答案】 A【分析】由题意联合流程图可知当i 2017时,程序应履行S S i,i i 4 2021,再次进入判断框时应当跳出循环,输出S 的值;联合所给的选项可知判断框内应填入的条件是i2017?.应选A.7.【吉林省长春市北京师范大学长春市隶属中学2019 届高三第四次模拟考试】依据如下图的程序框图,当输入的 x 值为3时,输出的y 值等于A . 1B .eC.e1 D.e2【答案】 C【分析】由题x 3 , x x 2 3 1,此时 x 0 ,持续运转,x 1 2 1 0 ,程序运转结束,得y e 1,应选C.8.【西南名校结盟重庆市第八中学2019 届高三 5 月高考适应性月考卷(六) 】履行如下图的程序框图,则输出的值为A . 4B .5C. 6 D. 7【答案】 C【分析】由题可得 S 3,i 2 S 7,i 3 S 15,i 4 S 31,i 5 S 63,i 6 ,此时结束循环,输出i 6 ,应选C.9 2019届高三二模】阅读如下图的程序框图,运转相应的程序,输出的S 的值等于.【山东省济宁市A.30 B .31C. 62 D. 63【答案】 B【分析】由流程图可知该算法的功能为计算S 1 21 22 23 24的值,即输出的值为S 1 21 22 23 24 1 (1 25 ) 31.应选 B.1 210.【辽宁省大连市2019 届高三第二次模拟考试】履行如下图的程序框图,若输出结果为1,则可输入的实数 x 值的个数为A .1B .2 C. 3 D. 4【答案】 Bx2 1, x 2x 的方程,即可获得可【剖析】依据程序框图的含义,获得分段函数 y ,分段解出对于log 2 x, x 2输入的实数 x 值的个数.【分析】依据题意,该框图的含义是:当 x 2 时,获得函数y x2 1 ;当x 2 时,获得函数y log 2 x ,所以,若输出的结果为 1 时,若 x 2 ,获得x211,解得x 2 ,若 x 2 ,获得log2x1,无解,所以,可输入的实数x 的值可能为 2 ,2,共有2个.应选B.11.【江西省新八校2019 届高三第二次联考】如下图的程序框图所实现的功能是A .输入a的值,计算(a 1) 32021 1 的值B.输入a的值,计算(a 1) 32020 1 的值C.输入a的值,计算(a 1) 32019 1的值D .输入a的值,计算(a 1) 32018 1的值【答案】 B【分析】由程序框图,可知a1 a , a n 13a n 2 ,由i的初值为1,末值为2019,可知,此递推公式共履行了2019 1 2020次,又由 a n 1 3a n 2 ,得 a n 1 1 3(a n 1) ,得 a n 1 ( a 1) 3n 1即 a n (a 1) 3n 1 1,故 a2021 (a 1) 32021 1 1 (a 1) 32020 1,应选B.12.【山西省 2019 届高三考前适应性训练(二模)】履行如下图的程序框图,则输出x的值为1 A .2 B .13 D.3C.2【答案】 A【剖析】依据程序框图进行模拟运算获得x 的值具备周期性,利用周期性的性质进行求解即可.【分析】∵ x 1 12 ;,∴当 i 1 时,x ; i 2 时, x213i 3 时, x 3 , i 4时,x 4,,即 x 的值周期性出现,周期数为2∵ 2018 504 4 2 ,则输出x的值为2,应选 A.【名师点睛】此题主要考察程序框图的辨别和判断,联合条件判断x 的值具备周期性是解决此题的关键,属于中档题.13.【青海省西宁市第四高级中学、第五中学、第十四中学三校2019 届高三 4 月联考】若某程序框图如图所示,则该程序运转后输出的值是A .5B .4C. 3 D. 2【答案】 B【剖析】模拟履行循环构造的程序获得n 与i的值,计算获得n 2 时知足判断框的条件,退出循环,输出结果,即可获得答案.【分析】模拟履行循环构造的程序框图,可得: n 6, i 1,第 1 次循环:n 3, i 2 ;第 2 次循环: n 4, i 3 ;第 3 次循环: n 2, i 4 ,此时知足判断框的条件,输出i 4 .应选B.【名师点睛】此题主要考察了循环构造的程序框图的应用,此中解答中依据给定的程序框图,依据判断框的条件推出循环,逐项正确计算输出结果是解答的重点,侧重考察了考生的运算与求解能力,属于基础题.14.【江苏省七市 (南通、泰州、扬州、徐州、淮安、宿迁、连云港)2019 届高三第三次调研】下列图是一个算法流程图.若输出的值为 4,则输入x 的值为______________.【答案】【分析】当1x 1时,由流程图得y 3x ,令 y 3 x 4 ,解得x 1 ,知足题意.当 x 1 时,由流程图得y 3 x ,令 y 3 x 4 ,解得x 1 ,不知足题意.故输入 x 的值为1.15.【北京市人大附中2019 届高三高考信息卷(三 )】履行如下图的程序框图,若输入 x 值知足 2 x 4,则输出 y 值的取值范围是______________.【答案】 [ 3,2]【分析】依据输入 x 值知足 2 x 4 ,利用函数的定义域,分红两部分:即﹣2 x 2 和 2 x 4 ,当﹣2 x 2 时,履行y x2 3 的关系式,故 3 y 1,当 2 x 4 时,履行y log 2 x 的关系式,故 1 y 2 .综上所述:y [ 3,2] ,故输出y 值的取值范围是[ 3,2] .。
