2012-2013第1学期《数理经济学》课程期中试卷
-2012-2013学年-高等数学(2-1)期中考试试卷---答案

-2012-2013学年-高等数学(2-1)期中考试试卷---答案2012—2013学年第一学期《高等数学(2-1)》期中试卷(工科)专业班级姓名学号开课系室基础数学系考试日期 2012年11月25日页号一二三四五六总分本页满分32 18 10 16 16 8本页得分阅卷人注意事项:1.请在试卷正面答题,反面及附页可作草稿纸;2.答题时请注意书写清楚,保持卷面清洁;3.本试卷共五道大题,满分100分;B .(0)f 是()f x 的极小值;C .(0,(0))f 是曲线()y f x =的拐点;D .(0)f 是()f x 的极大值.3. 当x →∞时,若21ax bx c++与11x +为等价无穷小,则,,a b c 之值为( B ). A .0,1,1a b c ===; B .0,1a b ==,c 为任意常数;C .0a =,,b c 为任意常数; D. ,,a b c 均为任意常数.4.设220()(),0x x f x x g x x ⎧>=≤⎩,其中()g x 是有界函数,则()f x 在 0x =处( D ). A .极限不存在;B.极限存在但不连续;C.连续但不可导;D.可导. 5. 设()f x 在0x 可导且01()2f x '=,则0x ∆→时,0|x x dy =是x ∆的( C ).A .等价无穷小;B.高阶无穷小;C.同阶但非等价无穷小;D 低阶无穷小.三、计算题(共4小题,每小题5分,共20分)1.求极限0x →解:(方法一)200sin 12lim lim 11cos 2x x x xx x→→==-;(方法二)001lim 11cos x x x →→==-; (方法三)洛比达法则001sin 11cos cos sin lim 1sin 2cos 21sin x x x x x x x x x x xx x →→→+-+-===+. 2. 设函数()y y x =由方程sin()(0,)xy y xe x x y ππ=>-<<确定,求其在1x =处的切线方程.解:两边取对数得:sin()(1)ln xy y x =-,两边对x 求导,有1cos()()ln y xy y xy y x x-''+=+, 又由于1x =时,sin 0y =,y ππ-<<,可得0y =,代入得(1)1y '=-,故在1x =处的切线方程为(1)y x =--,即10x y +-=.3. 设3arctan 6x t t y t t =+⎧⎪⎨=+⎪⎩,求221d y t dx =. 解:222363(1)111dy dy t dt t dx dx dt t +===+++; 22222()66(1)()1211d dy d y d dy t t t dt dx dx dx dx dx t dt t +====+++,故 2241d y t dx ==.本页满分10分本页得分4. 求极限21)(cos lim x x x →. 解:(方法一)2211cos 1cos 100lim(cos )lim(1cos 1)x x x x x x x x --→→=+- 20cos 11lim 2x x x e e →--==; (方法二)22222111sin 1222sin 2200lim(cos )lim (cos )lim(1sin )xx x x xx x x x x x e ---→→∞→==-=; (方法三)洛比达法则sin 2cos 220111ln(cos )lim 200lim(cos )lim x x x x x x x x x x e e e -→-→→===.四、应用题(共3小题,每小题8分,共24分)1. 已知()sin 2ln(1),0()1,0ax a b x x x x f x e x ++-⎧>⎪=⎨⎪-≤⎩在0x =处可导,试求出a 与b .解:由于()f x 在0x =处可导,必连续,故(0)(0)(0)0f f f -+===,又000()sin 2ln(1)()sin 2ln(1)(0)lim lim lim 2x x x a b x x a b x x f a b x x x++++→→→++-+-==+=+-,可得20a b +-=,即2a b +=;又由于()f x 在0x =处可导,则(0)(0)f f -+''=,又 01(0)lim ax x e f a x--→-'==, 本页满分16分 本页得分2200200()sin 2ln(1)sin ln(1)(0)lim 2lim 1cos 11lim lim [sin ]1(1)x x x x a b x x x x f x x x x x x x +++++→→→→++-+-'==--==--=--, 故1,3a b =-=.2. 有一底半径为R cm ,高为h cm 的圆锥容器,今以253cm /s 自顶部向容器内注水,试求当容器内水位等于锥高的一半时水面上升的速率.解:设t 时刻,水的体积,水面半径及水的深度分别为,,V r x ,由于2211()33V R h r h x ππ=--, 又从相似三角形可知:r h x R h -=,即h x r R h-=, 可得3222332211()1[()]333h x R V R h R h h x hh πππ-=-=--,两边对t 求导,得 222()dV R dx h x dt dt hπ=-, 由已知条件25dV dt =,2h x =,代入得2100dx dt R π=,即水面上升的速率为2100cm/s Rπ. 3. 试讨论方程)0(,ln >=a ax x 有几个实根.解:令()ln ,(0,)f x x ax x =-∈+∞,则 1()f x a x '=-,令()0f x '=,解得驻点1x a =,列表如下: x 10,a ⎛⎫ ⎪⎝⎭ 1a 1,a ⎛⎫+∞ ⎪⎝⎭ ()f x ' + 0 — 本页满分16分本页得分()f x 最大值1f a ⎛⎫ ⎪⎝⎭可得,()f x 的最大值为1(ln 1)f a a ⎛⎫=-+ ⎪⎝⎭,讨论如下: (1) 当1a e =时,10f a ⎛⎫= ⎪⎝⎭,方程ln x ax =有唯一的实根; (2) 当10a e <<时,10f a ⎛⎫> ⎪⎝⎭,又由于 00lim ()lim (ln )x x f x x ax ++→→=-=-∞; ln lim ()lim ()x x x f x x a x→+∞→+∞=-=-∞, 故方程ln x ax =有两实根,分别位于10,a ⎛⎫ ⎪⎝⎭与1,a ⎛⎫+∞ ⎪⎝⎭内; 当1a e >时,10f a ⎛⎫< ⎪⎝⎭,方程ln x ax =没有实根. 五、证明题(共2小题,每小题8分,共16分)1.设函数()f x 在[0,2]上连续,在(0,2)内可导,且(0)0f =,0)2(=f ,证明:存在(0,2)ξ∈,使得()()f f ξξ'=.证明:令()()x F x e f x -=,则()F x 在[0,2]上连续,在(0,2)内可导,且由于(0)0f =,0)2(=f ,易得(0)(2)0F F ==,根据罗尔定理,至少存在(0,2)ξ∈,使得()0F ξ'=,即()()0e f e f ξξξξ--'-+=,又0e ξ-≠,可得()()f f ξξ'=.本页满分8分本页2.证明:当0>x 时,x x x x <+<+)1ln(1. 证明:(方法一)设t t f ln )(=,则)(t f 在[1,1]x +上连续,在(1,1)x +内可导,由 Lagrange 中值定理,得ln(1)ln11x x ξ+-=,11x ξ<<+,故1111x ξ<<+,即1ln(1)11x x x +<<+,整理得,x x xx <+<+)1ln(1. (方法二):对()ln(1)f t t =+在[0,]x 上应用Lagrange 中值定理.(方法三):利用函数的单调性. 得分。
2012-2013-1概率论与数理统计A卷A

浙江科技学院考试试卷浙江科技学院2012 -2013学年第 I 学期考试试卷 A 卷考试科目 概率论与数理统计A 考试方式 闭卷 完成时限 2小时一、填空题。
将答案填在空格处(本大题共7小题,每小题3分, 总计21分)。
1、10把钥匙中有3把能打开门,今任取2把,则能把门打开的概率是 .2、若事件A , B 互不相容,且P (A ) =0.5,P (B ) =0.4,则()P AB = ,()P AB = .3、若连续型随机变量X 的分布函数为0, 0,(), 01,1, 1,x F x ax x x <⎧⎪=≤<⎨⎪≥⎩则a = ,{0.5 1.5}P X <<= .4、已知X 的概率密度为()X f x ,则22Y X =-的概率密度()Y f y = .5、右表给出了(X, Y ) 的分布, 则()E XY = ,X 与Y 的协方差(,)Cov X Y = .6、设123,,X X X 是取自总体X 的样本, X 为样本均值,若总体方差存在,则112d X X =-,2123121236d X X X =+-都是总体均值的 估计,最有效的是 . 专业班级 学号 姓名………………………………………………………………………装订线……………………………………………………………………………………浙江科技学院考试试卷7、设总体服从2(,)N μσ,1215(,,,)x x x 是取自该总体的一样本,计算得样本均值0.58x =,样本方差220.004s =,则2σ的置信度为0.95的置信区间为 .二、选择题。
将正确答案的代号填入题后括号中(本大题共7小题,每小题3分,共21分)。
1、从一批产品中,每次取出一个(取后不放回),抽取三次,用123(,,)i A i =表示“第i 次取到的是正品”,下列结论中不正确的是( ). (A)123123123123A A A A A A A A A A A A 表示“至少抽到2个正品”; (B)121323A A A A A A 表示“至少有1个是次品”;(C)123A A A 表示“至少有1个不是正品”;(D)123A A A 表示“至少有1个是正品”2、5(12)(1,2,)k k p a k ==⋅⋅⋅为某一离散型随机变量的概率分布,则常数a =( ). (A )1/2; (B )2; (C )1/5; (D )53、设2~(,)X N μσ,其概率密度2(3)()}4x f x +=-,则( ). ( A )3,2μσ==;( B )3,μσ==; ( C )3,2μσ=-=;( D )3,μσ=-=4、设两个随机变量X 与Y 相互独立且同分布,{1}{1}1/2P X P Y =-==-=, {1}{1}1/2P X P Y ====,则下列式子成立的是( ). (A )X Y =;(B ){}1P X Y ==;(C ){}1/2P X Y ==;(D ){}1/4P X Y ==。
厦大《数理经济学》--习题

《数理经济学》参考习题说明:以下习题主要在于帮助读者进一步理解和掌握相关的最优化方法。
而对相关数学最优化定理推导的深入理解将非常有助于对该原理的掌握,因此相关定理的证明可以作为习题,鉴于篇幅,在习题中不再重复。
另一方面,对经济学分析如何应用最优化数学方法,建议读者进一步阅读参考文献中的相关微观经济学和宏观经济学的高级教程。
另,以下习题中相关定理和例题的编号为教材中的编号。
第一部分 非线性规划与应用1. 如序中所提到的,目标函数和约束函数均为线性函数时称为线性规划问题,线性是非线性的一个特例,考虑以下的线性规划问题,min : T c x..:0s t Ax ≤ 0x ≥其中nx R ∈,c 为维向量,为n A m n ×矩阵。
导出该线性规划问题的Kuhn-Tucker 最优性条件。
2. 当非线性规划问题中的目标函数为二次函数,约束函数为线性函数时,称为二次规划问题。
导出以下二次规划问题的Kuhn-Tucker 最优性条件。
1min : 2T Ta c x x Hx ++..:s t Ax b =0x ≥其中为常数,为维向量,为a c n H n n ×对称矩阵,为A m n ×矩阵。
3. 考虑以下非线性规划问题:12max : x x −221..:0s t x x −+≤110x −≤ 20x −≤画图分析该问题的最优解,并讨论在最有解点是否满足Kuhn-Tucker 条件或Fritz John 条件。
14. 求解以下非线性规划问题:221122min : 23x x x x x −+− 212..:42s t x x −+≤1234x x +≤6)2 10x ≥,20x ≥5. 分析点*(4,3)是否为满足以下非线性规划问题的二阶条件的最优解:x =()(2212max : 34x x −+− 2212..:25s t x x +≤127x x +≥ 10x ≥,20x ≥6. 考虑下述含参数的非线性规划问题:11min : x u x −− 2212..:1s t x x u +≤−2用()x u 表示最优解,表示最优值函数,利用定理2.1.2和定理2.2.1的公式计算()u Φ()x u ∇,在和的值。
数理经济学课后题第2节

第二章 习题答案1.假设教材《数理经济学》的需求集为:{}6000|),(2==q p q p D ,其中,q 为需求量(万册),p 为价格(元)。
如果价格从20元提高为21元,则需求量将作如何变动? 解:2220206000212160001513.61p q p q q q ======当时,,得;当时,,得 所以,价格从20元提高为21元,则需求量从15万册下降到13.61万册。
2.设某厂商的成本函数为323151500)(q q q q C +-+=,证明,其边际成本总是正的。
证明:因为边际成本函数,()()22C'156331120q q q q =-+=-+>所以,其边际成本总是正的。
3.设某厂商的成本函数为q q q q C +++=1201000)(,求边际成本函数。
解:边际成本函数为()C'20q =++4.设某一商品的需求函数为:18000)(2+==p p q q D,其中:q 为需求量,p 为价格。
若价格从9下降为8.50,问需求量将作如何变动? 解:2280008000997.568.5109.22918.51p q p q ======++当时,;当时, 所以,价格从9下降为8.5时,需求量将从97.56上升为109.22.5.若某人的效用函数取下述形式:322121)3()2(),(++=x x x x u ,其中:u 为总效用函数,1x ,2x 为所消费商品的数量,要求计算:(1)每一商品的边际效用函数;(2)当消费的每种商品均为3个单位时,第一种商品的边际效用值。
解:(1)商品1的边际效用函数:()()3112223MU x x =++商品2的边际效用函数:()()22212323MU x x =++(2)123x x ==当时,()()31232332160MU =++= 6.假定某厂商的生产函数为:αα-=1),(L AK L K Q ,其中:0>A 及10<<α。
武汉大学2012-2013第一学期期中试题及答案(1)

= 2n−1 x2 cos(2x + nπ ) + 2n−1 nx cos(2x + (n − 1)π ) + 2n−3 n(n −1) cos(2x + (n − 2)π )
2
2
2
4) dy = d (sin(x2 + 1))4
= 4(sin( x2 + 1))3d sin( x2 + 1)
= 4(sin(x2 + 1))3 cos(x2 + 1)d (x2 + 1)
1 x2 2 x2
− lim x→0
2 x2 3 x2
=
−1 6
2)
由
lim ln(x
x→0
1
+ e2 x )sin x
=
lim ln(x + e2x )
x→0
x
=
lim
x→0
1 + 2e2x x + e2x
= 3,
1
得 lim( x + e2x )sin x = e3 ; x→0
3) 由
lim ln( 2 π x→+∞
2) 3) 且有
f
′(0)
=
lim
x→0
f
(x) − 0 x
=
lim
x→0
g(x) − e−x x2
= lim g′(x) + e−x = lim g′′( x) − e−x = 1 (g′′(0) − 1) .
x→0
2x
x→0
2
2
当 x ≠ 0 时,
f
′( x)
= ⎜⎜⎝⎛
g(x) − e−x x
(完整word版)数理经济学课后题第2章(word文档良心出品)

第二章习题答案1.假定教材《数理经济学》的需求集为: D ( p, q) | p2 q 6000 ,此中,q为需求量(万册), p 为价钱(元)。
假如价钱从20 元提升为21 元,则需求量将作怎样改动?解:当 p2q 6000,得 q 15;当 p26000,得20时,20 21时,21 q因此,价钱从 20 元提升为21 元,则需求量从15 万册降落到13.61 万册。
2.设某厂商的成本函数为 C (q) 1500 15q 3q 2 q3,证明,其边沿成本老是正的。
证明:由于边沿成本函数,C' q 15 6q 3q2212 0 3 q 1因此,其边沿成本老是正的。
3.设某厂商的成本函数为C(q) 1000 20q q 1 q ,求边沿成本函数。
解:边沿成本函数为qC' q 20 1 q2 1 q4.设某一商品的需求函数为:q q D ( p) 8000 ,此中: q 为需求量, p 为价钱。
若价p 2 1格从 9 降落为,问需求量将作怎样改动?解:当 p 9时, q 8000 ;当 p 时, q 800092 1 2 1因此,价钱从 9 降落为 8.5 时,需求量将从97.56 上升为 109.22.5.若某人的功效函数取下述形式:u( x , x ) ( x 2) 2 ( x 3)3,此中: u 为总功效函数,1 2 1 2x1 , x2 为所花费商品的数目,要求计算:(1)每一商品的边沿功效函数;(2)当花费的每种商品均为 3 个单位时,第一种商品的边沿功效值。
解:( 1)商品1 的边沿功效函数:MU 1 2 x1 2 x23 3商品 2 的边沿功效函数:MU 2 3 x12x22 2 3( 2)当 x1 x2 3时,2 3 2 332160MU 1 36.假定某厂商的生产函数为:Q( K , L) AK L1 ,此中: A 0 及 0 1。
证明:劳动的边沿产出是正的,且对于L 单一递减(固定K 时)。
-2012-2013学年-高等数学(2-1)期中考试试卷---答案

-2012-2013学年-高等数学(2-1)期中考试试卷---答案2012—2013学年第一学期《高等数学(2-1)》期中试卷(工科)专业班级姓名学号开课系室基础数学系考试日期 2012年11月25日页号一二三四五六总分本页满分32 18 10 16 16 8本页得分阅卷人注意事项:1.请在试卷正面答题,反面及附页可作草稿纸;2.答题时请注意书写清楚,保持卷面清洁;3.本试卷共五道大题,满分100分;4.试卷本请勿撕开,否则作废; 5.本试卷正文共6页。
一、 填空题(共5小题,每小题4分,共20分)1.设函数1(1sin ),0(),xx x f x a x ⎧⎪-≠=⎨⎪=⎩ 在0x =处连续,则a =1e - .2.设()f x 在2x =处连续,且2()lim32x f x x →=-,则(2)f '= 3 . 3.设22ln arctana y x a x=+,则dy=22x adx x a-+ . 4. 函数ln(12)y x =+,则()(0)n y = 1(1)(1)!2n n n --- . 5. 曲线21x y e -=-的下凸区间是____[22_____________________.二、选择题(共5小题,每小题4分,共20分) 1.设函数11()tan ()()xxe e xf x x e e +=-,则0x =是()f x 的( C ).A .连续点;B .可去间断点;C. 跳跃间断点;D .无穷间断点.2. 设()f x 有二阶连续导数且(0)0f '=,()lim 1||x f x x →''=,则下列说法正确的是( B ). A .(0)f 不是()f x 的极值,(0,(0))f 不是曲线()y f x =的拐点;本页满分32分 本页得分B .(0)f 是()f x 的极小值;C .(0,(0))f 是曲线()y f x =的拐点;D .(0)f 是()f x 的极大值. 3. 当x →∞时,若21ax bx c++与11x +为等价无穷小,则,,a b c 之值为( B ). A .0,1,1a b c ===; B .0,1a b ==,c 为任意常数; C .0a =,,b c 为任意常数; D. ,,a b c 均为任意常数.4. 设220()(),x x f x xx g x x ⎧>⎪=⎨⎪≤⎩,其中()g x 是有界函数,则()f x 在0x =处( D ).A .极限不存在;B.极限存在但不连续;C.连续但不可导;D.可导.5. 设()f x 在0x 可导且01()2f x '=,则0x ∆→时,0|x x dy =是x ∆的( C ).A .等价无穷小;B.高阶无穷小;C.同阶但非等价无穷小;D 低阶无穷小.三、计算题(共4小题,每小题5分,共20分) 1. 求极限01sin 1x x x →+-解:(方法一)200sin 1sin 12lim lim 11cos 2x x x xx x x x→→+==-; (方法二)2001sin 1lim11cos 1sin 1x x x x x x x x →→+==-++; (方法三)洛比达法则本页满分18分 本页得分01sin 11cos cos sin lim 1sin 2cos 21sin x x x x x x x x xx xx x →→→+-+-===+. 2. 设函数()y y x =由方程sin()(0,)xy y xe x x y ππ=>-<<确定,求其在1x =处的切线方程.解:两边取对数得:sin()(1)ln xy y x =-,两边对x 求导,有1cos()()ln y xy y xy y x x-''+=+, 又由于1x =时,sin 0y =,y ππ-<<,可得0y =,代入得(1)1y '=-,故在1x =处的切线方程为(1)y x =--,即10x y +-=.3. 设3arctan 6x t t y t t=+⎧⎪⎨=+⎪⎩,求221d y t dx =. 解:222363(1)111dydy t dt t dx dx dt t +===+++;22222()66(1)()1211d dy d y d dy t t t dt dx dx dx dx dx t dt t +====+++,故 2241d yt dx ==.本页满分10分 本页得分4. 求极限21)(cos lim x x x →.解:(方法一)2211cos 1cos 10lim(cos )lim(1cos 1)x x x x x x x x --→→=+-20cos 11lim2x x xe e→--==;(方法二)22222111sin 1222sin 22lim(cos )lim (cos )lim(1sin )x x x x x x x x x x x e---→→∞→==-=;(方法三)洛比达法则sin 2cos 22111ln(cos )lim 2lim(cos )lim xx xx x x x x x x e e e-→-→→===.四、应用题(共3小题,每小题8分,共24分)1. 已知()sin 2ln(1),0()1,0ax a b x x x x f x e x ++-⎧>⎪=⎨⎪-≤⎩在0x =处可导,试求出a 与b .解:由于()f x 在0x =处可导,必连续,故(0)(0)(0)0f f f -+===,又00()sin 2ln(1)()sin 2ln(1)(0)lim lim lim 2x x x a b x x a b x x f a b x x x++++→→→++-+-==+=+-,可得20a b +-=,即2a b +=;又由于()f x 在0x =处可导,则(0)(0)f f -+''=,又 01(0)lim ax x e f a x--→-'==, 本页满分16分 本页得分2200200()sin 2ln(1)sin ln(1)(0)lim 2lim1cos 11lim lim [sin ]1(1)x x x x a b x x x x f x x x x x x x +++++→→→→++-+-'==--==--=--, 故1,3a b =-=.2. 有一底半径为R cm ,高为h cm 的圆锥容器,今以253cm /s 自顶部向容器内注水,试求当容器内水位等于锥高的一半时水面上升的速率. 解:设t 时刻,水的体积,水面半径及水的深度分别为,,V r x ,由于2211()33V R h r h x ππ=--,又从相似三角形可知:r h x R h -=,即h xr R h-=,可得3222332211()1[()]333h x R V R h R h h x hh πππ-=-=--,两边对t 求导,得 222()dV R dxh x dt dt hπ=-, 由已知条件25dV dt =,2hx =,代入得2100dx dt R π=,即水面上升的速率为2100cm/s Rπ. 3. 试讨论方程)0(,ln >=a ax x 有几个实根. 解:令()ln ,(0,)f x x ax x =-∈+∞,则1()f x a x '=-,令()0f x '=,解得驻点1x a=,列表如下:x10,a ⎛⎫⎪⎝⎭ 1a1,a ⎛⎫+∞ ⎪⎝⎭()f x '+—本页满分16分 本页得分()f x最大值1f a ⎛⎫ ⎪⎝⎭可得,()f x 的最大值为1(ln 1)f a a ⎛⎫=-+ ⎪⎝⎭,讨论如下:(1) 当1a e =时,10f a ⎛⎫= ⎪⎝⎭,方程ln x ax =有唯一的实根;(2) 当10a e<<时,10f a ⎛⎫> ⎪⎝⎭,又由于 00lim ()lim (ln )x x f x x ax ++→→=-=-∞;ln lim ()lim ()x x xf x x a x→+∞→+∞=-=-∞, 故方程ln x ax =有两实根,分别位于10,a ⎛⎫ ⎪⎝⎭与1,a ⎛⎫+∞ ⎪⎝⎭内;当1a e >时,10f a ⎛⎫< ⎪⎝⎭,方程ln x ax =没有实根.五、证明题(共2小题,每小题8分,共16分)1.设函数()f x 在[0,2]上连续,在(0,2)内可导,且(0)0f =,0)2(=f ,证明:存在(0,2)ξ∈,使得()()f f ξξ'=.证明:令()()x F x e f x -=,则()F x 在[0,2]上连续,在(0,2)内可导,且由于(0)0f =,0)2(=f ,易得(0)(2)0F F ==,根据罗尔定理,至少存在(0,2)ξ∈,使得()0F ξ'=,即()()0e f e f ξξξξ--'-+=,又0e ξ-≠,可得()()f f ξξ'=.本页满分8分 本页2.证明:当0>x 时,x x xx<+<+)1ln(1. 证明:(方法一)设t t f ln )(=,则)(t f 在[1,1]x +上连续,在(1,1)x +内可导,由 Lagrange 中值定理,得ln(1)ln11x x ξ+-=,11x ξ<<+,故1111x ξ<<+,即1ln(1)11x x x +<<+,整理得,x x xx<+<+)1ln(1. (方法二):对()ln(1)f t t =+在[0,]x 上应用Lagrange 中值定理.(方法三):利用函数的单调性.得分。
《数理经济学》2010级期末试卷A答案
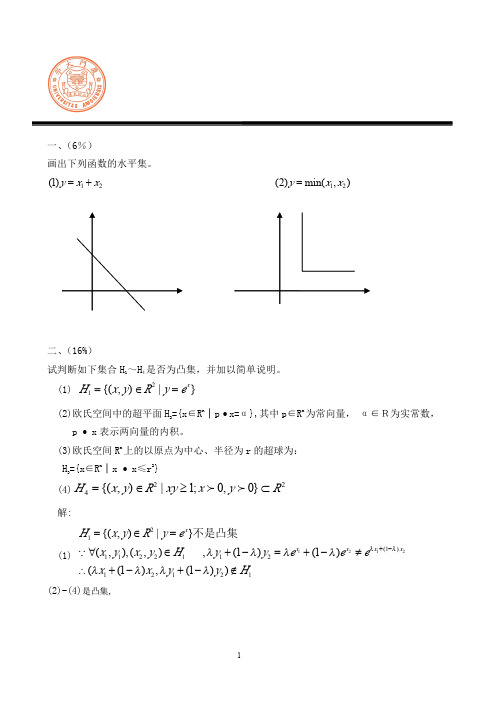
一、(6%)画出下列函数的水平集。
12 (1)y x x =+12 (2)min(,)y x x=二、(16%)试判断如下集合H 1~H 4是否为凸集,并加以简单说明。
(1)}|),{(21xe y R y x H =∈=(2)欧氏空间中的超平面H 2={x∈R n│p •x=α},其中p∈R n为常向量,α∈R为实常数,p •x 表示两向量的内积。
(3)欧氏空间R n上的以原点为中心、半径为r 的超球为:H 3={x∈R n │x •x≤r 2}(4)224}0,0;1|),{(R y x xy R y x H ⊂≥∈=≻≻解:(1)121221(1)112211212121{(,)|}(,),(,),(1)(1)((1),(1))x x x x x H x y R y e x y x y H y y e e e x x y y H λλλλλλλλλλ+−=∈=∀∈+−=+−≠∴+−+−∉∵不是凸集(2)-(4)是凸集,三、(10%)设某两个商品的需求量1q 和2q 分别是它们的价格1p 、2p 和收入I 的函数,形如:23/2121122126,4q p p I q p p I −−==。
目前的价格*1p =6,*2p =9,收入I *=2.当两种商品的价格均上升0.2,收入下降0.1时,1q 和2q 分别增加多少?1232212121211112222123133222221212121222121212::(,,)(0.2,0.2,0.1)*(6,9,2)6(*)4(*)1296448T Tx p p I x p p I F x p p I q q q pp I DF x q q q p p I p p I p p I p p p I p p I p p I −−−−−−−−∆=∆∆∆=−=⎛⎞⎜⎟=⎜⎟⎝⎠∂∂∂⎛⎞⎜⎟∂∂∂⎜⎟=⎜⎟∂∂∂⎜⎟∂∂∂⎝⎠⎛⎞−⎜⎟=⎜⎟−⎝⎠=解依题意1230.75 4.58/3 1.185232/3(*)(*)(*)0.230.75 4.50.9(*)0.28/3 1.185232/30.2370.1F x x F x DF x xq DF x x q −⎛⎞⎜⎟−⎝⎠+∆−≈∆⎛⎞∆−−⎛⎞⎛⎞⎛⎞⎜⎟≈∆≈≈⎜⎟⎜⎟⎜⎟⎜⎟∆−−⎝⎠⎝⎠⎝⎠⎜⎟−⎝⎠四、(12%)1/41/212121212121212/(,)(,)1(,)()(),x x f x x f x x f ff x x x x x x x y x =∂∂=+∂∂=保持不变的等产量线的斜率相等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1
一、叙述并证明含不等式约束的非线性规划问题的Kuhn-Tucker 充分和必要条件(必要条件的证明需包含对Fritz-John 条件的证明,其中可直接利用二择一等引理)。
二、求以下非线性规划问题的最优解。
2
12m in :-2x x
22
12113..:
2
2
s t x x x +-
≤-≤
三、考虑一个竞争厂商,两种投入12,x x 的价格分别为12,w w ,厂商的生产技术以科布道格拉斯函数表示:()1212,f x x x x α
β
=,其中+<1,>0,>0αβαβ。
(1)证明:()12,f x x 是严格凹函数。
(2)求出条件投入需求函数(),,=1,2i x w y i 、成本函数(),c w y 。
(3)利用包络定理证明
()(),=,,1,2i i
c w y x w y i w ∂=∂,并结合(2)的结论验证。
四、 两个生产同质产品的寡头垄断企业的成本函数为,=1,2i i i C c q i =,其中i c 为企业i 的边际成本,市场需求曲线为p Q θ=-,其中12Q q q =+,
(1)求出古诺(Cournot )均衡情况下的产量、价格和利润;
(2)为获得两个厂商进行生产的内点解(即两个厂商都生产正的产量),需要对参数12,,c c θ施加何种约束?其中1,c θ变化对均衡产量有何影响?
(3)假定厂商1先行动,求出该斯塔克伯格(Stackelberg )均衡情况下的产量、价格和利润;并与(1)的结果进行比较。
五、以下任选一题
1. 根据教材例题,用数理模型说明刚性工资的存在。
2. 根据课堂例题,用数理模型讨论逆向选择问题,说明信息不对称对效率的影响。
