第2章 随机过程与排队轮基础
排队论基础

通信网理论(三)排队论与通信网业务分析排队论基础纪阳北邮无线新技术研究室Tel: +86-10-62283522E-mail: jiyang@W T I排队论概述•排队系统–要求服务的顾客–提供服务的服务员W T I2排队论概述•排队系统的广泛性–顾客+服务→排队系统–矛盾统一,广义化:•通信中:–呼叫——线路–信息包——分组交换机–移动体——服务区•计算机:–总线指令——CPU处理–数据流——存储器•其它:–敌机——防空设施–客机——跑道W T I3排队论概述•排队现象存在的基础–资源的有限性–需求的随机性•排队系统的复杂性在于随机性–到达与离去(服务率)均不确定,工作于随机状态W T I4排队论概述•排队系统中的资源冲突–资源少——顾客排队长——服务质量下降–资源多——服务闲置——资源浪费•排队系统设计目标–为顾客提供满意服务同时提高资源利用率。
(与统计参数和工作方式有关)W T I5如何描述一个排队系统(1)•排队系统三要素: m,λ,μ–m-窗口数,表示资源的量•可同时向顾提供服务的设施数。
•(单窗口m=1;多窗口m>1)–λ-顾客到达率(平均)–μ:系统服务率(平均)W T I6如何描述一个排队系统(1)λ↓——负荷轻•此三量可已知或可测出,但描述排队系统,此三要素不充分•主要取决于ti 和τi的统计特性(分布)和排队规则7W T I如何描述一个排队系统(1)•此三量可已知或可测出,但描述排队系统,此三要素不充分•排队系统性能主要取决于–ti 和τi的统计特性(分布)–服务规则和排队规则8 W T I到达与服务的分布类型•M——指数分布–平稳性–稀疏性–独立性•泊松分布•Er——r阶爱尔兰分布•H R——R阶指数分布•D分布——确定性分布W T I9系统工作方式•服务规则–先到先服务First In, First Serve–后到先服务Last In, First Serve–优先制服务Priority•排队规则–等待型•不拒绝系统–截至型•n=m,即时拒绝,电话网•m<n,延时拒绝,缓冲区数据通信W T I1011W T I 排队过程的实例到达离去忙时T 闲时I 顾客数t 1t 2t n t 1τ2τn τ如何分析一个排队系统•排队队长k 的概率分布、均值、方差•等待时间w 的均值、方差•服务时间τ•系统时间S•系统效率η–窗口占用率,η=r/m•稳定性–ρ=λ/µ•if ρ>m, 不拒绝系统,not stable,•if ρ>m, 截至型系统,stableW T I1213W T I 队长k排队长度—t瞬间系统内的顾客数(含在窗口的)k —离散随机变量三种观察:d k —顾客到达时观察队长为k 的概率r k —顾客离去时观察队长为k 的概率(以上为有条件抽样)p k —(服务员)随机观察队长为k的概率在最简系统中,p k =r k =d k —平均队长,又称系统数k 注意:其他的系统中这几种观察的结果是不同的。
排队论基础

t时刻, k状态 则:Δ t—Δ t内到达1人概率
Δ t—Δ t内离去1人概率
t+Δt时刻处于k状态(概率 pk(tt)),由下述情 况形成:
t为k-1态,Δt内到达1人,无人离去,概率: p k 1 ( t) t( 1 t) p k 1 ( t) t
Network Laboratory
复杂性:在于随机性——到达与离去(服务 率)均不确定——工作于随机状态 资源少——顾客排队长——服务质量下降 资源多——服务闲置——资源浪费
Network Laboratory
目标:为顾客提供满意服务同时提高资 源利用率。(与统计参数和工作方 式有关)
在通信网的业务分析和性能计算中,排队论 是不可缺少的
k
pk k p0
Network Laboratory
求p0: 用归一化条件
1 pk
k0
(12 )p01 1p0
p01
p0——系统无人概率(空闲率) 1-p0=—系统有人概率(忙概率) 忙 太大不稳
得通解: pkkp0k(1)
无后效性
顾客到达时刻相互独立
不相交区间内到达顾客数相互独立
系统顾客数具有马氏性
稀疏性:
Δ t内到达2个或2个以上顾客概率为0
有限区间内的k为有限,或
p(k)0
Network Laboratory
(1)T内有k个顾客到达的概率
在以上假设下: T内到达顾客数为k
Δ=T/N
............ .....
Network Laboratory
1-Δ t-Δ t
Δ t
排队论知识点(一)

排队论知识点(一)排队论知识点详解什么是排队论排队论是应用概率论、随机过程和数学统计方法来研究队列系统的数学理论。
队列系统是指一些处理实体以确定的方式到达某个系统,被系统以某种方式处理,然后离开系统的系统模型。
排队论研究的目标是为了通过合理的设计和优化队列系统(如银行服务台、电话交换机等)的结构和参数,提高系统的效率和性能。
排队论的主要概念1. 到达过程到达过程是指实体到达队列系统的时间间隔的随机过程。
根据到达的规律性和随机性不同,到达过程可以分为不可预测的泊松到达过程和可预测的非泊松到达过程。
2. 服务过程服务过程是指队列中的实体被处理的时间间隔的随机过程。
根据服务的规律性和随机性不同,服务过程可以分为不可预测的指数服务过程和可预测的非指数服务过程。
3. 队列长度队列长度是指队列中正在等待服务的实体的个数,也可以看作是在系统中等待服务的实体的数学期望。
4. 平均等待时间平均等待时间是指实体在队列系统中等待服务的平均时间。
5. 利用率利用率是指队列系统中服务设备的利用情况,通常用平均到达率与平均服务率的比值来表示。
排队论的基本模型1. M/M/1模型M/M/1模型是排队论中最简单的模型之一,代表了一个单一服务台和一个队列的排队系统。
M/M/1模型的到达过程和服务过程都是泊松过程,服务设备能力为1。
2. M/M/C模型M/M/C模型是M/M/1模型的扩展,代表了含有C个服务台和一个队列的排队系统。
到达过程和服务过程仍然是泊松过程,但是服务设备能力为C。
3. M/G/1模型M/G/1模型是M/M/1模型的变体,代表了一个单一服务台和一个队列的排队系统,但是服务过程是一般分布。
到达过程仍然是泊松过程。
4. G/G/1模型G/G/1模型代表了一个单一服务台和一个队列的排队系统,到达过程和服务过程都是一般分布。
排队论的应用1. 交通拥堵排队论可以用来研究交通拥堵的原因和解决方案,进一步优化交通网络资源的利用和流量的分配。
(完整)排队论
5。
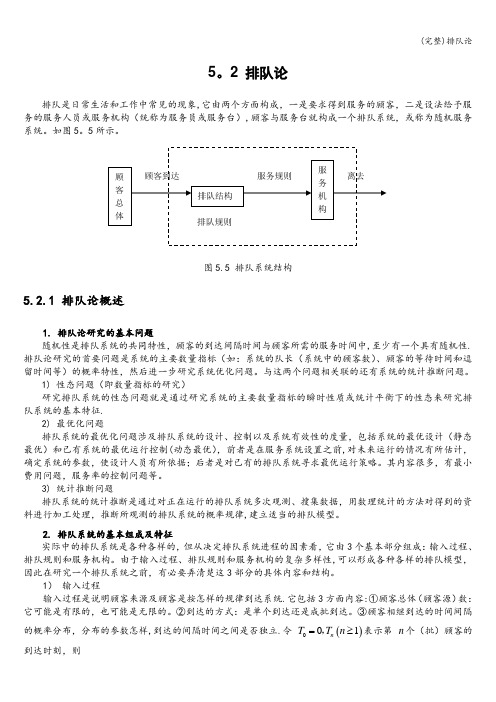
2 排队论排队是日常生活和工作中常见的现象,它由两个方面构成,一是要求得到服务的顾客,二是设法给予服务的服务人员或服务机构(统称为服务员或服务台),顾客与服务台就构成一个排队系统,或称为随机服务系统。
如图5。
5所示。
图5.5 排队系统结构5.2.1 排队论概述1. 排队论研究的基本问题随机性是排队系统的共同特性,顾客的到达间隔时间与顾客所需的服务时间中,至少有一个具有随机性.排队论研究的首要问题是系统的主要数量指标(如:系统的队长(系统中的顾客数)、顾客的等待时间和逗留时间等)的概率特性,然后进一步研究系统优化问题。
与这两个问题相关联的还有系统的统计推断问题。
1) 性态问题(即数量指标的研究)研究排队系统的性态问题就是通过研究系统的主要数量指标的瞬时性质或统计平衡下的性态来研究排队系统的基本特征.2) 最优化问题排队系统的最优化问题涉及排队系统的设计、控制以及系统有效性的度量,包括系统的最优设计(静态最优)和已有系统的最优运行控制(动态最优),前者是在服务系统设置之前,对未来运行的情况有所估计,确定系统的参数,使设计人员有所依据;后者是对已有的排队系统寻求最优运行策略。
其内容很多,有最小费用问题,服务率的控制问题等。
3) 统计推断问题排队系统的统计推断是通过对正在运行的排队系统多次观测、搜集数据,用数理统计的方法对得到的资料进行加工处理,推断所观测的排队系统的概率规律,建立适当的排队模型。
2. 排队系统的基本组成及特征实际中的排队系统是各种各样的,但从决定排队系统进程的因素看,它由3个基本部分组成:输入过程、排队规则和服务机构。
由于输入过程、排队规则和服务机构的复杂多样性,可以形成各种各样的排队模型,因此在研究一个排队系统之前,有必要弄清楚这3部分的具体内容和结构。
1) 输入过程输入过程是说明顾客来源及顾客是按怎样的规律到达系统.它包括3方面内容:①顾客总体(顾客源)数:它可能是有限的,也可能是无限的。
电子科大随机过程与排队论01

随机事件体F由Ω的全体子集(共26 =64个)构成; k F上的概率定义为P(A)= ,k为随机事件A包含 6 的样本点数;
(Ω,F,P)为概率空间。
2013-9-13
计算机科学与工程学院
顾小丰
20-12
古典概率空间
1) 样本空间由有限个样本点组成, Ω={ω1,ω2,…, ωn}; 2) 每个基本事件Ai={ωi},i=1,2,…,n出现的可能性 相等。
B发生的条件概率定义为:
P( AB) P(B | A) P( A)
给定概率空间(Ω,F,P),AF,且P(A)>0,对 任 意 BF 有 P(B|A) 对 应 , 则 条 件 概 率 P(B|A) 是 (Ω,F)上的概率,记P(B|A)=PA ,则(Ω,F,PA)也是 一个概率空间,称为条件概率空间。
设(Ω,F)是可测空间,如果定义随机事件体F上的实 值集函数P(A),AF满足: 1) 0≤P(A)≤1,AF; (非负性) 2) P(Ω)=1; (规范性) 3) AiF(i=1,2,…,),AiAj=Φ(i≠j),则等式
P( A i ) P( A i )成立 。
i 1 i 1
下一讲内容预告
随机变量及其分布程
• 随机变量、分布函数 • 离散型随机变量及其分布律 • 连续型随机变量及其概率密度
常见的随机变量及其分布
n维随机变量 随机变量函数的分布
2013-9-13 计算机科学与工程学院 顾小丰 20-22
2013-9-13 计算机科学与工程学院 顾小丰 20-8
二、样本空间、随机事件体
随机试验E的每一个最简单的试验结果,称 为样本点,记为。全体样本点构成的集合,称 为样本空间,记为Ω。 样本空间Ω的子集组成的集类F,如果满足: 1. ΩF; 2. 若AF,则 A F; 3. 若AiF(i=1,2,…,),则 A i F ;
运筹优化(十六)--排队论基础及其最优化求解

运筹优化(⼗六)--排队论基础及其最优化求解排队过程的⼀般表⽰下图1就是排队过程的⼀般模型。
各个顾客由顾客源(总体)出发,到达服务机构 (服务台、服务员)前排队等候接受服务, 服务完成后就离开。
排队结构指队列的数⽬和排列⽅式 , 排队规则和服务规则是说明顾客在排队系统中按怎样的规 则、次序接受服务的。
我们所说的排队系统就指图中虚线所包括的部分。
排队系统的组成和特征⼀般的排队系统都有三个基本组成部分 : 1输⼊过程 ; 2排队规则 ; 3服务机构。
1. 输⼊过程输⼊即指顾客到达排队系统 , 可能有下列各种不同情况 , 当然这些情况并不是彼此排斥的。
(1) 顾客的总体(称为顾客源)的组成可能是有限的,也可能是⽆限的。
上游河⽔流⼊⽔库可以认为总体是⽆限的 , ⼯⼚内停机待修的机器显然是有限的总体。
(2) 顾客到来的⽅式可能是⼀个⼀个的, 也可能是成批的。
例如到餐厅就餐就有单个到来的顾客和受邀请来参加宴会的成批顾客,我们将只研究单个到来的情形。
(3) 顾客相继到达的间隔时间可以是确定型的, 也可以是随机型的。
(4) 顾客的到达可以是相互独⽴的,就是说,以前的到达情况对以后顾客的到来没有影响 , 否则就是有关联的 。
(5) 输⼊过程可以是平稳的,或称对时间是齐次的,是指描述相继到达的间隔时间分布和所含参数(如期望值、⽅差等)都是与时间⽆关的, 否则称为⾮平稳的。
2. 排队规则(1) 顾客到达时, 如所有服务台都正被占⽤,在这种情形下顾客可以随即离去, 也可以排队等候。
随即离去的称为即时制或称损失制 , 因为这将失掉许多顾客 ; 排队等候的称为等待制。
普通市内电话的呼唤属于前者 , ⽽登记市外长途电话的呼唤属于后者。
对于等待制,为顾客进⾏服务的次序可以采⽤下列各种规则: 先到先服务, 后到先服 务 , 随机服务 , 有优先权的服务等。
先到先服务 , 即按到达次序接受服务 , 这是最通常的情形。
后到先服务,如乘⽤电梯的顾客常是后⼊先出的。
随机过程与排队论
随机过程与排队论任课教师:魏静萱副教授wjx@曾勇副教授第一节排队现象例一:电话系统:主叫用户和被叫用户之间提供语音服务,该服务承载于某条通信信道之上,即两个用户c个通道。
地需要一条通道,3个用户需要3个通道,4个用户需要6个通道。
一般的,n个用户需要2n球人口60亿,需要?通道。
海量通信接近天文数字。
解决:信道“公用”导致拥挤排队现象例二:排队现象举例排队系统的三大要素:1. 输入过程 2. 排队规则:队列允许的最大长度 3. 服务窗:顾客是怎样接受服务的1.输入过程:顾客按什么规则进入系统?一个个?成批?到达过程和到达时间间隔符合一定的分布,称到达分布。
假设:到达过程和到达时间是独立同分布的。
到达过程假定为平稳的,对时间是齐次的。
注:Markov 齐次过程 如果一个过程只依赖于现在,而不是过去。
表1 输入过程的三种随机过程描述按顾客到达过程的不同概率特性分类: ① 定长输入(D ):顾客等间隔到达,nc τ=n τ的分布函数为 1()()0n t c F t P t t cτ≥⎧=≤=⎨<⎩②Poisson 流输入(M): 系统的输入过程{M(t)>0}是Poission 流 满足4个条件:a) M(t)取值为非负数b) P(M(0)=0)=1, 即时间间隔为0时到达系统 的人数为0 c) 过程{M(t)} 具有平稳独立增量性 d) 每一个增量M(a+t)-M(a)非负,且服从参数为tλ的泊松分布(){()()}!k a t P M t a M a k e K λλ-+-==③ k 阶Erlang 输入(Ek)④ 一般独立输入(G):顾客的到达过程{n τ}是独立同分布的随机变量序列,其分布函数可以是任意函数。
⑤ 成批到达系统:顾客一批批到达系统,每批相继到达的时间间隔为上述各种分布之一。
2.排队与服务规则① 损失制 (无排队队列):顾客到达时,系统被占用,顾客离去,不再回来。
排队论
泊松输入中的顾客到达间隔时间 T 相互独立且服从同参数 λ 的负指数分 布,其密度函数为
其平均到达间隔时间为
λ 称为到达率。
三. 排队系统的主要特征
1. 输入过程 ⑴ 定长输入( D, Deterministic ) ⑵泊松输入 (最简单流, M ) ⑶ 一般独立输入( G,General Independent ) —— 指顾客到达间隔时间 T 为相互独立且同分布的随机变量。最简单 流是它的一个特例。 此外,在本章所讨论的排队系统中,总假定输入过程是平稳的,或 称对时间是齐次的。 平稳的输入过程 —— 指顾客到达间隔时间的分布与时间无关。否则就称 为非平稳的。
服务台m
服务台 1
⑸
服务台 2
服务台 1 服务台 2
···
···
服务台 m
服务台 m
三. 排队系统的主要特征
1. 输入过程 2. 服务时间 τ 的分布 3. 服务机构(服务台) 4. 服务规则
⑴ 先到先服务(FCFS) ⑵ 后到先服务(LCFS)
如信息处理、仓库中堆积的货物等。 ⑶ 随机服务(SIRO) ⑷ 优先权服务(PR) ⑸ 一般服务规则(GD)
1909年,由丹麦工程师爱尔朗(A.K.Erlang)在研究电话系统时初创的。
§l 排队论的基本概念及研究的问题
一.排队论中有两个基本概念:
顾客:把提出需求的对象称为顾客(或需求); 服务:把实现服务的设施称为服务机构(或服务台)。
顾客和服务机构组成一个排队系统,称为随机服务系统。 因此也称排队论为随机服务系统理论
⑴ 定长输入( D, Deterministic ) —— 每隔一定时间 α 到达一个顾客,顾客到达间隔时间 T 的分布函数为
三. 排队系统的主要特征
随机过程概要及概率基础
四、事件独立: P( AB) P( A)P(B)
n个事件独立, 2n n 1 个表达式。
随机变量独立:X1 , X 2 , , X n 独立,要求
联合密度为边缘密度之积,即:
F x1,, xn FX1 x1 FXn xn
F 其中, X j
xj
lim F xi
x1, , xn
随机过程概要及概率基 础
二、随机数学发展概述
随机数学
stochastic mathematics
概率论
probability theory
随机现象 偶然性
数理统计
Mathematical statistics
内在规律 必然性
随机过程
stochastic process
3 随机过程
➢Brown运动: 1827 年,Brown在显微镜下发现花 粉的无规则运动, 将此奇怪现象公诸于世, 无人能解 释原因. 1900年,法国数学家Bachelier给出 一维 Brown运动粗略模型, 其博士论文为《投机的理论》 ,研究证券价格的涨落,开创近代金融数学的先河, 但他的结果几十年之后才得到认可.
1.2 随机变量
随机变量X分布函数: Fx PX x
满足:
(ⅰ) 单调不减; (ⅱ) 右连续;
(ⅲ) F 0 ;
(ⅳ) F 1 ;
Fx f x
概率空间( , F, P) 实数a,{ : X () a} F;
这里指的是可测集《 , 实变函数》《应用数学基础》 讲Lebesgue可测,是指:{x D : f (x) a}为可测集.
同时, P Xn 1 (一般项趋于1), n 1
P(lim sup( X n
0)
1.这样无穷多个X
排队长度检测方法研究
摘要随着城市的发展,交通拥挤已成全世界的交通难题,车辆排队是交通拥挤的一种典型表现形式,因此车辆排队长度是一个很重要的交通信息参数。
本文基于二流理论,把真实交通流状态转换为二流运行状态,计算转换后得到一种车辆排队长度,即当量排队长度。
根据流量守恒方程,建立了单车道路段的当量排队长度模型,并在此基础上推出多车道的平均当量排队长度模型,并用VISSIM软件模拟交通拥堵路段,对该模型进行测试.仿真结果表明,模型计算出来的当量排队长度均大于实际车辆排队长度,实际排队长度变化时,当量排队长度相对稳定。
关键词交通流;交通拥挤;车辆排队长度;二流理论;当量排队长度AbstractWith the development of cities,traffic jam has become a whole world’s problem. Queue of vehicles is a typical manifestation of congestion. So the queue length is an important traffic information parameter。
A kind of queue length transformed by the real queue length,called equivalent queue length,which turns the real traffic flow into a two-fluid operation status, is brought forward in this article,based on the theory of two-fluid. On this basis,the equivalent queue length model is built for the single-lane sections according to flow conservation equation. And the multi-lane sections average equivalent queue length is built based on the single-lane model。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
k =0
(λ t ) − λ t (λ t ) = ∑e ( k − 1) ! k! k =1
k
∞
k
∞
= λ te
− λt
∑
k =1
(λt ) = λt ( k − 1) !
16
k −1
2012年3月
BUPT Information Theory & Technology Education & Research Center
其中λ>0是泊松流的强度,表示平均到达率; 且N(0) = 0;不相交区间上增量相互独立,即对 一切 0≤t1<t2<…<tn,N(t1), N(t2)-N(t1), N(t 3)N(t2), …, N(tn)-N(t n-1)相互独立。
应用:广泛用于各种随机事件的描述或近似,可用来描 述完全不可预测的随机事件和大量随机事件的叠加。
2012年3月
11
BUPT Information Theory & Technology Education & Research Center
Siméon Denis Poisson
• Born: 6/21/1781Pithiviers, France • Died: 4/25/1840Sceaux, France • “Life is good for only two things: discovering mathematics and teaching mathematics.”
∞
∞
= ∑ ( k − 1) e
k =1
− λt
(λ t ) −λt (λt ) = ( λt ) 2 + λt + ke ( k − 1) ! k=1 k ⋅ (k −1) !
k
∞
k
∑
D( X ) = E X − ( EX ) = λt
2 2
2012年3月 17
( )
Poisson过程的叠加和分解
2012年3月
8
BUPT Information Theory & Technology Education & Research Center
Poisson过程
定义:计数过程N(t)服从泊松分布的随机过程, 即长度为t的时间内到达k个事件的概率为
(λt ) k pk (t ) = k!
e
−λt
k = 0,1,2,⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅
BUPT Information Theory & Technology Education & Research Center
2012年3月
18
BUPT Information Theory & Technology Education & Research Center
Poisson过程的叠加
2012年3月 13
BUPT Information Theory & Technology Education & Research Center
Poisson’s education and work
• Poisson impressed his teachers Laplace and Lagrange with his abilities. • Unfortunately, the École Polytechnique specialized in geometry, and Poisson could not draw diagrams well. • However, his final paper on the theory of equations was so good he was allowed to graduate without taking the final examination. • After graduating, Poisson received his first teaching position at the École Polytechnique in Paris, which rarely happened. • Poisson did most of his work on ordinary and partial differential equations. He also worked on problems involving physical topics, such as pendulums and sound.
准备知识: 计数过程
随机过程{N(t),t≥0}称为一个计数过程。 N(t)表示到时刻t为止已发生的“事件”的总数。
� N(t)≥0; � N(t)是整数; � N(t)≥ N(s),当t ≥ s; � N(t) - N(s)代表时间区间[t, s) 中发生的“事件” 数
2012年3月
4
随机事件的两种描述法
BUPT Information Theory & Technology Education & Research Center
Poisson过程的分解
• 性质2-2:参数为 λ = λ1 + λ2 的Poisson流到达 交换局A后,每个呼叫将独立去两个不同方 向,且去两个方向的概率分别为 λi P = • i = 1,2 i λ • 则Poisson流被分解为两个独立的 Poisson 流,参数分别为 λ1和λ2
2012年3月
14
BUPT Information Theory & Technology Education & Research Center
Poisson’s accomplishments
• He has many mathematical and scientific tools named for him, including Poisson's integral, Poisson's equation in potential theory, Poisson brackets in differential equations, Poisson's ratio in elasticity, and Poisson's constant in electricity. He first published his Poisson distribution in 1837 in Recherches sur la probabilit é des jugements en matière criminelle et matière civile. Although this was important to probability and random processes, other French mathematicians did not see his work as significant. His accomplishments were more accepted outside France, such as in Russia, where Chebychev used Poisson ’s results to develop his own.
第二章 随机过程与排队轮基础
Communication Networks Theory Education & Research Center
信息与通信工程学院 通信网技术教研中心
通信网基础
无线通信与网络研究室
准备知识: 随机过程
BUPT Information Theory & Technology Education & Research Center
2012年3月 12
BUPT Information Theory & Technology Education & Research Center
Siméon Denis Poisson
• Poisson’s father originally wanted him to become a doctor. After a brief apprenticeship with an uncle, Poisson realized he did not want to be a doctor. • After the French Revolution, more opportunities became available for Poisson, whose family was not part of the nobility. • Poisson went to the École Centrale and later the École Polytechnique in Paris, where he excelled in mathematics, despite having much less formal education than his peers.
ψ (t ) = o (t )
t→0
∞
• (4)有限性:在任意有限区间内到达有限个 事件的概率为1,即 ∑ P ( t ) = 1
k k = 0
2012年3月
10
BUPT Information Theory & Technology Education & Research Center
例题分析
设电话呼叫按30次/小时的泊松过程进行,求5分钟 间隔内,(1)没有呼叫的概率;(2)呼叫3次的概率。 解:按题意λ= 30次/h = 0.5次/min t = 5min ,分别计算k = 0或k=3
P0 (5) = e −0.5×5 = 0.082
2.53 −0.5×5 P3 (5) = e = 0.214 3!
