§10.5 安培定律 磁力矩(打印稿)
安培力 磁力矩
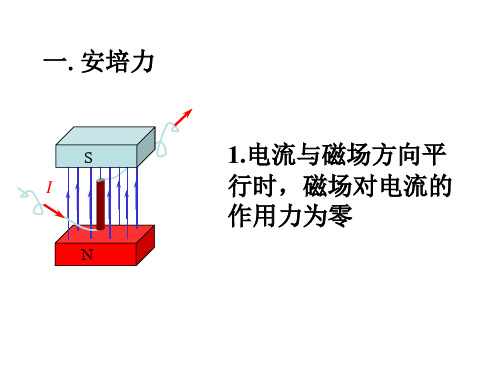
S I
1.电流与磁场方向平 电流与磁场方向平 行时, 行时,磁场对电流的 作用力为零
N
N F I B S
2.电流与磁场方向垂 电流与磁场方向垂 直时, 直时,磁场对电流的作 用力最大。 用力最大。 在匀强磁场中,当I与 在匀强磁场中, 与 B垂直时,安培力的大 垂直时, 垂直时 小为 F=BIL 方向用左手定则判断
二.磁力矩 磁力矩
I S
O θ
O’
通电线圈放入匀强磁场中, 通电线圈放入匀强磁场中,如果两条边 受到的安培力不在同一条直线上, 受到的安培力不在同一条直线上,通电线圈 就要受到磁力矩的作用。 就要受到磁力矩的作用。
O θ
F = BIa b ab M1 = F cosθ = BI cosθ 2 2
B2
B
B1
I
3.当电流 3.当电流I与磁感应 不垂直时, 强度B不垂直时,可将B 分解为平行于电流的分 量B1(对安培力无贡 ),和垂直于电流的 献),和垂直力F垂直于纸面向外 安培力 垂直于纸面向外
F
B I
安培力F 安培力 的方向总是垂 直于电流I 直于电流 与磁感应强 度B 所确定的平面
A、IBS 、 B、 IBS/2 、
O a I
b
B
c d S O’
C、√3IBS /2 、
D、由于导线框的边长及固定轴的位置未给以, 、由于导线框的边长及固定轴的位置未给以, 无法确定。 无法确定。
如图,条形磁铁平放于水平桌面上, 例2. 如图,条形磁铁平放于水平桌面上, 在它的正中央上方固定一根直导线, 在它的正中央上方固定一根直导线,导线 与磁场垂直, 与磁场垂直,现给导线中通以垂直于纸面 向外的电流,则下列说法正确的是: 向外的电流,则下列说法正确的是: A.磁铁对桌面的压力减小 . B.磁铁对桌面的压力增大 . C.磁铁对桌面的压力不变 . D.以上说法都不可能 .
安培环路定律 磁力 磁介质(附解析)
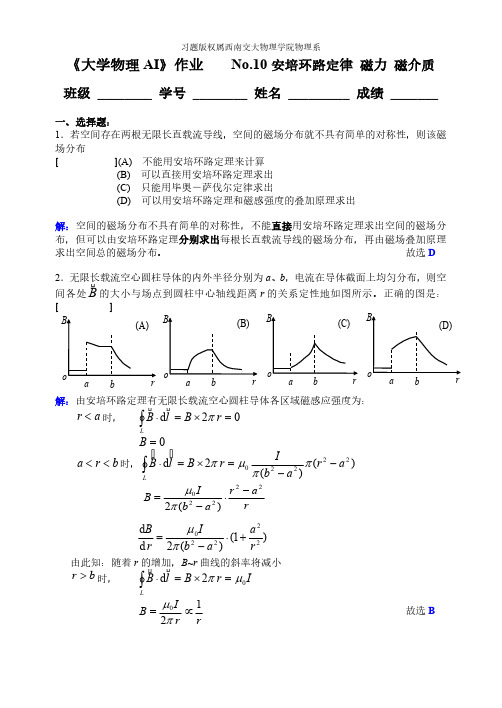
习题版权属西南交大物理学院物理系《大学物理AI 》作业No.10安培环路定律 磁力 磁介质班级 ________ 学号 ________ 姓名 _________ 成绩 _______一、选择题:1.若空间存在两根无限长直载流导线,空间的磁场分布就不具有简单的对称性,则该磁场分布 [ ](A) 不能用安培环路定理来计算 (B) 可以直接用安培环路定理求出 (C) 只能用毕奥-萨伐尔定律求出 (D) 可以用安培环路定理和磁感强度的叠加原理求出解:空间的磁场分布不具有简单的对称性,不能直接用安培环路定理求出空间的磁场分布,但可以由安培环路定理分别求出每根长直载流导线的磁场分布,再由磁场叠加原理求出空间总的磁场分布。
故选D 2.无限长载流空心圆柱导体的内外半径分别为a 、b ,电流在导体截面上均匀分布,则空间各处的大小与场点到圆柱中心轴线距离r 的关系定性地如图所示。
正确的图是:B 内[]解:由安培环路定理有无限长载流空心圆柱导体各区域磁感应强度为:时,a r <02d =⨯=⋅⎰r B l B Lπ内内0=B 时,b r a <<)()(2d 22220a r ab I r B l B L--=⨯=⋅⎰ππμπ内内r a r a b IB 22220)(2-⋅-=πμ)1()(2d d 22220ra ab I r B +⋅-=πμ由此知:随着r 的增加,B ~r 曲线的斜率将减小时,b r >I r B l B L02d μπ=⨯=⋅⎰内内故选Brr I B 120∝=πμ3.如图,线固定不动,则载流三角形线圈将:[ ] (A) 向着长直导线平移(B) (C) 转动(D) 不动解:建立如图所示的坐标轴,无限长直载流导线在x >0应强度为:方向xI B πμ201=⊗由安培定律可得不同位置a 为:l aII AB a I I F AB πμπμ22210210==30cos d 2d 30cos 2102x x I I l BI F F l a aCABC AC =︒⋅===⎰⎰︒+πμ式中为三角形边长,各力方向如图所示,则载流三角形线圈所受合力为:l 令,有)0(>=λλal0)23111(2231233321[2d )(d 210210<+--=+⨯--=∑λπμλπμλI I I I F x 又(无穷远处),所以载流线圈所受合力始终向着长直电流,可见载流三角0|0==∑λx F形线圈不可能转动,只能向着长直导线平动。
大学物理安培力磁力矩和功

力矩的功:
磁 力 的 功 : 转 动
A Md
F1
BIS sin d
载 流 线
I dBS cos
圈
d
B
I dm Im
F2
n
A Im
注:
1、任意一个闭合电流回路在磁场中改变位置或形状时,
只要电流不变,磁力或磁力矩作功都可按上式计算。
例:电流为 I 的长直导线附近,有一半径为 a, 质量
M方向:⊙
M M1 M2 BIl2l1 sin BIS sin
F2
S = l1l2 为线圈平面的面积 N匝线圈的磁力矩:
⊙
r
l1
B
M NBIS sin
n
F1
注:上式虽是从矩形闭合载流线圈推出,但适合于
均匀磁场中任意形状的闭合载流线圈。
磁 力 矩 用 磁 矩 表
M NBIS sin
线圈的磁矩:pm M
安培定律
磁 秤 测 量 原 理
例1: 磁秤:如图所示, 矩形线 圈的宽为b,长为l,共有N匝, 下端放在待测的均匀磁场中, 其平面与磁感应强度垂直,当 线圈中通有电流I时,线圈受 到一向上的作用力,天平失去 平衡,调节砝码m使两臂达到 平衡。用上述数据求待测磁场 的磁感应强度B。
I B
磁秤
F NBIb NBIb mg B mg NIb
例2、半径为R的铜丝环,载有电流I。现把圆环放在 均匀磁场中,环平面与磁场垂直。求(1)圆环受到 的合力。(2)铜丝内部的张力。
例 题
推论1:均匀磁场对闭合载流导线的作用合力为零。
:
圆
环
在
磁 场
y
dFy
dF
Fy
中
的
§7.8_安培定律_磁力矩

P. 18 / 25 .
磁偶极矩 ( 磁矩 ):
pm IS en ( A·m2 )
则磁力矩:
M
pm
B
M BIaSbsisnin
B
b
B
F1
a
I
en
F2
I
en
M
Chapter 10. 稳恒电流与稳恒磁作场者:杨茂§田10. 5 安培定律 磁力矩
P. 19 / 25 .
磁偶极矩 ( 磁矩 ):
2R
M I2 r 2
0I1
2R
sin
/2
W Md
0
I2
r2
0 I1
2R
/
2
sin
d
I1
0
I2 r
0r2
2R
I1I2
(解毕 )
P. 23 / 25 .
R
Chapter 10. 稳恒电流与稳恒磁作场者:杨茂§田10. 5 安培定律 磁力矩
P. 24 / 25 .
1. 安培定律:
b
dF Idl B F Idl B
P. 17 / 25 .
二、载流线圈所受的磁力矩
匀强磁场中: Fi 0
但合力矩: Mi 0 !
F1 F2 IBb
合力矩:M Mi
2F1
a 2
cos(2
)
BIaSbsisnin
B
b
B
F1
a
I
en
F2
I
en
M
Chapter 10. 稳恒电流与稳恒磁作场者:杨茂§田10. 5 安培定律 磁力矩
解 大线圈在其圆心处产生的磁场:
Bo
0I1
2R
安培力与磁力矩

•线圈所受有磁力矩
M=F1l1 cos
M=F1l1 cos
BIl2l1 si n
BIS sin
引入磁矩
M mB
•讨论:
=/2,线圈与磁场平行,磁通量F =0,力矩Mmax=ISB
=0,
垂直, F =BS,力矩M=0,平衡
=,
垂直, F =-BS,力矩M=0,平衡
例题2、证明转动带电园盘的磁矩 。
dF Idl B •对于有限长载流导线
F Idl B
例题1、有一段弯曲导线 ab 通有电流I ,求此导线在如图所示
均匀磁场中受的力?
b
F a Idl B
b
F
I ( a dl
)B
F Il B
dl
a
l
B
b
F IlB sin
l与磁感应强度B在同一平面内,所以,该
力方向垂直于纸面向外。
2020物理竞赛
安培力与磁力矩
11-6 载流导线在磁场中所受的力 11-7 磁场对载流线圈的作用
复习
•带电粒子在磁场中所受的力—— 洛伦兹力 Fm qv B
•带电粒子在磁场中的运动 速度方向与磁场方向平行——直线运动 垂直——圆周运动 有夹角——螺旋运动
•速度选择器
•霍耳效应——现象、规律、理论解释和应用
m 1 QR2
4
解: dq Q 2r dr R 2
dI
dq T
2
Q
R
2
2rdr
rdr
o r dr
dm dI r 2 r 3dr
m dm R r 3dr 1 QR2
0
4
二、磁电式电流计原理
•作用:测量电流
•原理:载流线圈在磁场中受
安培定律 洛仑兹力

推论
在均匀磁场中
任意形状闭合载流线圈受合力为零
练习
如图
求半圆导线所受安培力
f 2 BIR
方向竖直向上
I a
c B R b
平行电流的相互作用力
df1 B2 I1dl1
df 2 B1 I 2dl 2
0 I2 B2 2a
f洛
fe
Et
l
+ + + + + + + +
A
Bl
I qnld
U AA 1 IB nq d
I nqld
U AA
IB K d
总结
U AA
IB K d
1 K nq
(1) q>0时,K>0,
U AA 0 U AA 0
(1)会聚磁场中作螺旋运动的带正电的粒子掉向返转
带电粒子在磁场中的作用
(2)磁约束装置
带电粒子在磁场中的作用
(3)非均匀磁场的应用:范•艾仑(Van Allen)辐射带
11-8
一、霍耳效应概念
霍耳效应
厚度d,宽为 l 导电薄片,沿x轴通有电流强度I,当 在y轴方向加以匀强磁场B时,在导电薄片两侧 ( A, A ) 产生一电位差 U AA,这一现象称为 霍耳效应
q受力为:
f 洛 q B
f e q Et
大小:
大小:
f 洛 qB
f e qEt
方向:沿Z轴正向
方向:沿轴Z负向
当
即
f洛 fe
A A
时,
A
V
Et B 时,
磁感应强度和安培力课件
2.计算大小 (1)有效长度法: 公式 F=BIL 中的 L 是有效长度,弯曲导线的有效长度等于 连接两端点线段的长度.相应的电流沿 L 由始端流向末端,如图 所示.
(2)电流元法: 将导线分割成无限个小电流元,每一小段看成直导线,再按 直线电流的判断和计算.
(2016·海南)(多选)如图(a)所示,扬声器中有一线圈处 于磁场中,当音频电流信号通过线圈时,线圈带动纸盆振动,发 出声音.俯视图(b)表示处于辐射状磁场中的线圈(线圈平面即纸 面),磁场方向如图中箭头所示.在图(b)中( )
考点三 安培力的判断与计算
1.判断方向 (1)磁场和电流方向垂直的情况: 直接用左手定则判定. (2)磁场和电流方向不垂直的情况: 将磁感应强度沿电流和垂直电流方向分解,再用左手定则判 定垂直分量作用的安培力.
(3)通用结论: 不论磁场和电流方向是否垂直,安培力总是垂直于磁场和电 流方向所决定的平面. (4)常用推论: 两平行的直线电流作用时,同向电流吸引,异向电流排斥.
三、磁感线 意义:磁感线的疏密表示磁场的强弱,某点的切线方向
表示该点的磁场方向. 特点:磁感线是闭合曲线,在磁体外部从 N 极指向 S 极;
在磁体内部由 S 极指向 N 极.磁感线不相交.
安培定则:判定电流周围的磁场方向
磁场 项目
直线电流 的磁场
通电螺线管 的磁场
环形电流 的磁场
安培 定则
特点
无磁极、环 环形电流的两
绕 导线的同 与条形磁铁的磁场相似, 侧是 N 极和 S
心 圆,距导 管内为匀强磁场且最强, 极,离圆环中心
线 越远处磁 管外越远处磁场越弱. 越远磁场越弱.
场越弱
四、安培力 大小:F=BILsinθ(θ是 B 与 I 的夹角).
10.5 10.6 10.7 安培定律
F
.
B
10.5~10.7 安培定律
第十章 真空中的稳恒磁场
结论: 均匀磁场中,任意形状刚性闭合平面 通电线圈所受的力和力矩为
F 0, M m B 0 稳定平衡 m // B, M 0
m B , M M max mB , π / 2
Fm qvB sin
dF Fm qvd B dN
方向:右手螺旋
由于自由电子受到了磁场的作用力,使导线在宏 观上看起来受到了磁场的作用力 (安培定律的微观意 义)。
洛仑兹力的功: A Fm dl Fm vd dt 0
结论:洛仑兹力恒不作功。
dF2 B1I 2dl2 sin
90 ,sin 1
2π d 0 I 2 I1dl1 dF1 B2 I1dl1 2π d dF2 B1 I 2 dl2
d
dF2 dF1 0 I1I 2 dl2 dl1 2π d
0 I1 I 2 dl2
10.5~10.7 安培定律
2)方向相反 非稳定平衡
3)方向垂直
力矩最大
.
.
.
.
. .
.
. . I
F
. I . . + + + + + + F . . . I
+ F + + + + + + + + + +B+
.
0 ,M 0
π π , M 0 2 , M M max
.
.
.B .
§10.6安培定律 磁力矩 洛伦兹力
§10.6 安培定律 磁力矩 洛伦兹力1、如图,一个电荷为+q 、质量为m 的质点,以速度v v 沿x 轴射入磁感强度为B的均匀磁场中,磁场方向垂直纸面向里,其范围从x = 0延伸到无限远,如果质点在x = 0和y = 0处进入磁场,则它将以速度v v -从磁场中某一点出来,这点坐标是x = 0 和 [ ] (A) qB m y v +=. (B) qB m y v 2+=.(C)qB m y v 2−=.(D)qBm y v −=. 2、一运动电荷q ,质量为m ,进入均匀磁场中,[ ](A) 其动能改变,动量不变. (B) 其动能和动量都改变.(C) 其动能不变,动量改变. (D) 其动能、动量都不变. 3、如图,匀强磁场中有一矩形通电线圈,它的平面与磁场平行,在磁场作用下,线圈发生转动,其方向是[ ](A) ab 边转入纸内,cd 边转出纸外. (B) ab 边转出纸外,cd 边转入纸内. (C) ad 边转入纸内,bc 边转出纸外. (D) ad 边转出纸外,bc 边转入纸内.4、一运动电荷q ,质量为m ,垂直进入均匀磁场中,则[ ](A) 其速度大小和方向都改变.(B)其速度大小和方向都不变.(C) 其速度大小不变,速度方向改变.(D) 其速度大小改变,速度方向不变. 5、一质量为m ,电荷为+q 的粒子,以0v v 速度垂直进入均匀的稳恒磁场B v 中,电荷将作半径为______________的圆周运动6、如图所示,在真空中有一半径为a 的3/4圆弧形的导线,其中通以稳恒电流I ,导线置于均匀外磁场B v 中,且B v 与导线所在平面垂直.则该载流导线 bc所受的磁力大小为________________。
7、如图,无限长直载流导线与正三角形载流线圈在同一平面内,若长直导线固定不动,则载流三角形线圈将[ ](A) 向着长直导线平移.(B) 离开长直导线平移.(C) 转动.(D) 不动.I I(14)选择题8、有一根质量为m ,长为l 的直导线,放在磁感强度为 B v 的均匀磁场中,B v 的方向在水平面内,导线中电流方向如图所示,当导线所受磁力与重力平衡时,导线中电流I =__________.9、一带电粒子平行磁感线射入匀强磁场,则它作________________运动.若此带电粒子垂直磁感线射入匀强磁场,则它作________________运动.10、如图,一根载流导线被弯成半径为R 的1/4圆弧,放在磁感强度为B 的均匀磁场中,则载流导线ab 所受磁场的作用力的大小为____________,方向_________________.11、一电荷为q 的粒子在均匀磁场中运动,下列哪种说法是正确的?[ ](A) 只要速度大小相同,粒子所受的洛伦兹力就相同; (B) 在速度不变的前提下,若电荷q 变为-q ,则粒子受力反向,数值不变;(C) 粒子进入磁场后,其动能和动量都不变;(D) 洛伦兹力与速度方向垂直,所以带电粒子运动的轨迹必定是圆。
10-6 安培定律 磁力矩 洛伦兹力
y v
dF θ
v Idl
v B
v v v I dF = Idl × B o dFx = dF sinθ = BIdl sinθ dFy = dF cosθ = BIdl cosθ
Fx = ∫ d Fx = BI
Fy = ∫ dFy = BI ∫ dx = BIl
0 ∫0 d y l
P l
x
=0
v v v F = Fy = BIl j
线圈有N匝时 线圈有 匝时
v v v M = NIS en × B
磁力矩使磁矩方向有转向与磁场方向一致的趋势。 磁力矩使磁矩方向有转向与磁场方向一致的趋势。
第十章 运动电荷的磁场
10-6 安培定律 磁力矩 洛伦兹力
讨 论
v v 1)en方向与 B 相同 )
稳定平衡
+ + + + + +
2)方向相反 ) 不稳定平衡 . . . . . . . . .
v F3
M
P v
F3 = BIl2 sin( ̟ − θ ) v v F4 = − F3 v 4 v F = ∑ Fi = 0
i =1
v F1
I
ϕ
F2 v B
O
v N F4
v en
O,P
v F2
l2 M,N v F1
ϕ
θ
v en
v B
第十章 运动电荷的磁场
10-6 安培定律 磁力矩 洛伦兹力
v F3
z
v Fm
q+ θ v
v B
v v v Fm = qv × B
o x
y
Fm = qvB sin θ
v
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
y
I
Idl
B
B = Bcosθ B sinθ k i
z
o a
θ
b
x
dFx = I(Bzdy Bydz) = IBzdy
Fx = ∫ dFx = ∫ IBzdy = 0
0 0
( B在xoz平面内) xoz平面内)
6
Chapter 10. 稳恒电流与稳恒磁场
§10. 5 安培定律 磁力矩
dFy = I(Bxdz Bzdx) = IBcosθ dz + IB sinθ dx
F F
F = 2T
a
T
b
T
答案: T = IBR
× × × × × × ×
× ×I × × × × ×
× × × × × × ×
× × × × × × ×
× × × × ×B × × × × R × × × × × × × × × I × × ×
10
Chapter 10. 稳恒电流与稳恒磁场
§10. 5 安培定律 磁力矩
§10. 5 安培定律 磁力矩
如图,已知:I 例 如图,已知:I1,I2,R >> r,大线圈固定 .求当小 线圈从如图位置转到相互垂直时磁力矩作的功. 解 大线圈在其圆心处产生的磁场:
Bo =
0I1
2R
方向:
I1
pm = I2S2 = I2π r 2 小线圈:
当小线圈转到θ 位置时: 位置时:
I2
y ∞
o
I1 dF = I2dl ×B1= I2dl B1 sin90 j
I = I2dx 0 1 dF = dFy = I2dl B1 2π x
∴ F = Fy =
a+l
I2dl dF
a
o
l
∫
a
0I1I2 dx 2π x
I2
x x+ dx
x
0I1I2 a +l F= ln 竖直向上. 2π a (解毕 )
Chapter 10. 稳恒电流与稳恒磁场
§10. 5 安培定律 磁力矩
§10.5 安培定律 磁力矩
1
Chapter 10. 稳恒电流与稳恒磁场
§10. 5 安培定律 磁力矩
一,安培力 安培定律
电流元 Idl 受力:dF =
I b
B
dF = dN fm
dN = n S dl
fm = ev×B
}
dl θ
§10. 5 安培定律 磁力矩
定义
磁偶极矩 ( 磁矩 ):
pm = IS en
则磁力矩: :
( Am2 )
a
B
b
θ I
en
F2
M = pm ×B
上两式对 上两式对任意形状的载流线 的载流线
圈都成立.
B
I
θ
en
F 1
M
当θ = 0 时线圈处于最稳定状态.
12
Chapter 10. 稳恒电流与稳恒磁场
如图,匀强磁场B中,求该载流导线所受到的 B 课堂练习 如图, 磁力.已知:B 磁力.已知:B,R,I . 提示:用一导线将ab连接起来,则: 提示: 用一导线将ab连接起来,则:
Facba = 0
Facba = Facb + Fba
答案: Facb = 2IBR
× × × × I × × × × c × × × × × ×
二,载流线圈所受的磁力矩
匀强磁场中:∑Fi = 0 但合力矩: ∑Mi ≠ 0 !
B
a
b
θ I
en
F2
F = F2 = IBb 1
合力矩:M = ∑Mi
B
= 2F1 a cos(π θ ) 2 2 = BIab sinθ
I
θ
en
F 1
M
= BISsinθ
11
Chapter 10. 稳恒电流与稳恒磁场
a b
(安培定律) )
I a
dl θ
B
dF 大小: dF = Idl B sinθ
方向:右手定则.
I
S
B
电流元 Idl 沿电流方向,故上
亦为电流方向. 式的积分方向亦为电流方向. 式的
v
I
dl
fm
3
Chapter 10. 稳恒电流与稳恒磁场
§10. 5 安培定律 磁力矩
已知:I 例 已知:I1,I2,l,a,求两导线间的相互作用力. 解 建立坐标系如图所示
I a
B
I
S
dF = nSdl ev×B= neSvdl ×B
dq neSdl = neSv I= = dt dl / v
B
v
I
dl
fm
2
Chapter 10. 稳恒电流与稳恒磁场
§10. 5 安培定律 磁力矩
导线受到的磁力即为安培力: 导线受到的磁力即为 :
I b
B
dF = Idl ×B
F = ∫ Idl ×B
( The end15 )
�
a
∞
∞
5
Chapter 10. 稳恒电流与稳恒磁场
§10. 5 安培定律 磁力矩
试证: B 试证:在匀强磁场B中,任意形状的载流导线所受的磁 力为 F = I ab B sinθ .已知:I ,θ . .已知:I 建立坐标系如图所示 证明:
dF = Idl ×B
dl = dБайду номын сангаас + dy + dz k i j
r
R
M = pm ×B
M = pmB sinθ
= I2π r 2B sinθ
13
Chapter 10. 稳恒电流与稳恒磁场
§10. 5 安培定律 磁力矩
由于:R 由于:R >> r,则: B ≈ Bo =
0I1
2R
∴ M = I2π r
W=
π/2
2
0I1
2R
sinθ
∫ Mdθ
0
= I2π r
0I1 π / 2 2
7
Chapter 10. 稳恒电流与稳恒磁场
§10. 5 安培定律 磁力矩
推论1: B 推论 :在匀强磁场B中,载流直导线所受的磁力: 大小:F = I Bl 方向:l ×B 推论2: 推论 :在匀强磁场 B 中,任意 形状的闭合载流线圈所 形状的 载流线圈所 受到的磁力为零! 受到的磁力为 !
0I1 B1 = 2π x
∞
4
Chapter 10. 稳恒电流与稳恒磁场
§10. 5 安培定律 磁力矩
课堂练习 已知:I1,I2,a,求 已知:I ,求单位长度上两导线间的 两导线间的 相互作用力. 取元如图所示: 提示:取元如图所示: 2dl I
B1 =
∞
I1
∞
I2
0I1 2π a
dF2 = I2dl × B1
2R
2
0
∫ sinθ dθ
(解毕 )
I1
I2
r
R
=
π 0r
2R
I1I2
14
Chapter 10. 稳恒电流与稳恒磁场
§10. 5 安培定律 磁力矩
1. 安培定律:
dF = Idl ×B
F = ∫ Idl ×B
a
b
2. 磁力矩: M = pm ×B
其中磁偶极矩 ( 磁矩 ):pm = IS en 其中
相互吸引.
dF2 I2dl B1
答案:
dF2 0I1I2 F= = l dl 2π a
SI制中 制中安培定义 : 真空中两根 ∞ 载流直 定义 真空中两根∞
导线间距为1 导线间距为 1m , 通以相同大小的稳恒电流 , 通以相同大小的稳恒电流, 若导线上作用力为2×10-7 N/m,则每根导 若导线上作用力为 , 线中电流为1A. 线中电流为 .
× × × × × × ×
× × × × × R × ×
× × × × × × × × × R × × b × × × × × × × 2 × × ×R
× × × × B × × × F× ba × × × × a × ×
9
Chapter 10. 稳恒电流与稳恒磁场
§10. 5 安培定律 磁力矩
如图,在匀强磁场B中,垂直放置一个圆形载 B 课堂练习 如图,在 流线圈,求该线圈中的张力.已知:B 流线圈,求该线圈中的张力.已知:B,R,I . 提示: 提示: 以半个线圈作为研究对象,则:
× × × × a × ×
× × × × × ×
× × × F × ×I × × × × × × ×
× × × × × ×
× × B × × b × × × × × × × ×
B
I
8
Chapter 10. 稳恒电流与稳恒磁场
§10. 5 安培定律 磁力矩
Fy = ∫ dFy = ∫ IBcosθ dz + ∫ IB sinθ dx
0 0
xb
= IB ab sinθ
xa
y
I
Idl
dFz = I(Bydx Bxdy) = IBxdy
Fz = ∫ dFz = ∫ IBxdy = 0
0 0
B
z
o a
θ
b
x
∴
F = I B ab sinθ
( B在xoz平面内) xoz平面内)
