粒子群算法
基本粒子群算法

基本粒子群算法粒子群算法(Particle Swarm Optimization,PSO)是一种群体智能算法。
粒子群算法的灵感来源于模拟一群鸟的行为,这些鸟往往会通过互相沟通,得到更好的食物来源。
类比到优化问题中,粒子群算法的每个个体被称为粒子,它们互相传递信息,从而实现全局最优解的搜索。
在粒子群算法中,每个粒子代表了一个解空间内的可行解。
每个粒子的位置被编码成一组向量,这个向量就是这个粒子的位置,每个粒子还有一个速度向量,决定了它在解空间内的运动方向和速度大小。
在每一次迭代中,每个粒子会对自己的位置和速度进行更新,这依赖于当前的个体最优解,和全局最优解。
个体最优解是这个粒子对解空间的局部搜索结果,全局最优解是所有粒子对解空间的全局搜索结果。
粒子群算法通过不断迭代,更新每个粒子的位置和速度,直到达到收敛条件。
收敛条件可以通过迭代次数,目标函数的阈值等来定义。
在应用上,粒子群算法已被广泛应用于优化问题中,包括函数优化,组合优化,路径规划等等。
它的应用在电力系统,通信网络,机器人,图像处理和数据挖掘等领域也被证明是有效的。
在实际应用中,粒子群算法需要注意一些问题。
一是在选择惯性权重时需要遵守准则,即越接近最优解惯性权重应该越小,越远离最优解惯性权重应该越大。
二是需要确定好种群大小,如果种群太小,可能会导致粒子局限于局部最优解,而丢失全局优解的机会。
三是需要合适的约束条件,保证解空间的可行性,尤其是在优化问题中。
综上所述,粒子群算法是一种十分有用的优化算法,它通过模拟鸟群的行为,实现有效的搜索全局最优解。
但是在实际应用中需要注意一些问题,特别是在惯性权重,种群大小和约束条件的确定上,这样才能达到最好的优化效果。
粒子群算法及应用

粒子群算法及应用粒子群算法(Particle Swarm Optimization,PSO)是一种基于群体智能的优化算法,源于对鸟群集群行为的观察和模拟。
粒子群算法通过模拟鸟群中个体间的协作与信息传递,以寻找最优解。
在实际应用中,粒子群算法已被广泛应用于函数优化、组合优化、图像处理、各类工程设计等领域。
粒子群算法的基本原理是模拟鸟群中每只鸟(粒子)的行为。
每个粒子表示问题的一个候选解,在解空间中最优解。
算法从一个随机初始解的种子集合出发,通过迭代更新粒子位置和速度,直到满足终止条件。
每个粒子维护自身的历史最优解和全局最优解,通过个体经验和邻域协作来引导过程。
粒子在解空间中自由移动,并通过其中一种适应度函数评价解的质量,并更新自身位置和速度。
整个过程中,粒子会不断地向全局最优解靠拢,从而找出最优解。
粒子群算法广泛应用于函数优化问题。
对于复杂的多峰函数,粒子群算法能够通过群体间的信息共享来克服局部最优解,找到全局最优解。
此外,粒子群算法还可以解决许多实际问题,如资源调度、网络路由、机器学习等。
例如,在图像处理中,可以使用粒子群算法进行图像分割、图像识别和图像增强等任务,通过优化算法自动化地寻找最优解。
除了以上应用,粒子群算法还可以用于各种优化问题的求解。
例如,粒子群算法在组合优化问题中的应用表现得较为出色。
在组合优化问题中,需要从大量的解空间中找到最佳的组合方案。
通过粒子群算法的迭代和全局协作,可以有效地找到最优解。
另外,粒子群算法还可以用于工程设计中的自动优化。
在工程设计过程中,需要考虑多个目标和多个约束条件,粒子群算法可以通过多目标优化或多约束优化来处理复杂的工程设计问题。
总之,粒子群算法作为一种群体智能算法,在函数优化、组合优化、图像处理和工程设计等领域都得到了广泛的应用。
其优势在于全局寻优能力和自适应性,能够找到复杂问题的最优解。
随着对算法的研究和改进,粒子群算法有望在更多领域得到应用和推广。
粒子群算法粒子维度

粒子群算法粒子维度粒子群优化算法(Particle Swarm Optimization,PSO)是一种基于群体智能的优化算法,源自对鸟群行为的模拟。
它通过模拟鸟群在食物等目标时的行为,利用群体协作和信息交流来优化问题的解。
在粒子群算法中,解空间被表示为多维空间,每个解被称为一个粒子,粒子的位置表示解在各个维度上的取值。
每个粒子都有自己的位置和速度,通过更新速度和位置来更优的解。
粒子的移动策略是受到个体历史最优位置和全局最优位置的影响,个体历史最优位置是粒子自身的最优解,全局最优位置是整个群体中历史最优解。
粒子群算法的基本过程如下:(1)初始化群体的位置和速度;(2)根据适应度函数评估每个粒子的适应度;(3)更新每个粒子的速度和位置;(4)更新个体历史最优位置和全局最优位置;(5)重复步骤(2)到(4),直到达到指定的迭代次数或满足停止条件。
更新速度和位置的过程可以通过以下公式实现:速度更新公式:V[i] = w * V[i] + c1 * rand( * (P_best[i] -X[i]) + c2 * rand( * (G_best[i] - X[i])位置更新公式:X[i]=X[i]+V[i]其中,V[i]表示粒子i的速度,X[i]表示粒子i的位置,w是惯性权重,P_best[i]是粒子i的个体历史最优位置,G_best[i]是粒子i周围邻域中最优的全局最优位置,c1和c2是学习因子,rand(是一个随机数。
(1)全局能力强:通过群体的协作和信息交流,可以在解空间中进行全局,避免陷入局部最优解;(2)收敛速度快:通过粒子的速度更新,可以有效地引导过程,加快算法的收敛速度;(3)不依赖问题的具体形式:粒子群算法不需要对问题进行求导或者建立模型,适用于不同类型的问题。
然而,粒子群算法也存在一些不足之处:(1)对参数设置敏感:学习因子和惯性权重的选择对算法的性能有重要影响,需要进行合理的参数设置;(2)易陷入局部最优解:粒子群算法在过程中容易陷入局部最优解,特别是在解空间比较复杂的问题中,需要采取一些措施来增强其全局能力。
粒子群算法

粒子群算法原理及简单案例[ python ]介绍粒子群算法(Particle swarm optimization,PSO)是模拟群体智能所建立起来的一种优化算法,主要用于解决最优化问题(optimization problems)。
1995年由 Eberhart和Kennedy 提出,是基于对鸟群觅食行为的研究和模拟而来的。
假设一群鸟在觅食,在觅食范围内,只在一个地方有食物,所有鸟儿都看不到食物(即不知道食物的具体位置。
当然不知道了,知道了就不用觅食了),但是能闻到食物的味道(即能知道食物距离自己是远是近。
鸟的嗅觉是很灵敏的)。
假设鸟与鸟之间能共享信息(即互相知道每个鸟离食物多远。
这个是人工假定,实际上鸟们肯定不会也不愿意),那么最好的策略就是结合自己离食物最近的位置和鸟群中其他鸟距离食物最近的位置这2个因素综合考虑找到最好的搜索位置。
粒子群算法与《遗传算法》等进化算法有很多相似之处。
也需要初始化种群,计算适应度值,通过进化进行迭代等。
但是与遗传算法不同,它没有交叉,变异等进化操作。
与遗传算法比较,PSO的优势在于很容易编码,需要调整的参数也很少。
一、基本概念与遗传算法类似,PSO也有几个核心概念。
粒子(particle):一只鸟。
类似于遗传算法中的个体。
1.种群(population):一群鸟。
类似于遗传算法中的种群。
2.位置(position):一个粒子(鸟)当前所在的位置。
3.经验(best):一个粒子(鸟)自身曾经离食物最近的位置。
4.速度(velocity ):一个粒子(鸟)飞行的速度。
5.适应度(fitness):一个粒子(鸟)距离食物的远近。
与遗传算法中的适应度类似。
二、粒子群算法的过程可以看出,粒子群算法的过程比遗传算法还要简单。
1)根据问题需要,随机生成粒子,粒子的数量可自行控制。
2)将粒子组成一个种群。
这前2个过程一般合并在一起。
3)计算粒子适应度值。
4)更新种群中每个粒子的位置和速度。
粒子群算法详解

粒子群算法详解粒子群算法(Particle Swarm Optimization,PSO)是一种模拟鸟群觅食行为的优化算法,通过模拟个体之间的协作和信息共享来寻找最优解。
它是一种全局优化算法,可以应用于各种问题的求解。
粒子群算法的基本思想是通过模拟鸟群的行为来寻找最优解。
在算法中,将待优化问题看作一个多维空间中的搜索问题,将问题的解看作空间中的一个点。
每个解被称为一个粒子,粒子的位置代表当前解的状态,速度代表解的更新方向和速度。
粒子之间通过互相交流信息,以共同寻找最优解。
在粒子群算法中,每个粒子都有自己的位置和速度。
每个粒子根据自身的经验和邻域中最优解的经验来更新自己的速度和位置。
速度的更新由三个因素决定:当前速度、个体最优解和全局最优解。
粒子根据这些因素调整速度和位置,以期望找到更优的解。
通过不断迭代更新,粒子群逐渐收敛于最优解。
粒子群算法的核心是更新速度和位置。
速度的更新公式如下:v(t+1) = w * v(t) + c1 * rand() * (pbest - x(t)) + c2 * rand() * (gbest - x(t))其中,v(t+1)为下一时刻的速度,v(t)为当前速度,w为惯性权重,c1和c2为学习因子,rand()为[0,1]之间的随机数,pbest为个体最优解,gbest为全局最优解,x(t)为当前位置。
位置的更新公式如下:x(t+1) = x(t) + v(t+1)通过调整学习因子和惯性权重,可以影响粒子的搜索能力和收敛速度。
较大的学习因子和较小的惯性权重可以增强粒子的探索能力,但可能导致算法陷入局部最优解;较小的学习因子和较大的惯性权重可以加快算法的收敛速度,但可能导致算法过早收敛。
粒子群算法的优点是简单易实现,收敛速度较快,对于大多数问题都能得到较好的结果。
然而,粒子群算法也存在一些缺点。
首先,算法对于问题的初始解和参数设置较为敏感,不同的初始解和参数可能导致不同的结果。
粒子群优化算法-参数寻优
粒⼦群优化算法-参数寻优⼀、粒⼦群算法的概念 粒⼦群优化算法的基本思想:是通过群体中个体之间的协作和信息共享来寻找最优解. PSO的优势:在于简单容易实现并且没有许多参数的调节。
⽬前已被⼴泛应⽤于函数优化、神经⽹络训练、模糊系统控制以及其他遗传算法的应⽤领域。
⼆、粒⼦群算法分析1、基本思想 粒⼦群算法通过设计⼀种⽆质量的粒⼦来模拟鸟群中的鸟,粒⼦仅具有两个属性:速度和位置,速度代表移动的快慢,位置代表移动的⽅向。
每个粒⼦在搜索空间中单独的搜寻最优解,并将其记为当前个体极值,并将个体极值与整个粒⼦群⾥的其他粒⼦共享,找到最优的那个个体极值作为整个粒⼦群的当前全局最优解,粒⼦群中的所有粒⼦根据⾃⼰找到的当前个体极值和整个粒⼦群共享的当前全局最优解来调整⾃⼰的速度和位置。
2、粒⼦群算法的主要步骤如下:(1)对粒⼦群的随机位置和速度进⾏初始设定,同时设定迭代次数。
第⼆步:计算每个粒⼦的适应度值。
(2)对每个粒⼦,将其适应度值与所经历的最好位置Pbest;的适应度值进⾏⽐较,若较好,则将其作为当前的个体最优位置。
(3)对每个粒⼦,将其适应度值与全局所经历的最好位置Gbestg的适应度值进⾏⽐较,若较好,则将其作为当前的全局最优位置。
(4)根据公式(1), (2)对粒⼦的速度和位置进⾏优化,从⽽产⽣新的粒⼦。
(5)如未达到结束条件(通常为最⼤循环数或最⼩误差要求),则返回第⼆步。
3、本案例群体的初始参数列表:maxgen:⼀般为最⼤迭代次数以最⼩误差的要求满⾜的。
粒⼦群算法的最⼤迭代次数,也是终⽌条件数。
c1,c2:加速常数,取随机2左右的值。
w:惯性权重产⽣的。
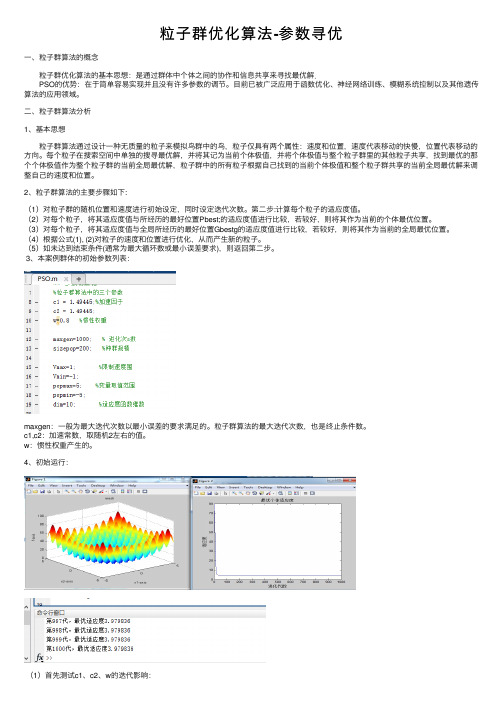
4、初始运⾏:(1)⾸先测试c1、c2、w的迭代影响:利⽤函数来表⽰各变量:运⾏得:逐渐迭代得:可以看出迭代收敛最早。
随着不断的迭代,最优适应度承不稳定状态。
(2)dim与sizepop的影响:适应度函数维数dim=12:适应度函数维数dim=8:适应度函数维数dim=5:适应度函数维数dim=3:种群规模sizepop=220:种群规模sizepop=200:种群规模sizepop=150:种群规模sizepop=130:将种群规模sizepop调制到<130时,迭代次数⽆法收敛到接近于0,所以判别种群规模sizepop在200最佳。
粒子群算法(基础精讲)课件
神经网络训练
神经网络训练是指通过训练神经网络来使其能够学习和模拟特定的输入输出关系 。粒子群算法可以应用于神经网络的训练过程中,通过优化神经网络的参数来提 高其性能。
例如,在机器视觉、语音识别、自然语言处理等领域中,神经网络被广泛应用于 各种任务。粒子群算法可以用于优化神经网络的结构和参数,从而提高其分类、 预测等任务的准确性。
优势
在许多优化问题中,粒子群算法表现出了良好的全局搜索能 力和鲁棒性,尤其在处理非线性、多峰值等复杂问题时具有 显著优势。
粒子群算法的核心要素
02
粒子个体
01
粒子
在粒子群算法中,每个解被称为一个粒子,代表问题的 一个潜在解。
02
粒子状态
每个粒子的位置和速度决定了其状态,其中位置表示解 的优劣,速度表示粒子改变方向的快慢。
社会认知策略的引入
总结词
引入社会认知策略可以增强粒子的社会性,提高算法的群体协作能力。
详细描述
社会认知策略是一种模拟群体行为的方法,通过引入社会认知策略,可以增强粒子的社会性,提高算 法的群体协作能力。在粒子群算法中引入社会认知策略,可以使粒子更加关注群体最优解,促进粒子 之间的信息交流和协作,从而提高算法的全局搜索能力和鲁棒性。
03 粒子群算法的实现步骤
初始化粒子群
随机初始化粒子群的 位置和速度。
初始化粒子的个体最 佳位置为随机位置, 全局最佳位置为随机 位置。
设置粒子的个体最佳 位置和全局最佳位置 。
更新粒子速度和位置
根据粒子个体和全局最佳位置计 算粒子的速度和位置更新公式。
更新粒子的速度和位置,使其向 全局最佳位置靠近。
每个粒子都有一个记录其历史最 佳位置的变量,用于指导粒子向
粒子群算法基本原理
粒子群算法基本原理粒子群算法(Particle Swarm Optimization, PSO)是一种基于群体智能的优化算法,模拟了鸟群或鱼群等生物群体在自然界中求解问题的行为。
粒子群算法是一种无约束优化算法,可以用于求解各种优化问题。
粒子群算法的基本原理是通过模拟粒子在解空间中的过程来寻找最优解。
每个粒子表示了一个潜在的解,其位置和速度表示了解的状态和速度。
整个粒子群可以看作是一个多维解空间中的群体,每个粒子都具有一个解向量和速度向量,通过不断调整速度和位置来寻找最优解。
1.初始化粒子群:根据问题的维度和约束条件,随机初始化粒子的位置和速度。
其中位置表示解向量,速度表示方向和速度。
2.计算粒子适应度:根据问题的定义,计算每个粒子的适应度。
适应度函数根据问题的不同而变化,可以是目标函数的取值或其他综合评价指标。
3.更新粒子速度和位置:通过利用粒子当前的位置、速度和历史最优解来更新粒子的速度和位置。
速度的更新过程包括两部分,第一部分是加速度项,其大小与粒子所处位置与个体最优解、群体最优解的距离有关;第二部分是惯性项,保持原有的速度方向并控制的范围。
位置的更新通过当前位置和速度得到新的位置。
4.更新个体最优解和群体最优解:将每个粒子的适应度与其历史最优解进行比较并更新。
个体最优解是粒子自身到的最优解,群体最优解是所有粒子中的最优解。
5.判断停止条件:根据预定的停止条件判断是否终止算法。
停止条件可以是达到最大迭代次数、适应度值达到一定阈值或范围满足一定条件等。
6.返回最优解:将群体最优解或个体最优解作为最终结果返回。
粒子群算法通过不断地更新粒子的速度和位置,通过粒子之间的信息交流和协作来找到最优解。
在算法的早期阶段,粒子的范围较大,有较高的探索性;随着的进行,粒子逐渐聚集在最优解周围,并逐渐减小范围,增强了局部的能力。
这种全局和局部的结合使得粒子群算法能够更好地求解多峰优化问题。
粒子群算法的优点是简单易实现、全局能力强,对于非线性、非凸性、多峰性问题有很好的适应性。
粒子群算法介绍
1.介绍:粒子群算法(Particle Swarm Optimization, PSO)最早是由Eberhart 和Kennedy于1995年提出,它的基本概念源于对鸟群觅食行为的研究。
设想这样一个场景:一群鸟在随机搜寻食物,在这个区域里只有一块食物,所有的鸟都不知道食物在哪里,但是它们知道当前的位置离食物还有多远。
那么找到食物的最优策略是什么呢?最简单有效的就是搜寻目前离食物最近的鸟的周围区域。
经过实践证明:全局版本的粒子群算法收敛速度快,但是容易陷入局部最优。
局部版本的粒子群算法收敛速度慢,但是很难陷入局部最优。
现在的粒子群算法大都在收敛速度与摆脱局部最优这两个方面下功夫。
其实这两个方面是矛盾的。
看如何更好的折中了。
粒子群算法主要分为4个大的分支:(1)标准粒子群算法的变形在这个分支中,主要是对标准粒子群算法的惯性因子、收敛因子(约束因子)、“认知”部分的c1,“社会”部分的c2进行变化与调节,希望获得好的效果。
惯性因子的原始版本是保持不变的,后来有人提出随着算法迭代的进行,惯性因子需要逐渐减小的思想。
算法开始阶段,大的惯性因子可以是算法不容易陷入局部最优,到算法的后期,小的惯性因子可以使收敛速度加快,使收敛更加平稳,不至于出现振荡现象。
经过本人测试,动态的减小惯性因子w,的确可以使算法更加稳定,效果比较好。
但是递减惯性因子采用什么样的方法呢?人们首先想到的是线型递减,这种策略的确很好,但是是不是最优的呢?于是有人对递减的策略作了研究,研究结果指出:线型函数的递减优于凸函数的递减策略,但是凹函数的递减策略又优于线型的递减,经过本人测试,实验结果基本符合这个结论,但是效果不是很明显。
对于收敛因子,经过证明如果收敛因子取0.729,可以确保算法的收敛,但是不能保证算法收敛到全局最优,经过本人测试,取收敛因子为0.729效果较好。
对于社会与认知的系数c2,c1也有人提出:c1先大后小,而c2先小后大的思想,因为在算法运行初期,每个鸟要有大的自己的认知部分而又比较小的社会部分,这个与我们自己一群人找东西的情形比较接近,因为在我们找东西的初期,我们基本依靠自己的知识取寻找,而后来,我们积累的经验越来越丰富,于是大家开始逐渐达成共识(社会知识),这样我们就开始依靠社会知识来寻找东西了。
粒子群算法粒子群算法简介
粒子群算法(1)----粒子群算法简介二、粒子群算法的具体表述上面罗嗦了半天,那些都是科研工作者写论文的语气,不过,PSO的历史就像上面说的那样。
下面通俗的解释PSO算法。
PSO算法就是模拟一群鸟寻找食物的过程,每个鸟就是PSO中的粒子,也就是我们需要求解问题的可能解,这些鸟在寻找食物的过程中,不停改变自己在空中飞行的位置与速度。
大家也可以观察一下,鸟群在寻找食物的过程中,开始鸟群比较分散,逐渐这些鸟就会聚成一群,这个群忽高忽低、忽左忽右,直到最后找到食物。
这个过程我们转化为一个数学问题。
寻找函数y=1-cos(3*x)*exp(-x)的在[0,4]最大值。
该函数的图形如下:当x=0.9350-0.9450,达到最大值y=1.3706。
为了得到该函数的最大值,我们在[0,4]之间随机的洒一些点,为了演示,我们放置两个点,并且计算这两个点的函数值,同时给这两个点设置在[0,4]之间的一个速度。
下面这些点就会按照一定的公式更改自己的位置,到达新位置后,再计算这两个点的值,然后再按照一定的公式更新自己的位置。
直到最后在y=1.3706这个点停止自己的更新。
这个过程与粒子群算法作为对照如下:这两个点就是粒子群算法中的粒子。
该函数的最大值就是鸟群中的食物计算两个点函数值就是粒子群算法中的适应值,计算用的函数就是粒子群算法中的适应度函数。
更新自己位置的一定公式就是粒子群算法中的位置速度更新公式。
下面演示一下这个算法运行一次的大概过程:第一次初始化第一次更新位置第二次更新位置第21次更新最后的结果(30次迭代)最后所有的点都集中在最大值的地方。
粒子群算法(2)----标准的粒子群算法在上一节的叙述中,唯一没有给大家介绍的就是函数的这些随机的点(粒子)是如何运动的,只是说按照一定的公式更新。
这个公式就是粒子群算法中的位置速度更新公式。
下面就介绍这个公式是什么。
在上一节中我们求取函数y=1-cos(3*x)*exp(-x)的在[0,4]最大值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Xi =Xi1,Xi 2 ,...,Xid
Study Factor
Here I am! x
pi
My best 最佳解 positio 運動向量 n
區域
全域 最佳解
慣性向量
pg The best position of team
v
03/08
AI course
03/08
AI course 鸟群(鱼群)行为
Particle Swarm Optimization 粒子群特性
03/08
AI course PSO概述
Particle Swarm Optimization
每个寻优的问题解都被想象成一只 鸟(鱼),称为 Particle
每个Particle都有记忆能力 所有的Particle都通过Fitness Function 来判断目前的位置之好坏 每个Particle通过Velocity Function来 决定移动的距离与方向
Vid:第 i 个 particle (有d个维度) 的速度 Pgd:所有 particle 到目前为止所出现的最佳位置
Xid:每个 particle 目前的所在位置
C2:学习常数
rand():0~1之间的随机数
03/08
AI course
Particle Swarm Optimization
根据 Fitness Function计算出其 Fitness Value 以作为判断每一Particle 之好坏
Minimize fi t
Maximize fi t
x t 100
i
i
2
y t 100
i
i
2
x t 100
2
y t 100
03/08
AI course PSO概述
Particle Swarm Optimization
起源
生物学家对鸟(鱼)群捕食的行为 研究 社会行为 (Social-Only Model)
个体认知 (Cognition-Only Model)
03/08
AI course 鸟群(鱼群)行为
Particle Swarm Optimization
03/08
AI course
Particle Swarm Optimization
Cooperation example
Discovery of
Particle Swarm Optimization
探索 粒子群优化算法
03//08
AI course Inventor (1)
Particle Swarm Optimization
Particle Swarm Optimization
1975 1953 1969
1989
1991
1995
03//08
AI course 最优化算法
Particle Swarm Optimization
解决最优化问题的方法
传统搜索方法 保证能找到最优解 Heuristic Search
不能保证找到最优解
PSO Velocity Function
PSO Velocity Function
Vid w Vid C1 rand () Pid X id t C2 rand () Pgd X id t
Vid:第 i 个 particle (有d个维度) 的速度
Particle Swarm Optimization
PSO Pseudo Code I) For each particle: Initialize particle II) Do: a) For each particle: 1) Calculate fitness value 2) If the fitness value is better than the best fitness value (Pbest) in history 3) Set current value as the new Pbest End b) For each particle: 1) Find in the particle neighborhood, the particle with the best fitness 2) Calculate particle velocity according to the velocity function 3) Update particle position according to the position function End While maximum iterations or minimum error criteria is not attained
产生初始族群 满足停止条件 No 计算适应度
更新速度和位置
产生新族群
03/08
AI course
Particle Swarm Optimization
PSO Velocity Function
PSO Velocity Function
| |
Cognition-Only Model + Social-Only Model
PSO Velocity Function
动能向量理论
vid (t 1) w vid (t ) c1 rand () ( pid xid (t )) c2 rand () ( pgd xid (t ))
xi (t 1) xi (t ) vi (t )
Pid:每个particle 到目前为止所出现的最佳位置
Pgd:所有 particle 到目前为止所出现的最佳位置 Xid:每个 particle 目前的所在位置 C1,C2:学习常数 w:惯性权重 rand():0~1之间的随机数
03/08
AI course
Particle Swarm Optimization
AI course PSO举例
Particle Swarm Optimization
Griewank
Rastrigin
Rosenbrock
03/08
AI course PSO举例
Particle Swarm Optimization
(见程序演示)
Optimum=0, Dimension=30 Best result after 40 000 evaluation
03/08
AI course
Particle Swarm Optimization
PSO Velocity Function
Cognition-Only Model
Vid Vid C1 rand () P X id t id
Vid:第 i 个 particle (有d个维度) 的速度 Pid:每个 particle 到目前为止所出现的最佳位置
03/08
AI course
Particle Swarm Optimization
PSO算法流程
Initial
将群族初始化,以随机的方式求出每一Particle 之初始位置与速度
03/08
AI course
Particle Swarm Optimization
PSO算法流程
Evaluation
Update the Position 根据 Velocity Function 更新每个Particle的移动方向与速度
回到 Evaluation 继续执行,直到符合终止条件为止
03/08
AI course
Particle Swarm Optimization
PSO 流程图
开始
设定参数
结束 Yes
PSO算法流程
Find the Gbest
找出所有Particle 到目前为止所搜寻到的全体最优解,此最优解我 们称之为Gbest
Global Best Solution
Past Best Solution
03/08
AI course
Particle Swarm Optimization
PSO算法流程
30D function Griewank Rastrigin Rosenbrock PSO 0.003944 82.95618 50.193877 Evolutionary algo. 0.4033 46.4689 1610.359
03/08
AI course
Particle Swarm Optimization
Russell Eberhart eberhart@
Russ Eberhart
03/08
AI course Inventor (2)
Particle Swarm Optimization
James Kennedy Kennedy_Jim@
James Kennedy
Xid:每个 particle 目前的所在位置
C1:学习常数
rand():0~1之間的随机数
03/08
AI course
Particle Swarm Optimization
PSO Velocity Function
Social-Only Model
Vid Vid C2 rand () Pgd X id t
Particle Swarm Optimization 粒子群算法
2011/03
03//08
AI course Outline
Particle Swarm Optimization
Introduction Discovery of Particle Swarm Optimization (PSO)
