六年级上册数学讲义-分数百分数比综合应用(二)-人教版(含答案)
第八讲 总复习分数百分数(讲义)人教版六年级上册数学
第8讲 小学数学总复习（五）——分数百分数思维启航一、训练目标知识传递：熟练应用解决分数应用题的几种方法。
能力强化：理解能力、分析能力、推算能力、综合能力。
思想方法：抓不变量法,倒推法,单位1转换法,方程思想，假设法，重组法，比例法。
二、知识与方法归纳1.简单分数应用题，必须先找出单位“1”，并且分析这个单位“1”是已知还是未知，初步确定方法.2.较复杂的分数应用题，如有多个“单位”1，第一可以考虑转化成同一个单位“1”，如果不好转化，可以一层一层的倒推。
对于需要某个条件而题目没告诉，且不具体时，还需要假设出某个数量，还可以结合方程，比例等综合使用方法使解题更加简化。
3.经济价格问题：从厂家购进的商品价格称为成本（也叫进价），商家在进价的基础上提高价格出售，称为售价，利润=售价－成本， 售价=成本×（1+利润率）， 利润率=成本利润×100% ，售价=原价×折扣4.浓度问题。
我们知道，将糖溶于水就得到了糖水，其中糖叫溶质，水叫溶剂，糖水叫溶液。
如果水的量不变，那么糖加得越多，糖水就越甜，也就是说糖水甜的程度是由糖（溶质）与糖水（溶液＝糖+水）二者质量的比值决定的。
这个比值就叫糖水的含糖量或糖含量。
类似地，酒精溶于水中，纯酒精与酒精溶液二者质量的比值叫酒精含量。
因而浓度就是溶质质量与溶液质量的比值，通常用百分数表示，即：浓度＝溶质质量溶液质量 ×100％＝溶质质量溶质质量+溶剂质量×100％ 5.工程问题：工作总量、工作时间（完成工作总量所需的时间）和工作效率（单位时间内完成的工作量）．工作效率×工作时间＝工作总量，工作总量÷工作时间＝工作效率，工作总量÷工作效率＝工作时间．思维进阶例1.甲、乙、丙、丁四人共同购买一个价值4200元的商品。
甲支付的现金是其他三人所支付现金总数的41，乙支付的现金比其他三人所支付的现金少50%，丙支付的现金占总支付的现金总数的41，那么丁支付现金多少元？例2.甲、乙两个书架共有1100本书，从甲书架借出13，从乙书架借出75%以后，甲书架是乙书架的2倍还多150本，乙书架原有多少本书？思维训练 1.六年级上学期男、女生共有300人，这一学期男生增加125，女生增加120，共增加了13人．这一学年六年级男、女生各有多少人?例3.某店原来将一批苹果按100%的利润(即利润是成本的100%)定价出售。
第7讲 百分数的应用-六年级上册数学讲义(含答案)
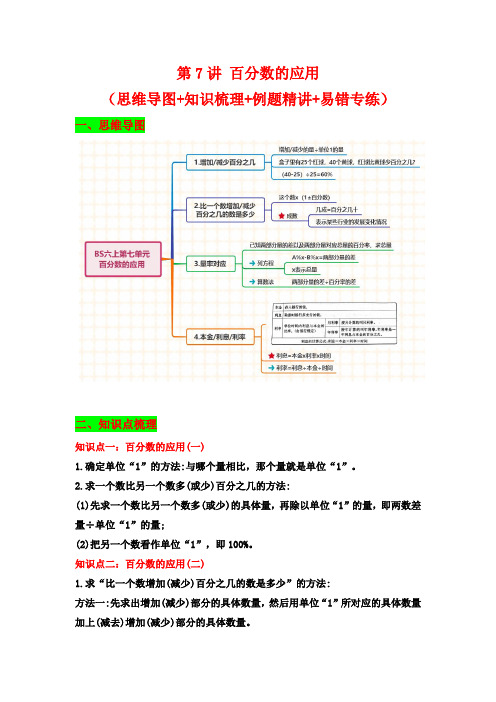
第7讲百分数的应用（思维导图+知识梳理+例题精讲+易错专练）一、思维导图二、知识点梳理知识点一：百分数的应用(一)1.确定单位“1”的方法:与哪个量相比，那个量就是单位“1”。
2.求一个数比另一个数多(或少)百分之几的方法:(1)先求一个数比另一个数多(或少)的具体量，再除以单位“1”的量，即两数差量÷单位“1”的量;(2)把另一个数看作单位“1”，即100%。
知识点二：百分数的应用(二)1.求“比一个数增加(减少)百分之几的数是多少”的方法:方法一:先求出增加(减少)部分的具体数量，然后用单位“1”所对应的具体数量加上(减去)增加(减少)部分的具体数量。
方法二:先求出增加(减少)后的数量是单位“1”的百分之几，然后用单位“1”所对应的具体数量乘这个百分数。
2.成数的意义。
在工农业生产和日常生活中经常用到成数，成数可以表示各行各业的发展变化情况。
“几成”就是十分之几，也就是百分之几十。
3.解决成数问题的方法。
解决成数的问题，关键是先将成数转化为百分数，然后按照百分数问题的解法进行解答。
知识点三：百分数的应用(三)1.已知两个部分量的差(和)及两个部分量对应的百分数，求总量，这类问题用方程解有两种方法:(1)A%x±B%x=两个部分量的差(和);(2)(A%±B%)x=两个部分量的差(和)。
(x代表总量;A%代表较大的部分量所占的百分数;B%代表较小的部分量所占的百分数)2.用方程解“已知比一个数增加百分之几的数是多少，求这个数”的问题有两种解答方法:(1)单位“1”的量×(1+比单位“1”多的百分率)=已知量;(2)单位“1”的量+单位“1”的量×比单位“1”多的百分率=已知量。
3.用方程解“已知一个部分量占总量的百分之几及另一个部分量，求总量”的问题有两种解答方法:(1)总量×(1-已知部分量占总量的百分率)=另一部分量;(2)总量-总量×已知部分量占总量的百分率=另一部分量。
新版六年级上册数学讲义-《分数(百分数)应用题》 北师大版
成都市六年级上期《分数（百分数）应用题》-复习课一、分数应用题主要讨论的是以下三者之间的关系。
1、分率：表示一个数是另一个数的几分之几，这几分之几通常称为分率。
2、标准量：解答分数应用题时，通常把题目中作为单位“1”的那个数，称为标准量。
（也叫单位“1”的数量）3、比较量：解答分数应用题时，通常把题目中同标准量比较的那个数，称为比较量。
（也叫分率对应的数量）三种数量有如下关系：标准量×分率=比较量，比较量÷标准量=分率，比较量÷分率=标准量。
二、找单位1：（1）当两种数量比较时，抓关键词找准单位“1”分数应用题，题目中经常出现“是”、“占”、“比”、“等于”、“相当于”这些词，一般来说，单位“1”的量就隐藏在这些关键字的后面的量就是单位“1”。
一般“的”前面是单位“1”（2）部分数和总数有些分数应用题，存在着整体和部分两个数量，部分数和总数作比较关系时，部分数通常作为比较量，而总数则作为标准量，那么总数就是单位“1”。
例如：食堂买来100千克白菜，吃了2/5，吃了多少千克？在这里，食堂一共买来的白菜是总数，吃掉的是部分数，所以100千克白菜就是单位“1”。
（3）、原数量与现数量有的关键句中不是很明显地带有一些指向性特征的词语，也不是部分数和总数的关系。
这类分数应用题的单位“1”比较难找。
例如：水结成冰后体积增加了1/10，冰融化成水后，体积减少了1/12。
象这样的水和冰两种数量到底谁作为单位“1”？两句关键句的单位“1”是不是相同？用上面讲过的两种方法不容易找出单位“1”。
其实我们只要看，原来的数量是谁？这个原来的数量就是单位“1”！三、分数应用题的分类。
（三类）1.1 直接求一个数是另一个数的百分之几一个数÷另一个数1.2 求一个数比另一个数多百分之几差量（多的部分）÷单位11.3 求一个数比另一个数少百分之几差量（少的部分）÷单位12.1直接求一个数的百分之几是多少单位1×分率2.2求比一个数多百分之几的数是多少单位1×（1＋分率）2.3 求比一个数少百分之几的数是多少单位1×（1－分率）3.1已知一个数的百分之几是多少，求这个数。
学大精品讲义六上数学(含答案)第十二讲分数百分数比综合应用(二)
一、知识梳理分数乘除法和百分数的综合应用题：（1）单位“ 1”的量和数量关系：（2）解答“求一个数的几分之几（或百分之几）是多少”的应用题；（3）解答一个数比另一个数多（或少）几分之几（或百分之几）的应用题;百分数应用题：（1）纳税和利率；（2）折扣和利润；比的应用：按比例分配二、方法归纳分数和百分数的应用题（1）求一个数是另一个数的几分之几（或百分之几）的应用题一个数十另一个数=分率一个数十另一个数X100%=百分之几5（2）求一个数的几分之几（或百分之几）是多少的应用题 一个数X 分率=多少 一个数X 百分之几=多少（3） 求一个数比另一个数多（或少）几分之几（或百分之几）是多少的应用题 另一个数X （ 1+分率）=一个数 或者 另一个数X （ 1-分率）=一个数另一个数X （ 1+百分之几）=一个数 或者 另一个数X （ 1-百分之几）=一个数 （4） 已知一个数的几分之几（或百分之几）是多少，求这个数的应用题 多少十几分之几=这个数 多少十百分之几=这个数（5） 已知一个数比另一个数多（或少）几分之几（或百分之几）是多少，求另一个数的 应用题一个数+（ 1+分率）=另一个数 或 一个数+（ 1-分率）=另一个数 一个数+（ 1+百分之几）=另一个数 或一个数+（ 1-百分之几）=另一个数按比例按分配的应用题： 总量十总份数=每一份的数三、课堂精讲1 例1. 一桶油第一次用去 来这桶油有多少千克？，第二次比第一次多用去20千克，还剩下22千克。
原【规律方法】画线段图能将题目中抽象的数量关系，直观形象地表示出来5【搭配课堂训练题】 【难度分级】A 1. 修路队修一段铁路，修了一天后，已修和未修的比是1:4。
第二天修了 3200千米，这5时已修的是全长―。
这条路长多少千米？92. 修路队3天修完一条公路。
第一天修了 36千米，第二天又修了余下天修了 12千米。
这条路长多少千米？720，比男职工少144人，缝纫机厂共有职工多少5的，第三8例2 .缝纫机厂女职工占全厂职工人数的 人？【规律方法】解题关键是找到与具体数量144人的相对应的分率。
人教版小学六年级数学上册同步培训讲义(精品)
人教版数学六年级上册讲义目录第一讲：分数乘整数第二讲：分数乘分数第三讲：分数乘加、乘减混合运算及简算第四讲：倒数的认识第五讲：“求一个数的几分之几是多少”的应用题第六讲：“求比一个数多（或少）几分之几的数是多少”的实际问题第七讲：位置与方向第八讲：分数除法的意义和法则第九讲：分数四则混合运算第十讲：“已知一个数的几分之几是多少，求这个数”的实际问题第十一讲：稍复杂的“已知一个数的几分之几是多少，求这个数”的实际问题第十二讲：比的意义和基本性质（一）第十三讲：比的意义和基本性质（二）第十四讲：比的应用第十五讲;圆的认识第十六讲：轴对称图形第十七讲：圆的周长第十八讲：圆的面积第十九讲：百分数的意义和写法第二十讲：百分数与小数、分数的互化（2节）第二十一讲;百分数应用题（3节）第二十二讲：折扣第二十三讲：纳税第二十四讲：利率第二十五讲：百分数应用题分类第二十六讲：统计第二十七讲：数学广角第二十八讲：整数、分数、百分数应用题结构类型第一讲：分数乘法（一）一、知识讲解（一）分数乘法意义：1、分数乘整数的意义与整数乘法的意义相同，就是求几个相同加数的和的简便运算。
注：“分数乘整数”指的是第二个因数必须是整数，不能是分数。
例如：53×7表示: 求7个53的和是多少？ 或表示：53的7倍是多少？ 2、一个数乘分数的意义就是求一个数的几分之几是多少。
注：“一个数乘分数”指的是第二个因数必须是分数，不能是整数。
（第一个因数是什么都可以）例如：53×61表示: 求53的61是多少？9 ×61表示: 求9的61是多少？ A × 61表示: 求a 的61是多少？（二）分数乘法计算法则：分子与整数相乘，分母不变。
注：（1）为了计算简便能约分的可先约分再计算。
（整数和分母约分）（2）约分是用整数和下面的分母约掉最大公因数。
（整数千万不能与分母相乘，计算结果必须是最简分数）二、过关练习1、分数乘整数年 班 姓名一、想一想，填一填。
人教版六年级数学上册分数应用题及答案
人教版六年级数学上册分数应用题及答案This manuscript was revised by the office on December 22, 2012（人教版）六年级数学上册分数应用题（二）及答案（一）（1）一条水渠，第一天挖了，还剩175米没挖，第一天修了多少米？（2）洗衣机厂上半年生产洗机厂完成了全年计划的，下半年生产的和上半年同样多，实际超额完成100台，计划生产洗衣机多少台？（3）李明看一本书，第一天看了全书的，第二天看了39页，这时正好看了全书的一半，这本书共有多少页？（4）一辆汽车从甲地开往乙地，第一天行了全程的，第二天行了全程的，离乙地还有112千米。
甲、乙两地相距多远？（5）李看一本书，第一天看了全书的，第二天看了全书的，第三天看了12页，还剩20页没看，这本书共有多少页？（6）建华水泥厂上半年完成全年计划的，下半年生产了12.8万吨，实际全年产量超过计划的，今年计划生产水泥多少吨？（7）挖一条水渠第一周挖了全长的，第二周挖了全长的，第二周比第一周多挖20米，这条水渠全长多少米？参考答案（1）175÷（1－）×＝175××＝25（米）答：第一天修了25米。
（2）解：设计划生产x台。
答：计划生产500台洗衣机。
（3）＝＝130（页）答：这本书共有130页。
（4）解：设甲乙两地相距千米。
答：甲乙两地相距320千米。
（5）（页）答：这本书共64页。
（6）解：全年计划生产水泥吨。
答：全年生产水泥24吨。
（7）解：（米）答：这条水渠长400米。
六年级上册数学讲义-分数百分数比综合应用(一)-人教版(含答案)
第十一讲分数、百分数和比的综合应用（一）一、知识梳理分数乘除法和百分数的综合应用题：（1）单位“1”的量和数量关系:（2）解答“求一个数的几分之几（或百分之几）是多少”的应用题；（3）解答一个数比另一个数多（或少）几分之几（或百分之几）的应用题；百分数应用题：（1）纳税和利率；（2）折扣和利润；比的应用：按比例分配二、方法归纳分数和百分数的应用题（1）求一个数是另一个数的几分之几（或百分之几）的应用题一个数÷另一个数=分率一个数÷另一个数× 100%=百分之几（2）求一个数的几分之几（或百分之几）是多少的应用题一个数×分率=多少一个数×百分之几=多少（3）求一个数比另一个数多（或少）几分之几（或百分之几）是多少的应用题另一个数×（1+分率）=一个数或者另一个数×（1-分率）=一个数另一个数×（1+百分之几）=一个数或者另一个数×（1-百分之几）=一个数（4）已知一个数的几分之几（或百分之几）是多少，求这个数的应用题多少÷几分之几=这个数多少÷百分之几=这个数（5）已知一个数比另一个数多（或少）几分之几（或百分之几）是多少，求另一个数的应用题一个数÷（1+分率）=另一个数或一个数÷（1-分率）=另一个数一个数÷（1+百分之几）=另一个数或一个数÷（1-百分之几）=另一个数按比例按分配的应用题：总量÷总份数=每一份的数三、课堂精讲（一）求一个数是另一个数的几分之几（或百分之几）的应用题例1. 六年级2 班有学生42 人，在某次计算题比赛中得优的有18 人，得良的有15 人，及格的有7 人，再努力的有2 人，求得优人数占全班人数的百分之几？及格人数占全班人数的百分之几？【规律方法】要求得优人数占全班人数的百分之几，就是把全班人数看成单位“1”，得优人数是比较量，即求18 人占42 人的百分之几即就是优秀率；求及格人数占全班人数的百分之几，就是求及格率。
小学六年级数学上册《分数百分数应用题》PPT课件
分数百分数应用 题的知识结构图
求一个数是另一个数的几分之几（或百分之几）是多少
1求分率应用题
求一个数比另一个数多或少几分之几（或百分之几） 是多少
简单的求一个数的几分之几（或百分之几）是多少
分 数
2分数百分数乘法应用题 稍复杂的求一个数的几分之几（或百分之几）是多少 连续求一个数的几分之几（或百分之几）是多少
少页没看？ 例3.书店运进105本书，第一天卖出1/3，第二天卖出40%两
天共卖出多少本？
3、 连续求一个数的几分之几（或百分之几）是多 少的应用题。
特征：条件中给出两个分率句，分率句中的单位 “1”是不相同的（一个已知，一个间接已知） 关键：清楚每一步中谁是单位“1”，谁是谁的几分 之几，同时找准中间量。
2、稍复杂的“已知一个数的几分之几是多少，求这个数” 的应用题
特征：单位“1”的量未知，已知的数量与所给的分率不对应。 方法：1、方程解法：a.确定单位“1”，设单位“1”为x
b.找出题目中的数量关系，列出等量关系式 c.单位“1”的量（x）×（1±几分之几）=问题的 量 2、算术方法：先求出已知量对应的分率（1±几分之 几），再用对应量÷对应分率=单位“1”的量 例1.一堆煤，运走2/5，还剩75吨，这堆煤有多少吨？ 例2.一种彩电，现在售价900元，比原价降低了20%，原价 多少元？ 例3.学校五年级有150人，比四年级多25%，四年级有多少 人？
分数、百分数应用题
（归类总结）
分百应用题是六年级上册的重点，也是 一个难点，它涉及了第二，第三，第五以及 第六单元的部分内容，所占比例很大。要想 让学生们准确地掌握好各个类型应用题的特 点，以及解答方法，首先，要对应用题进行 分类，让学生掌握应用题的解题策略。其次， 对于一些平时练习出现的易混易错的典型应 用题进行对比，归类，从而掌握其正确的解 答方法。最后还要对学生进行不同类型应用 题的分组练习，从而进一步提高学生分析解 决应用题的能力。
秋季六年级数学同步课程第十二讲 分数百分数比综合应用(二)
第十二讲分数、百分数和比的综合应用（二）一、知识梳理分数乘除法和百分数的综合应用题：（1）单位“1”的量和数量关系:（2）解答“求一个数的几分之几（或百分之几）是多少”的应用题；（3）解答一个数比另一个数多（或少）几分之几（或百分之几）的应用题；百分数应用题：（1）纳税和利率；（2）折扣和利润；比的应用：按比例分配二、方法归纳分数和百分数的应用题（1）求一个数是另一个数的几分之几（或百分之几）的应用题一个数÷另一个数=分率一个数÷另一个数×100%=百分之几（2）求一个数的几分之几（或百分之几）是多少的应用题 一个数×分率=多少 一个数×百分之几=多少（3）求一个数比另一个数多（或少）几分之几（或百分之几）是多少的应用题 另一个数×（1+分率）=一个数 或者 另一个数×（1-分率）=一个数 另一个数×（1+百分之几）=一个数 或者 另一个数×（1-百分之几）=一个数 （4）已知一个数的几分之几（或百分之几）是多少，求这个数的应用题 多少÷几分之几=这个数 多少÷百分之几=这个数（5）已知一个数比另一个数多（或少）几分之几（或百分之几）是多少，求另一个数的应用题一个数÷（1+分率）=另一个数 或 一个数÷（1-分率）=另一个数 一个数÷（1+百分之几）=另一个数 或 一个数÷（1-百分之几）=另一个数按比例按分配的应用题：总量÷总份数=每一份的数三、课堂精讲例1. 一桶油第一次用去51，第二次比第一次多用去20千克，还剩下22千克。
原 来这桶油有多少千克？【规律方法】画线段图能将题目中抽象的数量关系，直观形象地表示出来【搭配课堂训练题】 【难度分级】 A1．修路队修一段铁路，修了一天后，已修和未修的比是1:4。
第二天修了3200千米，这时已修的是全长95。
人教版人教版六年级数学上册 第六单元百分数的应用题其二：百分数与比应用题的结合(原卷版)
六年级数学上册第六单元百分数的应用题其二：百分数与比应用题的结合本专题是第六单元百分数的应用题其二：百分数与比应用题的结合，先头内容为《第六单元百分数的应用题其一：百分数与分数乘除法应用题的结合》，后续内容为《第六单元百分数的应用题其三：百分率问题》和《第六单元百分数的应用题其四：浓度问题》。
本部分内容主要是百分数与比应用题的结合问题，由于比的应用题主要体现在第四单元内容中，所以，本部分内容考点划分较为笼统，比的应用题详细内容请参考第四单元的典型例题系列。
该部分内容多考察应用题型，综合性较强，题目难度稍大，建议结合比的应用题作为重点部分和复习内容进行讲解，共划分为六个考点，欢迎使用。
【考点一】百分数与比应用题的结合其一：和比问题。
【方法点拨】根据按比例分配问题的方法，在和比问题中，前提条件是已知和与比，因此，题目中没有和或比的时候，要先求出和与比。
【典型例题】王叔叔家的菜地共800 平方米，准备用40%的菜地种西红柿，剩下的再按2:1的面积比种黄瓜和茄子。
三种蔬菜的面积分别是多少平方米？【对应练习】小明家8月份共缴纳水费、电费、煤气费140元，其中电费占整个费用的60%，水费与煤气费的比是1:3，李惠家水费、电费、煤气费各付多少元？【考点二】百分数与比应用题的结合其二：化连比问题。
【方法点拨】根据按比例分配问题的方法，先求出各部分量的比，再化连比，最后根据按比例分配应用题的方法先求出每份数，即和÷份数和=每份数，再分别求出各部分数量是多少。
【典型例题1】盒子里有三种颜色的球，黄球个数与红球个数的比是2:3，红球个数是白球个数的80%，已知三种颜色的球共175个，三种颜色的各球有多少个？【对应练习】艾迪、大宽、薇儿给地主做长工，已知艾迪一个月的工资与大宽一个月的工资比是1:2，大宽一个月的工资是薇儿一个月工资的75%，地主每个月给他们一共51元钱的工资，那么艾迪的工资为多少元？【典型例题2】某奥数课外班共有3个班，其中普通班人数比提高班人数多20%，提高班人数比尖子班人数多20%，普通班人数比尖子班多11 人，尖子班有学生多少人？【考点三】百分数与比应用题的结合其三：先求比，再按比例分配。
六年级上册数学讲义— 分数(百分数)应用题人教新课标
分数（百分数）应用题：1、求一个数是另一个数的几（百）分之几？部分量÷“1”=百分率2、求一个数的几分之几是多少？“1”×分率=部分量3、已知一个数是另一个数的几分之几，求这个数？“1”（x）×分率=部分量“1”已知ד1”↙↘未知设x比“1”多（＋）比“1”少（－）4、求一个数比另一个数多百分之几（少百分之几）多的数量多百分之几÷“1”=少的数量少百分之几百分数应用题：发芽数量（部分量）发芽率（百分率）=──────────×100%总数量（“1”）不发芽率（百分率）=100%－发芽率出勤人数合格数量出勤率=─────X100％合格率=─────X100％总人数总数量面粉数量成活棵树出粉率=─────X100％成活率=────X100％小麦数量总棵树命中次数达标人数命中率=────X100％达标率=────X100％总次数总人数油的重量糖的重量出油率=────X100％含糖率=────X100％花生重量甘蔗的重量再生物质的数量再生率=───────X100％废料物质的数量按比例分配应用题1、题目特点：已知总量和各部分的比。
2、解题关键：先求出各部分量占总量的几分之几。
3、解题方法：求一个数的几分之几是多少，用乘法进行计算。
正、反比列应用题1、找量：在条件、问题中找出两个相关联的量2、判断：判断这两个量之间存在什么比例关系，写出数量关系式↗同扩同缩：正｛｝↘一扩一缩：反｛×｝3、列比例：利用关系式列出比例。
折扣、纳税、利息等应用题：1、折扣：九折表示现价是原价的90％现价比原价降低10％。
｛100％─90％2、纳税：求一个数的百分之几是多少，用乘法进行计算。
3、利息：〔1〕本金：存入银行的钱。
〔2〕利息：银行多支付的钱。
〔3〕利息=本金X利率X时间〔银行多给你的〕〔4〕利率：是一个百分数。
利率=利息÷本金〔国家规定〕〔5〕利息税=利息X5％〔上交国家的，5％是国家规定的〕〔6〕税后利息=利息─利息税〔自己的〕共取回=本金+税后利息。
六年级上册数学讲义-分数百分数比综合应用(一)-人教版(含答案)
第十一讲分数、百分数和比的综合应用（一）一、知识梳理分数乘除法和百分数的综合应用题：（1）单位“1”的量和数量关系:（2）解答“求一个数的几分之几（或百分之几）是多少”的应用题；（3）解答一个数比另一个数多（或少）几分之几（或百分之几）的应用题；百分数应用题：（1）纳税和利率；（2）折扣和利润；比的应用：按比例分配二、方法归纳分数和百分数的应用题（1）求一个数是另一个数的几分之几（或百分之几）的应用题一个数÷另一个数=分率一个数÷另一个数× 100%=百分之几（2）求一个数的几分之几（或百分之几）是多少的应用题一个数×分率=多少一个数×百分之几=多少（3）求一个数比另一个数多（或少）几分之几（或百分之几）是多少的应用题另一个数×（1+分率）=一个数或者另一个数×（1-分率）=一个数另一个数×（1+百分之几）=一个数或者另一个数×（1-百分之几）=一个数（4）已知一个数的几分之几（或百分之几）是多少，求这个数的应用题多少÷几分之几=这个数多少÷百分之几=这个数（5）已知一个数比另一个数多（或少）几分之几（或百分之几）是多少，求另一个数的应用题一个数÷（1+分率）=另一个数或一个数÷（1-分率）=另一个数一个数÷（1+百分之几）=另一个数或一个数÷（1-百分之几）=另一个数按比例按分配的应用题：总量÷总份数=每一份的数三、课堂精讲（一）求一个数是另一个数的几分之几（或百分之几）的应用题例1. 六年级2 班有学生42 人，在某次计算题比赛中得优的有18 人，得良的有15 人，及格的有7 人，再努力的有2 人，求得优人数占全班人数的百分之几？及格人数占全班人数的百分之几？【规律方法】要求得优人数占全班人数的百分之几，就是把全班人数看成单位“1”，得优人数是比较量，即求18 人占42 人的百分之几即就是优秀率；求及格人数占全班人数的百分之几，就是求及格率。
最新人教版六年级数学上册《分数、百分数应用题复习》教学讲义ppt课件
A，：第一二本周书读90了0页全，书第的一1周读了全书的
1 9
，
10
（1）第一周读了多少页？————对应的分率是第一周
读了（ ）
（2）第二周读了多少页？————对应的分率是第二周
读了（ ）
（3）还剩下多少页？————对应的分率是还剩（
）没读
（4）两周一共读多少页？————对应的分率是两周一
共读了（ ）
相差量÷单位“1”=相差分率
（1）一台电视机，原价8000元， 现价6000元，降价了百分之几？ （2）一台电视机，原价8000元 ，降价2000元，降价了百分之几 ？ （3）一台电视机，现价6000元 ，比原价降了2000元，降价了百 分之几？
（二）求一个数的几（百）分之几是多少：
单位“1”×对应分率=所求量
已知量÷已知量的对应分率＝单位“1”
已知量÷已知量的对应分率＝单位“1”
1、一堆煤用去了4吨，正好用了这堆煤
的 2 ，这堆煤有多少吨？ 2、3一堆煤，用去 2 后还剩2吨，这堆煤
有多少吨？
3
3去、15一，堆两煤次，共第用一去次5用.2去吨，23 ，这第堆煤二有次多用 少吨？
4、用一批花生榨油，共得到花生油500
（2）糖10克，溶入水中制成糖 水100克。求含糖率。
（3）一些糖溶入100克水中制 成糖水110克。求含糖率。
2、相差量÷标准量=相差分率
（1）机床厂去年生产机床800台，今年 计划生产1000台。今年计划产量比去年 增产百分之几？ （2）机床厂去年生产机床800台，今年 计划比去年多生产200台。今年计划比 去年增产百分之几？
3、停车场里有18辆小汽车， 是大汽车数量的，190大汽车的 数量是运货车的 4 。运货车
人教版六年级数学上册《分数、百分数应用题(二)》教学设计
4、边长1厘米的正方形面积比边长2厘米的正方形面积少百分之几？
5、修一条公路，实际造价84万元，比原计划增加了5％，增加了多少万元？
出示：
1、花园小学五年级男生有150人，女生人数是男生的 ，已知五年级人数占全校学生人数的25％。全校有多少名学生？
2、引导学生分析百分数应用题的数量关系，解答稍复杂的百分数应用题，掌握百分数应用题的解答方法。
3、通过综合分析、解答、比较，进一步提高学生的分析能力和解答能力。
教学重、难点
重点：掌握百分数应用题的解答方法难点：正确分析数量关系
教学具准备
小黑板
教学环节
教师活动
学生活动
基本练习
出示：
1、什么叫百分数？百分数又叫做什么？怎样进行百分数、分数、小数的互化。
个别学生上台板演，并说说自己的解题思路。
学生独立完成。
作业
课堂作业本
学生独立完成。
课后反思
理清知识体系要充分调动学生的主动性和积极性，要让学生自己动手动脑，教师的作用主要是引导、帮助、点拨和补充。学生经过自己的努力而整理出来的知识体系，学生理解得更深刻，记忆得特别牢固，而且能有效地锻炼和培养学生的自学能力。总之,使学习的知识系统化，也明确了各知识点的共性和个性，表示了学生对知识的理解，更重要的是渗透了学生对各类信息的整合、梳理，培养了科学的学习方法，让学生学会学习。
总之使学习的知识系统化也明确了各知识点的共性和个性表示了学生对知识的理解更重要的是渗透了学生对各类信息的整合梳理培养了科学的学习方法让学生学会学习
《分数、百分数应用题（二）》教学设计
教学内容
分数、百分数应用题（二）
人教版六年级数学上册第六单元百分数的应用题其一：百分数与分数乘除法应用题的结合(解析版)
六年级数学上册典型例题系列之第六单元百分数的应用题其一：百分数与分数乘除法应用题的结合（解析版）编者的话：《六年级数学上册典型例题系列》是基于教材知识点和常年考点考题总结和编辑而成的，其优点在于选题典型，考点丰富，变式多样。
本专题是第六单元百分数的应用题其一：百分数与分数乘除法应用题的结合，后续内容为《第六单元百分数的应用题其二：百分数与比应用题的结合》、《第六单元百分数的应用题其三：百分率问题》和《第六单元百分数的应用题其四：浓度问题》。
本部分内容是百分数与分数乘除法应用题的结合问题，由于分数乘除法应用题主要体现在第一、三单元的内容中，所以，本部分内容考点划分较为笼统，分数乘除法应用题详细内容请参考第一、三单元的典型例题系列。
该部分内容多考察填空、选择、应用等题型，综合性较强，题目难度稍大，建议结合分数乘除法应用题作为重点部分和复习内容进行讲解，共划分为六个考点，欢迎使用。
【考点一】百分数与分数乘法应用题的结合其一：基本类型题。
【方法点拨】1.百分数应用题多是在分数乘除法应用题的基础上进行变式，因此，掌握了分数乘除法应用题也就掌握了百分数应用题。
（注意：分数乘除法应用题的详细考点请参考编者的第一、三单元典型例题系列）2.百分数应用题与分数乘法应用题的结合：（1）求一个数的百分之几是多少？（单位“1”已知）单位“1”×百分率=分率所对应的量（2）求一个数比另一个数多（少）百分之几的数是多少？单位“1”×（1+百分率）=分率所对应的数量【典型例题1】东风化肥厂九月份计算生产化肥2800万袋，实际上半月完成计划的59%，下半月完成计划的65%。
全月超额生产化肥多少袋？解析： 2800×（59%+65%）-2800=672（袋）答：略。
【典型例题2】从1997年至今，我国铁路进行多次提速。
有一列火车，原来每小时行驶80千米，提速后，这列火车的速度比原来增加了40%。
现在这列火车每小时行驶多少千米？解析：80×（1+40%）=112（千米）答：略。
人教版新课标数学六年级上册《用百分数解决问题(二)》课件
填一填
①80千克比50千克多（ 30）千克， 多（ 60）%。
②50千克比80千克少（ 30）千克， 少（37.5）%。
③50千克是80千克的（62.5）%。
④80千克是50千克的（160 ）%。
1. 小飞家原来每月用水约10t，更换了节水龙头后 每月用水约9t，每月用水比原来节约了百分之几？
求现在每月用水比原来节约了百分之几，就是求 现在每月比原来每月少用的用水量是原来每月用 水量的百分之几。原来每月的用水量是单位 “1”。
辨一辨
（1）甲校的图书是乙校的150%，甲校比乙校 的图书多百分之几？
（2）王生储蓄的钱数比张华多20%，王生储蓄 的钱数是张华的百分之几？
（3）甲的岁数和乙的岁数的比是4︰5，甲的岁
数是乙的百分之几？
（4）农场葡萄园的公顷数是苹果园面积的 萄园的面积比苹果园少百分之几？
4 5
,葡
数学诊所
①一个足球运动员，经训练速度提高了2%米。（×） ②甲数比乙数多10%，乙数就比甲数少10%。（×）
单位“1”的量未知,可用方程解 。
答
现成本
解：设原来每件成本x元。
现成本占单位 “1”的百分率
x－15%x＝37.4 37.4 ÷（1－15%）
单位
1、龙泉镇去年有小学生2800人，今年比“去1” 年 减少了0.5%。今年有小学生多少人？
理解：今年比去年减少了0.5%。（今年比去年
减少的学生人数是去年学“1生” 人数的0.5%
• 一件衣服120元，一条裤子90元，衣服比裤 子多几分之几？
一个乡去年原计划造林12公顷，实际造林14 公顷。实际造林比原计划多百分之几？
﹋﹋多的﹋公﹋顷数﹋占计﹋划﹋的百﹋分之几
人教版新课标数学六年级上册分数百分数应用题课件(共13张PPT)
我来寻找单位 1、六年级学生“占1全”校学生的15%。
2、汽车制造厂计划生产小客车4500辆，实际多生产了1 。
5
3、甲车间的人数调出1给乙车间。 3
4、猴子只数的25%相当于松鼠的只数。
方法：抓住含有倍数关系的句子，确定
单位“1”。
1、求一个数是另一个的几分之几或百分之几？
解：设第二单元考了X分。
X+10%X=99
99÷(1+10%)
1.1X=99
X=90
答：李明第二单元考了90分。
小明家去年实际用水100吨， 比计划勤俭了15 ，小明家实际比 计划勤俭用水多少吨？
思考
考考你，你能完整解答下列各题吗？
3、商店运来大米100kg，上午卖出了70%，下午又卖出了
1 5
7 6
，男生有多少人？
24× 7 ＝ 28（人）
6
例2：一本120页的小说，已经看了45%，还剩 多少页？
120×(1－45%)＝ 55(页)
例3：妈妈每月收入3000元。按国家规定月收入 超过2000元的部分按10%缴纳个人所得税。 妈妈今年该缴多少税?
（3000－2000)×10%×12=1200(元)
解题方法：
一个数÷另一个数＝几分之几或百分之几（分率）
例1：某班有男生20人，女生24人，男生人数是 女生的几分之几？
20÷24＝ 20 ＝ 5
24 6
例2：某校五年级160名学生，已到达国家体锻 标准的有120，达标的占百分之几？
120÷160×100%＝ 75%
例3：某县种子推广站，用300粒玉米种子作发芽 实验，结果有288粒种子发芽。求发芽率？
一共看了55页。这本书有多少页？
六年级上册 分数、百分数和比应用的综合应用 课件
2、饲养场养鸡、鸭一共2000只，已知鸡的只数是 鸭的1.5倍，饲养场养鸡、鸭各多少只？ 3、水果店运来苹果300千克，运来的橘子比苹果 少 ，水果店运来橘子多少千克？
通过本节课学习，你有什么收获？
果园里有梨树600棵，比苹果树多20%， 果园里有苹果树多少棵？
①梨树棵数占苹果树棵数：1＋20%＝120% ②梨树棵数与苹果树棵数的比：120%＝6︰5 ③苹果树树棵数：600÷6×5＝500（棵）
1（1）林业部门要配制一种一种农药灭虫， 药粉和水的比是1︰500，现要配制农药5010 千克，需要药粉和水各多少千克？
北师大版小学数学6年级上册《比的应用》第二课时
分数、百分数和比应用的综合应用
学习目标： 1、在具体情境问题中，会把比转化成分数 或者把百分数转化成分数，分数转化成比来 解题，提高学生分析问题的综合能力。 2、在解答具体问题中，能用不同的方法来 解题，沟通知识间的内在联系，培养多元化 思维，学会用多种策略来解决数学实际问题。 3、在探究和交流中，向学生渗透转化思想 思想和方法。 4、培养学生善于倾听的良好品质，体验成 功的收获，增强自信心。
想一想，填一填
1、 ＝（ ）︰（ ） 2、（ ）︰（ ）＝ （）＝1－20%
（） 3、男生人数与女生人数的比是3︰4，男生人数占女 生人数的（ ），女生人数占全班人数的（ ）。 4、盐水的含盐率为10%，则盐占盐水的 ，盐和 水的比是（ ）︰（ ）。 5、苹果树棵数是梨树棵数的2.5倍，苹果树与梨树棵 数的比是（ ）︰（ ）。
果园里有梨树600棵，比苹果树多2 果园里有苹果树多少棵？
苹果树：
六年级上册数学讲义-第六章6.5分数,比,百分数综合题型 人教版 含答案
第5讲分数，比，百分数综合题型【知识巩固】1.“归一”问题：此类应用题中暗含着单一量不变,文字叙述中多带有类似“照这样计算”的字样,其解题的关键是从已知的一种对应量中求出单一量（即归一）,再以它为标准,根据题目要求算出所求量.2.“归总”问题：此类题中暗含着总量不变,即乘积不变.其解题的关键是先求出总数（即归总）,再根据总数算出所求量.3.量率对应问题此类题中需要先确定单位“1”，在找到对应分率与对应量，通过单位“1”、对应分率与对应量之间的关系解答问题【典例精讲】题型一：量率对应问题例1.某中学上年度高中男、女生共290人，这一年度高中男生增加4%，女生增加5%，共增加了13人，本年度该校有男、女生各多少人？题型二：部分量不变例2.100千克刚采下的鲜蘑菇含水量为99%，稍微晾晒后，含水量下降到98%，那么这100千克的蘑菇现在还有多少千克呢？题型三：总量不变例3.甲校原有图书是乙校原有图书的140%，如果甲校给乙校650本，甲校原有图书是乙校原有图书的75%．原来甲校有图书多少本？题型四：相差量不变例4.有两段布，一段布长40米，另一段长30米，把两段布都用去同样长的一部分后，发现短的一段布剩下的长度是长的一段布所剩长度的60%，每段布用去多少米？【课堂练习】题型一：量率对应问题【基础练习】1.甲、乙两仓库共存粮95 吨，现从甲仓库运出存粮的53，从乙仓库运出存粮的40%，这时甲、乙两仓库剩下的粮同样多，甲、乙两仓库原来各存粮多少吨？2.某中学参加文艺汇演的共80人，其中男生人数的40%和女生人数的50%共37人，问男、女生各多少人？【提高练习】1.甲、乙两种商品，成本共2200元，甲商品按20%的利润定价，乙商品按15%的利润定价，后来都按定价的90%打折出售，结果仍获利131元，甲商品的成本是多少元.？2.如图，将两根木棒垂直插入装满沙子的圆柱型容器中（到底），较短的木棒露出的部分占其全长的20%，较长的木棒露出的部分占其全长的31，已知长木棒比短木棒长12厘米，求圆柱形容器的高是多少厘米？3.某次会议，昨天参加会议的男代表比女代表多700人，今天男代表减少10%，女代表增加了5%，今天共1995人出席会议，那么昨天参加会议的有多少人？4.二年级两个班共有学生90人，其中少先队员有71人，又知一班少先队员占全班人数的75%，二班少先队员占全班人数的65，求两个班各有多少人？题型二：部分量不变【基础练习】1.100千克刚采下的鲜蘑菇含水量为99%，稍微晾晒后，含水量下降到98%，那么这100千克的蘑菇现在还有多少千克呢？2.有一堆糖果,其中奶糖占45%,再放入16块水果糖后,奶糖就只占25%.那么,这堆糖中有奶糖多少块？【提高练习】1.一堆围棋子黑白两种颜色，拿走15枚白棋子后，白子个数是黑子个数的50%；再拿走45枚黑棋子后，黑子个数是白子的个数的20%，求开始时黑棋子、白棋子各有多少枚？2.学校有足球蓝球共65个，其中足球是蓝球数量的25%，今年又买回一些足球，这时足球是篮球数量的75%，今年买回足球多少个？3.有两堆棋子,A 堆有黑子350个和白子500个,B 堆有黑子400个和白子100个,为了使A 堆中黑子占50%,B 堆中黑子占75%,要从B 堆中拿到A 堆;黑子和白子各有多少个？4.有若干堆围棋子，每堆棋子数一样多，且每堆中白子都占28％．小明从某一堆中拿走一半棋子，而且拿走的都是黑子，现在，在所有的棋子中，白子将占32％．那么，共有棋子多少堆?题型三：总量不变【基础练习】1.有两筐梨.乙筐是甲筐的60%，从甲筐取出5千克梨放入乙筐后，乙筐的梨是甲筐的79， 甲、乙两筐梨共重多少千克？2.小明是从昨天开始看这本书的，昨天读完以后，小明已经读完的页数是还没读的页数10%，他今天比昨天多读了12页，这时已经读完的页数是还没读的页数的25%，问题是，这本书共有多少页？【提高练习】1.学校阅览室里有学生在看书，其中女生占男生的32，后来又有14名女生来看书，但有14名男生离开图书馆，这时女生人数占所有看书人数的75%．问原来女生有多少人?2.把一个正方形的一边减少20%,另一边增加2米,得到一个长方形.它与原来的正方形面积相等.那么正方形的面积是多少平方米？3.小莉和小刚分别有一些玻璃球，如果小莉给小刚24个，则小莉的玻璃球比小刚少73；如果小刚给小莉24个，则小刚的玻璃球比小莉少62.5%，小莉和小刚原来共有玻璃球多少个？4.甲、乙两个书架共有1100本书，从甲书架借出31，从乙书架借出75%以后，甲书架是乙书架的2倍还多150本，问乙书架原有多少本书？题型四：相差量不变【基础练习】1.有两根塑料绳，一根长80米，另一根长40米，如果从两根上各剪去同样长的一段后，短绳剩下的长度是长绳剩下的27，两根绳各剪去多少米？2.今年父亲40岁，儿子12岁，当儿子的年龄是父亲的512时，儿子多少岁？【提高练习】1.仓库里原来存大米和面粉袋数相等，运出800袋大米和500袋面粉后，仓库里所剩的大米袋数时面粉的75%，仓库里原有大米和面粉各多少袋？2.某小学六年级有两个班，六年一班有学生人数是六年级二班学生人数的76，两个班各转出4人后，六年二班人数还比六年一班人数多112，原来六一班和六二班各有多少人？ 3.甲乙两数，开始时甲比乙多25%，甲乙两数同时加上5后，现在甲比乙多214，原来乙和甲分别是多少？4.由奶糖和巧克力混合成的一堆糖中，如果增加10个奶糖，巧克力就占总数的60％，再增加30个巧克力，则巧克力占总数的75％。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第十二讲分数、百分数和比的综合应用（二）一、知识梳理分数乘除法和百分数的综合应用题：（1）单位“1”的量和数量关系:（2）解答“求一个数的几分之几（或百分之几）是多少”的应用题；（3）解答一个数比另一个数多（或少）几分之几（或百分之几）的应用题；百分数应用题：（1）纳税和利率；（2）折扣和利润；比的应用：按比例分配二、方法归纳分数和百分数的应用题（1）求一个数是另一个数的几分之几（或百分之几）的应用题一个数÷另一个数=分率一个数÷另一个数×100%=百分之几（2）求一个数的几分之几（或百分之几）是多少的应用题一个数×分率=多少一个数×百分之几=多少（3）求一个数比另一个数多（或少）几分之几（或百分之几）是多少的应用题另一个数×（1+分率）=一个数或者另一个数×（1-分率）=一个数另一个数×（1+百分之几）=一个数或者另一个数×（1-百分之几）=一个数（4）已知一个数的几分之几（或百分之几）是多少，求这个数的应用题多少÷几分之几=这个数多少÷百分之几=这个数（5）已知一个数比另一个数多（或少）几分之几（或百分之几）是多少，求另一个数的应用题一个数÷（1+分率）=另一个数或一个数÷（1-分率）=另一个数一个数÷（1+百分之几）=另一个数或一个数÷（1-百分之几）=另一个数按比例按分配的应用题：总量÷总份数=每一份的数三、课堂精讲1例1. 一桶油第一次用去，第二次比第一次多用去 20 千克，还剩下 22 千克。
原5来这桶油有多少千克？【规律方法】画线段图能将题目中抽象的数量关系，直观形象地表示出来【搭配课堂训练题】【难度分级】 A1.修路队修一段铁路，修了一天后，已修和未修的比是 1:4。
第二天修了 3200 千米，这5时已修的是全长。
这条路长多少千米？952.修路队3 天修完一条公路。
第一天修了36 千米，第二天又修了余下的，第三8天修了 12 千米。
这条路长多少千米？7例2．缝纫机厂女职工占全厂职工人数的，比男职工少144 人，缝纫机厂共有职工多少20人？【规律方法】解题关键是找到与具体数量144 人的相对应的分率。
4．某车间一天出席人数与缺席人数的比是8:1，缺席人数比出席人数少35人。
这个车间原【搭配课堂训练题】 【难度分级】 A1 3. 菜农张大伯卖一批大白菜，第一天卖出这批大白菜的32 ，第二天卖出余下的 5，这时还剩下 240 千克大白菜未卖，这批大白菜共有多少千克？【难度分级】B有多少人？4 例 3．男生人数是女生人数的5，男生人数是学生总人数的几分之几？4 【规律方法】男生人数是女生的 5，是将女生人数看作单位“1”，平均分成 5 份，男生是这样的 4 份，学生总人数为这样的（4+5）份，求男生人数是学生总人数的几分之几？就是求 4 份是（4+5）份的几分之几？【搭配课堂训练题】 【难度分级】 B4 5.兄弟两人各有人民币若干元，其中弟的钱数是兄的5 2，若弟给兄 4 元，则弟的钱数是兄的，求兄弟两人原来各有多少元？36.有两桶油，甲桶比乙桶少 20 千克。
从甲桶倒出 5 千克，这时甲桶与乙桶的重量比是1:4。
乙桶原有多少千克？2例4．甲是乙的3，乙是丙的 80% ，甲是丙的的几分之几？2 2【规律方法】甲是乙的3是多少？，乙是丙的 80% ，求甲是丙的的几分之几？就是求 80% 的3【搭配课堂训练题】【难度分级】 B37.某工厂计划一月份生产一批零件，由于改进生产工艺，结果上半月生产了计划的，下5半月比上半月多生产了 20% ，这样全月实际生产了 1980 个零件，一月份计划生产多少个？48.小宇三天读一本 116 页的书，第二天读的页数是第一天的3半多 2 页，那么他第一天读了多少页？，第三天读的比第二天的一3例5．甲的 80%等于乙的7，甲是乙的几分之几？3【规律方法】由条件可得等式：甲×80% =乙×方法1：等式两边同除以 80%得：甲×80%=乙×18 73÷ 80% 7甲=乙×253方法2：根据比例的基本性质得：甲∶乙=718 ∶ 80%化简得：甲∶乙=15：28即甲是乙的。
2510. 甲车间和乙车间共有工人 93 人。
甲车间人数的 等于乙车间人数的 54 【搭配课堂训练题】 【难度分级】 B9. 五（2）班有学生 54 人，男生人数的 75%和女生人数的 80%都参加了课外兴趣小组，而未参加课外兴趣小组的男、女生人数刚好相等，这个班男、女生各有多少人？75%。
甲车间有多少人？9 例 6．有两种糖放在一起，其中软糖占 2025%，求软糖有多少块？，再放入 16 块硬糖以后，软糖占两种糖总数的【规律方法】根据题意，硬糖块数、两种糖的总块数都发生变化，但软糖块数不变，可以 9确定软糖块数为单位“1”，则原来硬糖块数是软糖块数的（1－209）÷20 9= 倍。
加11入 16 块硬糖 以后，后来硬糖块数是软糖块数的（1－25%）÷ 25%=3 倍，这样 16 块硬糖9 16 相当于软糖的 3－ = 11 9倍，从而求出软糖的块数。
【搭配课堂训练题】 【难度分级】 B5 11. 五金工厂两个车间，甲车间人数是乙车间的8人数的比是 3:4。
甲车间有多少人？。
乙车间调走 64 人后，甲车间与乙车间1 例 7．小明看一本课外读物，读了几天后，已读的页数是剩下页数的 81，后来他又读了 20 页，这时已读的页数是剩下页数的 6，这本课外读物共有多少页？【规律方法】根据题意，已读页数和未读页数都发生了变化，但这本书的总页数不变，可 1把总页数看作单位“1”，原来已读页数占总页数的8 +1 ，又读了 20 页后，这时已读页数占总页数的 1 6 +1 ，这 20 页占这本书总页数的（ 1 － 6 +1 1 8 +1），则这本课外读物的页数 为 ： 20÷（【搭配课堂训练题】 【难度分级】 A1 － 6 +1 1 8 +1 ）=630（页）1 12. 兄弟三人合买一台彩电，老大出的钱是其他两人出钱总数的21，老二出的钱是其他两人出钱总数的 3，老三比老二多出 400 元。
问这台彩电多少钱？13. 李师傅加工一批零件，已加工与未加工的个数比是 1:3，再加工 400 个后，已1加工的占总数的 3。
这时加工的零件有多少个？【规律方法】根据题意，有如下数量关系：第一车间人数+40 人=第二车间人数－40 人列方程进行解答。
【搭配课堂训练题】 【难度分级】B14. 老师买来一些本子和铅笔作奖品，已知本子本数与铅笔支数的比是 4∶3，每位竞赛获奖的同学奖 8 本本子和 5 支铅笔，奖了 7 位同学后，剩下的本子本数与铅笔支数的比是 3∶4， 老师买来本子、铅笔各多少？例8.某工厂第一车间人数比第二车间的 多16人，如果从第二车间调40人到第 一车间， 5这时两个车间的人数正好相等，原来两个车间各有多少人？42．当人体的上半身与下半身的长度之比满足 0.618:1 时，可以给人美的感觉，这个比例称之为“黄金比例”，在绘画、摄影等领域经常使用。
已知女生菲菲上半身长 61.8 厘米，下半身长 95 厘米。
根据“黄金比例”可知，她最适合穿 厘米的高跟鞋。
四、讲练结合题1、（ 年应元二中）《数学天地》和《数学故事》册数的比试 4：6，《数学故事》的册数比《数学天地》的册数多（ ）％。
3．（年育才实验）判断：2 甲班人数的 33 等于乙班人数的 4，甲乙两班人数的比是 8：9。
（ ）4.（应元二中）小红看一本书，第一天看了 16 页，第二天看 42 页，这时已看的与未看的页数之比是 2：3。
这本书共有多少页？3 4 5. 小林体重的 等于小胡体重的，那么小林与小胡的体重比是（ ）45A.3：5B.5：3C.15：16D.16：1556. 水果店运来一堆水果，第一天卖出这堆水果的 8剩水果 14 吨，问这堆水果有多少吨？2 多3 吨，第二天卖出余下水果的 ，还32 7.（学而思）琦琦有铅笔和圆珠笔若干支。
铅笔占总数的72,若少 22 根圆珠笔，则圆珠笔占两种笔总数的5,那么原来琦琦的圆珠笔比铅笔多几支？8.（黄埔广附）库房有一批货物，第一天运走1，第二天比第一天多运 8 吨，还剩5这批货物总重量的14，这批货物有多少吨？259.（白云广雅）小明读了一本书，上午读了一部分，这时读的页数与未读页数的比是 1：9，下午比上午多读 6 页，这里已读的页数与未读的页数的比变成了 1：3，这本书共有多少页？10. （广雅）丽丽、贝贝、甜甜三个好朋友共收集废旧电池 420 节，其中甜甜收集1的比贝贝少3，贝贝和丽丽收集的废旧电池的比是 4:5，那么三个人各收集废旧电池多少节？五．课后自测练习3 1.六一班男生人数的44与女生人数的5相等，则男生与女生的最简整数比是（）2.旅行车经过一段山路（只有上坡和下坡），其中上坡路和下坡路的长度比为 3：2，旅行车上坡每小时行 45 千米，下坡每小时行 60 千米，求旅行车的平均速度是多少？53.雅）今年父亲 40 岁，儿子12 岁，当儿子的年龄是父亲的12时，儿子多少岁？4．（太和华附）仓库有一批货物，运走货物与剩下的货物的重量比是 2:7，如果又3运走 64 吨，那么剩下的货物只有仓库原来的，仓库原有货物多少吨？51 5.（育才实验）一套西服的价格是 250 元，其中上衣价钱的 6相等。
问：上衣价钱比裤子价钱贵多少元？1 正好与裤子价钱的46.（应元二中）小明购买甲乙两种书共 60 本，总价值 780 元，如果把购买的甲乙两种书的本数交换一下，共需付 720 元，已知甲乙两种书的单价比为 3：2，两种书的单价各是多少元？7.（中大附中）某人拿了一筐桔子到集市上出售，第一人尝了 1 个后，买了余下的多 2 个。
这时，框中还剩1 。
第二人尝了2 个后，再买了余下的 1 。
第三人买了余下的 13 下 18 个桔子。
原来框中有多少个？ 3 68. （华赛杯）某商品有 76 件，出售给 33 位顾客，每位顾客最多买三件。
买一件按原价，买两件降价 10%，买三件降价 20%。
最后结算，平均每件恰好按原定价的 85%出售，那么买三件的顾客有多少人？9.（高斯数学）过年了，小高与小斯收到的压岁钱数之比为 8：5，假期花掉的钱数的比为8:3，结果假期结束小高还剩下 240 元，小斯还剩 270 元，问两人各收多少压岁钱？第十二讲 分数、百分数和比的综合应用（二）【答案】例 1．解;原来这桶油的重量:（20 + 22）÷（1- 15,- 1）5(千克).答:原来这桶油有 70 千克.【搭配课堂训练题】5 11. 解：3200 ÷（5 + 4 - ） 4 +1,,(米).答:这段铁路长 9000 米.2.12 ÷（1- 5）+ 368= 32 + 36 = 6（8 千米）答：这条公路长 58 千米。