圆周等分系数参照表
圆的等分系数三篇

圆的等分系数三篇圆的等分系数也叫等分圆周直径系数!是已知圆的直径,求圆内接正n边形边长时,所利用到的一个参数。
下面是为大家带来的,希望能帮助到大家!圆的等分系数1计算公式设圆的直径为d,圆内接正n边形,等分系数为:k则:正n边形的边长a=k*d这里的k根据n的取值不同,有不同的对应值!下面给出圆的等分系数表:1--0.000002--1.000003--0.866034--0.707115--0.587796--0.500007--0.433888--0.382689--0.3420210--0.3090211--0.2817312--0.2588213--0.2393214--0.2225215--0.2079116--0.1950917--0.1837518--0.1736519--0.1645920--0.15643(其中前面的数字就是n的取值,后面的为取值为n的时候系数k 的取值!)下面补充下上面系数表的算法问题:以求内接正n边形的边长为例子!依然设圆的直径为d,等分系数为k,我们来探讨下k的取值!每条边对应的角度为:2/n然后求每条边的长度,实际就是求边所在的弦的长度!选取任意一条边AB,那么连接该边两个端点AB与圆心O,得到AOB=2/n延长AO交圆于C,连接CB,得到直角三角形CAB,其中:ACB=AOB/2=/n 则所求的AB的长度为:AB=AC*sinACB=d*sin(/n)而AB=k*d因此k=sin(/n)圆的等分系数2记弦长为t,圆的半径为r,有以下几种情况:1.3等分时,t=2rsin602.5等分时,t=2rsin363.6等分时,t=2rsin304.8等分时,t=2rsin45圆的等分系数3圆的等分系数也叫等分圆周直径系数!是已知圆的直径,求圆内接正n边形边长时,所利用到的一个参数。
计算公式:圆内接正n边形,等分系数为:k则:K=Sin(/n)sin是正弦,比如sin(/6)=1/2如果圆的直径为d,则:正n边形的边长a=k*d当n=6时,a=d/2六边形是3.14除以6等于0.5吗?那么八边形系数0.38268九边形系数0.34202十边形系数0.30902如何得来?追答:n=6,sin(/6)=sin30=0.5n=8,sin(/8)=sin22.5=0.38268n=9,sin(/9)=sin20=0.34202n=10,sin(/10)=sin18=0.30902内容仅供参考。
圆的等分系数表

• 使用圆弧和扇形公式计算尺寸和形状
圆的等分系数表在计算机软件设计中的应用
计算机辅助设
计(CAD)软
利用圆的等分
件 -广泛应用
系数表在CAD
提高计算机软
于建筑设计、
软件中绘制圆
件设计效率
机械制造等领
形图形
域
01
• 可以方便地绘制圆形图形
02
03
• 输入圆的半径和圆心角
• 简化计算过程
THANK YOU FOR WATCHING
谢谢观看
CREATE TOGETHER
DOCS
• 如:Coursera、Udemy等在线教育平台
• 提供关于圆的性质和计算的课程和资源
圆的等分系数表的书籍与教材
数学教材和工具书
• 如:《数学词典》
• 包含圆的等分系数表的相关知识
工程技术类书籍
• 如:《机械设计手册》
• 提供圆的等分系数表在工程设计中的应用实例
专业书籍和教材
• 如:《圆弧及扇形计算》
• 使用圆的周长公式
• 选择合适的半径范围
• 计算每个半径的圆的周长
• 如:1-100mm
将计算结果整理成表格形式
优化和取整等分系数表
• 列出半径和对应的周长
• 对计算结果进行优化和取整
• 方便查阅和应用
• 使得表格更加精确和实用
圆的等分系数表的优化与改进
提高计算精度
⌛️
• 使用更精确的圆周率值
• 如:使用35位小数的π
质
圆的等分系数表
• 制造业和工程领域
• 随着数学的发展,人们对圆的认识
• 在绘画、雕塑和建筑等领域
等分圆周系数表

等分圆周系数表
等分圆周系数表是指在圆周内等分若干份的系数表。
这份系数表可以用于计算圆内接正多边形的面积,以及圆的周长等。
下面是一份等分圆周系数表,其中每一项是一个整数,表示将圆周等分为多少个等份,每个等份的大小为该数字乘以圆的周长。
| 整数 | 等分圆周系数 |
| ----- | -------- |
| 0 | 1 |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
| 6 | 6 |
| 7 | 7 |
| 8 | 8 |
| 9 | 9 |
| 10 | 10 |
| 11 | 11 |
| 12 | 12 |
| 13 | 13 |
| 14 | 14 |
| 15 | 15 |
| 16 | 16 |
| 17 | 17 |
| 18 | 18 |
| 19 | 19 |
| 20 | 20 |
这份等分圆周系数表是根据圆的周长和半径计算出的。
当圆的周长为 C,半径为 r 时,圆内接正 n 边形的面积为:
πr^2 × (n-2)!
其中,n 表示正 n 边形的边数,! 表示阶乘运算。
另外,圆的周长为:
C = 2πr
因此,可以通过计算πr^2 和 2πr 之间的系数,来制作等分圆周系数表。
等分圆周系数表还可以用于计算圆的面积、圆周长、正多边形的面积等。
在制作等分圆周系数表时,需要考虑到小数点后的位数,以确保计算结果的准确性。
圆等分系数表

圆等分系数表
1圆的等分系数表圆的等分系数表:
10.0000021.0000030.8660340.7071150.5877960.5000070.4338880.3826 890.34202100.30902110.28173120.25882130.23932140.22252150.20791 160.19509170.18375180.17365
2190.16459200.15643
圆的等分系数也叫等分圆周直径系数!是已知圆的直径,求圆内接正n边形边长时,所利用到的一个参数。
计算公式:设圆的直径为d,圆内接正n边形,等分系数为:k
则:正n边形的边长a=k*d
这里的k根据n的取值不同,有不同的对应值!(其中前面的数字就是n的取值,后面的为取值为n的时候系数k的取值!)
下面补充下上面系数表的算法问题:
以求内接正n边形的边长为例子!依然设圆的直径为d,等分系数为k,我们来探讨下k的取值!
每条边对应的角度为:2π/n
然后求每条边的长度,实际就是求边所在的弦的长度!选取任意一条边AB,那么连接该边两个端点AB与圆心O,得到<AOB=2π/n延长AO交圆于C,连接CB,得到直角三角形CAB,其中:<ACB=<AOB/2=π/n 则所求的AB的长度为:AB=AC*sin<ACB=d*sin(π/n)
而AB=k*d
因此k=sin(π/n)。
圆周等分弦长系数表打印正式稿
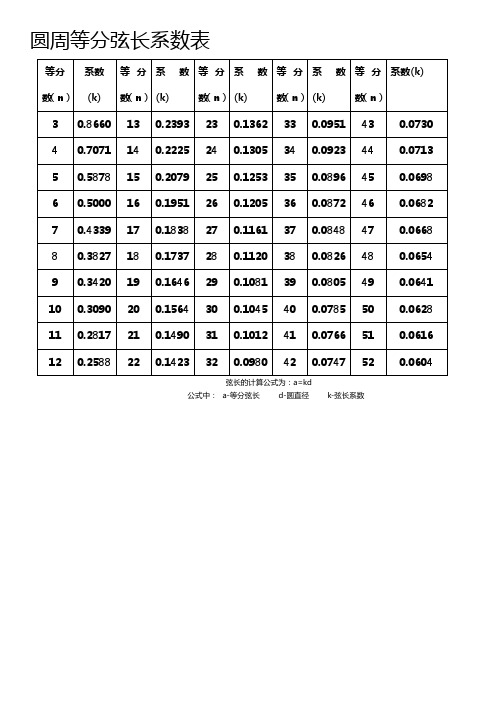
圆周等分弦长系数表弦长的计算公式为:a=kd公式中:a-等分弦长d-圆直径k-弦长系数90度虾米腰弯头放样展开简易计算公式关于虾米腰弯头放样展开的方法,好多网友问到具体的放样展开方便的方法,因为1:1画图展开太麻烦了,也不够精确。
我总结了一下,归纳了下面的计算表格,根据此表格,可以比较方便的展开90度多节(2~19节)弯头。
圆周等分数为16等份只能是90度的虾米腰弯头,请先按照虾米腰节数选出K值,带入到左面表格的公式中,计算出17个点的坐标,然后可在钢板上直接画出第一节展开图或放出样板。
,我举个实际例子比如:5节弯头(取值K=0.1989),直径219,弯曲半径300点1 X=0*219 Y=0.1989*(300-0.5*219)点2 X=0.196*219 Y=0.1989*(300-0.462*219)点3 X=0.393*219 Y=0.1989*(300-0.354*219)点9 X=1.571*219 Y=0.1989*(300+0.5*219多节的弯头叫作“虾米腰”。
手工放样步骤:(以一节为例,其余方法相同)1)先按实际尺寸画出弯头侧面投影。
包括接缝线。
2)按线把每一个封闭线框图形分割成独立的图形。
(可以裁剪,也可以单独再画。
3)取一个图样,(将中心线垂直的设置)画在另一张纸上,沿图样高度画两条上下平行的横线,并与中心线垂直,长度正好是图样直径的圆周长。
(封闭的长方形)4)将图样垂直方向作等分,并作好标记,然后将这些等分线垂直的画到刚才画的展开的长方形内,注意展开图上的点一定要对应投影图样上的点。
5)将图样上斜线沿水平方向作等分。
并平行的拉到展开的图样上,并对应相应的点。
把展开样上得到的交点圆滑连接,就是展开的曲线。
等分作的越密,曲线越准。
6)放出咬口的量,和板厚处理。
弯头下料必须知道弯曲半径,厚度、几节。
图12、画展开图:在端节的一端以aa’为直径画一个半圆弧,将半圆弧六等分(等分的越多就越精确)。
圆周等分系数表

圆周等分系数表圆周等分系数表是一种数学概念,它是指将一个圆周等分为若干份,每份所占的角度等于360°(一周)÷若干份。
它是可逆的,如果一个角的圆周等分系数是x,那么2x的那个角的圆周等分系数是2x,以此类推a x的那个角的圆周等分系数是ax。
圆周等分系数用在测定圆周上物体的角度,也用来测量圆心的角度,以便为圆作图。
常见的圆周等分系数也可以用来表示正多边形的顶点之间的角度,正多边形的圆周等分系数与这个正多边形的边数有关。
以下是常见的圆周等分系数表:1. 一边:12. 两边:23. 三边:34. 四边:45. 五边:56. 六边:67. 七边:78. 八边:89. 九边:910. 十边:1011. 十一边:1112. 十二边:1213. 十三边:1314. 十四边:1415. 十五边:1516. 十六边:1617. 十七边:1718. 十八边:1819. 十九边:1920. 二十边:2021. 二十一边:2122. 二十二边:2223. 二十三边:2324. 二十四边:2425. 二十五边:2526. 二十六边:2627. 二十七边:2728. 二十八边:2829. 二十九边:2930. 三十边:3031. 三十一边及以上:每个正多边形的圆周等分系数可以由其拥有的边数来计算。
圆周等分系数表是有用的数学概念,有助于我们了解圆周上各个角度的大小,也有助于我们给圆上的物体定位,从而更好地掌握圆周的绘图,我们可以应用圆周等分系数表来测量多边形的每个角落,而且在测量圆周上物体位置时,我们也可以用到圆周等分系数表。
