测量平差习题集
测量平差习题集

第二部分 自测题第一章 自测题一、判断题(每题2分,共20分)1、 通过平差可以消除误差,从而消除观测值之间的矛盾。
( )2、 观测值i L 与其偶然真误差i ∆必定等精度。
( )3、 测量条件相同,观测值的精度相同,它们的中误差、真误差也相同。
( )4、 或然误差为最或然值与观测值之差。
( )5、 若X 、Y 向量的维数相同,则YX XY Q Q =。
( )6、 最小二乘原理要求观测值必须服从正态分布。
( )7、 若真误差向量的数学期望为0,即0=∆)(E ,则表示观测值中仅含偶然误差。
( ) 8、 单位权中误差变化,但权比及中误差均不变。
( ) 9、 权或权倒数可以有单位。
( )10、相关观测值权逆阵Q 的对角线元素ii Q 与权阵P 的对角线元素ii P 之间的关系为1=ii ii P Q 。
( )二、填空题(每空0.5分,共20分)1、测量平差就是在 基础上,依据 原则,对观测值进行合理的调整,即分别给以适当的 ,使矛盾消除,从而得到一组最可靠的结果,并进行 。
2、测量条件包括 、 、 和 ,由于测量条件的不可能绝对理想,使得一切测量结果必然含有 。
3、测量误差定义为 ,按其性质可分为 、 和 。
经典测量平差主要研究的是 误差。
4、偶然误差服从 分布,它的概率特性为 、 和 。
仅含偶然误差的观测值线性函数服从 分布。
5、最优估计量应具有的性质为 、 和 。
若模型为线性模型,则所得最优估计量称为 ,最优估计量主要针对观测值中仅含 误差而言。
要证明某估计量为最优估计量,只需证明其满足 性和 性即可。
6、限差是 的最大误差限,它的概率依据是 ,测量上常用于制定 的误差限。
7、若已知观测值向量L 或其偶然真误差向量∆的协方差阵为∑,则L 或∆的权阵定义为L P =∆P = ,由于验前精度∑难以精确求得,实用中定权公式有 、 、 ,特别是对独立等精度观测向量L 而言,其权阵可简单取为L P = 。
测量平差所有习题
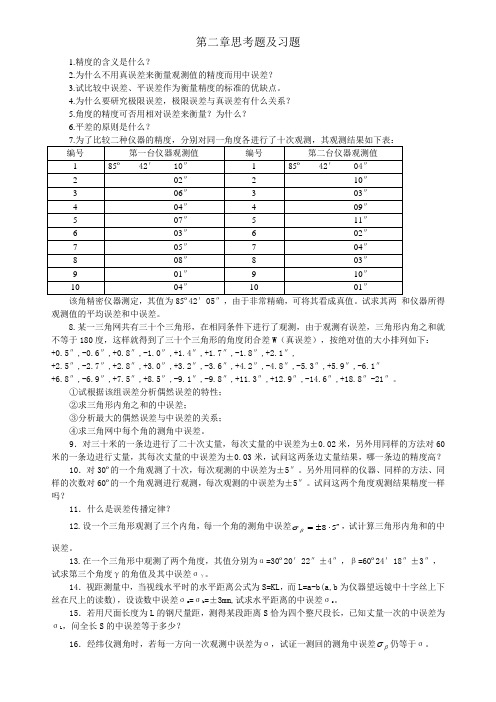
第二章思考题及习题1.精度的含义是什么?2.为什么不用真误差来衡量观测值的精度而用中误差?3.试比较中误差、平误差作为衡量精度的标准的优缺点。
4.为什么要研究极限误差,极限误差与真误差有什么关系?5.角度的精度可否用相对误差来衡量?为什么?6.平差的原则是什么?观测值的平均误差和中误差。
8.某一三角网共有三十个三角形,在相同条件下进行了观测,由于观测有误差,三角形内角之和就不等于180度,这样就得到了三十个三角形的角度闭合差W(真误差),按绝对值的大小排列如下:+0.5″,-0.6″,+0.8″,-1.0″,+1.4″,+1.7″,-1.8″,+2.1″,+2.5″,-2.7″,+2.8″,+3.0″,+3.2″,-3.6″,+4.2″,-4.8″,-5.3″,+5.9″,-6.1″+6.8″,-6.9″,+7.5″,+8.5″,-9.1″,-9.8″,+11.3″,+12.9″,-14.6″,+18.8″-21″。
①试根据该组误差分析偶然误差的特性;②求三角形内角之和的中误差;③分析最大的偶然误差与中误差的关系;④求三角网中每个角的测角中误差。
9.对三十米的一条边进行了二十次丈量,每次丈量的中误差为±0.02米,另外用同样的方法对60米的一条边进行丈量,其每次丈量的中误差为±0.03米,试问这两条边丈量结果,哪一条边的精度高?10.对30º的一个角观测了十次,每次观测的中误差为±5″。
另外用同样的仪器、同样的方法、同样的次数对60º的一个角观测进行观测,每次观测的中误差为±5″。
试问这两个角度观测结果精度一样吗?11.什么是误差传播定律?12.设一个三角形观测了三个内角,每一个角的测角中误差58''⋅±=βσ,试计算三角形内角和的中误差。
13.在一个三角形中观测了两个角度,其值分别为α=30º20′22″±4″,β=60º24′18″±3″,试求第三个角度γ的角值及其中误差σγ。
测量平差练习题

测量平差练习题1.如图,高差观测值h 1=15.752米±5毫米,h 2=7.305米±3毫米,h 3=9.532米±4毫米,试求A 到D 间的高差及中误差。
2.已知函数式()32121L L L X ++=,式中的()1,2,3i L i =均为等精度独立观测值,其中误差为σ,试求X 的中误差。
3.设函数为44332211L a L a L a L a F +--=,式中观测值L1、L2、L3和L4 相应有权为P1、P2、P3和P4 ,求F 的权倒数。
4.使用两种类型的经纬仪观测某一角度得29331241''±'''︒=L ,84231242''±'''︒=L ,求该角最或是值及其中误差。
5.设观测值L1、L2和L3的权为1、2及4,观测值L2的中误差为6",求观测值L1和L3的中误差。
6.如图,这是一个单结点水准网,A 、B 、C 为已知水准点,其中000.10=A H 米,000.13=B H 米,000.11=C H 米,E 为待定点,高差观测值383.11=h 米、612.12-=h 米、396.03=h 米,试列出改正数条件方程式。
7.如图所示的水准网。
其中A 点为已知高程点,其高程已知值为HA=100.000m ,其余各点为高程未知点。
各条路线的观测高差及路线长如下:h1=0.023m ,S1=5km ; h2=1.114m ,S2=5km ; h3=1.142m ,S3=5km ; h4=0.078m , S 4=2km; h5=0.099m ,S5=2km ; h6=1.216m ,S6=2km 。
①试列出该水准网按条件平差时的条件方程式;②设C=10,确定出各条路线观测高差的权。
8.如图为一大地四边形,试判断各类条件数目并列出改正数条件方程式。
误差理论与测量平差基础习题集

第一章绪论§1-1观测误差1.1.01为什么说观测值总是带有误差,而且观测误差是不可避免的?1.1.02观测条件是由哪些因素构成的?它与观测结果的质量有什么联系?1.1.03测量误差分为哪几类?它们各自是怎样定义的?对观测成果有何影响?试举例说明。
1.1.04用钢尺丈量距离,有下列几种情况使量得的结果产生误差,试分别判定误差的性质及符号:(1)长不准确;(2)尺尺不水平;(3)估读小数不准确;(4)尺垂曲;(5)尺端偏离直线方向。
1.1.05在水准测量中,有下列几种情况使水准尺读数带有误差,试判别误差的性质及符号:(1)视准轴与水准轴不平行;(2)仪器下沉;(3)读数不准确;(4)水准尺下沆。
§1-2测量平差学科的研究对象1.2.06 何谓多余观测?测量中为什么要进行多余观测?1.2.07 测量平差的基本任务是什么?§1-3测量平差的简史和发展1.3.08 高斯于哪一年提出最小二乘法?其主要是为了解决什么问题?1.3.09 自20世纪五六十年代开始,测量平差得到了很大发展,主要表现在那些方面?§1-4 本课程的任务和内容1.4.10 本课程主要讲述哪些内容?其教学目的是什么?第二章误差分析与精度指标§2-1 正态分布2.1.01 为什么说正态分布是一种重要的分布?试写出一维随机变量X的正态分布概率密度式。
§2-2 偶然误差的规律性2.2.02 观测值的真误差是怎样定义的?三角形的闭合差是什么观测值的真误差?2.2.03 在相同的观测条件下,大量的偶然误差呈现出什么样的规律性?2.2.04 偶然误差*服从什么分布?它的数学期望和方差各是多少?§2-3 衡量精度的指标2.3.05 何谓精度?通常采用哪几种指标来衡量精度?2.3.06 在相同的观测条件下,对同一个量进行若干次观测得到一组观测值,这些观测值的精度是否相同?能否认为误差小的观测值比误差大的观测值精度高?2.3.07 若有两个观测值的中误差相同,那么,是否可以说这两个观测值的真误差一定相同?为什么?2.3.08 为了鉴定经纬度的精度,对已知精确测定的水平角α=45O00’00”作12次观测,结果为:45o00’06” 44o59’55” 44o59’58” 45o00’04”45o00’03” 45o00’04” 45o00’00” 44o59’58”44o59’59” 44o59’59” 45o00’06” 45o00’03”设α没有误差,试求观测值的中误差。
测量平差试题一

协因数阵为 QXˆXˆ
0.25 0.15
0.15 0.75
,且单位权方差
ˆ
2 0
3.0cm2
,
(1)计算 P1 点纵、横坐标中误差和点位中误差;
(2)计算 P1 点误差椭圆三要素E、E、 F ; (3)计算 P1 点在方位角为 90 方向上的位差。
(17 分)
一、FFFFT 二、相等 三、aabcd
六. (1)ˆx
3 2
cm,,ˆ y
1.5cm
ˆ p
3cm
(2)E =74. 5或254. 5,E, 1.54cm F 0.79cm
(3)
ˆ
90
1.5cm
9.定权时 0 可任意给定,它仅起比例常数的作用( )。
10.设有两个水平角的测角中误差相等,则角度值大的那个水平角相对精度高( )。
二、 用“相等”或“相同”或“不等”填空(8 分)。
已知两段距离的长度及其中误差为 300.158m±3.5cm; 600.686m±3.5cm。则:
1.这两段距离的中误差(
的测回数 N=( )。
a) 25
b) 20
c) 45
QQYXXX
Q XY QYY
=
0.5 0.25
0.25
0.5
单位权方差 0 2 =±2.0。则 P 点误差椭圆的方位角 T=( )。
a) 90
b) 135
c) 120
4.设 L 的权为 1,则乘积 4L 的权 P=( )。
)。
2.这两段距离的误差的最大限差(
)。
3.它们的精度(
)。
4.它们的相对精度(
)。
三、 选择填空。只选择一个正确答案(25 分)。
测量平差超级经典试卷含答案汇总

一、填空题(每空1分,共20分) 1、测量平差就是在 多余观测 基础上,依据 一定的 原则,对观测值进行合理的调整,即分别给以适当的 改正数 ,使矛盾消除,从而得到一组最可靠的结果,并进行 精度评估 。
2、条件平差中,条件方程式的选取要求满足 、 。
3已知条件平差的法方程为024322421=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡k k ,则PVVT= ,μ= ,1k p = ,2k p = 。
4、已知某平差问题,观测值个数为79,必要观测量个数为35,则按条件平差进行求解时,条件方程式个数为 ,法方程式个数为 。
5、已知某平差问题观测值个数为50,必要观测量个数为22,若选6个独立参数按具有参数的条件平差进行求解,则函数模型个数为 ,联系数法方程式的个数为 ;若在22个独立参数的基础上,又选了4个非独立参数按具有条件的参数平差进行求解,则函数模型个数为 ,联系数法方程式的个数为 。
6、间接平差中误差方程的个数等于________________,所选参数的个数等于_______________。
7、已知真误差向量1⨯∆n 及其权阵P ,则单位权中误差公式为 ,当权阵P 为 此公式变为中误差公式。
二、选择题(每题2分,共20分)1、观测条件是指:A)产生观测误差的几个主要因素:仪器,观测者,外界条件等的综合B)测量时的几个基本操作:仪器的对中,整平,照准,度盘配置,读数等要素的综合C)测量时的外界环境:温度,湿度,气压,大气折光……等因素的综合.D)观测时的天气状况与观测点地理状况诸因素的综合答:_____2、已知观测向量()L L L T=12的协方差阵为D L =--⎛⎝⎫⎭⎪3112,若有观测值函数Y 1=2L 1,Y 2=L 1+L 2,则σy y 12等于? (A)1/4(B)21/2(D)4答:__3、已知观测向量()L L L T=12的权阵P L =--⎛⎝ ⎫⎭⎪2113,单位权方差σ025=,则观测值L 1的方差σL 12等于:(A)0.4 (B)2.5(C)3 (D)253答:____4、已知测角网如下图,观测了各三角形的内角,判断下列结果,选出正确答案。
文档:误差理论与测量平差基础习题集(二期)

误差理论与测量平差基础题库集1.1 设对一段距离丈量了三次,三次结果分别为9.98m ,10.00m ,10.02m ,试根据测量平差概念,按独立等精度最小二乘原理(21min ni i v ==∑)求这段距离的平差值以及消除矛盾时各次结果所得的最或然改正数。
11223311231.1ˆˆˆ 9.98 ˆˆˆ 10 ˆˆˆ 10.0219.98ˆ110110.02ˆ()130103ˆ9.982ˆ100ˆ10.022T T L X V XL X V XL X V XV X XB B B l V Xcm V Xcm V Xcm ->>⎧==-⎪⎪==-⎨⎪==-⎪⎩⎡⎤⎡⎤⎢⎥⎢⎥=-⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦==⨯==-==-==-=-1.2 一段距离丈量了三次,三次结果分别为9.98m ,10.00m ,10.02m ,令三次结果的权分别为1,2,1,试按独立非等精度最小二乘原理(21min ni i i p v ==∑)求这段距离的平差值以及消除矛盾时各次结果所得的最或然改正数。
111231.21001001000202001001ˆ()1(9.9810210.02)104ˆ9.982ˆ100ˆ10.022T T Q P Q X B PB B Pl V Xcm V Xcm V Xcm -->>⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=⇒==⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎣⎦==⨯+⨯+==-==-==-=-1.3 设一平面三角形三内角观测值为A 、B 、C ,180W A B C =++-︒为三角形闭合差,试根据测量平差概念,按独立等精度最小二乘原理证明三内角的评差值为ˆ3W AA =-、ˆ3W BB =-、ˆ3W C C =-。
()1231231231.3ˆˆˆ18001800011100AB C A V B V C V V V V W V V W V AV W P E Q E>>++-︒=+++++-︒=+++=⎡⎤⎢⎥+=⎢⎥⎢⎥⎣⎦+===按条件平差法有1123()111311313131ˆ31ˆ31ˆ3T T T T V QA K A K A AA W WW W W A A V A W B B V B W C C V C W -===-⎡⎤⎢⎥=-⎢⎥⎢⎥⎣⎦⎡⎤-⎢⎥⎢⎥⎢⎥=-⎢⎥⎢⎥⎢⎥-⎣⎦=+=-=+=-=+=-123ˆˆˆ ˆˆˆ ˆˆˆˆˆ+180 +18010ˆ01ˆ11180ˆˆA A B B A B A B A B A B A X V X A B X V X B C X X V X X C A XV B X C X X ⎧==-⎪⎪==-⎨⎪=--︒=--︒-⎪⎩⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥=-⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦---︒⎢⎥⎢⎥⎣⎦⎣⎦⎡⎤⎢⎥⎢⎣⎦按参数平差11()101011010101101111180121801321801331ˆ31ˆ31ˆˆˆ1801803T TB PB B Pl A BC A WA B C A B C B W AA W BB W CA B A W B --=⎥⎡⎤⎡⎤⎛⎫⎛⎫--⎛⎫⎛⎫⎢⎥⎢⎥ ⎪ ⎪= ⎪ ⎪⎢⎥⎢⎥ ⎪ ⎪--⎝⎭⎝⎭ ⎪ ⎪⎢⎥⎢⎥---︒⎝⎭⎝⎭⎣⎦⎣⎦⎡⎤-⎢⎥--+︒⎡⎤==⎢⎥⎢⎥-+-+︒⎣⎦⎢⎥-⎢⎥⎣⎦=-=-=︒--=︒-+-+即132180313W A B C W CC W=︒---++=-1.4 已知独立等精度观测某三角锁段共得15个三角形,其闭合差如下表 所示。
测量平差习题集答案

测量平差习题集答案测量平差习题集答案在测量工作中,平差是一项非常重要的环节。
它通过对测量数据进行处理和分析,消除误差,得到更加准确的测量结果。
为了帮助大家更好地理解和掌握平差的方法和技巧,下面将为大家提供一些测量平差习题集的答案。
1. 题目:某测量队在进行水平控制网的测量时,测得A、B两点的水平角为α1=90°30'20",α2=269°29'40",A、B两点的距离为1000米。
已知A点的坐标为(1000, 1000),求B点的坐标。
解答:根据水平角的定义,可以得到以下关系式:α1 = α2 + 180°即90°30'20" = 269°29'40" + 180°化简得90°30'20" = 449°29'40"由于角度超过360°,需要将其转化为小于360°的形式,可以通过减去360°来实现,即:90°30'20" - 360° = 89°29'40"所以,B点的水平角为89°29'40"。
接下来,根据已知的A点坐标和AB距离,可以利用正弦定理来求解B点的坐标。
设B点的坐标为(x, y),则有:(x - 1000)^2 + (y - 1000)^2 = 1000^2根据正弦定理,可以得到以下关系式:sin(89°29'40") = (x - 1000) / 1000化简得:(x - 1000) = 1000 * sin(89°29'40")解得:x ≈ 1999.999同理,可得:y ≈ 1000.000所以,B点的坐标为(1999.999, 1000.000)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二部分 自测题第一章 自测题一、判断题(每题2分,共20分)1、 通过平差可以消除误差,从而消除观测值之间的矛盾。
( )2、 观测值i L 与其偶然真误差i ∆必定等精度。
( )3、 测量条件相同,观测值的精度相同,它们的中误差、真误差也相同。
( )4、 或然误差为最或然值与观测值之差。
( )5、 若X 、Y 向量的维数相同,则YX XY Q Q =。
( )6、 最小二乘原理要求观测值必须服从正态分布。
( )7、 若真误差向量的数学期望为0,即0=∆)(E ,则表示观测值中仅含偶然误差。
( ) 8、 单位权中误差变化,但权比及中误差均不变。
( ) 9、 权或权倒数可以有单位。
( )10、相关观测值权逆阵Q 的对角线元素ii Q 与权阵P 的对角线元素ii P 之间的关系为1=ii ii P Q 。
( )二、填空题(每空0.5分,共20分)1、测量平差就是在 基础上,依据 原则,对观测值进行合理的调整,即分别给以适当的 ,使矛盾消除,从而得到一组最可靠的结果,并进行 。
2、测量条件包括 、 、 和 ,由于测量条件的不可能绝对理想,使得一切测量结果必然含有 。
3、测量误差定义为 ,按其性质可分为 、 和 。
经典测量平差主要研究的是 误差。
4、偶然误差服从 分布,它的概率特性为 、 和 。
仅含偶然误差的观测值线性函数服从 分布。
5、最优估计量应具有的性质为 、 和 。
若模型为线性模型,则所得最优估计量称为 ,最优估计量主要针对观测值中仅含 误差而言。
要证明某估计量为最优估计量,只需证明其满足 性和 性即可。
6、限差是 的最大误差限,它的概率依据是 ,测量上常用于制定 的误差限。
7、若已知观测值向量L 或其偶然真误差向量∆的协方差阵为∑,则L 或∆的权阵定义为L P =∆P = ,由于验前精度∑难以精确求得,实用中定权公式有 、 、,特别是对独立等精度观测向量L 而言,其权阵可简单取为L P = 。
8、已知真误差向量1⨯∆n 及其权阵P ,则单位权中误差公式为 ,当权阵P 为 此公式变为中误差公式。
式中,1⨯∆n 可以为同一观测量的真误差,也可以为 观测量的真误差。
9、已知独立非等精度观测向量1⨯n L 的非线性函数变量为)(L f z =,则2z m = ,zp 1= 。
10、已知某量z 的权倒数zp 1及单位权中误差μ,则z m = 。
三、选择题(每题2分,共20分)1、已知方位角1213245''±'''=οAP T ,±=km s AP 10 时点位纵横向精度基本相同(5102⨯≈ρ)。
A 、1mB 、1cmC 、5cmD 、5mm2、已知)180(3ˆο-++=-=C B A W WA A,m m m m C B A ===,m m W 3=,则A m ˆ= 。
A 、m 32 B 、m 32C 、m 32 D 、m 23 3、长方形地块的面积由长和宽得到,已知长度的测量值cm m a 14±=,若要求面积的中误差25dm m S ≤,则宽度测量值m b 3=的中误差应限制在 范围。
A 、1cmB 、2cmC 、3cmD 、4cm4、A 、B 两点按双次观测得高差'i h 、"i h )8,,2,1(K =i ,各高差之间相互独立,每一高差的中误差均为mm 2±,则全长高差算术中数的中误差为± 。
A 、2mmB 、4mmC 、8mmD 、16mm5、水准测量中,10km 观测高差值权为8,则5km 高差之权为 。
A 、2B 、4C 、8D 、16 6、已知⎥⎦⎤⎢⎣⎡=∆3112P ,则2L p = 。
A 、2B 、3C 、25D 、35 7、已知三角形闭合差向量1⨯n W 及其相关权阵W P ,i W 中i A 的权为i p ,则i A 的中误差为。
A 、n W P W W T ±B 、i W T np W P W ±C 、nWP W W T 3± D 、i W T np W P W 3±8、已知观测值L 的中误差为L m ,L x 2=,2L y =,则xy m = 。
A 、24L Lm B 、L Lm 4 C 、22L Lm D 、L Lm 29、已知),,2,1(n i L x v i i K =-=,[]nL x =,观测值iL 独立等精度,其权均为1,则21v v p=。
A 、nB 、n -C 、n 1 D 、n1- 10、随机向量1⨯n X 的协方差阵X ∑还可写为 。
A 、)()()(X E X E X X E T T -B 、)()(X E X E TC 、)()(X E X E TD 、)()()(XE X E XX E TT-第二章 自测题一、判断题(每题2分,共20分)1、参数平差中,当误差方程为线性时,未知参数近似值可以任意选取,不会影响平差值及其精度。
( )2、 观测值i L ),,2,1(n i K =之间误差独立,则平差值iL ˆ之间也一定误差独立。
( ) 3、提高平差值精度的关键是增加观测次数。
( )4、参数平差中要求未知参数i x ˆ之间函数独立,所以它们之间的协方差一定为0。
( )5、对于一定的平差问题,一定有∆∆≤P PV V TT。
( )6、参数平差中,若X F Z Tˆδ=,则)(1F N F tn PV V T T Z --=∑。
( )7、 参数平差中,当观测值之间相互独立时,若某一误差方程式中不含有未知参数,但自由项不为0,则此误差方程式对组成法方程不起作用。
( )8、 数平差定权时,随单位权中误差的选取不同,会导致观测量平差值的不同。
( ) 9、 差值的精度一定高于其观测值的精度。
( )10、因为V L L +=ˆ,故V L LQ Q Q +=ˆ。
( )二、填空题(每空1分,共25分)1、参数平差中,未知参数的选取要求满足 、 。
2、已知某平差问题,观测值个数为79,多余观测量个数为35,则按参数平差进行求解时,误差方程式个数为 ,法方程式个数为 。
3、非线性误差方程式i t i i L x x x f v -=)ˆ,,ˆ,ˆ(21K 的线性化形式为 。
未知参数的近似值越靠近 ,线性化程度就越高;当线性化程度不高时,可以采用 法进行求解。
4、参数平差中,已知⎥⎦⎤⎢⎣⎡=4223N ,2±=μ,则=1ˆx p ,=1ˆx m ,=2ˆx p ,=2ˆx m 。
若1ˆˆ221++=x x z ,则=z p ,=z m 。
5、已知36=Pl l T,4=n ,法方程为024ˆˆ322421=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡x x δδ,则PV V T= ,μ= ,1ˆx m = ,2ˆx m = 。
6、设观测值的权阵为P ,将其各元素同乘以某大于0的常数λ后重新进行平差,则下列各量:X ˆ、V 、μ、Xˆ∑、V Q 中,数值改变的有 、 ,数值不改变的有 、 、 。
7、V L ˆ∑= ,V X ˆ∑= ,LV ∑= 。
三、选择题(每题2分,共10分)1、参数平差的法方程可以写为 。
A 、0ˆˆ=+U X Q XB 、0ˆˆ=+U P X XC 、0ˆ=+U Q X UD 、0ˆ=+U X Q U2、参数平差中,已知⎥⎦⎤⎢⎣⎡=211121ˆX P ,41ˆ±=xm ,则±=μ。
A 、1B 、2C 、4D 、83、以L m 、∆m 、v m 分别表示某一量的观测值、真误差、观测值残差的中误差,则2L m 、2∆m 、2v m 之间的关系为 。
A 、222∆<=m m m v LB 、222v L m m m >=∆ C 、222∆==m m m v L D 、222L v m m m <=∆4、参数平差中,L Q ˆ= 。
A 、TA AN 1- B 、A N A T1-C 、T A AN P11--- D 、A N A P T 11---5、参数平差中,L X Q ˆ= 。
A 、TA AN 1- B 、A N A T1-C 、1-NA TD 、T A N1-第三章 自测题一、判断题(每题2分,共20分)1、 同一平差问题,参数平差与条件平差所得观测值的平差值及其绝对精度一定相同。
( )2、若n n L k L k L k z ˆˆˆ2211+++=Λ,则2ˆ22ˆ222ˆ21221nL n L Lz m k m k m k m +++=Λ。
( ) 3、条件平差中,0)(>∆-V B 。
( )4、条件平差中,一定有∆∆≤P PV V TT 。
( )5、若某一条件方程式的闭合差为0,则此条件方程式对求解不起作用。
( )6、若有条件方程为011101021140151=⎥⎦⎤⎢⎣⎡-+⎥⎥⎦⎤⎢⎢⎣⎡⎥⎦⎤⎢⎣⎡--v v M ,观测值间相互独立,则2L 一定不得改正数。
( )7、 若参数平差模型为l X A V +=ˆδ,条件平差模型为0=+W BV ,则Bl W -=。
( )8、 无论参数平差还是条件平差,均有0=LV Q 。
( ) 9、 条件平差中,若0)(=∆E ,则0)(=W E 。
( ) 10、条件平差中,P Q V 为幂等阵。
( )二、填空题(每空1分,共20分)1、条件平差中,条件方程式的选取要求满足 、 。
2、已知某平差问题,观测值个数为79,必要观测量个数为35,则按条件平差进行求解时,条件方程式个数为 ,法方程式个数为 。
3、非线性条件方程式in i f L L L f 021)ˆ,,ˆ,ˆ(=K (i f 0为常数)的线性化形式为 。
4、测量平差中,为消除多余观测所引起的矛盾,当所列方程为 方程时,称为参数平差;当所列方程为 方程时,称为条件平差。
由于单纯消除矛盾而给的观测值改正数有无穷多组,为求出唯一估值,参数平差和条件平差都必须依据 原则求出极值,一般称参数平差的极值问题为 极值,条件平差的极值问题为 极值。
5、已知条件平差的法方程为024322421=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡k k ,则PV V T = ,μ= ,1k p = ,2k p = ,=21k k m 。
若21k k z +=,则=z m 。
6、V L ˆ∑= ,L K ˆ∑= ,L W ˆ∑= ,WK Q = 。
三、选择题(每题2分,共10分)1、条件平差的法方程等价于 。
A 、0=+W K Q KB 、0=+W Q K WC 、0=+W P K WD 、0=+W P K K2、条件平差中,已知⎥⎦⎤⎢⎣⎡=8224W Q ,2±=μ,则±=1k m 。
