§5.5 布里渊区
布里渊区图示
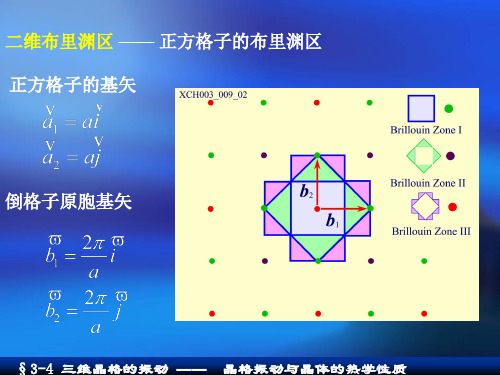
a 3 正格子原胞基矢 a1 ai, a2 i aj 2 2 取单位矢量k垂直于i, j 则,a1,a2和k构成的体积 3 2 a 2
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
倒格子原胞的基矢为 2 (a2 k ) 2 2 b1 i j a 3a 2 (k a1 ) 4 b2 j 3a
的垂直平分线和第一 布里渊区边界所围成 —— 第二布里渊区大小
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
第三布里渊区
由4个倒格点
的垂直平分线和第二布 里渊区边界边界所围成 第三布里渊区大小
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
第一、第二和第三布里渊区
§3-4 三维晶格的振动 ——
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
选一个倒格点为原点,原点的最近邻倒格矢有6个,分别是
b1 , b2 , (b1 b2 )
§3-4 三维晶格的振动 —— 晶格振动与晶体的热学性质
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
晶格振动与晶体的热学性质
正方格子其它布里渊区的形成
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
正方格子其它布里渊 和第一布里渊 区重合
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
二维斜格子的第一布里渊区
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
二维斜格子其它布里渊区的形成
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
二维斜格子其它布里渊区的形状
布里渊区通俗理解

布里渊区通俗理解-概述说明以及解释1.引言1.1 概述布里渊区是一个在物理和数学领域中具有重要意义的概念,它主要用来描述在给定条件下某一物体或物体集合的邻域。
布里渊区的概念源于法国物理学家亚历山大·布里渊的研究成果,他发现了一种描述物体在空间中的局部特性的方法。
布里渊区的概念不仅在物理学领域中被广泛应用,同时也在计算机图形学、材料科学、生物学等领域中具有重要作用。
在本文中,我们将深入探讨布里渊区的概念、应用以及重要性,希望能够对读者有所启发和帮助。
通过了解布里渊区的相关知识,我们可以更好地理解物体在空间中的局部结构和特性,为我们探索和应用这些知识提供了理论基础。
在日常生活中,布里渊区的概念也有着重要的意义,可以帮助我们更好地理解世界的复杂性,促进科学技术的发展和创新。
展望未来,布里渊区的研究和应用将会不断深化和拓展,为人类社会的进步和发展做出更大的贡献。
1.2 文章结构本文将分为三个主要部分来讨论布里渊区的通俗理解。
在引言部分,我们将简要介绍布里渊区的概念、文章结构和撰写本文的目的。
在正文部分,我们将详细探讨布里渊区的概念,其在实际应用中的情况以及在各领域中的重要性。
最后,在结论部分,我们将总结布里渊区的作用,讨论其在日常生活中的意义,并展望未来布里渊区的发展方向。
通过这样的结构安排,读者可以系统地了解布里渊区的相关知识,并深入理解其在现实生活中的应用和意义。
1.3 目的2.正文2.1 布里渊区的概念布里渊区(英文名为Boulevard区)是一种在计算机科学领域中常用的概念,用于描述一种数据结构的布局方式。
布里渊区是指内存中的一段连续地址空间,通常用来存储程序代码、全局变量和静态变量。
在操作系统中,布里渊区还可以用于存放动态链接库和共享库的代码段和数据段。
布里渊区的特点是具有一定的大小和位置,可以在运行时被操作系统动态地分配和回收。
布里渊区的概念主要用于优化内存管理和提高程序的执行效率。
布里渊区图示

a 3 正格子原胞基矢 a1 = ai, a2 = i + aj 2 2 取单位矢量k垂直于i, j 则,a1,a2和k构成的体积 3 2 Ω= a 2
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
倒格子原胞的基矢为 2π (a2 × k ) 2π 2π b1 = i− j = Ω a 3a 2π (k × a1 ) 4π b2 = = j Ω 3a
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
正方格子其它布里渊区的形成
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
正方格子其它布里渊区的形状
—— 每个布 里渊区经过适 当的平移之后 和第一布里渊 区重合
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
二维斜格子的第一布里渊区
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
二维斜格子其它布里渊区的形成
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
二维斜格子其它布里渊区的形状
—— 每个布里 渊区经过适当 的平移之后和 第一布里渊区 重合
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
平面正三角形,相邻原子间距为 求正格矢和倒格矢 求正格矢和倒格矢, 平面正三角形,相邻原子间距为a,求正格矢和倒格矢,画 出第一和第二布里渊区
的垂直平分线和第一 布里渊区边界所围成 —— 第二布里渊区大小
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
第三布里渊区 由4个倒格点 个倒格点
的垂直平分线和第二布 里渊区边界边界所围成 第三布里渊区大小
§3-4 三维晶格的振动 ——
倒格子和布里渊区

于是:
Gh1h2 h3 CA a1 a3 (h1b1 h2b2 h3b3 ) ( ) h1 h3 2 2 0
同理 Gh1h2 h3 CB 0 而且 CA, CB 都在(ABC)面上, 所以 Gh1h2h3 与晶面系 (h1h2h3 ) 正交。
三维例子:
正点阵为简 单点阵,倒 易点阵也是 简单点阵。
正格子空间中长 的基矢a3对应于 倒格子空间短的 基矢b3,反之亦 然。推广,正格 子空间长的线条 对应于倒格子空 间短的线条。
正点阵为有心点阵时,倒易点阵也是有心点阵, 但有心类型可能不同,例如:体心立方点阵的倒格子 为面心立方点阵。
而面心立方点阵的倒格子为体心立方点阵。
倒易点阵仍是简立方点阵:
2 2 2 b1 i, b2 j , b3 k, a a a
所以倒格子也是布拉菲格子。 六角点阵: 六角点阵的倒易点阵: 见Ashcroft p88 c 轴方向不变,a 轴在垂直于c 轴的 平面上旋转30度。
正格子空间六方结构,在倒格子空间亦为六方结 构。不过其基矢尺寸关系发生变化,基矢方向也转了 一个角度。
显然 : b1 a 2 a 3 , b 2 a 3 a1 , b 3 a1 a 2 ,
b1 2 2 3 a1 a 2 a3 a3 a1 b2 2 a1 a 2 a3 a1 a 2 b3 2 a1 a 2 a3
G G ( k ) 0 2
k
k
G 2
G
G 2
正方点阵布里渊区
第二到第九Brillouin区约化到第一布里渊区
布里渊区

布里渊区
主讲人: 主讲人:许本超 答疑人: 答疑人:李海龙 封福明
固体物理 固体物理
内容
• • • • • • • • • 1.倒易空间 2. 布里渊区基本概念 3. 典型格子的第一布里渊区 4.布里渊区的几何性质 5. 衍射条件在布里渊区诠释 6.布里渊区中的K点 7.布里渊区和能带的关系 8.布里渊区和费米面 9.MS计算能带实例图
14
固体物理 固体物理
7.2布里渊区和能带的关系
能带论的基本出发点: 能带论的基本出发点 固体中的电子可以在整个固体中运动 电子在运动过程中要受晶格原子势场的作用 由于周期场的微扰, 由于周期场的微扰,
E
E6
E(k)函数在布里渊区 函数在布里渊区
允许带
E5
边界k=± 边界 ±nπ/a处出现 处出现
3.2体心立方晶格的F.B.Z 体心立方晶格的F.B.Z 体心立方晶格的 体心立方晶格的倒格子为面心立方晶格
可以看出, 可以看出,面心立方倒 格子(即体心立方晶格) 格子(即体心立方晶格) 的F.B.Z为正菱形十二 为正菱形十二 面体(非正十二面体) 面体(非正十二面体)
8
固体物理 固体物理
3.3面心立方晶格的F.B.Z 面心立方晶格的 面心立方晶格的F.B.Z 面心立方晶格的倒格子为体心立方晶格
如右图所示, 如右图所示,黑框为体心立方 倒格子,取其体心(黄点) 倒格子,取其体心(黄点)作 为原点,红点(8个 为原点,红点(8个)为此原 点最相邻的倒格点,蓝点(6 点最相邻的倒格点,蓝点( 个)为此原点次相邻倒格点 可以看出, 可以看出,体心立方倒 格子(即面心立方晶格) 格子(即面心立方晶格) 的F.B.Z为截角的八面体 为截角的八面体 十四面体) (十四面体)
布里渊区gamma点的物理意义

布里渊区gamma点的物理意义
【原创版】
目录
1.布里渊区的定义与物理意义
2.布里渊区与倒格子的关系
3.γ点的定义及其在布里渊区中的作用
4.γ点在晶体电子态中的应用
5.总结
正文
布里渊区是固体物理学中的一个重要概念,它描述了晶体中电子状态的分布情况。
布里渊区可以用波矢 k 来描述,其中 kx、ky、kz 构成一个 k 空间(属于倒格子)。
晶体电子的所有状态对应的全部 k,都将均匀分布在倒格子的一个 W-S 原胞中,这个原胞就称为布里渊区。
布里渊区与倒格子有密切的关系。
倒格子是实际空间中晶格点的倒数空间,而布里渊区是描述电子状态的虚拟空间。
在波矢空间中,倒格子的体积就是第一布里渊区所围成的空间的体积。
也就是说,它们实际上是同一个空间,只是基矢不同而已。
在布里渊区中,γ点是一个重要的概念。
γ点是倒格子中的一个特殊点,它与晶体中的电子态有直接的关系。
γ点在布里渊区中的作用是描述电子态的能量和动量。
通过γ点,我们可以了解电子在晶体中的行为和性质。
γ点在晶体电子态中的应用非常广泛。
在晶体的能带理论中,各种电子态按照它们的波矢分类。
通过γ点,我们可以研究电子态的能量分布、电子态的相互作用以及电子态的激发等物理现象。
此外,γ点还可以用于分析晶体的光学性质、电学性质以及磁学性质等。
总之,布里渊区和γ点是固体物理学中非常重要的概念。
布里渊区的积分

(9)
(10)
I (E ) =
V
f (k )δ (E − ε(k ))dk =
i=1
pi Ii (E )
(11)
其中 Ii (E ) =
V
µi (x, y, z )δ (E − εl (x, y, z ))dxdydz
(12)
对于i=1,2,3,4,有µi (x,y,z)=1,x,y,z。 这样,I(E)变为四个独立的积分。接下来换元,令
计算体积分的一种办法是对面积分I(e)进行数值积分: J (E ) =
E −∞
I (e)de =
E Emin
I (e)de
(22)
但是我们更希望得到解析解。 首先对J(E)作变换: J (E ) =
tetra
f (k )θ (E − ε(k )) d3 k = Vtetra (E ) f occ
x = f (e, u, v )
y = g (e, u, v ) z = h(e, u, v )
(13)
3
4
ε1<e<ε2
ε2<e<ε3
4
ε3<e<ε4
4
e
e 1 3
1
e 3
1
3
2
2
2
Figure 2: 图2 得到εl (x,y,z)= εl (e,u,v)=e。于是 Ii (E ) =
对于三维体系由于二次曲面形式复杂除了态密度dos即ie中的被积函数恒等于1的计算能做到解析求解23以外目前最多只能做到半解析求解10即在某些维度上是解析的其它维度上是数值的因此积分的计算量稍大
布里渊区的积分
January 20, 2007
§5.5 布里渊区

§5.5 布里渊区本节我们举例说明二维和三维晶格的布里渊区。
一、二维正方格子正格子原胞基矢 a a a a == 2,1; 倒格子原胞基矢 ab a b π=π=22,21 。
如图5.10所示,倒格子空间离原点最近的倒格点有四个,相应的倒格矢为b b b b 2,2,1,1--, 它们的垂直平分线的坐标是 ak x π±= 及 a k y π±= 这些垂直平分线围成的区域就是简约布里渊区。
它也是一个正方形,其中一些特殊点和线有惯用的符号表示,中心:Γ; 边界线中心:X ; 角顶点:M; ΓX 线:∆; ΓM 线:∑。
离Γ点次近邻的四个倒格点相应的倒格矢是b b b b b b b b 21,21),2(1,21+--+-+它们的垂直平分线,同第一布里渊区边界围成的区域合起来成为第二布里渊区,这个区的各部分别平移一个倒格矢,可以同第一个区重合。
同理可得第三,第四,……,一系列布里渊区。
二、体心立方格子正基矢 )(21k j i a a ++-=, )(22a a +-= , )(23a a -+= 。
可证倒基矢 )(21k j ab +π= , )(22k i ab +π= , )(23i j ab +π= 。
(习题:证明bcc 的倒格子是fcc 。
)倒格矢:图5.10])21()31()32[(2332211k n n j n n i n n ab n b n b n G n +++++π=++= 离原点最近的有12个倒格点,其坐标可一般地写为)21,31,32(2n n n n n n a +++π. 具体写出是)0,1,1(2a π, )0,1,1(2aπ )0,1,1(2a π, )0,1,1(2aπ )1,0,1(2a π, )1,0,1(2aπ )1,0,1(2a π, )1,0,1(2aπ )1,1,0(2a π, )1,1,0(2aπ )1,1,0(2a π, )1,1,0(2aπ 相应的倒格矢长度为 π=22),,(321an n n G 这12个倒格矢的中垂线围成菱形正面体,称为简约布里渊区,如图5.11所示,其体积正好是倒格子原胞的大小。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§5.5 布里渊区
本节我们举例说明二维和三维晶格的布里渊区。
一、二维正方格子
正格子原胞基矢 a a a a == 2,
1; 倒格子原胞基矢 a
b a b π=π=22,21 。
如图5.10所示,倒格子空间离原点最近的倒格点
有四个,相应的倒格矢为
b b b b 2,
2,1,1--, 它们的垂直平分线的坐标是 a
k x π±= 及 a k y π±= 这些垂直平分线围成的区域就是简约布里渊区。
它也是一个正方形,其中一些特殊点和线有惯用的符号表示,
中心:Γ; 边界线中心:X ; 角顶点:M; ΓX 线:∆; ΓM 线:∑。
离Γ点次近邻的四个倒格点相应的倒格矢是
b b b b b b b b 21,21),2(1,21+--+-+
它们的垂直平分线,同第一布里渊区边界围成的区域合起来成为第二布里渊区,这个区的各部分别平移一个倒格矢,可以同第一个区重合。
同理可得第三,第四,……,一系列布里渊区。
二、体心立方格子
正基矢 )(2
1k j i a a ++-=, )(2
2a a +-= , )(2
3a a -+= 。
可证倒基矢 )(21k j a
b +π= , )(22k i a
b +π= , )(23i j a
b +π= 。
(习题:证明bc
c 的倒格子是fcc 。
)
倒格矢:
图
5.10
])21()31()32[(2332211k n n j n n i n n a
b n b n b n G n +++++π=++= 离原点最近的有12个倒格点,其坐标可一般地写为
)2
1,31,32(2n n n n n n a +++π. 具体写出是
)0,1,1(2a π, )0,1,1(2a
π )0,1,1(2a π, )0,1,1(2a
π )1,0,1(2a π, )1,0,1(2a
π )1,0,1(2a π, )1,0,1(2a
π )1,1,0(2a π, )1,1,0(2a
π )1,1,0(2a π, )1,1,0(2a
π 相应的倒格矢长度为 π=22),,(321a
n n n G 这12个倒格矢的中垂线围成菱形正面体,称为简约布里渊区,如图5.11所示,其体积正好是倒格子原胞的大小。
简约区中的高对称点和线(如图5.11):
(点))0,0,0(2:a πΓ;)0,0,1(2:a H π;)21,21,21(2:a P π;)0,2
1,21(2:a N π; (线))10(),0,0,(2:<δ<δπ∆a
,
图5.11
)2
10(),0,,(2:<σ<σσπ∑a , )210(),,,(2:
<λ<λλλπΛa 。
三、面心立方格子
正基矢 )(21k j a a += ;)(22k i a a += ;)(2
3j i a a += , 倒基矢 )(21a b ++-=
π ;)(22a b +-=π ;)(23a b -+=π , 倒格矢 ])321()321()321[(2332211k n n n j n n n i n n n a
b n b n b n G n -+++-+++-π=++=其倒格子是bc
c ,配为数为8,离原点最近的8个倒格点的坐标是:
)1,1,1(2a π,)1,1,1(2a
π, )1,1,1(2a π,)1,1,1(2a
π, )1,1,1(2a π,)1,1,1(2a
π, )1,1,1(2a π,)1,1,1(2a
π, 他们的中垂面围成一个正八面体,其体积比倒格子原胞的体积大,为构造简约布里渊区,需再考虑6个次近邻倒格点;
)0,0,2(2±πa ,)0,2,0(2±πa ,)2,0,0(2±πa
, 他们相应的倒格矢的中垂面截去八面体的六个顶角,形成截角八面体(truncated octahedron ),它是一个十四面体,这个十四面体的体积正好等于原胞体积,称为fcc 的第一布里渊区,如图5.12所示。
布里渊区中一些对称点和线的惯用符号(如图5.12):
(点))0,0,0(2:a πΓ;)0,0,1(2:a X π;)0,43,43(2:a K π;)2
1,21,21(2:a L π;
图5.12
(线))10(),0,0,(2:<δ<δπ∆a
, )2
10(),0,,(2:<σ<σσπ∑a , )210(),,,(2:
<λ<λλλπΛa 。
四、高布里渊区
图5.13示出了bcc 和fcc 晶格第一,第二,第三布里渊区的形状。
图5.13。
