布里渊区图示
合集下载
布里渊区1

—— 简单立方格子 —— 第一布里渊区
2) 体心立方格子 —— 正格子基矢 —— 倒格子基矢
第一布里渊区 —— 边长
的面心立方格子
—— 第一布里渊区 原点和12个近邻格点连线的垂直平分面围成的正十二面体
—— 体心立方格子第一布里渊区各点的标记
3) 面心立方格子 —— 正格子基矢 —— 倒格子基矢
布里渊区和能带 —— 在k空间把原点和所 每个区域内 E ~ k 是连续变化的
而在这些区域的边界上能量E(k)发生突变 这些区域称为布里渊区
—— 布里渊区
简单立方晶格k空间的二维示意图
—— 属于同一个布里渊区的能级构成一个能带 —— 不同的布里渊区对应不同的能带 —— 每一个布里渊区的体积相同___倒格子原胞的体积 —— 每个能带的量子态数目 _____ 2N (计入自旋)
第一布里渊区 —— 边长
的体心立方格子
—— 第一布里渊区为原点和8个近邻格点连线的垂直平分 面围成的正八面体,和沿立方轴的6个次近邻格点连 线的垂直平分面割去八面体的六个角, 形成的14面体
面心立方格子 —— 第一布里渊区 —— 八个面是正六边形 —— 六个面是正四边形
布里渊区图示
a 3 正格子原胞基矢 a1 ai, a2 i aj 2 2 取单位矢量k垂直于i, j 则,a1,a2和k构成的体积 3 2 a 2
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
倒格子原胞的基矢为 2 (a2 k ) 2 2 b1 i j a 3a 2 (k a1 ) 4 b2 j 3a
的垂直平分线和第一 布里渊区边界所围成 —— 第二布里渊区大小
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
第三布里渊区
由4个倒格点
的垂直平分线和第二布 里渊区边界边界所围成 第三布里渊区大小
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
第一、第二和第三布里渊区
§3-4 三维晶格的振动 ——
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
选一个倒格点为原点,原点的最近邻倒格矢有6个,分别是
b1 , b2 , (b1 b2 )
§3-4 三维晶格的振动 —— 晶格振动与晶体的热学性质
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
晶格振动与晶体的热学性质
正方格子其它布里渊区的形成
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
正方格子其它布里渊 和第一布里渊 区重合
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
二维斜格子的第一布里渊区
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
二维斜格子其它布里渊区的形成
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
二维斜格子其它布里渊区的形状
布里渊区

可以展开为傅立叶级数
2
2
f (x) f0 p1 Cp cos( a
px)
p 1
S p sin( a
px)
(2.4.6)
其中 p 是整数, f0 ,Cp , S p 是傅立叶系数。
这个展开式可以写成更简洁的形式
2
f (x)
p
f p exp(i a
px)
(2.4.7)
系数 f p 由 f0 , Cp , S p 给出。
倒格子的原胞基矢为
b1
2
a
i
b2
2
a
j
离原点最近的的倒格点有四个:
b1 , -b1 , b2 , - b2 它们的垂直平分线围成的区域 就是简约布里渊区,即第一布里渊 区.显然,第一布里渊区是一个正 方形,面积为 S*=(2π)2/a2 .
二维方格子布里渊区
可以看出,倒格子点阵也是正方点阵,点阵常数为 2
a
正八面体的体积是 9 (2 )3
2a
比倒格子的原胞体积大 1 (2 )3
2a
可见这个八面体不是第一布里渊区。
必须再考虑次紧邻的六个倒格点,倒格矢为:2 (2i )
a
2 ( j )
a
2 (k )
a
它们的中垂面截去了正八面体的 6 个顶角,形成一个截角八面体,
它有八个正六边形和六个正方形,即十四面体。而截去的体积恰好是
2
a
i
b2
2
a
j
2
b3 a k
所以,倒格子也是简立方结构,其第一布里渊区仍然是一个简立方。
(4)体心立方结构晶体点阵的布里渊区 对于体心立方结构晶体点阵,如果正格子基矢取为:
布里渊区图示

的垂直平分线和第一 布里渊区边界所围成 —— 第二布里渊区大小
§3-4 三维晶格的振动 —— 晶格振动与晶体的热学性质
第三布里渊区 由4个倒格点
的垂直平分线和第二布 里渊区边界边界所围成 第三布里渊区大小
§3-4 三维晶格的振动 —— 晶格振动与晶体的热学性质
第一、第二和第三布里渊区
§3-4 三维晶格的振动 —— 晶格振动与晶体的热学性质
正格子原胞基矢
a1
ai, a2
a 2
i
3 aj 2取单位矢 Nhomakorabeak垂直于i, j
则,a1,a2和k构成的体积
3 a2 2
§3-4 三维晶格的振动 —— 晶格振动与晶体的热学性质
倒格子原胞的基矢为
b1
2
(a2
k)
2
a
i
2
3a
j
b2
2
(k
a1 )
4
3a
j
§3-4 三维晶格的振动 —— 晶格振动与晶体的热学性质
二维斜格子其它布里渊区的形成
§3-4 三维晶格的振动 —— 晶格振动与晶体的热学性质
二维斜格子其它布里渊区的形状
—— 每个布里 渊区经过适当 的平移之后和 第一布里渊区 重合
§3-4 三维晶格的振动 —— 晶格振动与晶体的热学性质
平面正三角形,相邻原子间距为a,求正格矢和倒格矢,画 出第一和第二布里渊区
选一个倒格点为原点,原点的最近邻倒格矢有6个,分别是
b1, b2 , (b1 b2 )
§3-4 三维晶格的振动 —— 晶格振动与晶体的热学性质
§3-4 三维晶格的振动 —— 晶格振动与晶体的热学性质
§3-4 三维晶格的振动 —— 晶格振动与晶体的热学性质
第三布里渊区 由4个倒格点
的垂直平分线和第二布 里渊区边界边界所围成 第三布里渊区大小
§3-4 三维晶格的振动 —— 晶格振动与晶体的热学性质
第一、第二和第三布里渊区
§3-4 三维晶格的振动 —— 晶格振动与晶体的热学性质
正格子原胞基矢
a1
ai, a2
a 2
i
3 aj 2取单位矢 Nhomakorabeak垂直于i, j
则,a1,a2和k构成的体积
3 a2 2
§3-4 三维晶格的振动 —— 晶格振动与晶体的热学性质
倒格子原胞的基矢为
b1
2
(a2
k)
2
a
i
2
3a
j
b2
2
(k
a1 )
4
3a
j
§3-4 三维晶格的振动 —— 晶格振动与晶体的热学性质
二维斜格子其它布里渊区的形成
§3-4 三维晶格的振动 —— 晶格振动与晶体的热学性质
二维斜格子其它布里渊区的形状
—— 每个布里 渊区经过适当 的平移之后和 第一布里渊区 重合
§3-4 三维晶格的振动 —— 晶格振动与晶体的热学性质
平面正三角形,相邻原子间距为a,求正格矢和倒格矢,画 出第一和第二布里渊区
选一个倒格点为原点,原点的最近邻倒格矢有6个,分别是
b1, b2 , (b1 b2 )
§3-4 三维晶格的振动 —— 晶格振动与晶体的热学性质
§3-4 三维晶格的振动 —— 晶格振动与晶体的热学性质
lecture 7 布里渊区
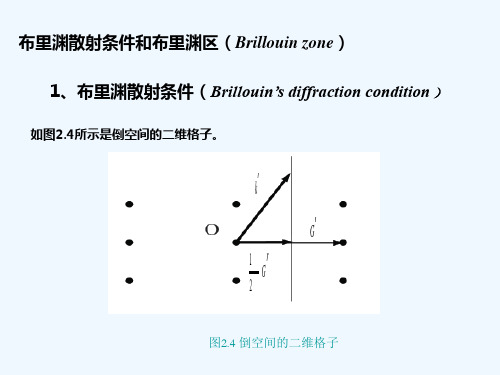
布里渊散射条件和布里渊区(Brillouin zone) 1、布里渊散射条件(Brillouin’s diffraction condition )
如图2.4所示是倒空间的二维格子。
k
G
1 G 2
图2.4 倒空间的二维格子
O 点是到空间的原点,考虑连接原点和任意一个倒格点的倒格 矢。作垂直平分线(三维情形将是垂直平分面),如果入射波 矢满足(2.3.2)式,将(2.3.2)式两边同除以4,散射条件 则可写成
Homework
1. 考虑一个ABAB…AB原子线,A-B键长为 a 2 A,B原子的散射因子分别为
,
f A 和 fB
入射X射线垂直于原子线。 (1) 给出θ方向(θ是衍射光束与原子线之间的夹角)衍射加 强条件; (2)计算衍射强度; (3)讨论 fA fB 情况。
A B A B
a/2
通过这四个矢量的中点
1 b i, 1 2 a
1 b2 j 2 a
分别作四个垂直平分面,就形成了第一布里渊区的边界。 再作离原点次近邻的倒格点的倒格矢分别为
b ( h 1 , h 1 ) ,( b h 1 , h 1 ) 1 1 2 2 1 2
a a i j k) 1 ( 2
原胞体积为
a a i j k) 2 ( 2
a a (i j k) 3 2
3 a ( a a ) a / 2 1 2 3
则三个倒格子基矢为:
2 2 b ( a a ) ( j k ) 1 2 3 a
3 a ( a a ) a / 4 1 2 3
倒格子原胞基矢为:
2 2 b ( aa ) ( i j k ) 1 2 3 a
如图2.4所示是倒空间的二维格子。
k
G
1 G 2
图2.4 倒空间的二维格子
O 点是到空间的原点,考虑连接原点和任意一个倒格点的倒格 矢。作垂直平分线(三维情形将是垂直平分面),如果入射波 矢满足(2.3.2)式,将(2.3.2)式两边同除以4,散射条件 则可写成
Homework
1. 考虑一个ABAB…AB原子线,A-B键长为 a 2 A,B原子的散射因子分别为
,
f A 和 fB
入射X射线垂直于原子线。 (1) 给出θ方向(θ是衍射光束与原子线之间的夹角)衍射加 强条件; (2)计算衍射强度; (3)讨论 fA fB 情况。
A B A B
a/2
通过这四个矢量的中点
1 b i, 1 2 a
1 b2 j 2 a
分别作四个垂直平分面,就形成了第一布里渊区的边界。 再作离原点次近邻的倒格点的倒格矢分别为
b ( h 1 , h 1 ) ,( b h 1 , h 1 ) 1 1 2 2 1 2
a a i j k) 1 ( 2
原胞体积为
a a i j k) 2 ( 2
a a (i j k) 3 2
3 a ( a a ) a / 2 1 2 3
则三个倒格子基矢为:
2 2 b ( a a ) ( j k ) 1 2 3 a
3 a ( a a ) a / 4 1 2 3
倒格子原胞基矢为:
2 2 b ( aa ) ( i j k ) 1 2 3 a
布里渊区图示

a 3 正格子原胞基矢 a1 = ai, a2 = i + aj 2 2 取单位矢量k垂直于i, j 则,a1,a2和k构成的体积 3 2 Ω= a 2
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
倒格子原胞的基矢为 2π (a2 × k ) 2π 2π b1 = i− j = Ω a 3a 2π (k × a1 ) 4π b2 = = j Ω 3a
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
正方格子其它布里渊区的形成
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
正方格子其它布里渊区的形状
—— 每个布 里渊区经过适 当的平移之后 和第一布里渊 区重合
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
二维斜格子的第一布里渊区
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
二维斜格子其它布里渊区的形成
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
二维斜格子其它布里渊区的形状
—— 每个布里 渊区经过适当 的平移之后和 第一布里渊区 重合
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
平面正三角形,相邻原子间距为 求正格矢和倒格矢 求正格矢和倒格矢, 平面正三角形,相邻原子间距为a,求正格矢和倒格矢,画 出第一和第二布里渊区
的垂直平分线和第一 布里渊区边界所围成 —— 第二布里渊区大小
§3-4 三维晶格的振动 ——
晶格振动与晶体的热学性质
第三布里渊区 由4个倒格点 个倒格点
的垂直平分线和第二布 里渊区边界边界所围成 第三布里渊区大小
§3-4 三维晶格的振动 ——
lecture 7 布里渊区.ppt

Homework
1.
考虑一个ABAB…AB原子线,A-B键长为
a 2
A,B原子的散射因子分别为 f A 和 f B
,入射X射线垂直于原子线。
(1) 给出θ方向(θ是衍射光束与原子线之间的夹角)衍射加
强条件;
(2)计算衍射强度;
(3)讨论
f A f B 情况。
A
B
A
B
a/2
a/2
2. 用波长为λ 的X射线,照射晶格常数为a 的金刚石结构晶体, 问要得到衍射面指数为(220)的衍射斑点,对应的布拉格 角应是多少?
如图2.7所示是一个十二面体。
第一布里渊区种典型 对称点的坐标为:
: 2 (0, 0, 0)
a
H : 2 (1, 0, 0)
a
N : 2 (1 , 1 , 0)
a 22
P : 2 (1 , 1 , 1)
a 222
图2.7 体心立方正格子的第一布里渊区
(5)面心立方结构晶体点阵的布里渊区 取面心立方的原胞基矢为:
布里渊散射条件和布里渊区(Brillouin zone)
1、布里渊散射条件(Brillouin’s diffraction condition )
如图2.4所示是倒空间的二维格子。
r k
r G
1
r G
2ቤተ መጻሕፍቲ ባይዱ
图2.4 倒空间的二维格子
O 点是到空间的原点,考虑连接原点和任意一个倒格点的倒格 矢。作垂直平分线(三维情形将是垂直平分面),如果入射波 矢满足(2.3.2)式,将(2.3.2)式两边同除以4,散射条件 则可写成
对于三维简立方结构晶格点阵来说,其正格子基矢为
r a1
r ai
30 布里渊区的知识

������
*简谐近似是晶格动力学处理许多物理问题的出发点!
* 对热膨胀和热传导等问题必须考虑高阶项 --- 特别是3次和4次项的作用 → 这称为非谐项或非谐作用 – V非谐 * 具体处理问题时,把非谐项看成是对起主要作用 的简谐项的微扰!
简正振动模式:在简谐近似下, 由N个原子构成的晶体的晶格振 动, 可变为3N个独立的谐振子的振动. 每个谐振子的振动模式称 为简正振动模式 简正振动模式对应着所有的原子都以该模式的频率做振动, 它是 晶格振动模式中最简单最基本的振动方式. 原子的振动 —格波振动通常是这3N个简正振动模式的线形迭加.
2
a
i
倒格矢的垂直平分面 构成第一布里渊区
a
O
一维晶格点阵
b
-π/a
O
倒格子点阵
π/a
二维晶格点阵的布里渊区 取正格子基矢为 a1 ai 和a2 a j 可求出倒格子基矢为
2 2 b1 i 和b2 j a a
作原点0至其它倒格点连线的中垂线,它们将二维倒 格子平面分割成许多区域
第三章 晶格动力学和 晶体的热学性质
固体的许多性质都可以基于静态模型来理解(即晶体点阵模型), 即认为构成固体的原子在空间做严格的周期性排列,在该框架内, 我们讨论了X 光衍射发生的条件,求出了晶体的结合能,以后还将 在此框架内,建立能带论,计算金属大量的平衡性质。然而它只 是实际原(离)子构形的一种近似,因为原子或离子是不可能严 格的固定在其平衡位置上的,而是在固体温度所控制的能量范围 内在平衡位置附近做微振动。只有深入地了解了晶格振动的规律, 更多的晶体性质才能得到理解。如:固体热容,热膨胀,热传导, 融化,声的传播,电导率,压电现象,某些光学和介电性质,位 移性相变,超导现象,晶体和辐射波的相互作用等等。
*简谐近似是晶格动力学处理许多物理问题的出发点!
* 对热膨胀和热传导等问题必须考虑高阶项 --- 特别是3次和4次项的作用 → 这称为非谐项或非谐作用 – V非谐 * 具体处理问题时,把非谐项看成是对起主要作用 的简谐项的微扰!
简正振动模式:在简谐近似下, 由N个原子构成的晶体的晶格振 动, 可变为3N个独立的谐振子的振动. 每个谐振子的振动模式称 为简正振动模式 简正振动模式对应着所有的原子都以该模式的频率做振动, 它是 晶格振动模式中最简单最基本的振动方式. 原子的振动 —格波振动通常是这3N个简正振动模式的线形迭加.
2
a
i
倒格矢的垂直平分面 构成第一布里渊区
a
O
一维晶格点阵
b
-π/a
O
倒格子点阵
π/a
二维晶格点阵的布里渊区 取正格子基矢为 a1 ai 和a2 a j 可求出倒格子基矢为
2 2 b1 i 和b2 j a a
作原点0至其它倒格点连线的中垂线,它们将二维倒 格子平面分割成许多区域
第三章 晶格动力学和 晶体的热学性质
固体的许多性质都可以基于静态模型来理解(即晶体点阵模型), 即认为构成固体的原子在空间做严格的周期性排列,在该框架内, 我们讨论了X 光衍射发生的条件,求出了晶体的结合能,以后还将 在此框架内,建立能带论,计算金属大量的平衡性质。然而它只 是实际原(离)子构形的一种近似,因为原子或离子是不可能严 格的固定在其平衡位置上的,而是在固体温度所控制的能量范围 内在平衡位置附近做微振动。只有深入地了解了晶格振动的规律, 更多的晶体性质才能得到理解。如:固体热容,热膨胀,热传导, 融化,声的传播,电导率,压电现象,某些光学和介电性质,位 移性相变,超导现象,晶体和辐射波的相互作用等等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
重合
平面正三角形,相邻原子间距为a,求正格矢和倒格矢,画 出第一和第二布里渊区
正格子原胞基矢
a1
ai, a2
a 2
i
3 aj 2
取单位矢量k垂直于i, j
ቤተ መጻሕፍቲ ባይዱ
则,a1,a2和k构成的体积
3 a2 2
倒格子原胞的基矢为
b1
2 (a2 k)
2
a
i
2
3a
j
b2
2
(k
a1 )
4
3a
j
选一个倒格点为原点,原点的最近邻倒格矢有6个,分别是
b1, b2 , (b1 b2 )
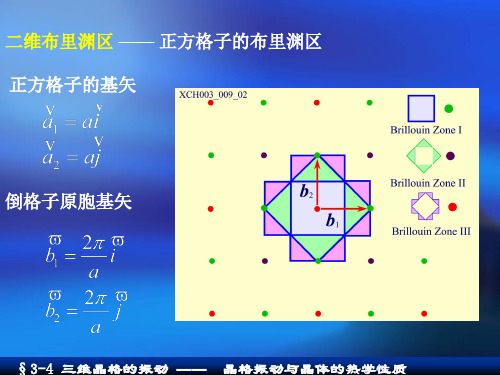
二维布里渊区 —— 正方格子的布里渊区 正方格子的基矢
倒格子原胞基矢
第一布里渊区 倒格子空间离原点最近的四个倒格点 垂直平分线方程
—— 第一布里渊区 大小
第二布里渊区 由4个倒格点
的垂直平分线和第一 布里渊区边界所围成 —— 第二布里渊区大小
第三布里渊区 由4个倒格点
的垂直平分线和第二布 里渊区边界边界所围成
第三布里渊区大小
第一、第二和第三布里渊区
正方格子其它布里渊区的形成
正方格子其它布里渊区的形状
—— 每个布 里渊区经过适 当的平移之后 和第一布里渊
区重合
二维斜格子的第一布里渊区
二维斜格子其它布里渊区的形成
二维斜格子其它布里渊区的形状
—— 每个布里 渊区经过适当 的平移之后和 第一布里渊区
平面正三角形,相邻原子间距为a,求正格矢和倒格矢,画 出第一和第二布里渊区
正格子原胞基矢
a1
ai, a2
a 2
i
3 aj 2
取单位矢量k垂直于i, j
ቤተ መጻሕፍቲ ባይዱ
则,a1,a2和k构成的体积
3 a2 2
倒格子原胞的基矢为
b1
2 (a2 k)
2
a
i
2
3a
j
b2
2
(k
a1 )
4
3a
j
选一个倒格点为原点,原点的最近邻倒格矢有6个,分别是
b1, b2 , (b1 b2 )
二维布里渊区 —— 正方格子的布里渊区 正方格子的基矢
倒格子原胞基矢
第一布里渊区 倒格子空间离原点最近的四个倒格点 垂直平分线方程
—— 第一布里渊区 大小
第二布里渊区 由4个倒格点
的垂直平分线和第一 布里渊区边界所围成 —— 第二布里渊区大小
第三布里渊区 由4个倒格点
的垂直平分线和第二布 里渊区边界边界所围成
第三布里渊区大小
第一、第二和第三布里渊区
正方格子其它布里渊区的形成
正方格子其它布里渊区的形状
—— 每个布 里渊区经过适 当的平移之后 和第一布里渊
区重合
二维斜格子的第一布里渊区
二维斜格子其它布里渊区的形成
二维斜格子其它布里渊区的形状
—— 每个布里 渊区经过适当 的平移之后和 第一布里渊区
