布里渊区
布里渊区通俗理解

布里渊区通俗理解-概述说明以及解释1.引言1.1 概述布里渊区是一个在物理和数学领域中具有重要意义的概念,它主要用来描述在给定条件下某一物体或物体集合的邻域。
布里渊区的概念源于法国物理学家亚历山大·布里渊的研究成果,他发现了一种描述物体在空间中的局部特性的方法。
布里渊区的概念不仅在物理学领域中被广泛应用,同时也在计算机图形学、材料科学、生物学等领域中具有重要作用。
在本文中,我们将深入探讨布里渊区的概念、应用以及重要性,希望能够对读者有所启发和帮助。
通过了解布里渊区的相关知识,我们可以更好地理解物体在空间中的局部结构和特性,为我们探索和应用这些知识提供了理论基础。
在日常生活中,布里渊区的概念也有着重要的意义,可以帮助我们更好地理解世界的复杂性,促进科学技术的发展和创新。
展望未来,布里渊区的研究和应用将会不断深化和拓展,为人类社会的进步和发展做出更大的贡献。
1.2 文章结构本文将分为三个主要部分来讨论布里渊区的通俗理解。
在引言部分,我们将简要介绍布里渊区的概念、文章结构和撰写本文的目的。
在正文部分,我们将详细探讨布里渊区的概念,其在实际应用中的情况以及在各领域中的重要性。
最后,在结论部分,我们将总结布里渊区的作用,讨论其在日常生活中的意义,并展望未来布里渊区的发展方向。
通过这样的结构安排,读者可以系统地了解布里渊区的相关知识,并深入理解其在现实生活中的应用和意义。
1.3 目的2.正文2.1 布里渊区的概念布里渊区(英文名为Boulevard区)是一种在计算机科学领域中常用的概念,用于描述一种数据结构的布局方式。
布里渊区是指内存中的一段连续地址空间,通常用来存储程序代码、全局变量和静态变量。
在操作系统中,布里渊区还可以用于存放动态链接库和共享库的代码段和数据段。
布里渊区的特点是具有一定的大小和位置,可以在运行时被操作系统动态地分配和回收。
布里渊区的概念主要用于优化内存管理和提高程序的执行效率。
布里渊区

2
a
i
b2
2
a
j
2
b3 a k
所以,倒格子也是简立方结构,其第一布里渊区仍然是一个简立方。
(4)体心立方结构晶体点阵的布里渊区 对于体心立方结构晶体点阵,如果正格子基矢取为:
a1
a 2
(i
j
k)
a2
a 2
(i
j
k)
a a3 2 (i j k )
原胞体积为 a1 (a2 a3 ) a3 / 2
b1(h1 1, h2 1), b2(h1 1, h2 1)
通过这四个倒个是的中点,即
1 2
b1
1 2
b2
a
i
a
j
分别作四个垂直平分面,即可得到第二布里渊区的边界。
照此可以画出第二布区、第三布区等。如右图所示。 可以看出,布区的序号越大,分离的区域越多;但不论分离的区域数
目是多少,各布区的面积是相等的。
The first Brillouin zone is the Wigner-Seitz primitive cell in the reciprocal lattice.
§2.4 原子的形状因子和结构因子 (atomic form factor and structure factor )
一、散射波振幅(Diffraction amplitude)
可以展开为傅立叶级数
2
2
f (x) f0 p1 Cp cos( a
px)
p 1
S p sin( a
px)
(2.4.6)
其中 p 是整数, f0 ,Cp , S p 是傅立叶系数。
这个展开式可以写成更简洁的形式
2
2013固体物理-2.3_布里渊区
2k ⋅G = G2
D
GD
k1
k
⋅
1
G
=
1
G
2
2 2
k2 O G/2 GC C
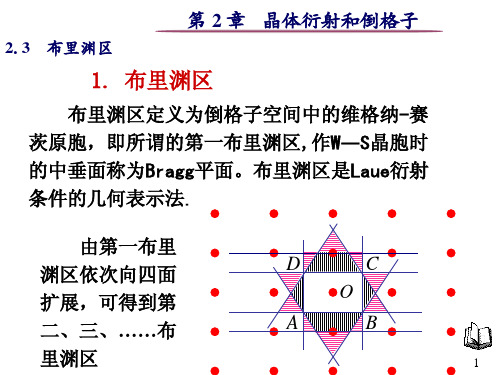
任何从原点到 G 的垂直平分面的矢量都满足衍射 条件,这些平面正是布里渊区的边界。布里渊区包含
了所有能在晶体上发生布拉格反射的波的波矢 k
3
2.3 布里渊区
第 2 章 晶体衍射和倒格子
2.3. 1 简单立方晶格的倒格子
8
2.3 布里渊区
第 2 章 晶体衍射和倒格子
最短的倒格矢是以下8个矢量
2π (±i ± j ± k) a
上述8个矢量的垂直平 分面围成一个正八面体, 另外由以下6个倒格矢
2π (±2i); 2π (±2 j ); 2π (±2k)
a
a
a
的垂直平分面切割这个八面体的6个角,得 到的截角八面体或十四面体即为第一布里 渊区
K : 2π ( 3 , 3 ,0) a 44
其中 0 < δ < 1, 0 < λ < 1 , 0 < σ < 3
2
4
10
a
a
a
第一布里渊区由上述12个矢量的
垂直平分面围成,是一个正十二面体
6
2.3 布里渊区
第 2 章 晶体衍射和倒格子
体心立方晶格的布里渊区中一些
具有较高对称性的点或轴的坐标
Γ : 2π (0,0,0) a
∆ : 2π (δ ,0,0)
a
Λ : 2π (λ,λ,λ)
a
Σ : 2π (σ ,σ ,0)
a
2.3 布里渊区
第 2 章 晶体衍射和倒格子
§5.5 布里渊区

§5.5 布里渊区本节我们举例说明二维和三维晶格的布里渊区。
一、二维正方格子正格子原胞基矢 a a a a == 2,1; 倒格子原胞基矢 ab a b π=π=22,21 。
如图5.10所示,倒格子空间离原点最近的倒格点有四个,相应的倒格矢为b b b b 2,2,1,1--, 它们的垂直平分线的坐标是 ak x π±= 及 a k y π±= 这些垂直平分线围成的区域就是简约布里渊区。
它也是一个正方形,其中一些特殊点和线有惯用的符号表示,中心:Γ; 边界线中心:X ; 角顶点:M; ΓX 线:∆; ΓM 线:∑。
离Γ点次近邻的四个倒格点相应的倒格矢是b b b b b b b b 21,21),2(1,21+--+-+它们的垂直平分线,同第一布里渊区边界围成的区域合起来成为第二布里渊区,这个区的各部分别平移一个倒格矢,可以同第一个区重合。
同理可得第三,第四,……,一系列布里渊区。
二、体心立方格子正基矢 )(21k j i a a ++-=, )(22a a +-= , )(23a a -+= 。
可证倒基矢 )(21k j ab +π= , )(22k i ab +π= , )(23i j ab +π= 。
(习题:证明bcc 的倒格子是fcc 。
)倒格矢:图5.10])21()31()32[(2332211k n n j n n i n n ab n b n b n G n +++++π=++= 离原点最近的有12个倒格点,其坐标可一般地写为)21,31,32(2n n n n n n a +++π. 具体写出是)0,1,1(2a π, )0,1,1(2aπ )0,1,1(2a π, )0,1,1(2aπ )1,0,1(2a π, )1,0,1(2aπ )1,0,1(2a π, )1,0,1(2aπ )1,1,0(2a π, )1,1,0(2aπ )1,1,0(2a π, )1,1,0(2aπ 相应的倒格矢长度为 π=22),,(321an n n G 这12个倒格矢的中垂线围成菱形正面体,称为简约布里渊区,如图5.11所示,其体积正好是倒格子原胞的大小。
布里渊区

倒格矢的垂直平分面,倒易空间被这些平面分成许多包围原
点的多面体区域,这些区域称作布里渊区,其中最靠近原点
的平面所围成的区域称作第一布里渊区,第一布里渊区界面
与次远垂直平分面所围成的区域称作第二布里渊区,依次类
பைடு நூலகம்
推得到二维正方格子的布里渊区图见下页。
对一种晶体来说,它的所有布里渊区都有同
样大小的体积,利用平移对称性可以找出第一布 里渊区和所有较高的布里渊区之间的全等性。
见黄昆书图4-13 (p179)
倒易点阵和14种晶体点阵是一一对应的,因 此也只有14种类型的倒易点阵和14种不同形状的 第一布里渊区。第一布里渊区的形状只与晶体的 布拉维点阵的几何性质有关,与晶体的化学成分、 晶胞中的原子数目无关。
布里渊区是一个对称性原胞,它保留了相应
的布拉菲点阵的点群对称性。因此第一布里渊区 里依然可以划分为几个完全等同的区域。
由于布里渊区界面是某倒格矢
r
ur G
的垂直平分面,如果
用 k 表示从原点出发、端点落在布里渊区界面上的倒易空
间矢量,它必然满足方程:
k G
1
G2
2
该方程称作布里渊区的界面方程
正方点阵布里渊区
第二到第九Brillouin区约化到第一布里渊区
各布里渊区的形状,不管被分成多少部分,对原点都是对称的
六方点阵布里渊区图
见黄昆书图4-24 (p194)
Kittel (p28) 黄昆书图4-12(p179)
见黄昆书图4-12 (p179)
体心立方的Wigner-Seitz原胞及第一布里渊区
面心立方的Wigner-Seitz原胞及第一布里渊区
固体物理学:布里渊区(brillouin zone )

2π i j k a
已知体心立方正格基矢:
a1
a
a 2 a
2
i
i
j
jk k
a3
2 a
2
i
jk
可见,面心立方的倒格子是体心立方。
同上例,先写出 倒格矢,再写出 离原点最近的倒 格点坐标,最后 做中垂面。
可以得到面心立方 的布里渊区。如图 所示,为截角8面 体或叫14面体。
a
3
2 a
2
i
j
可见,体心立方的倒格子是面心立方。离原 点最近邻的有12个倒格点,它们分别位于:
2 (1,1,0); 2 (1,1,0); 2 (1,1,0); 2 (1,1,0);
a
a
a
a
2 (1,0,1); 2 (1,0,1); 2 (1,0,1); 2 (1,0,1);
a
a
a
a
2 (0,1,1); 2 (0,1,1); 2 (0,1,1); 2 (0,1,1)
高序号布里渊区的各个分散的碎片平 移一个或几个倒格矢进入简约布里渊区, 形成布里渊区的简约区图。
二维正方晶格的十个布里渊区
第一区 第二区 第三区 第四区 第五区 第六区 第七区 第八区 第九区 第十区
例1: 简单立方格子
解:
正格子基矢:
倒格子基矢:
简单立方格子的第一布里渊区:原点和6个近 邻格点的垂直平分面围成的立方体。
布里渊区(brillouin zone ) (1)布里渊区的定义
在k空间(倒格子空间)中,以任意一个倒 格点为原点,做原点和其它所有倒格点连线(倒 格矢)的中垂面(或中垂线),这些中垂面(或中 垂线)将倒格子空间分割成许多区域,每个区域 内 E ~ k 是连续变化的, 而在这些区域的边界上 能量E(k)发生突变, 这些区域称为布里渊区。
布里渊区的名词解释

布里渊区的名词解释布里渊区是指在光学和无线电工程中,光纤或导波管中因材料非线性而产生的相位调制现象。
这个现象是由于不同频率的光波在光纤中传播时,会发生频率的混合与干涉,导致光波的相位发生变化。
在布里渊区内,光纤中的光波与光纤内部的声波相互作用产生布里渊散射。
布里渊散射是指当光纤中的光波与声波相互作用时,部分光能被散射出去。
这种散射现象是由光波与光纤中声波的相互作用引起的。
光纤中的声波可以由光波引导产生。
当光波在光纤中传播时,由于光纤材料的非线性特性,光波的电场强度会随着光纤中的声波的存在而发生变化。
这种变化会导致光波的相位发生调制。
在布里渊区内,声波的频率与光波的频率非常接近,使得声波与光波发生有效的相互作用。
布里渊区的大小取决于光纤的参数以及传输信号的频率。
对于光纤通信系统来说,布里渊区的存在会对信号的传输产生一定的影响。
当信号频率位于布里渊区时,光纤中的声波与光波的相互作用会导致信号的相位失真和功率损耗。
因此,在设计和实施光纤通信系统时,需要考虑布里渊散射对信号传输的影响,并采取相应的措施来减小布里渊区对信号质量的影响。
布里渊区的现象不仅存在于光纤中,还可以在其他一些导波管(如微纳米波导)中观察到。
这些导波管中的布里渊散射现象也会对波导中传输的信号产生影响。
除了在通信领域中的应用,布里渊区的现象还在光纤传感、光子晶体等领域有着广泛的应用。
通过利用布里渊区的特性,可以设计出基于布里渊散射的传感器,用于测量温度、压力等物理量。
此外,在光子晶体中,布里渊散射也起着重要的作用,可以用于控制和调制光子的传输和储存。
总的来说,布里渊区是光纤或导波管中由于材料非线性而产生的相位调制现象。
它在光纤通信、光纤传感和光子晶体等领域都有着重要的应用。
在光纤通信领域,布里渊散射的存在对信号的传输质量产生一定的影响,因此需要在系统设计中考虑并采取相应的措施来减小布里渊区对信号的影响。
布里渊区

jk
,
b2
2
a
k+i
,
b3
2
a
i j
K n n1b1 n2b2 n3b3
2 a
n2 n3 i n1 n3 j n1 n2 k
20
4
a
b1
b2
b3
21
3.离原点最近的倒格点 体心立方的倒格子是面心立方,离原点最近的倒格点有十二个。在直角坐标系中的坐标分别为:
11
6.二维正方格子的能带交叠 第一布里渊区在k方向上能量最高点A,k'方向上能量最高点C。 C点的能量比第二布里渊区B点高。
12
二维(包括三维)和一维情形有一个重要的区别—不同能带在能量上不一定 分隔开而可以发生能带之间的交叠。第一布里渊区和第二布里渊区能带 的重叠。
13
7.二维斜格子的第一布里渊区
第一布里渊区—倒格子空间中的WS原胞。
1
2.布里渊区的特点 (1)各布里渊区的体积相等,都等于倒格子原胞的体积。
=b1 b2 b3
2 3
(2)波矢k的代表点是均匀分布的,每个代表点的体积为:
1 N1
b1
2 N2
b2
3 N3
b3
14
8.二维六角格子其它布里渊区的形成
15
9.二维六角格子其它布里渊区的形状 每个布里渊区经过适当的 平移之后和第一布里渊区 重合
16
10.二维格子布里渊区的特点 (1)尽管布里渊区在图中看起来好像被分割为不相连的若干小区, 但是,实际上能量 是连续的。属于一个布里渊区的能级构成一个能带。不同的布里渊区对应不同的 能带。 (2)每个布里渊区的形状尽管各异,但是面积都相等, 等于倒格子原胞的面积。 (3)计入自旋,每个能带包含2N个量子态。 (4)每个布里渊区经过适当的平移之后和第一布里渊区重合。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Kittel (p29),黄昆书图4-13(p179)
见黄昆书图4-13 (p179)
倒易点阵和14种晶体点阵是一一对应的,因 此也只有14种类型的倒易点阵和14种不同形状的 第一布里渊区。第一布里渊区的形状只与晶体的 布拉维点阵的几何性质有关,与晶体的化学成分、 晶胞中的原子数目无关。 布里渊区是一个对称性原胞,它保留了相应 的布拉菲点阵的点群对称性。因此第一布里渊区 里依然可以划分为几个完全等同的区域。 对一种晶体来说,它的所有布里渊区都有同 样大小的体积,利用平移对称性可以找出第一布 里渊区和所有较高的布里渊区之间的全等性。
第二到第九Brillouin区约化到第一布里渊区
各布里渊区的形状,不管被分成多少部分,对原点都是对称的
六方点阵布里渊区图
)
黄昆书图4-12(p179)
见黄昆书图4-12 (p179)
体心立方的Wigner-Seitz原胞及第一布里渊区
面心立方的Wigner-Seitz原胞及第一布里渊区
五. 布里渊区: 第一布里渊区的确定:取法和正点阵中Wigner-Seitz 原胞取法相同。它是倒易点阵的原胞。
Léon Brilliouin
(1889-1969)
布里渊区定义:在倒易点阵中,以某一格点为坐标原点,做所有 倒格矢的垂直平分面,倒易空间被这些平面分成许多包围原 点的多面体区域,这些区域称作布里渊区,其中最靠近原点 的平面所围成的区域称作第一布里渊区,第一布里渊区界面
与次远垂直平分面所围成的区域称作第二布里渊区,依次类
推得到二维正方格子的布里渊区图见下页。 由于布里渊区界面是某倒格矢 G 的垂直平分面,如果 用 k 表示从原点出发、端点落在布里渊区界面上的倒易空 间矢量,它必然满足方程:
1 2 k G G 2
该方程称作布里渊区的界面方程
正方点阵布里渊区
