八年级下册数学图形与坐标
湘教版八年级下册数学第3章 图形与坐标含答案(参考答案)
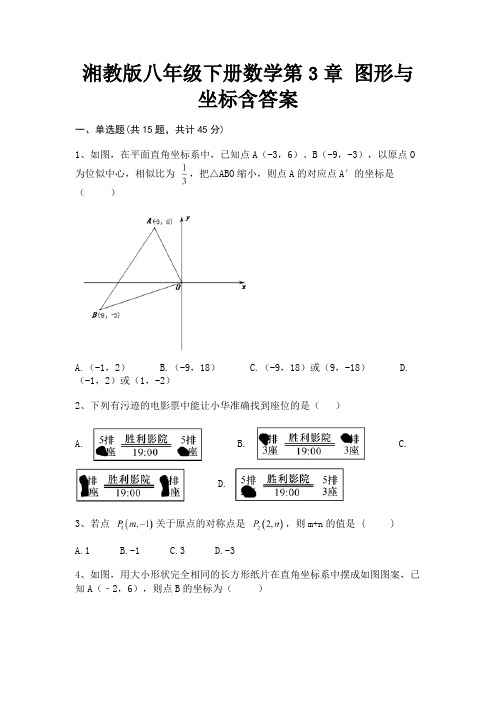
湘教版八年级下册数学第3章图形与坐标含答案一、单选题(共15题,共计45分)1、如图,在平面直角坐标系中,已知点A(-3,6)、B(-9,-3),以原点O 为位似中心,相似比为,把△ABO缩小,则点A的对应点A′的坐标是()A.(-1,2)B.(-9,18)C.(-9,18)或(9,-18)D.(-1,2)或(1,-2)2、下列有污迹的电影票中能让小华准确找到座位的是()A. B. C.D.3、若点关于原点的对称点是,则m+n的值是 ( )A.1B.-1C.3D.-34、如图,用大小形状完全相同的长方形纸片在直角坐标系中摆成如图图案,已知A(﹣2,6),则点B的坐标为()A.(﹣6,4)B.(,)C.(﹣6,5)D.(,4)5、在平面直角坐标系中,点P(-8,2012)在第( )象限.A.一B.二C.三D.四6、如图是一所学校的部分平面示意图,在同一平面直角坐标系中,若体育馆A 的坐标为,科技馆B的坐标为,则教学楼C的坐标为()A. B. C. D.7、如图,点在函数的图象上,且,过点作轴于点,则的周长为()A. B. C. D.8、如图,在平面直角坐标系中,平行四边形OABC的边OA在x轴的正半轴上,A,C两点的坐标分别为(2,0),(1,2),点B在第一象限,将直线沿y轴向上平移m个单位.若平移后的直线与边BC有交点,则m的取值范围是( )A. B. C. D.9、已知点P(a+1,﹣+1)关于y轴的对称点在第一象限,则a的范围在数轴上表示正确的是()A. B. C.D.10、在平面直角坐标系中,点P(﹣2,﹣3)到y轴的距离为()A.3B.﹣3C.2D.﹣211、在平面直角坐标系中,点A(2,5)与点B关于y轴对称,则点B的坐标是()A.(-5,-2)B.(-2,-5)C.(-2,5)D.(2,-5)12、点(,5)在()A.第一象限B.第二象限C.第三象限D.第四象限13、将点向左平移个单位长度,在向上平移个单位长度得到点,则点的坐标是()A. B. C. D.14、如图,点A(t,3)在第一象限,OA与x轴所夹的锐角为α,tanα=,则t的值是()A.1B.1.5C.2D.315、已知|x-2|+ =0,则点P(x,y)在直角坐标系中()A.第一象限B.第二象限C.第三象限D.第四象限二、填空题(共10题,共计30分)16、如图所示,线段,,的长度分别为,,,且平分.若将点表示为,点表示为,则点可表示为________.17、平面直角坐标系xOy中,点A(4,3),点B(3,0),点C(5,3),点E在x轴上.当CE=AB时,点E的坐标为________.18、点P(m−1,m+3)在平面直角坐标系的y轴上,则P点坐标为________.19、若点P(2a+3b,﹣2)关于原点的对称点为Q(3,a﹣2b),则(3a+b)2020=________.20、如图,在平面直角坐标系中,点A(4,0),B(4,4),点P在半径为2的圆O上运动,则的最小值为________.21、如图,是象棋盘的一部分,若“帅”位于点(2,﹣1)上,“相”位于点(4,﹣1)上,则“炮”所在的点的坐标是________.22、坐标平面内的点与________ 是一一对应的.23、点P(2-a,a+1)在y轴上,则a=________。
冀教版数学八年级下册《图形变化与图形上点的坐标之间的关系》教学设计

冀教版数学八年级下册《图形变化与图形上点的坐标之间的关系》教学设计一. 教材分析冀教版数学八年级下册《图形变化与图形上点的坐标之间的关系》这一章节主要介绍了图形在坐标系中的变换,包括平移、旋转和轴对称等,以及这些变换与图形上点的坐标之间的关系。
通过本章的学习,学生能够理解图形变换的实质,掌握图形变换的方法,并能运用坐标表示和计算图形变换后点的坐标。
二. 学情分析学生在七年级已经学习了坐标系和坐标的概念,对坐标系有一定的认识,但对于图形变换和坐标之间的关系可能还没有完全理解。
因此,在教学过程中,需要引导学生通过实际操作和思考,逐步理解图形变换与坐标之间的关系。
三. 教学目标1.理解图形变换的实质,掌握图形变换的方法。
2.能够运用坐标表示和计算图形变换后点的坐标。
3.培养学生的空间想象能力和逻辑思维能力。
四. 教学重难点1.图形变换的实质和方法的掌握。
2.图形变换与坐标之间的关系的理解。
五. 教学方法1.采用问题驱动的教学方法,引导学生通过实际操作和思考,探索图形变换与坐标之间的关系。
2.运用多媒体辅助教学,直观展示图形变换的过程,帮助学生理解和掌握。
3.采用小组合作学习,鼓励学生互相讨论和交流,提高学生的合作能力和沟通能力。
六. 教学准备1.多媒体教学设备。
2.坐标纸、直尺、圆规等学习工具。
3.教学课件和练习题。
七. 教学过程1.导入(5分钟)通过一个简单的图形变换实例,引导学生思考图形变换的过程和坐标的变化。
例如,将一个点(2,3)进行平移,让学生观察坐标的变化。
2.呈现(15分钟)利用多媒体展示各种图形变换的实例,包括平移、旋转和轴对称等,并引导学生思考这些变换与坐标之间的关系。
3.操练(15分钟)让学生分组进行实际操作,利用坐标纸和学具进行图形变换,并记录变换后点的坐标。
教师巡回指导,解答学生的疑问。
4.巩固(10分钟)让学生独立完成一些图形变换的练习题,巩固所学知识。
教师选取部分学生的作业进行点评和讲解。
冀教版八年级数学下册19.4坐标与图形的变化公开课优质教案

《18.3图形与坐标2》教学案例一、教材说明:1、教材版本:冀教版八年级(上)第十八章第3节《图形与坐标》第2课时。
2、“平面直角坐标系”是学习函数及其图象、的基础,是沟通数与形的桥梁。
这节课是在学习了坐标系与有关几何知识的基础上,进行函数图像在坐标系中变化,,学生在学习平面直角坐标系的概念,继续探究坐标系中点、图形变化的特征,为以后学习图形的平移、函数图像的平移打下基础。
本节内容需3课时,本设计为第2课时,本人大胆尝试,改编教材原有内容,结合学生现有水平,充分运用多媒体课件及导学案,创新编排,由点的平移拓展到图形的平移,符合学生的认知规律。
二、教学目标:(一)知识目标1、感受平面直角坐标系中图形的变化过程;2、探索平面直角坐标系中图形的变化过程及规律。
(二)技能目标1、会正确画出平面直角坐标系中图形的变化过程;2、在给定的平面直角坐标系中,能够根据坐标指出点的位置,并且已知点的位置写出它对应的坐标;3、在给定的条件下,能够根据象限内点的特征与图形变化的特征,解决一些简单的数学问题;4、初步培养学生探索总结规律的能力。
(三)情感目标1、能使学生感受到数学与现实世界的联系,增强学生“用数学”的意识,感受数学之用;2、培养学生严谨朴实的科学态度和勤奋自强的探索精神,以及独立思考与合作交流的学习习惯,感受数学之实。
3、让学生得到尝试、成功的情感体验,感受数学之美。
三、教学重点与难点:1、教学重点:能在给定的平面直角坐标系中,结合图形的变化求相应点的坐标。
2、教学难点:探索象限内图形变化而产生的坐标变化特征,以及它们特征的简单运用。
四、教学媒体和教学技术选用1、提供学习资源:导学案(前一天发给学生自主完成)2、教学媒体:实物投影、多媒体课件五、教学过程:(一)、自学引路:(课前以导学案的形式发给学生,学生独立完成)根据右图完成下列问题: 1、写出图中各点的坐标:点A( )点B( )点C( )点P( )2、将点A向右平移5个单位长度,得到点A1( );3、将点B向左平移2个单位长度,得到点B1( );4、将点P向上平移4个单位长度,得到点P1( ) ;5、将点C向下平移3个单位长度,得到点C1( );归纳总结:根据以上平移过程及结果,你发现了什么变化规律? 想一想,做一做:点C(2,1)经过如何变化得到点C 2(5,4) 点A(-1,-1)经过如何变化得到点A 2(2,3).使用说明:课前教师检查学生完成情况,确定课堂教学任务。
八年级数学下册第三章《图形与坐标》测试题-湘教版(含答案)

八年级数学下册第三章《图形与坐标》测试题-湘教版(含答案)一.选择题1.当2<m<3时,点P(m﹣2,m﹣3)在第()A.一象限B.二象限C.三象限D.四象限2.在直角坐标系中,M(﹣3,4),M到x、y轴的距离与M′到x、y轴的距离相等,则M′的坐标不可能为()A.(﹣3,﹣4)B.(3,4)C.(3,﹣4)D.(3,0)3.若点(a,﹣3)与点(2,b)关于y轴对称,则a,b的值为()A.a=2,b=3B.a=2,b=﹣3C.a=﹣2,b=﹣3D.a=﹣2,b=3 4.在平面直角坐标系中,点Q(﹣1,3)向右平移3个单位长度后的坐标为()A.(﹣1,0)B.(﹣1,6)C.(2,3)D.(2,6)5.如果点A(2,﹣3)和点B关于原点对称,则点B的坐标为()A.(﹣2,3)B.(﹣2,﹣3)C.(2,﹣3)D.(2,3)6.如图,一个动点P在平面直角坐标系中按箭头所示方向做折线运动,即第一次从原点运动到(1,1),第二次从(1,1)运动到(2,0),第三次从(2,0)运动到(3,2),第四次从(3,2)运动到(4,0),第五次从(4,0)运动到(5,1),…,按这样的运动规律,经过第2013次运动后,动点P的坐标是()A.(2012,1)B.(2012,2)C.(2013,1)D.(2013,2)7.在y轴上,与点A(3,﹣2)的距离等于3的点有()A.1个B.2个C.4个D.0个8.如图,在直角坐标系中,▱OABC的顶点A为(1,3)、C为(5,0),则B的坐标为()A.(6,3)B.(5,5)C.(4,3)D.无法确定9.如图,△AOB关于x轴对称图形△A′OB,若△AOB内任意一点P的坐标是(a,b),则△A′OB中的对应点Q的坐标是()A.(a,b)B.(﹣a,b)C.(﹣a,﹣b)D.(a,﹣b)10.根据指令[s,A](s≥0,0°≤A<360°)机器人在平面上能完成如下动作:先在原地顺时针旋转角度A,再朝其面对的方向沿直线行走距离s.现在机器人在平面直角坐标系的原点,且面对y轴的负方向,为使其移动到点(﹣3,0),应下的指令是()A.[3,90°]B.[90°,3]C.[﹣3,90°]D.[3,270°]二.填空题11.已知点A(2,3)在第一象限,则与点A关于x轴对称的点的坐标为,与点A 关于y轴对称的点的坐标为,与点A关于原点对称的点的坐标为.12.若点A(﹣1,a),B(b,2)两点关于y轴对称,则a=,b=.13.点P(1,2)关于点Q(﹣1,1)的对称点的坐标为.14.定义:在平面直角坐标系内,对于点P(x,y),我们把Q(﹣y+1,x+3)叫做它的伴随点.如点(2,1)的伴随点为(﹣1+1,2+3),即(0,5).若点M的伴随点坐标为(﹣5,3),则点M的坐标为.15.将点N(﹣1,2)向右平移3个单位,再向下平移4个单位后,其坐标变为.16.坐标系中M(﹣3,2),N(3,2)之间距离是.17.点M(﹣3,5)关于直线x=1对称的点M′的坐标为.18.如图,规定列号写在前面,行号写在后面,如用数对的方法,棋盘中“帅”与“卒”的位置可分别表示为(e,4)和(g,3),则“马”的位置可表示为.19.在x轴上与点(0,﹣2)距离是4个单位长度的点有.20.如图,直线OD与x轴所夹的锐角为30°,OA1的长为1,△A1A2B1,△A2A3B2,△A3A4B3,…,△A n A n+1B n均为等边三角形,点A1,A2,A3,…,A n+1在x轴的正半轴上依次排列,点B1,B2,B3,…,B n在直线OD上依次排列,那么B2020的坐标为.三.解答题21.自然数按如图规律排列,14这个数位于第4行,第3列,记作(4,3),那么124这个数记作什么?…12510……43611……98712….…16151413………………….22.已知平面直角坐标系中,点P(1﹣a,2a﹣5)到两坐标轴的距离相等,求a值并确定点P的坐标.23.已知A(0,0)、D(4,2)、E(6,6)、C(2,4),依次连接各点得到四边形ADEC,按要求绘制下列图形.(1)横坐标、纵坐标都乘以﹣1;(2)纵坐标不变,横坐标扩大为原来的2倍;(3)横坐标都加2,同时纵坐标都减5;(4)如果坐标不变,纵坐标都扩大为原来的2倍,同时再加上3,不画图,你能叙述图形的变化吗?24.点P(x+1,2x﹣1)关于原点的对称点在第一象限,试化简:|x﹣3|﹣|1﹣x|25.如图,分别说明:△ABC从(1)→(2),再从(2)→(3)…一直到(5),它的横、纵坐标依次是如何变化的?26.当m为何值时,点P(3m﹣1,m﹣2)到y轴的距离是到x轴距离的3倍?求出此时点P到原点的距离.27.已知在平面直角坐标系中,点A、B的坐标分别为:A(﹣3,4),B(4,﹣2).(1)求点A、B关于y轴对称的点的坐标;(2)在平面直角坐标系中分别作出点A、B关于x轴的对称点M、N,顺次连接AM、BM、BN、AN,求四边形AMBN的面积.参考答案一.选择题1.解:∵2<m<3时,∴m﹣2>0,m﹣3<0,∴点P在第四象限.故选:D.2.解:∵M点的坐标为(﹣3,4),∴M到x、y轴的距离分别为4,3,而M到x、y轴的距离与M′到x、y轴的距离相等,∴M′到x、y轴的距离也为4,3,结合各选项A、B、C到x、y轴的距离分别为4,3,D到x、y轴的距离分别为0,3,故D符合题意.故选:D.3.解:∵点(a,﹣3)与点(2,6)关于y轴对称,∴a=﹣2,b=﹣3,故选:C.4.解:点Q(﹣1,3)向右平移3个单位长度后的坐标为(2,3).故选:C.5.解:∵点A(2,﹣3)和点B关于原点对称,∴点B的坐标为(﹣2,3).故选:A.6.解:∵第一次从原点运动到(1,1),第二次从(1,1)运动到(2,0),第三次从(2,0)运动到(3,2),第四次从(3,2)运动到(4,0),第五次从(4,0)运动到(5,1),…,∴按这样的运动规律,第几次横坐标即为几,纵坐标为:1,0,2,0,1,0,2,0 (4)个一循环,∵=503…1,∴经过第2013次运动后,动点P的坐标是:(2013,1).故选:C.7.解:在y轴上,与点A(3,﹣2)的距离等于3的点有(0,﹣2),即只有1个点.故选:A.8.解:由题意得AB∥x轴,那么点A和B的纵坐标相等为3,∵OC=5,那么点B的横坐标为1+5=6.故选:A.9.解:∵△AOB与△A'OB关于x轴对称,∴点P(a,b)关于x轴的对称点为(a,﹣b),∴点P的对应点Q的坐标是(a,﹣b).故选:D.10.解:根据点(0,0)到点(﹣3,0),即可知机器人先顺时针转动90°,再向左平移3个单位,于是应下指令为[3,90°].故选:A.二.填空题11.解:∵点A(2,3)在第一象限,∴与点A关于x轴对称的点的坐标为:(2,﹣3),与点A关于y轴对称的点的坐标为:(﹣2,3),与点A关于原点对称的点的坐标为:(﹣2,﹣3).故答案为:(2,﹣3),(﹣2,3),(﹣2,﹣3).12.解:∵点A(﹣1,a),B(b,2)两点关于y轴对称,∴b=1,a=2,故答案为:2;1.13.解:设点P(1,2)关于点Q(﹣1,1)的对称点的坐标为(a,b),则=﹣1,=1,解得:a=﹣3,b=0,∴点P(1,2)关于点Q(﹣1,1)的对称点的坐标为(﹣3,0),故答案为:(﹣3,0).14.解:设点M(m,n),则它的伴随点为(﹣n+1,m+3),∵点M的伴随点坐标为(﹣5,3),∴﹣n+1=﹣5,m+3=3,解得,m=0,n=6,∴M(0,6).故答案为(0,6).15.解:点N(﹣1,2)向右平移3个单位,再向下平移4个单位后,其坐标为(﹣1+3,2﹣4),即:(2,﹣2),故答案为:(2,﹣2).16.解:∵M(﹣3,2),N(3,2),∴MN∥x轴,∴MN=3﹣(﹣3)=3+3=6.故答案为:6.17.解:∵点M(﹣3,5)与点N关于直线x=1对称,而1×2﹣(﹣3)=5,∴点M(﹣3,5)关于直线x=1对称的点N的坐标是(5,5),故答案为(5,5).18.解:根据题意知“马”的位置可表示为(c,3),故答案为:(c,3).19.解:∵点在x轴上,∴点的纵坐标为0,∵距离(0,﹣2)的距离是4,∴所求点的横坐标为±=±2,∴所求点的坐标是(2,0)或(﹣2,0).故答案填:(2,0)或(﹣2,0).20.解:∵△A1B1A2为等边三角形,∴∠B1A1A2=60°,∵∠B1OA2=30°,∴∠B1OA2=∠A1B1O=30°,∴OA2=2OA1=2,同理可得,OA n=2n﹣1,∵∠B n OA n+1=30°,∠B n A n A n+1=60°,∴∠B n OA n+1=∠OB n A n=30°,∴B n A n=OA n=2n﹣1,即△A n B n A n+1的边长为2n﹣1,则可求得其高为×2n﹣1=×2n﹣2,∴点B n的横坐标为×2n﹣1+2n﹣1=×2n﹣1=3×2n﹣2,∴点B n的坐标为(3×2n﹣2,×2n﹣2),∴点B2020的坐标为(3×22018,×22018).故答案为(3×22018,×22018).三.解答题21.解:第一单元是:1,第二单元是:2,3,4,第三单元是:5,6,7,8,9,第四单元是:10,11,12,13,14,15,16,第五单元是:17,18,19,20,21,22,23,24,25,…,所以,124在第12单元,第3个数,即第3行第12个数,∴124这个数记作(3,12).22.解:∵点P(1﹣a,2a﹣5)到两坐标轴的距离相等,∴符合题的点P的横、纵坐标相等或互为相反数,∴|1﹣a|=|2a﹣5|,∴1﹣a=±(2a﹣5)解得:a=2或a=4,则1﹣2=﹣1,2×2﹣5=﹣1,1﹣4=﹣3,2×4﹣5=3,所以P的坐标为(﹣1,﹣1)或(﹣3,3).23.解:(1)如图所示:四边形A′D′E′C′即为所求;(2)如图所示:四边形A″D″E″C″即为所求;(3)如图所示:四边形A1D1E1C1即为所求;(4)图形在原基础上各点向上平移纵坐标个单位后,再将整体图形向上平移3个单位.24.解:∵点P(x+1,2x﹣1)关于原点的对称点P′的坐标为(﹣x﹣1,﹣2x+1),而P′在第一象限,∴﹣x﹣1>0,且﹣2x+1>0,∴x<﹣1,∴|x﹣3|﹣|1﹣x|=﹣(x﹣3)﹣(1﹣x)=﹣x+3﹣1+x=2.25.解:(1)→(2)纵坐标不变,横坐标都加1,(2)→(3)横坐标不变,纵坐标都加1,(3)→(4)横、纵坐标都乘以﹣1,(4)→(5)横坐标不变,纵坐标都乘以﹣1.26.解:根据题意得到|3m﹣1|=3|m﹣2|,两边平方,解得m=因而P的坐标是(,﹣),则OP=.27.解:(1)根据轴对称的性质,得A(﹣3,4)关于y轴对称的点的坐标是(3,4);点B(4,﹣2)关于y轴对称的点的坐标是(﹣4,﹣2).(2)根据题意:点M、N与点A、B关于x轴对称,可得M(﹣3,﹣4),N(4,2);进而可得四边形AMBN为梯形,且AM=8,BN=4.故四边形AMBN的面积为•(8+4)×7=42.。
初中数学八年级下册第3章图形与坐标3.1平面直角坐标系教学

我思 我进步
通过本节课,你有什么收获? 你还存在哪些疑问,和同伴交流.
练习
3.如图是某动物园的部分平面示意图,试建立适当的 平面直角坐标系, 用坐标表示大门、百鸟园、大象馆、 狮子馆和猴山的位置.
解:如图,以大门所在点为原点O,在网格中以过点O
的水平直线和垂直直线分别作为x 轴,y 轴建立平面直
角坐标系.
y
由图可知大门、百鸟园、大象
馆、狮子馆和猴山的位置为:
大门(0,0),百鸟园(5,
2 O1 学校
-5-4-3-2-1 1 2 3 4 5 x -1
B电影院-2 -3
有时还可借助方向和距离(或称方 位) 来刻画两物体的相对位置.
-4 -5 C汽车站
思考
(1)如图,李亮家距学校1000 m,如何用方向和距离来
描述李亮家相对于学校的位置?(2)反过来,学校相对
于李亮家的位置怎样描述呢?
如图,以学校所在位置为原点,分别以正东、正北方向为x
轴, y 轴的正方向,建立平面直角坐标系, 规定1 个单位长
度代表100 m长. 根据题目条件,点A(5,4.5) 是书
北
y 5
A书店
4
店的位置,点B(-2.5,-3)是电影
3
院的位置, 点C(4,-6) 是汽车站 的位置. 在日常生活中, 除了用平面直角 坐标系刻画物体之间的位置关系外,
分析:如图,设H 岛所在的位置 为C,△ABC 是直角三角形, ∠CAB = 90°,利用勾股定理可 以求出BC间的距离.
解:在Rt△ABC 中, ∵ AC = 30海里, AB = 40海里,∠CAB = 90°,
BC AC2 AB2 302 402 50海里.
由于在点B处测得H岛在北偏西 53°6′的方向上, 则∠BCA = 53°6′. 故此时,渔政船在H岛南偏东53°6′ 的方向, 距H岛50海里的位置.
冀教版数学八年级下册19.4《坐标与图形的变化》教学设计

冀教版数学八年级下册19.4《坐标与图形的变化》教学设计一. 教材分析冀教版数学八年级下册19.4《坐标与图形的变化》是本册教材中的重要内容,主要介绍了坐标系中图形的平移和旋转。
这部分内容不仅是初中数学的基础,而且与现实生活紧密相连,具有较高的实用价值。
通过学习本节内容,学生能够理解平移和旋转的性质,掌握平移和旋转的计算方法,并能够运用平移和旋转解决实际问题。
二. 学情分析八年级的学生已经掌握了坐标系的基础知识,对图形的平移和旋转有了初步的认识。
但是,对于复杂的图形变换,学生可能还存在理解上的困难。
因此,在教学过程中,教师需要结合学生的实际情况,用生动形象的语言和具体的例子,帮助学生理解和掌握平移和旋转的性质和计算方法。
三. 教学目标1.理解平移和旋转的定义和性质;2.掌握平移和旋转的计算方法;3.能够运用平移和旋转解决实际问题。
四. 教学重难点1.教学重点:平移和旋转的定义和性质,平移和旋转的计算方法;2.教学难点:对复杂图形进行平移和旋转的计算和应用。
五. 教学方法采用问题驱动法、案例教学法和合作学习法。
通过设置问题,引导学生主动探索和思考;通过具体的案例,让学生理解和掌握平移和旋转的性质和计算方法;通过合作学习,培养学生团队协作的能力。
六. 教学准备1.准备相关的教学案例和图片;2.准备平移和旋转的计算练习题;3.准备课堂用的坐标系图。
七. 教学过程1.导入(5分钟)通过一个简单的图形变换案例,引导学生思考平移和旋转的性质。
例如,展示一个三角形在坐标系中的平移和旋转,让学生观察和描述平移和旋转的方向和距离。
2.呈现(10分钟)通过PPT或者黑板,呈现平移和旋转的定义和性质,以及平移和旋转的计算方法。
用生动的语言和具体的例子,帮助学生理解和掌握平移和旋转的性质和计算方法。
3.操练(10分钟)让学生通过实际操作,进行平移和旋转的计算。
可以设置一些练习题,让学生独立完成,然后互相交流和讨论。
4.巩固(10分钟)通过一些综合性的练习题,让学生运用平移和旋转的性质和计算方法,解决实际问题。
冀教版八年级数学下册第十九章《坐标与图形的位置》公开课课件

作业
➢ 图示为某废墟示意图,由于雨水冲蚀,残缺 不全,依稀可见钟楼坐标为A(5, 2),街口坐 标为B(5,-2),资料记载比德先生的祖居坐标 为(1,1),你能帮助比德先生找到他家的老屋 吗?
x
A(5, 2)
(5,0)
y
(1,1)
B(5,-2)
(0,0)
(0,0)、(0,-5)、(-2,-2),以这三点为平形四边形的
三个顶点,则第四个顶点不可能在第__一__象限。
➢ 已知:矩形OABC在平面直角坐标系中的位置如右
图所示,点B的坐标为(3,-2),则矩形的面积等于
_6_____
y
G E
C
O
x
F
A
B(3,-2)
反思与评价
1、通过这节课你有哪些收获? 2、你还有什么想法?
课堂延伸
➢ 如图,在直角坐标系 中,右边的图案是由 左边的图案经过平移 得到的,左图案中左 右眼睛的坐标分别是 (-4,2),(-2,2),右图 案中左眼的坐标是 (3,4),则右图案中 右眼的坐标是( ) (5,4)
仔细观察坐标 特点,有助于 解决问题。
小试牛刀
如图,某战役缴获敌人防
御工事坐标地图碎片,
顶点C的坐标是( C )
A.(3,7) B.(5,3) C.(7,3) D.(8,2)
y
D
(A) OP
C BQ x
小测验
➢ 如左图所示,若在象棋盘上建立直角坐标 系,使“将”位于点(1,-2),“象”位于点 (3,-2),则“炮”位于点( B ) A.(1,-1) B.(-1,1) C.(-1,2) D.(1,-2)
➢ 15、一年之计,莫如树谷;十年之计,莫如树木;终身之计,莫如树人。2021年7月2021/7/292021/7/292021/7/297/29/2021
(新课标)最新湘教版八年级数学下册《图形与坐标》单元提升卷及答案解析

湘教版八年级数学(下)第三章《图形与坐标》提升卷(含答案)一、选择题(每小题3分,共30分)1.平面直角坐标系内有一点A(a,b),若ab=0,则点A的位置在()A.原点;B,x 轴上;C,y 轴上; D.坐标轴上;2.在平面直角坐标系中,已知点P(a,b)在第四象限,则点Q(b-l,-a)所在的象限是()A.第一象限;B.第二象限;C.第三象限;D.第四象限;3.如图所示,线段AB经过平移得到线段A′B′,其中点A,B的对应点分别为点A′,B′,这四个点都在格点上.若线段AB上有一个点P(a,b),则点P在A′B′上的对应点P′的坐标为()A.(a-2,b+3);B.(a-2,b -3);C.(a+2,b+3);D.(a+2,b -3);4.若某四边形顶点的横坐标变为原来的相反数,而纵坐标不变,此时图形位置也不变,则这四边形一定不是()A.矩形B.正方形C.直角梯形D.菱形5.在平面直角坐标系中,将点A(l,2)的横坐标乘以-1,纵坐标不变,得到点A′,则点A与点A′的关系是()A.关于x轴对称;B.关于y 轴对称;C.关于原点对称; D.将点A向x轴负方向平移一个单位得点A;6.点P在x轴的下侧、y 轴的左侧,距离每个坐标轴都是3个单位长度,则点P的坐标为()A.(3,3)B.(-3,3) C,(-3,-3) D.(3,-3)7.在平面直角坐标系中,把点P(-3,2)绕原点O顺时针旋转180°,所得到的对应点P′的坐标为()A.(3,2) B.(2,-3)C.(-3,-2) D.(3,-2)8.如图,在方格纸上摆出了六枚棋子,如果用(2,-1)表示棋子A,用(6,-2)表示棋子B,那么(5,3)表示的是()A.棋子E B.棋子DC.棋子C D.棋子F9.已知点M 到x 轴的距离为3,到y 轴的距离为2,则M点的坐标为()A,(3,2) B.(-3,-2)C.(3,-2)D.(2,3),(2,-3),(-2,3),(-2,-3)10.A(-3,2)关于原点的对称点是B,B 关于x 轴的对称点是C,则点C的坐标是()A.(3,2) B.( -3,2) C,(3,-2)D.(-2,3)二、填空题(每小题3分,共24分)11.以点(4,0)为圆心,以5为半径的圆与y 轴交点的坐标为. 12.已知等边△ABC的两个顶点坐标为A(-4,0),B (2,0),则点C的坐标为。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章 平面直角坐标系
单元测试题
(时限:100分钟 总分:100分)
班级 姓名 总分 一、 选择题(本题共8小题,每小题4分,共32分) 1. 在平面直角坐标系中,点(1,2)在( )
A .第一象限 B.第二象限 C.第三象限 D.第四象限 2. 在平面直角坐标系中,若点P (-3,m +1)在第三象限,则m 的值为 ( ) A .-1
B .m >-3
C .m <-1
D .m >-1
3. 在y 轴上,与点A (3,-2)的距离等于3的点有( )
A.1个
B.2个
C.4个
D. 0个 4. 点A (1,2)向右平移2个单位得到对应点'A ,则点'A 的坐标是( ) A.(1,4) B.(1,0) C.(-l ,2) D.(3,2) 5. 如图,小明从点O 出发,先向西走40米,再向南走30米 到达点M ,如果点M 的位置用(-40,-30)表示,那么 (10,20)表示的位置是( ) A .点A B .点B C .点C D .点D
6. 点P (a ,b )的纵坐标b 不变,而横坐标a 减少3,则点P ( ). A .向左平移了3个单位 B.向右平移了3个单位 C.向上平移了3个单位 D.向下平移了3个单位
7. 在平面直角坐标系中,若点(a ,b )在x 轴上,则( ) A.00a b =≠, B .0b = C.
1a
b
= D.0a b +=且0a ≠ 8. 若点P (m ,1-2m )的横坐标与纵坐标互为相反数,则点P 一定在( )
第5题图
A .第一象限 B.第二象限 C. 第三象限 D .第四象限 二、填空题(本题共8小题,每小题4分,共32分)
9. 如果用(6,1)表示一张6排1号的电影票,那么15排2号的电影票可表示为________ . 10. 若点M (2a -,23a +)是y 轴上的点,则a 的值为___________.
11.一个长方形在平面直角坐标系中三个顶点的坐标为(–1,–1)、(–1,2)、(3,–1),则第四个顶点的坐标为 .
12. 如图在直角坐标系中,右边的图案是由左边的图案 经过平移以后得到的. 左图中左右眼睛的坐标分别 是(-4,2),(-2,2),右图中左眼的坐标是(3,4), 则右图中右眼的坐标是 .
13. 如图所示的围棋盘放在平面直角坐标系内,黑棋A 的 坐标为(-1,2),那么白棋B 的坐标是 . 14.已知点P 的坐标是(2a -,36a +),且点P 到两 坐标轴的距离相等,则点P 的坐标是_____________. 15. 如图,在平面直角坐标系中,将线段AB 绕点A 按逆 时针方向旋转90°后,得到线段AB ′,则点B ′的坐标 为 .
16. 在平面直角坐标系中,已知点A (-4,0),B (4,0), 点C 在坐标轴上,且AC +BC =10,写出满足条件的 所有点C 的坐标________.
三、解答题(本题共5小题,共36分) 17.(本小题满分6分)
写出图中点A 、B 、C 、D 、E 、F 的坐标.
第12题图
第15题图
18. (本小题满分6分)
如图,小海龟位于图中点A(2,1)处,按下述路线移动:(2,1)→(2,4)→(7,4)→(7,7)→(1,7)→(1,1)→(2,1).用粗线将小海龟经过的路线描出来,看一看是什么图形.
19. (本小题满分10分)
如图,菱形ABCD,四个顶点分别是A(-2,-1),
B(1,-3),C(4,-1),D(1,1).将菱形沿x
轴负方向平移3个单位长度,各个顶点的坐标变为
多少?将它沿y轴正方向平移4个单位长度呢?并
分别画出平移后的图形.
20. (本小题满分6分)
如图是某市市区几个旅游景点的示意图(图中每个小正方形的边长为1个单位长度).请
坐标表示下列景点的位置.
光岳楼____ __;
金凤广场_ _ ____;
动物园____ __;
山峡会馆___ ___;
湖心岛____ _.
21.(本小题满分8分)
如图,四边形ABCD各个顶点的坐标分别为(–2,8),(–11,6),(–14,0),(0,0).
(1)确定这个四边形的面积,你是怎么做的?
(2)如果把原来ABCD各个顶点纵坐标保持不变,横坐标增加2,所得的四边形面积又是
多少?
参考答案
第三章 平面直角坐标系
一、选择题:
1.A ;
2.C ;
3. A ;
4.D ;
5.B ;
6.A ;
7.B ; 8 D. 二、填空题:
9. (15,2) ; 10. 2; 11. (3,2); 12. (5,4);
13. (-3,-2) ; 14. (3,3)或(6,-6); 15(4,2);16. (5,0)±, (0,3)±. 三、解答题:
17. A (-2,-2),B (-5,4),C (5,-4),D (0,-3),E (2,5),F (-3,0). 18. 略
19. 将菱形沿x 轴负方向平移3个单位长度,各个顶点的坐标变为 (-5,-1),(-2,-3),(1,-1),(-2,1).
将它沿y 轴正方向平移4个单位长度,各个顶点的坐标变为 (-2,3),(1,1),(4,3),(1,5).图略.
20. 光岳楼(0,0);金凤广场(-2,-1.5);动物园(6,3);山峡会馆(4,-1);
湖心岛(-1.5,1).
21.(1)80(可分别割成直角三角形和长方形或补直角三角形成长方形); (2)80.。
