圆柱的表面积练习课
《圆柱的表面积》练习2课件

(2)一个底面直径是4分米,高是4分米的圆柱形通风管, 需要铁皮(50.24 )平方分米。
50cm
10cm
6、一个圆柱底面半径是4cm,高是6cm,沿这个圆柱 的底面直径将圆柱平均分成两份(如图),这时表面 积比原来增加多少平方厘米?
4cm
6cm
7、一个圆柱侧面展开后是一个边长为 31.4cm的正方形,这个圆柱的表面积是 多少?
8、一个圆柱的侧面积是18.84cm2,底 面周长是6.28cm,求这个圆柱的表面积?
9、一个圆柱的侧面积是188.4cm2,底 面半径是2cm,它的高是多少?
10、一个圆柱被截去5cm后,圆柱的表面积减 少了31.4cm2,求原来圆柱的表面积?
5cm
20cm
C. 它的侧面展开图一定是正方形
(2)一个圆柱的侧面展开后是正方形,这个圆柱的高和底 面直径比是( A )
A. π∶1 B. 1∶π C. 1∶1
3、求下列各图形的表面积
15cm
6cm
5Байду номын сангаасm
9cm
10cm
6cm
4、书P18第17题
10cm
10cm
5、要将路灯座(如右图) 漆上白色的油漆,要漆多 少平方米?
(3)一个圆柱体,它的底面半径是2厘米,高是5厘米,它的 底面积是( 12.56cm2),它的底面周长是( 12.56cm),它的 侧面积是( 62.8cm2),它的表面积是( 87.92cm2 )
圆柱的表面积练习课

6.一个圆柱的侧面积是188.4平 方分米,底面半径是2分米.它 的高是多少?
7、把一根长5分米的圆柱体木料沿着直径 劈成相等的两半,表面积增加了20平方分 米。这根木料的直径是( )。
8、把右图中的长方形ABCD以其中的一条边 为轴旋转一周,得到一个立体图形,这个 立体图形的底面半径和侧面积各是多少? (BC=10厘米,AB=4厘米)
列式:求下面各图形的表面积(单位:cm)
( 1) 7 7 7 ( 3) 4 ( 4) 6 10 30 10 ( 2) 5 3
联系生活实际,说说生活中的问题与哪些面积有 关?(填A、B、C、D) A求底面积 B求侧面积 C求1个底面积与侧面积 D求表面积 (1)圆形水池的占地面积。( ) (2)做一节烟囱所需铁皮面积。( ) (3)求易拉罐上商标纸的面积。( ) (4)做茶叶桶所需铁皮面积。( ) (5)做一个无盖水桶所需铁皮面积。( ) (6)往大厅的柱子上涂漆,求涂漆部分面积。( ) (7)在水池的内壁和底面抹水泥,求抹水泥部分的 面积。 ( ) (8)做一个油桶所需铁皮面积。( ) (9)压路机的滚筒转动一周,求压路面积。( ) (10)做一个塑料笔筒所需塑料面积。( )
课本P18(1)要将路灯(如图)漆上白 色的油漆,要漆多少平方米?(2)街心 公园有30个这样的灯座,如果漆每平方 米所用的材料费是50元,一共需要多少 元?
三、解决问题:
1、做50节同样大小的圆柱形通风管,每节 长4米,管口直径是10厘米,至少需要多少 平方米的铁皮?
2、压路机的滚筒是一个圆柱形,它的宽是1.5 米,滚筒横截面的半径是0.6米,以每分钟滚 动5周计算,每分钟压路的面积是多少平方米?
圆柱的表面积教案

圆柱的表面积教案圆柱的表面积教案1教材内容:23-24页教学目标:1、进一步巩固圆柱侧面积、底面积、表面积的计算方法,体会这些计算方法的联系和区别。
2、引导学生运用所学的圆柱表面积的知识解决相关的实际问题。
教学重难点:通过解决实际问题,加深学生对圆柱表面积计算方法的理解,培养学生灵活运用所学的知识解决实际问题的能力,发展学生的空间观念。
教学具准备:与练习六中的练习相关的图片。
教学过程:一、复习引入1、什么是圆柱的表面积?包括哪几个部分?怎么求圆柱的表面积?其中圆柱的底面积怎么算?侧面积呢?2、揭示要求:这节课,我们要运用所学的有关知识,解决生活中的相关问题,希望通过问题的解决,来加深对圆柱表面积的认识。
二、基本练习1、出示练习六第3题,理解表格意思。
2、第一行中,已知什么?怎么算出这个圆柱的侧面积、底面积和表面积?各自计算,算后填写在书中表格里,再交流方法和得数。
3、第二行中,已知什么?怎么算出这个圆柱的侧面积、底面积和表面积?各自计算,算后填写在书中表格里,再交流方法和得数。
4、如果已知一个圆柱的底面周长是6.28分米,高是3分米,怎么算出这个圆柱的侧面积、底面积和表面积?各自计算,算后交流方法和得数。
三、综合练习1、完成练习六第4题。
⑴讨论:求做这个通风管要多大的铁皮,实际上是算哪个面的面积?为什么?⑵各自练习后交流算法。
2、完成练习六第5题。
⑴讨论:需要糊彩纸的面是什么?要求彩纸的面积就是算圆柱的哪几个面积?为什么?⑵各自练习后交流算法和结果。
3、讨论练习六第7题。
⑴出示“博士帽”问:认识它吗?什么样的人可以拥有博士帽?⑵看看,这个博士帽是怎么做成的,包括哪几个部分?⑶出示条件:这个博士帽上面是边长30厘米的正方形,下面的底面直径16厘米,高为10厘米的圆柱。
你能算出,做一顶这样的博士帽需要多少平方分米的黑色卡纸?⑷各自计算,算后交流算法和结果。
⑸如果要做10顶呢?怎么算?3、讨论练习六第8题。
人教版六下数学《圆柱的表面积》微课精讲+课件教案试卷

人教版六下数学《圆柱的表面积》微课精讲+课件教案试卷知识点:1.沿圆柱的高剪开,圆柱的侧面展开图是一个长方形(或正方形)。
(如果不是沿高剪开,有可能还会是平行四边形)2.圆柱的侧面积=底面周长×高,用字母表示为:S侧=ch。
3.圆柱的侧面积公式的应用:(1)已知底面周长和高,求侧面积,可运用公式:S侧=ch;(2)已知底面直径和高,求侧面积,可运用公式:S侧=πd h;(3)已知底面半径和高,求侧面积,可运用公式:S侧=2πr h4.根据不同条件求圆柱表面积的思维图5.圆柱表面积的计算方法的特殊应用:练习:1.一个底面周长和高相等的圆柱,如果高增加1 dm,它的侧面积就增加6.28 dm2,这个圆柱的底面周长是多少?6.28÷1=6.28(dm)答:这个圆柱的底面周长是6.28分米。
2.一个容器,从正面看和从上面看如下图,求这个立体图形的表面积是多少?3.14×( )2×2+3.14×4×6+5×1×4=120.48(cm2)答:这个立体图形的表面积是120.48平方厘米。
3.如图,一个高为24 cm的圆柱被截去4 cm后,圆柱的表面积减少了25.12 cm2。
原来圆柱的侧面积是多少平方厘米?25.12÷4×24=150.72(cm2)答:原来圆柱的侧面积是150.72平方厘米。
4.某宾馆有4根圆柱形柱子,每根柱子高是6 m,底面周长为2.512 m,现要给这些柱子贴上墙纸,如果每平方米墙纸45元,给这些柱子贴墙纸一共需要多少元?2.512×6×4×45=2712.96(元)答:给这些柱子贴墙纸一共需要2712.96元。
5.用一个滚刷往墙壁上刷涂料,滚刷的半径是6 cm,长30 cm。
如果每蘸一次涂料,滚刷可以滚动四圈,那么可以刷多少平方厘米的墙壁?2×3.14×6=37.68(cm)37.68×30×4=4521.6(cm2)答:可以刷4521.6平方厘米的墙壁。
圆柱体表面积练习题含答案

圆柱体表面积练习题含答案圆柱体表面积练习题含答案圆柱体是我们在日常生活中经常遇到的几何体之一,它具有很多有趣的特性。
其中一个重要的特性就是它的表面积。
在本文中,我们将介绍一些关于圆柱体表面积的练习题,并提供答案供大家参考。
练习题1:一个圆柱体的底面半径为5cm,高为10cm,求其表面积是多少?解答:首先,我们需要计算出圆柱体的侧面积和底面积,然后将它们相加。
底面积可以通过公式πr²来计算,其中r为底面半径。
所以底面积为π × 5² = 25π cm²。
侧面积可以通过公式2πrh来计算,其中r为底面半径,h为圆柱体的高。
所以侧面积为2π × 5 × 10 = 100π cm²。
最后,将底面积和侧面积相加得到总表面积。
总表面积为25π + 100π = 125π cm²。
练习题2:一个圆柱体的底面积为50π cm²,高为8cm,求其表面积是多少?解答:首先,我们需要计算出圆柱体的侧面积和底面积,然后将它们相加。
已知底面积为50π cm²,可以通过公式πr²来计算。
所以,50π = πr²,解得r² = 50,即r = √50 ≈ 7.07 cm。
侧面积可以通过公式2πrh来计算,其中r为底面半径,h为圆柱体的高。
所以侧面积为2π × 7.07 × 8 ≈ 112.8π cm²。
最后,将底面积和侧面积相加得到总表面积。
总表面积为50π + 112.8π ≈ 162.8π cm²。
练习题3:一个圆柱体的总表面积为300π cm²,高为12cm,求其底面半径是多少?解答:已知总表面积为300π cm²,可以通过公式计算出侧面积和底面积的和。
侧面积可以通过公式2πrh来计算,其中r为底面半径,h为圆柱体的高。
所以侧面积为2πrh。
第三单元圆柱表面积练习课(课件)-六年级下册数学人教版

在一个零件(如图)的表面涂一层防锈材料。这个零件是由Байду номын сангаас
两个圆柱组成的,小圆柱的底面直径是4cm,高是2cm;大圆
柱的底面直径是6cm,高是5cm。这个零件涂防锈材料的面积
是多少平方厘米?
方法一:
小圆柱的表面积 大圆柱的表面积
- 小圆柱的两个 底面积
在一个零件(如图)的表面涂一层防锈材料。这个零件是由 两个圆柱组成的,小圆柱的底面直径是4cm,高是2cm;大圆 柱的底面直径是6cm,高是5cm。这个零件涂防锈材料的面积 是多少平方厘米?
下面是一张长方形纸板,剪下的阴影部分刚好能做成一个圆柱 (接头处忽略不计),做成的圆柱的表面积是多少?
d h C底 =πd
51.4cm
d
S表=2S底 + S侧
r r、h
或d、h
2d + πd =51.4
下面是一张长方形钢板,剪下的阴影部分刚好能做成一个圆 柱形带盖的水桶(接头处忽略不计),这个水桶表面积是多少?
h
d
C底 =πd
20.7dm
圆柱表面积 拓展练习
P 课本 19 4、如下图,上排图中切完后的截面或剪完后展开的
侧面分别是什么形状?请与下排图连一连。
横切
纵切
一根圆柱形状的木料,底面直径是10厘米,高是12厘米。 把这块木料分成相等的两块,原木料的表面积增加了多少?
课本P19
11、一根圆柱形木料的底面半径是0.5m,长是2m。如图所
5cm 12cm
把一个圆柱体木块过底面圆心从上到下劈成两半,表面积增 加64平方厘米。这个圆柱体木块原来的侧面积是多少平方厘米?
一个圆柱体木块,底面半径5cm,沿直径切成两个完全相同 的半圆柱,表面积增加160cm2。原来这个圆柱体木块的表面 积是多少平方厘米?
苏教版六年级数学圆柱的表面积和体积练习

苏教版六年级数学——圆柱的表面积和体积练习教学内容:圆柱表面积和体积计算综合练习教学目标:提高学生应用公式解决实际问题的能力,帮助学生在具体的情境中进一步感受所学知识的应用价值。
教学重难点:进一步培养学生的空间想像能力和综合应用数学知识解决实际问题的能力。
教学对策:补充一些有关圆柱表面积和体积计算的基本练习及解决问题的练习,指导学生灵活运用所学知识解决问题。
教学准备:多媒体教学设备教学过程:一、揭示课题前几节课,我们学习了圆柱表面积和圆柱体积计算,运用这些知识能解决很多实际问题。
这节课,我们将这部分知识进行综合练习。
(板书课题)二、知识梳理,练习巩固。
1、知识整理。
(1)已知圆的半径和高,怎样求圆柱的表面积和体积?(2)已知圆的直径和高,怎样求圆柱的表面积和体积?(3)已知圆的周长和高,怎样求圆柱的表面积和体积?同桌之间可以互相说说,可以说说运用哪些计算公式进行计算。
2、求下面各圆柱的体积⑴底面积0.6平方米,高0.5米⑵半径4厘米,高12厘米⑶直径5分米,高6分米学生独立计算,然后指名交流,教师及时了解学生计算情况。
3、一个圆柱形水池,直径10米,深1米。
(1)这个水池占地面积是多少?(2)在池底及池壁抹一层水泥,抹水泥部分的面积是多少?(3)挖成这个水池,共需挖土多少立方米?学生读题后,独立思考并解答,交流时指名学生说说每一个问题要求的是什么?三、综合练习1、求下面圆柱的体积和表面积。
底面半径:3米,高:10米2、有两个底面积相等的圆柱,第一个圆柱的高是第二个圆柱的4/7。
第一个圆柱的体积是24立方厘米,第二个圆柱的的体积比第一个圆柱多多少立方厘米?3、压路机的滚筒是个圆柱,它的长是2米,滚筒横截面半径是1米,如果滚筒每分钟滚动5周,那么10分钟可压路多少平方米?4、在直径0.8米的水管中,水流速度是每秒2米,那么1分钟流过的水有多少立方米?四、补充练习:课前思考:通过本课练习,让学生在解决实际问题的过程中,进一步理解和掌握圆柱的体积公式,感受所学的数学知识的应用价值。
圆柱的表面积练习课2
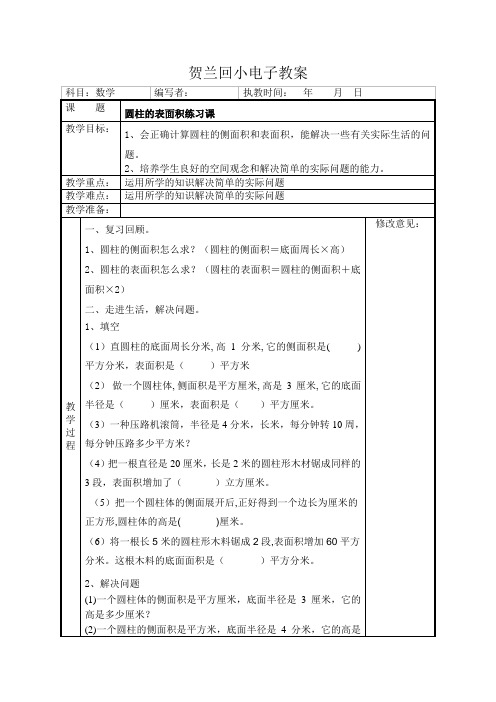
1、圆柱的侧面积怎么求?(圆柱的侧面积=底面周长×高)
2、圆柱的表面积怎么求?(圆柱的表面积=圆柱的侧面积+底面积×2)
二、走进生活,解决问题。
1、填空
(1)直圆柱的底面周长分米,高1分米,它的侧面积是()平方分米,表面积是()平方米
(2)做一个圆柱体,侧面积是平方厘米,高是3厘米,它的底面半径是()厘米,表面积是()平方厘米。
(5)做5节底面直径是2分米,长8分米的圆柱形通风管,至少需要多少铁皮?
(6)某宾馆大堂有6根圆柱形大柱,高10米,大柱周长分米,要全部涂上油漆,如果按每平方米的油漆费为80元计算,需用多少钱?
(7)一个没有盖的圆柱形铁皮水桶,高是24厘米,底面直径是20厘米,做这个水桶至少要用铁皮多少平方厘米?(接口处不计,得三、布置作业: 练习题
四、回顾全课,课堂小结。
这节课你有哪些收获?
修改意见:
板书设计
圆柱的表面积练习课
圆柱的侧面积=底面周长×高
圆柱的表面积=圆柱的侧面积+底面积×2
长方体的表面积=(长×宽+长×高+宽×高)×2
正方体的表面积=棱长×棱长×6
贺兰回小电子教案
科目:数学
编写者:
执教时间:年月日
课题
圆柱的表面积练习课
教学目标:
1、会正确计算圆柱的侧面积和表面积,能解决一些有关实际生活的问题。
2、培养学生良好的空间观念和解决简单的实际问题的能力。
教学重点:
运用所学的知识解决简单的实际问题
教学难点:
运用所学的Байду номын сангаас识解决简单的实际问题
教学准备:
教学过程
2、解决问题
(1)一个圆柱体的侧面积是平方厘米,底面半径是3厘米,它的高是多少厘米?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
答:它的高是15dm。
如果一段圆柱形的木头,截成两截, 它的表面积会有什么变化呢?
表面积增加了
一个圆柱形木棒,底面半径2厘米,高3厘米, 截成两截,表面积之和增加( )平方厘 C 米。
A: 15.7
B:12.56
C:25.12
一个圆柱形木棒,底面半径2厘米,高3厘米, 沿底面直径纵剖,表面积之和增加( ) 平方厘米。 B
答:他用了2355平方厘米的彩纸。
3 (1)底面直径: 12 9(dm) 4
(2)铁皮面积: 3.14×(9÷2)2+3.14×9×12 =63.585+339.12
=402.705(dm2) 答:做这个水桶大约要用402.705dm2铁皮。
188.4÷(2×3.14×2) =188.4÷12.56 =15(dm)
圆柱表面积=底面周长×(半径+高)
(1)花布的面积(侧面积): 3.14×18×80 =56.52×80 =4521.6(cm2) (2)黄布的面积(两个底面积): 3.14×(18÷2)2×2 =254.34×2 =508.68(cm2)
答:花布需要4521.6平方厘米,黄布需要508.68平方厘米。
达 标 检 测
1、计算下面各圆柱的侧面积和表面积。 ①C=9.42厘米,h=5厘米 ②d=8米,h=3米 ③r=2分米,h=6分米 2、填空。 ①用一张长5厘米、宽8厘米的长方形纸围成一个圆 柱体,这个圆柱体的侧面积是( 40 )平方厘米。 ②做一节底面直径是10厘米、长95厘米的圆柱体 通风管,至少用一张长( 314 )厘米宽( 95 )厘 米的长方形铁皮。
一台压路机的 滚筒长2米,直径为 1.2米。如果它滚动 100周,压路的面积 是多少平方米?
1.2×3.14×2=7.536(平方厘米)
要 包 装 100 个 圆 柱形易拉罐的侧面, 至少共需要多少平方 分米的广告纸?(得
数保留整数)
练
习
二
横切
纵切
(1)横切成两个圆柱,表面积之和发生了什么变化? 横切成3个圆柱呢? (2)一个圆柱从底面圆心纵切成两半,表面积之和 发生了什么变化?
=3.14 × 50 + 3.14×120 =3.14 × 10 × 17
=157+ =3.14 ×367.8 170
22 =533.8(cm =533.8(cm ))
πr2×2+2πr×h =2πr2+2πr×h =2πr×r+2πr×h
=2πr×(r+h)
底面周长×(半径+高)
13.求下面各图形的表面积。
3.14×3.5×12 =3.14×42
=131.88(cm2)
答:制作中间的轴需要131.88cm2的硬纸板。
提示:求彩纸的面积就是用灯笼的表面积减去两个78.5㎝2
(1)侧面积:3.14×20×30=1884(cm)2 (2)底面积:3.14×(20 ÷2)2×2=628(cm)2
(3)彩纸的面积:1884+628-78.5×2=2355(cm)2
13.求下面各图形的表面积。
(10×10)×2+(10×15)×4 =100×2+150×4 =200+600 =800(cm2)
13.求下面各图形的表面积。
62×6 =36×6 =216(cm2)
13.求下面各图形的表面积。
2× 3.14 ×5 2+ × 3.14×5×12 2 ×3.14 × 5× (52 + 12)
圆柱的表面积 练习课
复习:
1.把圆柱体的侧面沿高展开, 可能得到一个( 长方 )形,
也可能得到一个( 正方 )
2. 把一个圆柱侧面沿高展开, 可得到一个长方形, 这个 长方形的长等于圆柱的(底面周长 ), 宽等于圆柱( 高)。 3. 圆柱两底面之间的( 有( 无数 )条。 4.圆柱的侧面积= 5.圆柱的表面积= 距离 )叫做它的高, 它的高
A: 12 B:24 C:25.12
一根圆柱形木材长 20 分米 , 把截成 4 个相等 的圆柱体,表面积增加了 18.84 平方分米。 求底面的面积是多少。
人的大脑和肢体一样, 多用则灵,不用则废。
-茅以升
