同济大学朱慈勉结构力学第4章习题答案.doc
同济大学朱慈勉结构力学第4章习题答案.doc
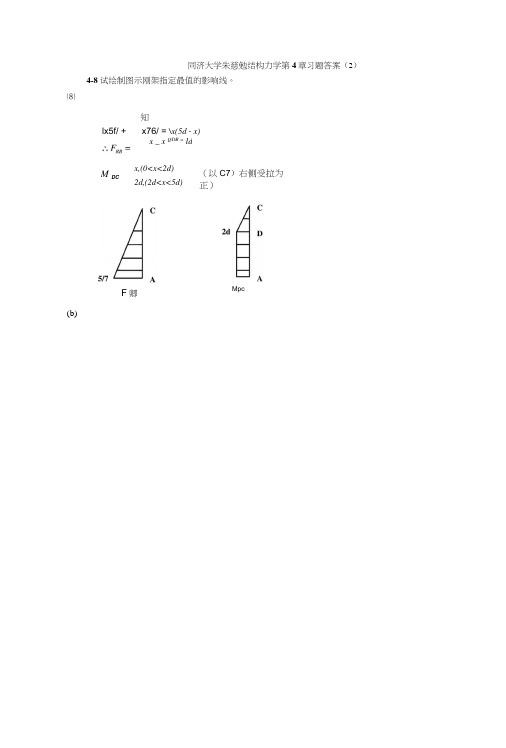
同济大学朱慈勉结构力学第4章习题答案(2)4-8试绘制图示刚架指定最值的影响线。
⑻知lx5f/ + x76/ = \x(5d - x)MDCx _ x QDB = ldx,(0<x<2d)2d,(2d<x<5d)(以C7)右侧受拉为正)(b) F卿Mpc以A为坐标原点,向右为x轴正方向。
弯矩M以右侧受拉为正当0<x<a时;£M F=O + F RA=l — i(T) a分析F以右部分,GCD为附属部分,可不考虑当寸,去掉AF, GCD附属部分结构,分析中问部分M E=(2a~x), F NE = —1<x< 4^/时,由= 0知M E=x-4a, E RD=-―—=—-3,F NE =-4 + —a a a1XF NE的影响线4-9试绘制图示桁架指定杆的内力影响线,分别考虑荷载为上承和卜'承河种情况。
(a)上承荷载时:以A点为坐标原点,句右力X轴正方向。
F RA=1-^(T)当0S*<8(C点以左财,取卜1截面左侧考虑由= 0 —>F N3 = |(10% — x) — (1 xl0|/2 = —i当12幺;^20( D点以右)时,(1-—)x10音 _ 5由E M T = 0 4 F N3 =——22_ =F N3在CD之间的影响线用C点及£>的值。
直线相连。
=0^1_^+当0 2x^8时,取1-1截面左侧分析由F N2 sin45° =1知F N2=-x-y/2 由SF>0^F N1=-F3 +F N2CO s45、4-i下承荷载情况可同样方法考虑(b)= O^lx(8^/-x) = F RA x8d/^F RA=1-上承荷载时当O<x0时, S4d<x<8M SO<x< 4樹,取1 -1截面右侧分析。
I F; = 0 4 F N, x取1 -1截面左侧分析0^F y=0^F NI 取2-2截而右侧分析。
(完整版)完整的结构力学答案-同济大学朱慈勉
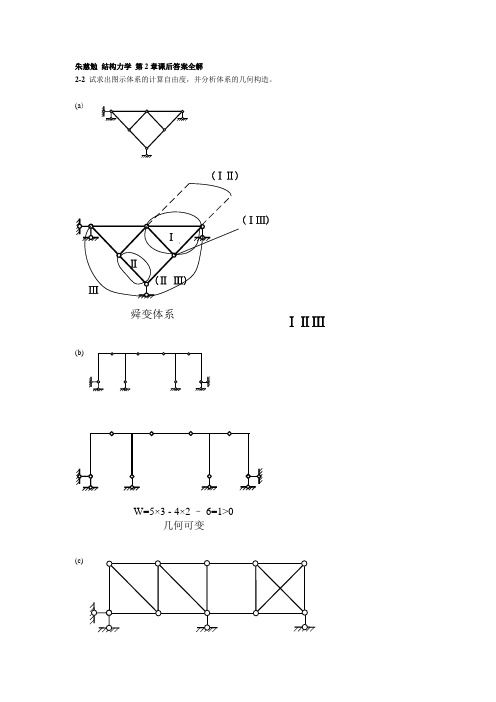
朱慈勉 结构力学 第2章课后答案全解2-2 试求出图示体系的计算自由度,并分析体系的几何构造。
(a )(ⅠⅡ)(ⅠⅢ)舜变体系ⅠⅡⅢ(b)W=5×3 - 4×2 – 6=1>0几何可变(c)有一个多余约束的几何不变体系(d)W=3×3 - 2×2 – 4=1>0可变体系2-3 试分析图示体系的几何构造。
(a)(ⅡⅢ)Ⅲ几何不变2-4 试分析图示体系的几何构造。
(a)几何不变(b)W=4×3 -3×2 -5=1>0几何可变体系(ⅠⅢ)(ⅡⅢ)几何不变(d)Ⅲ(ⅠⅢ)有一个多余约束的几何不变体(ⅠⅢ)(ⅡⅢ)(ⅠⅡ)舜变体系(f)(ⅠⅢ)(ⅡⅢ)无多余约束内部几何不变(h)二元体W=3×8 - 9×2 – 7= -1, 有1个多余约束2-5 试从两种不同的角度分析图示体系的几何构造。
(a)(ⅠⅢ)ⅠⅡⅢ(ⅠⅡ)(ⅡⅢ)舜变体系(b)Ⅲ(ⅡⅢ)(ⅠⅢ)同济大学朱慈勉 结构力学 第3章习题答案3-2 试作图示多跨静定梁的弯矩图和剪力图。
(a)2P F a 2P F a4P F Q34P F 2P F(b)aaaa a2m6m2m4m2m2020Q10/326/310(c)18060(d)3m2m2m3m3m4m3m2m2m2mA2m 2m2m2m7.5514482.524MQ3-3 试作图示刚架的内力图。
(a)242018616MQ18(b)4kN ·m 3m3m6m1k N /m2kN A CBD6m10kN3m3m 40kN ·mABC D30303011010QM 210(c)45MQ(d)3m3m 6m6m2m 2m444444/32MQN(e)4481``(f)4m4m2m3m4m222220M3-4 试找出下列各弯矩图形的错误之处,并加以改正。
(a)F P(b)(c)(d)(e)(f)F3-5 试按图示梁的BC 跨跨中截面的弯矩与截面B 和C 的弯矩绝对值都相等的条件,确定E 、F 两铰的位置。
同济大学朱慈勉 结构力学 第4章习题答案(1).

同济大学朱慈勉结构力学第 4章习题答案(14-5 试用静力法作图示结构中指定量值的影响线。
(alF P =1M A 、 F Q A 、 M C 、F Q C, 10, 0(( , 1(A QA P C QC P C QC M x F F C M F x a F C M x a a x F x a =-== =≤=--=-=≥坐标原点设在 A处,由静力平衡可知当在点以左时, 当在点以右时, M A 的影响线F Q A 的影响线M C 的影响线的影响线(b1R B 、 M C 、 F Q C/(/,(0(,( ,( ,( cos ,(0 (1,( C QC A x l x l a l x a l a x a M aa x a a x l x a l xx a l F x a x l l αα=-≤≤⎧⨯-≤⎧⎪==⎨⎨⨯>-≥≥⎩⎪⎩⎧-≤≤⎪⎪=⎨⎪-≤≤⎪⎩RB RB RB RA 以为坐标原点,方向如图所示假设 F 向上为正,由静力分析知 F F F F R B 的影响线 M C 的影响线F 2a cos lα(1alα-F Q C 的影响线(cF N CD 、 M E 、 M C 、 F Q C R 3355 041(7 05121232(5,(05532,(5753,(030,(373311,(03 ,(03544371,(37 ,(37 544B NCD NCD NCDENCDCNCDRQCNCDM F x F xF x xMF xx xMxF x x xFF x x x=⨯⨯-⨯-=→=- ⎧⨯⨯--≤≤⎪⎪=⎨⎪⨯⨯≤≤⎪⎩-≤≤⎧=⎨≤≤⎩⎧⎧-≤≤-≤≤⎪⎪⎪⎪==⎨⎨⎪⎪≤≤-≤≤⎪⎪⎩⎩∑由知,3NCDF 的影响线 EM 的影响线CM 的影响线341RQCF 的影响线(d5mM C 、 F Q C 111 , ,848 RB C QC Dx x x F M F---===以点为坐标原点,向右为正1494189 8CM 的影响线 QCF 的影响线(e1,(0 0,(0, 0,(7 1,(70,(05 ,(05 , 1,(57 4,(57LR QAQA QC C x a x a F F a x a a x a x a x a x a F M a x a a a x a -≤≤≤≤⎧⎧==⎨⎨≤≤≤≤⎩⎩≤≤-≤≤⎧⎧==⎨⎨≤≤≤≤⎩⎩2a 4a F Q A 、 F Q A 、 F Q C 、 M CL R(fF R A 、 F Q B 、 M E 、 F Q F1,(02 ,(02 , 220,(25 0,(25,(02 ,(0 423,(2, ,(242220,(25 5,(45 22RA QB E QF x xx a x a F F a aa x a a x a x xx a x a a x xM a a x a F ax a aa x a x a x a a ⎧⎧-≤≤-≤≤⎪⎪==⎨⎨⎪⎪≤≤≤≤⎩⎩⎧⎧≤≤≤≤⎪⎪⎪⎪⎪⎪=-≤≤=-≤≤⎨⎨⎪⎪≤≤⎪⎪-≤≤⎪⎪⎩⎩11RA F 的影响线QB F 的影响线a/21/21/21/2E M 的影响线QF F 的影响线4-6 试用机动法作图示结构中指定量值的影响线。
结构力学1-9章答案
1 8
2 36
1 4
3 ( 1 3 2 1 6 2 (3) 1 (6))
6EI 2
2
+ 2 6 1 2 5 ()
6EI
2EI
(c)
2kN/m 6m
2kN 2kN
B 2EI C
EI
EI
1
A
D
3m 3m 3m
1 6
2
2
3
3
42
18
36
30
6
MP
M
xc
6
3 2EI
(2
18
2
0
C
F RC [( 1 ) a] a (方向与图示一致)
h
h
(b)
c1 c2 c3
A A′
2a
BC
D
B′ C′
D′
Δ C
a
2a
1
0.5
1.5
0
FR 图
yc
t h
M ds
t
5 4
5
+t 5 5 t (1) 12 t ( 1 4 3 2 4 3)
4
2
h2
54.5t()
5-10 试求图示结构在支座位移作用下的位移:(a) ΔC ;(b) ΔyC , ΔC 。 (a)
C D
D′
E E′
C′ΔC
h
b
A
l 2
B
B′
l 2
a
1
1
1
h
h
0
A
B
C
D
E
FG
H
2m 2m 2m 2m 2m 2m 2m 3m
A
M 7.5
结构力学课后习题答案(朱慈勉)

朱慈勉 结构力学 第2章课后答案全解2-2 试求出图示体系的计算自由度,并分析体系的几何构造。
(a)(ⅠⅡ)(ⅠⅢ)舜变体系ⅠⅡⅢ(b)W=5×3 - 4×2 – 6=1>0几何可变(c)有一个多余约束的几何不变体系(d)W=3×3 - 2×2 – 4=1>0可变体系2-3 试分析图示体系的几何构造。
(a)(ⅡⅢ)Ⅲ几何不变2-4 试分析图示体系的几何构造。
(a)几何不变(b)W=4×3 -3×2 -5=1>0几何可变体系(ⅠⅢ)(ⅡⅢ)几何不变(d)Ⅲ(ⅠⅢ)有一个多余约束的几何不变体(ⅠⅢ)(ⅡⅢ)(ⅠⅡ)舜变体系(f)(ⅠⅢ)(ⅡⅢ)无多余约束内部几何不变(h)二元体W=3×8 - 9×2 – 7= -1, 有1个多余约束2-5 试从两种不同的角度分析图示体系的几何构造。
(a)(ⅠⅢ)ⅠⅡⅢ(ⅠⅡ)(ⅡⅢ)舜变体系(b)Ⅲ(ⅡⅢ)(ⅠⅢ)同济大学朱慈勉 结构力学 第3章习题答案3-2 试作图示多跨静定梁的弯矩图和剪力图。
(a)2P F a 2P F a4P F Q34P F 2P F(b)aa aaa2m6m2m4m2m2020Q10/326/310(c)18060(d)3m2m2m3m3m4m3m2m2m2mA2m 2m2m2m7.5514482.524MQ3-3 试作图示刚架的内力图。
(a)242018616MQ18(b)4kNm3m3m6m1k N /m2kN A CBD6m10kN3m3m 40kNmABC D30303011010QM 210(c)45MQ(d)3m3m6m6m2m 2m444444/32MQN(e)4481``(f)4m4m2m3m4m222220M3-4 试找出下列各弯矩图形的错误之处,并加以改正。
(a)F P(b)(c)(d)(e)(f)F3-5 试按图示梁的BC 跨跨中截面的弯矩与截面B 和C 的弯矩绝对值都相等的条件,确定E 、F 两铰的位置。
结构力学答案-同济大学朱慈勉

FP
FP
4
1
FP
4
31
3
2
FP 2
பைடு நூலகம்
2
B
FP
1
3 4
FP
C
1
.1
2
3
.
4
FN1 = −
2 2 FP
∑ . 由 MB = 0,可求得FC = 0.75FP
.
X1
X2
D
FN 3 =
2 2
FP
∑ 由 MD = 0,可求得x1 = −FP → x2 = FP
由节点法,对C分析可求得FN 2
=
FP 4
3-15 试求图示桁架各指定杆件的内力。 (a)
qa 2
qa 2 2
qa 2qa
1.5qa
3-11 试指出图示桁架中的零杆。
1.5qa
FP
FP
页 19 / 180
结构力学答案-同济大学朱慈勉
FP
FP
FP
、
3-12 试求图示桁架各指定杆件的内力。 (b)
3m
3 ×3m
先求出支座反力,如图所示。零杆亦示于图中。 取1-1截面以上部分分析
F3
FBC
然后再依次隔离A, B, D点不难求得 F2 = −7.5KN (−), FBD = 3KN , F1 = −4KN (−)
=
0
→
FB x
=
4 3
P
∑ M C = 0 → FN 4 = −2P
1C
3 2 4D
2P 5 P FP
2
∑
取虚线所示的两个隔离体有:
M B = 0,
2 2
×
FN 2
结构力学 第四章 作业参考答案

结构力学 第四章习题 参考答案2005级4-1 图示抛物线拱的轴线方程24(fy x l l=−)x ,试求截面K 的内力。
解:(1) 求支座反力801155 kN 16AV AV F F ×=== 0805(5580)0.351500.93625 kN 16BV BV F F ×==−×+×== 0Mc 55880350 kN 4H F f ×−×===(2) 把及代入拱轴方程有:16m l =4m f =(16)16xy =−x (1)由此可得:(8)tan '8x y θ−==(2) 把截面K 的横坐标 ,代入(1),(2)两式可求得: 5m x ==>, 3.44m y =tan 0.375θ= 由此可得:20.56θ= 则有sin 0.351θ=,cos 0.936θ=最后得出截面k 处的内力为: (上标L 表示截面K 在作用力左边,R 则表示截面在作用力右边)055550 3.44103 kN m K H M M F y =−=×−×=i0cos sin 550.936500.35133.93 kN L sK s H F F F θθ=−=×−×= (5580)0.936500.35140.95 kN R sK F =−×−×==40.95 KN 0sin cos 550.351500.93666.1 kN L NK s H F F F θθ=+=×+×= (5580)0.351500.93638.03 kN R NK F =−×+×=4-2 试求拉杆的半圆三铰拱截面K 的内力。
解:(1)以水平方向为X 轴,竖直方向为Y 轴取直角坐标系,可得K 点的坐标为:2m6mK K x y =⎧⎪⎨==⎪⎩ (2)三铰拱整体分别对A ,B 两点取矩,由平衡方程可解得支座反力:0 20210500 20210500 2100A By B Ay x Ax M F M F F F ⎧=×−××⎪⎪=×+××⎨⎪=−×=⎪⎩∑∑∑=== => 5 kN ()20 kN () 5 kN ()Ay Ax By F F F =−⎧⎪=−⎨⎪=⎩向下向上向左(3)把拱的右半部分隔离,对中间铰取矩,列平衡方程可求得横拉杆轴力为:CN 0 105100MF =×−×∑=>N 5 kN F =(4)去如图所示的α角,则有:=>cos 0.6sin 0.8θθ=⎧⎨=⎩于是可得出K 截面的内力,其中:22(6)206525644 kN m 2K M ×=−+×−×−×=isK F (20265)sin 5cos 0.6 kN θθ=−×−×−×=− NK F (20265)cos 5sin 5.8 kN θθ=−−×−×−×=−13K M F r Fr ==(内侧受拉) K 截面作用有力,剪力有突变 且有01sin3032LSK 2F F F F =−=−×=− (2) 22R SK F FF F =−=(3)011sin30(326NKF F F F ==×=拉力)(4)4-4 试求图示三铰拱在均布荷载作用下的合理拱轴线方程。
同济大学朱慈勉 结构力学 第4章习题答案(1).

同济大学朱慈勉结构力学第 4章习题答案(14-5 试用静力法作图示结构中指定量值的影响线。
(alF P =1M A 、 F Q A 、 M C 、F Q C, 10, 0(( , 1(A QA P C QC P C QC M x F F C M F x a F C M x a a x F x a =-== =≤=--=-=≥坐标原点设在 A处,由静力平衡可知当在点以左时, 当在点以右时, M A 的影响线F Q A 的影响线M C 的影响线的影响线(b1R B 、 M C 、 F Q C/(/,(0(,( ,( ,( cos ,(0 (1,( C QC A x l x l a l x a l a x a M aa x a a x l x a l xx a l F x a x l l αα=-≤≤⎧⨯-≤⎧⎪==⎨⎨⨯>-≥≥⎩⎪⎩⎧-≤≤⎪⎪=⎨⎪-≤≤⎪⎩RB RB RB RA 以为坐标原点,方向如图所示假设 F 向上为正,由静力分析知 F F F F R B 的影响线 M C 的影响线F 2a cos lα(1alα-F Q C 的影响线(cF N CD 、 M E 、 M C 、 F Q C R 3355 041(7 05121232(5,(05532,(5753,(030,(373311,(03 ,(03544371,(37 ,(37 544B NCD NCD NCDENCDCNCDRQCNCDM F x F xF x xMF xx xMxF x x xFF x x x=⨯⨯-⨯-=→=- ⎧⨯⨯--≤≤⎪⎪=⎨⎪⨯⨯≤≤⎪⎩-≤≤⎧=⎨≤≤⎩⎧⎧-≤≤-≤≤⎪⎪⎪⎪==⎨⎨⎪⎪≤≤-≤≤⎪⎪⎩⎩∑由知,3NCDF 的影响线 EM 的影响线CM 的影响线341RQCF 的影响线(d5mM C 、 F Q C 111 , ,848 RB C QC Dx x x F M F---===以点为坐标原点,向右为正1494189 8CM 的影响线 QCF 的影响线(e1,(0 0,(0, 0,(7 1,(70,(05 ,(05 , 1,(57 4,(57LR QAQA QC C x a x a F F a x a a x a x a x a x a F M a x a a a x a -≤≤≤≤⎧⎧==⎨⎨≤≤≤≤⎩⎩≤≤-≤≤⎧⎧==⎨⎨≤≤≤≤⎩⎩2a 4a F Q A 、 F Q A 、 F Q C 、 M CL R(fF R A 、 F Q B 、 M E 、 F Q F1,(02 ,(02 , 220,(25 0,(25,(02 ,(0 423,(2, ,(242220,(25 5,(45 22RA QB E QF x xx a x a F F a aa x a a x a x xx a x a a x xM a a x a F ax a aa x a x a x a a ⎧⎧-≤≤-≤≤⎪⎪==⎨⎨⎪⎪≤≤≤≤⎩⎩⎧⎧≤≤≤≤⎪⎪⎪⎪⎪⎪=-≤≤=-≤≤⎨⎨⎪⎪≤≤⎪⎪-≤≤⎪⎪⎩⎩11RA F 的影响线QB F 的影响线a/21/21/21/2E M 的影响线QF F 的影响线4-6 试用机动法作图示结构中指定量值的影响线。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
同济大学朱慈勉结构力学第4章习题答案(2)4-8试绘制图示刚架指定最值的影响线。
⑻知lx5f/ + x76/ = \x(5d - x)MDCx _ x QDB = ldx,(0<x<2d)2d,(2d<x<5d)(以C7)右侧受拉为正)(b) F卿Mpc以A为坐标原点,向右为x轴正方向。
弯矩M以右侧受拉为正当0<x<a时;£M F=O + F RA=l — i(T) a分析F以右部分,GCD为附属部分,可不考虑当寸,去掉AF, GCD附属部分结构,分析中问部分M E=(2a~x), F NE = —1<x< 4^/时,由= 0知M E=x-4a, E RD=-―—=—-3,F NE =-4 + —a a a1XF NE的影响线4-9试绘制图示桁架指定杆的内力影响线,分别考虑荷载为上承和卜'承河种情况。
(a)上承荷载时:以A点为坐标原点,句右力X轴正方向。
F RA=1-^(T)当0S*<8(C点以左财,取卜1截面左侧考虑由= 0 —>F N3 = |(10% — x) — (1 xl0|/2 = —i当12幺;^20( D点以右)时,(1-—)x10音 _ 5由E M T = 0 4 F N3 =——22_ =F N3在CD之间的影响线用C点及£>的值。
直线相连。
=0^1_^+当0 2x^8时,取1-1截面左侧分析由F N2 sin45° =1知F N2=-x-y/2 由SF>0^F N1=-F3 +F N2CO s45、4-i下承荷载情况可同样方法考虑(b)= O^lx(8^/-x) = F RA x8d/^F RA=1-上承荷载时当O<x0时, S4d<x<8M SO<x< 4樹,取1 -1截面右侧分析。
I F; = 0 4 F N, x取1 -1截面左侧分析0^F y=0^F NI 取2-2截而右侧分析。
y/5x~~[6dF.KAy/5x 75 =----------- 1 ---I6d23xS M K =0^F RB X3^=F N3X2^^F N3=~^当86/时,取2-2截而左侧分析。
= 0 F RA x4f/ + F N2 x2t/ = 0 F N2 = — - 25 SrX M K = 0 —F KA x 56/ = F N3x2^^F N3=-- —2 16d r7|下称荷载吋,用同样方法分析,得到影响线如下4-13试求图示简支梁在吊车竖向荷载作川下B 支座的最人反力。
设一台吊车轮压为F PI =F P2=285kN ,>}一台 轮压为Fp 3=F P4=250kN,轮距及车挡限位的最小车距如图所示。
B 支座反力的影响线如卜:300综上所述,R max = 548.62/CNF N2NlF P2或F P3置点时,B 支座可能取得最大反力 F P2置于S 点时-x 285+ 285SF P +FPCR _655A2KN>^^=35扁1.92KN<23127:R285+250x(丽+WF P3置于B 点时1 231 27«R B =285+-x285 + 250x(- + -) = 547.5^231 R-300x 285+ 250 79.2A7V 〉ZE L 250 x19 6013.2A7V250 +25() x37.525K/V <PC_19丛=54.9231 19此时R 。
=250+ f - x 285 十 250 x —= 548.62 AW4-15试求在阁示分布移动荷载作用下6支座反力的最大值。
当7.5dS 12时,一二-0.3x + 2.7 = 0^x = 9y 此时八二2. 7x9—81x0.15-7. 425=4. 725 dx 当0<x<7.5日d, A ln .ix = — x7.5 + —= 4.3875 nwx 斗 4 /. A Illax =4.725 4S=qA=4.725x56 = 264.6AW ,此时x = 90求影响线需求得当F P 作用于AB 屮点及K 点两侧吋的^值。
首先,用静力法求得当F p =l 作用于屮点吋F N1 F N2 F N3 M K F QK 的值。
采用节点法 C 节ft个F NCD枳擗对ft 性pQC^ O F QC F QC = F QC途F^c = F QC =则 F MCD = 1 -2F QCF P =1 'DtUiX 样使州节点ifc"JftF N2于是F NCD =j ,F NI =j>/^1.49 F N2=^-^1.37 F N3=|1 2FQK =F QC =7 M K =-F QC X 4 = --(以下侧受拉为正)B 支座的反力影响线如农图所示 求5=(^的最大值设荷载左端距A 结点为X ,求A 1 4 , x x + 4.5, ,广、r 45x Vi-) (0-x -7-5) 6A :1X 18X |-1X -A1 (13.5-x)21.8 4.05 —x + ------- 4 4(0<x<7.5) (7.5<x<12) =-x[1^—^ + 13'5~X]x4.5 (12<x<13.5) 2 5 5-0.15x 2+2.7x-7.425 (7.5<x<12)-0.9x+14.175 (12<x<13.5)17F NCD =乎(1-2F OC )?E 节氏K 枰鞭用法可行J ;M A =O^F N 3=2F (X :,BP采用联合法求解求L F N2已影响线吋,只需求得当心=1作JTI TAB 巾点吋杆1,2,3的轴力。
求人的影响线,需求得当F p =1作用于AB 屮点与K 点吋M K 的值。
FNCD =-2F QCF N2 = —F NCD =-^F QC F NI = ^FNCD= -275F QC F N3 = -F^Z M A =OF N38 = |xl2 + F QC .xl6^F QC =-iF N2的影晌线P0.33Fk 釣影晌线4-11试利川影响线计算阁示荷载作川下吣和的值。
⑻当巧=1作用于K 点时,可把体系看成一对对称荷载与一对反对称荷载的脊加 a.对称体系 由节点法可得... M {K a>=-F QC x4 = lCD 杆轴力等于0->F N1FYB =-| Z M B =°->E2X=()M 卜F YA xl2 = 1.5 F Q V) = F YA YA/.M K =1 + 1.5 = 2.5 F^K =- + - = - F Q L K(b)=M41 3 5FN1的影响线先不考虑力偶产生的内力M K =F yA x3.6 = -6/W 嗜 F Q R K =F yA =-y/W综上所述 M K =64.8-6 二 58.8AW*"7 F Q R K =-18- —= -19.67/C?/64.83 4106 yA 6根据对称性,以二0447试求图示简支梁在移动荷载组作用下的绝对最大弯矩,并与跨中截而的最大弯矩相比较,⑻(b)M K 的影响线2 2 2F Q KK 的影响线50kNF R4mI l50kN I IlOOkN6-—z/z 36-—m3显然,1OOKN 为产生最人弯矩的临界荷载2 2 100x(6——) + 50x(10——)---------- 2 ------------ 2_=S3.3KN122.M K =F yA x(6 + -)-50x4 = 355.6^e/z/当100/C7V 作用于跨中时,跨中弯矩最大5()kNlOOkNM. = 100x3 + 50 = 35()/C7V显然只有300KN和最左的100KN可能是产生最大弯矩的临界荷载对300KN进行分析5<iiF yA = F R x (5 — 0.375) /10 = 31QKN M niax=370x(5-0.375) - 200 x 1.5 = 1411.25 AW • m对100K7V进行分析F R = 800ZW20CKK 30CKX IMBCK 1«KX/= ----------------- ------------------------------------------ -------------- 1 ----------- -------------F yli = F R x(5 - 0.375) /10 = 370AWM max =370x(5 - 0.375) -100x1.5-100x3 = 1261.25AT7V因此,最大冇矩为141 L25KN 所以,当300KN作用于跨中时游中弯矩綾大Al Cmax = 300 x 2.5 + 200 x 1.75 +100 x (1.75 + 1.0 + 0.25) = 1400KN • m。
