北邮通信原理课件A-3随机过程
合集下载
通信原理随机过程

4
通信原理
2.随机过程的均值及相关函数 (时域) (1) 均值: E X (t) mX (t)
任何随机过程都可以看成是一个零均值随机 过程与一个确定函数的和。 X (t) X (t) mX (t)
(2) 相关函数:自相关函数 E X (t1)X (t2) RX (t1,t2) 互相关函数 E X (t1)Y (t2 ) RXY (t1,t2)
(2)自相关函数
RY (t1,t2 ) E[Y (t)Y (t )]
E[ X (t u)X (t v)h(u)h(v)dvdu]
RX ( u v)h(u)h(v)dvdu RY ( )
(6) 零均值随机过程和确定信号之和的功率谱密度为PX ( f ) Pm( f )
7
通返信回原目理录
3.2 平稳随机过程
1.定义 2.各态历经性(遍历性) 3.联合平稳 4.复平稳过程 5.零均值平稳过程通过滤波器 6.平稳序列 7.循环平稳过程
1.定义
(1)严平稳随机过程(狭义平稳)
如果对于任意n和t1, t2 , …,tn以及 有
通信原理
安建伟
北京科技大学通信工程系
第3章随机过程
3.1 随机过程的统计特性 3.2 平稳随机过程 3.3 高斯过程 3.4 高斯白噪声 3.5 匹配滤波器
2
通信原理
引言
为什么研究随机过程?
– 通信中,信号、干扰、噪声等都是随机信号, 具有一定的统计规律性。
– 随机过程是随机信号的数学模型。
研究什么?
T 2T T
时间平均
1T
lim x(t)
x(t )dt
北邮通信原理讲义
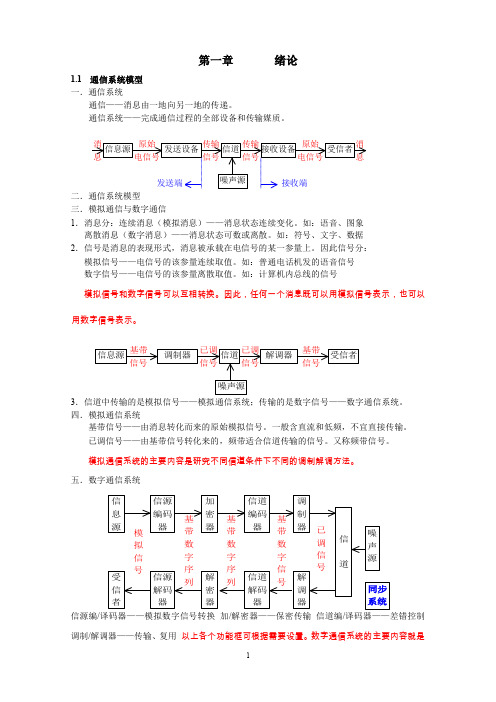
线性 时移 频移 比例
a
n 1
n f n (t )
a
n 1
N
n
Fn ( w)
f (t t 0 ) f (t ) e jw0t
f (at )
F ( w) e jwt0 F ( w w0 )
1 F ( w a) a
2f (w)
对偶 复共轭 微 分 时域
F (t )
f * (t )
S f ( w)dw S f ( f )df
பைடு நூலகம்
5.无限周期信号的平均功率和功率谱密度 功率谱密度 S f ( w) 2
n
| C
n
| 2 ( w nwT ) , 平均功率 P
n
| C
n
|2
Cn 为各个频率点的幅度,|Cn|2 为 nwT 分量的平均功率 四.信号通过线性系统 1.系统的传递函数 以冲激函数 δ (t)作为激励,通过系统后
信噪比
信号平均功率 噪声平均功率
二.数字通信系统性能指标 1. 速度指标 码元速率 RBN:每秒传送码元的数目。单位:B 信息速率 Rb:每秒传送的信息 量。单位:b/s, bps Rb = RBN log2 N (bit/s) 2. 质量指标 误码率 P B:码元被错误接收的概率。 误信率 Pb:传输每比特信息发生错误接收的概率。
第二章
2.1 确知信号的频谱分析 一.付立叶变换
随机信号分析
任一信号有两种表示方法:时域表示法 f (t ) :信号的大小随时间的变化。
频域表示法 F ( w) :信号的振幅和相位随频率成分的变化。两种表示法互相对应,记做:
f (t ) F (w) 。变换式为: f (t )
通信原理-随机过程课件

一个随机过程在时间上是否具有某种 稳定的统计特性。如果一个随机过程 在长时间观察下表现出稳定的统计特 性,则称该随机过程具有遍历性。
遍历性的数学描述
对于一个随机过程,如果存在一个常 数$c$,使得对于任意的时间$t$,有 $E[X(t)]=c$,则称该随机过程具有遍 历性。其中$X(t)$表示在时刻$t$的随 机变量的取值。
标量乘法
标量乘法满足结合律和分 配律,即对于任意标量a 和任意随机过程X,有 a(X+Y)=aX+aY。
线性变换的应用
信号处理
在通信系统中,信号经常 需要进行线性变换以实现 调制、解调、滤波等操作 。
控制系统
在控制系统中,线性变换 被广泛应用于系统的分析 和设计,如传递函数、状 态方程等。
图像处理
在图像处理中,线性变换 被广泛应用于图像的增强 、滤波、变换等操作。
04
CATALOGUE
随机过程的平稳性
平稳性的定义
平稳性定义
一个随机过程如果对于任何正整数n,以及任何非负整数k,其n维联合分布函 数与n+k维联合分布函数相同,则称该随机过程是严平稳的。
数学表达式
若对于任意的正整数n和任意的非负整数k,都有P(X_1, X_2, ..., X_n) = P(X_1+k, X_2+k, ..., X_n+k),则称随机过程{X_t}是严平稳的。
06
CATALOGUE
随机过程的功率谱密度
功率谱密度的定义
功率谱密度
表示随机信号的功率随频率的分布, 是描述随机信号频域特性的重要参数 。
定义方式
功率谱密度函数通常由傅里叶变换来 定义,将随机信号的时域表示转换为 频域表示。
遍历性的数学描述
对于一个随机过程,如果存在一个常 数$c$,使得对于任意的时间$t$,有 $E[X(t)]=c$,则称该随机过程具有遍 历性。其中$X(t)$表示在时刻$t$的随 机变量的取值。
标量乘法
标量乘法满足结合律和分 配律,即对于任意标量a 和任意随机过程X,有 a(X+Y)=aX+aY。
线性变换的应用
信号处理
在通信系统中,信号经常 需要进行线性变换以实现 调制、解调、滤波等操作 。
控制系统
在控制系统中,线性变换 被广泛应用于系统的分析 和设计,如传递函数、状 态方程等。
图像处理
在图像处理中,线性变换 被广泛应用于图像的增强 、滤波、变换等操作。
04
CATALOGUE
随机过程的平稳性
平稳性的定义
平稳性定义
一个随机过程如果对于任何正整数n,以及任何非负整数k,其n维联合分布函 数与n+k维联合分布函数相同,则称该随机过程是严平稳的。
数学表达式
若对于任意的正整数n和任意的非负整数k,都有P(X_1, X_2, ..., X_n) = P(X_1+k, X_2+k, ..., X_n+k),则称随机过程{X_t}是严平稳的。
06
CATALOGUE
随机过程的功率谱密度
功率谱密度的定义
功率谱密度
表示随机信号的功率随频率的分布, 是描述随机信号频域特性的重要参数 。
定义方式
功率谱密度函数通常由傅里叶变换来 定义,将随机信号的时域表示转换为 频域表示。
北邮 移动通信原理课件

10
BUPT Information Theory & Technology Education & Research Center
• 在前三代移动通信中,除了上述物理层关键技术的不 断发展外,在网络层其功能也在逐步完善。它主要体 现有: • 1)网络协议逐步走向规范化,到了第三代(3G)已初步形 成了横向三层:物理层、链路层、网络高层;纵向两 个平面:用户业务平面与控制平面的初步规范结构。 • 2)逐步增强并完善网络层辅助物理层实现对三重动态 性的匹配功能,加强并完善对无线资源管理、移动性 管理以及接入分配、调度算法的实现。 • 3)第二代(2G)开始逐步引入智能网,实现交换与控制的 分离,并通过业务生成系统快速生成新业务。
第一章 绪 论
• §1.1 移动通信的主要特点
• 移动通信是通信领域中最具有活力,最具有发 展前途的一种通信方式。它是当今信息社会中 最具有个性化特征的通信手段。它的发展与普 及改变了社会也改变了人类的生活方式,它让 人们领悟到现代化与信息化的气息。 • 移动通信,顾名思义其最本质的特色是“移动” 二字,就是说这类通信不是传统静态的固定式 通信,而是动态的移动式通信。
4
BUPT Information Theory & Technology Education & Research Center
1.2 移动通信的发展
•移动通信,确切地说蜂窝式移动通信,就正式商业运营 而言,至今也不过只有20多年的历史,就其发展历程 看,大约每十年更新一代。目前正处于第二代(2G)与第三 代(3G)交接期。 •自上世纪八十年代我国引入模拟式(TACS)移动通信网以 来,经过短短二十多年的发展,截止2002年底,我国已 拥有2亿以上的移动通信用户,成为全球头号移动用户大 国。我国的第一代移动通信TACS系统目前已完成其历史 任务而被淘汰;第二代移动通信GSM系统是全球第一, 规模最大、用户最多,CDMA系统目前也是数一数二, 并即将成为全球第一;第三代移动通信,我国目前还处 于即将投入运营的阶段。
BUPT Information Theory & Technology Education & Research Center
• 在前三代移动通信中,除了上述物理层关键技术的不 断发展外,在网络层其功能也在逐步完善。它主要体 现有: • 1)网络协议逐步走向规范化,到了第三代(3G)已初步形 成了横向三层:物理层、链路层、网络高层;纵向两 个平面:用户业务平面与控制平面的初步规范结构。 • 2)逐步增强并完善网络层辅助物理层实现对三重动态 性的匹配功能,加强并完善对无线资源管理、移动性 管理以及接入分配、调度算法的实现。 • 3)第二代(2G)开始逐步引入智能网,实现交换与控制的 分离,并通过业务生成系统快速生成新业务。
第一章 绪 论
• §1.1 移动通信的主要特点
• 移动通信是通信领域中最具有活力,最具有发 展前途的一种通信方式。它是当今信息社会中 最具有个性化特征的通信手段。它的发展与普 及改变了社会也改变了人类的生活方式,它让 人们领悟到现代化与信息化的气息。 • 移动通信,顾名思义其最本质的特色是“移动” 二字,就是说这类通信不是传统静态的固定式 通信,而是动态的移动式通信。
4
BUPT Information Theory & Technology Education & Research Center
1.2 移动通信的发展
•移动通信,确切地说蜂窝式移动通信,就正式商业运营 而言,至今也不过只有20多年的历史,就其发展历程 看,大约每十年更新一代。目前正处于第二代(2G)与第三 代(3G)交接期。 •自上世纪八十年代我国引入模拟式(TACS)移动通信网以 来,经过短短二十多年的发展,截止2002年底,我国已 拥有2亿以上的移动通信用户,成为全球头号移动用户大 国。我国的第一代移动通信TACS系统目前已完成其历史 任务而被淘汰;第二代移动通信GSM系统是全球第一, 规模最大、用户最多,CDMA系统目前也是数一数二, 并即将成为全球第一;第三代移动通信,我国目前还处 于即将投入运营的阶段。
通信原理教程3-随机过程

X (t1 ) 和 X (t2 ) 分别是在时刻
t1 、 t 2 观察X(t)
得到的两个随机变量。自相关函数表示在两个时 刻对同一个随机过程抽样的两个随机值的相关程 度。
平稳随机过程
平稳随机过程的定义:
统计特性与时间起点无关的随机过程。 所谓平稳随机过程,是指它的统计特性不随时间的推移 而变化。 设随机过程{X(t),t∈T},若对于任意n和任意选定t1 <t2<…<tn, tk∈T, k=1, 2, …, n,以及h为任意值,且 x1, x2, …, xn∈R,有
随机过程的统计特性
随机过程的统计特性用分布函数、概率密度函数或数字 特征来描述。 设X(t)表示一个随机过程,在任意给定的时刻t1∈T, 其 取值X(t1)是一个一维随机变量。而随机变量的统计特性可以 用分布函数或概率密度函数来描述。我们把随机变量X(t1)小 于或等于某一数值x1 的概率P[X(t1)≤x1 ],简记为FX(x1, t1), 即 FX(x1,t1)=P[X(t1)≤x1]
E[ ST j d
R( ) PX ( f )e
j
df
上式表明,PX(f )和R( )是一对傅里叶变换:
PX(f
)的性质:
PX(f ) 0, 并且PX(f )是实函数。 PX(f ) =PX(-f ),即PX(f )是偶函数。
【例】某随机相位余弦波X(t)=Acos(ωc t+θ), 其中A和ωc均为常数,θ是在(0, 2π)内均匀分 布的随机变量。 (1) 求X(t)的自相关函数与功率谱密度; (2) 讨论X(t)是否具有各态历经性。
解 (1) 先考察ξ(t)是否广义平稳。 X(t)的数学期望为
t1 、 t 2 观察X(t)
得到的两个随机变量。自相关函数表示在两个时 刻对同一个随机过程抽样的两个随机值的相关程 度。
平稳随机过程
平稳随机过程的定义:
统计特性与时间起点无关的随机过程。 所谓平稳随机过程,是指它的统计特性不随时间的推移 而变化。 设随机过程{X(t),t∈T},若对于任意n和任意选定t1 <t2<…<tn, tk∈T, k=1, 2, …, n,以及h为任意值,且 x1, x2, …, xn∈R,有
随机过程的统计特性
随机过程的统计特性用分布函数、概率密度函数或数字 特征来描述。 设X(t)表示一个随机过程,在任意给定的时刻t1∈T, 其 取值X(t1)是一个一维随机变量。而随机变量的统计特性可以 用分布函数或概率密度函数来描述。我们把随机变量X(t1)小 于或等于某一数值x1 的概率P[X(t1)≤x1 ],简记为FX(x1, t1), 即 FX(x1,t1)=P[X(t1)≤x1]
E[ ST j d
R( ) PX ( f )e
j
df
上式表明,PX(f )和R( )是一对傅里叶变换:
PX(f
)的性质:
PX(f ) 0, 并且PX(f )是实函数。 PX(f ) =PX(-f ),即PX(f )是偶函数。
【例】某随机相位余弦波X(t)=Acos(ωc t+θ), 其中A和ωc均为常数,θ是在(0, 2π)内均匀分 布的随机变量。 (1) 求X(t)的自相关函数与功率谱密度; (2) 讨论X(t)是否具有各态历经性。
解 (1) 先考察ξ(t)是否广义平稳。 X(t)的数学期望为
北邮通信原理讲义

当 T∞时,其平均功率为:
P lim
T
1 T2 2 1 f ( t ) dt T T T 2 2
| FT ( w) | dw lim T T
2
定义:功率谱密度 S f ( w)
| FT ( w) | 2 1 平均功率 P lim 2 T T
|t| |t|
n
Sa(
nw1 ) ( w nw1 ) 2
w1
2 T
A |t| A T (t ) { 0
ASa (
2
w ) 2
4
5 阶越函数
u (t )
( w)
1 jw
6 指数函数
e
a t
2a a w2
2
三.功率谱密度和能量谱密度 1.功率信号:时间无限的信号,具有无限的能量,但平均功率有限。 2.能量信号:时间有限的信号,信号能量有限,在全部时间内的平均功率为 0。 3.信号的功率(能量) :电压(电流) f (t) 加在单位电阻上消耗的功率(或能量) 。 信号的瞬时功率(能量)为 f (t ) ,总功率(能量)为 4.能量信号的能量和能量谱密度
输入信号 f (t) F(w) 系统 h(t) H(w) 输出信号 r (t) R(w)
的响应 h (t)为该系统的传递函数 2.线性系统——满足叠加定理 若激励 f1 (t)和 f2 (t)的响应分别是 r1 (t)和 r2 (t),则激励 af1 (t)+bf2 (t) 的响应是 ar1 (t)+br2 (t)。 3.确知信号通过线性系统 已知:h (t) =δ (t) * h (t) 利用时域卷积定理: R(w)=F(w)H(w) 2.2 随机过程 利用叠加定理: r (t) = f (t) * h (t)
第三章通信原理 随机过程

或随机过程的一次实现。 全部样本函数构成的总
体 x1t, x2 ,t,就,是xn 一t个
随机过程,记作 。
t
因此从这个角度得到随机过程的这种定义: 随机过程是所有样本函数的集合。
角度2:现在,我们在某一特定时刻如 时t1刻观察
各台接收机的噪声,可以发现在同一时刻,每个接 收机的输出噪声值是不同的,它在随机变化。
(1)随机过程的协方差函数:B(t1,t2) 描述了随机过程§(t)在任意两个时刻t1和t2,相对
均值的起伏量之间的相关程度。
B(t1, t2 ) E (t1) a(t1) (t2 ) a(t2 )
B(t1, t2 ) x1 a(t1 ) x2 a(t2 ) f2( x1, x2;t1, t2 )dx1dx2
f1x,t
F1x, t
x
F1x, t
x
f1 y, tdy
F1和x, t f即1x是, t 的函数,x 又是时间 的函数。t很显然,
一维分布函数及一维概率密度函数仅仅表示了随机过程 在任一瞬间的统计特性,它对随机过程的描述很不充分, 通常需要在足够多的时间上考察随机过程的多维分布。
测试结果表明,得到的 n张记录图形并不因为有 相同的条件而输出相同 的波形。恰恰相反,即 使n足够大,也找不到两 个完全相同的波形。这 就是说,通信机输出的 噪声电压随时间的变化 是不可预知的,因而它 是一个随机过程。
N部通信机的噪声输出记录
测试结果的每一个记录, 都是一个确定的时间函
数 ,xi 称t 之为样本函数
式中 是一个离散随机变量,且
P
、0
1 2
P 2, 试12求 和E 1。 R 0,1
体 x1t, x2 ,t,就,是xn 一t个
随机过程,记作 。
t
因此从这个角度得到随机过程的这种定义: 随机过程是所有样本函数的集合。
角度2:现在,我们在某一特定时刻如 时t1刻观察
各台接收机的噪声,可以发现在同一时刻,每个接 收机的输出噪声值是不同的,它在随机变化。
(1)随机过程的协方差函数:B(t1,t2) 描述了随机过程§(t)在任意两个时刻t1和t2,相对
均值的起伏量之间的相关程度。
B(t1, t2 ) E (t1) a(t1) (t2 ) a(t2 )
B(t1, t2 ) x1 a(t1 ) x2 a(t2 ) f2( x1, x2;t1, t2 )dx1dx2
f1x,t
F1x, t
x
F1x, t
x
f1 y, tdy
F1和x, t f即1x是, t 的函数,x 又是时间 的函数。t很显然,
一维分布函数及一维概率密度函数仅仅表示了随机过程 在任一瞬间的统计特性,它对随机过程的描述很不充分, 通常需要在足够多的时间上考察随机过程的多维分布。
测试结果表明,得到的 n张记录图形并不因为有 相同的条件而输出相同 的波形。恰恰相反,即 使n足够大,也找不到两 个完全相同的波形。这 就是说,通信机输出的 噪声电压随时间的变化 是不可预知的,因而它 是一个随机过程。
N部通信机的噪声输出记录
测试结果的每一个记录, 都是一个确定的时间函
数 ,xi 称t 之为样本函数
式中 是一个离散随机变量,且
P
、0
1 2
P 2, 试12求 和E 1。 R 0,1
通信原理课件第3章_随机过程

严平稳随机过程的数字特征: (1)其均值与t无关,为常数a; (2)自相关函数只与时间间隔有关。 4.广义平稳随机过程 把同时满足(1)和(2)的过程定义为广义平稳随机过程。 意义: ●具有各态历经性平稳随机过程--十分有趣,非常有用。
●平稳随机过程的统计特性不随时间的推移而改变,即它的 一维分布函数与时间t无关:
f1 ( x1 , t1 ) f1 ( x1 )
●而二维分布函数只与时间间隔 = t2 – t1有关:
f 2 ( x1 , x2 ; t1 , t 2 ) f 2 ( x1 , x2 ; )
3. 数字特征
E (t ) x1 f1 ( x1 )dx1 a
2017/2/12
通信原理
6
第3章 随机过程
概括:
随机过程ξ(t)的含义/属性有两点: (1)ξ(t)是t 的函数; (2)ξ(t)在任一时刻 t1上的取值ξ(t1)不是确定的,是一个 随机变量。即每个时刻上的函数值是按照一定的概率分布 的。 概率论:随机变量分析--分布函数和概率密度
研究内容--随机过程统计特征: 3.1.1 随机过程的分布函数 3.1.2 随机过程的数字特征
2 (t )
n (t )
t1 t2
t
图3-1 n部接收机的输出波形 讨论: ●在任一给定时刻t1上,每一个样本函数i (t)都是一个确定的 数值i (t1),但是每个i (t1)都是不可预知的--为随机量。 ●换句话说,随机过程在任意时刻t1的值ξ(t1)是一个随机变量。 ●因此,又可以把随机过程看作是在时间进程中处于不同时 刻的随机变量的集合。
2017/2/12
Hale Waihona Puke 通信原理7第3章 随机过程
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三、 高斯白噪声—频域特性
频域特性——近似白噪声
白噪声:功率谱密度在整个频域内都均匀分布 单边功率谱密度函数为: Pn(f)=n0(W/Hz)
Pn(f) n0 0
双边功率谱密度函数 为:Pn(f)=n0/2(W/Hz)
Pn(f) n0/2
f
通信系统中的热噪声,在相当宽的频域内具有 平坦的功率谱,故近似认为是白噪声。
二、统计特性
概率分布 数学期望(均值) 方差 协方差函数 相关函数
1. 概率分布
随机过程ξ(t) 在任一时刻t1的取值是随机变量, 则随机变量ξ(t1)的取值小于等于某一数值x1 的概率为ξ(t)的一维概率分布函数:
F1(x1,t1) P{ (t1) x1}
ξ
(t)的一维概率密度函数:
F1 ( x 1 , t 1 ) f 1 ( x 1 , t1 ) x1
概率分布(续)
ξ (t)的n维概率分布函数和n维概率密度 函数分别是:
Fn (x1, x2 xn ;t1 ,t2 tn ) P{(t1 ) x1, (t2 ) x2 (tn ) xn }
4.概率分布:若ξi(t)是高斯型的,经过线性系统 后的ξo(t)也是高斯型的。
例题
求双边功率谱密度为n0/2(W/Hz)的白噪声通 过理想低通滤波器后的功率谱密度、自相 关函数和噪声功率。
H(f) K
-fH
O
fH
f
二、随机过程通过乘法器(调制器)
平稳随机过程X(t)经过调制器,输出随机过 程Y(t),Y(t)的功率谱为SY(ω),自相关函数为 RY(t, t+τ)
特点
a (t)a; R(t1,t2)R(τ)
特点(续)
各态历经性:设x (t)是ξ(t)的任一实现,ξ(t)的统 计平均= x (t)的算术平均
a a lim
T
1 T2 x(t )dt T T 2
T
R( ) R( ) lim
1 T2 x(t ) x(t )dt T T 2
3.2 随机过程
一、概念 二、统计特性
一、概念
样本函数: 随机过程 的一个实现 随机过程: 样本函数 的集合 任意时刻 的取值为随 机变量
S1
S2 Sn
样本空 间
x1 (t) t
x2 (t)
t
(t )
xn (t) t tk
随机过程没有确定的时间函数,只能从统计角 度,用概率分布和数字特征来描述。
E( X ) xf ( x)dx 定义 物理意义
表示随机变量的均值
性质
C是常数,则E(C)=C。 C是常数,则E(C·X)=C·E(X)。 X 、Y 是 任 意 两 个 随 机 变 量 , 则 E(X+Y)=E(X)+E(Y)。 X 、Y 是 两个 互 相 独立 的 随 机变 量 , 则 E(X· Y)=E(X)· E(Y)。
2 X
随机变量X的协方差
定义 C O V ( X , Y ) Ex E ( X )y E ( Y ) E( X Y ) E( X ) E(Y )
E(XY)称相关函数
物理意义
描述两维随机变量(X,Y)的相互关系
几个概念
独立 不相关 正交 f(x,y)=f(x)f(y) COV(X,Y)=0 E(XY)=0
一、随机过程通过线性系统 二、随机过程通过乘法器(调制器)
一、随机过程通过线性系统
随机过程ξi(t)通过线性系统h (t),其
输出也是随机过程
输入信号 ξi(t) Pi(ω) 系统 h(t) H(ω) 输出信号 ξo (t) Po(ω)
o (t) i (t) h(t)
随机过程通过线性系统(续)
c c c
X
c
c
c
RY(t, t+τ)与t有关,所以Y(t)不平稳,取其时间平均 cos R ( ) R ( t , t ) R ( ) 与t无关, 2
. c Y Y x
SY () RY ( ) 1 SY () [S X ( c ) S X ( c )] 4
意义:随机过程中的任一实现都经历了随机过程的所 有可能状态。因此, 只需从任意一个随机过程的样 本函数中就可获得它的所有的数字特征, 从而使 “统计平均”化为“时间平均”,使实际测量和计算 的问题大为简化。
例题(例3-1)
设一个随机相位的正弦波为 (t) Acos(ct ) 其中,A和c均为常数;是在(0, 2π)内均匀分布的随 机变量。试讨论(t)是否具有各态历经性。 【解】
性质: 若ξi(t)是平稳随机过程,则
1.均值:E[ξo(t)] = E[ξi(t)] H (0)与 t 无关 2.自相关函数:Ro(t1, t1+τ) = Ro(τ) 与t1无关
3.功率谱密度函数:
P () R ( )e
o
j
o
d P () H ()
i
2
1
(2 )
n/2
1 2 ... n B
exp 1/ 2
1 B 2 B j 1 k 1
n
n
( jk
x j aj
x a
k
j
)(
k
k
)
高斯过程只依赖数字特征,即均值和协方差函数 高斯过程若是宽平稳的,也是严平稳的 高斯过程不同时刻的取值若互不相关,则彼此独立 高斯过程经过线性系统后仍是高斯过程 各种起伏噪声,在任一时刻,噪声的振幅都符合 均值a=0的高斯分布,故称为高斯噪声。
随机变量X的方差
定义
D ( X ) E x E ( X ) [ x E ( X )] 2 f ( x ) dx
2
E ( X 2 ) E ( X ) 2
物理意义
表示随机变量与均值的偏离程度
方差一般也 表示,其平方根 X 称为标准方 用差
第三章 随机过程
随机变量 随机过程 平稳随机过程及其特点 高斯过程与高斯白噪声 随机过程通过系统 窄带高斯过程与窄带高斯白噪声 正弦波加窄带高斯噪声
3.1 随机变量
一、概念 二、统计特性 随机变量X,概率密度函数f(x)
三、数字特征 ——数学期望 ——方差 ——协方差
随机变量X的数学期望
fH
f
例题
求随机相位正弦波ξ(t)=Acos(wct+θ)的自相关函数 和功率谱密度,在(0, 2π)内均匀分布。
解:
证明(t)是广义平稳过程 求自相关函数 A2 R( ) cos c 2 2 A 功率谱密度
P () 2
[ ( c ) ( c )]
X (t) S X (w) Cos w c t Y (t) S y (w)
随机过程通过乘法器(续)
R ( t, t ) E[Y (t)Y (t )] E[ X (t) X (t ) cos t cos (t )]
Y c c
E[ X (t) X (t )] [cos cos(2 t )] 2 R ( ) [cos cos(2 t )] 2
f x
1 2π
-x 2 e2
O
a
x
几个定义
定义
概率积分函数: (x) Q函数:
Q(x) 1 2
2
2
x
1
x
exp( z2
z )dz 2 )dz
2
exp (
2
P( x ) Q (
xa
)
误差函数: erf ( x )
互补误差函数: 2 erfc(x) 1 erf ( x )
xx0e z dz2
e
z 2
dz 2Q ( 2 x)
二、高斯白噪声—时域特性
随机过程ξ(t),在任一时刻的取值(随机变量)都 符合高斯分布,则称ξ(t)服从高斯分布。其n维概率 密度函数为: f n (x1 , x2 ,..., xn;t1 , t 2 ,..., tn )
( t)
a (t )
1 ( t ) 2 (t) n (t)
0
t
3. 方差
D( (t)] E{ (t) E[ (t)]}2 2 (t)
物理意义:表示随机过程在某时刻的取值 (随机变量)对该时刻的期望的偏离程度 (t)
σ (t )
1 ( t ) 2 ( t) n ( t)
ξ(t)的平均功率:S = E[ξ2(t)] = R(0) ξ(t)的直流功率:a2 = E2 [ξ(t)] = R(∞) ξ(t)的交流功率:σ2 = R(0) - R(∞)
相关函数其他性质
R(τ)=R(-τ) | R(τ)|≤R(0)
R(0)为上界
特点(续)
以相关函数表示随机过程的频域特性
j () R() R ( ) e d 即:P P ( ) ξ(t)的功率谱:
维纳-辛钦关系 ξ(t)的平均功率:
1 S 2
P ()d
P ( f )df
Po()
即:平均功率= 功率谱曲线下的面积
