通信原理习题课(4)
北邮版通信原理课后习题的答案第四章-精品
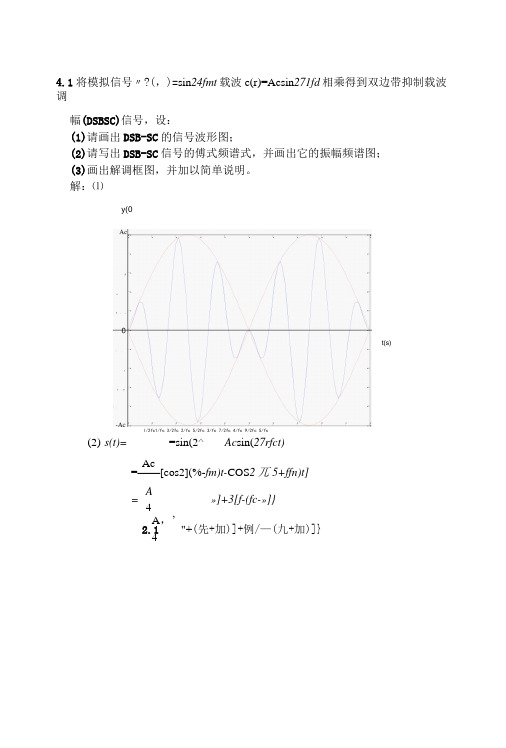
4.1将模拟信号〃?(,)=sin 24fmt 载波c(r)=Acsin 271fd 相乘得到双边带抑制载波调幅(DSBSC)信号,设:(1)请画出DSB-SC 的信号波形图;(2)请写出DSB-SC 信号的傅式频谱式,并画出它的振幅频谱图; (3)画出解调框图,并加以简单说明。
解:⑴(2) s(t)= =sin(2^ Ac sin(27rfct)Ac=——[cos2](%-fm)t-COS 2兀5+ffn)t] A = »]+3[f-(fc-»]} 4A ,’ 2.1 "+(先+加)]+例/—(九+加)]} 4y(0l/2fc1/fc 3/2fc 2/fc 5/2fc 3/fc 7/2fc 4/fc 9/2fc 5/fct(s)S ⑴八3Ac/4- Ac/2.Ac/4(3)相干解调Cos(Wct)与发端相干偏调相干解调:将接收信号与载波信号sin(2乙加)相乘,得至U A cr(t)sin(2^fct)=Acm(t)sin(2^fct)sin(2^fit)=--cos(44fct)]通过低通滤波器抑制载频的二倍频分量,得到解调信号为刈⑺=与机⑺ 2.2 已知某调幅波的展开式为:s(t)=cos(2/rxl()4r)+4COS (2TT xl.lxl040+cos(2万xl.2xl04r) (1)求调幅系数和调制信号频率;(2)写出该信号的傅式频谱式,画出它的振幅频谱图; (3)画出该信号的解调框图。
解:⑴sQ)=cos(24xl04r)+4cos(2乃xl.lxl04r)+cos(2万xl.2xl04r)=4cos(2%xl.lxl04r)[l+0.5cos(2万x0.1xl04r)] 调制系数是a=0.5;信号频率是f=1000Hz(2)S(/)=;U(/+104)+演f —i04)]+2[Mf+l.lxl()4)+5(/—1.1X104)]+-W+1.2X 104)+^(/-1.2X 104)]-fm-fc ・fc -fc+fm。
天津大学现代通信原理课后习题答案(1-4章)

天津大学现代通信原理课后习题答案(1-4章)《现代通信原理》课后习题解答第一章绪论1-1设英文字母C出现的概率为0.023,E出现的概率为0.105,试求C与E的信息量。
11IClog2log25.44bit解:p(某)0.023IElog213.25bit0.1051-2设某地方的天气预报晴占4/8,阴占2/8,小雨占1/8,大雨占1/8,试求各每个消息的信息量。
解:8log21bit晴:阴:2bit小雨:3bit大雨:3bit。
41-3设有四个信息A、B、C、D分别以概率1/4,1/8,1/8和1/2传递,每一消息的出现的是相互独立的。
试计算其平均信息量。
解:1111H(某)P(A)log2P(B)log2P(C)log2P(D)log2P(A)P(B)P(C)P(D)11111111log2log2log2log211114882()()()()48821.75bit/符号1-4一个离散信号源每毫秒发出4种符号中的一个,各相互独立符号出现的概率分别为0.4,0.3,0.2,0.1。
求该信号源的平均信息量与信息传输速率。
解:111H(某)0.4log20.3log20.2log20.40.30.210.2log21.84bit/符号0.21.841840bit/1061-5设一信息源的输出由128个不同的符号组成,其中16个出现的概率为1/32,R其余112个出现概率为1/224,信息源每秒钟发1000个符号,且每个符号彼此独立,试计算该信息源的平均信息速率。
11解:H(某)16(1/32)log2112(1/224)log2(1/32)(1/224)6.405bit/符号Rb6.40510006405bit/第1页共26页1-6设一数字传输系统传递二进制码元的速率为1200B,试求该系统的信息传输速率,若该系统改为8进制码元传递,传码率仍为1200B,此时信息传输速率又为多少?解:Rb=RB=1200b/RbRBlog2N1200log28120033600b/1-7已知二进制数字信号的传输速率为2400b/。
通信原理课程通信原理-习题课

《通信原理》习题课1. 已知二进制OOK 数字通信系统中发送的二元信号是()1cos2c s t A f t π=、()20s t =,持续时间为0b t T ≤<。
OOK 信号传输中受到功率密度为02N 的加性高斯白噪声()n t 的干扰,接收信号为()()()i r t s t n t =+,1,2i =(1)请分别画出最佳相干接收框图。
(2)设s1(t)和s2(t)等概出现,推导相干接收时的平均误比特率。
(知识点:数字频带通信系统)2.设有恒参信道模型如下图所示,求其幅频特性、相频特性、时延特性和群时延特性,并说明它们对信号传输的影响。
(知识点:信道)3.已知在高斯信道理想通信系统传送某一信息所需带宽为106Hz,信噪比为20dB ,若将所需信噪比降低10dB ,求无差错传输所需信道带宽。
(知识点:香农信道容量公式)4.某一待传输的图片约含2.5×106个像素,每像素量化为16个亮度电平。
假若所有这些亮度电平等概出现且互不相关,并设加性高斯噪声信道中的信噪比为30dB ,试计算用3分钟传送一张这样的图片所需的最小信道带宽(假设不进行压缩编码)。
(知识点:信息量计算;香农公式)5.对10路模拟信号分别进行A 律13折线PCM 编码(每样值8比特编码),然后进行时分复用,再经过滚降因子为α=0.5的升余弦脉冲成型滤波器进行无ISI 传输,该升余弦基带系统的截止频率为480kHz 。
(1)求该系统的最大信息传输速率;(2)求允许每路模拟信号的最高频率分量f H 的值。
(知识点:抽样定理;升余弦滤波器带宽)6. 一个由字母A ,B ,C ,D 组成的字。
对于传输的每一个字母用二进制脉冲编码,00代替A ,01代替B ,10代替C ,11代替D ,每个脉冲宽度为5ms 。
(1)不同的字母是等可能出现时,试计算传输的平均信息速率; (2)若每个字母出现的可能性分别为P A =1/5,P B =1/4,P C =1/4,P D =3/10试计算传输的平均信息速率。
通信原理课后练习答案经典.ppt

统计独立。
⑴ 试证明 z(t)是广义平稳的;
⑵ 试画出自相关函数 Rz ( ) 的波形; ⑶ 试求功率谱密度Pz ( f ) 及功率S。
10
.精品课件.
第3章课后作业解答
⑴ 试证明 z(t)是广义平稳的; 只要证明z(t) 的均值为常数,自相关函数仅与时间
间隔 有关即可。
E[z(t )] E[m(t )cos(ct )] E[m(t )] E[cos(ct )]
E{cos[c (t1
t2 )
2 ]
cos[c (t2
t1 )]}
1 2
E{cos[c (t1
t2 )
2 ]}
1 2
cos c
0 12
.精品课件.
第3章课后作业解答
⑵ 试画出自相关函数 Rz ( ) 的波形;
Rz (
)
1 2
Rm (
) cosc
1 / 2 Rz ( )
1
1
⑶ 试求功率谱密度Pz ( f ) 及功率S。 1 / 2
E[m(t1 )cos(ct1 ) m(t2 )cos(ct2 )]
E[m(t1 ) m(t2 )] E[cos(ct1 ) cos(ct2 )]
Rm ( ) E[cos(ct1 ) cos(ct2 )]
E[cos(ct1 ) cos(ct2 )]
1 2
作业 习题:3-5、3-6、3-7、3-8
9
.精品课件.
第3章课后作业解答
3-5 已知随机过程z(t ) m(t )cos(ct ),其中,m(t)
是广义平稳过程,且自相关函数为
1 Rm ( )
1 1 0
Rm ( ) 1 0 1
0
数字通信原理第二版课后习题答案 第4章

即 n =1, k = 3 31 。 根据带通信号的抽样定理,理论上信号不失真的最小抽样频率为
3 k f s = 2 B(1 + ) =2 × 3100 × ( 1 + )= 6800 Hz n 31
13
12
《通信原理》习题第四章
n×
1 1 + =0.3,可求得 n ≈ 3.2,所以量化值取 3。故 c5 c6 c7 c8 =0011。 64 3.93 所以输出的二进制码组为 11100011。 习题 4.8 试述 PCM、DPCM 和增量调制三者之间的关系和区别。 答:PCM、DPCM 和增量调制都是将模拟信号转换成数字信号的三种较简单和
图 4-2 习题 4.4 图
习题 4.5 设有一个均匀量化器,它具有 256 个量化电平,试问其输出信号量噪 比等于多少分贝? 解:由题意 M=256,根据均匀量化量噪比公式得
(S
q
N q )dB = 20 lg M = 20 lg 256 = 48.16dB
习题 4.6 试比较非均匀量化的 A 律和 µ 律的优缺点。 答:对非均匀量化:A 律中,A=87.6; µ 律中,A=94.18。一般地,当 A 越大时, 在大电压段曲线的斜率越小,信号量噪比越差。即对大信号而言,非均匀量化的 µ 律 的信号量噪比比 A 律稍差;而对小信号而言,非均匀量化的 µ 律的信号量噪比比 A 律稍好。 习题 4.7 在 A 律 PCM 语音通信系统中,试写出当归一化输入信号抽样值等于 0.3 时,输出的二进制码组。 解:信号抽样值等于 0.3,所以极性码 c1 =1。 查表可得 0.3 ∈ ( 1 3.93 , 1 1.98 ) , 所以 0.3 的段号为 7, 段落码为 110, 故 c2 c3c4 =110。 第 7 段内的动态范围为: (1 1.98 − 1 3.93) 1 ≈ ,该段内量化码为 n ,则 16 64
通信原理(陈启兴版)第4章课后习题答案

第四章模拟调制4.1学习指导4.1.1要点模拟调制的要点主要包括幅度调制、频率调制和相位调制的工作原理。
1.幅度调制幅度调制是用调制信号去控制载波信号的幅度,使之随调制信号作线性变化的过程。
在时域上,已调信号的振幅随基带信号的规律成正比变化;在频谱结构上,它的频谱是基带信号频谱在频域内的简单平移。
由于这种平移是线性的,因此,振幅调制通常又被称为线性调制。
但是,这里的“线性”并不是已调信号与调制信号之间符合线性变换关系。
事实上,任何调制过程都是一种非线性的变换过程。
幅度调制包括标准调幅(简称调幅)、双边带调幅、单边带调幅和残留边带调幅。
如果调制信号m(t)的直流分量为0,则将其与一个直流量A0相叠加后,再与载波信号相乘,就得到了调幅信号,其时域表达式为stAmttAtmttAM()0()cosc0cosc()cosc(4-1)如果调制信号m(t)的频谱为M(ω),则调幅信号的频谱为1S()πA()()M()M()(4-2)AM0cccc2调幅信号的频谱包括载波份量和上下两个边带。
上边带的频谱结构与原调制信号的频谱结构相同,下边带是上边带的镜像。
由波形可以看出,当满足条件|m(t)|A0(4-3)时,其包络与调制信号波形相同,因此可以用包络检波法很容易恢复出原始调制信号。
否则,出现“过调幅”现象。
这时用包络检波将发生失真,可以采用其他的解调方法,如同步检波。
调幅信号的一个重要参数是调幅度m,其定义为m A m(t)Am(t)0max0minAm(t)Am(t)0max0min(4-4)AM信号带宽B AM是基带信号最高频率分量f H的两倍。
AM信号可以采用相干解调方法实现解调。
当调幅度不大于1时,也可以采用非相干解调方法,即包络检波,实现解调。
双边带信号的时域表达式为stmttDSB()()cosc(4-5)其中,调制信号m(t)中没有直流分量。
如果调制信号m(t)的频谱为M(ω),双边带信号的频谱为1S()M()M()(4-6)DSBcc2与AM信号相比,双边带信号中不含载波分量,全部功率都用于传输用用信号,调制效率达到100%。
现代通信原理与技术 课后习题答案4
则SSB信号的时域表达式
4-10证设AM信号为
式中, 输入噪声为
则解调器输入的信号功率 和噪声功率 分别为
设同步检测(相干解调)中,相干载波为 ,则
故输出有用信号和输出噪AM信号为 ,且 ,则
式中,Pc为载波功率,Ps为边带功率。
又
故
(2)假定 ,则理想包络检波输出为
4-14解(1)该角调波的瞬时角频率为
故最大频偏
调频指数
而最大相偏
因为FM波与PM波的带宽形式相同,即
所以带宽为
(2)因为不知调制信号m(t)的形式,所以无法确定该角调波sm(t)究竟是FM信号还是PM信号。
4-15解:(1)设单音调制信号 ,其中 , ;载波 ,其中A=2, ,则NBFM信号为
而AM信号为
4-1解AM信号
DSB信号
USB信号
LSB信号
频谱图略
4-2解 设载波 ,
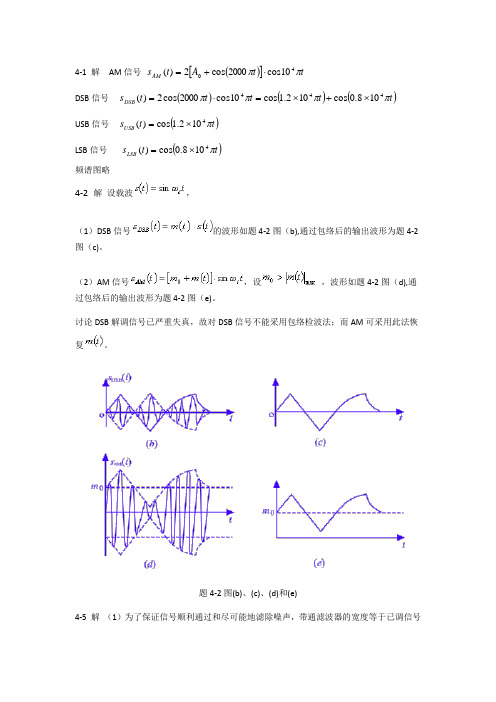
(1)DSB信号 的波形如题4-2图(b),通过包络后的输出波形为题4-2图(c)。
(2)AM信号 ,设 ,波形如题4-2图(d),通过包络后的输出波形为题4-2图(e)。
讨论DSB解调信号已严重失真,故对DSB信号不能采用包络检波法;而AM可采用此法恢复 。
因此输出噪声 的功率谱密度
功率谱图略
4-6解方法如上题
(1)
(2) (3)
4-7解
练习题4-7图接收机模型
(1)设双边带信号 ,则输入信号功率
(2)双边带信号采用相干解调的输出为 ,故输出信号功率
(3)因 ,则
故输出信噪比
或由 ,得
4-8解设发射机输出功率为 ,损耗 ,已知 ,
(1)DSB/SC方式:
现代通信原理与技术课后答案完整版-张辉第四章
4-1 解 AM 信号 ()[]t t A t s AM ππ4010cos 2000cos 2)(⋅+=DSB 信号 ()()()t t t t t s DSB ππππ444108.0cos 102.1cos 10cos 2000cos 2)(⨯+⨯=⋅= USB 信号 ()t t s USB π4102.1cos )(⨯=LSB 信号 ()t t s LSB π4108.0cos )(⨯=频谱图略4-2 解 设载波,(1)DSB 信号的波形如题4-2图(b),通过包络后的输出波形为题4-2图(c)。
(2)AM 信号,设 ,波形如题4-2图(d),通过包络后的输出波形为题4-2图(e)。
讨论DSB 解调信号已严重失真,故对DSB 信号不能采用包络检波法;而AM 可采用此法恢复。
题4-2图(b)、(c)、(d)和(e)4-5 解 (1)为了保证信号顺利通过和尽可能地滤除噪声,带通滤波器的宽度等于已调信号带宽,即kHz f B m 8422=⨯==,其中心频率为100kHz ,故有为常数,其中其他,,K kHzf kHz K H ⎩⎨⎧≤≤=010496)(ω。
(2)已知解调器的输入信号功率W mW S i 31022-⨯==,输入噪声功率为)(1032101021082)(26633W f P B N n i ---⨯=⨯⨯⨯⨯⨯=⋅=故输入信噪比5.62=iiN S (3)因为DSB 调制制度增益2=DSB G ,故解调器的输出信噪比 1252==ii o o N SN S (4)根据相干解调器的输出噪声与输入噪声功率关系)(108416W N N i o -⨯==又因解调器中低通滤波器的截止频率为kHz f m 4=,故输出噪声的功率谱密度kHz f Hz W f N f P m o N o 4)/(1011081082)(336≤⨯=⨯⨯==--, μ 或者,根据相干解调器的输出噪声与输入噪声功率关系)(21)(t n t n c o =,其中)(t n c 是解调器输入端高斯窄带噪声的同相分量,其功率谱密度kHz f Hz W f P f P n nc 4)/(104)(2)(3≤⨯==-, μ因此输出噪声)(t n o 的功率谱密度kHz f Hz W f P f P nc no 4)/(101)(41)(3≤⨯==-, μ 功率谱图略4-6 解 方法如上题 (1)为常数,其中其他,,K kHzf kHz K H ⎩⎨⎧≤≤=010096)(ω(2)125=i i N S (3)125=oo N S4-7 解练习题4-7图 接收机模型(1)设双边带信号,则输入信号功率(2)双边带信号采用相干解调的输出为,故输出信号功率(3)因,则故输出信噪比或由,得4-8 解设发射机输出功率为,损耗,已知,(1)DSB/SC方式:因,则又因,则所以(2)SSB/SC 方式:因,则又因,则所以讨论 若要获得相同的输出信噪比,采用DSB 传输是所需的小于SSB 的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
0
t
T
1 2
fm
图P9-2
解:设抽样信号 q(t) 的中心位置的三角波形为q0(t) 。可见,q0(t)
是两个门函数的卷积,即
q0
(t
)
1
dr
(t
)
d
r
(t
)
其频谱函数 Q0 (w) 为
Q0 (w)
sinc2
w
2
抽样信号q(t) 可表示为 q(t) q0 (t) t nT
解:(1)由抽样频率 fs 8kHz
,可知抽样间隔 T 1 1 (s)
fs 8000
又对抽样信号8级量化,故需要3位二进制码编码,每个码元占
用的时间为
Tb
T 3
1 3 8000
1 (s) 24000
因为占空比为1,所以每个码元的矩形脉冲宽度
Tb
1 (s) 24000
故PCM基带信号频谱第一零点频率
m s (t)
H1(w)
m s (t)
m(t)
H2 (w)
r (t)
发送端
接收端 (b)
解:(1)M (w) 通过 H1(w) 后的最高频率仍为 f1 ,故抽样速率 为 fs 2 f1
(2)若抽样速率 fs 3 f1 ,理想抽样信号 ms (t) 的频谱M s (w)如图
9-18所示
Ms(w)
(1)试问抽样速率应为多少?
(2)若抽样速率fs 3 f1,试画出已抽样信号ms (t) 的频谱;
(3)试问接收端的接收网路应具有怎样的传输函数H2(w) , 才能由 ms (t) 不失真地恢复 m(t) ?
1 M(w)
w1
w1
H1(w)
1
m(t)
w 2w1
(a)
2w1 w
图P9-1
m'(t)
9-1 已知一低通信号 m(t) 的频谱 M ( f ) 为
M
(
f
)
1
|f| 200
0
| f | 200Hz 其他
(1)假设以 fs 300 Hz 的速率对m(t) 进行理想抽样,试画 出抽样信号ms (t) 频谱草图;
(2)若用 fs 400 Hz 的速率抽样,重做上题。
解:(1)由题意知,已抽样信号为 ms (t) m(t) T (t)
MS( f )
300
MS( f )
400
150
-200
0 200 300 f (a)
-200 0 200 400
f
(b)
图9-16 频谱图(—)
9-2 已知一基带信号m(t) cos2t 2 cos4t ,对其进行 理想抽样: (1)为了在接收端能不失真地从抽样信号ms (t) 中恢复m(t) , 试问抽样间隔应如何选择? (2)若抽样间隔取为0.2s,试画出已抽样信号的频谱图。
解:(1)接收端收到的码组c1c2c3c4c5c6c7c8 01010011 。由c1 0 知,信号为负值;由段落码 c2c3c4 101 知,信号样值位于第6
段,起点电平为256,量化间隔为16;由段内码 c5c6c7c8 0011
(采用折叠码)可知,信号样值位于第6段的第5级(序号为4),
x)dx
0.75
(
x
0.5)2
(0.75
x)dx
0.25
0.25
0.75
4 (x
0.5)2
(0.5
0.5
x)dx
0.25
0.75
4 (x 0.25
0.5)2 0.5dx
0.75
(x
0.25
0.5)3
dx
1 48
信号功率
Sq
3
2
4
1
2 (1
0.5
x)dx
1 4
2
0.5
2 (1
Tb
1 (s) 240000
故传输此时分复用PCM信号所需的奈奎斯特基带带宽
B 1 120(kHz)
2
9-14 一单路话音信号的最高频率为4kHz,抽样频率为 8kHz,以PCM方式传输。设传输信号的波形为矩形脉冲,
其宽度为 ,且占空比为1;
(1)若抽样后信号按8级量化,试求PCM基带信号频谱的 第一零点频率; (2)若抽样后信号按128级量化,则PCM基带信号频谱的 第一零点频率又为多少?
)
1 T
M(f
n
nfs )H ( f )
2
T
M(
n
f
nfs )sinc(2
f)
式中,T
1 2 fm
,
fs
2
fm
9-6 设输入抽样器的信号为门函数Gr (t) ,宽度 20ms , 若忽略其频谱第10个零点以外的频率分量,试求最小抽样频 率。
解:门函数的频谱函数为
G( f ) sinc( f ) 它的第一个零点频率 f 1 50Hz ,其余零点之间的间隔为
故译码器输出
I0
256
4 16
16 2
328
(2)均匀量化11位码为
00101000000
9-11 采用13折线A律编码,最小量化间隔为1个量化单位, 已知抽样脉冲值为-95量化单位; (1)试求此时编码器输出码组,并计算量化误差;
(2)试写出对应于该7位码(不包括极性码)的均匀量化 11位码。
3 f1
3w1
w1
w1
3w1
w
图9-18 频谱图(三)
(3)根据信号无失真传输原理,接收网络的传输函数 H1(w)
应设计为
1
H
2
(w)
H1
(
w)
w w1
0
w w1
此时能由ms (t) 不失真的恢复出 m(t)
9-4 已知信号m(t) 的最高频率为 fm ,若用图P9-2所示的q(t)
对m(t) 进行抽样,试确定已抽样信号频谱的表达式,并画出 其示意图。
解:(1)因为样值为负值,所以极性码c1 0 ,而64 95 128
所以码组位于第四段,段落码为 c2c3c4 011 ,量化间隔为4. 由于95 64 74 3,所以段内码为 c5c6c7c8 0111
故编码器输出为
c1c2c3c4c5c6c7c8 00110111
量化误差为3个单位。
解:因为25 40 26 ,所以所需的二进制码组的位数 N 6
量化级间隔
v 20 0.5(V ) 40
9-8 已知模拟信号抽样值的概率密度 f (x) 如图P9-3所示。 若按4电平进行均匀量化,试计算信号量化噪声功率比。
解:量化间隔 x 2 0.5
f (x)
4
1
量化区间终点依次为:
1
2
M (w) Q(w)
1
T
M
(w) Q0 (4 nfm )
n
w
4 nfm
1
T
Q0 (4
n
nfm )
w
4
nfm
T
sinc2 (2 nfm )
n
w
4 nfm
M (w)和 M s (w)的频谱如图9-19(a)和9-19(b)所示。
M (w)
Ms(w)
wm
0
wm
w
2
0
图9-19 频谱图(四)
B 1 24(kHz)
(2)若抽样信号128级量化,故需要7位二进制码编码, 每个码元的矩形脉冲宽度为
Tb
T 7
1 7 8000
1 (s) 56000
故PCM基带信号频谱第一零点频率
B 1 56(kHz)
9-15 若12路话音信号(每路信号的最高频率均为4kHz) 进行抽样和时分复用,将所得的脉冲用PCM系统传输, 重做上题。
M s f fs M ( f nfs ) 5 M ( f 5n)
n
其频谱图如图9-17所示。
MS( f )
5
2.5
-4 -2 0
2
4
f
图9-17 频谱图(二)
9-3 已知某信号m(t) 的频谱 M (w) 如图P9-1(a)所示。将它通 过传输函数为 H1(w) 的滤波器(如图P9-1(b))后再进行理想 抽样。
解:12路信号时分复用后传输,所需带宽相应扩大12倍,所以
(1)B 24 12 288 (kHz) (2)B 56 12 672 (kHz)
n
其频谱函数 Q(w) 为
Q(w)
Q0 (w)
2
T
w nn2T将T1 2 fm
和Q0(w) 的表达式代入上式,可得
Q(w)
2
T
Q0 (4nfm ) w 4nfm
n
若用 q(t) 对m(t) 进行抽样,则已抽样信号ms (t) 为
ms (t) m(t)q(t)
其频谱为
MS
1 ,所以第10个零点的位置 f10 10 f1 500 Hz 。忽略第
10个零点以外的频率分量后,最小抽样频率为 fs 2 f10 1000 Hz
9-7 设信号 m(t) 9 Acoswt ,其中 A 10V 。若 m(t)被均
匀量化为40个电平,试确定所需的二进制码组的位数N和
量化间隔 v 。
n
式中,q(t)是宽度为 2 、幅度为1抽样脉冲,其频谱函数(即
脉冲形成电路的传输函数)为
Q( f ) H ( f ) 2 sinc(2 f )
ms (t)是理想抽样信号,其频谱函数为
M S ( f )
1 T
M(f
n
nfs )
故已抽样信号的频谱为
M H (F )
MS( f
