第一讲 平行线的构造与应用
平行线课件

通过平行线的判定定理可以推导 出平行线的性质,同样地,通过 平行线的性质也可以推导出平行
线的判定定理。
06
平行线在实际生活中的应用
BIG DATA EMPOWERS TO CREATE A NEW
ERA
在工程制图中的应用
01
02
03
04
平行线在工程制图中被广泛应 用,例如在机械制图、电子工 程制图和土木工程制图等领域
平行线还用于确定建筑物的对 称性和比例,以确保建筑物外 观的协调性和美感。
在道路设计中的应用
在道路设计中,平行线被用来确 定道路的路径和宽度。
平行线还用于确定路标、交通标 志和道路边界等元素的位置。
通过使用平行线,道路设计师可 以确保道路的连续性和安全性, 以及为驾驶员提供清晰的导航指
示。
THANKS
感谢观看
两把直角尺
准备工具
两把直角尺。
移动第一把直角尺
将第一把直角尺移动到下一个位置,并重 复上述步骤,直到画出所需的平行线。
描线
沿着第二把直角尺的边缘描出直线。
固定第一把直角尺
将第一把直角尺放置在画板上,并使其保 持水平。
调整第二把直角尺
将第二把直角尺的一边紧贴第一把直角尺 ,并将另一边调整到与第一把直角尺成90 度角。
02 03
详细描述
根据平行线的性质,如果两条直线平行于第三条直线,那么这两条直线 上与第三条直线相交的点到第三条直线的距离相等。利用这个性质,我 们可以证明线段相等。
示例
在三角形ABC中,AB平行于CD,那么AB和CD上的高相等。
用于证明两直线平行
总结词
平行线可以用于证明两直线平行 。
平行线的性质课件

利用平行线性质解决几何最值问题
平行线定义:在同一平面内,永不 相交的两条直线
几何最值问题:求线段、角度、面 积等几何量的最大值或最小值
添加标题
添加标题
添加标题
添加标题
平行线性质:平行线之间的线段相 等
利用平行线性质解决几何最值问题 的方法:通过平行线之间的线段相 等,找到几何量的最大值或最小值
平行线的性质在解析几 何中的应用
面的交点
平行线与平面 的夹角:平行 线与平面的夹 角为直线与平
面的夹角
平行线与平面的 平行性:平行线 与平面的平行性 为直线与平面的
平行性
总结与思考
总结平行线的性质及其应用
平行线的定义: 在同一平面内, 永不相交的两
条直线
平行线的性质: 平行线之间的 角度相等,平 行线之间的线
段相等
平行线的应用: 在几何证明、 工程测量、建 筑设计等领域
利用平行线性质解决函数问题
平行线与函数的 关系:平行线是 函数的基本性质 之一,可以应用 于求解函数问题
平行线性质的应 用:利用平行线 性质可以求解函 数的最大值、最 小值、极值等问
题
平行线性质的证 明:利用平行线 性质可以 在更高级的数学 领域中也有广泛 的应用,如微积 分、线性代数等
平行线的性质在代数中 的应用
利用平行线性质解决线性方程组问题
平行线性质:两条直线平行,同位角相等
线性方程组:一组线性方程组成的方程组
利用平行线性质解线性方程组:通过观察方程组中的同位角,找出方程组中的平行线, 从而解出方程组
应用实例:求解线性方程组,如3x+2y=5,4x+3y=6,通过观察方程组中的同位角, 找出方程组中的平行线,从而解出方程组
平行线构造和应用讲义(含答案)
二、平行线中构造平行线
5. 已知 AB ∥ CD,点 P 为平面内一点,连接 AP、CP. (1) 探究:如图 (1)∠PAB = 145°,∠PCD = 135°,则 ∠APC 的度数是; 如图 (2)∠PAB = 45°,∠PCD = 60°,则 ∠APC 的度数是. (2) 在图 2 中试探究 ∠APC ,∠PAB,∠PCD 之间的数量关系,并说明理由. (3) 拓展探究:当点 P 在直线 AB ,CD 外,如图 (3)、(4) 所示的位置时,请分别直接写出 ∠APC ,∠PAB,∠PCD 之间的数量关系.
·2·
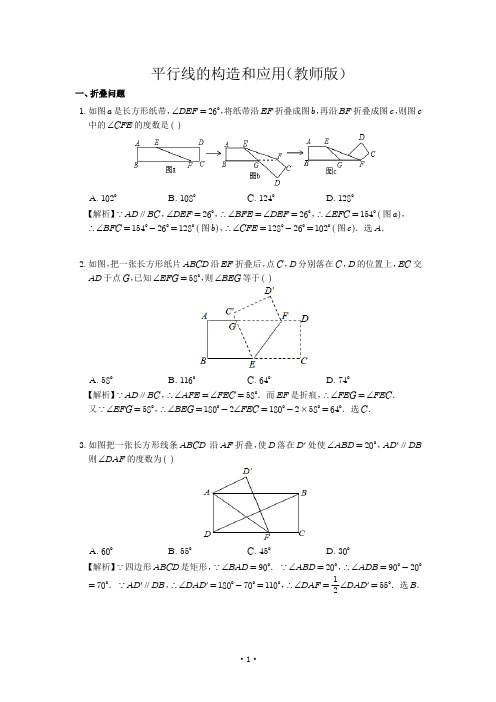
6. (1) 如图①,∠CEF = 90°,点 B 在射线 EF 上,AB ∥ CD,若 ∠ABE = 130°,求 ∠C 的度数; (2) 如图②,把 “∠CEF = 90°” 改为 “∠CEF = 120°”,点 B 在射线 EF 上,AB ∥ CD. 猜想 ∠ABE 与 ∠C 的数量关系,并说明理由.
3. 如图把一张长方形线条 ABCD 沿 AF 折叠,使 D 落在 D′ 处使 ∠ABD = 20°,AD′ ∥ DB 则 ∠DAF 的度数为 ( )
A. 60°
B. 55°
C. 45°
D. 30°
【解析】∵ 四边形 ABCD 是矩形,∵ ∠BAD = 90°. ∵ ∠ABD = 20°,∴ ∠ADB = 90° - 20° = 70°. ∵ AD′ ∥ DB,∴ ∠DAD′ = 180° - 70° = 110°,∴ ∠DAF = 21 ∠DAD′ = 55°.选 B.
【解析】(1) 如图 1,分别过点 E,F 作 EM ∥ AB,FN ∥ AB, ∴ EM ∥ AB ∥ FN ,∴ ∠ B = ∠ BEM = 30 ° ,∠ MEF = ∠EFN ,又 ∵ AB ∥ CD,AB ∥ FN ,∴ CD ∥ FN , ∴ ∠D + ∠DFN = 180°,又 ∵ ∠D = 120°,∴ ∠DFN = 60°, ∴ ∠BEF = ∠MEF + 30°,∠EFD = ∠EFN + 60°, ∴ ∠EFD = ∠MEF + 60° ∴ ∠EFD = ∠BEF + 30° = 90°; (2) 如图 1,分别过点 E,F 作 EM ∥ AB,FN ∥ AB, ∴ EM ∥ AB ∥ FN ,∴ ∠ B = ∠ BEM = 30 ° ,∠ MEF = ∠EFN ,又 ∵ AB ∥ CD,AB ∥ FN ,∴ CD ∥ FN , ∴ ∠D + ∠DFN = 180°,又 ∵ ∠D = 120°,∴ ∠DFN = 60°, ∴ ∠BEF = ∠MEF + 30°,∠EFD = ∠EFN + 60°, ∴ ∠EFD = ∠MEF + 60°,∴ ∠EFD = ∠BEF + 30°;
平行线课件

三角形内角和定理
01
三角形三个内角之和等于180度。
平行线与三角形内角关系
02
若一条直线平行于三角形的一条边,则该直线与三角形另外两
边所构成的同位角或内错角相等。
应用举例
03
通过平行线的性质,可以方便地求出三角形中某个内角的度数
,或者证明三角形内角之间的关系。
利用平行线证明三角形相似或全等
相似三角形判定
如果两个三角形对应的角相等, 那么这两个三角形相似。平行线 可以方便地构造出对应角相等的
条件。
全等三角形判定
如果两个三角形在对应角相等的 同时,还有一对对应边相等,那 么这两个三角形全等。平行线同
样可以辅助证明全等条件。
应用举例
在证明三角形相似或全等时,可 以通过构造平行线来找到对应角 或对应边,从而简化证明过程。
典型例题解析与思路拓展
解析
作DF平行于AB交AC于F点。由于DF平行于AB且AD = DE,根据平行线性质和等腰三 角形性质可知,角DFC等于角ABC且DF = CE。又因为AB = AC,所以角ABC等于角 ACB。因此,角DFC等于角DCB。根据等腰三角形性质可知,BD = DF。所以BD = CE
在性。
综合法
结合观察法、作图法和 代数法等多种方法,综 合分析平行线的存在性
。
图形变换下平行线
05
保持性质探究
平移变换下平行线保持性质说明
平移变换不改变图形的形状和大小, 因此平行线在平移后仍然保持平行。
在平移过程中,平行线之间的距离也 不会发生变化。
平移变换可以沿着任意方向进行,但 无论方向如何,平行线的性质都保持 不变。
四边形的性质
平行线ppt课件

02
平行线判定方法的 误用
提醒学生注意不同判定方法的使 用条件和限制,避免误用或混淆。
03
忽略平行线的存在 性
提醒学生在解题时,不要忽略题 目中可能存在的平行线,否则可 能导致解题错误。
拓展延伸内容推荐
平行线与相似三角形的关系
探讨平行线与相似三角形之间的联系,以及如 何利用平行线的性质解决相似三角形的问题。
交通信号灯
交通信号灯中的红灯、绿灯、黄灯等灯光的排列 也遵循平行线的原则,使得驾驶员和行人能够清 晰地辨认交通信号。
导向标志 道路两侧的导向标志牌上的文字、图案等也采用 平行线排列,方便驾驶员快速获取道路信息。
日常生活用品设计美学体现
家居用品
家居用品中的桌子、椅子、床等家具的设计中经常运用到平行线, 使得家具外观简洁大方,符合现代审美。
图形示例
判定步骤
首先确定两条被截直线和截线,然后 找出同旁内角并测量其角度之和是否 为180度,如果是,则两条直线平行。
在图形中,画出两条被第三条直线所 截的直线,并标出同旁内角。
实际应用场景分析
建筑设计中
在建筑设计中,平行线的概念经常被用来确保建筑物的稳定性和美观性。例如,在设计墙壁、 地板和天花板时,需要确保它们是平行的,以避免出现倾斜或不平整的情况。
在物理学中,平行线的概念被广泛应用于光 学、力学等领域的研究中,如光的反射、折 射等现象都与平行线密切相关。
计算机图形学
工程测量与建设
在计算机图形学中,平行线的绘制和处理是 图形渲染、图像处理等任务中的重要环节之 一。
在工程测量与建设中,平行线的运用可以确 保建筑物的精确度和稳定性,提高工程质量。
05
预备工作
建议学生提前预习相关知识点,回顾平行线的定义、性质及判 定方法,并尝试思考一些与平行线相关的实际问题,为下一讲 的学习做好准备。
平行线的性质及应用

平行线的性质及应用平行线是几何学中的重要概念,它在许多数学问题和实际应用中起到了重要的作用。
本文将探讨平行线的性质以及其在几何学和实际生活中的应用。
一、平行线的定义与性质平行线是指在同一个平面内,永不相交的两条直线。
根据平行线的定义,我们可以得出以下性质:1. 平行线的对应角是相等的:当两条平行线被一条横截线所交叉时,同位角(对应角)是相等的。
这个性质被称为同位角性质。
2. 平行线的内错角是互补的:当两条平行线被一条横截线所交叉时,内错角(相邻内角)之和等于180度。
这个性质被称为内错角性质。
3. 平行线的外错角是相等的:当两条平行线被一条横截线所交叉时,外错角(相邻外角)是相等的。
这个性质被称为外错角性质。
这些基本性质使得平行线成为几何学中一个重要的对象。
通过这些性质,我们可以解决许多几何问题。
二、平行线的应用1. 三角形的判定平行线的性质可以用来判定三角形之间的关系。
例如,当一条直线与两条平行线相交时,我们可以通过内错角性质得到两个内角是互补的,从而判定这个三角形是直角三角形。
2. 平行四边形的性质平行线的性质在研究平行四边形时也起到了重要的作用。
平行四边形是指具有两对平行边的四边形。
通过平行线的性质,我们可以证明平行四边形的对边相等、对角线等分等一系列性质。
3. 实际应用平行线不仅在几何学中有重要应用,在实际生活中也扮演着重要角色。
以下是几个实际应用的例子:a) 建筑设计:在建筑设计中,平行线的概念用来确定墙壁和地板的平行关系,确保建筑结构的稳定和美观。
b) 路网规划:在城市规划中,平行线可以用来规划并确定道路的位置和方向,使交通更加便利和高效。
c) 测量和绘图:在测量和绘图中,平行线用于确保准确和精确的测量和绘制。
例如,在制作地图时,通过描绘平行线网格,可以更好地表示地理信息。
总结:平行线在几何学和实际应用中都具有重要地位。
通过了解平行线的定义与性质,我们可以解决许多几何问题,并应用于实际生活中的建筑设计、道路规划以及测量绘图等领域。
平行线课件

3
隧道测量
在隧道测量中,平行线的概念被用于确定隧道的 走向和截面形状,以及测量隧道内部的各项参数 。
其他领域中的平行线应用
摄影
在摄影中,平行线的概念被用于构图和视觉引导,例如利用平行线 来引导观众的视线,突出照片的主题。
艺术
在艺术创作中,平行线的概念被用于创造平衡、和谐和动态感,例 如在绘画、雕塑和建筑艺术中都可以看到平行线的运用。
平行线间夹角
两条平行线间的夹角等于它们与 x轴或y轴夹角的差。
利用坐标系解决平行线问题
判断两直线是否平行
01
通过比较两直线的斜率或方向向量,可以判断它们是否平行。
求两平行线间的距离
02
利用两平行线的方程,可以求出它们之间的距离。
解决平行线与其他几何图形的问题
03
结合坐标系和几何图形的性质,可以解决平行线与点、线段、
计算机图形学
在计算机图形学中,平行线的概念被用于生成三维模型的线条和轮廓 ,以及进行光线追踪和渲染等计算。
06
总结与回顾
重点知识点总结
平行线的定义和性质
在同一平面内,不相交的两条直线叫做平行线。平行线的性质包 括同位角相等、内错角相等、同旁内角互补等。
平行线的判定方法
通过同位角、内错角或同旁内角的关系,可以判定两条直线是否平 行。
截距相等法
在直角坐标系中,如果两 条直线与同一坐标轴的截 距相等,则这两条直线平 行。
方向向量法
在向量空间中,两条直线 平行当且仅当它们的方向 向量共线。
平行线与坐标轴夹角关系
平行线与x轴夹角
平行于x轴的直线与x轴夹角为0° ,倾斜角也为0°。
平行线与y轴夹角
平行于y轴的直线与y轴夹角为 90°,倾斜角不存在。
认识平行线ppt优秀课件

平行线理论的发展历程
随着数学的发展,人们对平行线 理论的认识逐渐深入。
中世纪欧洲数学家进一步探索了 平行线的性质和定理,并尝试解
决一些关于平行线的难题。
19世纪,非欧几里德几何学的 出现对平行线理论产生了深远影 响,人们开始认识到平行线并非
总是相交于无穷远点。
平行线在现代数学中的应用
01
02
03
02 平行线的应用
CHAPTER
几何作图中的应用
平行线在几何作图中具有重要作用, 可以用于确定图形的基本形状和尺寸 。
平行线还可以用于解决几何作图问题 ,例如通过平行线将一个复杂图形分 解为简单图形,便于分析和计算。
通过平行线,可以绘制出各种几何图 形,如三角形、四边形、圆形等,为 进一步研究几何性质和定理奠定基础 。
03 平行线的历史与发展
CHAPTER
平行线理论的起源
平行线理论最早可以追溯到古 希腊时期,当时数学家们开始 研究几何学,并探索了平行线 的性质和定义。
欧几里德在《几何原本》中首 次给出了平行线的定义,并研 究了它们的性质和定理。
古希腊数学家还发现了一些关 于平行线的有趣定理,如“平 行线间的角相等”和“同位角 相等”。
平行线具有传递性、同位角相等、内 错角相等、同旁内角互补等性质。
平行线的表示方法
用平行符号“//”表示两条直线平行 。
平行线的性质
同位角相等
内错角相等
两条平行线被一条横截线所截,同位角相 等。
两条平行线被一条横截线所截,内错角相 等。
同旁内角互补
平行线的性质的应用
两条平行线被一条横截线所截,同旁内角 互补,即两个同旁内角之和为180度。
在线性代数中,向量空间中的子空间可以由平行线定义,而线性变换可以用来研究平行线的 性质和行为。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一讲平行线的构造与应用
1、如图1,直线A B∥CD,∠EFA=30°,∠FGH=90°,∠HMN=30°,∠CNP=50°,则∠GHM
的大小是。
2、图2中ABCD是个直角梯形(∠DAB=∠ABC=90°),以AD为一边向外作长方形ADEF,
其面积为6.36平方厘米,连结BE交AD于P,连结PC,求图中阴影部分的面积是多少平方厘米?
3、如图3所示,AB∥ED,∠1=∠A+∠E,∠2=∠B+∠C+∠D,证明∠2=2∠1。
4、如图4,在折线ABCDEFG中,已知∠1=∠2=∠3=∠4=∠5,延长AB、GF交于点M,试探
索∠AMG与∠3的关系,并说明理由。
5、如图5,已知AB∥EF,∠C=90°,求x+y-z的度数。
6、 如图6,已知,CD ∥EF ,∠C +∠F =∠ABC ,求证AB ∥GF 。
7、 如图7,已知AB ∥CD ,∠EAF =41∠EAB ,∠ECF =41∠ECD ,求证:∠AFC =4
3∠AEC 。
8、如图8,点E 、F 分别是矩形ABCD 的边AB 、BC 的中点,连AF 、CE 交于点G ,则S □AGCD :S □ABCD = 。
9、如图9,AB ∥CD ,EP ⊥FP ,已知∠1=30°,∠2=20°,则∠F 的度数为 。
10、如图10,CD 是⊿ABC 的角平分线,D E ∥AC 交BC 于点E ,EF ∥CD 交AB 于点F ,求证:EF 平分∠BED 。
11、已知:如图11,∠A +∠C +∠E =∠B +∠D +∠F ,求证:AF ∥CD 。
12、如图12,已知:AB∥CD,∠ABP和∠CDP的平分线相交于点E,∠ABE和∠CDE的平分线相交于点F,∠BFD=54°,求∠BPD与∠BED的度数。
13、如图13,已知∠3=∠1+∠2,求证:∠A+∠B+∠C+∠D=180°。
