电工技术第2章(李中发版)课后习题及详细解答 (1)
电工学第2章习题答案
解 选取C为研究对象 1、如图所示，由平衡方程得 ∑Fx=0 FAC Cos30o－FBCCos30o=0 ∑Fy=0 FAC Sin30o－F＋FBCSin30o =0 解得 FAC =FBC=F
2、许用应力为 杆AC的承载极限：
F1 σ A C A A C 1 6 0 1 0 2 1 2 .7 4 1 0
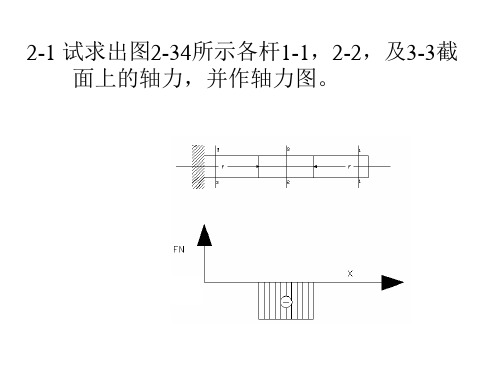
解b 使用截面法，沿截面1-1将杆分 成两段，取出右段并画出受力图（b） 用FN1表示左段对右段的作用， 由平衡方程∑Fx=0，得FN1 =F（拉）
同理，可以计算横截面2-2上的轴 力FN2，由截面2-2右段图（c）的平 衡方程Fx=0 ∑，得FN2= F（压）
同理，可以计算横截面3-3上的轴力 FN3，由截面3-3左段图（d）的平衡 方程∑Fx=0，得FN3=F（拉）
3 3
σp
1
5 10 2 d
σ p 200 M P a
得
d 9mm
综上可知
d 14m m
2- 8 如图2-41所示，齿轮与轴用平键连 接，已知轴直径d=70mm，键的尺寸 b h 20m m 12m m 100m m ，传递的力偶矩 M 2 K N m ；键材料的许用应力 τ
6 4
4 0 6 .7 8 K N
杆BC的承载极限：
F2 σ
BC
A B C 1 0 0 1 0 3 5 .5 8 1 0
6
4
3 5 5 .8 K N
由
得
FA C FB C F 3 5 5 .8 K N
F 3 5 5 .8 K N
2-6 图2-39所示结构中梁AB的变形及重量 可忽略不计。杆1为钢制圆杆，直径 d1=20mm，E1=200GPa；杆2为铜制圆杆， 直径d2=25mm，E2=100GPa。试问：(1)载 荷F加在何处，才能使梁AB受力后仍保持 水平? (2)若此时F=30kN，求两拉杆内横 截面上的正应力。
《电工电子技术(第2版)》课后习题一答案
03 电子技术基础题目解析
半导体器件题目解析
半导体材料特性
二极管与三极管
解答涉及半导体材料的导电性、热敏 性和光敏性等特性，以及其在电子器 件中的应用。
针对二极管和三极管的符号、工作原 理、特性曲线及主要参数进行深入解 析，并讨论其在电路中的应用。
PN结形成与特性
详细解析PN结的形成过程、工作原理 和特性，包括单向导电性、击穿电压 等概念。
提高实践能力
除了理论学习外，还需要注重实践能力的培养和提高，通 过参加实验、课程设计等实践活动来加深对理论知识的理 解和应用。
关注新技术发展
随着科技的不断发展，电工电子技术也在不断更新换代， 需要关注新技术的发展动态和应用前景。
拓展相关学科知识
电工电子技术与其他学科有着密切的联系和交叉，可以拓 展相关学科知识的学习和应用，如物理学、数学、计算机 科学等。
05 电机与变压器基础题目解 析
变压器工作原理及特性参数计算
变压器工作原理
基于电磁感应原理，通过变换电 压和电流来实现电能的传输和分 配。主要构件包括铁芯和绕组， 铁芯上绕有一次绕组和二次绕组。
特性参数计算
包括额定电压、额定电流、额定 容量、变比、空载电流、空载损 耗、短路阻抗和效率等。这些参 数对于变压器的选择和使用具有
02 电路基础题目解析
直流电路题目解析
电阻、电容、电感等元件的串并联计算
掌握元件的基本性质，熟练运用串并联公式进行计算。
欧姆定律和基尔霍夫定律的应用
理解定律原理，能够准确运用在复杂直流电路的分析中。
电源的等效变换
掌握电压源、电流源的等效变换方法，能够简化电路结构。
叠加定理和戴维南定理的应用
理解定理条件，能够运用定理求解复杂直流电路。
(完整版)《电力电子技术(第二版)》课后习题及解答
《电力电子技术》习题及解答第1章思考题与习题1.1晶闸管的导通条件是什么? 导通后流过晶闸管的电流和负载上的电压由什么决定?答：晶闸管的导通条件是：晶闸管阳极和阳极间施加正向电压，并在门极和阳极间施加正向触发电压和电流（或脉冲）。
导通后流过晶闸管的电流由负载阻抗决定，负载上电压由输入阳极电压U A决定。
1.2晶闸管的关断条件是什么?如何实现?晶闸管处于阻断状态时其两端的电压大小由什么决定?答：晶闸管的关断条件是：要使晶闸管由正向导通状态转变为阻断状态，可采用阳极电压反向使阳极电流I A减小，I A下降到维持电流I H以下时，晶闸管内部建立的正反馈无法进行。
进而实现晶闸管的关断，其两端电压大小由电源电压U A决定。
1.3温度升高时，晶闸管的触发电流、正反向漏电流、维持电流以及正向转折电压和反向击穿电压如何变化？答：温度升高时，晶闸管的触发电流随温度升高而减小，正反向漏电流随温度升高而增大，维持电流I H会减小，正向转折电压和反向击穿电压随温度升高而减小。
1.4晶闸管的非正常导通方式有哪几种？答：非正常导通方式有：(1) I g=0，阳极电压升高至相当高的数值；(1) 阳极电压上升率du/dt 过高；(3) 结温过高。
1.5请简述晶闸管的关断时间定义。
答：晶闸管从正向阳极电流下降为零到它恢复正向阻断能力所需的这段时间称为关断时间。
即gr rr q t t t +=。
1.6试说明晶闸管有哪些派生器件？答：快速晶闸管、双向晶闸管、逆导晶闸管、光控晶闸管等。
1.7请简述光控晶闸管的有关特征。
答：光控晶闸管是在普通晶闸管的门极区集成了一个光电二极管，在光的照射下，光电二极管电流增加，此电流便可作为门极电触发电流使晶闸管开通。
主要用于高压大功率场合。
1.8型号为KP100-3，维持电流I H =4mA 的晶闸管，使用在图题1.8所示电路中是否合理，为什么?(暂不考虑电压电流裕量)图题1.8答：（a ）因为H A I mA K V I <=Ω=250100，所以不合理。
电工与电子技术第二章课后习题参考答案
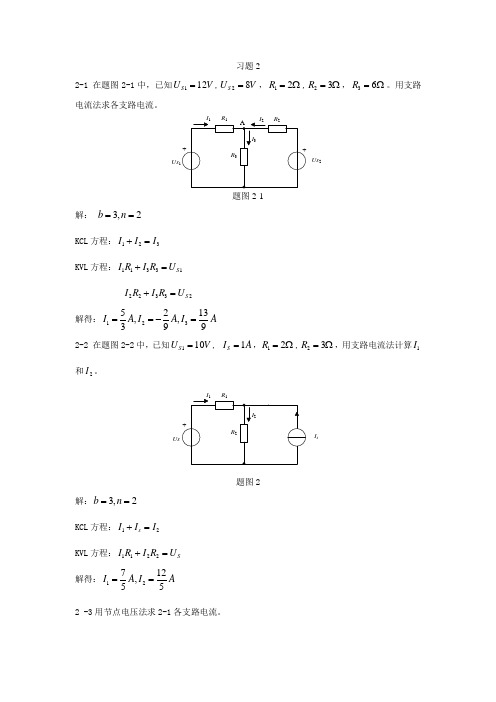
习题22-1 在题图2-1中，已知112S U V =,28S U V =，12R =Ω,23R =Ω，36R =Ω。
用支路电流法求各支路电流。
Us 2Us题图2-1解： 3,2b n == KCL 方程：123I I I += KVL 方程：11331S I R I R U += 22332S I R I R U += 解得：1235213,,399I A I A I A ==-= 2-2 在题图2-2中，已知110S U V =, 1S I A =，12R =Ω,23R =Ω，用支路电流法计算1I 和2I 。
IsUs题图2解：3,2b n == KCL 方程：12s I I I += KVL 方程：1122S I R I R U += 解得：12712,55I A I A ==2 -3用节点电压法求2-1各支路电流。
解：121212312882623611111133236s S abU U R R U V R R R ++===+=++++ 11126125323s abU U I A R --=== 2222682339S abU U I A R --===- 332613369ab U I A R ===2-4用节点电压法求2-2的电流1I 和2I 。
解：112101627.211115236sS abU I R U V R R ++====++111107.21.42s ab U U I A R --=== 227.2 2.43ab U I A R ===或211 1.41 2.4S I I I A =+=+= 2-5 在题图2-5中，已知110s U V =, 26S U V =, 2S I A =,12R =Ω,23R =Ω，36R =Ω，1S R =Ω，用节点电压法求电流1I 和2I 和3I 。
sR U题图2-5解：设上面的节点为a ，下面的节点为b 则12121231262236111111236s S S abU U I R R U V R R R +-+-===++++11112632S ab U U I A R --=== 2226603S ab U U I A R --===33616ab U I A R === 2-6在题图2-6中，已知10S U V =, 2S I A =，14R =Ω,22R =Ω，38R =Ω。
电工电子技术基础(第二版)-部分习题参考答案-李中发-50848308
部分习题参考答案第1章1.1 （1）5ab =U V ；（2）5ab =U V ；（3）2-=I A ；（4）2=I A1.2 （a ）－10W ；（b ）－48W ，30W ；（c ）－50W ，25W1.3 （3）5601-=P W ，5402-=P W ，6003=P W ，3204=P W ，1805=P W1.4 23-=I mA 。
603=U V1.5 50=P W1.6 26ac =U V ，7bd =U V1.7 11ab =U V ，32-=I A ，23=I A ，5.53=R Ω1.8 －18W ，－18W ，4W1.9 0ab =U V ，0=I A1.10 75.8S2=U V1.11 （a ）8.2Ω；（b ）12.5Ω；（c ）2Ω1.12 4=U V1.13 5.2=I A ，7ab =U V1.14 1=I A1.15 1ab =U V1.16 31=I A ，82=I A ，113=I A1.17 11-=I A ，12=I A1.18 21=I A ，22-=I A ，4.03=I A1.19 71=I A ，5.112-=I A ，5.33=I A ，14-=I A1.20 （a ）7OC =U V ，60=R Ω；（b ）100OC =U V ，150=R Ω1.20 （a ）5.1=I A ；（b ）2=I A1.22 4=I A1.23 2=I A1.24 （a ）14OC =U V ，20=R Ω（b ）60OC =U V ，60=R Ω（c ）14OC =U V ，100=R Ω1.25 （a ）4OC =U V ，80=R Ω；（b ）3OC =U V ，340=R Ω电工电子技术基础（第二版） 2 1.26 1=I A1.27 25.0=I A1.28 5.0=I A第2章2.2 （1）)45100sin(210︒+=t i πA ；（2）90°，102A2.4 1366.14j B A +=+，366.2j B A +-=-，︒∠=1.83100AB ，︒∠=1.231/B A2.7 A )34.21314sin(8.1221︒+=+t i i ，A )67.98314sin(8.1221︒+=-t i i 2.8 )4510sin(210006︒+=t u s V2.9 )45sin(707.0︒+=t i A ，)45sin(07.7C ︒-=t u V2.10 )752sin(20︒+=t i A2.11 5A ，1A ，7A2.12 （a ）7.07V ；（b ）7.07V2.13 0.065H2.14 （a ）︒-∠4522Ω；（b ）︒∠452Ω；（c ）︒-∠4522Ω2.15 （1）)4510sin(23︒-=t i A ，)4510sin(203R ︒-=t u V ，)4510sin(403L ︒+=t u V ，)13510sin(203C ︒-=t u V ；（2）6.112=f H ，t i 310sin 22=A ，t u 3R 10sin 220=V ， )9010sin(403L ︒+=t u V ，)9010sin(403C ︒-=t u V 2.16 )4510sin(225.04︒+=t i A ，t i 4R 10sin 25.0=A ，)9010sin(25.04L ︒-=t i A ，)9010sin(5.04C ︒+=t i A2.17 ︒∠=45101I A ，︒∠=902102I A ，︒-∠=45103I A ，︒-∠=1.8100SU V 2.18 ︒∠=4525.01I A ，︒∠=9012I A ，︒-∠=4525.03I A 1.19 880=P W ，660=Q Var ，1100=S VA ，︒∠=9.3644Z2.20 200=r Ω，12.3=L H2.21 （1）2528=P W ，766.040cos =︒；（2）60=C μF2.22 55.0cos =ϕ，6=R Ω，22.9=X Ω2.23 350=R Ω，5=L mH2.24 ︒∠=6.2636.22UV ，150=P W ，50-=Q Var ，158=S VA ，95.0=λ 2.25 100=R Ω，3.57=L mH ，6.17=C μF2.26 120C =X Ω2.27 4010=ωrad/s ，2=I A ，8000L =U V ，160=Q2.28 19=L mH ，05.0=C μF部分习题参考答案 32.30 44P =I A ，44L =I A ，0N =I2.31 18.4L =I A ，18.4YP =I A ，42.2P =∆I A2.32 2.46j 5.61+=Z Ω2.33 8687W ，26061W第3章3.1 4)0(C =+u V ，1)0(1=+i A ，1)0(C =+i A ，0)0(2=+i A3.2 3)0(L =+u V ，3)0(L =+i A ，5.1)0(1=+i A ，5.1)0(2=+i A3.3 6)0(C =+u V ，6)0(L =+u V ，0)0(L =+i A ，0)0(C =+i A ，0)0(=+i A3.4 0)0(C =+u V ，0)0(L =+u V ，3)0(L =+i A ，0)0(C =+i A ，3)0(=+i A3.5 )e 1(2C t u -+=V ，t i --=e 2C A3.6 t i 5L e 1--=A ，t u 5L e 5-=V3.7 )e 1(44000C t u -+=V3.8 t u 2000C e 48--=V3.9 t u 1000C e 20-=V3.10 )e 1(425.0C t u -+=V 3.11 )e 1(4592000C t u --=V ，t i 92000C e 30-=mA ， t i 920001e 5.225.7-+=mA ，)e 1(5.7920002t i --=mA3.12 t u 5.0C e 32-+=V3.13 t i 5.1L e -=A ，t u 5.1L e 5.1--=V 3.14 t i 34L e 82-+=A ，t u 34L e 332--=V 3.15 t i 2L e 35--=A ，t u 2L e 6-=V ，t i 21e 2--=A ，t i 22e 23--= A 3.16 t i 34L e 21--= A第4章4.2 33盏；25.21=I A ，75.132=I A4.3 10=k ，78.0=P W4.4 1.7=k ；51=U V ，71.02=U V ；5.121=I mA ，892=I mA ，63=P mW电工电子技术基础（第二版） 4 4.5 （1）10001=N 匝，1642=N 匝；（2）197.01=I A ，2.12=I A4.6 （1）362=U V ，243=U V ；（2）69.11=I A ，52=I A ，83=I A ；（3）130Ω4.8 230V ，133V ；133V ，133V4.9 10；310；10；3/104.10 （1）77.51N =I A ，3.144N 2=I A ；（2）1000盏；（3）500盏4.11 500匝，7.221=I A ，202=I A4.13 （1）280A ；（2）4.375A第5章5.4 2=p ，转速为0时1=s ，转速为1440 r/min 时04.0=s5.5 3=p5.6 04.0N =s ，22=f Hz5.15 （1）04.0N =s ，6.11N =I A ，5.36N =T N ·m ；（2）2.81=st I A ，2.80max =T N ·m ，2.80=st T N ·m ，43.61=P kW5.18 （1）3.131N =T N ·m ； （2）89.0cos = ；（3）7.106Yst =I A ，9.56Yst =T N ·m ；（4）不能起动第7章7.4 （1）1V ，0.5%；（2）0.5级7.5 5%；2.5%7.6 电流量程为0.5A 时：0.125W/div ，0.25W/div ，0.5W/div ，1W/div ； 电流量程为1A 时：0.25W/div ，0.5W/div ，1W/div ，1W/div ；7.7 41Ω，959Ω7.8 249.975k Ω，2250 k Ω第8章8.1 （a ）0.7V ；（b ）1.5V ；（c ）4.3V8.5 （a ）放大，7V ；（b ）饱和，0.3V ；（c ）截止，5V8.8 （1）50B =I μA ，2C =I mA ，6CE =U V8.9 3CE =U V 时：160B =R k Ω，75B =I μA ，3C =I mA部分习题参考答案 55.1C =I mA 时：320B =R k Ω，5.37B =I μA ，5.7CE =U V8.10 50B =I μA ，4C =I mA ，3.0CE =U V ，三极管饱和8.11 5.2C =R k Ω，200B =R k Ω8.13 （a ）50B =I μA ，2C =I mA ，6CE =U V（b ）33B =I μA ，33.1C =I mA ，8CE =U V8.14 空载时：180u -=A ；接上负载时：90u -=A8.15 （1）16B =I μA ，8.0C =I mA ，2.7CE =U V（3）76.1i =r k Ω，3o =r k Ω（4）5.37u -=A ，24us -=A8.16 （1）12BQ =I μA ，2.1CQ =I mA ，6CEQ =U V（3）3.2i =r k Ω，3o =r k Ω（4）6.6u -=A ，3.6us -=A8.17 （1）25B =I μA ，5.1C =I mA ，5.4CE =U V（3）92i =r k Ω，3o =r k Ω（4）73.0u -=A8.18 （1）25B =I μA ，5.2C =I mA ，7CE =U V（3）85i =r k Ω，13o =r Ω（4）99.0u =A8.19 （1）34B2B1==I I μA ，7.1C2C1==I I mA ，2.5CE2CE1==U U V（3）30u1-=A ，50u2-=A ，1500u =A8.20 （1）20B1=I μA ，1C1=I mA ，4CE1=U V40B2=I μA ，2C2=I mA ，6CE2=U V（3）116u1-=A ，98.0u2=A ，114u -=A8.21 （1）10B1=I μA ，5.0C1=I mA ，5.10CE1=U V20B2=I μA ，1C2=I mA ，8.5CE2=U V（3）95.0u1=A ，153u2-=A ，146u -=A第9章9.1 6~0o -=u V9.2 12~6o =u V9.3 50μA9.4 （1）o x 5.0Ru R =；（2）10=R k Ω 9.5 Ru i i o =电工电子技术基础（第二版） 6 9.6 Ru i i o =9.7 R U i =o 9.8 i F3F2F1F2F11o 1u R R R R R R u ⎪⎪⎭⎫ ⎝⎛++-= 9.9 )(i2i1o u u u +-= 9.10 )(2i1i2o u u u -=9.11 i o 30u u = 9.12 i 12o 1u R R u ⎪⎪⎭⎫ ⎝⎛+= 9.13 )(4i2i1o u u u +-=9.14 )(5.0i2i1o u u u +=9.15 )(4i1i2o u u u -=9.16 i3i2i1o 436u u u u -+=9.18 1=t s 时6o =u V ，2=t s 时12o =u V ，3=t s 时12o =u V9.19 2500=A ，01.0=F9.20 100f =A ，%1.0d ff =A A 9.26 16=f kHz ，40F ≥R k Ω第10章10.2 562=U V ，1782=I mA ；80D =I mA ，79RM =U V10.3 （1）13.75mA ；（2）19.44mA ；（3）244V10.4 （1）9V ，90mA ；（2）4.5V ，45mA ；（3）短路；（4）12V 10.6 （1）24V ；（2）20V10.9 二极管：75D =I mA ，3.35RM =U V ；电容：250=C μF ，耐压大于35.3V 10.11 （1）9.4omin =U V ，3.21omax =U V ；（2）P 21R R R == 10.12 （2）5.15=k ，250D =I mA ，20RM =U V ，100021==C C μF第11章11.1 100000011011，81B部分习题参考答案 711.2 5，25711.3 16102)37()55()110111(==，16102)D 4()77()1001101(== 11.4 111001101100，0011 0110 1001 001011.5 2345，92911.7 （1）011、101、110、111；（2）011、100、101；（3）001、010、100、111；（4）000、001、010、100 11.9 （1）C A AB F +=；（2）1=F ；（3）D AC CD A BC AB F +++=；（4）D B A F +=；（5）B F =；（6）B A F =；（7）0=F ；（8）B A F += 11.10 （1）ABC F =1，C B A F ++=211.11 （a ）AB F =；（b ）B A F += 11.12 AB F =1，B A F +=2，B A F ⊕=3，AB F =4，B A F +=5，B A F ⊕=6 11.13 C AB F +=1，B AC F +=2，C B B A F ⊕⊕⊕=3，CA BC AB F ++=4 11.14 （a ）BC C A AB F ++=；（b ）D BC D C C B A AB +++ 11.15 （a ）C A B A AB F ++=；（b ）BCD B A F +=11.16 （a ）B A AB F +=；（b ）D C B A F ⊕+⊕=11.17 （a ）D C B A F ⊕⊕⊕=；（b ）C B A F ⊕⊕=1，CA BC AB F ++=2 11.18 （a ）D C B A F ⊕⊕⊕=（b ）33B F =，232B B F ⊕=，121B B F ⊕=，010B B F ⊕= （c ）M B F ⊕=22，M B F ⊕=11，M B F ⊕=00 11.19 C B C A F +=1，ABC C B A C B A B A F +++=2，CA BC AB F ++=3 A C BC B A F ++=411.20（1）BCD ACD ABD ABC Y +++=（2）D C B A Y ⊕⊕⊕=（3）D C B A Y ⊕⊕⊕=（4）ABCD D C B A Y +=11.21 （1）0B Y =（2）0123012301230123B B B B B B B B B B B B B B B B Y +++=（3）02123B B B B B Y ++= （4）02123B B B B B Y ++= 11.22 D C B A Y ⊕⊕⊕=11.23 红灯AB Y =1，黄灯AC Y =2，白灯B A Y =311.24 红灯A C C B B A Y 1++=，黄灯C AB C B A BC A C B A Y +++= 2， 绿灯ABC Y =3 11.25 ACD ABC ABD BCD D C B D C A D B A C B A X +++++++= CD BD BC AD AC AB Y +++++=电工电子技术基础（第二版） 8 第12章12.12 2位二进制同步可逆计数器12.13 五进制同步计数器12.14 六进制异步计数器12.17 （a ）8421码8进制计数器；（b ）5421码6进制计数器；（c ）8421码7进制计数器12.18 （a ）10进制计数器；（b ）11进制计数器 12.19 （a ）50进制计数器；（b ）137进制计数器 12.20 （1）2Q CR =，02Q Q LD =；（2）045Q Q Q CR =，145Q Q Q LD =；（3）0156Q Q Q Q CR =，256Q Q Q LD =；（4）367Q Q Q CR =，01267Q Q Q Q Q LD = 12.21 （1）030B 0A Q Q R R ==；（2）02450B 0A Q Q Q Q R R ==；（3）460B 0A Q Q R R ==；（4）34560B 0A Q Q Q Q R R ==12.24 11s12.26 0.05V12.27 －4.5625V12.28 －4.98V ，－3.75V ，－0.0195V12.29 －3.75V。
电工技术第2章李中发版课后习题及详细解答
电工技术第2章(李中发版)课后习题及详细解答第2章电路的基本分析方法2.1 试求如图2.3所示各电路a、b两端的等效电阻。
图2.3 习题2.1的图分析本题考查电阻串联、电阻并联电路总电阻的计算，电阻串联电路的总电阻为，电阻并联电路的总电阻为。
解对图2.3（a）所示电路，6Ω电阻和上面12Ω电阻并联后再与下面12Ω电阻串联，其总电阻为Ω，该16Ω电阻与4Ω电阻并联后再与5Ω电阻串联，因此a、b两点之间的总电阻为：（Ω）对图2.3（b）所示电路，左右两边4个10Ω电阻并联后再与中间的10Ω电阻串联，因此a、b两点之间的总电阻为：（Ω）对图2.3（c）所示电路，6Ω电阻和12Ω电阻并联后再与下面4Ω电阻串联，其总电阻为Ω，该8Ω电阻再与左边8Ω电阻以及右边4Ω电阻并联，因此a、b两点之间的总电阻为：（Ω）2.2 试求如图2.4所示电路中的电压U。
分析电阻串、并联电路电流和电压的计算，一般可先利用电阻串、并联公式求出电路的总电阻，然后根据欧姆定律求出总电流，最后利用欧姆定律或分压公式和分流公式计算各个电阻的电压或电流。
解标出总电流和待求支路电流的参考方向，如图2.5所示。
电路的总电阻为：（Ω）图2.4 习题2.2的图图2.5 习题2.2解答用图总电流为：（A）待求支路的电流为：（A）待求电压为：（V）2.3 试求如图2.6所示电路中的电流I和电压U ab。
分析本题考查电阻串联、电阻并联电路电流和电压的计算。
由于对外电路而言，恒流源与电阻串联可等效于该恒流源，故本题可先用分流公式计算出两并联电阻支路的电流，然后再计算a、b 之间的电压。
解设8Ω电阻与2Ω电阻串联支路的电流为，如图2.7所示。
由分流公式得：（A）（A）a、b之间的电压为：（V）图2.6 习题2.3的图图2.7 习题2.3解答用图2.4 试求如图2.8所示电路中的电流I。
分析3Ω电阻和下面6Ω电阻并联后再与上面6Ω电阻串联，然后与2Ω电阻并联接到8V恒压源上，故待求电流与2Ω电阻是否并联无关。
电工技术第二章 电路的分析方法习题解答
第二章电路的分析方法本章以电阻电路为例，依据电路的基本定律，主要讨论了支路电流法、弥尔曼定理等电路的分析方法以及线性电路的两个基本定理：叠加定理和戴维宁定理。
1．线性电路的基本分析方法包括支路电流法和结点电压法等。
（1）支路电流法：以支路电流为未知量，根据基尔霍夫电流定律（KCL）和电压定律(KVL)列出所需的方程组，从中求解各支路电流，进而求解各元件的电压及功率。
适用于支路较少的电路计算。
（2）结点电压法：在电路中任选一个结点作参考结点，其它结点与参考结点之间的电压称为结点电压。
以结点电压作为未知量，列写结点电压的方程，求解结点电压，然后用欧姆定理求出支路电流。
本章只讨论电路中仅有两个结点的情况，此时的结点电压法称为弥尔曼定理。
2 ．线性电路的基本定理包括叠加定理、戴维宁定理与诺顿定理，是分析线性电路的重要定理，也适用于交流电路。
（1）叠加定理：在由多个电源共同作用的线性电路中，任一支路电压（或电流）等于各个电源分别单独作用时在该支路上产生的电压（或电流）的叠加（代数和）。
①“除源”方法（a）电压源不作用：电压源短路即可。
（b）电流源不作用：电流源开路即可。
②叠加定理只适用于电压、电流的叠加，对功率不满足。
（2）等效电源定理包括戴维宁定理和诺顿定理。
它们将一个复杂的线性有源二端网络等效为一个电压源形式或电流源形式的简单电路。
在分析复杂电路某一支路时有重要意义。
①戴维宁定理：任何一个线性含源的二端网络，对外电路来说，可以用一个理想电压源和一个电阻的串联组合来等效代替，其中理想电压源的电压等于含源二端网络的开路电压，电阻等于该二端网络中全部独立电源置零以后的等效电阻。
②诺顿定理：任何一个线性含源的二端网络，对外电路来说，可以用一个理想电流源和一个电阻的并联组合来等效代替。
此理想电流源的电流等于含源二端网络的短路电流，电阻等于该二端网络中全部独立电源置零以后的等效电阻。
3 ．含受控源电路的分析对含有受控源的电路，根据受控源的特点，选择相应的电路的分析方法进行分析。
电工技术习题答案第二章
第二章电路的分析方法习题参考答案1.用支路电流法求I1、I2、I3, U1、U2、U3。
图2-12 习题1的电路解：根据KCL 列方程组：123112312134 I A I AI A =--=-=-==--=-根据KVL列方程组123642628426 U V U V U V =-==+==+=所以得：I1=-2A、I2=2A、I3=-4A, U1=2V、U2=8V、U3=6V 2.求图2-13所示电路中的I S和U 。
图2-13 习题2的电路解：如图所示设流过2Ω电流为I 1,流过5Ω电流为I 2,得：()12126323*361515356155*615ABS AB AC I A U V I A I I I AU U U V===+===∴=+==-=--=-则3.电路如图2-14所示，已知E 1=8V ，E 2=4V ，E 3=6V ，R 1=2Ω，R 2=4Ω，R 3=1Ω，求各支路电流。
图2-14 习题3的电路解：根据KCL,KVL 列方程组 11222133311321R I E R I E E R I I E I I I +-=++=+=把已知条件代入，解方程组得：I 1=1.429A, I 2=2.286A, I 3=-0.857A4.电路如图2-15所示，用叠加原理求各支路电流。
(I 1=0.2A, I 2=1.2A)图2-15 习题4的电路解：原图可以等效为以下两个电路的叠加：则有：''12200.81015I I A ===+ 及 ''''12''''1210151I I I I =-+=得''''120.6,0.4I A I A =-= '''111'''2220.21.2I I I AI I I A ∴=+==+=5. 如图2-16所示电路，已知U S1=U S2=U S3=1V ，R 1=R 2=R 3=1Ω，用叠加定理求流过Ｒ1的电流。
(完整版)电工2章
第2章 习题解答(部分)2.3.3 计算图2.13中的电流 I 3。
解: 用电源等值互换法将电流源变换成电压源，将电阻R 2和R 3合并成电阻R 23，其中 V R I U R S S 2125.043,2=⨯=⨯=Ω=参考方向如图2.34所示。
求电路中电流IA R R R U U I S 2.115.012143,211=+++=+++= I 即为原电路中R 1上流过的电流，用分流公式，可求原电路中I 3A I R R R I 6.02.11113223=⨯+=⨯+= 2.4.1 图2.16是两台发电机并联运行的电路。
已知E 1=230V , R 01=0.5Ω，E 2=226V , R 02=0.3 Ω,负载电阻R L =5.5Ω，试分别用支路电流法和结点电压法求各支路电流 。
解:（1）用支路电流法：各支路电流参考方向已画在图2.16中。
列结点电压方程 L I I I =+21列回路电压方程L L 0222LL 0111R I R I E R I R I E +=+=S Ω 图 2.13 习题2.3.3的图U S U 图解 2.34101202图2.16 习题2.4.1的图联立求解上述三各方程式组成的方程组，可得A 40A2021===L I I I验算：按非独立回路方程进行02201121R I R I E E -=-代入数据443.0205.020226230==⨯-⨯=- （正确！）（2）用结点电压法求解：先求端电压U ，有V 2205.513.015.013.02265.02301110201022011=+++=+++=L R R R R E R E U A 405.0220A 205.0220226A 205.022023002220111====-=-==-=-=L L R U I R U E I R U E I 结果与上相同。
2.5.1 试用结点电压法求图2.18所示电路中的各支路电流解:在原图2.18中用O 和O ’标明两个结点，则有A 5.0505025V 505015015015025501005025a O ,O'-=-==++++=I U A 5.0505025A 15050100c b -=-==-=I I 2.6.1 用叠加原理计算图2.19中各支路的电流。
电工技术第2章习题答案
2.1.1 选择题（1）在图2-73所示电路中，发出功率的元件是Ａ。
（Ａ）仅是5Ｖ的电源（Ｂ）仅是2Ｖ的电源（Ｃ）仅是电流源（Ｄ）电压源和电流源都发出功率（Ｅ）条件不足图2-73题2.1.1（1）图图2-74题2.1.1（2）图（2）在图2-74所示电路中，当增大时，恒流源两端的电压Ｕ。
（A）不变（B）升高（C）降低（3）在图2-75所示电路中，当开关S闭合后，P点的电位。
（A）不变（B）升高（C）为零（4）在图2-76所示电路中，对负载电阻R而言，点画线框中的电路可用一个等效电源代替，该等效电源是。
（A）理想电压源（B）理想电流源（C）不能确定图2-75题2.1.1（3）图图2-76题2.1.1（4）图(5) 实验测的某有源二端线性网络的开路电压为10V，当外接3Ω的电阻时，其端电压为6V，则该网络的戴维南等效电压的参数为(C)。
(a)6V，R0=3Ω(b)8V，R0=3Ω (c)10V，R0=2Ω(6) 实验测得某有源二端线性网络的开路电压为6V，短路电流为3A。
当外接电阻为4Ω时，流过该电阻的电流I为( A )。
(a)1A (b)2A (c)3A(7) 在图2-77所示电路中，已知1=4V，2=4V，当2单独作用时，电阻R中的电流为1，那么当1单独作用时，电压是（A）（A）1V （B）3V （C）-3V图2-77题2.1.1（7）图（8）一个具有几个结点，b条支路的电路，其独立的方程为（B）a)（1）个 b)（1）个（9）一个具有几个结点，b条支路的电路，要确定全部支路电流，最少要测量（B）a)（1）次 b)（1）次（10）一个具有n个结点，b条支路的电路，要确定全部支路电压，最少要测量（A）a)（1）次 b)（1）次（11）电阻并联时，电阻值越大的电阻：（A）a)消耗功率越小； b)消耗功率越大。
（12）两个电阻并联时，电阻值，越小的电阻（B）a)该支路分得的电流愈小； b)该支路分得的电流愈大。
《电工技术(李中发版)》课后习题及详细解答(全面版)
图1.29 习题1.16的图
1.17 试求如图1.30所示电路中 a 点的电位。 分析 本题运用 KCL 和 KVL 求出电路中的各个电流后，即可运用电位的概念求出 a 点 的电位。
分析 本题考查电流、电压参考方向的关联性和功率，题目不难，但一不小心就容易出
错。运用功率公式计算时，电压和电流参考方向关联时采用公式
，非关联时采用公
式
。此外，由于元件3产生10W 功率，故
W；元件4产生 W 功率，故
W，实际上元件4吸收了10W 功率。 解 （1）元件1的电流与电压是关联参考方向，根据功率计算公式得：
根据 KVL 列出如图1.16所示两个回路的方程，为：
第 5 页 共 135 页
解之，得：
（A）
（V）
图1.15 习题1.8的图 1.8解答用图
图1.16 习题
1.9 在如图1.17所示的电路中，已知
V，
Ω， kΩ。求开关 S 在不同位
置时，电流表和电压表的读数各为多少？
分析 开关 S 在不同位置时，电路电路分别处于不同的工作状态：在位置1时处于负载状
（V） 电流表的读数为：
（A） 1.10 求如图1.18所示电路中负载吸收的功率。 分析 欲求负载吸收的功率，必须先求出负载的电流和电压，而负载的电流和电压可利
用基尔霍夫定律求出。
解 设负载的电流、电压参考方向关联，即设负载两端电压的参考方向为上正下负，根
据基尔霍夫定律得：
（A）
所以，负载吸收的功率为：
1.14 指出如图1.25所示电路有多少节点和支路，并求电压 Uab 和电流 I。 分析 本题将 KCL 推广到封闭曲面即可求出电流 I，进而可求出电压 Uab。 解 电路有2个节点和3条支路。作封闭曲面如图1.26所示，根据 KCL，得：
电工技术II练习册答案(带解析)
电工技术II习题解答习题1——电路模型和电路定律1-1 根据图示参考方向，判断各元件是吸收还是发出功率，其功率各为多少？解：元件1吸收10W；元件2吸收10W；元件3发出10W；元件4发出10W；1-2 各元件的条件如图所示。
(1)若元件A吸收功率为10 W，求I a；(2)若元件B产生功率为(－10 W)，求U b；(3)若元件C吸收功率为(－10 W)，求I c；(4)求元件D吸收的功率。
解：I a＝-1A;U b＝-10V;I c＝-1A;P＝-4mW.1-3某直流电源的额定功率为P N=200W，额定电压为U N=50V，内阻R0=0.5Ω，负载电阻R可以调节，如图所示，试求：（1）额定状态下的电流及负载电阻；（2）空载状态下的电压；（3）短路状态下的电流。
解：(1) P N＝U N×I N ----> I N=4A;负载电阻R= U N/I N =12.5Ω(2) U=E= U N+ R o×I N = 52V(3)I st=E/R0 =104AE1-4 某有源支路接在U =230V 的电源上，电路如下图所示，支路电阻为R 0=0.5Ω，测得电路中的电流I =10安培。
求： （1）该有源支路的电动势E ；（2）此支路是从电网吸收电能还是向电网输送电能？ 解：（1）E= U + R o ×I =235V（2）P =U ×I >0, 输送1-5 (1)求图 (a)电路中受控电压源的端电压和它的功率；(2)求图 (b)电路中受控电流源的电流和它的功率；解：（a ）U 1＝3×4 =12V ，受控电压源的端电压2U 1＝24V ，P 发=3×24 =72W （b ）I 2＝0.5A ，受控电流源的电流6I 2＝3A ，P 吸=5×3 =15W1-6 求图示各电路中的U ab ，设端口a 、b 均为开路。
解：（a ）U ab ＝-2+4=2V （b ）U ab ＝-1+8=7V （c ）i =5/20 =0.25 AU ab ＝3i +10i =3.25V （d ）U ab ＝-3+5×1＝2VE习题2——等效电路分析方法2-1 求各电路的等效电阻R ab 。
50916 《电工电子技术与技能 第2版》课后习题答案
《电工电子技术及技能》习题参考答案第1章认识电工实训室与安全用电1-1 解：常用电工工具除螺丝刀、测电笔、钢丝钳、电工刀和剥线钳外，还有尖嘴钳、断线钳、电烙铁、活络扳手等；常用电工仪表除电压表、电流表、钳形电流表、万用表、兆欧表外，还有绝缘电阻表、功率表、电能表、示波器、、电桥、仪用互感器等。
1-2 解：常见导致触电的因素有：（1）电气线路或设备安装不良、绝缘损坏、维护不当，当人体接触绝缘损坏的导线或漏电设备时，发生触电；（2）非电气人员缺乏电器常识而进行电气作业，乱拉乱接，错误接线，造成触电；（3）用电人员或电气工作人员违反操作规程，缺乏安全意识，思想麻痹，导致触电；（4）电器产品质量低劣导致触电事故发生；（5）偶然因素如大风挂断电线而落在人身上，误入有跨步电压的区域等。
1-3 解：（1）按照触电事故的构成方式，触电事故可分为电击和电伤。
电击是电流对人体内部组织的伤害，是最危险的一种伤害，绝大多数的死亡事故都是由电击造成的；电伤是由电流的热效应、化学效应、机械效应等对人体造成的伤害。
（2）按照人体触及带电体的方式和电流流过人体的途径，电击可分为单相触电、两相触电和跨步电压触电。
1-4 解：对呼吸减弱或已经停止的触电者，口对口人工呼吸法是维持体内外的气体交换行之有效的方法，施行口对口人工呼吸前，应迅速将触电者身上障碍呼吸的衣领、上衣、裤带解开，并迅速取出触电者口腔内妨碍呼吸的食物，脱落的假牙、血块、粘液等，以免堵塞呼吸道。
作口对口人工呼吸时，应使触电者仰卧，并使其头部充分后仰，（最好一只手托在触电者颈后），使鼻孔朝上，以利呼吸道畅通。
口对口人工呼吸法操作步骤：（1）使触电者鼻孔紧闭，救护人员深吸一口气后紧贴触电者的口向内吹气，为时约2秒钟；（2）吹气完毕，立即离开触电者的口，并松开触电者的鼻孔，让他自行呼气，为时约3秒钟。
1-5 解：胸外心脏压挤法是在触电者心脏停止跳动时行之有效的施救方法。
应使触电者抑卧在比较坚实的地方，动作要领如下：（1）救护人员跪在触电者一侧或骑跪在其腰部两侧，两手相叠，手掌根部在心窝上方，胸骨下三分之一至二分之一处。
《电子技术》_李中发主编_前六章问题详解
第1章半导体存器件1.1 在如下列图的各个电路中，直流电压V，电阻kΩ，二极管的正向压降为，求U o。
图1.4 习题的图分析U o的值与二极管的工作状态有关，所以必须先判断二极管是导通还是截止。
假如二极管两端电压为正向偏置如此导通，可将其等效为一个Ｖ的恒压源；假如二极管两端电压为反向偏置如此截止，如此可将其视为开路。
解对图〔a〕所示电路，由于V，二极管VD承受正向电压，处于导通状态，故：〔V〕对图〔b〕所示电路，由于V，二极管VD承受反向电压截止，故：〔V〕对图〔c〕所示电路，由于V，二极管VD承受正向电压导通，故：〔V〕1.2 在如下列图的各个电路中，输入电压V，二极管的正向压降可忽略不计，试分别画出各电路的输入电压u i和输出电压u o的波形。
分析在u i和5V电源作用下，分析出在哪个时间段二极管正向导通，哪个时间段二极管反向截止。
在忽略正向压降的情况下，正向导通时可视为短路，截止时可视为开路，由此可画出各电路的输入、输出电压的波形。
图1.5 习题的图解对图〔a〕所示电路，输出电压u o为：u≥5V时二极管VD承受正向电压导通，U D=0，u o=5V；u i<5V时二极管VD承受反i向电压截止，电阻R中无电流，u R=0，u o= u i。
输入电压u i和输出电压u o的波形如图〔a〕所示。
图1.6 习题解答用图对图〔b〕所示电路，输出电压u o为：u≥5V时二极管VD承受正向电压导通，U D=0，u o=u i；u i<5V时二极管VD承受反i向电压截止，电阻R中无电流，u R=0，u o=5V。
输入电压u i和输出电压u o的波形如图〔b〕所示。
对图〔c〕所示电路，输出电压u o为：ui≥5V时二极管VD承受反向电压截止，电阻R中无电流，u R=0，u o= u i；u i<5V 时二极管VD承受正向电压导通，U D=0，u o=5V。
输入电压u i和输出电压u o的波形如图〔c〕所示。
电工学第2章习题及答案
2.4.1 图所示电路原 已稳定。在 t = 0 时将开关 S 从 a 端换接到 b 端。试 求换路后的响应 iL 和 uL。24 V
2Ω
US
R2
6Ω
uL
iL L
1H
返 回
第2章 电路的暂态分析
2.4.2 图所示电路原 已处于稳态。试求 S 闭合 后的 i2 、iL 和 uL，并画出 其变化曲线。
i1
S
IS
R1
24 A
i2
1.5 Ω 3Ω
7Ω
R3
R2
iL L uL 0.4 H
a
S
b
R1
3Ω
2.4.3 图所示电路 原已处于稳态。在 t = 0 时将开关 S 从 a 端改合 到 b 端。试求换路后的 iL 和 uL，并说明是什么 响应。
U S1
6V
US2
6V 6Ω
3Ω
R3
iL L
R2 6 i1 (0) i L ( 0) 3 A 1.8 A R1 R2 46 R1 4 i 2 ( 0) i L ( 0) 3 A 1.2 A R1 R2 46
返 回练习题题集 下一页 上一题 下一题
U S 12 uL (0) A 3A R1 4
返 回练习题题集 上一页 上一题 下一题
第2章 电路的暂态分析
2.3.3 图所示电路原已稳定，求开关 S 闭合后的响应 uC 和 i1、 i2 ，并画出其变化曲线。
S
R1
i1
20 V
4kΩ
R3 iC
R2
1.6kΩ
US
uC
iC
C 2.5F
6kΩ
电工学—电工技术课后答案
第二章 电路的分析方法P39 习题二 2-1题2-1图题2-1等效图 解：334424144I R R I R I RR I ⋅=⋅+⎪⎪⎭⎫⎝⎛+⋅①33341445I R E I I R R I R ⋅-=⎥⎦⎤⎢⎣⎡++ ② 344443363I I I I =+⎪⎭⎫⎝⎛+，344215I I = 34815I I = ①33444621I I I I -=⎪⎭⎫⎝⎛++，345623I I -= 3410123I I -=，34506015I I -=，A 2930,302933==I I 代入 ①A 2916,293081544=⨯=⨯I I 另外，戴维南等效图A 29549296I 5==回归原图3355I R I R E ⋅=⋅-，所以A 293042954163=⨯-=I2-2答 由并联输出功率400w 所以每个R 获得功率RU P 2,W 1004400==)(484,2201002Ω==R R改串联后：W 25422220P P 222=⨯===总消耗输出R U 2-33R 2R4R5R3I1I5I4IE +- 1R2I 6V+ -Ω1Ω920 5I题2-3等效图Ω=++⨯=++⋅=313212123121112111R R R R R R ，Ω=++⨯=++⨯=13213223121123122R R R R R RΩ=++⨯=++⋅=213213123121123133R R R R R R)(913910312953125225231ab Ω=+=+=+⨯+=R2-4题2-4 △-Y 变换（一）图题2-4 △-Y 变换（二）图题2-4 △-Y 变换（三）图题2-4 等效星型图2-5 解：ab cR 31 R 32 R 32 R 32 R 31 R 31 bcR 92 R 92 R 92 aR 31 R 31 R 31 bacR 95R 95 R 95 b1Ω1Ω2ΩΩ31 Ω21 a12 3+-10V Ω2Ω25A题2-5 （a)图2-6 用两种电源等效互换的方法，求电路中5Ω电阻上消耗的功率。
电工技术习题答案第二章
第二章 电阻电路的分析本章的主要任务是学习电阻电路的分析计算方法，并运用这些方法分析计算各种电阻电路中的电流、电压和功率。
本章基本要求1． 正确理解等效电路的概念，并利用等效变换化简电路。
2． 掌握电阻串、并联等效变换、电阻的Y 形连接与Δ形连接的等效变换、电源的等效变换。
3． 电阻电路的分压公式和分流公式的应用。
4． 运用支路电流法和结点电压法分析计算电路。
5． 运用叠加定理分析计算电路。
6． 熟练应用戴维宁定理和诺顿定理分析计算电路。
7． 应用戴维宁定理或诺顿定理求解电路中负载电阻获得的最大功率。
8． 学会含有受控源电路的分析计算。
9． 了解非线性电阻电路的分析方法。
2－1 电路如图2－1解 将ADE 、DBF然后将图2-1(a)由图2-1(c)即可得到原电路的Y 形电路和△形电路，分别如图2-1(d)和(e)所示。
图2-1(a) 图2-1(b)BA C 6ΩAB C2－2Ω。
试求支路电流I 1、I 2和I 3。
解 8363661+⨯+由分流公式得A 8936312=+=I I ， A 4936613=+=I I2－3 试用电源等效变换法将图2－3所示的各电路化简。
U S 6（a ）(b) aAB C 3Ω 3Ω图2-1(c) 图2-1(d) B A C图2-3解 将原电路逐步等效变换，最终化简成为最简电路。
化简过程如图所示。
2－4 电路如图2－4所示，试用电源等效变换法求电流I 。
(c)39VΩI图2-3(d) a bb 6或(d) a a ba b ab2或解 首先利用电源的等效变换求出Ω1电阻以左部分的最简等效电路，逐步等效化简过程如图所示。
2。
试用支路电流法求各==+00033111I R I R U s代入数据 并整理得：⎪⎩⎪⎨⎧=+-=+=+-906055052003221321I I I I I I I解得： A 16371-=I ，A 432-=I ，A 16253=I 2－6 如图2－6所示，已知电压源U s1＝80V ，U s2＝30V ，U s3＝220V ，电阻 R 1＝20Ω，R 2＝5Ω，R 3＝10Ω，R 4＝4Ω。
电工技术II练习册答案(带解析)
习题1——电路模型和电路定律1-1 根据图示参考方向，判断各元件是吸收还是发出功率，其功率各为多少解：元件1吸收10W ；元件2吸收10W ；元件3发出10W ；元件4发出10W ；1-2 各元件的条件如图所示。
(1)若元件A 吸收功率为10 W ，求I a ； (2)若元件B 产生功率为(－10 W)，求U b ； (3)若元件C 吸收功率为(－10 W)，求I c ；(4)求元件D 吸收的功率。
解：I a ＝-1A;U b ＝-10V; I c ＝-1A; P ＝-4mW.1-3某直流电源的额定功率为P N =200W ，额定电压为U N =50V ，内阻R 0=Ω，负载电阻R 可以调节，如图所示，试求：（1） 额定状态下的电流及负载电阻； （2） 空载状态下的电压； （3） 短路状态下的电流。
解：(1) P N ＝U N ×I N ----> I N =4A;负载电阻 R = U N /I N =ΩR 0-E+R(2) U =E= U N + R o ×I N = 52V (3) I st =E /R 0 =104A1-4 某有源支路接在U =230V 的电源上，电路如下图所示，支路电阻为R 0=Ω，测得电路中的电流I =10安培。
求： （1）该有源支路的电动势E ；（2）此支路是从电网吸收电能还是向电网输送电能解：（1）E= U + R o ×I =235V（2）P =U ×I >0, 输送1-5 (1)求图 (a)电路中受控电压源的端电压和它的功率；(2)求图 (b)电路中受控电流源的电流和它的功率；解：（a ）U 1＝3×4 =12V ，受控电压源的端电压2U 1＝24V ，P 发=3×24 =72W （b ）I 2＝，受控电流源的电流6I 2＝3A ，P 吸=5×3 =15W1-6 求图示各电路中的U ab ，设端口a 、b 均为开路。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第2章电路的基本分析方法2.1 试求如图2.3所示各电路a、b两端的等效电阻。
图2.3 习题2.1的图分析本题考查电阻串联、电阻并联电路总电阻的计算，电阻串联电路的总电阻为，电阻并联电路的总电阻为。
解对图2.3（a）所示电路，6Ω电阻和上面12Ω电阻并联后再与下面12Ω电阻串联，其总电阻为Ω，该16Ω电阻与4Ω电阻并联后再与5Ω电阻串联，因此a、b两点之间的总电阻为：（Ω）对图2.3（b）所示电路，左右两边4个10Ω电阻并联后再与中间的10Ω电阻串联，因此a、b 两点之间的总电阻为：（Ω）对图2.3（c）所示电路，6Ω电阻和12Ω电阻并联后再与下面4Ω电阻串联，其总电阻为Ω，该8Ω电阻再与左边8Ω电阻以及右边4Ω电阻并联，因此a、b两点之间的总电阻为：（Ω）2.2 试求如图2.4所示电路中的电压U。
分析电阻串、并联电路电流和电压的计算，一般可先利用电阻串、并联公式求出电路的总电阻，然后根据欧姆定律求出总电流，最后利用欧姆定律或分压公式和分流公式计算各个电阻的电压或电流。
解标出总电流和待求支路电流的参考方向，如图2.5所示。
电路的总电阻为：（Ω）图2.4 习题2.2的图图2.5 习题2.2解答用图总电流为：（A）待求支路的电流为：（A）待求电压为：（V）2.3 试求如图2.6所示电路中的电流I和电压U ab。
分析本题考查电阻串联、电阻并联电路电流和电压的计算。
由于对外电路而言，恒流源与电阻串联可等效于该恒流源，故本题可先用分流公式计算出两并联电阻支路的电流，然后再计算a、b之间的电压。
解设8Ω电阻与2Ω电阻串联支路的电流为，如图2.7所示。
由分流公式得：（A）（A）a、b之间的电压为：（V）图2.6 习题2.3的图图2.7 习题2.3解答用图2.4 试求如图2.8所示电路中的电流I。
分析3Ω电阻和下面6Ω电阻并联后再与上面6Ω电阻串联，然后与2Ω电阻并联接到8V 恒压源上，故待求电流与2Ω电阻是否并联无关。
解3Ω电阻和下面6Ω电阻并联后再与上面6Ω电阻串联，总电阻为：（Ω）待求电流为：（A）2.5 试求如图2.9所示电路中的电压U ab。
图2.8 习题2.4的图图2.9 习题2.5的图分析用分流公式计算出两并联支路的电流后，即可计算出a、b之间的电压。
解1Ω电阻和2Ω电阻串联支路的电流为：（A）两个3Ω电阻串联支路的电流为：（A）两支路电流的方向均向下。
a、b之间的电压为：（V）2.6 在如图2.10所示的电路中，已知V，V，Ω，Ω，Ω，试用支路电流法计算各支路电流，并证明电源产生的功率等于所有电阻消耗的总功率。
分析本题电路有2个节点3条支路，需要列3个独立的方程才能解出3个支路电流I1、I2、I3。
2个节点可列出1个方程，另外两个方程可由左右两个回路列出。
解根据KCL对上面节点列电流方程，设流入节点的电流为正，流出节点的电流为负，则有：设左边回路的绕行方向为顺时针方向，根据KVL，有：设右边回路的绕行方向为逆时针方向，根据KVL，有：将题设数据代入以上3个方程，得：联立以上3个方程求解，得：AAA3个电阻总共吸收的功率为：（W）两个电源的功率为：（W）可见两个电源均发出功率，共2748W，3个电阻总共吸收的功率也是2748W，电路的功率平衡。
2.7 在如图2.11所示电路中，试用支路电流法计算各支路电流。
图2.10 习题2.6的图图2.11 习题2.7的图分析本题电路虽有3条支路，但由于恒流源支路的电流已知，故只有两个未知电流I1、I2，只需要列2个独立的方程。
2个节点可列出1个方程，另外1个方程可由右边回路列出。
注意：列KVL方程时要尽量避开恒流源支路，否则，因为恒流源两端的电压未知，反而要多列1个方程。
解根据KCL对上面节点列电流方程，设流入节点的电流为正，流出节点的电流为负，则有：设右边回路的绕行方向为逆时针方向，根据KVL，有：联立以上3个方程求解，得：AA说明其实际方向与图中所标的参考方向相反。
2.8 在如图2.12所示电路中，试用支路电流法计算各支路电流。
分析本题电路虽有4条支路，但也只有3个未知电流I1、I2、I3，只需要列3个独立的方程。
2个节点可列出1个方程，另外2个方程可由右边两个回路列出。
解根据KCL对上面节点列电流方程，设流入节点的电流为正，流出节点的电流为负，则有：设右边两个回路的绕行方向均为顺时针方向，根据KVL，有：将题设数据代入以上3个方程，得：联立以上3个方程求解，得：AAA说明其实际方向与图中所标的参考方向相反。
2.9 在如图2.13所示电路中，已知V，V，Ω，Ω，试用节点电压法计算各支路电流。
图2.12 习题2.8的图图2.13 习题2.9的图分析本题电路有2个节点，4条支路，用节点电压法求出两个节点间的电压后，即可求出各支路电流。
解设两节点间电压的参考方向为上正下负，根据弥尔曼公式得：（V）由此可计算出各支路电流分别为：（A）（A）（A）（A）I2和I4为负值，说明它们的实际方向与图中所标的参考方向相反。
2.10 在如图2.14所示电路中，试用节点电压法计算各支路电流。
分析本题电路有2个节点，4条支路，但只有3个未知电流I1、I2、I3。
用节点电压法求出两个节点间的电压后，即可求出各支路电流。
解设两节点间电压的参考方向为上正下负，根据弥尔曼公式得：（V）由此可计算出各支路电流分别为：（A）（A）（A）说明其实际方向与图中所标的参考方向相反。
2.11 在如图2.15所示电路中，试用节点电压法计算各支路电流。
分析本题电路有3个节点，可以假设任意一个节点为参考节点，用KCL列出其余各节点的电流方程，再用KVL或欧姆定律写出各支路电流的表达式，代入各电流方程求解，即可求出其余各节点的电位，进而可求出各支路的电流。
解设下面的节点为参考节点，上面左右两个节点的电位分别为U a、U b。
应用KCL分别对上面左右两个节点列方程，得：图2.14 习题2.10的图图2.15 习题2.11的图根据欧姆定律或KVL，由图2.15可得各支路电流为：将以上4式代入KCL方程，得：解之，得：VV由此可计算出各支路电流分别为：AAAA说明其实际方向与图中所标的参考方向相反。
2.12 将如图2.16所示的两个电路分别化为一个恒压源与一个电阻串联的电路。
分析本题考查电源之间的等效变换。
利用电压源和电流源的等效变换逐步化简，即可将如图2.16所示的两个电路分别化为一个恒压源与一个电阻串联的电路。
在变换过程中，当有多个恒流源并联时，可等效为一个恒流源，等效后的恒流源的电流等于原来的多个恒流源电流的代数和；当有多个恒压源串联时，可等效为一个恒压源，等效后的恒压源的电压等于原来的多个恒压源电压的代数和。
图2.16 习题2.12的图解对图2.16（a）所示电路，首先将2个电压源等效变换为电流源，然后将2个并联的恒流源等效为一个恒流源，将两个并联的电阻等效为一个电阻，即化为一个电流源，最后将该电流源等效变换为电压源，等效变换过程如图1.17所示。
图2.17 图2.16（a）的变换过程对图2.16（b）所示电路，首先将两个电流源等效变换为电压源，然后将两个串联的恒压源等效为一个恒压源，将两个串联的电阻等效为一个电阻，即化为一个电压源，等效变换过程如图1.18所示。
图2.18 图2.16（b）的变换过程2.13 电路如图2.19所示，试用电压源与电流源等效变换的方法计算流过2Ω电阻的电流I。
分析本题有2个电压源和1个电流源，在变换过程中需注意电流和电压的方向，变换前后电压源的正极性端与电流源电流流出的一端对应。
解首先将左边两个电压源等效变化为电流源；将上面的电流源等效变化为电压源，并将其内阻与电路中串联的1Ω电阻合并。
画出变换后的电路，如图2.20所示。
然后将图2.20所示电路根据图2.21的变换次序，最后化简为图2.21（c）所示的电路。
由图2.21（c）可得流过2Ω电阻的电流为：（A）图2.19 习题2.13的图图2.20 图2.19的等效电路图2.21 图2.20的等效变换过程2.14 写出如图2.22所示电路中输出电压U2与输入电压U1的比值。
分析本题可用电压源和电流源的等效变换逐步化简后求解，也可用电阻串并联方法求解，还可用戴维南定理求解，这里采用第一种方法。
解将输入电压U1看作恒压源，则其与电阻R串联的支路可等效变换为电流源，再将2个并联的电阻等效为一个电阻，得如图2.23（a）所示电路。
最后将如图2.23（a）所示电路的电流源等效变换为电压源，得如图2.23（b）所示电路。
由图2.23（b）得：图2.22 习题2.14的图图2.23 习题2.14解答用图2.15 试用电压源与电流源等效变换的方法求如图2.24所示各电路中的电流I。
图2.24 习题2.15的电路分析图2.24（a）电路有2个电压源，将它们等效变换为电流源后，再将2个电流源等效变换为1个电流源，即可利用分流公式求出待求电流。
图2.24（b）电路有1个电流源和1个电压源，先将电压源等效变换为电流源，然后将2个电流源等效变换为1个电流源，即可利用分流公式求出待求电流。
解对图2.24（a）所示电路，根据图2.25的变换次序，最后化简为如图2.25（c）所示的电路。
由图2.25（c）得：（A）图2.25 图2.24（a）解答用图对图2.24（b）所示电路，根据图2.26的变换次序，最后化简为如图2.26（c）所示的电路。
由图2.26（c）得：（A）图2.26 图2.24（b）解答用图2.16 试用叠加定理计算如图2.27所示电路中流过4Ω电阻的电流I。
分析本题有1个10A恒流源和1个10V恒压源。
利用叠加定理求解时，10A恒流源单独作用时10V恒压源短路，这时5Ω电阻也被短路，1Ω电阻和4Ω电阻并联；10V恒压源单独作用时10A恒流源开路，这时1Ω电阻和4Ω电阻串联。
解10A恒流源单独作用时的电路如图2.28（a）所示，由图可得：（A）10V恒压源单独作用时的电路如图2.28（b）所示，由图可得：（A）2个电源共同作用时，根据叠加定理得待求电流为：（A）图2.27 习题2.16的图图2.28 习题2.16解答用图2.17 试用叠加定理计算如图2.29所示电路中流过3Ω电阻的电流I。
分析2A恒流源单独作用时6V恒压源短路，这时3Ω电阻和6Ω电阻并联；6V恒压源单独作用时2A恒流源开路，这时3Ω电阻和6Ω电阻串联。
解2A恒流源单独作用时的电路如图2.30（a）所示，由图可得：（A）6V恒压源单独作用时的电路如图2.30（b）所示，由图可得：（A）2个电源共同作用时，根据叠加定理得待求电流为：（A）图2.29 习题2.17的图图2.30 习题2.17解答用图2.18 如图2.31（a）所示，V，，V。