2018届江苏省赣榆县海头高级中学高三上学期数学周考10
江苏省赣榆县海头高级中学2018届高三上学期数学周考4

考点:难度:2一、填空题1、设集合则A B =_____.2、“3a ≥”是“2[1,2],0x x a ∀∈-≤”为真命题的_____条件.(在“充分不必要”、“必要不充分”、“既不充分又不必要”、“充要”中选择填空).3、函数[]),0(cos 3sin π∈-=x x x y 的值域是_____.4、已知命题R p ∈∃ϕ:,使)sin()(ϕ+=x x f 为偶函数;命题R x q ∈∀:,03sin 42cos <-+x x ,则下列命题:①q p ∧;②q p ∨⌝)(;③)(q p ⌝∨;④)()(q p ⌝∧⌝. 其中真命题有_____(填序号). 5、已知02<<-x π,且51cos sin =+x x ,则=x tan _____. 6、将函数)0)(2sin(2πϕϕ<<+=x y 的图象沿x 轴向左平移8π个单位,得到函数)(x f y =的图象,若函数)(x f y =的图象过原点,则ϕ的值为_____.7、已知函数)6sin(2)(πϖ-=x x f 的最小正周期为π,且函数)(x f y =在⎥⎦⎤⎢⎣⎡2,0π上的单调递增区间为[]b a ,,则实数=+b a _____.8、在平面坐标系xOy 中,若角α的始边与x 轴的正半轴重合,终边在射线)0(3>-=x x y 上,则α5sin =_____.9、⎩⎨⎧≥<-=1213)(x x b x x f x ,若4))65((=f f ,则b =_____. 10、设α为锐角,且54)6cos(=+πα,则)122sin(πα+的值为_____. 11、已知函数)(x f 是定义在R 上的奇函数,且当0≤x 时,a x x x f +--=3)(2,则不等式4)1(+->-x x f 的解集是_____.12、设函数x m x x f +=ln )(,若0>>a b 有1)()(<--ab a f b f 成立,则m 的取值范围为_____.13、若不等式2ln 9x x c bx ≤++,对任意的())3,0(,,0∈+∞∈b x 恒成立,则实数c 的取值范围是_____.14、已知函数⎪⎩⎪⎨⎧>+--≤=031302)(2x x x x x f ,若存在唯一的整数x ,使得0)(>-xa x f 成立,则实数a 的取值范围为_____.二、解答题15、(本题满分14分)已知直线2=y 与函数)0(1cos sin 32sin 2)(2>-+=ϖϖϖϖx x x x f 的图象的两相邻交点之间的距离为π.(1)求函数)(x f y =的解析式,并求出函数)(x f y =的单调递增区间;(2)将函数)(x f y =的图象向左平移4π个单位后得到函数)(x g y =的图象,求函数)(x g y =在⎥⎦⎤⎢⎣⎡2,0π的最大值和最小值.16、(本题满分14分)已知函数.(1)求的值;(2)设求cos()αβ+的值.17、(本题满分14分)如图①,一条宽为km 1的两平行河岸有村庄A 和供电站C ,村庄B 与C A ,的直线距离都是km 2,BC 与河岸垂直,垂足为D .现要修建电缆,从供电站C 向村庄B A ,供电.修建地下电缆、水下电缆的费用分别是2万元km /、4万元km /.(1)已知村庄A 与B 之间原来铺设有旧电缆,需要改造,旧电缆的改造费用是0.518、(本题满分16分)设二次函数c bx ax x f ++=2)(在区间[]2,2-上的最大值、最小值分别是M 、m ,集合{}x x f x A ==)(|.(1)若{}2,1=A ,且2)0(=f ,求M 和m 的值; (2)若{}1=A ,且1≥a ,记m M a g +=)(,求)(a g 的最小值19、(本题满分16分)已知函数()21f x x ax =-+,()442x x a g x -=-⋅,其中a ∈R .(1)当0a =时,求函数()g x 的值域;(2)若对任意[]0,2x ∈,均有()2f x ≤,求a 的取值范围;(3)当0a <时,设()()(),,,f x x a h x g x x a>⎧⎪=⎨≤⎪⎩,若()h x 的最小值为72-,求实数a 的值.20、(本题满分16分)已知函数x a x a x x f ln )12()(2++-=.(1)当1=a 时,求函数)(x f 的单调增区间;(2)求函数)(x f 在区间]1[e ,上的最小值;(3)设x a x g )1()(-=,若存在]1[0e e x ,∈,使得)()(00x g x f ≥成立,求实数a 的取值范围.。
江苏省赣榆县海头高级中学2018届高三上学期数学周练16 Word版缺答案

江苏省海头高中2018届高三年级第一学期周练(16)数 学 试 题一、填空题:本大题共14小题,每小题5分,共70分.请把答案填写在答题卡相应位置.......上. 1.命题:“1>∀x ,32≥x ”的否定为 ▲ ; 2.满足}3,2,1{}1{⊆⊆A 的集合A 的个数为 ▲ ;3.已知复数))(1(i a i z -+=(i 为虚数单位)为纯虚数,则实数a 的值为 ▲ ; 4.如图所示的流程图,是一个算法流程图,则输出的n 的值是 ▲ ; 5.甲、乙两盒中各有除颜色外完全相同的2个红球和1个白球,现从甲、乙两盒中随机各取一个球,则至少有一个红球的概率为 ▲ ;6.已知样本数据x 1,x 2,…,x n 的方差52=s ,则样本数据2x 1+1,2x 2+1,…, 2x n +1的方差为 ▲ ; 7.已知2lg =a ,3lg =b ,则=53lg▲ ;(用a ,b 表示) 8.已知等差数列}{n a 前n 项和为n S ,且62118=-a a ,则=9S ▲ ;9.设实数y x ,满足⎪⎩⎪⎨⎧≤--≥-≤+22142y x y x y x ,则y x z +=的最小值为 ▲ ;10.已知锐角θ满足54)62sin(=+πθ,则=+)65cos(πθ ▲ ; 11.已知正数y x ,满足42=++y x xy ,则y x +的最小值为 ▲ ; 12.如图,半圆O 的直径为2,A 为直径延长线上的一点,2=OA ,B 为半圆上任意一点。
以AB 为斜边作等腰直角三角形ABC 且3πα=,则=⋅ ▲ ;13.已知圆O :122=+y x 和点)0,2(-A ,若存在异于点A 的定点B 和常数λ满足:对圆O 上任意一点M ,都有MA MB λ=,则点B 的坐标为 ▲ ;14.若0112<+-mx x m (0≠m )对于一切4≥x 恒成立,则实数m 的取值范围是 ▲ . 二、解答题:本大题共6小题,共计90分,请在答题纸指定的区域内作答...........,解答题应写出文(第4题)字说明、证明过程或演算步骤. 15.(本题满分14分)如图,在四棱锥ABCD P -中,底面ABCD 是矩形,平面⊥PCD 平面ABCD ,M 为PC 中点,求证:(Ⅰ)//PA 平面MBD ;(Ⅱ)BC PD ⊥。
江苏省赣榆县海头高级中学2018届高三上学期数学周考4

考点:难度:2一、填空题1、已知全集1234{}U =,,,,集合{}}1434{A B =,,=,,则_____.2、若复数z 满足,其中i 为虚数单位, 为复数z 的共轭复数,则复数z 的模为_____.3、若角α的终边经过点)6,(-x P ,且53tan -=α,则x 的值为_____. 4、右图是一个算法流程图,则输出的k 的值是_____.5、设53)6cos(=+πα,则)3sin(πα-=____.6、已知a 、b 的夹角为120︒,||3,||a a b =+= ,则||b =_____.7、若()323f x x ax x =-+在[)2,+∞上是增函数,则a 的取值范围 是_____.8、已知函数()f x 是定义在R 上且周期为4的偶函数.当]4[2x ∈,时,43f(x)=|log (x-)|2, 则)21(f 的值为_____.9、已知两条直线b a ,与两个平面βα,,α⊥b ,则下列命题中正确的是_____. ① 若α//a ,则b a ⊥;②若b a ⊥,则α//a③若β⊥b ,则βα//;④若βα⊥,则β//b10、如图,在矩形ABCD 中,2,2==BC AB ,点E 为BC 的中点,点F 在边CD 上,若2=⋅AF AB ,则⋅的值为_____.11、设函数⎪⎩⎪⎨⎧≥<=-11)(311x xx e x f x ,则使得2)(≤x f 成立的x 的取值范围是_____.12、已知直线)20(παα<<=x 与函数x x f sin )(=和函数x x g cos )(=的图象分别交于N M ,两点,若51=MN ,则线段MN 的中点的纵坐标为_____. 13、已知函数],0[,3)(2m x x x x f ∈-=,其中,R m ∈当函数)(x f 的值域为]2,0[时,则实数m 的取值范围为_____.14、已知函数⎪⎩⎪⎨⎧<≥-=0,30,4)(2x xx x x x f 若函数()()3g x f x x b =-+有三个零点,则实数b 的取值范围为_____.二、解答题15、(本题满分14分)已知向量2()2a cos sin αα=,,b=(2sina,t),a (0,)2π∈. (1)若2a-b=(,0)5,求t 的值; (2)若1t =,且•1a b =,求tan(2a+)4π的值.16、(本题满分14分)如图,已知直三棱柱111ABC A B C -的侧面11ACC A 是正方形,点O 是侧面11ACC A 的中心,,M 是棱BC 的中点.(1)求证://OM 平面11ABB A ;(2)求证:⊥1AC 平面BC A 1.17、(本题满分14分)如图是一个半圆形湖面景点的平面示意图.已知AB 为直径,且2AB =km,O 为圆心,C 为圆周上靠近A 的一点,D 为圆周上靠近B 的一点,且CD ∥AB .现在准备从A 经过C 到D 建造一条观光路线,其中A 到C 是圆弧AC ,C 到D 是线段CD .设rad AOC x ∠=,观光路线总长为km y .(1)求y 关于x 的函数解析式,并指出该函数的定义域;(2)求观光路线总长的最大值.18、(本题满分16分)已知二次函数()f x 满足(1)()2f x f x x +-=且(0)1f =.(1)求()f x 的解析式;(2)当[1,1]x ∈-时,不等式:()2f x x m >+恒成立,求实数m 的范围.(3)设[]()(2),1,1g t f t a t =+∈-,求()g t 的最大值19、(本题满分16分)已知函数()f x =2axx b +,在1x =处取得极值2.(1)求函数()f x 的解析式;(2)m 满足什么条件时,区间(,21)m m +为函数()f x 的单调增区间?(3)设直线l 为曲线()f x =2axx b +的切线,求直线l 的斜率的取值范围.20、(本题满分16分) 已知函数333)(1++-=+x x ax f 是定义在R 上的奇函数.(1)求a 的值;(2)存在t R ∈,不等式()()2222f t t f t k -<-有解,求k 的取值范围;(3)若函数()g x 满足()()()12333x x f x g x -⋅+=-⎡⎤⎣⎦,若对任意x R ∈,不等式()()211g x m g x ≥⋅-恒成立,求实数m 的最大值.。
2018届江苏省赣榆县海头高级中学高三上学期数学周练11

江苏省海头高中2018届高三年级第一学期周练(11)数 学 试 题一、填空题:本大题共14小题,每小题5分,共70分.请把答案填写在答题卡相应位置.......上. 1.已知集合}1,0,1{-=A ,集合}1|{->=x x B ,则=B A ; 2.设复数)()2R a i a a z ∈-+=(,且2||=z ,则=z ;3.不等式0123>--xx 的解集为 ; 4.双曲线)0,0(12222>>=-b a by a x 的渐近线方程为y x 2±=,则该双曲线的离心率为 ;5.为了得到函数)62sin(π-=x y 的图像,可以将x y 2cos =的图像向右平移)0(>m m 个单位,则m 的最小值为 ;6.已知如图是9位评委给某作品打出的分数茎叶图,那么9位评委打出的分数的方差为 ;7.在区间],[ππ-上任取一个数x ,则使得21cos -≥x 成立的概率是 ; 8.过点)6,0(A 且与圆01010:22=+++y x y x C 切于原点的圆的一般方程是 ;9.已知z y x ,,均为大于1的实数,且32,,z y x 成等比数列,则zyx y lg lg lg lg +的最小值为 ;10.已知等比数列{a n }的前n 项和为S n ,若3222+=a S ,3233+=a S ,则公比q 的值为 ;11.已知16960cos sin =θθ,且24πθπ<<,则=-)3sin(πθ ; 12.在ABC ∆中,60=∠A ,4=AB ,A ∠的平分线交边BC 于M ,且CM 41=,则AM 的长度为 ;13.设1F 是椭圆13222=+y x 的左焦点,P 为椭圆上任意一点,Q 的坐标为)1,66(,则898 9 91 12 23 4PQ PF +1的最大值为 ;14.已知函数⎩⎨⎧>+-≤-+=ax x ax ax x x f ,ln 1,2)(2有三个不同的零点,则实数a 的取值范围是 ;二、解答题:本大题共6小题,共计90分,请在答题纸指定的区域内作答...........,解答题应写出文字说明、证明过程或演算步骤. 15.(本题满分14分)如图,在矩形ABCD 中,3=AB ,1=AD ,点E 在边CD 上,且EC DE 2=, (1)求AEB ∠cos ; (2)求CAE ∠tan 。
江苏省赣榆县海头高级中学2018届高三上学期数学文小题

高三数学小题训练11.不等式1121≤+-x x 的解集是 ;2.幂函数3222)1(----=m m x m m y ,当),0(+∞∈x是 ;3.执行如图所示的伪代码,当输入,a b 的值分别为1,3时,最后输出 的a 的值为 ;4.若命题“存在20,4R x ax x a ∈++≤”为假命题,则实数a 的 取值范围是 ; 5.P :522x -> ,q:21045x x >+-,则p ⌝是q ⌝的 条件;6.已知函数c x x y +-=33的图像与x 轴恰有两个公共点,则=c ;7.函数22,0,()1,0x x f x x x ⎧⎪=⎨-+>⎪⎩≤的值域为 ;8.已知12sin()413x π-=,且04x π<<,则cos 2cos()4x x π=+ ;9.已知)(x f 是定义在]1,1[-上的奇函数,当0<x 时,)1()(-=x x x f ,则关于m 的不等式0)1()1(2<-+-m f m f 的解集为 ;10.函数)(x f 的定义域为R ,2)0(=f ,对任意R x ∈,1)()(>'+x f x f ,则不等1)(+>⋅x x e x f e 的解集为 ;11.已知函数R m m x x x f ∈++=,2sin 3cos 2)(2 ⑴当R x ∈时,求)(x f 的单调递增区间;⑵当⎥⎦⎤⎢⎣⎡∈2,0πx 时,且)(x f 的最小值为2,求m 的值12.已知命题:p 方程0222=-+ax x a 在[]1,1-上有解;命题:q 只有一个实数x 满足不等式0222≤++a ax x 。
若命题“p 或q ”是假命题。
求a 的取值范围。
江苏省赣榆县海头高级中学高三上学期数学周练10(文科)
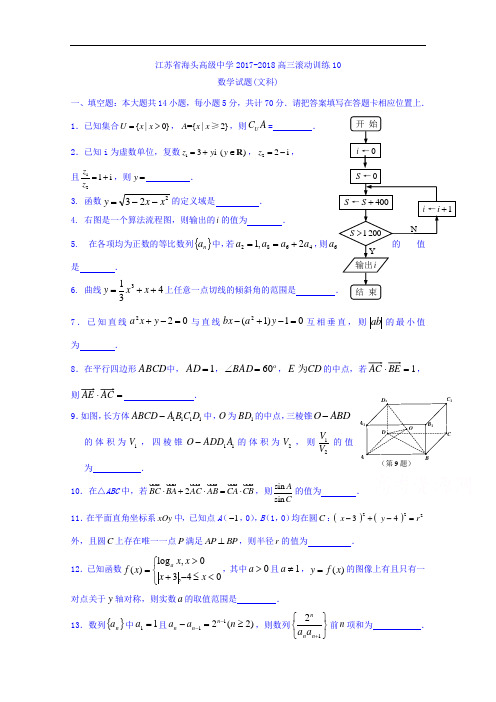
1A 江苏省海头高级中学2017-2018高三滚动训练10数学试题(文科)一、填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答题卡相应位置上. 1.已知集合{|0}U x x =>,={|2}A x x ≥,则A C U = . 2.已知i 为虚数单位,复数13i z y =+()R y ∈,22i z =-, 且121i z z =+,则y = . 3. 函数223x x y --=的定义域是 . 4. 右图是一个算法流程图,则输出的i 的值为 .5. 在各项均为正数的等比数列{}n a 中,若46822,1a a a a +==,则6a 是 .6. 曲线4313++=x x y 上任意一点切线的倾斜角的范围是 .7.已知直线022=-+y x a 与直线01)1(2=-+-y a bx 互相垂直,则ab 的最小值为 .8.在平行四边形ABCD 中,1=AD ,60=∠BAD ,E CD 为的中点,若1=⋅BE AC ,则=⋅ .9.如图,长方体1111ABCD A B C D -中,O 为1BD 的中点,三棱锥O ABD -的体积为1V ,四棱锥11O ADD A -的体积为2V ,则12VV 的值为 .10.在△ABC 中,若2BC BA AC AB CA CB ⋅+⋅=⋅,则sin sin AC的值为 . 11.在平面直角坐标系xOy 中,已知点A (1-,0),B (1,0)均在圆C :()()22234x y r -+-=外,且圆C 上存在唯一一点P 满足AP BP ⊥,则半径r 的值为 . 12.已知函数⎩⎨⎧<≤-+>=04,30,log )(x x x x x f a ,其中0>a 且1≠a ,)(x f y =的图像上有且只有一对点关于y 轴对称,则实数a 的取值范围是 . 13.数列{}n a 中11=a 且)2(211≥=---n a a n n n ,则数列⎭⎬⎫⎩⎨⎧+12n n n a a 前n 项和为 .14.已知函数⎩⎨⎧>-≤-=05042x e x x x f x ,,)(,若关于x 的方程05=--ax x f )(恰有三个不同的实数解,则满足条件的所有实数a 的取值集合为 .二、解答题:本大题共6小题,共计90分.请在答题卡...指定区域....内作答.解答时应写出文字 说明、证明过程或演算步骤.15.(本小题满分14分)如图,在直三棱柱111ABC A B C -中,AC BC =,点M 为棱11A B 的中点.求证:(1)//AB 平面11A B C ;(2)平面1C CM ⊥平面11A B C .16.(本小题满分14分)设△ABC 的内角A ,B ,C 所对边分别为a ,b ,c .向量()a b =m ,()sin cos B A =-,n ,且⊥m n .(1)求A 的大小;(2)若=n ,求cos C 的值.ABCA 1B 1C 1M(第15题)17.(本小题满分14分)如图,在平面直角坐标系xOy 中,已知圆22:40C x y x +-=及点(1,0)A -,(1,2)B .(1)若直线l 平行于AB ,与圆C 相交于M ,N 两点,MN AB =,求直线l 的方程; (2)在圆C 上是否存在点P ,使得2212PA PB +=?若存在,求点P 的个数;若不存在,说明理由.18.(本小题满分16分) 将2张边长均为1分米的正方形纸片分别按甲、乙两种方式剪裁并废弃阴影部分.(1)在图甲的方式下,剩余部分恰能完全覆盖某圆锥的表面,求该圆锥的母线长及底面半径; (2)在图乙的方式下,剩余部分能完全覆盖一个长方体的表面,求长方体体积的最大值.(第18题)甲乙19.(本小题满分16分)对于给定的正整数k ,如果各项均为正数的数列{}n a 满足:对任意正整数()n n k >,21111k n k n k n n n k n k n a a a a a a a --+-++-+⋅⋅⋅⋅⋅⋅=总成立,那么称{}n a 是“()Q k 数列”. (1)若{}n a 是各项均为正数的等比数列,判断{}n a 是否为“(2)Q 数列”,并说明理由; (2)若{}n a 既是“(2)Q 数列”,又是“(3)Q 数列”,求证:{}n a 是等比数列.20. (本小题满分16分)设命题p :对任意的)π02x ⎡∈⎢⎣,,sin tan x ax b x +≤≤恒成立,其中a b∈R,.(1)若10,,求证:命题p为真命题.a b==(2)若命题p为真命题,求a b,的所有值.。
2018届江苏省赣榆县海头高级中学高三上学期数学周考(6)
江苏省海头高中2018届高三年级第一学期周考(6)数学试题(文科)一.填空题:本大题共14小题,每题5分,共70分.请把答案填写在答题卡相应位置.......上. 1. 设集合U ={1,2,3,4},A ={1,2,3},B ={2, 3,4},则∁U (A ∩B )= ▲ . 2. 函数()f x =的定义域为 ▲ .3. 已知平面向量a ,b 满足|a |=1,|b |=2,a 与b 的夹角为60°,则|2a -b|的值为 ▲ . 4. 右图是一个算法流程图,则输出的k 的值是 ▲ .5. 已知函数()()23020x x x f x f x x ⎧-⎪=⎨+<⎪⎩,≥,,,则()9f -= ▲ .6.设等差数列{}n a 的前n 项和为n S .若公差2d =,510a =,则10S 的值是 ▲ .7. 已知函数()ln 4f x x x =+-的零点在区间()1k k +,内,则正整数k 的值为 ▲ .8. 已知函数()3213f x ax x x =-+在区间()02,上是单调增函数,则实数a 的取值范围为 ▲ .9.已知圆锥的侧面展开图是半径为3,圆心角为2π3的扇形,则这个圆锥的高为 ▲ . 10.若指数函数()f x 的图象过点()24-,,则不等式()()52f x f x +-<的解集为 ▲ . 11.已知函数()()()sin 00πf x x ωϕωϕ=+><<,的周期为4,将函数f (x )的图象向右平移13个单位后,所得图象关于原点对称,则函数y =f (x )在[]01,上的值域为▲ .12.如图,在四边形ABCD 中,AB AD ⋅=5,BD =4,O 为BD 的中点,且AO =3OC ,则CB CD ⋅= ▲ . 13.已知函数()()2342ln 2f x x a x x =++-在区间()12,上存在最值,则实数a 的取值范围是 ▲ .14.在△ABC 中,若1tan A ,2tan C ,1tan B成等差数列,则cos C 的最小值为 ▲ . BADOC(第12题图)(第4题)(第16题)ABCDP M N二、解答题:本大题共6小题,共90分.请在答题卡指定区域内........作答,解答时应写出文字说明、证明过程或演算步骤.15.已知π03x ⎡⎤∈⎢⎥⎣⎦,,设向量()sin cos m x x =,,()312n =,. (1)若m ∥n ,求x 的值; (2)若35m n ⋅=,求()πsin 12x -的值.16.如图,在四棱锥P ABCD -中,底面ABCD 是矩形,平面PAD ⊥平面ABCD ,AP=AD ,M ,N 分别为棱PD ,PC 的中点. 求证:(1)MN ∥平面PAB ; (2)AM ⊥平面PCD .17.在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,若c -b =2b cos A . (1)求证:A =2B ; (2)若cos B =34,c =5,求△ABC 的面积.18.如图,矩形ABCD 是某小区户外活动空地的平面示意图,其中AB =503米,AD =100米.现拟在直角三角形OMN 内栽植草坪供儿童踢球娱乐(其中,点O 为AD 的中点,OM ⊥ON ,点M 在AB 上,点N 在CD 上),将破旧的道路AM 重新铺设.已知草坪成本为每平方米20元,新道路AM 成本为每米500元,设∠OMA =θ,记草坪栽植与新道路铺设所需的总费用为f (θ). (1)求f (θ)关于θ函数关系式,并写出定义域;(2)为节约投入成本,当tan θ为何值时,总费用 f (θ)最小?OABCDMNθ(第18题图)19.已知二次函数()f x 为偶函数且图象经过原点,其导函数()'f x 的图象过点()12,. (1)求函数()f x 的解析式;(2)设函数()()()'g x f x f x m =+-,其中m 为常数,求函数()g x 的最小值.20.设函数()1ln 1f x a x x=+-. (1)当2a =时,求函数()f x 在点()()11f ,处的切线方程; (2)讨论函数()f x 的单调性;(3)当102a <<时,求证:对任意()1+2x ∈∞,,都有()1e x aa x ++<.。
江苏省赣榆县海头高级中学2018届高三上学期数学小题11
考点:难度:2一、填空题1、全集{}1,2,3,4,5,6I =,{}{}1,3,5,2,3,6A B ==,则()I C A B =_____. 2、设i 是虚数单位,则复数ii +2的模为_____. 3、若m ∈R , 命题“若0m >,则20x x m +-=有实根”的逆否命题是_____4、“0a =” 是“函数()()32f x x ax x R =+∈为奇函数”的_____条件(填充要关系).5、已知)0(πα,∈,53)4sin(-=+πα,则=αtan _____. 6、已知不等式210ax bx +->的解集为()2,3,则ab =_____.7、已知函数)(x f 为定义在R 上的奇函数,当0≥x 时,m x x f x ++=22)((m 为常数),则)1(-f 的值为_____.8、函数xe xf x=)(的单调减区间为_____. 9、已知函数⎩⎨⎧<+≥=mx x m x x f x ,,12)(错误!未找到引用源。
的值域为R ,则实数m 的取值范围是_____.10、若函数()()2lg 1f x x ax =--在区间()1,+∞是增函数,则a 的取值范围是_____. 11、矩形ABCD 中, P 为矩形ABCD 所在平面内一点,且满足3,4PA PC ==,矩形对角线6AC =,则=⋅_____.12、如图,在ABC ∆中,已知B=3π,D 为BC 边上一点.若AB AD =,则A D C ∆的周长的最大值为_____.13、已知函数x x x f 2)(2+=图像上有两点0),(),(212211<<x x y x B y x A ,、,若曲线)(x f y =分别在点A B 、处的切线互相垂直,则212x x -的最大值是_____.14、函数⎩⎨⎧≥-<+-=0101)(2x x x x x g ,,,若m x g g y 2))((-=有3个不同的零点,则m 的取值范围是_____.。
2018届江苏省赣榆县海头高级中学高三上学期数学周练10(文科)
1A 江苏省海头高级中学2017-2018高三滚动训练10数学试题(文科)一、填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答题卡相应位置上. 1.已知集合{|0}U x x =>,={|2}A x x ≥,则A C U = . 2.已知i 为虚数单位,复数13i z y =+()R y ∈,22i z =-, 且121i z z =+,则y = . 3. 函数223x x y --=的定义域是 . 4. 右图是一个算法流程图,则输出的i 的值为 .5. 在各项均为正数的等比数列{}n a 中,若46822,1a a a a +==,则6a 是 .6. 曲线4313++=x x y 上任意一点切线的倾斜角的范围是 .7.已知直线022=-+y x a 与直线01)1(2=-+-y a bx 互相垂直,则ab 的最小值为 .8.在平行四边形ABCD 中,1=AD ,60=∠BAD ,E CD 为的中点,若1=⋅BE AC ,则=⋅ .9.如图,长方体1111ABCD A BC D -中,O 为1BD 的中点,三棱锥O ABD -的体积为1V ,四棱锥11O ADD A -的体积为2V ,则12VV 的值为 .10.在△ABC 中,若2BC BA AC AB CA CB ⋅+⋅=⋅,则sin sin AC的值为 . 11.在平面直角坐标系xOy 中,已知点A (1-,0),B (1,0)均在圆C :()()22234x y r -+-=外,且圆C 上存在唯一一点P 满足AP BP ⊥,则半径r 的值为 . 12.已知函数⎩⎨⎧<≤-+>=04,30,log )(x x x x x f a ,其中0>a 且1≠a ,)(x f y =的图像上有且只有一对点关于y 轴对称,则实数a 的取值范围是 .13.数列{}n a 中11=a 且)2(211≥=---n a a n n n ,则数列⎭⎬⎫⎩⎨⎧+12n n n a a 前n 项和为 .14.已知函数⎩⎨⎧>-≤-=05042x e x x x f x ,,)(,若关于x 的方程05=--ax x f )(恰有三个不同的实数解,则满足条件的所有实数a 的取值集合为 .二、解答题:本大题共6小题,共计90分.请在答题卡...指定区域....内作答.解答时应写出文字 说明、证明过程或演算步骤.15.(本小题满分14分)如图,在直三棱柱111ABC A B C -中,AC BC =,点M 为棱11A B 的中点.求证:(1)//AB 平面11A B C ;(2)平面1C CM ⊥平面11A B C .16.(本小题满分14分)设△ABC 的内角A ,B ,C 所对边分别为a ,b ,c .向量()a =m ,()sin cos B A =-,n ,且⊥m n .(1)求A 的大小;(2)若=n ,求cos C 的值.ABCA 1B 1C 1M(第15题)17.(本小题满分14分)如图,在平面直角坐标系xOy 中,已知圆22:40C x y x +-=及点(1,0)A -,(1,2)B .(1)若直线l 平行于AB ,与圆C 相交于M ,N 两点,MN AB =,求直线l 的方程; (2)在圆C 上是否存在点P ,使得2212PA PB +=?若存在,求点P 的个数;若不存在,说明理由.18.(本小题满分16分) 将2张边长均为1分米的正方形纸片分别按甲、乙两种方式剪裁并废弃阴影部分.(1)在图甲的方式下,剩余部分恰能完全覆盖某圆锥的表面,求该圆锥的母线长及底面半径; (2)在图乙的方式下,剩余部分能完全覆盖一个长方体的表面,求长方体体积的最大值.(第18题)甲乙19.(本小题满分16分)对于给定的正整数k ,如果各项均为正数的数列{}na 满足:对任意正整数()n n k >,21111k n k n k n n n k n k n a a a a a a a --+-++-+⋅⋅⋅⋅⋅⋅=总成立,那么称{}n a 是“()Q k 数列”. (1)若{}n a 是各项均为正数的等比数列,判断{}n a 是否为“(2)Q 数列”,并说明理由; (2)若{}n a 既是“(2)Q 数列”,又是“(3)Q 数列”,求证:{}n a 是等比数列.20. (本小题满分16分)设命题p :对任意的)π0x ⎡∈⎢⎣,,sin tan x ax b x +≤≤恒成立,其中a b∈R,.(1)若10,,求证:命题p为真命题.a b==(2)若命题p为真命题,求a b,的所有值.。
江苏省赣榆县海头高级中学2018届高三上学期数学文基础题训练9,10 精品
高三文科基础题训练91.函数x x x f 21)3ln()(-+=的定义域是 ;2.若1{1,0,,2}3α∈-,则使函数y x α=的定义域为R ,且在(-∞,0)上单调递增 的α值为 ;3.函数xx x f ln )(=的单调减区间是 ;4.函数22,0,()1,0x x f x x x ⎧⎪=⎨-+>⎪⎩≤的值域为 ;5.在ABC ∆中,设,,a b c 分别为角,,A B C 的对边,若5a =,4A π=,3cos 5B =,则边c = ;6.已知函数)(x f 的定义在R 上的奇函数,当0>x 时,x x f --=21)(,则不等式21)(-<x f 的解集是 .7.已知1cos7α=,13cos()14αβ-=,且π2βα<<<.(Ⅰ)求tan2α的值;(Ⅱ)求β.高三文科基础题训练101.命题“x ∃∈R ,sin 1x ≤”的否定是 ;2.设等差数列{}n a 的前n 项和为n S .若公差2d =,510a =,则10S 的值是 ;3.设函数()f x 是定义在R 上的偶函数,当0x ≥时,()21xf x =+.若()3f a =,则实数a 的值为 ;4.已知向量,满足()32=-⋅,()1,1,1==,则与的夹角为 。
5.已知条件:|1|2,p x +>条件:,q x a >且p ⌝是q ⌝的充分不必要条件,则a 的取值 范是 .6.如图,在ABC ∆中, 120=∠BAC , 12==AC AB ,, D 是边BC 上一点,2=,则=⋅ ;7.已知32()f x ax bx cx d =+++为奇函数,且在点(2,(2))f 处的切线方程为9160x y --=。
(1)求()f x 的解析式;(2)若()y f x m =+的图象与x 轴仅有一个公共点,求m 的范围。
ABCD。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
江苏省海头高中2018届高三年级第一学期周考(10)
数 学 试 题(理)
一、填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答题卡相应位置上. 1.设集合{1,2,3}A =,{2,4,6}B =,则A
B =▲.
2.已知复数z 满足(1i)i z +=,其中i 为虚数单位,则复数z 的实部为▲. 3.已知幂函数2
2*()m m y x
m -=∈N 在(0,)+∞是增函数,则实数m 的值是▲.
4.已知曲线3
()ln f x ax x =+在(1,(1))f 处的切线的斜率为2,则实数a 的值是▲.
5.函数sin(2)(0)2
y x ϕϕπ
=+<<图象的一条对称轴是12x π=,则ϕ的值是▲.
6.已知1>x ,且1=-y x ,则y
x 1
+
的最小值为▲. 7.已知平面向量b a ,
21==,a 与b 的夹角为 60
,则-2的值为▲. 8.已知公差不为零的等差数列{}n a 的前n 项和为n S ,且26a =,若137,,a a a 成等比数列,
则8S 的值为▲.
9.若实数y x ,满足⎪⎩
⎪
⎨⎧≥≤--≤-+1
010
2x y x y x ,则x y x z +=的最大值为▲.
10.设)326(58cos 3sin παπαα<<=
+,则)3
22sin(πα+=▲. 11.若直线b kx y +=是函数x y ln =图象的一条切线,则b k +的最小值为▲.
12.某罐头生产厂计划制造一种圆柱形的密封铁皮罐头盒,其表面积为定值S .若罐头盒的底面半径为r ,则当=r ▲时,罐头盒的体积最大(用S 表示).
13.已知点P 是圆22:4O x y +=上的动点,点(4,0)A ,若直线1y kx =+上总存在点Q ,使点Q 恰是线段AP 的中点,则实数k 的取值范围为▲.
14.已知函数32
()2f x x x a =--,若存在(]0,x a ∈-∞,使0)(0≥x f ,则实数a 的取值范
围为▲.
二、解答题:本大题共6小题,共计90分.请在答题卡指定区域.......内作答.解答时应写出文字 说明、证明过程或演算步骤.
在ABC ∆中,设向量)sin ,sin (sin C B A m +=,)sin ,sin (sin C B A n -+=,
B A n m sin sin 3⋅=⋅.
(1)求C 的值;
(2)求B A sin sin +的取值范围.
16.(本小题满分14分)
已知数列{}n a 的前n 项和是n S ,且满足11a =,*
131()n n S S n +=+∈N .
(1)求数列{}n a 的通项公式; (2)在数列{}n b 中,13b =,*1
1()n n n n
a b b n a ++-=∈N ,令n n n b a c ⋅=,求:数列{}n c 的前n 项和.
如图,有一块半圆形空地,开发商计划建一个矩形游泳池ABCD 及其矩形附属设施EFGH ,并将剩余空地进行绿化,园林局要求绿化面积应最大化.其中半圆的圆心为O ,半径为R ,矩形的一边AB 在直径上,点C 、D 、G 、H 在圆周上,E 、F 在边CD 上,且3
B O G π
∠=,
设BOC θ∠=.
(1)记游泳池及其附属设施的占地面积为()f θ,求()f θ的表达式; (2)怎样设计才能符合园林局的要求?
18.(本小题满分16分)
在平面直角坐标系xOy 中,曲线162+-=x x y 与坐标轴的交点都在圆C 上. (1)求圆C 的方程;
(2)若过点)4,29(A 的直线l 与圆C 交于Q P ,两点,且圆弧PQ 恰为圆C 周长的
3
1
,求直线l 的方程;
(3)从圆C 外一点M 向圆C 引一条切线,切点为T ,若MO MT =,求MT 的最小值.
(第17题)
O
C
D
E
F
G
H
19.(本小题满分16分)
已知数列{}n a 的前n 项和为n S ,满足21n n S a =-,*n ∈N .数列{}n b 满足
1(1)(1)n n nb n b n n +-+=+,*n ∈N ,且11b =.
(1)求数列{}n a 和{}n b 的通项公式;
(2)若n n c a ={}n c 的前n 项和为n T ,对任意的*n ∈N ,都有n n T nS a ≤-,求实数a 的取值范围;
(3)是否存在正整数m ,n ,使1b ,m a ,n b (1n >)成等差数列,若存在,求出所有满足条件的m , n ,若不存在,请说明理由.
20. (本小题满分16分)
已知函数()(1)e x
f x ax =-(0a ≠,e 是自然对数的底数).
(1)若函数()f x 在区间[]1,2上是单调减函数,求实数a 的取值范围;
(2)求函数
()f x 的极值;
(3)设函数()f x 图象上任意一点处的切线为l ,求l 在x 轴上的截距的取值范围.。
