2019-2020年高三数学上学期解析几何14抛物线的方程及其性质(1)教学案(无答案)
高中数学抛物线的几何性质总结课件

开口方向与开口大小的关系
开口方向与开口大小的相互影响
开口方向和开口大小是相互影响的,一般来说,向上开口的抛物线开口会逐渐变小,向下开口的抛物线开口会逐 渐变大。
特殊情况下的关系
当a=0时,抛物线退化为一条直线,此时开口方向和大小无法定义。
04 抛物线的对称性
抛物线的对称轴
抛物线关于其对称轴对称,对称轴是 一条垂直于x轴的直线。
对称轴是抛物线几何性质的一个重要 特征,它决定了抛物线的形状和位置 。
对于标准形式的抛物线 y=ax^2+bx+c,其对称轴的方程是 x=-b/2a。
抛物线的对称中心
抛物线的对称中心是其顶点的位 置,顶点坐标可以通过二次函数 的顶点式y=a(x-h)^2+k得到。
抛物线上的任意一点 到焦点的距离等于该 点到准线的距离。
抛物线的标准方程
开口向右的抛物线方程为 $y^2 = 2px$,其中 $p$ 是焦 距。
开口向左的抛物线方程为 $y^2 = -2px$,其中 $p$ 是 焦距。
ቤተ መጻሕፍቲ ባይዱ
抛物线的标准方程可以根据焦 点和准线的位置进行变换。
抛物线的几何性质
01
02
03
开口方向与函数值变化趋势
开口方向与函数值随x的变化趋势一致,向上开口时函数值随x增大而增大,向 下开口时函数值随x增大而减小。
抛物线的开口大小
开口大小与二次项系数的绝对值大小
开口大小由二次项系数的绝对值|a|决定,|a|越大,抛物线开口越小;|a|越小,抛 物线开口越大。
开口大小与函数值变化幅度的关系
高二数学人选修课件抛物线的简单几何性质

02
抛物线的几何特征
抛物线的焦点和准线
抛物线的焦点: 抛物线与x轴的
交点
焦点到准线的距 离:p(抛物线
的参数)
准线:抛物线与 y轴的交点
抛物线的标准 方程:
y^2=2px (p>0)
抛物线的开口方向和大小
开口方向:抛物线开口方向由其系数a决定,a>0时开口向上,a<0时开口向下。 开口大小:抛物线开口大小由其系数b决定,b>0时开口较大,b<0时开口较小。 抛物线顶点:抛物线顶点是抛物线与x轴的交点,其横坐标为-b/2a。 抛物线对称性:抛物线关于其顶点对称,顶点将抛物线分为对称的两部分。
抛物线的顶点和离心率
顶点:抛物线的最高点或最低点,决定了抛物线的位置和形状 离心率:抛物线开口的大小,决定了抛物线的扁平程度 顶点的坐标:可以通过二次公式求解得到 离心率的计算:可以通过二次公式求解得到,也可以根据顶点和焦点的位置关系求解得到
03
抛物线与坐标轴的 交点
抛物线与x轴的交点
抛物线与x轴的交点称为x轴的交点,是抛物线与x轴的公共点。 x轴的交点决定了抛物线的开口方向和大小。 x轴的交点可以通过求解二次方程得到。 x轴的交点在图形上表现为抛物线与x轴的交点,是抛物0时, 抛物线与y轴的 交点为(0,y1)和 (0,y2),其中y1 和y2是抛物线 与y轴的交点坐 标。
0 2
抛物线与坐标轴 的交点个数:抛 物线与x轴和y轴 的交点个数等于 抛物线的解数, 即抛物线与x轴 和y轴的交点坐 标的个数。
0 3
抛物线与坐标轴 的交点性质:抛 物线与x轴和y轴 的交点坐标决定 了抛物线的开口 方向、对称轴位 置和顶点位置等 几何性质。
抛物线与直线垂直 :当直线与抛物线 相交,且交点在抛 物线上时,这两个 直线在抛物线上垂 直。
高三数学《抛物线》教案

高三数学《抛物线》教案一、教学内容本节课选自高三数学教材下册第五章《圆锥曲线与方程》中的第二节《抛物线》。
详细内容包括:1. 抛物线的定义与标准方程;2. 抛物线的简单几何性质;3. 抛物线的焦点、准线及其应用;4. 实践活动中抛物线的绘制。
二、教学目标1. 让学生掌握抛物线的定义、标准方程及简单几何性质;2. 培养学生运用抛物线的焦点、准线解决实际问题的能力;3. 激发学生学习兴趣,培养空间想象力和逻辑思维能力。
三、教学难点与重点重点:抛物线的定义、标准方程、简单几何性质及焦点、准线。
难点:抛物线焦点、准线的求解与应用。
四、教具与学具准备1. 教具:多媒体课件、黑板、粉笔;2. 学具:直尺、圆规、量角器。
五、教学过程1. 引入:通过展示生活中抛物线的实例(如抛物线运动、拱桥等),引出本节课的主题——抛物线。
2. 新课导入:讲解抛物线的定义,引导学生观察抛物线的特点,推导抛物线的标准方程。
3. 知识讲解:(1)抛物线的定义与标准方程;(2)抛物线的简单几何性质;(3)抛物线的焦点、准线及其应用。
4. 例题讲解:(1)求抛物线的标准方程;(2)求抛物线的焦点、准线;(3)抛物线在实际问题中的应用。
5. 随堂练习:针对例题进行变式训练,巩固所学知识。
6. 实践活动:分组讨论,利用学具绘制抛物线,观察抛物线的性质,加深对知识的理解。
六、板书设计1. 定义:抛物线是平面内到一个定点(焦点)距离等于到一条定直线(准线)距离的点的轨迹;2. 标准方程:y^2=2px(p>0);3. 简单几何性质:对称性、开口方向、顶点、渐近线;4. 焦点、准线:F(p,0),x=p;5. 例题与解答。
七、作业设计1. 作业题目:(1)求抛物线y^2=8x的焦点、准线;(2)求抛物线x^2=4y的顶点、对称轴;(3)抛物线y^2=4x与直线y=2x+1相交,求交点坐标。
2. 答案:(1)焦点F(2,0),准线x=2;(2)顶点(0,0),对称轴y轴;(3)交点(2,5)。
高三数学《抛物线》教案

高三数学《抛物线》教案一、教学内容本节课选自高三数学教材下册第五章《圆锥曲线与方程》中的抛物线部分。
具体内容包括:抛物线的定义、性质、标准方程及其应用。
二、教学目标1. 理解并掌握抛物线的定义、性质和标准方程。
2. 能够运用抛物线的性质解决实际问题,提高数学应用能力。
3. 培养学生的空间想象能力和逻辑思维能力。
三、教学难点与重点重点:抛物线的定义、性质和标准方程。
难点:抛物线标准方程的推导及其在实际问题中的应用。
四、教具与学具准备1. 教具:多媒体课件、黑板、粉笔。
2. 学具:直尺、圆规、量角器。
五、教学过程1. 导入:通过展示生活中的抛物线实例,如拱桥、篮球抛物线等,引导学生思考抛物线的性质和用途。
2. 基本概念:(1)抛物线的定义:介绍抛物线的起源,引导学生理解抛物线的定义。
(2)抛物线的性质:通过动画演示,让学生观察抛物线的对称性、顶点、焦点等性质。
(3)抛物线的标准方程:引导学生根据性质推导出抛物线的标准方程。
3. 例题讲解:(1)求抛物线的标准方程。
(2)已知抛物线上一点,求该点处的切线方程。
4. 随堂练习:(1)判断下列图形是否为抛物线。
(2)求下列抛物线的标准方程。
5. 应用拓展:(1)抛物线在实际问题中的应用。
(2)抛物线与圆、直线等图形的位置关系。
六、板书设计1. 定义、性质、标准方程。
2. 例题解答步骤。
3. 课后作业及答案。
七、作业设计1. 作业题目:(1)求下列抛物线的标准方程:① y²=4x;② x²=4y;③ y²=8x;④ x²=8y。
(2)已知抛物线y²=4x上一点(1,2),求该点处的切线方程。
2. 答案:(1)① y²=4x,焦点(1,0),顶点(0,0);② x²=4y,焦点(0,1),顶点(0,0);③ y²=8x,焦点(2,0),顶点(0,0);④ x²=8y,焦点(0,2),顶点(0,0)。
2019-2020年高三数学 抛物线的几何性质教案 新人教A版

2019-2020年高三数学抛物线的几何性质教案新人教A版(1)抛物线的几何性质下面我们类比椭圆、双曲线的几何性质,从抛物线的标准方程y2=2px(p>0)出发来研究它的几何性质.(二)几何性质怎样由抛物线的标准方程确定它的几何性质?以y2=2px(p>0)为例,用小黑板给出下表,请学生对比、研究和填写.(2)例题的讲解与引申例3有2种解法;解法一运用了抛物线的重要性质:抛物线上任一点到焦点的距离(即此点的焦半径)等于此点到准线的距离.可得焦半径公式设P(x0,这个性质在解决许多有关焦点的弦的问题中经常用到,因此必须熟练掌握.(2)由焦半径不难得出焦点弦长公式:设AB是过抛物线焦点的一条弦(焦点弦),若A(x1,y1)、B(x2,y2)则有|AB|=x1+x2+p.特别地:当AB⊥x轴,抛物线的通径|AB|=2p例4涉及直线与圆锥曲线相交时,常把直线与圆锥曲线方程联立,消去一个变量,得到关于另一变量的一元二次方程,然后用韦达定理求解,这是解决这类问题的一种常用方法.附教学教案2019-2020年高三数学抽样方法教案同步教案新人教A版一、本讲进度1.1抽样方法1.2总体分布的估计课本第4页至第14页二、本讲主要内容1.三种抽样方法的概念及比较2.总体分布的估计——总体密度曲线三、学习指导1.随着当今社会信息化程度的日益提高,为了及时获取信息,我们往往不是对所研究的对象进行全面调查,而是采取抽样调查的方法,通过样本推测全体对象的情况,“抽样调查”一词已成为常用词汇。
那么,怎样根据问题的需要和对象的特征,合理地抽取样本呢?一般有常用的三种抽样方法:(Ⅰ)简单随机抽样:定义见课本P.4(1)特点:被抽取样本的总体的个体数有限,从总体中逐个地进行抽取且不放回抽样。
它是一种等概率抽样,不仅每次从总体中抽取一个个体时,各个个体被抽取的概率相等,而且在整个抽样过程中,各个个体被抽取的概率也相等,这样就保证了这种抽样方法的公平性。
2019-2020学年高二数学上学期《抛物线的几何性质》学案
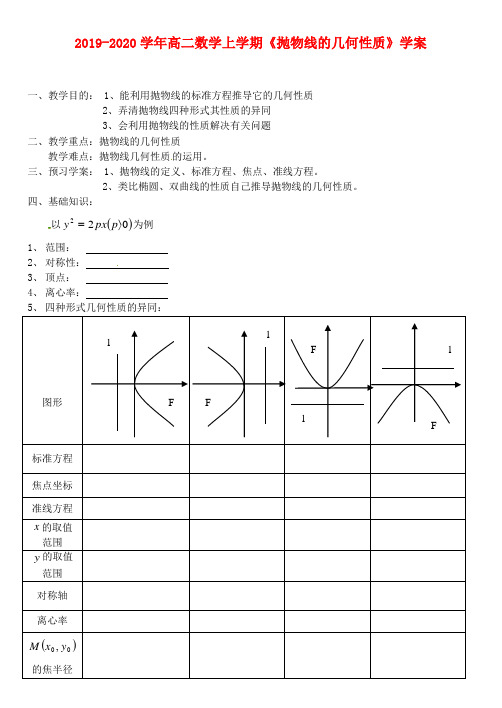
2019-2020学年高二数学上学期《抛物线的几何性质》学案一、教学目的: 1、能利用抛物线的标准方程推导它的几何性质2、弄清抛物线四种形式其性质的异同3、会利用抛物线的性质解决有关问题二、教学重点:抛物线的几何性质教学难点:抛物线几何性质的运用。
三、预习学案: 1、抛物线的定义、标准方程、焦点、准线方程。
2、类比椭圆、双曲线的性质自己推导抛物线的几何性质。
四、基础知识:以()022〉=p px y 为例1、 范围:2、 对称性:3、 顶点:4、 离心率: 图形标准方程焦点坐标 准线方程x 的取值范围 y 的取值范围 对称轴 离心率()00,y x M 的焦半径F lFlFFll6、 焦半径:抛物线上一点M 与焦点F 连线的线段MF 叫做焦半径。
设抛物线()022〉=p px y 上一点M(x,y)由抛物线的定义,易知20p x MF += 7、 焦点弦:过焦点的弦设AB 是过抛物线()022〉=p px y 焦点F 的一条弦,()()2211,,,y x B y x A 则有:①p x x AB ++=21 ②221221,4p y y p x x -=⋅=⋅ 特别地,当焦点弦垂直于对称轴时,又称作正焦弦(“通径”)此时p AB 2=,从而p 刻画了抛物线开口大小,p 越大,开口越宽.p 越小,开口越窄. 五、典型例题(一)利用性质求抛物线标准方程例1、抛物线以x 轴为轴,顶点在坐标原点,开口向右,且过()32,4M ,求抛物线的标准方程.若抛物线顶点在坐标原点,过()32,4M ,该抛物线标准方程为练习:抛物线以x 轴为轴,顶点在坐标原点,且顶点与焦点的距离等于3,则抛物线标准方程为(二)焦点弦问题例2、已知抛物线x y 42=过焦点F 的弦为AB ,且8=AB ,求AB 中点的横坐标.练习:已知()()()332211,,,,,y x C y x B y x A 是抛物线()022〉=p px y 上三点,F 为焦点,若CF BF AF ,,成等差数列。
高中数学抛物线的几何性质总结课件

准线上的点到抛物线焦点的距离相等 。
抛物线的离心率与焦距的关系
01
02
03
04
离心率
抛物线的离心率等于1。
焦距
抛物线的焦距等于2p,其中p 是抛物线的准线到焦点的距离
。
关系
离心率与焦距之间存在直接关 系,离心率越大,焦距越小;
离心率越小,焦距越大。
应用
了解离心率与焦距的关系有助 于解决一些与抛物线相关的几
将直线方程代入抛物线方 程,得到一元二次方程, 利用判别式非负求出交点 。
参数方程法
设定参数表示交点的坐标 ,代入抛物线方程和直线 方程,解出参数。
交点的性质
对称性
抛物线与直线交点的对称 性取决于抛物线的对称性 和直线的斜率。
唯一性
当直线与抛物线相切时, 交点唯一;当直线与抛物 线相交时,交点可能有两 个。
02
抛物线的几何性质
抛物线的对称性
总结词
抛物线具有对称性,其对称轴是 抛物线的准线。
详细描述
抛物线关于其准线对称,这意味着 对于抛物线上的任意一点P,其关 于准线的对称点也在抛物线上。
数学表达
如果点P(x,y)在抛物线上,那么点 P'(-x,-y)也在抛物线上。
抛物线的范围
01
总结词
抛物线在x轴上方的部分是连续且封闭的。
何问题。
THANK YOU
感谢各位观看
02 03
详细描述
对于开口向上的抛物线,其顶点是最低点,对于开口向下的抛物线,其 顶点是最高点。抛物线在x轴上方的部分是连续且封闭的,形成一个完 整的图形。
数学表达
对于标准形式的抛物线y=ax^2+bx+c,当a>0时,顶点为最低点;当 a<0时,顶点为最高点。
2021-2022年高三数学上学期解析几何14抛物线的方程及其性质(1)教学案(无答案)

2021年高三数学上学期解析几何14抛物线的方程及其性质(1)教学案(无答案)【教学目标】掌握抛物线的定义、标准方程、几何图形,以及它的简单几何性质.【教学重点】能利用抛物线的定义、几何性质解决一些简单的数学问题.【教学难点】抛物线标准方程的四种不同形式.【教学过程】一、知识梳理:1.抛物线定义:平面内到一个定点F和一条定直线l(Fl)的距离的点的轨迹叫做抛物线;点F叫做抛物线的,直线l叫做抛物线的.2.标准方程、焦点、准线、图形(其中,表示焦点F到准线的距离)标准方程抛物线的图形焦点坐标准线方程开口方向焦半径3(1)范围:.(2)对称性:.(3)顶点:.(4)开口方向:.二、基础自测:1.抛物线2x2+y=0的焦点坐标是.2.抛物线y=4x2的准线方程为.3.已知抛物线y2=2px(p>0)的准线与圆(x-3)2+y2=16相切,则p的值为________.4.已知抛物线的顶点在原点,焦点在y 轴上,抛物线上的点P (m ,-2)到焦点的距离为4, 则m 的值为________.三、典型例题: 反思: 例1.根据下列条件求抛物线的标准方程.(1)抛物线的焦点是双曲线16x 2-9y 2=144的左顶点;(2)过点P (2,-4);(3)抛物线的焦点在x 轴上,直线y =-3与抛物线交于点A ,AF =5.【变式拓展】如图,过抛物线y 2=2px (p >0)的焦点F 的直线l 交抛物线于A ,B 两点,交其准线于点C .若BC =2BF ,且AF =3,则此抛物线的方程为__________________.例2.已知曲线上的每一点到点A (0,2)的距离减去它到x 轴的距离的差都是2,求曲线的方程.【变式拓展】已知动圆P 过点F (0,14)且与直线y =-14相切,动圆的圆心为P . (1)求点P 的轨迹C 的方程;(2)过点F 作一条直线交轨迹C 于A ,B 两点,轨迹C 在A ,B 两点处的切线相交于点N ,M 为线段AB 的中点,求证:MN ⊥x 轴.例3.已知抛物线y 2=2x 焦点是F ,点P 是抛物线上的动点,又有点A (3,2),求PA +PF 的最小值,并求出取最小值时P 点的坐标.【变式拓展】(xx 年南京模拟)已知点A (-2,1),y 2=-4x 的焦点是F ,P 是y 2=-4x 上的点,为使PA +PF 取得最小值,求P 点的坐标.四、课堂反馈:1.若抛物线y 2=2px (p >0)的焦点也是双曲线x 2-y 2=8的一个焦点,则p = .2.若抛物线x 2=ay 过点A ⎝ ⎛⎭⎪⎫1,14,则点A 到此抛物线的焦点的距离为 . 3.若抛物线y 2=2px (p >0)上的点A (2,m )到焦点的距离为6,则p = .4.若点P 到直线y =-1的距离比它到点(0,3)的距离小2,则点P 的轨迹方程是 .五、课后作业: 学生姓名:___________1.抛物线y =-12x 2的焦点坐标是 . 2.抛物线y 2=8x 的焦点到准线的距离是 .3.点M (5,3)到抛物线y =ax 2的准线的距离为6,那么抛物线的方程是 . 4.若双曲线x 23-16y 2p 2=1的左焦点在抛物线y 2=2px 的准线上,则p 的值为________. 5.已知双曲线x 24-y 212=1的离心率为e ,抛物线x =2py 2的焦点为(e,0),则p 的值为 . 6.若抛物线y 2=2px 的焦点与椭圆x 26+y 22=1的右焦点重合,则p 的值为 . 7.过抛物线y 2=4x 的焦点作直线交抛物线于A (x 1,y 1),B (x 2,y 2)两点,若x 1+x 2=6, 那么AB 等于 .8.直线l 过抛物线y 2=ax 焦点,并且垂直于x 轴,若直线l 被抛物线截得线段长为4,则a = .9.若动圆与圆(x -2)2+y 2=1外切,又与直线x +1=0相切,求动圆圆心的轨迹方程.10.在路边安装路灯,灯柱与地面垂直,灯杆与灯柱所在平面与道路垂直,且,路灯采用锥形灯罩,射出的光线如图中阴影部分所示,已知,路宽米,设灯柱高(米),(1)求灯柱的高(用表示);(2)若灯杆与灯柱所用材料相同,记此用料长度和为,求关于的函数表达式,并求出的最小值. CB A D。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2019-2020年高三数学上学期解析几何14抛物线的方程及其性质(1)教学案
(无答案)
【教学目标】掌握抛物线的定义、标准方程、几何图形,以及它的简单几何性质. 【教学重点】能利用抛物线的定义、几何性质解决一些简单的数学问题.
【教学难点】抛物线标准方程的四种不同形式.
【教学过程】
一、知识梳理:
1.抛物线定义:平面内到一个定点F 和一条定直线l (F ∉l )的距离 的点的轨迹叫做抛物线;点F 叫做抛物线的 ,直线l 叫做抛物线的 .
2.标准方程、焦点、准线、图形(其中0>p ,表示焦点F 到准线l 的距离)
3.抛物线的几何性质:以)0(2>=p px y 为例: (1)范围: . (2)对称性: .
(3)顶点: . (4)开口方向: .
二、基础自测:
1.抛物线2x 2+y =0的焦点坐标是 .
2.抛物线y =4x 2
的准线方程为 .
3.已知抛物线y 2=2px (p >0)的准线与圆(x -3)2+y 2=16相切,则p 的值为________.
4.已知抛物线的顶点在原点,焦点在y 轴上,抛物线上的点P (m ,-2)到焦点的距离为4,
则m 的值为________.
三、典型例题: 反思: 例1.根据下列条件求抛物线的标准方程.
(1)抛物线的焦点是双曲线16x 2-9y 2
=144的左顶点;
(2)过点P (2,-4);
(3)抛物线的焦点在x 轴上,直线y =-3与抛物线交于点A ,AF =5.
【变式拓展】如图,过抛物线y 2=2px (p >0)的焦点F 的直线l 交抛物线于A ,B 两点,交其
准线于点C .若BC =2BF ,且AF =3,则此抛物线的方程为__________________.
例2.已知曲线上的每一点到点A (0,2)的距离减去它到x 轴的距离的差都是2,求曲线的方程.
【变式拓展】已知动圆P 过点F (0,14)且与直线y =-14
相切,动圆的圆心为P . (1)求点P 的轨迹C 的方程;
(2)过点F 作一条直线交轨迹C 于A ,B 两点,轨迹C 在A ,B 两点处的切线相交于点N ,
M 为线段AB 的中点,求证:MN ⊥x 轴.
例3.已知抛物线y 2=2x 焦点是F ,点P 是抛物线上的动点,又有点A (3,2),求PA +PF 的最小值,并
求出取最小值时P 点的坐标.
【变式拓展】(2011年南京模拟)已知点A (-2,1),y 2=-4x 的焦点是F ,P 是y 2=-4x 上的点,
为使PA +PF 取得最小值,求P 点的坐标.
四、课堂反馈:
1.若抛物线y 2=2px (p >0)的焦点也是双曲线x 2-y 2=8的一个焦点,则p = .
2.若抛物线x 2=ay 过点A ⎝ ⎛⎭
⎪⎫1,14,则点A 到此抛物线的焦点的距离为 . 3.若抛物线y 2
=2px (p >0)上的点A (2,m )到焦点的距离为6,则p = .
4.若点P 到直线y =-1的距离比它到点(0,3)的距离小2,则点P 的轨迹方程是 .
五、课后作业: 学生姓名:___________
1.抛物线y =-12
x 2的焦点坐标是 . 2.抛物线y 2=8x 的焦点到准线的距离是 .
3.点M (5,3)到抛物线y =ax 2
的准线的距离为6,那么抛物线的方程是 . 4.若双曲线x 23-16y 2
p 2=1的左焦点在抛物线y 2=2px 的准线上,则p 的值为________. 5.已知双曲线x 24-y 212
=1的离心率为e ,抛物线x =2py 2的焦点为(e,0),则p 的值为 . 6.若抛物线y 2=2px 的焦点与椭圆x 26+y 22
=1的右焦点重合,则p 的值为 . 7.过抛物线y 2=4x 的焦点作直线交抛物线于A (x 1,y 1),B (x 2,y 2)两点,若x 1+x 2=6, 那么AB 等于 .
8.直线l 过抛物线y 2=ax 焦点,并且垂直于x 轴,若直线l 被抛物线截得线段长为4,则a = .
9.若动圆与圆(x -2)2+y 2=1外切,又与直线x +1=0相切,求动圆圆心的轨迹方程.
10.在路边安装路灯,灯柱AB 与地面垂直,灯杆BC 与灯柱AB 所在平面与道路垂直,且 120=∠ABC ,路灯C 采用锥形灯罩,射出的光线如图中阴影部分所示,已知 60=∠ACD ,路宽24=AD 米,设灯柱高h AB =(米),θACB =∠()
4530≤≤θ
(1)求灯柱的高h (用θ表示);
(2)若灯杆BC 与灯柱AB 所用材料相同,记此用料长度和为S ,求S 关于θ的函数表达式,并求
出S 的最小值. C
B A D。
