柯布-道格拉斯(Cobb-Douglas)生产函数模型
柯布道格拉斯生产函数

柯布道格拉斯生产函数柯布道格拉斯生产函数是经济学家柯布道格拉斯提出的一种描述生产关系的数学模型。
它是一种生产函数,描述了生产过程中输入要素和产出之间的关系。
柯布道格拉斯生产函数被广泛应用于经济学研究中,可以帮助我们理解和分析不同要素对产出的影响。
柯布道格拉斯生产函数的基本形式为:Y = A * (K^α) * (L^β) * (M^γ)其中,Y表示产出,K表示资本输入,L表示劳动输入,M表示其他要素输入,A表示全要素生产率,α、β、γ表示要素的弹性系数。
柯布道格拉斯生产函数的核心思想是,通过将输入要素(如资本和劳动)与全要素生产率相结合,可以预测产出的变化。
这个模型假设生产过程中的技术水平是固定的,并且每个要素对产出的贡献程度是固定的。
柯布道格拉斯生产函数的形式化表述可能有些晦涩难懂,但是我们可以通过一个简单的例子来理解它的应用。
假设一个农场使用了一定数量的土地和劳动力来种植农作物。
我们可以将土地和劳动力作为输入要素,农作物的产量作为输出。
通过柯布道格拉斯生产函数,我们可以分析不同的土地和劳动力对农作物产量的影响,并找出最佳的要素组合方式。
在柯布道格拉斯生产函数中,弹性系数α、β和γ表示了不同要素对产出的敏感性。
当α大于1时,资本输入对产出的增长影响更大;当α小于1时,劳动输入对产出的增长影响更大;当α等于1时,资本和劳动的影响是等价的。
柯布道格拉斯生产函数还可以用来分析全要素生产率的增长。
通过对全要素生产率的改进,可以提高产出水平而不需要增加输入要素。
这对于发展中国家和企业来说具有重要意义,因为他们可以通过提高技术水平来实现经济增长,而不仅仅依靠增加资本和劳动力的投入。
然而,柯布道格拉斯生产函数也存在一些限制。
它假设了技术水平是固定的,这在现实生产过程中并不成立。
现代经济往往面临着科技进步和创新的快速变化,传统的柯布道格拉斯生产函数无法很好地解释这种变化。
此外,柯布道格拉斯生产函数忽略了其他可能影响产出的因素,如市场需求、政府政策等。
数据建立柯布道格拉斯生产函数分析美国某行业的投入产出情况
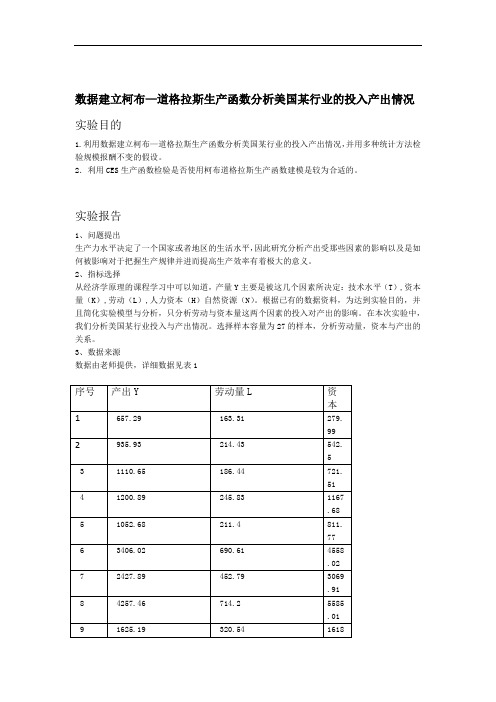
数据建立柯布—道格拉斯生产函数分析美国某行业的投入产出情况实验目的1.利用数据建立柯布—道格拉斯生产函数分析美国某行业的投入产出情况,并用多种统计方法检验规模报酬不变的假设。
2.利用CES生产函数检验是否使用柯布道格拉斯生产函数建模是较为合适的。
实验报告1、问题提出生产力水平决定了一个国家或者地区的生活水平,因此研究分析产出受那些因素的影响以及是如何被影响对于把握生产规律并进而提高生产效率有着极大的意义。
2、指标选择从经济学原理的课程学习中可以知道,产量Y主要是被这几个因素所决定:技术水平(T),资本量(K),劳动(L),人力资本(H)自然资源(N)。
根据已有的数据资料,为达到实验目的,并且简化实验模型与分析,只分析劳动与资本量这两个因素的投入对产出的影响。
在本次实验中,我们分析美国某行业投入与产出情况。
选择样本容量为27的样本,分析劳动量,资本与产出的关系。
3、数据来源数据由老师提供,详细数据见表14.数据处理将表1中的实验数据化为其对数,方便建模时分析,如表2所示5.09565.367985.228105.50465.353756.537576.115426.571165.770005.534065.465694.946845.0372 15.481766.285497.355535.368866.987586.25715.71986.728255.648975.015755.560336.209795.6174 94.8978表25.数据分析而且没有发现明显产出越多。
投入越多,K与资本L可以明显的发现劳动量数据,1观察表.不符合实际的数据。
但是其中的幂函数关系需要通过进一步的分析发现。
6.建立模型通过数理经济学的学习我们还了解到,生产函数常以柯布-道格拉斯(Cobb-Douglas)幂函数的形式出现。
柯布-道格拉斯生产函数最初是美国数学家柯布(Cobb)和经济学家道格拉斯(Douglas)共同探讨投入生产关系时创立的生产函数,他们根据历史资料,研究了1899-1922年美国资本和劳动对生产的影响,认为在技术不变的情况下产出与投入的劳动力??LAKY?及资本的关系可以表示为:,其中Y表示产量,A表示技术水平,K表示投入的资本量,L表示投入的劳动量,α、β分别表示K和L的产出弹性。
道格拉斯函数

固定投入比例生产函数:
柯布-道格拉斯生产函数 - 应用
柯布—道格拉斯生产函数模型是广泛应用的一种 生产函数。美国科学家道格拉斯和数学家柯布合作, 研究了劳动投入与资本投入和产出之间的关系,得 出如下柯布—道格拉斯生产函数模型: Y=ax1b1x2b2 柯布—道格拉斯生产函数模型广泛应用于经济数量 分析,对于农业技术经济数量分析具有特殊意义。 柯布—道格拉斯生产函数模型具有以下的特点: 1、柯布—道格拉斯生产函数模型中,a,b1,b2是 固定参数。 2、可线性化。
பைடு நூலகம் 应用
3、参数估计和其它代数方程相比,计算比较
方便。 4、运用柯布—道格拉斯生产函数模型进行技 术经济分析,由于数据特性,计算分析结论 更准确。 正是由于这些特点,该模型在农业生产的技 术经济分析中得到了广泛的应用。
谢谢!
根据柯布-道格拉斯生产函数可以得到下列经济参 数(设μ=1): ①劳动力边际生产力 表示在资产不变时 增加单位劳动力所增加的产值。 ②资产边际生产力 表示在劳动力不变时 增加单位资产所增加的产值。 ③劳力对资产的边际代换率 表示 产值不变时增加单位劳动力所能减少的资产值。 ④劳动力产出弹性系数 ,表示劳动力投入的 变化引起产值的变化的速率。 ⑤资产产出弹性系数 ,表示资产投入的变化 引起产值变化的速率。 国际上一般取α=0.2~0.4,β=0.8~0.6。中国根据 国家计委测算一般可取α=0.2~0.3,β=0.8~0.7。 "
三种类型
从这个模型看出,决定工业系统发展水平的主 要因素是投入的劳动力数、固定资产和综合技术水 平(包括经营管理水平、劳动力素质、引进先进技 术等),根据α 和β的组合情况,它有三种类型: ①α+β>1, 称为递增报酬型,表明按现有技术用扩 大生产规模来增加产出是有利的。 ②α+β<1, 称为递减报酬型,表明按现有技术用扩大 生产规模来增加产出是得不偿失的。 ③α+β=1, 称为不变报酬型,表明生产效率并不会 随着生产规模的扩大而提高,只有提高技术水平, 才会提高经济效益。
柯布-道格拉斯生产函数

柯布-道格拉斯生产函数柯布—道格拉斯生产函数最初是美国数学家柯布(C.W.Cobb)和经济学家保罗·道格拉斯(PaulH.Douglas)共同探讨投入和产出的关系时创造的生产函数,是以美国数学家C.W.柯布和经济学家保罗.H.道格拉斯的名字命名的,是在生产函数的一般形式上作出的改进,引入了技术资源这一因素。
用来预测国家和地区的工业系统或大企业的生产和分析发展生产的途径的一种经济数学模型,简称生产函数。
是经济学中使用最广泛的一种生产函数形式,它在数理经济学与经济计量学的研究与应用中都具有重要的地位。
柯布-道格拉斯生产函数-简介保罗·道格拉斯柯布和道格拉斯研究的是1899年至1922年美国制造业的生产函数。
他们指出,制造业的投资分为,以机器和建筑物为主要形式的固定资本投资和以原料、半成品和仓库里的成品为主要形式的流动资本投资,同时还包括对土地的投资。
在他们看来,在商品生产中起作用的资本,是不包括流动资本的。
这是因为,他们认为,流动资本属于制造过程的结果,而非原因。
同时,他们还排除了对土地的投资。
这是因为,他们认为,这部分投资受土地价值的异常增值的影响较大。
因此,在他们的生产函数中,资本这一要素只包括对机器、工具、设备和工厂建筑的投资。
而对劳动这一要素的度量,他们选用的是制造业的雇佣工人数。
但是,不幸地是,由于当时对这些生产要素的统计工作既不是每年连续的,也不是恰好按他们的分析需要来分类统计的。
因而,他们不得不尽可能地利用有的一些其它数据,来估计出他们打算使用的数据的数值。
比如,用生铁、钢、钢材、木材、焦炭、水泥、砖和铜等用于生产机器和建筑物的原料的数量变化来估计机器和建筑物的数量的变化;用美国一两个州的雇佣工人数的变化来代表整个美国的雇佣工人数的变化等等。
经过一番处理,他们得到关于1899年至1922年间,产出量P、资本C和劳动L的相对变化的数据(以1899年为基准)。
令人佩服的是,在没有计算机的年代里,他们从这些数据中,得到了如下的生产函数公式:P=1.01L3/4C1/4柯布(C.W.Cobb)这一结果虽然与现代计算机统计软件的计算结果不同,但两者无本质上的差别。
cobb-douglas生产函数

cobb-douglas生产函数
,
近年来,经济学家们成功地将Cobb-Douglas生产函数应用于互联网行业,用以阐明它们在生产中优势的特点及影响因素,相比之下,标准生产函数受到许多限制,无法实现经济效率的极高的效用。
Cobb-Douglas生产函数即Cobb-Douglas产函数,是由Cobb和Douglas于1928年提出的,是经济学中乘积型生产函数中的一种。
它假设商品的生产、消耗及交换活动的参与者都是理性的,个体的行为是完全由其自身的利益考虑呈现的。
这个函数基于参与者的理性行为对产出的预测模型,因此它能够有效衡量出个体理性考虑决定生产者在受到资源限制和相同科技水平下的最优产出结果。
应用于互联网行业的Cobb-Douglas生产函数,能够通过识别人的需求和技术环境的变化,充分结合市场和技术条件,优化商品生产分配。
其对产品电商领域的客户行为分析也是极为重要的,例如客户总体满意度以及服务价格比例等,所有这些都可以通过Cobb-Douglas生产函数深入地分析出来,用以为公司更加精准地制定出更具有商业价值的策略。
Cobb-Douglas生产函数在互联网行业的应用举足轻重,有效地提高了互联网行业对生产资源的利用效率,提高了产品的技术水平,并且有利于企业优化市场分配与营销策略,让企业可以有效挖掘出更多的商业价值。
米道格拉斯生产函数

米道格拉斯生产函数(一)米道格拉斯生产函数产生的背景米道格拉斯生产函数最初由美国数学家柯布(C.W.Cobb)和经济学家保罗·道格拉斯(Paul H. Douglas)于20世纪30年代共同创建。
他们在探讨投入与产出的关系时,基于劳动投入、资本投入与产出之间的联系,建立了这一被命名为柯布-道格拉斯生产函数的理论模型。
此生产函数一经提出便得到了广泛的应用,原因就在于它具有明确的经济意义,并能够解释要素的边际产量、边际替代率、产出弹性、替代弹性以及技术进步等诸多方面。
(二)米道格拉斯生产函数的概念米道格拉斯生产函数是由美国科学家道格拉斯和数学家柯布基于劳动投入、资本米道格拉斯生产函数是由美国科学家道格拉斯和数学家柯布基于劳动投入、资本投入与产出之间的关系进行研究而建立的,被广泛应用在经济学领域。
它的基本形式为:Y = A(t)LαKβμ,其中Y代表工业总产值,At表示综合技术水平,L是投入的劳动力数,K代表投入的资本(一般指固定资产净值),α和β分别是劳动力产出与资本产出的弹性系数,而μ则表示随机干扰的影响。
从这个模型中我们可以明显看到,影响工业系统发展的主要因素包括投入的劳动力数、固定资产以及综合技术水平等。
此外,根据α和β的组合情况,这个生产函数可以被划分为三种类型:①α+β>1, 这种情况被称为递增报酬型,表明按现有技术通过扩大规模来增加产出将是有利的;②α+β=1, 这是规模报酬不变的类型;③α+β<1, 这被称作递减报酬型,意味着如果增加生产要素的投入,其产量的增加幅度会逐渐减小。
(三)米道格拉斯生产函数的应用米道格拉斯生产函数是一种广泛应用的经济数学模型,主要用于预测国家和地区的工业系统或大企业的生产和分析发展生产的途径。
具体来说,它可以分析要素投入对产出的贡献率、规模收益等一系列问题,从而了解各种生产要素(例如劳动力和资本)的分配和使用效率,进而优化生产资源配置。
数据建立柯布—道格拉斯生产函数分析美国某行业的投入产出情况
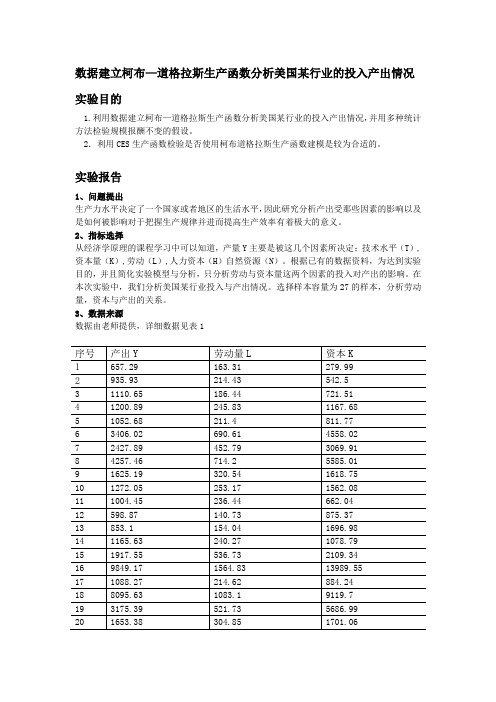
数据建立柯布—道格拉斯生产函数分析美国某行业的投入产出情况实验目的1.利用数据建立柯布—道格拉斯生产函数分析美国某行业的投入产出情况,并用多种统计方法检验规模报酬不变的假设。
2.利用CES生产函数检验是否使用柯布道格拉斯生产函数建模是较为合适的。
实验报告1、问题提出生产力水平决定了一个国家或者地区的生活水平,因此研究分析产出受那些因素的影响以及是如何被影响对于把握生产规律并进而提高生产效率有着极大的意义。
2、指标选择从经济学原理的课程学习中可以知道,产量Y主要是被这几个因素所决定:技术水平(T),资本量(K),劳动(L),人力资本(H)自然资源(N)。
根据已有的数据资料,为达到实验目的,并且简化实验模型与分析,只分析劳动与资本量这两个因素的投入对产出的影响。
在本次实验中,我们分析美国某行业投入与产出情况。
选择样本容量为27的样本,分析劳动量,资本与产出的关系。
3、数据来源数据由老师提供,详细数据见表14.数据处理将表1中的实验数据化为其对数,方便建模时分析,如表2所示表25.数据分析观察表1数据,可以明显的发现劳动量L与资本K投入越多,产出越多。
而且没有发现明显不符合实际的数据。
但是其中的幂函数关系需要通过进一步的分析发现。
6.建立模型通过数理经济学的学习我们还了解到,生产函数常以柯布-道格拉斯(Cobb-Douglas )幂函数的形式出现。
柯布-道格拉斯生产函数最初是美国数学家柯布(Cobb )和经济学家道格拉斯(Douglas )共同探讨投入生产关系时创立的生产函数,他们根据历史资料,研究了1899-1922年美国资本和劳动对生产的影响,认为在技术不变的情况下产出与投入的劳动力及资本的关系可以表示为:Y AK L βα=,其中Y 表示产量,A 表示技术水平,K 表示投入的资本量,L 表示投入的劳动量,α、β分别表示K 和L 的产出弹性。
由于柯布-道格拉斯(Cobb-Douglas )生产函数是一个非线性模型,对生产函数取对数,可得:ln ln lnL Y A K αβ=++建立线性模型:11220X +X i i Y βββμ=++ 利用样本数据用Eviews 做lnY 对lnK 和lnL 的回归Dependent Variable: LNY Method: Least Squares Date: 10/27/16 Time: 12:46 Sample: 1 27Included observations: 27Variable Coefficient Std. Error t-Statistic Prob. LNK 0.373400 0.087246 4.279838 0.0003 LNL 0.606563 0.129114 4.697887 0.0001 C1.1663130.330983 3.5237830.0017R-squared 0.942420 Mean dependent var 7.443631 Adjusted R-squared 0.937622 S.D. dependent var 0.761153 S.E. of regression 0.190103 Akaike info criterion -0.378063 Sum squared resid 0.867339 Schwarz criterion -0.234081 Log likelihood 8.103847 Hannan-Quinn criter. -0.335249 F-statistic 196.4056 Durbin-Watson stat 1.854054Prob(F-statistic)0.000000得出回归方程:Y=0.373400lnK+0.606563lnL+1.166313 7.模型检验Y 对lnK 与lnL 的回归模型的检验经济检验:α为0.373400,说明产出与资本投入成正相关,且在其他条件保持不变的情况下,资本投入增加1%,产出增加约0.37%β为0.606563,说明产出与劳动量成正相关,且在其他条件保持不变的情况下,资本投入增加1%,产出增加约0.61%,对α与β的估计符合经济理论,故通过经济检验。
柯布-道格拉斯生产函数的

柯布-道格拉斯生产函数的
答:柯布-道格拉斯生产函数的基本形式为:
Y=A(t)LαKβμ
式中Y是工业总产值,At是综合技术水平,L是投入的劳动力数(单位是万人或人),K是投入的资本,一般指固定资产净值(单位是亿元或万元,但必须与劳动力数的单位相对应,如劳动力用万人作单位,固定资产净值就用亿元作单位),α是劳动力产出的弹性系数,β是资本产出的弹性系数,μ表示随机干扰的影响,
μ≤1。
从这个模型看出,决定工业系统发展水平的主要因素是投入的劳动力数、固定资产和综合技术水平(包括经营管理水平、劳动力素质、引进先进技术等)。
根据α和β的组合情况,它有三种类型:
1、α+β>1,称为递增报酬型,表明按现有技术用扩大生产规模来增加产出是有利的。
2、α+β<1,称为递减报酬型,表明按现有技术用扩大生产规模来增加产出是得不偿失的。
3、α+β=1,称为不变报酬型,表明生产效率并不会随着生产规模的扩大而提高,只有提高技术水平,才会提高经济效益。
