数据建立柯布道格拉斯生产函数分析美国某行业的投入产出情况
柯布-道格拉斯生产函数例题

柯布-道格拉斯生产函数例题Y=A·K^α·L^β其中,Y代表产出,A代表全要素生产率,K代表资本投入,L代表劳动力投入,α和β是生产函数的弹性系数。
下面我们通过一个例题来具体说明柯布-道格拉斯生产函数的具体应用。
假设一个工厂使用柯布-道格拉斯生产函数来描述其生产过程。
在其中一时期,该工厂的全要素生产率A为1,资本投入K为100,劳动力投入L为50。
利用柯布-道格拉斯生产函数求出该工厂的产出。
根据柯布-道格拉斯生产函数,将给定的参数代入公式,可以得到:Y=1·100^α·50^β对于具体的弹性系数α和β,我们可以根据实际情况来确定。
假设α为0.5,β为0.5,则可以计算出产出为:Y=1·100^0.5·50^0.5=1·10·7.071=70.71因此,该工厂在给定的资本投入和劳动力投入下,可以获得70.71的产出。
接下来,我们来分析一下这个例题的结果。
首先,从数值上可以看出,产出随着资本和劳动力的增加而增加,但增加的速度逐渐减缓。
也就是说,在资本投入和劳动力投入增加时,每增加一个单位的投入,产出的增加逐渐变小。
这是柯布-道格拉斯生产函数的典型特征。
其次,我们可以通过调整参数来观察产出的变化。
比如,如果我们将资本投入K增加到200,劳动力投入L保持不变,则可以计算出产出为:Y=1·200^0.5·50^0.5=1·14.142=14.142可以看到,当资本投入翻倍时,产出并没有翻倍,而是略微增加了。
这说明随着资本投入的增加,产出的增长速度逐渐减缓,即边际产出递减。
最后,我们还可以通过改变全要素生产率A来观察产出的变化。
比如,如果我们将全要素生产率A增加到2,而资本投入和劳动力投入保持不变,则可以计算出产出为:Y=2·100^0.5·50^0.5=2·10·7.071=141.42可以看到,当全要素生产率增加一倍时,产出也相应增加一倍。
【原创】用excel来构建柯布-道格拉斯Cobb-Douglas生产函数的可视化数据分析报告论文(代码+数据)

咨询QQ:3025393450有问题百度搜索“”就可以了欢迎登陆官网:/datablog用excel来构建柯布-道格拉斯Cobb-Douglas生产函数的可视化数据分析报告来源:大数据部落| 有问题百度一下“”就可以了原文:/?p=3430我使用excel来构建Cobb-Douglas生产函数的可视化。
生产函数将任何给定公司的输出表示为两个输入(人工和资本)和参数(α和β)的函数。
当α和β之和等于1时,可以证明它们分别代表劳动力和资本的产出份额。
这种情况也意味着公司的经营规模不断回报。
当公司将其投入扩大一定百分比时,产出增加相同的数量。
如果我们指定alpha和beta,我们可以在xyz空间中绘制每个劳动力,资本和产出量。
我们这样做是为了劳动力和资本,范围从1到100,alpha = beta = .5。
结果是Cobb-Douglas生产表面,资本和劳动力各占50%的投入。
咨询QQ:3025393450有问题百度搜索“”就可以了欢迎登陆官网:/datablog请注意,分隔不同颜色区域的线条间隔相等。
这是规模收益递增的特性。
当劳动力和资本扩张时,效用水平按比例稳定增长。
从上方观察表面也很有用。
咨询QQ:3025393450有问题百度搜索“”就可以了欢迎登陆官网:/datablog那些L形曲线被称为等长或矩形双曲线。
它们代表产生相同(“iso”)输出量(“quant”)的劳动力和资本的不同组合。
例如,L = 4且K = 4,L = 16且K = 1,并且L = 1且K = 16都产生O = 4的输出水平。
对于Q = 4,L形曲线简单地连接这些点。
当曲线向西北方向移动时,它们会绘制组合以获得更高的输出值。
柯布—道格拉斯+eviews6.0
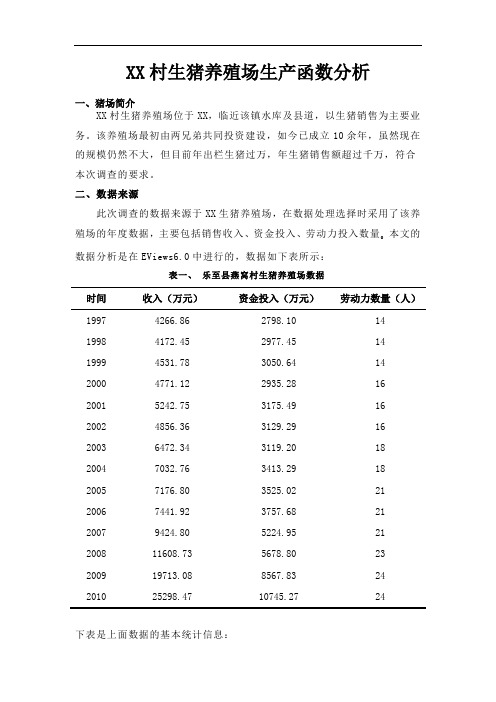
XX村生猪养殖场生产函数分析一、猪场简介XX村生猪养殖场位于XX,临近该镇水库及县道,以生猪销售为主要业务。
该养殖场最初由两兄弟共同投资建设,如今已成立10余年,虽然现在的规模仍然不大,但目前年出栏生猪过万,年生猪销售额超过千万,符合本次调查的要求。
二、数据来源此次调查的数据来源于XX生猪养殖场,在数据处理选择时采用了该养殖场的年度数据,主要包括销售收入、资金投入、劳动力投入数量。
本文的数据分析是在EViews6.0中进行的,数据如下表所示:表一、乐至县燕窝村生猪养殖场数据时间收入(万元)资金投入(万元)劳动力数量(人)1997 4266.86 2798.10 141998 4172.45 2977.45 141999 4531.78 3050.64 142000 4771.12 2935.28 162001 5242.75 3175.49 162002 4856.36 3129.29 162003 6472.34 3119.20 182004 7032.76 3413.29 182005 7176.80 3525.02 212006 7441.92 3757.68 212007 9424.80 5224.95 212008 11608.73 5678.80 232009 19713.08 8567.83 242010 25298.47 10745.27 24下表是上面数据的基本统计信息:表二:数据信息统计表Range: 1 14 -- 14 obs Object CountData Pointsseries 4 56 coef 1 751 Total5807三、模型的设定及变量的假定柯布-道格拉斯生产函数最初是美国数学家柯布(C.W.Cobb )和经济学家道格拉斯(P.H.Douglas )共同探讨投入生产关系时创立的生产函数,是在生产函数的一般形式上作出了改进,引入了技术资源这一因素。
他们根据历史资料,研究了1899-1922年美国资本和劳动对生产的影响,认为在技术不变的情况下产出与投入的劳动力及资本的关系可以表示为:Y AK L αβ=其中Y 表示产量,A 表示技术水平,K 表示投入的资本量,L 表示投入的劳动量,α、β分别表示K 和L 的产出弹性。
柯布道格拉斯函数拓展分析.

一定历史时期的生产函数是反映当时的社会生产力 水平的。只有明确一定历史阶段的社会生产力特征才能 构造出最能反映当时生产力发展水平的生产函数。在工 业时代,生产力水 平是以单位量的资本和劳动力的投入所能获得的产成品 的数量来衡量的。柯布——道格拉斯生产函数正是在 工业经济时代所构造出的反映工业经济时代生产力特征 的函数模型。当人类 进入到信息经济时代,由于信息资源的加入、技术的不 断进步,导致生产力发展的特征和能发生了根本变化, 信息时代的经济发展特征是以性能、质量、产品的差异 性组合,客户服务和信息管理等为主要竞争手段的。如 果我们仍然以工业时代测算生产力的方法去考察信息时 代中信息技术对生产力的作用的话,肯定无法对其做出 准确的判断。所以,原有的柯布——道格拉斯生产函 数已经不能再适应新的经济发展形态。
柯布——道格拉斯生产函 数
戚瓅丹 154
从三方面介绍C-D函数
• 传统的柯布——道格拉斯生产函数及其性质 • 对柯布——道格拉斯生产函的质疑 • 对柯布——道格拉斯生产函数所做的改进
传统的柯布——道格拉斯生产函数及其性质
柯布——道格拉斯生产函数是经济学中使用最为广泛 的生产函数,通常简称为C—D生产函数。它是由美国 数学家柯布(c.w.Cobb)和经济学家道格拉斯 (P.H.Douglas)根据1899年~1922年间美国制造业部 门的有关数据构造出来的。两人共同探讨投入和产出 的关系时,在生产函数的一般形式上引入了技术资源 因素,于1928年提出了这一函数形式。他们认为,在 技术经济条件不变的情况下,产出与投入的劳动力和 资本的关系可以表示为:
• 索洛经济增长速度方程表明产出增长率为技术进步速度和资本、劳动投入的 增长率的加权和。其表现形式为:
• 其中,P、a、k和1分别表示产出量、技术进步、资本投入和劳动投入的增长 速度,α、β分别表示资本和劳动的产出弹性。
微观经济学实验三:估计柯布-道格拉斯生产函数PPT课件

可编辑
3
3.实验原理
★ 柯布-道格拉斯生产函数
柯布-道格拉斯生产函数是由数学家C.柯布与经济学 家P.道格拉斯于20世纪30年代初一起提出来的。他们根据 美国1899—1922年的工业生产统计资料,得出这一时期 美国的生产函数。柯布-道格拉斯生产函数的表达式为:
Q = ALαKβ 式中Q代表总产量,L代表劳动投入量,K代表资本 投入量 。A、α、β为常数,且 0<α<1 ,0<β<1 。
8
4.实验步骤
1)设计回归模型
对柯布- 道格拉斯生产函数取其对数形式,因而设计 回归模型如下:
ln Q = C+ αln l + βln k + u 其中,Q代表总产出,l代表劳动投入量,k代表资本投 入量, α、β分别代表回归系数。
可编辑
9
4.实验步骤
2) 利用EViews软件进行回归分析,得到回归方程:
以国民经济中某一个行业或某一企业为对象,收集相关 数据进行回归分析,估计它的规模报酬状况。
1、根据我国钢铁行业的有关数据,研究其生产函数、规 模报酬及其变化趋势。
2、根据我国粮食生产的有关数据,研究其生产函数、规 模报酬及其变化趋势。
LOG(Y) = 1.168 + 0.607*LOG(L) + 0.372*LOG(K)
劳动的产出弹性α=0.607,资本的产出弹性β= 0.372 。
2)无约束条件的系数估计值α+β=0.607+0.372=0.979, 经Wald检验,无法拒绝原假设,即α+β=1,说明该行业生 产遵循规模报酬不变的假设。
在本实验中,最初提出的C-D生产函数中,假定参
数满足 + =1 ,也就是假定研究对象满足规模报酬不 变。即当资本与劳动的数量同时增长倍时,产出量也增 长 倍。
微观经济学实验三:估计柯布-道格拉斯生产函数

18
14
• 选择View/Coefficient Tests/Omitted Variables—Likelihood Ration,在打开的 对话框中,列出检验统计量名,用至少一 个空格相互隔开。
15
5.实验结果分析
1) 根据回归结果可知,美国金属行业生产的柯布-道格拉 斯生产函数为: LOG(Y) = 1.168 + 0.607*LOG(L) + 0.372*LOG(K) 劳动的产出弹性α=0.607,资本的产出弹性β= 0.372 。 2)无约束条件的系数估计值α+β=0.607+0.372=0.979, 经Wald检验,无法拒绝原假设,即α+β=1,说明该行业生产 遵循规模报酬不变的假设。 1937年,提出了C-D生产函数的改进型,即取消了 + =1 的假定,允许要素的产出弹性之和大于1或小于1,即承 认研究对象可以是规模报酬递增的,也可以是规模报酬递减 的,取决于参数的估计结果。因而基于C-D生产函数的改进 型,也可以说该行业的生产存在一定程度的规模报酬递减的 情况。
11
4.实验步骤
3)Wald系数检验----有约束条件的检验
利用EViews软件进行Wald检验,结果如下(原假设: 约束条件有效):
EViews显示F统计量和 2 统计量及相应的P值。它们 的P值表明我们可以确定地接受规模报酬不变的原假设。
12
4.实验步骤
4)遗漏变量检验
这一检验能给现有方程添加变量,而且判断添加的变 量对解释因变量变动是否有显著作用,以期完善原有模型 的设计。原假设H0是添加变量不显著。 本实验中,超越对数生产函数模型
柯补道格拉斯生产函数的成本函数

柯布-道格拉斯(Cobb-Douglas)生产函数是描述生产过程中输入与产出关系的数学模型。
在经济学中,柯布-道格拉斯生产函数广泛应用于描述企业的生产过程,并且对于企业的成本分析具有重要的意义。
本文将深入探讨柯布-道格拉斯生产函数的成本函数,分析其在企业经济中的应用和意义。
1. 柯布-道格拉斯生产函数简介柯布-道格拉斯生产函数最初由美国经济学家查尔斯·柯布和保罗·道格拉斯提出,用于描述输入与产出之间的关系。
其一般形式为:Q = A * L^a * K^b,其中Q表示产出,L表示劳动力输入,K表示资本输入,A为总要素生产率(Total Factor Productivity,TFP),a和b分别为劳动力和资本的弹性系数。
该函数表明产出与劳动力和资本的投入量成正比,同时与总要素生产率的影响呈现指数关系。
2. 柯布-道格拉斯生产函数的成本函数在企业经济中,成本是企业经营活动的核心指标之一。
柯布-道格拉斯生产函数可以通过对数变换后转化为成本函数形式,描述企业的生产成本与输入要素之间的关系。
成本函数的一般形式为:C = wL + rK,其中C表示总成本,w表示单位劳动力的工资,L表示劳动力投入量,r表示单位资本的租金,K表示资本投入量。
该成本函数表明总成本与劳动力和资本的投入成本成正比。
3. 柯布-道格拉斯生产函数的应用柯布-道格拉斯生产函数的成本函数在企业经济中具有重要的应用价值。
通过成本函数可以对企业的成本进行有效的管理和控制。
企业可以根据成本函数分析各项要素成本的相对重要性,通过控制劳动力和资本的投入量来实现成本最小化,从而提高生产效率和经济效益。
成本函数还可以为企业的产量规划和定价提供重要依据。
通过成本函数分析企业的生产要素价格和产出水平,可以有效制定合理的产量规划和产品定价策略,以实现企业利润最大化。
4. 柯布-道格拉斯生产函数的意义在现代经济学理论中,柯布-道格拉斯生产函数的成本函数对企业经济管理具有深远的意义。
柯布--道格拉斯生产函数

柯布--道格拉斯生产函数柯布-道格拉斯生产函数是一种用来描述产出与产出要素输入之间关系的经济学模型。
该模型是由美国经济学家柯布和道格拉斯在20世纪20年代提出的,被广泛应用于宏观经济学中的生产函数分析。
Y = A L^α K^β其中,Y表示产出, L表示劳动力输入量, K表示资本输入量, A表示全要素生产率, α和β是生产函数中劳动力因素和资本因素的弹性系数,而α+β的总和表示生产函数的规模收益。
所谓规模收益是指生产要素的总量增加一倍,能使产出增加的比例。
即α+β大于1时,存在递增规模收益;等于1时,存在恒等规模收益;小于1时,存在递减规模收益。
该生产函数的基本思想是,产出量可以用输入的各种生产要素数量来解释,而生产效率的提升可以通过升级技术和管理方法等手段来实现。
这一经济学模型通过科学地评估生产要素的投入和产出之间的关系,从而有效地指导产品生产的决策,同时也为企业实现成本最小化和效益最大化提供了理论基础。
优点:1.全要素生产率是该模型的核心概念,所包含的生产要素非常广泛,可以更全面地反映产出与产出要素之间的关系。
2.该模型能够帮助企业优化生产要素的投入,提高生产效率和效益。
3.对于某些复杂的生产运营系统,利用柯布-道格拉斯生产函数可以更加精细地建立生产模型,以便于深入分析和研究。
1.柯布-道格拉斯生产函数基于某一市场的生产数据,不适用于所有市场,无法复刻到所有不同形式的生产环境中。
2.该模型忽略了信息、技能和组织等非生产要素对企业产出的影响,对于这些影响因素的分析不够完备。
3.由于该模型只考虑单一生产函数,可能无法很好地解释某些特殊的产出情况。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数据建立柯布—道格拉斯生产函数分析美国某行业的投入产出情况实验目的
1.利用数据建立柯布—道格拉斯生产函数分析美国某行业的投入产出情况,并用多种统计方法检验规模报酬不变的假设。
2.利用CES生产函数检验是否使用柯布道格拉斯生产函数建模是较为合适的。
实验报告
1、问题提出
生产力水平决定了一个国家或者地区的生活水平,因此研究分析产出受那些因素的影响以及是如何被影响对于把握生产规律并进而提高生产效率有着极大的意义。
2、指标选择
从经济学原理的课程学习中可以知道,产量Y主要是被这几个因素所决定:技术水平(T),资本量(K),劳动(L),人力资本(H)自然资源(N)。
根据已有的数据资料,为达到实验目的,并且简化实验模型与分析,只分析劳动与资本量这两个因素的投入对产出的影响。
在本次实验中,我们分析美国某行业投入与产出情况。
选择样本容量为27的样本,分析劳动量,资本与产出的关系。
3、数据来源
数据由老师提供,详细数据见表1
4.数据处理
将表1中的实验数据化为其对数,方便建模时分析,如表2所示
5.09565.367985.228105.50465.35375
6.537576.115426.571165.770005.534065.465694.946845.0372 15.481766.28549
7.355535.368866.987586.25715.71986.728255.648975.015755.560336.209795.6174 94.8978
表2
5.数据分析
而且没有发现明显产出越多。
投入越多,K与资本L可以明显的发现劳动量数据,1观察表.
不符合实际的数据。
但是其中的幂函数关系需要通过进一步的分析发现。
6.建立模型
通过数理经济学的学习我们还了解到,生产函数常以柯布-道格拉斯(Cobb-Douglas)幂函数的形式出现。
柯布-道格拉斯生产函数最初是美国数学家柯布(Cobb)和经济学家道格拉斯(Douglas)共同探讨投入生产关系时创立的生产函数,他们根据历史资料,研究了1899-1922年美国资本和劳动对生产的影响,认为在技术不变的情况下产出与投入的劳动力??LAKY?及资本的关系可以表示为:,其中Y表示产量,A表示技术水平,K表示投入的资本量,L表示投入的劳动量,α、β分别表示K和L的产出弹性。
由于柯布-道格拉斯(Cobb-Douglas)生产函数是一个非线性模型,对生产函数取对数,可得: ??lnL K??ln Y?ln A
?????X Y??X+建立线性模型:利用样本数据用Eviews做lnY对lnK和lnL i21i021的回归
Dependent Variable: LNY
Method: Least Squares
Date: 10/27/16 Time: 12:46
Sample: 1 27
Included observations: 27
Prob. Std. Error Coefficient Variable t-Statistic
0.0003 0.373400 0.087246 4.279838 LNK
0.0001 0.129114 4.697887 LNL 0.606563
0.0017 3.523783
0.330983 1.166313
C
0.942420 R-squared
Mean dependent var 7.443631
0.937622 S.D. dependent var 0.761153 Adjusted R-squared
S.E. of regression Akaike info criterion 0.190103 -0.378063
Sum squared resid Schwarz criterion -0.234081 0.867339
Log likelihood -0.335249 8.103847 Hannan-Quinn criter.
F-statistic 1.854054
Durbin-Watson stat 196.4056
Prob(F-statistic)
0.000000
得出回归方程:Y=0.373400lnK+0.606563lnL+1.166313
7.模型检验
Y对lnK与lnL的回归模型的检验
经济检验:
α为0.373400,说明产出与资本投入成正相关,且在其他条件保持不变的情况下,资本投入增
加1%,产出增加约0.37%
β为,说明产出与劳动量成正相关,且在其他条件保持不变的情况下,资本0.606563的估计符
合经济理论,故通过经济检验。
β与α,对0.61%,产出增加约1%投入增加.
统计检验:
2R说明模型整体上对样本数据拟)拟合优度检验:=0.0.942420,修整的决定系数1( Y的大部分差异作出了解释。
K和L对合很好,即解释变量表明F(2,24)=3.40,5%的显著性水平下,F 统计量的临界值(2)显著性检验:在0.05因此t(24)=2.0639,24的t统计量的临界值为模型的线性关系显著成立。
自由度为0.025 lnL的参数显著性的异于零。
lnK与延伸问题:
,但是,很接近于1L的产出弹性之和为0.97996估计的资本量投入K与劳动量投入,即估计的生产函数是否,下面从它统计学的意义上考察,看它是否显著不为1并不为1 具有规模收益不变的特征。
生产函数可以化为如下形式=1,则Cobb-Dauglasα若+β?ln(K/L)
ln(Y/L)=lnA+???+Y?+X:的回归建立受约束线性模型利用,Eviews做ln(Y/L)对ln(K/L)0ii11 Dependent Variable: Y
Method: Least Squares
Date: 10/27/16 Time: 14:41
Sample: 1 27
Included observations: 27
Prob. t-Statistic Variable
Coefficient Std. Error
0.0001 4.717486 0.076543 X 0.361091
0.0000 8.022381
C
0.133562 1.071482
0.470952 R-squared 1.678343 Mean dependent var
0.449790 Adjusted R-squared 0.251624 S.D. dependent var
0.186645 S.E. of regression -0.448030 Akaike info criterion
0.870909 Sum squared resid -0.352042 Schwarz criterion
8.048399 Log likelihood -0.419487 Hannan-Quinn criter.
22.25467 Durbin-Watson stat 1.870391
F-statistic
0.000077 Prob(F-statistic)
得出回归方程:ln(Y/L)=0.361091ln(K/L)+1.071482
从回归结果看,无约束回归模型的残差平方和为0.867339,受约束回归模型的残差平方和为0.870909,样本容量n=27,计算F统计量为: F=0.098785
在5%的显著性水平下,自由度为(1,24)的F统计量的临界值为4.26,大于计算的F值,故不能拒绝该行业投入产出具有规模收益不变这一假设,即该行业产出投入的规模收益不变。
8.结果解释
利用柯布-道格拉斯(Cobb-Douglas)函数对美国某行业进行回归分析,发现该行业的产出与资本及劳动投入的关系基本满足柯布-道格拉斯的函数形式,这一定量的结果为产业调控产出提供了一定的理论依据。
同时,在0.05的显著性水平下,我们接受了资本投入量与劳动投入量的弹性之和为1的假定,即接受了该行业规模经济不变。
