自动控制原理实验一
实验报告-自动控制原理
________________________________________________________________________________
〖分析பைடு நூலகம்：______________________________________________________________________
_______________________________________________________________________________
说明：特征参数为比例增益K和微分时间常数T。
1)R2=R1=100KΩ, C2=0.01µF，C1=1µF；特征参数实际值：K=______，T=________。
波形如下所示：
2)R2=R1=100KΩ, C2=0.01µF，C1=0.1µF；特征参数实际值：K= 1，T=0.01。
波形如下所示：
四、实验心得体会
实验报告
班级
姓名
学号
所属课程
《自动控制原理》
课时
2
实践环节
实验3控制系统的稳定性分析
地点
实字4#318
所需设备
电脑、工具箱
一、实验目的
1.观察系统的不稳定现象。
2.研究系统开环增益和时间常数对稳定性的影响
3.学习用MATLAB仿真软件对实验内容中的电路进行仿真。
2、实验步骤
_______________________________________________________________________________
自动控制原理 实验一 控制系统的电子模拟实验
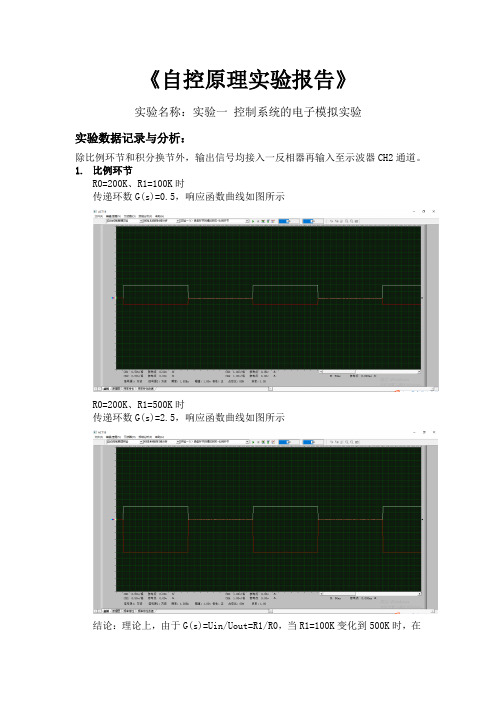
《自控原理实验报告》实验名称：实验一控制系统的电子模拟实验实验数据记录与分析：除比例环节和积分换节外，输出信号均接入一反相器再输入至示波器CH2通道。
1.比例环节R0=200K、R1=100K时传递环数G(s)=0.5，响应函数曲线如图所示R0=200K、R1=500K时传递环数G(s)=2.5，响应函数曲线如图所示结论：理论上，由于G(s)=Uin/Uout=R1/R0，当R1=100K变化到500K时，在输入信号不变的情况下，输出信号幅值应当变为原来的5倍。
由虚拟示波器图像可知输出红线（CH2）代表Uout，当R1=100K变化到500K时，其幅值变为原来的5倍。
这一结果符合理论分析结果。
2.积分环节R0=500K、C=1uF时传递环数G(s)=2/s，响应函数曲线如图所示R0=500K、C=2uF时传递环数G(s)=1/s，响应函数曲线如图所示R0=500K、C=3uF时传递环数G(s)=2/3s，响应函数曲线如图所示结论：理论上，由于G(s)分别为2/s、1/s、2/3s，可知响应曲线图像为斜率分别为2、1、1.5的直线，在输入信号为1V、1Hz的方波时，在有信号输入的阶段响应曲线上升但是斜率不相同，在无信号输入的阶段响应曲线保持不变。
由虚拟示波器图像可知输出红线（CH2）代表Uout。
结果符合理论分析结果。
3.惯性环节R0=200K、R1=200K、C=1uF时测量所得时间常数T=201.667ms理论上，传递环数G(s)=1/(0.2s+1),时间常数理论值为0.2s，响应函数曲线如图所示R0=200K、R1=200K、C=2uF时测量所得时间常数T=416.667ms理论上，传递环数G(s)=1/(0.4s+1),时间常数理论值为0.4s，响应函数曲线如图所示R0=200K、R1=100K、C=1uF时测量所得时间常数T=120ms理论上，传递环数G(s)=0.5/(0.1s+1),时间常数理论值为0.1s，响应函数曲线如图所示结论：实验测得时间常数与理论值基本符合。
自动控制原理实验一 典型系统的时域响应和稳定性分析
实验一典型系统的时域响应和稳定性分析一、实验目的1．研究二阶系统的特征参量(ξ、ωn) 对过渡过程的影响。
2．研究二阶对象的三种阻尼比下的响应曲线及系统的稳定性。
3．熟悉Routh判据，用Routh判据对三阶系统进行稳定性分析。
二、实验设备PC机一台，TD-ACC+教学实验系统一套。
三、实验原理及内容1．典型的二阶系统稳定性分析(1) 结构框图：如图1-1所示。
图1-1(2)图1-2(3) 理论分析系统开环传递函数为：G(s)=K1T0⁄s(T1s+1)开环增益：K= K1T0⁄先算出临界阻尼、欠阻尼、过阻尼时电阻R的理论值，再将理论值应用于模拟电路中，观察二阶系统的动态性能及稳定性，应与理论分析基本吻合。
在此实验中由图1-2，可以确地1-1中的参数。
T0= 1s , T1= 0.1s ,K1= 200R , K= 200R系统闭环传递函数为：W(s)=5Ks2+5s+5K其中自然振荡角频率：?n ω= 10√10R；阻尼比：?ζ= √10R402．典型的三阶系统稳定性分析(1) 结构框图：如图1-3所示。
图1-3(2) 模拟电路图：如图1-4所示。
图1-4(3) 理论分析系统的开环传函为: G(s)H(s)=20K s 3+12s 2+20s系统的特征方程为:1()()0G s H s += : s 3+12s 2+20s+20K=0 (4) 实验内容实验前由Routh 判断得Routh 行列式为：S 3 1 20 S 2 12 20K S 1 20-5/3*K 0 S 0 20K为了保证系统稳定，第一列各值应为正数，因此可以确定系统稳定 K 值的范围 : 0<K <12 R >41.7k系统临界稳定K: K=12 R =41.7k 系统不稳定K 值的范围: K >12 R <41.7k四、实验步骤1）将信号源单元的“ST ”端插针与“S ”端插针用“短路块”短接。
自动控制原理实验一
自动控制理论实验报告姓名学号班级同组人实验一典型系统的阶跃响应分析一、实验目的1. 熟悉一阶系统、二阶系统的阶跃响应特性及模拟电路；2. 测量一阶系统、二阶系统的阶跃响应曲线，并了解参数变化对其动态特性的影响；3. 掌握系统动态性能的测试方法。
二、实验内容1. 设计并搭建一阶系统、二阶系统的模拟电路；2. 观测一阶系统的阶跃响应，并研究参数变化对其输出响应的影响；σ、3. 观测二阶系统的阻尼比0<ξ<1时的单位阶跃响应曲线；并求取系统的超调量%调节时间t s(Δ= ±0.05)；并研究参数变化对其输出响应的影响。
三、实验结果（一）一阶系统阶跃响应研究1. 一阶系统模拟电路如图1-1所示，推导其传递函数G（s）=K/(Ts+1)，其中R0=200K。
图1-1 一阶系统模拟电路2. 将阶跃信号发生器的输出端接至系统的输入端。
3. 若K=1、T=1s时，取：R1=100K，R2=100K，C=10uF（K= R2/ R1=1，T=R2C=100K×10uF=1）。
当T=1，光标为起点和终值：光标为起点和0.95的终值：传递函数为:(R2/R1)/(R2CS+1)4 若K=1、T=0.1s时，重复上述步骤（R1=100K，R2=100K，C=1uF(K= R2/ R1=1,T=R2C=100K×1uF=0.1)）。
当T=0.1时，光标为起点和终值;光标为起点和0.95终值:6. 保存实验过程中的波形，记录相关的实验数据.，参数变化对系统动态特性的影响分析。
传递函数为:(R2/R1)/(R2CS+1), t=3T ，当T 减小需要达到稳定的时间也会减少，（二）二阶系统阶跃响应研究二阶系统模拟电路如图1-2所示，Rx 阻值可调范围为0～470K 。
图1-2 二阶系统模拟电路传递函数为1. n ω值一定（取10n ω=）时：1.1 当ξ=0.2时，各元件取值：C=1uF ，R=100K ， R X =250K （实际操作时可用200k+51k=251k 代替），理论计算系统的%σ，t s (Δ= ±0.05)，记录此时系统的阶跃响应曲线（阶跃信号的幅值自定），在曲线上求取系统的%σ，t s (Δ= ±0.05)，并与理论值进行比较。
自动控制原理实验.doc
实验一 典型环节的模拟研究一、实验目的：1． 了解并掌握XG2003自控理论教学实验系统模拟电路的使用方法，掌握典型环节模拟电路的构成方法，培养学生实验技能。
2． 熟悉各种典型环节的阶跃响应曲线。
3． 了解参数变化对典型环节动态特性的影响。
二、实验要求：1． 观测各种典型环节的阶跃响应曲线。
2． 观测参数变化对典型环节阶跃响应的影响。
三、实验仪器：1． XG2003教学实验板 一台 2． 示波器一台 3． 万用表一块四、实验原理和电路：本实验是利用运算放大器的基本特性（开环增益高、输入阻抗大、输出阻抗小等），设置不同的反馈网络来模拟各种典型环节。
典型环节块图及其模拟电路如下：1．比例（P ）环节。
其方块图如图1-1A 所示。
图1-1B 比例环节模拟电路比例环节的模拟电路如图1—1B 所示，其传递函数为1)()(R R s Ui s Uo = (1-2)比较式(1-1)和(1-2)得 K = R1/R0 (1-3)当输入为单位阶跃信号时，即)()(t l t U i = 时，SS U i 1)(=则由式(1-1)得 SKS U 1)(0= ， 所以输出响应为 K t U =)(0 (t ≥0) (1-4) 其输出方波如图1-1C 。
2．积输分（I ）环节。
其方块图如图1—2A 所示。
图1-1C 比例环节输出波形图 图1-2A 积分环节方块图 其传递函数为TSs Ui s Uo 1)()(=(1-5) 积分环节的模拟电路如图1—2B 所示。
图1-2B 积分环节模拟电路 积分环节模拟电路的传递函数为RoCSs Ui s Uo 1)()(=(1-6) 比较式(1-5)和(1-6)得C R T 0= 当输入为单位阶跃信号，即)()(t l t U i =时，S S U i 1)(=，则由式(1-5)得到TS S U 1)(0=·S 1=21TS 所以输出响应为：t T t U 1)(0=其输出波形如图1-2C 所示。
自动控制原理实验报告 (1)
实验1 控制系统典型环节的模拟实验（一）实验目的：1．掌握控制系统中各典型环节的电路模拟及其参数的测定方法。
2．测量典型环节的阶跃响应曲线，了解参数变化对环节输出性能的影响。
实验原理：控制系统模拟实验采用复合网络法来模拟各种典型环节，即利用运算放大器不同的输入网络和反馈网络模拟各种典型环节，然后按照给定系统的结构图将这些模拟环节连接起来，便得到了相应的模拟系统。
再将输入信号加到模拟系统的输入端，并利用计算机等测量仪器，测量系统的输出，便可得到系统的动态响应曲线及性能指标。
实验内容及步骤实验内容：观测比例、惯性和积分环节的阶跃响应曲线。
实验步骤：分别按比例，惯性和积分实验电路原理图连线，完成相关参数设置，运行。
①按各典型环节的模拟电路图将线接好(先接比例)。
(PID先不接)②将模拟电路输入端(U i)与阶跃信号的输出端Y相连接；模拟电路的输出端(Uo)接至示波器。
③按下按钮(或松开按钮)SP时，用示波器观测输出端的实际响应曲线Uo(t)，且将结果记下。
改变比例参数，重新观测结果。
④同理得积分和惯性环节的实际响应曲线，它们的理想曲线和实际响应曲线。
实验数据实验二控制系统典型环节的模拟实验（二）实验目的1．掌握控制系统中各典型环节的电路模拟及其参数的测定方法。
2．测量典型环节的阶跃响应曲线，了解参数变化对环节输出性能的影响。
实验仪器1．自动控制系统实验箱一台2．计算机一台实验原理控制系统模拟实验采用复合网络法来模拟各种典型环节，即利用运算放大器不同的输入网络和反馈网络模拟各种典型环节，然后按照给定系统的结构图将这些模拟环节连接起来，便得到了相应的模拟系统。
再将输入信号加到模拟系统的输入端，并利用计算机等测量仪器，测量系统的输出，便可得到系统的动态响应曲线及性能指标。
实验内容及步骤内容：观测PI，PD和PID环节的阶跃响应曲线。
步骤：分别按PI，PD和PID实验电路原理图连线，完成相关参数设置，运行①按各典型环节的模拟电路图将线接好。
自动控制原理实验（1）
实验一 典型环节的电路模拟一、实验目的1．熟悉THKKL-5型 控制理论·计算机控制技术实验箱及“THKKL-5”软件的使用； 2．熟悉各典型环节的阶跃响应特性及其电路模拟；3．测量各典型环节的阶跃响应曲线，并了解参数变化对其动态特性的影响。
二、实验设备1．THKKL-5型 控制理论·计算机控制技术实验箱；2．PC 机一台(含“THKKL-5”软件)、USB 数据采集卡、37针通信线1根、16芯数据排线、USB 接口线。
三、实验内容1．设计并组建各典型环节的模拟电路；2．测量各典型环节的阶跃响应，并研究参数变化对其输出响应的影响。
四、实验原理自控系统是由比例、积分、微分、惯性等环节按一定的关系组建而成。
熟悉这些典型环节的结构及其对阶跃输入的响应，将对系统的设计和分析十分有益。
本实验中的典型环节都是以运放为核心元件构成，其原理框图 如图1-1所示。
图中Z 1和Z 2表示由R 、C 构成的复数阻抗。
1．比例（P ）环节比例环节的特点是输出不失真、不延迟、成比例地复现输出信号的变化。
图1-1 它的传递函数与方框图分别为：KS U S U S G i O ==)()()(当U i (S)输入端输入一个单位阶跃信号，且比例系数为K 时的响应曲线如图1-2所示。
2．积分（I ）环节 图1-2积分环节的输出量与其输入量对时间的积分成正比。
它的传递函数与方框图分别为：设U i (S)为一单位阶跃信号，当积分系数为T 时的响应曲线如图1-3所示。
TsS U S U s G i O 1)()()(==图1-33．比例积分(PI)环节比例积分环节的传递函数与方框图分别为：)11(11)()()(21211212CS R R R CS R R R CS R CS R S U S U s G i O +=+=+==其中T=R 2C ，K=R 2/R 1设U i (S)为一单位阶跃信号，图1-4示出了比例系数(K)为1、积分系数为T 时的PI 输出响应曲线。
自动控制原理实验报告一
【范例 2-3】
【解】
将系统 G（s）=
转化为部分分式展开式 ������������ +������������������ +������
������������ +������������+������
MATLAB 程序为： >> num=[1,5,6];den=[1,2,1,0] >> [r,p,k]=residue(num,den) r = -5 -2 6 p = -1 -1 0 k = []
������������(������+������) ������+������.������ ������+������ (������+������)
【范例 2-2】
已知系统传递函数 G（s）= 的零极点模型 【解】MATLAB 程序为： >> k=10 >> z=[-5] >> p=[-0.5,-2,-3] >> sys=zpk(z,p,k) Zero/pole/gain:
试建立控制系统
3
控制系统的数学模型
10 (s+5) ------------------(s+0.5) (s+2) (s+3)
【自我实践 2-2】
建立控制系统的零极点模型 1） 2） G(s)= G(s)=
������ ������+������−������ (������+������+������) ������������ ������+������ ������+������ (������������ +������) ������ ������ ������+������ (������������ +������������ +������)
自动控制原理实验
自动控制原理实验
C
输 入
R2 R1 +
输 出 -1
Ui
0
t
Uo Uo 2 1
K=2
Ui=-1V
0
图 1-3 惯性环节实验原理图和输出波形
t
3.积分环节
积分环节实验原理图如图 1-4 所示。
G( S )
Z 2 1CS 1 Z1 R1 TS
， T=R1*C
当输入为单位阶跃信号，即 ui(t)=-1V 时，ui（s）= 所以输出响应为 uo（t）=
-1-
自动控制原理实验
R2
输 入
Ui
R1 +
0
输 出 -1 Uo Uo 2 1 k=2
t
Ui=-1V
0
图 1-2 比例环节实验原理图和输出波形
t
实验步骤： （1）调整示波器： 选择输入通道 CH1 或 CH2。 逆时针调节示波器的时间旋钮“TIME/DIV”到底， 使光标为一点， 并调节上下“位 移”旋钮使光标位于 0 线上。 调整示波器的输入幅度档位选择开关， 选择合适的档位使信号幅度便于观察， 例如 选择档位为 1V 档。 将输入幅度档位选择开关中心的微调旋钮顺时针旋到底。 将信号选择开关打到 DC 档。 （2）顺时针调节实验箱的旋钮，使阶跃信号为负（绿灯亮） 。 （ 3 ）阶跃信号接到示波器上，调节实验箱的幅度旋钮。使负跳变幅度为一格（即 Ui=-1V） 。 （4）接好实验线路，按下阶跃信号按钮，观察示波器的波形。 预习思考：输出幅度跳变应为……? 2.惯性环节 惯性环节实验原理图如图 1-3 所示。 其传递函数为： G( S )
-8-
自动控制原理实验
大使稳态误差进一步减小，直到等于零。因此， “比例+积分(PI)”控制器，可以使系统在进 入稳态后无稳态误差。 这是相位滞后校正，滞后校正器的基本特性，是相频曲线具有负相 移（滞后相位角） 。滞后校正器实际是一个低通滤波器，基本原理主要是利用其滞后网络的 高频衰减特性，以降低系统的开环截止频率，从而使已校正系统获得足够的相角裕度。 比例微分（PD）控制：在微分控制中，控制器的输出与输入误差信号的微分（即误差 的变化率） 成正比关系。 自动控制系统在克服误差的调节过程中可能会出现振荡甚至失稳。 其原因是由于存在有较大惯性组件（环节）或有滞后 (delay)组件，具有抑制误差的作用， 其变化总是落后于误差的变化。解决的办法是使抑制误差的作用的变化“超前” ，即在误差 接近零时，抑制误差的作用就应该是零。这就是说，在控制器中仅引入“比例”项往往是不 够的，比例项的作用仅是放大误差的幅值，而目前需要增加的是“微分项” ，它能预测误差 变化的趋势，这样，具有“比例+微分”的控制器，就能够提前使抑制误差的控制作用等于 零， 甚至为负值， 从而避免了被控量的严重超调。 所以对有较大惯性或滞后的被控对象， “比 例+微分(PD)”控制器能改善系统在调节过程中的动态特性，是“超前”校正。超前校正的 原理是利用微分环节的超前调节作用， 实际上是利用了 RC 微分电路的高通特性进行超前校 正的。 “滞后-超前（PID） ”校正包含 PI 和 PD 这两种校正，其对系统性能的影响是上述两种 校正对系统作用的综合， 这种校正方法兼有滞后校正和超前校正的优点， 因此可以取长补短， 比单独使用超前或滞后校正方法能满足更多的性能要求。 “滞后-超前”校正器不仅能提高系 统的稳定性能，还可以减少超调量、加快系统响应速度。合理应用 PID 可以取得更好的校 正效果。
自动控制原理实验
返回
实验二 典型环节的模拟研究(2学时) 实验三 典型二阶系统实验(2学时)
1、 实验目的：（1）学习系统（或环节）频率特 性的测量方法；（2）学习用频率特性确定数学模型的 方法 。 2、 实验要求：（1）测量并绘制一阶和二阶典型 环节的频率特性；（2）根据一阶和二阶典型环节的频 率特性确定其传递函数；（3）测量并绘制一个闭环系 统的频率特性
返回
实验六 系统的串联校正(2学时)
返回
实验四 根轨迹曲线的计算机绘制(2学时)
1、实验目的（1）训练学生应用计算机进行根轨迹 辅助分析；（2）让学生进一步加深系统零极点分布 对根轨迹形状的影响。 2、实验要求：（1）教师提供辅助分析软件，让学 生尽快学会使用；（2）每个学生做十例以上，并记 录各种根轨迹图。
返回
实验五 频率特性的研究 (2学时)
1、 实验目的：（1）学习正确选择校正装置的 种类及参数；（2）学习系统的调试方法。 2、 实验要求：（1）学生必须根据给定的条件及 指标要求确定校正装置的传递函数；（2）测出系统 的开环频率特性和闭环频率特性；（3）根据频率特 性求取系统的性能指标。
返回
1、 实验目的：（1）学习用阻容元件及线性组件 组成一个二阶系统进行各种实验的方法；（2）研 究阻尼比ξ和无阻尼自然振荡频率ω 对阶跃响应的
n
影响。 2、 实验要求：（1）要求学生画出实验电路图， 选择元器件并按照原理图连接成控制系统；（2） 改变参数，用长余辉示波器观察系统阶跃响应的变 化并记录。
自动控制原理实验(全面)
自动控制原理实验实验一 典型环节的电模拟及其阶跃响应分析一、实验目的⑴ 熟悉典型环节的电模拟方法。
⑵ 掌握参数变化对动态性能的影响。
二、实验设备⑴ CAE2000系统（主要使用模拟机，模/数转换，微机，打印机等）。
⑵ 数字万用表。
三、实验内容１．比例环节的模拟及其阶跃响应微分方程 )()(t Kr t c -= 传递函数 =)(s G )()(s R s C K -= 负号表示比例器的反相作用。
模拟机排题图如图9-1所示，分别求取K=1，K=2时的阶跃响应曲线，并打印曲线。
图9-1 比例环节排题图 图9-2 积分环节排题图 ２．积分环节的模拟及其阶跃响应微分方程 )()(t r dtt dc T= 传递函数 sKTs s G ==1)(模拟机排题图如图9-2所示，分别求取K=1，K=0.5时的阶跃响应曲线，并打印曲线。
３．一阶惯性环节的模拟及其阶跃响应微分方程 )()()(t Kr t c dtt dc T=+ 传递函数 1)(+=TS KS G模拟机排题图如图３所示，分别求取K=1, T=1; K=1, T=2; K=2, T=2 时的阶跃响应曲线，并打印曲线。
４．二阶系统的模拟及其阶跃响应微分方程 )()()(2)(222t r t c dt t dc T dt t c d T =++ξ传递函数 121)(22++=Ts s T s G ξ2222nn n s s ωξωω++= 画出二阶环节模拟机排题图，并分别求取打印： ⑴ T=1，ξ=0.1、0.5、1时的阶跃响应曲线。
⑵ T=2，ξ=0.5 时的阶跃响应曲线。
四、实验步骤⑴ 接通电源，用万用表将输入阶跃信号调整为2V 。
⑵ 调整相应系数器；按排题图接线，不用的放大器切勿断开反馈回路（接线时，阶跃开关处于关断状态）；将输出信号接至数/模转换通道。
⑶ 检查接线无误后，开启微机、打印机电源；进入CAE2000软件，组态A/D ，运行实时仿真；开启阶跃输入信号开关，显示、打印曲线。
自动控制原理实验(1)
实验一 典型环节的电路模拟一、实验目的1．熟悉THKKL-5型 控制理论·计算机控制技术实验箱及“THKKL-5”软件的使用； 2．熟悉各典型环节的阶跃响应特性及其电路模拟；3．测量各典型环节的阶跃响应曲线，并了解参数变化对其动态特性的影响。
二、实验设备1．THKKL-5型 控制理论·计算机控制技术实验箱；2．PC 机一台(含“THKKL-5”软件)、USB 数据采集卡、37针通信线1根、16芯数据排线、USB 接口线。
三、实验内容1．设计并组建各典型环节的模拟电路；2．测量各典型环节的阶跃响应，并研究参数变化对其输出响应的影响。
四、实验原理自控系统是由比例、积分、微分、惯性等环节按一定的关系组建而成。
熟悉这些典型环节的结构及其对阶跃输入的响应，将对系统的设计和分析十分有益。
本实验中的典型环节都是以运放为核心元件构成，其原理框图 如图1-1所示。
图中Z 1和Z 2表示由R 、C 构成的复数阻抗。
1．比例（P ）环节比例环节的特点是输出不失真、不延迟、成比例地复现输出信号的变化。
图1-1 它的传递函数与方框图分别为：KS U S U S G i O ==)()()(当U i (S)输入端输入一个单位阶跃信号，且比例系数为K 时的响应曲线如图1-2所示。
2．积分（I ）环节 图1-2积分环节的输出量与其输入量对时间的积分成正比。
它的传递函数与方框图分别为：设U i (S)为一单位阶跃信号，当积分系数为T 时的响应曲线如图1-3所示。
TsS U S Us G i O1)()()(==图1-33．比例积分(PI)环节比例积分环节的传递函数与方框图分别为：)11(11)()()(21211212CSR R R CSR R R CSR CS R S U S U s G i O +=+=+==其中T=R 2C ，K=R 2/R 1设U i (S)为一单位阶跃信号，图1-4示出了比例系数(K)为1、积分系数为T 时的PI 输出响应曲线。
自动控制原理实验报告
自动控制原理实验报告姓 名班 级学 号指导教师1自动控制原理实验报告（一）一．实验目的1.了解掌握各典型环节模拟电路的构成方法、传递函数表达式及输出时域函数表达式。
2.观察分析各典型环节的阶跃响应曲线，了解各项电路参数对典型环节动态特性的影响。
3.了解掌握典型二阶系统模拟电路的构成方法及Ⅰ型二阶闭环系统的传递函数标准式。
4.研究Ⅰ型二阶闭环系统的结构参数--无阻尼振荡频率ωn 、阻尼比ξ对过渡过程的影响。
5.掌握欠阻尼Ⅰ型二阶闭环系统在阶跃信号输入时的动态性能指标σ%、t p 、t s 的计算。
6.观察和分析Ⅰ型二阶闭环系统在欠阻尼、临界阻尼、过阻尼的瞬态响应曲线，及在阶跃信号输入时的动态性能指标σ%、t p 值，并与理论计算值作比对。
二．实验过程与结果1.观察比例环节的阶跃响应曲线1.1模拟电路图1.2传递函数(s)G(s)()o i U K U s == 10R K R =1.3单位阶跃响应U(t)K 1.4实验结果1.5实验截图2342.观察惯性环节的阶跃响应曲线2.1模拟电路图2.2传递函数(s)G(s)()1o i U KU s TS ==+10R K R =1T R C =2.3单位阶跃响应0(t)K(1e)tTU-=-2.4实验结果2.5 实验截图5673.观察积分环节的阶跃响应曲线3.1模拟电路图3.2传递函数(s)1G(s)()TS o i U U s ==i 0T =R C3.3单位阶跃响应01(t)i U t T =3.4 实验结果3.5 实验截图89104.观察比例积分环节的阶跃响应曲线4.1模拟电路图4.2传递函数0(s)1(s)(1)(s)i i U G K U T S ==+10K R R =1i T R C=4.3单位阶跃响应1 (t)(1)U K tT=+ 4.4实验结果4.5实验截图1112135.观察比例微分环节的阶跃响应曲线5.1模拟电路图5.2传递函数0(s)1(s)()(s)1i U TSG K U S τ+==+12312(R )D R R T CR R =++3R C τ=120R R K R +=141233(R //R )R D K R +=0.06D D T K sτ=⨯=5.3单位阶跃响应0(t)()U KT t Kδ=+5.4实验结果截图6.观察比例积分微分（PID ）环节的响应曲线6.1模拟电路图156.2传递函数0(s)(s)(s)p p p d i i K U G K K T S U T S ==++123212(R )C d R R T R R =++i 121(R R )C T =+120p R R K R +=1233(R //R )R D K R +=32R C τ= D D T K τ=⨯6.3单位阶跃响应0(t)()p p D p K U K T t K tTδ=++6.4实验观察结果截图16三．实验心得这个实验，收获最多的一点：就是合作。
自动控制原理-实验一
实验一 典型环节的模拟研究一．实验目的：1、了解并掌握ACLS-1控制理论实验箱模拟电路的使用方法，掌握典型环节模拟电路的构成方法，培养学生实验技能。
2、熟悉各种典型环节的阶跃响应曲线。
3、了解参数变化对典型环节动态特性的影响。
二．实验要求：1、观测各种典型环节的阶跃响应曲线。
2、观测参数变化对典型环节阶跃响应的影响。
三．实验仪器：1、ACLS-1控制理论实验箱 一台2、超低频示波器 一台3、万用表 一块四．实验原理和电路：实验是利用运算放大器和其它元器件构成的网络来模拟各种典型环节，接线方法见附录一和ACLS-1控制理论实验箱原理图。
典型环节方块图及其模拟电路如下：1.比例（P）环节：i当输入为单位阶跃信号，即)(1)(t t U i =时，SS U i 1)(=。
则由式（1－1） 得到：SK S U o 1)(•=其传递函数为：TSS U S U i o 1)()(= （1－5）积分环节的模拟电路如图1-2B 所示。
积分环节接线图：把图1－1B（b）中的R1换为C 即可。
积分环节模拟电路的传递函数为：CSR S U S U i o 01)()(= （1－6）比较式（1-5）和（1-6）得: C R T 0= （1－7） 当输入为单位阶跃信号，即)(1)(t t U i =时，SS U i 1)(=。
则由式（1－5） 得到：2111)(TS S TS S U o =•=比例积分环节的模拟电路如图1-3B 所示。
比例－积分环节接线图：把图1－1B（b）中的R1换成R1和C 串联即可。
其传递函数为：CSR R R CS R CS R S U S U i o 0010111)()(+=+= （1－10）比较式（1-9）和（1-10）得:当输入为单位阶跃信号，即)(1)(t t U i =时，SS U i 1)(=。
则由式（1－9） 得到：STS K S U o 1)1()(•+=惯性环节的接线图：把图1－1B（b）中的R1换成R1和C 并联即可。
自动控制原理实验
⾃动控制原理实验实验⼀典型系统动态性能和稳定性分析⼀．实验⽬的1．学习和掌握动态性能指标的测试⽅法。
2．研究典型系统参数对系统动态性能和稳定性的影响。
⼆．实验内容观测⼆阶系统的阶跃响应，测出其超调量和调节时间，并研究其参数变化对动态性能和稳定性的影响。
三．实验步骤1．熟悉实验箱，利⽤实验箱上的模拟电路单元，参考本实验附录中的图2.1.1和图2.1.2，设计并连接由⼀个积分环节和⼀个惯性环节组成的⼆阶闭环系统的模拟电路（如⽤U9、U15、U11和U8连成）。
注意实验接线前必须对运放仔细调零（出⼚已调好，⽆需调节）。
信号输出采⽤U3单元的O1、信号检测采⽤U3单元的I1、锁零接U3单元的G1。
2．利⽤实验设备观测该⼆阶系统模拟电路的阶跃特性，并测出其超调量和调节时间。
3．改变该⼆阶系统模拟电路的参数，观测参数对系统动态性能的影响。
4．分析实验结果，完成实验报告。
软件界⾯上的操作步骤如下：①按通道接线情况:通过上位机界⾯中“通道选择”选择I1、I2路A/D通道作为被测环节的检测端⼝,选择D/A通道的O1（“测试信号1”）作为被测对象的信号发⽣端⼝.不同的通道,图形显⽰控件中波形的颜⾊将不同。
②硬件接线完毕后,检查USB⼝通讯连线和实验箱电源后，运⾏上位机软件程序,如果有问题请求指导教师帮助。
③进⼊实验模式后，先对显⽰模式进⾏设置：选择“X-t模式”；选择“T/DIV”为1s/1HZ。
④完成上述实验设置，然后设置实验参数，在界⾯的右边可以设置系统测试信号参数，选择“测试信号”为“周期阶跃信号”，选择“占空⽐”为50%，选择“T/DIV ”为“1000ms ”，选择“幅值”为“3V ”，可以根据实验需要调整幅值，以得到较好的实验曲线，将“偏移”设为“0”。
以上除必须选择“周期阶跃信号”外，其余的选择都不是唯⼀的。
要特别注意，除单个⽐例环节外，对其它环节和系统都必须考虑环节或系统的时间常数，如仍选择“输⼊波形占空⽐”为50%，那么“T/DIV ”⾄少是环节或系统中最⼤时间常数的6～8倍。
自动控制原理实验1-6
⾃动控制原理实验1-6实验⼀MATLAB 仿真基础⼀、实验⽬的：（1）熟悉MATLAB 实验环境，掌握MATLAB 命令窗⼝的基本操作。
（2）掌握MATLAB 建⽴控制系统数学模型的命令及模型相互转换的⽅法。
（3）掌握使⽤MATLAB 命令化简模型基本连接的⽅法。
（4）学会使⽤Simulink 模型结构图化简复杂控制系统模型的⽅法。
⼆、实验设备和仪器 1．计算机；2. MATLAB 软件三、实验原理函数tf ( ) 来建⽴控制系统的传递函数模型，⽤函数printsys ( ) 来输出控制系统的函数，⽤函数命令zpk ( ) 来建⽴系统的零极点增益模型，其函数调⽤格式为：sys = zpk ( z, p, k )零极点模型转换为多项式模型[num , den] = zp2tf ( z, p, k ) 多项式模型转化为零极点模型 [z , p , k] = tf2zp ( num, den )两个环节反馈连接后，其等效传递函数可⽤feedback ( ) 函数求得。
则feedback （）函数调⽤格式为： sys = feedback（sys1, sys2, sign ）其中sign 是反馈极性，sign 缺省时，默认为负反馈，sign ＝-1；正反馈时，sign ＝1；单位反馈时，sys2＝1，且不能省略。
四、实验内容：1.已知系统传递函数，建⽴传递函数模型2.已知系统传递函数，建⽴零极点增益模型3．将多项式模型转化为零极点模型12s 2s s 3s (s)23++++=G )12()1()76()2(5)(3322++++++=s s s s s s s s G 12s 2s s 3s (s)23++++=G )12()1()76()2(5)(3322++++++=s s s s s s s s G4. 已知系统前向通道的传递函数反馈通道的传递函数求负反馈闭环传递函数5、⽤系统Simulink 模型结构图化简控制系统模型已知系统结构图，求系统闭环传递函数。
自动控制原理实验一控制系统的阶跃响应
自动控制原理实验一控制系统的阶跃响应实验目的：通过实验，掌握控制系统的阶跃响应的测量方法，了解控制系统的响应特性，并研究控制系统的参数对阶跃响应的影响。
实验原理：阶跃响应是指当控制系统输入信号突然从零变为常数时，系统的输出信号的响应过程。
通过观察阶跃响应可以了解控制系统的稳态误差、超调量、调节时间等参数，从而评估和改善控制系统的性能。
在实验中，常用的控制系统模型是一阶惯性环节，其传递函数为：G(s)=K/(Ts+1)其中，K为系统的增益，T为系统的时间常数。
通过改变K和T的值，可以观察到控制系统阶跃响应的变化。
实验仪器和材料：1.控制系统阶跃响应实验台2.配套的实验软件3.电脑实验步骤：1.打开实验软件，并连接实验台和电脑。
2.在软件中选择阶跃响应实验，并设置初始参数。
3.点击开始实验按钮，系统开始运行，记录实验数据。
4.观察实验数据的变化，并绘制出阶跃响应曲线。
5.改变控制系统的参数，如增益K和时间常数T的值，重新进行实验测量。
6.比较不同参数下的阶跃响应曲线，分析参数对响应的影响。
7.根据实验结果，评估系统的性能，并提出改进措施。
实验注意事项：1.实验过程中要保持实验台和电脑的连接良好，确保数据的准确性。
2.实验中应注意安全防护，避免操作中发生意外。
3.实验前要熟悉实验仪器的操作方法和实验原理，确保能够正确进行实验。
4.实验结束后，要及时清理实验台和关闭相关设备。
实验结果：通过实验测量得到的阶跃响应曲线，可以用于评估控制系统的性能。
通常，我们关注的参数包括稳态误差、超调量、调节时间等。
稳态误差是指系统在稳定状态下的输出值与期望值之间的差值。
通过观察阶跃响应曲线的稳态值，可以评估系统的稳态误差。
稳态误差越小，系统的控制性能越好。
超调量是指系统响应过程中最大超过期望值的幅值，通常以百分比形式表示。
通过观察阶跃响应曲线的峰值，可以评估系统的超调量。
超调量越小，系统的控制性能越好。
调节时间是指控制系统从初始状态到稳态所需的时间。
自控原理实验报告1
自动控制原理实验——第一次实验姓名：乔佳楠班级：06110901学号：20091419一、实验目的了解MATLAB在自动控制原理课程中的应用，学习MATLAB的基本使用方法。
通过上机实验操作学习线性系统的分析与设计，学习传递函数的描述方法，自控系统结构框图的模型表示以及线性系统的时域分析。
其中本节重点掌握结构框图中的串联，并联和反馈结构的模型表示方法，并能正确分析不同结构模型之间的关系。
二、实验要求运用MATLAB软件解决下列三个问题，并绘制出每个函数的单位阶跃响应图像，标出其上升时间，过渡过程时间，计算出超调量。
三、实验内容1．给出下列两个函数，分别求出在串联，并联和反馈结构中的系统传递函数，并画出阶跃响应曲线，标出上升时间，过渡过程时间以及超调量。
①G1=tf(10,[1,2,3]) ②G2=tf(1,[1,2])Step1:串联结构，即G=G1*G2>> G1=tf(10,[1,2,3]);>> G2=tf(1,[1,2]);>> G=series(G1,G2)Transfer function:10---------------------s^3 + 4 s^2 + 7 s + 6>> step(G)起调量：（1.77-1.66）/1.66*100%=6.63% 上升时间： 2.97 sec过渡过程时间：5.89 secStep2:并联结构，即G=G1+G2>> G1=tf(10,[1,2,3]);>> G2=tf(1,[1,2]);>> G=parallel(G1,G2)Transfer function:s^2 + 12 s + 23---------------------s^3 + 4 s^2 + 7 s + 6>> step(G)起调量：（4.19-3.83）/3.83*100%=9.40% 上升时间： 2.23 sec过渡过程时间：5.78 secStep3：反馈结构，即G=G1/(1+G1G2)>> G1=tf(10,[1,2,3]);>> G2=tf(1,[1,2]);>> G=feedback(G1,G2,-1)Transfer function:10 s + 20----------------------s^3 + 4 s^2 + 7 s + 16 >> step(G)起调量：（2.25-1.25）/1.25*100%=80.0%上升时间： 1.29 sec过渡过程时间：16.7 sec2.根据系统的结构框图，求出系统总的传递函数。
自动控制原理实验.
实验一控制系统典型环节的模拟 一、实验目的 (1)熟悉超低频扫描示波器的使用方法。
(2)掌握用运放组成控制系统典型环节的模拟电路。
(3)测量典型环节的阶跃响应曲线。
(4)通过实验了解典型环节中参数的变化对输出动态性能的影响。
二、实验所需挂件及附件DJK01 、DJK15、双踪慢扫描示波器、万用表三、实验线路及原理以运算放大器为核心元件，由其不同的R-C 输入网络和反馈网络组成的各种典型环节，如图8-1所示。
图中Z 1和Z 2为复数阻抗，它们都是由R 、C 构成。
基于图中A 点的电位为虚地，略去流入运放的电流，则由图8-1得：由上式可求得，由下列模拟电路组成的典型环节的传递函数及其单位阶跃响应。
(1)比例环节比例环节的模拟电路如图8-2所示：图8-1 运放的反馈连接图8-2 比例环节(2)惯性环节 (1) )(12Z Z u u S G i o =-=2=410820==12K K Z Z )S (G 111/1/)(21212212+=+⋅=+==TS K CS R R R R CS R CS R Z Z S G取参考值R1=100K，R2=100K，C=1uF图8-3 惯性环节(3)积分环节式中积分时间常数T=RC,取参考值R=200K，C=1uF图8-4 积分环节(4)比例微分环节（PD），其接线图如图及阶跃响应如图8-5所示。
参考值R1=200K，R2=410K，C=0.1uF）（311/1)(12TSRCSRCSZZSG====CR=T,=K(4)1+=1+•=1+==1D1211211212RR)ST(K)CSR(RRCS/RCS/RRZZ)S(GD其中图8-5 比例微分环节(5)比例积分环节，其接线图单位阶跃响应如图8-6所示。
参考值R1=100K R2=200K C=0.1uF图8-6 比例积分环节(6)振荡环节，其原理框图、接线图及单位阶跃响应波形分别如图8-7、8-8所示。
图8-8为振荡环节的模拟线路图，它是由惯性环节，积分环节和一个反号器组成。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
《自动控制原理》MATLAB仿真实验控制系统理论、计算方法与计算机技术的结合是当代控制理论发展的标志，因此在以MATLAB为代表的软件平台上，对控制系统进行分析、设计与仿真就成了控制工程师必须熟练掌握的重要知识与技能。
控制系统CAD及仿真是建立在古典控制理论、现代控制理论、计算方法、计算机技术等多方面知识上的综合性学科，是一门综合性与实践性较强的专业课，目前已成为自动化学科重要的研究分支，灵活地掌握与运用它有助于我们深刻理解已学过的有关课程内容，为今后从事控制系统领域的研究与开发工作提供坚实的基础。
本书是编者们对教学、实验与科研工作的总结，并在借鉴国内外控制领域专家、学者研究成果的基础上编写而成的。
在内容编排上具有如下几方面的特点：1、将MATLAB的使用方法和程序设计以简练的篇幅进行介绍，使得直接、快速地了解和掌握MATLAB软件平台成为可能，并采用由浅到深，由易到难逐步深入的方式对控制系统应用MATLAB软件进行刻化；2、在已学习的古典与现代控制理论的基础上，介绍在MATLAB软件平台上对系统进行分析和设计的方法；3、重点介绍目前控制系统仿真技术中状态空间法和Simulink仿真的主要思想，达到学以致用的效果；4、所有的实验、习题都经过精心选择，书中所有的用MATLAB描述的程序都经过严格的上机调试，保证所写程序的可用性，是本书的最重要的特色。
准备工作 熟悉MATLAB的仿真实验环境一、实验目的1．学习了解MATLAB的仿真实验环境2．练习MATLAB命令的基本操作；3．练习MATLAB的m文件的基本操作。
二、实验步骤1．学习了解MATLAB仿真实验环境开机执行程序进入MATLAB环境在命令提示符位置键入下述命令：help显示MATLAB的功能目录．并浏览内容。
intro显示MATLAB语言的基本介绍，如矩阵输人、数值激位计算、曲线绘图等，阅读命令平台上的注释，内容，以尽快MATLAB函数的应用方法。
内容，以尽快了解毗LAn函数的应用方法。
help heLp显示联机帮助查阅功能(要求用中文作简要记录)。
info显示工具箱中各种工具箱组件信息和开发商的联络信息；demoMATLAB的各种功能演水。
help control阅读控制系统工具箱命令清单，阅读如下命令的帮助文件内容：help stephelp impulehelp cloophelp printsys2.练习MATLAB命令的基本操作键人常数矩阵输人命令a＝[1 2 3]与a＝[1；2；3]记录结果，比较显示结果有何不同、b＝[1 2 5]与b=[l 2 5];记录结果，比较显示结果有何不同!a a’b b’记录结果，比较变量加“'”后的区别。
c=a*b c＝a*b'记录显示结果与出错原因。
a＝[1 2 3；4 5 6；7 8 0] a^2 a^0.5记录显示结果。
作循环命令程序makesum=0;for i＝1:1:100makesum＝makesum+i;end键入makesum，按回车键，记录计算结果。
分别执行下列命令a＝[1 2 3；4 5 6；7 8 0]poly(a) rank(a) det(a) trace(a)inv(a) eig(a)观察、记录显示结果，键人help函数名，查问相应m函数的意义和函数格式，并作记录。
3．练习m文件的基本操作打开用file菜单，其中有“Open m-file” 用于打开m文件“Run m-file” 用于执行m文件可以自由练习上述两项操作。
(注意：大部分m文件需要相应的数据才可以运行．此时命令平台上给出警告提示。
)例如打开：plot. m 阅读绘图命令的功能以及变量格式执行：penddemo.m 可以观察倒立摆控制系统的演示实验一 数学模型的处理一、实验目的1．观察学习、掌握Laplace 的变换与反变换；2．观察学习、掌握一般多项式的运算；3．观察学习、掌握一般微分方程的求解；二、实验步骤1．开机执行程序c ：＼matlab ＼bin ＼matlab.exe(或用鼠标双击图标)进人MATLAB 命令窗口2.建立系统模型系统模型的建立一般从时域开始，根据实际系统的各种物理关系与实际联接的关系导出表述系统逻辑关系的微分方程式。
（关系较复杂）为便于进一步处理，使用微分方程表述系统逻辑关系的时域表达式进入复数域进行分析与计算，即拉普拉斯变换与反变换，进而前涉到多项式的运算。
（a ）微分方程的求解：命令（微分方程的求解）：dsolve('方程l'，'方程2'，…)函数应用格式说明：(]) 可多至12个微分方程的求解；(2) 默认白变量为'x'，并可任意指定自变量为‘t ’、’u ’等；(3) 微分方程的各阶导数项以大写字母’D ’作为标识，后接数字阶数，再接解变量名，例如：Dy 表示dy/dx 、D2y 表示d 2y/dx 2等(4) 初始条件以符号代数方程结出，如‘y(a)＝b'、Dy(a)=b'等，其中a 、b 为常数。
如果初始始条件项省缺，其默认常数为C1，C2，…等。
(5)返回变量格式为：[Y1,Y2，…]=dsolve(…)返回方程得解Y1,Y2,…。
例： 已知0输入线型微分方程与初始条件为0)(2)(2)(22=++x c x c dx d x c dx d c(0)=0, c’(0)=0 求该微分方程得解；再MATLAB 环境下，输入下列语句：>> y=dsolve('D2c+2*Dc+2*c=0','c(0)=1','Dc(0)=0','x') ％求解微分方程>> ezplot(y,[1,10]); ％作出响应图>> grid ％作出网格 得到微分方程的解与响应图。
y =exp(-x)*sin(x)+exp(-x)*cos(x)（b ）求Laplace 变换命令（求Laplace 变换）：laplace(ft,t,s)例求方程22)(2++=t t t f 的拉是变换；解：在MATLAB 命令窗口上，键入以下命令;syms s t %定义变量Ft=t^2+2*t+2;St=laplace(Ft,t,s)得到拉普拉斯变换式为：St =2/s^3+2/s^2+2/s ；即：ss s s F 222)(23++=求F(s)的逆变换：Syms s tFt=2/s^3+2/s^2+2/s ;St=ilaplace(Ft,s,t) 运行程序得到：St =t^2+2*t+2求f(t)=sinwt 得拉氏变换，输入以下程序syms s t w %定义变量Ft=sin(w*t);St=laplace(Ft,t,s)运行得到：St = w/(s^2+w^2) %w 再MATLAB 中代表频率ω； 例 求1-e -at的拉氏变换解：该题是两项拉氏变换之和，即1*t 0和（-e -at ）拉氏变换之和。
syms t a %定义变量fb=laplace(-exp(-a*t))syms t %定义变量fc=laplace(1*t^0)fa=fc+fb运行后得到;fa =1/s-1/(s+a)=a/s(+a);(c) 多项式运算命令(多项式运算): roots(p); poly(r); conv(p,q); polyval(n,s); 求根用：roots(p);由根建立多项式：poly(r);多项式运算：conv(p,q);多项式求值：polyval(n,s)；例 求多项式43)(23++=s s s p 的根解：在MATLAB 命令窗口上，键入以下命令;p=[1 3 0 4]r=roots(p)运行求得根为：r1 = -3.3553 （负实根） 和共轭虚根 r2=0.1777 + 1.0773i r3= 0.1777 - 1.0773i 键入：p=poly(r)求得多项式系数为：p = 1.0000 3.0000 0.0000 4.0000 即原方程。
例 求两多项式相乘)4)(123(3+++s s s ，求s=－5时的值。
键入：p=[3 2 1];q=[1 4];n=conv(p,q)运行得到：n = 3 14 9 4键入：vlaue=polyval(n,-5) 运行得到值：vlaue = -66(d) z 变换与反变换命令(z 变换与反变换): 求f 的z 变换可用： F ＝ztrans(f)求F 的z 反变换可用：f=iztrans(F,t)例 求 f(t)=t 的z 变换输入以下程序：%%%% 求f的z变换syms t T;f=t*T;F=ztrans(f) %F=T*z/(z-1)^2%%%% 求F的反变换syms z Tf=iztrans(F,t); %=t*T三. 实验内容（a ）求解下列微分方程：（1）6)(6)(5)(22=++t y dxt dy dx t y d 初始条件： c(0)=0, c’(0)=2 （2）29)(29)(4)(2233=++dx t dy dx t y d dx t y d 初始条件： c(0)=0, c’(0)=17，c’’=－122 （b ）求下列函数拉氏变换及反变换(1) t t t f 4cos 4sin )(+=(2) 2)(42++=t e t t f(3) at n e t t f =)((4) t e t t f 22)1()(−=（c ）求下列函数z 变换;及反变换(1) k a t e =)((2) t a t e at ωsin )(−= (3) )()(a s s ks E +=（4）))((1)(b s a s s E ++=（d ）求下列函数z 反变换 (1) )5.0()(−=z zz E（2） )2)(1()(−−=z z zz E (3) ))(()(bT aT e z e z zz E −−−−=四、按要求完成实验报告；（1）求解（a）微分方程；（2）求解（b）函数拉氏变换及反变换；(3) 求解(c)、(d) 的z变换与z反变换；。