自动控制原理实验1-6
自动控制原理实验资料

自动控制原理实验实验1 控制系统典型环节的模拟利用运算放大器的基本特性,如:开环增益高,输入阻抗大、输出阻抗小等,通过设置不同的反馈网络,可以模拟各种典型环节。
一.实验目的● 掌握用运算放大器组成控制系统典型环节的电子电路原理。
● 观察几种典型环节的阶跃响应曲线。
● 了解参数变化对典型环节输出动态性能(即阶跃响应)的影响。
二.实验仪器● THSCC-1实验箱一台。
● 示波器一台。
三.实验内容 1.比例环节比例(P )环节的方框图如图1-1所示。
图1-1比例环节方框图K Z Z S u S u S G i o ==-=12)()()(当输入为单位阶跃信号,即u i =-1V 时,u i (s )=s 1,则u o (s )=K s1,所以输出响应为:u o (t )=K (t ≥0)。
比例环节实验原理图如图1-2所示。
选择:K=R2/R1=2,例如选择R2=820k ,R1=410k ,或选择R2=100k ,R1=51k 。
R2图1-2 比例环节实验原理图和输出波形实验步骤:(1)调整示波器:● 选择输入通道CH1或CH2。
● 逆时针调节示波器的时间旋钮“TIME/DIV ”到底,使光标为一点,并调节上下“位移”旋钮使光标位于0线上。
● 调整示波器的输入幅度档位选择开关,选择合适的档位使信号幅度便于观察,例如选择档位为1V 档。
● 将输入幅度档位选择开关中心的微调旋钮顺时针旋到底。
● 将信号选择开关打到DC 档。
(2)顺时针调节实验箱的旋钮,使阶跃信号为负(绿灯亮)。
(3)阶跃信号接到示波器上,调节实验箱的幅度旋钮。
使负跳变幅度为一格(即Ui=-1V )。
(4)接好实验线路,按下阶跃信号按钮,观察示波器的波形。
预习思考:输出幅度跳变应为……? 2.惯性环节惯性环节实验原理图如图1-3所示。
其传递函数为:11)()()(+==TS Ks u s u S G i o , K= R2/R1,T=R2*C 当输入为单位阶跃信号,即u i (t )=-1V 时,u i (s )=S 1,则u o (s )=S11TS 1⋅+ 所以输出响应为u o (t )=)e1(K Tt--。
自动控制原理实验指导书五个实验).docx

自动控制原理实验指导书电力学院自动控制原理实验室二OO八年三月实验一典型环节的电路模拟与软件仿真 (2)实验二线性定常系统的瞬态响应 (6)实验三线性系统稳态误差的研究 (8)实验四系统频率特性的测量 (11)实验五线性定常系统的串联校正 (13)附:THBDC-1控制理论•计算机控制技术实验平台简介 (16)实验一典型环节的电路模拟与软件仿真一、实验目的1.熟悉并寧握THBDC-1型控制理论•计算机控制技术实验平台及上位机软件的使用方法。
2.熟悉各典型环节的电路传递函数及其特性,学握典型环节的电路模拟与软件仿真研究。
3.测虽各典型环节的阶跃响应曲线,并了解参数变化对其动态特性的影响。
二、实验设备1.THBDC-1型控制理论・计算机控制技术实验平台2.PC机1台(含上位机软件)USB数据采集卡37针通信线1根16芯数据排线USB接口线3.双踪慢扫描示波器1台(可选)4.万用表1只三、实验内容1.设计并组建各典型环节的模拟电路;2.测量各典型环节的阶跃响应,并研究参数变化对其输出响应的影响;3.在上位机界血•上,填入各典型环节数学模型的实际参数,据此完成它们对阶跃响应的软件仿真,并与模拟电路测试的结果相比较。
四、实验原理自控系统是山比例、积分、微分、惯性等典型环节按一定的关系连接而成。
熟悉这些环节对阶跃输入的响应,对分析线性系统将是十分冇益的。
在附录屮介绍了典型环节的传递函数、理论的阶跃响W曲线和环节的模拟电路图。
五、实验步骤1.熟悉实验台,利用实验台上的各电路单元,构建所设计比例环节(可参考本实验附录)的模拟电路并连接好实验电路;待检杳电路接线无课示,接通实验台的电源总开关,并开启± 5V, ± 15V 直流稳压电源。
2.把采集卡接口单元的输出端DA1、输入端AD2与电路的输入端Ui相连,电路的输出端U。
则与采集卡接口单元屮的输入端AD1相连。
连接好采集卡接口单元与PC上位机的通信线。
自动控制原理实验指导书

⾃动控制原理实验指导书⽬录第⼀章⾃动控制原理实验 (1)实验⼀典型环节模拟⽅法及动态特性 (1)实验⼆典型⼆阶系统的动态特性 (4)实验三典型调节规律的模拟电路设计及动态特性测试 (6)实验四调节系统的稳态误差分析 (8)实验五三阶系统模拟电路设计及动态特性和稳定性分析 (11)实验六单回路系统中的PI调节器参数改变对系统稳定性影响 (13)实验七典型⾮线性环节的模拟⽅法 (15)实验⼋线性系统的相平⾯分析 (17)第⼆章控制理论实验箱及DS3042M(40M)⽰波器简介 (19)第⼀节⾃动控制理论实验箱的简介 (19)第⼆节数字存储⽰波器简介 (20)第⼀章⾃动控制原理实验实验⼀典型环节模拟⽅法及动态特性⼀、实验⽬的1、掌握⽐例、积分、实际微分及惯性环节的模拟⽅法。
2、通过实验熟悉各种典型环节的传递函数和动态特性。
⼆、实验设备及器材配置1、⾃动控制理论实验系统。
2、数字存储⽰波器。
3、数字万⽤表。
4、各种长度联接导线。
三、实验内容分别模拟⽐例环节、积分环节、实际微分环节、惯性环节,输⼊阶跃信号,观察变化情况。
1、⽐例环节实验模拟电路见图1-1所⽰传递函数:K R R V V I -=-=120阶跃输⼊信号:2V实验参数:(1) R 1=100K R 2=100K(2) R 1=100K R 2=200K2、积分环节实验模拟电路见图1-2所⽰传递函数:ST V V I I O 1-= ,其中T I阶跃输⼊信号:2V 实验参数:(1) R=100K C=1µf(2) R=100K C=2µf 3、实际微分环节实验模拟电路见图1-3所⽰传递函数:K ST S T V V D D I O +-=1 其中 T D =R 1C K=12R R 阶跃输⼊信号:2V实验参数:(1) R 1=100K R 2=100K (2)R 1=100K R 2=200K C=1µf4、惯性环节实验模拟电路见图1-4所⽰传递函数:1+-=TS K V V I O 其中 T=R 2C K=12R R 阶跃输⼊:2V 实验参数:(1) R 1=100K R 2=100K C=1µf(2) R=100K R 2=100K C=2µfR四、实验步骤1、熟悉实验设备并在实验设备上分别联接各种典型环节。
自动控制原理实验实验指导书

自动控制原理实验目录实验一二阶系统阶跃响应(验证性实验) (1)实验三控制系统的稳定性分析(验证性实验) (9)实验三系统稳态误差分析(综合性实验) (15)预备实验典型环节及其阶跃响应一、实验目的1.学习构成典型环节的模拟电路,了解电路参数对环节特性的影响。
2.学习典型环节阶跃响应测量方法,并学会由阶跃响应曲线计算典型环节传递函数。
二、实验内容搭建下述典型环节的模拟电路,并测量其阶跃响应。
1.比例(P)环节的模拟电路及其传递函数示于图1-1。
2.惯性(T)环节的模拟电路及其传递函数示于图1-2。
3.积分(I)环节的模拟电路及其传递函数示于图1-3。
4. 比例积分(PI)环节的模拟电路及其传递函数示于图1-4。
5.比例微分(PD)环节的模拟电路及其传递函数示于图1-5。
6.比例积分微分(PID)环节的模拟电路及其传递函数示于图1-6。
三、实验报告1.画出惯性环节、积分环节、比例积分环节、比例微分环节、比例积分微分环节的模拟电路图,用坐标纸画出所记录的各环节的阶跃响应曲线。
2.由阶跃响应曲线计算出惯性环节、积分环节的传递函数,并与由模拟电路计算的结果相比较。
附1:预备实验典型环节及其阶跃响应效果参考图比例环节阶跃响应惯性环节阶跃响应积分环节阶跃响应比例积分环节阶跃响应比例微分环节阶跃响应比例积分微分环节阶跃响应附2:由模拟电路推导传递函数的参考方法1. 惯性环节令输入信号为U 1(s) 输出信号为U 2(s) 根据模电中虚短和虚断的概念列出公式:整理得进一步简化可以得到如果令R 2/R 1=K ,R 2C=T ,则系统的传递函数可写成下面的形式:()1KG s TS =-+当输入r(t)为单位脉冲函数时 则有输入U 1(s)=1输出U 2(s)=G(s)U 1(s)= 1KTS-+由拉氏反变换可得到单位脉冲响应如下:/(),0t TK k t e t T-=-≥ 当输入r(t)为单位阶跃函数时 则有输入U 1(s)=1/s输出U 2(s)=G(s)U 1(s)= 11K TS s-+由拉氏反变换可得到单位阶跃响应如下:/()(1),0t T h t K e t -=--≥当输入r(t)为单位斜坡函数时 则有输入U 1(s)=21s输出U 2(s)=G(s)U 1(s)=2323R R C T R R =+2Cs12Cs-(s)U R10-(s)U 21R R +-=12212)Cs (Cs 1(s)U (s)U )(G R R R s +-==12212)Cs 1((s)U (s)U )(G R R R s +-==由拉氏反变换可得到单位斜坡响应如下:/()(1),0t T c t Kt KT e t -=--≥2. 比例微分环节令输入信号为U 1(s) 输出信号为U 2(s) 根据模电中虚短和虚断的概念列出公式:(s)(s)(s)(s)(s)U100-U U 0U 2=1R1R23(4)CSU R R '''---=++由前一个等式得到 ()1()2/1U s U s R R '=- 带入方程组中消去()U s '可得1()1()2/11()2/12()1134U s U s R R U s R R U s R R R CS+=--+由于14R C〈〈,则可将R4忽略,则可将两边化简得到传递函数如下: 2()23232323()(1)1()11123U s R R R R R R R R G s CS CS U s R R R R R ++==--=-++如果令K=231R R R +, T=2323R R C R R +,则系统的传递函数可写成下面的形式:()(1)G s K TS =-+当输入r(t)为单位脉冲函数时,单位脉冲响应不稳定,讨论起来无意义 当输入r(t)为单位阶跃函数时 则有输入U 1(s)=1/s输出U 2(s)=G(s)U 1(s)=(1)K TS S-+由拉氏反变换可得到单位阶跃响应如下:()(),0h t KT t K t δ=+≥当输入r(t)为单位斜坡函数时 则有输入U 1(s)=21s输出U 2(s)=G(s)U 1(s)=2(1)K TS S -+由拉氏反变换可得到单位斜坡响应如下:(),0c t Kt KT t =+≥实验一 二阶系统阶跃响应(验证性实验)一、实验目的研究二阶系统的两个重要参数阻尼比ξ和无阻尼自然频率n ω对系统动态性能的影响。
(完整word版)中国矿业大学常俊林版《自动控制原理》1-6章课后习题解答汇总
(3)不稳定,右半平面一个根,一对纯虚根
(4)不稳定,右半平面一个根,一对纯虚根
3.7
3.8
3.9
(1)
(2)将 代入闭环特征方程后,整理得
,解得
3.10
加入局部反馈前:开环传递函数 , 。
加入局部反馈后:开环传递函数 , 。
3.11
第一章
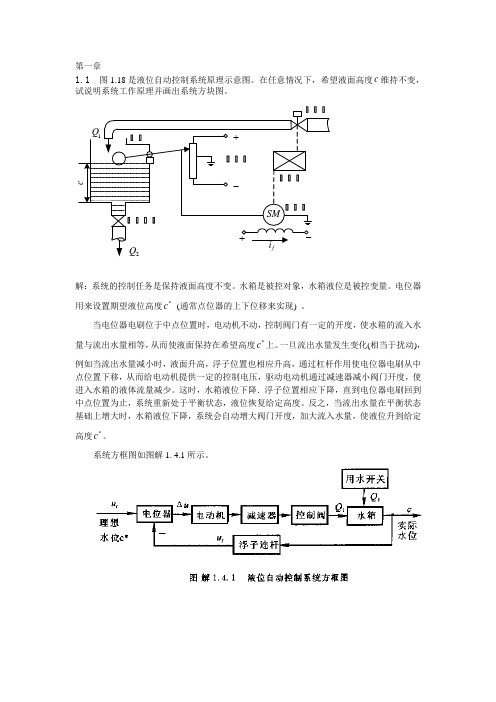
1.1图1.18是液位自动控制系统原理示意图。在任意情况下,希望液面高度 维持不变,试说明系统工作原理并画出系统方块图。
解:系统的控制任务是保持液面高度不变。水箱是被控对象,水箱液位是被控变量。电位器用来设置期望液位高度 (通常点位器的上下位移来实现)。
当电位器电刷位于中点位置时,电动机不动,控制阀门有一定的开度,使水箱的流入水量与流出水量相等,从而使液面保持在希望高度 上。一旦流出水量发生变化(相当于扰动),例如当流出水量减小时,液面升高,浮子位置也相应升高,通过杠杆作用使电位器电刷从中点位置下移,从而给电动机提供一定的控制电压,驱动电动机通过减速器减小阀门开度,使进入水箱的液体流量减少。这时,水箱液位下降.浮子位置相应下降,直到电位器电刷回到中点位置为止,系统重新处于平衡状态,液位恢复给定高度。反之,当流出水量在平衡状态基础上增大时,水箱液位下降,系统会自动增大阀门开度,加大流入水量,使液位升到给定高度 。
系统中,热交换器是被控对象,实际热物料温度为被控变量,冷水流量是干扰量。
系统方框图如图解1.4.4所示。
这是一个按干扰补偿的复合控制系统。
1.5
解带上负载后,由于负载的影响,图(a)与图(b)中的发电机端电压开始时都要下降,但图(a)中所示系统的电压能恢复到110 v,而图(b)中的系统却不能。理由如下;
自动控制原理实验

自动控制原理实验实验一 控制系统的数学模型一、 实验目的1. 熟悉Matlab 的实验环境,掌握Matlab 建立系统数学模型的方法。
2. 学习构成典型环节的模拟电路并掌握典型环节的软件仿真方法。
3. 学习由阶跃响应计算典型环节的传递函数。
二、 实验内容1. 已知图1.1中()G s 和()H s 两方框相对应的微分方程分别是:()610()20()()205()10()dc t c t e t dtdb t b t c t dt+=+=且满足零初始条件,用Matlab 求传递函数()()C s R s 和()()E s R s 。
图1.1 系统结构图2. 构成比例环节、惯性环节、积分环节、比例-积分环节、比例-微分环节和比例-积分-微分环节的模拟电路并用Matlab 仿真;3. 求以上各个环节的单位阶跃响应。
三、 实验原理1. 构成比例环节的模拟电路如图1.2所示,该电路的传递函数为:21().R G s R =-图1.2 比例环节的模拟电路原理图2. 构成惯性环节的模拟电路如图1.3所示,该电路的传递函数为:221(),,.1R KG s K T R C Ts R =-==+图1.2 惯性环节的模拟电路原理图3. 构成积分环节的模拟电路如图1.3所示,该电路的传递函数为:1(),.G s T RC Ts==图1.3 积分环节的模拟电路原理图4. 构成比例-积分环节的模拟电路如图1.4所示,该电路的传递函数为:2211()1,,.R G s K K T R C Ts R ⎛⎫=-+== ⎪⎝⎭图1.4 比例-积分环节的模拟电路原理图5. 构成比例-微分环节的模拟电路如图1.5所示,该电路的传递函数为:221()(1),,.R G s K Ts K T R C R =-+==图1.5 比例-微分环节的模拟电路原理图6. 构成比例-积分-微分环节的模拟电路如图1.6所示,该电路的传递函数为:121211212121121()1(1)()()()()()p d i f p i i ff i f f f f f d f f G s K T s T s R R R R C K R R C T R CT R R C R R C R R R R R R CC T R R C R R C⎛⎫=++ ⎪⎝⎭++=+==+++++=+++图1.6 比例-积分-微分环节的模拟电路原理图四、实验要求1.画出各环节的模拟电路图。
《自动控制原理》实验指导书(正文全)

实验一基于MATLAB实验平台的系统被控对象的建立与转换[说明]一个控制系统主要由被控对象、检测测量装置、控制器和执行器四大部分构成。
用于自控原理实验方面的被控对象可以有①用于实际生产的实际系统的真实被控对象,如进行温度控制的锅炉、进行转速控制的电机等;②用于实验研究的真实被控对象,如进行温度控制的实验用锅炉、进行转速控制的电机等;③用运算放大器等电子器件搭建的电模拟被控对象(电路板形式),它们的数学模型与真实被控对象的数学模型基本一致,而且比真实被控对象更典型,更精准。
它们是实物型原理仿真被控对象。
④计算机仿真的被控对象,它们是非实物型原理仿真被控对象,是以各种形式展现的被控对象的数学模型。
它们通过计算机屏幕展示,或是公式形式的数学算式,或是数字形式的数表、矩阵,或是图形形式的结构框图,或是动画形式的真实被控对象实物的动态图形。
在自控原理实验中,①极少用;②用的不多;③用的较多;④在MATLAB软件广泛使用后,用的较多。
③、④各有其优缺点。
MATLAB软件的应用对提高控制系统的分析、设计和应用水平起着十分重要的作用。
我们的实验采用的是④:采用MATLAB软件平台的计算机仿真的被控对象。
这里“被控对象的建立”,指在MATLAB软件平台上怎样正确表示被控对象的数学模型。
[实验目的]1.了解MATLAB软件的基本特点和功能;2.掌握线性系统被控对象传递函数数学模型在MATLAB环境下的表示方法及转换;3.掌握多环节串联、并联、反馈连接时整体传递函数的求取方法;4.掌握在SIMULINK环境下系统结构图的形成及整体传递函数的求取方法。
[实验指导]一、被控对象模型的建立在线性系统理论中,一般常用的描述系统的数学模型形式有:(1)传递函数模型——有理多项式分式表达式(2)传递函数模型——零极点增益表达式(3)状态空间模型(系统的内部模型)这些模型之间都有着内在的联系,可以相互进行转换。
1、传递函数模型——有理多项式分式表达式设系统的传递函数模型为1110111......)()()(a s a s a s a b s b s b s b s R s C s G n n n n m m m m ++++++++==---- 对线性定常系统,式中s 的系数均为常数,且a n 不等于零。
自动控制原理实验

2014-2015学年第二学期自动控制原理实验报告姓名:王丽学号:20122527班级:交控3班指导教师:周慧实验一:典型系统的瞬态响应和稳定性1. 比例环节的阶跃响应曲线图(1:1)比例环节的阶跃响应曲线图(1:2)2. 积分环节的阶跃响应曲线图(c=1uf)3. 比例积分环节的阶跃响应曲线图(c=1uf)比例积分环节的阶跃响应曲线图(c=2uf)4. 惯性环节的阶跃响应曲线图(c=1uf)惯性环节的阶跃响应曲线图(c=2uf)5. 比例微分环节的阶跃响应曲线图(r=100k)比例微分环节的阶跃响应曲线图(r=200k)6. 比例积分微分环节的阶跃响应曲线图(r=100k)比例积分微分环节的阶跃响应曲线图(r=200k)实验结论1. 积分环节的阶跃响应曲线图可以看出,积分环节有两个明显的特征:(1)输出信号是斜坡信号(2)积分常数越大,达到顶峰需要的时间就越长2. 比例积分环节就是把比例环节与积分环节并联,分别取得结果之后再叠加起来,所以从图像上看,施加了阶跃信号以后,输出信号先有一个乘了系数K的阶跃,之后则逐渐按斜坡形式增加,形式同比例和积分的加和是相同的,因而验证了这一假设。
3. 微分环节对于阶跃信号的响应,在理论上,由于阶跃信号在施加的一瞬间有跳变,造成其微分结果为无穷大,之后阶跃信号不再变化,微分为0,表现为输出信号开始衰减。
4. PID环节同时具备了比例、积分、微分三个环节的特性,输出图像其实也就是三个环节输出特性的叠加。
三个环节在整个系统中的工作实际上是相互独立的,这也与它们是并联关系的事实相符合。
5.惯性环节的传递函数输出函数:可以看到,当t→∞时,r(t)≈Ku(t),这与图中的曲线是匹配的。
实验心得通过本实验我对试验箱更加熟悉,会连接电路;更直观的看到电路的数学模型和电路的响应曲线图三者之间的关系,这让我能够将在此之前所学的知识联系到一起。
不管是什么电路,如果要研究它首先就是得到它的数学模型,然后再通过对数学模型的研究间接的来研究该电路。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验一 MATLAB 仿真基础、实验目的:(1) 熟悉MATLAB 实验环境,掌握MATLAB 命令窗口的基本操作。
(2) 掌握MATLAB 建立控制系统数学模型的命令及模型相互转换的方法。
(3) 掌握使用MATLAB 命令化简模型基本连接的方法。
(4) 学会使用Simulink 模型结构图化简复杂控制系统模型的方法。
二、实验设备和仪器1 •计算机;2. MATLAB 软件三、实验原理函数tf ()来建立控制系统的传递函数模型,用函数printsys ()来输出控制系 统的函数,用函数命令zpk ()来建立系统的零极点增益模型,其函数调用格式 为:sys = zpk( z, p, k 零极点模型转换为多项式模型[num , den] = zp2tf ( z, p, k ) 多项式模型转化为零极点模型[z , p , k] = tf2zp ( num, den )两个环节反馈连接后,其等效传递函数可用 feedback ()函数求得。
则 feedback ()函数调用格式为:sys = feedback (sysl, sys2, sigh其中sign 是反馈极性,sign 缺省时,默认为负反馈,sign = -1;正反馈时, sign = 1;单位反馈时,sys2= 1,且不能省略。
四、实验内容:1. 已知系统传递函数,建立传递函数模型2 2 5(s 2) (s6s 7) 33s(s 1) (s2s 1)2.已知系统传递函数,建立零极点增益模型s 3 飞2~s 2s 2s 13 •将多项式模型转化为零极点模型5(s 2)2(s 2 6s 7)G(s) s 3s 3 2s 22s 1G(s)G(s)4.已知系统前向通道的传递函数G(s)2 s2 5s 1 s2 2s 3反馈通道的传递函数H(s) s 10求负反馈闭环传递函数5、用系统Simulink模型结构图化简控制系统模型已知系统结构图,求系统闭环传递函数。
五、实验过程及结果:1. (1) num=[1 3];de n=[1 2 2 1];pri ntsys( num,de n)num/den 二s + 3s n3 + 2 s*2 + 2 s + 1(2) num=5*c onv(con v([1 2],[1 2]),[1 6 7]);den=conv( conv(conv([1 0],[1 1]),co nv([1 1],[1 1])),[1 0 2 1]);Gs=tf( nu m,de n)Trarsffunc七人口口;5 s 4 + 50 s3 + s 2 十260 s + 140s'7 + 3 s*6 + 5 s'5 4- 8 s'4 4- 9 £*3 + 5 s'2 + s2. k=10;z=[-5];p=[-0.5,-2,-3]; Gs=zpk(z,p,k)Zero/pole/gam:10 (s+5)(s+0» 5) (s+2) (s+3)3. num=[1 ,5,6];den=[1,2,1,0];[z,p,k]=tf2zp(num,den); Gs=zpk(z,p,k)2ero/pole/gain:(s+3) (s+2)s (s+1) A24. numg=[2,5,1];deng=[1,2,3]; numh=[5,10];denh=[1,10];[nu m,de n]=feedback (nu mg,de ng,nu mh,de nh);pri ntsys (nu m,de n) rum/ den 二2 s'3 + 25 s*2 + 51 s + 1011 s'3 + 57『2 + 78 s + 405. (1)用梅森公式求G1=1/(S+1); =5/(s+2);phi=factor(((G1+1)* G2/(1+2*G1+G1*G2));phi =(5*(s + 2))/(s'2 + 5*s + 11)⑵.用simulink结构图模型求传递函数» [九 B. C, D]=linnod C smF),Va^rin^: tfsir^ a default value of 0. 2 foT naxinum st ep size, the siiii'l s+i "m 只十pp si vi1' hp 十n or1 7rn ran disable this di Agnostic by setting J Airtoiat ic solver parameterEelect ion diagnosl ic to ‘ none’ in the Diagnostics paje of tKe confiEiir ail Dr. p^rajieters di aloe> In dJinnod at 1::In Linnizd'Wt 吊g»[nuxj den] =Es2tf B, C, D)print sys (nu^ij d呱 '『)nW伽=6 s + W实验二典型环节动态特性、实验目的:1 •熟悉MATLA桌面和命令窗口,初步了解SIMULINK功能模块的使用方法。
2 •通过观察典型环节在单位阶跃信号作用下的动态特性,加深对各典型环节响应曲线的理解。
3. 定性了解各参数变化对典型环节动态特性的影响。
二、实验设备和仪器1. 计算机;2. MATLAB软件三、实验原理典型环节的概念对系统建模、分析和研究很有用,但应强调典型环节的数学模型是对各种物理系统元、部件的机理和特性高度理想化以后的结果,重要的是,在一定条件下,典型模型的确定能在一定程度上忠实地描述那些元、部件物理过程的本质特征。
各典型环节的传递函数:①比例环节G1(S)=1和G2(S)=2 惯性环节G1(S)=1/(S+1)和G2(S)=1/(0.5S+1) ③积分环节G1(S)=(1/S)和G2(S)=(1/ ( 0.5S ) ④微分环节G1(S)=0.5S 和G2(S)=2S⑤比例微分环节G1(S)=(2+S)和G2(S)=(1+2S) ⑥比例积分环节(PI) G1(S)=(1+1/S)和G2( S) =2 (1+1/2S)四、实验过程启动MATLAB7.0进入Simulink后新建文档,分别在各文档绘制各典型环节的结构框图。
双击各传递函数模块,在出现的对话框内设置相应的参数。
然后点击工具栏的口按钮或simulation菜单下的start命令进行仿真,双击示波器模块观察仿真结果。
在仿真时设置各阶跃输入信号的幅度为1,开始时间为0 (微分环节起始设为0.5,以便于观察)传递函数的参数设置为框图的数中值,自己可以修改为其他数值再仿真观察其响应结果。
实验也可用程序实现得到响应曲线。
1. 比例环节G1(S)=1 和G2(S)=22. 惯性环节G1(S)=1/(S+1)和G2(S)=1/(0.5S+1)3. 积分环节G1(S)=1/S 和G2(S)=1/ (0.5S)■匸I工Inum=[1];den=[1,0]; G=tf(num,den), step(G)4. 微分环节G1(S)=0.5S 和G2(S)=Snum=[1];den=[1]; G=tf(num,den), step(G)num=[1];den=[1,1]; G=tf(num,den), step(G)6上匕例积分:G1 (S ) =1+1/S 和 G2( S ) =2 (1+1/2S )五、实验结果分析:比较前后两个阶跃曲线的区别与联系,作出相应的实验分析结果。
1. 比例环节比例环节的输出量与输入量成正比, 既无输出也无延迟,响应 速度快,因此系统易受外界干扰信号影响,从而导致系统不稳定。
2.惯性环节 惯 性环节使得输出波形在开始时以指数曲线上升,上升速度与时间长是有关,时间 常数越小,上升得越快。
3.积分环节积分环节的输出量反映了输入量随时间 的积累,积分作用随着时间而逐渐增强,其反应速度较比例环节迟缓。
4微分环节微分环节的输出反映了输入信号的变化速度,即微分环节能预示输入信号 的变化趋势,若输入为一定值,则输出为 0.5比例微分环节。
6.比例积分环节 积分和比例一起起作5.比例微分环节: G1(S)=2+S 和 G2(S)=1+2S num=[1];den=[0.5]; G=tf(num,den), step(G)du/dt 2 Derivative GainStep > du/dtDerivative 1 Gain 1Gain 2Add Scope 1 Ql W …9 324 G 6 10Add 1Gain 1num=[1,1];den=[1,0]; G=tf(num,den), step(G)Scope用时的响应速度变化加快,其输出与积分的时间长是有关。
实验三二阶系统阶跃响应一、实验目的1. 研究二阶系统的特征参数,阻尼比Z和无阻尼自然频率3 n对系统动态性能的影响,定量分析Z和3 n与最大超调量c箱口调节时间ts之间的关系。
2. 学会根据系统的阶跃响应曲线确定传递函数3. 学习用MATLA B真软件对实验内容中的电路进行仿真。
二、实验设备和仪器1. 计算机;2. MATLAB^件三、实验原理图3-1欠阻尼二阶系统的单位阶跃响应曲线典型二阶闭环系统的单位阶跃响应分为四种情况:1. 欠阻尼二阶系统如图3-2所示,由稳态和瞬态两部分组成:稳态部分等于1,瞬态部分是振荡衰减的过程,振荡角频率为阻尼振荡角频率,其值由阻尼比Z和自然振荡角频率3 n决定。
(1)性能指标:调节时间tS:单位阶跃响应C(t)进人土5%有时也取土2%误差带,并且不再超出该误差带的最小时间。
超调量c % ;单位阶跃响应中最大超出量与稳态值之比。
峰值时间tP :单位阶跃响应C(t)超过稳态值达到第一个峰值所需要的时间。
结构参数E:直接影响单位阶跃响应性能。
(2)平稳性:阻尼比E越小,平稳性越差(3)快速性:E过小时因振荡强烈,衰减缓慢,调节时间tS长,三过大时,系统响应迟钝,调节时间tS也长,快速性差。
0.7调节时间最短,快速性最好。
0.7时超调量c %<% ,平稳性也好,故称0.7为最佳阻尼比。
2. 临界阻尼二阶系统仁=1)系统有两个相同的负实根,临界阻尼二阶系统单位阶跃响应是无超调的,无振荡单调上升的,不存在稳态误差。
3. 无阻尼二阶系统仁二0时)此时系统有两个纯虚根,单位阶跃响应是等幅振荡的,系统不稳定。
4. 过阻尼二阶系统(E >1)时此时系统有两个不相等的负实根,过阻尼二阶系统的单位阶跃响应无振荡无超调无稳态误差,上升速度由小加大有一拐点。
