抽样信号与抽样定理
信号抽样与抽样定理

− nω
s
)
F (ω − n ω
)
矩形脉冲抽样——频谱结构 二. 矩形脉冲抽样 频谱结构
转 化
f (t )
FT
乘
0
1
0
.exe .exe
t
P (t )
τ
FT
− 2π
P (ω ) Eτω s
τ
2π
ω
卷
0
Ts
t
FT
−ωs
0
f s (t )
Fs (ω )
Eτ Ts
ωs
τ
ω
t
0
−
2π
2π
τ
−ωs
)
三.冲激抽样——频谱结构 冲激抽样 频谱结构
f (t )
0
FT
P (t )
∞
1
0
p (ω ) = ω s
∞
F (ω )
t
n=−∞
(1)
0
δT (t) = ∑δ (t − nTs )
FT
(ω s )
−ωs
0
n = −∞
∑ δ (ω − nω
ω
s
)
Ts
t
相 乘 相 卷
FT
ω ω
s
f s (t )
1 Ts
1 Ts
0
抽样频率
F1 (ω )
ωs<2 ωm
f (t)
0
− ωs
0
1 Ts
ω ωs F1 (ω )
ωs=2 ωm
Ts
t
ω s = 2ω m
− ωs
0
ωs ω
Nyquist,美国物理学家 , 1889 , 美国物理学家, 年出生在瑞典。 年在Texas 年出生在瑞典 。 1976年在 Texas 逝 年在 Texas逝 他对信息论做出了重大贡献。 世。他对信息论做出了重大贡献。 1907年移民到美国并于 年移民到美国并于1912年进入 年移民到美国并于 年进入 北达克塔大学学习。 北达克塔大学学习。1917年在耶鲁 年在耶鲁 要想抽样后能够不失真的还原出原信号,则抽 ~ 大学获得物理学博士学位。 大学获得物理学博士学位。1917~ 1934年在 年在AT&T公司工作 公司工作, 年在 公司工作 样频率必须大于两倍信号谱的最高频率。,后转入 Bell电话实验室工作 电话实验室工作。 Bell电话实验室工作。
实验四抽样定理
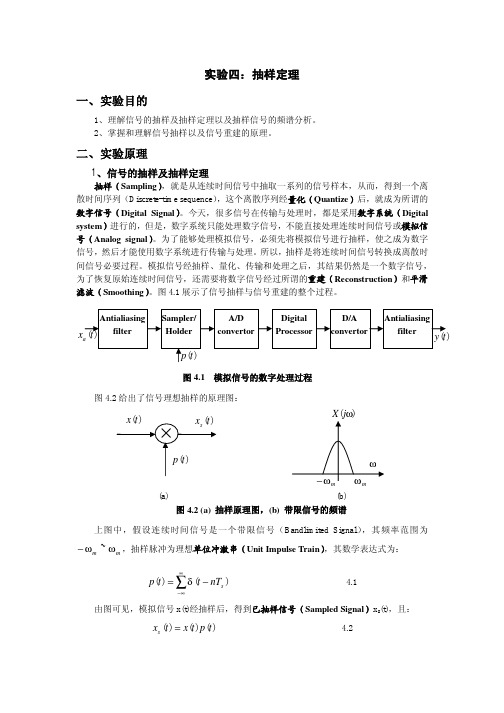
如果满足抽样定理,那么,我们就可以唯一地由已抽样信号 x[n] 恢复出原连续时间信 号 x(t)。在理想情况下,可以将离散时间序列通过一个理想低通滤波器,图 4.6 给出了理想 情况下信号重建的原理示意图。
⊗ x(t)
x p (t) Ideal Lowpass
Filter
p(t)
xr (t)
X = X + x*exp(-j*t'*(w-k*ws))*dt; end subplot(222)
plot(w,abs(Xa)) title('Magnitude spectrum of x(t)'), grid on axis([-60,60,0,1.8*max(abs(Xa))]) subplot(224) plot(w,abs(X)) title('Magnitude spectrum of x[n]'), xlabel('Frequency in radians/s'),grid on axis([-60,60,0,1.8*max(abs(Xa))]) 本程序可以用来观察在不同的抽样频率条件下,已抽样信号的频谱的混叠程度,从而更 加牢固地理解抽样定理。但是,提请注意的是,在 for 循环程序段中,计算已抽样信号的频 谱 X 时,没有乘以系数 1/Ts,是为了便于比较 X 与 Xa 之间的区别,从而方便观察频谱的 混叠程度。另外,程序中的时间步长 dt 的选择应该与抽样周期 Ts 保持一定的比例关系,建 议 Ts 不应小于 10dt,否则,计算得到的已抽样信号的频谱将出现错误。
−∞
显然,已抽样信号 xs(t) 也是一个冲激串,只是这个冲激串的冲激强度被 x(nTs) 加权了。 从频域上来看,p(t) 的频谱也是冲激序列,且为:
《信号与系统实验》信号的采样与恢复(抽样定理)实验

《信号与系统实验》信号的采样与恢复(抽样定理)实验一、实验目的1、了解电信号的采样方法与过程以及信号恢复的方法。
2、验证抽样定理。
二、实验设备1、信号与系统实验箱2、双踪示波器三、原理说明1、离散时间信号可以从离散信号源获得,也可以从连续时间信号抽样而得。
抽样信号f s(t)可以看成连续f(t)和一组开关函数s (t)的乘积。
s (t)是一组周期性窄脉冲,见实验图5-1,T s(t)称为抽样周期,其倒数f s(t)= 1/T s称为抽样频率。
图5-1 矩形抽样脉冲对抽样信号进行傅立叶分析可知,抽样信号的频率包括了原连续信号以及无限个经过平移的信号频率。
平移的频率等于抽样频率f s(t)及其谐波频率2f s、3f s》》》》》》。
当抽样信号是周期性窄脉冲时,平移后的频率幅度(sinx)/x规律衰减。
抽样信号的频谱是原信号频谱周期的延拓,它占有的频带要比原信号频谱宽得多。
2、正如测得了足够的实验数据以后,我们可以在坐标纸上把一系列数据点连起来,得到一条光滑的曲线一样,抽样信号在一定条件下也可以恢复到原信号。
只要用一截止频率等于原信号频谱中最高频率f n的低通滤波器,滤除高频分量,经滤波后得到的信号包含了原信号频谱的全部内容,故在低通滤波器输出可以得到恢复后的原信号。
3、但原信号得以恢复的条件是f s 2,其中f s为抽样频率,为原信号占有的频带宽度。
而f min=2 为最低抽样频率又称“柰奎斯特抽样率”。
当f s<2 时,抽样信号的频谱会发生混迭,从发生混迭后的频谱中我们无法用低通滤波器获得原信号频谱的全部内容。
在实际使用中,仅包含有限频率的信号是及少的,因此即使f s=2 ,恢复后的信号失真还是难免的。
图5-2画出了当抽样频率f s>2 (不混叠时)f s<2 (混叠时)两种情况下冲激抽样信号的频谱。
t f(t)0F()t 0m ωm ω-(a)连续信号的频谱Ts t 0f s (t)F()t0m ωm ω-s ω-s ω()(b)高抽样频率时的抽样信号及频谱 不混叠图5-2 冲激抽样信号的频谱实验中f s >2 、f s =2 、f s <2 三种抽样频率对连续信号进行抽样,以验证抽样定理——要使信号采样后能不失真地还原,抽样频率f s 必须大于信号频率中最高频率的两倍。
信号与系统中抽样的概念

信号与系统中抽样的概念抽样是信号与系统中一个重要的概念。
在信号处理中,抽样是指对连续时间信号进行离散化处理,将连续时间信号转换为离散时间信号的过程。
抽样的目的是为了将连续时间信号转换为数字信号,使得信号可以通过数字方式进行存储、传输和处理。
抽样过程可以看作是在连续时间域上对信号进行定时取样。
抽样过程中,我们使用采样定理(奈奎斯特定理)来保证抽样后的信号不失真。
采样定理指出,为了避免信号采样引起的混叠现象,抽样频率必须大于等于原始信号中最高频率的两倍,也就是满足奈奎斯特频率。
在实际应用中,我们通常采用理想脉冲序列作为采样信号。
理想脉冲序列是一个周期为T的序列,每个周期内有一个脉冲,其他时间点上为零。
理想脉冲序列的傅里叶变换是一个周期序列(频率为1/T)的线性组合。
对连续时间信号x(t)进行抽样,可以通过将x(t)与理想脉冲序列进行卷积来实现。
即将x(t)乘以理想脉冲序列,然后对乘积信号进行积分。
抽样后得到的信号为离散时间信号x[n],其中n为整数,表示采样时刻。
离散时间信号x[n]可以看作是连续时间信号x(t)在采样时刻的取样值。
为了重构x(t),可以通过将x[n]与插值函数进行卷积来实现。
插值函数可以看作是理想脉冲序列的反变换,即将理想脉冲序列的傅里叶变换除以周期序列的傅里叶变换。
抽样引入了两个重要的参数,即采样间隔和采样频率。
采样间隔为采样时刻之间的时间间隔,采样频率为采样时刻之间的倒数,即采样频率等于1/采样间隔。
采样频率越高,采样精度越高,重构信号的失真越小。
但是,采样频率过高也会导致计算和存储的需求增加。
抽样过程中,还存在一个概念叫做抽样定理。
抽样定理指出,在有限频带B内的连续时间信号,可以通过以准确率误差小于ε的方式进行采样和重构,只需要满足采样频率f_s大于等于2B。
这是由带限信号在频域中没有重叠而导致的。
如果信号的频域存在重叠,则需要进一步提高采样频率以避免混叠现象。
在实际应用中,我们使用的信号不一定是有限频带的信号,因此在抽样过程中,可能会引入混叠现象。
信号抽样原理

信号抽样原理
在信号处理中,抽样是指采集连续信号在一定时间间隔内的离散样本。
抽样原理基于奈奎斯特-香农采样定理,该定理表明
如果信号的最高频率为fmax,那么采样频率fs必须大于
2*fmax,才能保证采样后的离散信号能够完整还原原始信号。
抽样过程中,采样器将原始信号在不同时刻的幅度值进行测量,并将这些测量值进行离散化,得到离散信号序列。
这些样本点可以用来表示原始信号的近似形式,从而方便后续的处理和传输。
通常,采样过程可以用以下步骤描述:
1. 确定采样频率fs:根据信号的最高频率fmax,确定一个采
样频率fs,使得fs > 2*fmax。
这样做可以避免信号的频谱出
现混叠现象,即高频成分被错误地映射到低频区域。
2. 进行采样:在确定了采样频率后,采样器以固定时间间隔取样信号。
每个样本点对应于一个特定的时间,采集信号在该时刻的幅度值。
采样过程可以使用模拟-数字转换器(ADC)完成。
3. 离散化:将连续的采样信号转换为离散的信号序列。
这可以通过将每个采样点的幅度值用数字表示来实现。
离散化可以使用数字信号处理器(DSP)或其他离散化设备来完成。
4. 重构原始信号:通过插值或其他方法,使用离散信号序列重建原始信号。
重建后的信号能够以较高的精度近似原始信号,
使得后续的信号处理过程更加有效和准确。
通过抽样原理,连续信号可以被转换为离散信号进行处理和传输,从而在数字系统中实现各种信号处理算法和技术。
诸如音频、视频等多媒体数据的数字化处理都离不开抽样原理的应用。
§3.6--信号抽样与抽样定理(信号抽样-时域抽样定理-连续时间信号的重建--)

所以抽样信号的频谱为
其中, 为抽样角频率, 为抽样间隔 , 为抽样频率,
在时域抽样(离散化)相当于频域周期化
频谱是原连续信号的频谱以抽样角频率为间隔周期地延拓,频谱幅度受抽样脉冲序列的傅立叶系数加权。
(1) 冲激抽样若抽样脉冲是冲激序列,则这种抽样称为冲激抽样或理想抽样。
谢谢大家
二、时域抽样定理
二、时域抽样定理
时域抽样定理的图解:假定信号 f (t)的频谱只占据 的范围,若以间隔 对 f (t)进行抽样,抽样信号 fs (t)的频谱 FS(ω) 是以 ωS 为周期重复,在此情况下,只有满足条件 各频移的频谱才不会相互重叠。这样,抽样信号 fs (t) 保留了原连续信号f (t)的全部信息,完全可以用 fs (t) 唯一地表示 f (t) ,或者说, f (t)完全可以由恢复出 fs (t) 。
§ 3.6 信号抽样与抽样定理
信号抽样也称为取样或采样,是利用抽样脉冲序列 p (t) 从连续信号 f (t) 中抽取一系列的离散样值,通过抽样过程得到的离散样值信号称为抽样信号,用 fs (t) 表示。
一、信号抽样
抽样的原理方框图:
一、信号抽样
连续信号经抽样后变成抽样信号,往往还需要再经量化、编码等步骤变成数字信号。这种数字信号经传输、处理等步骤后,再经过上述过程的逆过程就可连续信号频谱在周期重复过程中,各频移的频谱将相互重叠,就不能从抽样信号中恢复原连续信号。频谱重叠的这种现象称为频率混叠现象。
二、时域抽样定理
在满足抽样定理的条件下,可用一截止频率为 的理想低通滤波器,即可从抽样信号 fs(t) 中无失真恢复原连续信号 f (t) 。
三、连续时间信号的重建
因为所以,选理想低通滤波器的频率特性为若选定 ,则有理想低通滤波器的冲激响应为若选 ,则而冲激抽样信号为
信号抽样与抽样定理

解:信号在时域抽样、周期化过程中频谱的变化规律:
(1)信号在时域周期化,周期为 T ,则频谱离散化,
抽样间隔为 ω0=2π/T。 (2)信号在时域抽样,抽样间隔为 TS ,则频谱周期化,
重复周期为 ωS=2π/TS 。
信号与系统
四、频域抽样与频域抽样定理
矩形单脉冲信号的频谱 F ( ) E Sa 0
1 s n
0 E
Ts
n0 Sa 2 m
( ns m0 )
信号与系统
四、频域抽样与频域抽样定理
f 0 t
E
2
E
F0 ( )
0
a
E
2
t
2
0
2
f1 t
b
F1
E 0
T
唯一地表示,抽样间隔为 s ,它必须满足条件 T
s
2tm ,其中 Ts
s 2
信号与系统
四、频域抽样与频域抽样定理
例: 大致画出图所示周期矩形信号冲激抽样后信号的频谱。
f1 (t )
E
T
0
2
T
2
t
f s (t )
E
T
0
2
T
2
t
信号与系统
四、频域抽样与频域抽样定理
2. 在什么条件下可从抽样信号 fs (t)中无失真地恢复原连
续信号 f (t) 。
信号与系统
一、信号抽样
假设原连续信号 f (t)的频谱为 F(ω),即
f (t ) F ( )
抽样脉冲 p (t) 是一个周期信号,它的频谱为
第6章采样频谱及采样定理

∫
∞
1n H ( jω ) 1+ω
2
−∞
dω < ∞
PT s (t ) =
n = −∞
s
∑ g(t − nT )
r s
P T (t)
∞
1
-Ts -τ oτ 2 2
Ts
t
图 5.1-2 抽样脉冲序列PTs(t)
f s (t ) = f (t ) ⋅ PTs (t )
2πτ PTs (t ) ↔ Ts
1 F [ f s (t )] = 2π
nΩτ ∑ Sa 2 n = −∞
1.周期矩形脉冲抽样 周期矩形脉冲抽样 图 5.1-1 所示的抽样原理从理论上分析可表述为f(t)与抽 样脉冲序列PTs(t)的乘积,即
f s (t ) = f (t ) ⋅ PT s (t )
f (t) f (t) fs(t) fs(t)
抽样器 o t
图 5.1-1 信号的抽样
o T s
t
式中的抽样脉冲序列PTs如图 5.1-2 所示。它实际上就是周期 矩形脉冲函数,可表示为
Fs (ω ) =
n =−∞ +∞
2π )对 f (t ) 进行抽样, 则抽样后, 信号 f s (t ) 的频谱 Fs (ω ) 是 F (ω ) Ts
∑ c F (ω − nω )
n s
(5.2-1)
在此情况下,只有满足 ωs ≥ 2ωm 的抽样定理条件, Fs (ω ) 才不会产生频谱的混叠,如图 5.2-1(b)所示。 这样,如果将 Fs (ω ) 通过理想低通滤波器,就可以从 Fs (ω ) 中恢复出 F (ω ) 。也就是说,抽样信号 f s (t ) 保留了 原连续信号 f (t ) 的全部信息,完全可以用 f s (t ) 唯一地表示 f (t ) 。如果 ωs < 2ωm ,此时不满足抽样定理条件, Fs (ω ) 将产生频谱的混迭,如图 5.2-1(c)所示,此时将不能从 Fs (ω ) 中恢复出 F (ω ) ,也即不能完全用 f s (t ) 唯 一地表示 f (t ) 。这就是说,取样的时间间隔过长,即取样速率太慢,将会造成信息丢失。 通过上面的讨论可见,为了使抽样信号 f s (t ) 保留原信号 f (t ) 的全部信息,要求 f s (t ) 的频谱 Fs (ω ) 不产 生混迭现象,此时必须满足 (5.2-2a) ωs ≥ 2ωm 即 ωs = 2π f s ≥ 2ωm = 2 × 2π f m (5.2-2b) 所以
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
理想抽样
1 F ) F ( n s( s) T sn
非理想抽样
p ( t ) ( t ) ( t nT ) T s
n
p ( t) G t nT ( s)
n
p ( ) ( n s s)
n
由频域卷积定理得,时域相乘的傅立叶变换等于它 们的频谱在频域里相卷积。 1 F ( w ) F ( w ) P ( w ) s 2 把计算出的P(w)代入上式得:
抽样性 周期
信号在时域被抽样后,它的频谱Fs(w)是连续 信号的频谱F(w)以抽样频率Ws为间隔周期地重复 而得到的。在重复过程中,幅度被抽样脉冲p(t)的 傅立叶系数所加权,加权系数取决于抽样脉冲序列 的形状。
时域理想抽样的傅立叶变换
f (t )
F()
FT
FT
相乘
1 F ) F ( n s( s) T sn
1 2
相卷积
T(t) (t nT s)
n
FT
p ( ) ( n s s)
n
n 1 E jn t s s P p ( t ) e dt Sa n T T 2 s
连续
抽样 还原(有条件)
离散
自然抽样 (矩形抽样)
时域 理想抽样 (冲激抽样)
抽样 频域 平顶抽样
低通
带通(3-42)
二. 时域 抽样
抽样过程可以看成由原信号f(t)和一个开关函数p(t) 的乘积来描述。 fs( t ) f( t ) p ( t )
时域抽样简图
连续信 号f(t) 抽样脉冲
抽样信号 fs(t)
T s 2 T s s 2
关于非理想抽样
n E s F ( ) Sa F ( n ) s s T 2 sn
1 p ( ) 2 P ( n ( ) F ( ) * p ( ) n s) F s n 2
F (w )
1
F ) s(w
E w s
- w m
w m
w
抽 样 后 频 谱
w w m w s
抽 样 前 频 谱
由以上推导可知,当抽样脉冲为矩形抽样脉冲时, 幅度以Sa函数的规律变化。从Fs(w)的频谱图可见 抽样后的信号频谱包括有原信号的频谱以及无限个 经过平移的原信号的频谱,平移的频率为抽样频率 及其各次谐波频率。且平移后的频谱幅值随频率而 呈Sa函数分布。但因矩形脉冲占空系数很小,所 以其频谱所占的频带几乎是无限宽的。
量化 编码
数字信号
1)矩形脉冲的抽样(自然抽样) 此时的抽样脉冲p(t)是矩形。由于fs(t)=f(t)p(t) 抽样信号在抽样期间脉冲顶部随f(t)变化,故这种 采样称为“自然抽样”。
*抽样信号频谱推导:
令模拟带限信号傅立叶变换为F(w).即f(t)F(w)
抽样脉冲序列的傅立叶变换为p(t) P(w) 设抽样为均匀抽样,周期为Ts,则抽样频率为 由于p(t)是周期信号,可知p(t)的傅立叶变换为: 其中
1 F w ) F ( w nw s( s) T s
上式表明:由于冲激序列的傅立叶系数Pn为常数, 所以F(w)是以ws为周期等幅地重复,如下图所示:
F(w) Fs(w) 1/Ts
-wm
wm
w
-ws
ws
w
抽样前信号频谱
抽样后信号频谱
下面对矩形脉冲抽样和冲激抽样进行比较和 小结:
p ( ) 2 P ( n n s)
n
Pn
1 Ts
E n s P Sa n T 2 s
1 F ( ) F ( ) * p ( ) s 2
1 F ( ) F ( ) * p ( ) s 2
2 w fs s 2 T s
n 1 E jnw t s s s
T s 2 T s s 2
p ( w ) 2 P ( w nw n s)
n
nw E s F ( w ) Sa ( ) F ( w nw ) s s T 2 sn 上式表明:
(2)通过冲激抽样的方法在数字信号处理中有着广泛的应用。 (点抽样;均匀抽样)
2)冲激抽样
若抽样脉冲是冲激序列,此时称为“冲激抽样” 或“理想抽样”。设Ts为抽样间隔,则抽样脉冲为
p ( t ) ( t ) ( t nT T s)
由于T(t)的傅立叶系数为: T s 1 2 1 jn t w s P ( t ) e dt T n T s T T s s 2 所以冲激抽样信号的频谱为:
数 字
语 音 信 号 输 出
语 音
信 号 输 入
A/D
pulse code modulation(PCM)
DCM
时域抽样简图:
连续信 号f(t) 抽样脉冲
抽样信号 fs(t)
量化 编码
数字信号
问题:
1)抽样后离散信号的频谱是什么样的?它与 未被抽样的连续信号的频谱有什么关系? 2)连续信号被抽样后,是否保留了原信号的 所有信息?即在什么条件下,可以从抽样的 信号还原成原始信号?
§3.10~3.11抽样信号与抽样定理
*时间抽样与空间抽样的实例演示
模 拟 信 号 输 入
A/ D 转换器
数字信号 处理器
模 拟 信 号 输
D/ A 转换器
出
数字信号处理系统简单框图
一.抽样的目的及所遇到的问题
模 拟
目的 : 模拟信号变成 比特流的数字 信号
反混迭失真
滤波器 取 样 量 化 码 化 器
* 抽样率的选择 s m m
s 2 m
结语:抽样率必须选得大于信号频谱最高频率的两倍。
若 0时 矩 形 脉 冲 冲 激 信 号
表示为一系列的冲激函 数:
(1)如果抽样脉冲宽度与系统中各时间常数相比十分小的时 候,这个冲激函数的假定将是一个很好的近似,它将使分 析简化。
