§3-8 抽样信号的傅里叶变换与抽样定理
§3.10-抽样信号的傅里叶变换

1.矩形脉冲抽样
第 3
页
(1)抽样信号
f(t)
连 续 信 号 f t
抽样信号
fs t
o
t
p(t)
抽样脉冲
pt
o TS
t
连续:信f号 t
抽样脉冲 : p序 t 列
fS(t)
抽样 : fst信 ftp 号 t o TS
t
X
频谱关系 连续:信 ft号 ;
第 4 页
f t F ( m m )
抽样脉冲:序 pt列 pt P,
限带
信号
抽样:信 fst号
fst F s
fstftpt Fs21πFP
•越小,越能反刻 映之 离, 值 散从 时信号传输, 角
更关f心 st中有无 ft的全部信息,必 fst须 的考 频虑
谱结构。
X
第
抽样信号的频谱结构
5 页
F sF ftpt2 1 πF P
pt P2πP nns n
Ts
o m
事 业 单 位 人员 进行2017年 度 个人的 意义在 于使事 业单位 人员不 断提升 自身的 政 治 素 养 、 业务水 平和综 合能力 。以下 是小编 为大家 精心整 理的事 业单位 人员 2017年 度 , 欢 迎 大 家阅读 。 事 业 单 位 人员 2017年 度个人 工作总 结一在 局领导 和 部 门 领 导 的正确 带领下 ,与同 事们的 齐心协 力、共 同努力 、大力 支持与 密切配 合 下 , 使 我 的工作 取得了 一定的 成绩。 对于不 利于团 结的话 不说, 不力于 工作的 事 不 做 , 对 于违法 的事坚 决不干 。现将 一年来 的工作 总结如 下: 一 、 学 习方 面 深 入 学 习科 学发展 观,并 且认真 学习邓 小平理 论和三 个代表 重要思 想、中 央 新 疆 工 作 座谈会 精神, 全面提 高了自 己的思 想道德 素质和 科学文 化素质 ;全心全 意 为 局 里 的 大事小 事服务 、处处 事事以 集体利 益为重 ,增强 了责任 感和自 觉性。 在 工 作 中 , 通过学 习和实 践科学 发展观 ,以及 相关业 务知识 ,不断 提高自 己的综 合 素质。 二 、工作 方面 1、电 话方面 :对待 上级部 门的来 电,问 清什么 事, 什 么 要 求 , 及时向 领导汇 报。对 待北京 的来电 ,问清 什么事 ,都是 让他们 通过
抽样定理
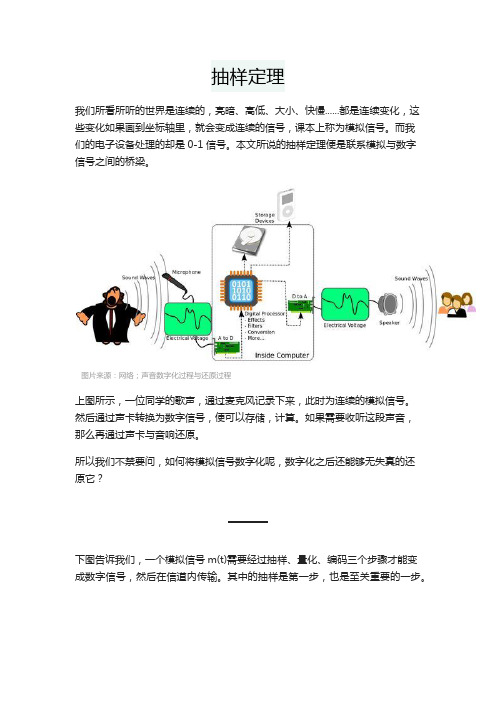
抽样定理我们所看所听的世界是连续的,亮暗、高低、大小、快慢......都是连续变化,这些变化如果画到坐标轴里,就会变成连续的信号,课本上称为模拟信号。
而我们的电子设备处理的却是0-1信号。
本文所说的抽样定理便是联系模拟与数字信号之间的桥梁。
图片来源:网络;声音数字化过程与还原过程上图所示,一位同学的歌声,通过麦克风记录下来,此时为连续的模拟信号。
然后通过声卡转换为数字信号,便可以存储,计算。
如果需要收听这段声音,那么再通过声卡与音响还原。
所以我们不禁要问,如何将模拟信号数字化呢,数字化之后还能够无失真的还原它?下图告诉我们,一个模拟信号m(t)需要经过抽样、量化、编码三个步骤才能变成数字信号,然后在信道内传输。
其中的抽样是第一步,也是至关重要的一步。
图片来源:网络;模拟信号数字化如果让小朋友来解决这个问题,他们也会想到,对于一个连续的曲线,我在其中抽出一定的点来,这些点不就变成了离散的信号了吗?然后我们再量化编码变成数字信号。
没错,我们本文要说的就是,怎么抽样,按照什么样的频率进行?图片来源:网络;对模拟信号“筛选”冲激抽样之前我们学习过冲激函数,我们用冲激函数去乘以函数f(t),会得到冲激处的函数值,我们当时称之为“筛选”特性,没错,这个就是抽样。
假设函数为f(t),抽样函数为p(t)为周期冲激函数,现在用p(t)对f(t)进行抽样,得出的抽样结果为fs(t)。
这三个函数的频域表达式分别为F(w),P(w),Fs(w)。
信号f(t)的傅里叶变换为F(w),最大频率为Wm。
抽样函数p(t)的傅里叶系数为Pn,傅里叶变换为P(w),那么fs(t)=f(t)*p(t),其傅里叶变换为Fs(w)。
在这种情况下抽样信号fs(t)是由一系列冲激函数构成,每个冲激的间隔为Ts而强度等于连续信号的抽样值f(nTs),如上图所示。
周期信号的傅里叶变换我们用周期冲激信号去抽样原始的信号?那么周期间隔Ts如何确定?如果间隔太大,看起来会丢失太多的信息;如果间隔太小,是不是信息又有点冗余了?抽样频率选择稀疏点?还是密集些呢?时域抽样定理一个频率受限的信号f(t),如果频谱只占据-W m~Wm的范围,则信号f(t)可以用等间隔的抽样值唯一的的表示。
抽样信号的傅里叶变换与序列的傅里叶变换探讨

摘
要 : 抽样 信 号 的傅 里 叶 变换 与序 列 的傅 里 叶 变 换二 者之 间 的 关 系进 行 了探 讨 。 对
关 键 词 : 里 叶 变换 ; 样 信 号 ; 列 傅 抽 序 中 图分 类 号 : N l . T 91 7 文 献标 识 码 : A 中 文 章 编 号 :0 8 7 5 (0 2 0 — 1 7 0 10 — 3 4 2 1 }1 0 6 — 2
’●1
l
D  ̄ [ ( ) ( ) T xn ] =
n : ∞
( )e ( ) n・ 1
讨 设 )为连 续 时间 信号 , t为周 期 性抽 样 脉 冲信 ft ( P()
号 。 进 行 理 论 分 析 的 时 候 , 常选 定 周 期 冲 激 信 号 8() 在 通 ,t 作 为 P() 此 处 ,r ) 8 tn , 整 数 (= , l 2 t( 8( = t ( )n取 — n 0± , , ±
熊文 杰 王 勉 z 邝 先 飞 。
(. 山 师范 学 院 物理 与 电子 工程 系 , 东 1 韩 广 潮州 5 14 ;. 西 现 代 职业 技 术 学 院 , 2 0 12 江 江西 304 ) 30 5 南昌 30 9 ;. 西农 业 大 3 0 53江 学理学院 . 江西 南 昌
1 离 散 时 间信 号 一 序 列
(: ∑F 一 ) ( (n 2 ) 孕 J 1 )
n ∞ 1
式() 31 2为 .O节 中给出的(一 O ) 。显然 , 3 l 2式 不能 直观
地 看 出式 ( 与 式 () 间 有什 么联 系 。 1 ) 2 之
4 二 者 之 间的 联 系
利 用傅里 叶变换 的定义 , 激抽样信 号 冲
抽样定理

抽样定理定义:在一个频带限制在(0,f h)内的时间连续信号f(t),如果以1/2 f h的时间间隔对它进行抽样,那么根据这些抽样值就能完全恢复原信号。
或者说,如果一个连续信号f(t)的频谱中最高频率不超过f h,当抽样频率f S≥2 f h时,抽样后的信号就包含原连续的全部信息。
抽样定理在实际应用中应注意在抽样前后模拟信号进行滤波,把高于二分之一抽样频率的频率滤掉。
这是抽样中必不可少的步骤。
07年的抽样定理:设时间连续信号f(t),其最高截止频率为f m ,如果用时间间隔为T<=1/2f m的开关信号对f(t)进行抽样时,则f(t)就可被样值信号唯一地表示。
什么是A/D转换和D/A转换?什么是A/D转换和D/A转换?一。
什么是a/d.d/a转换:随着数字技术,特别是信息技术的飞速发展与普及,在现代控制。
通信及检测等领域,为了提高系统的性能指标,对信号的处理广泛采用了数字计算机技术。
由于系统的实际对象往往都是一些模拟量(如温度。
压力。
位移。
图像等),要使计算机或数字仪表能识别。
处理这些信号,必须首先将这些模拟信号转换成数字信号;而经计算机分析。
处理后输出的数字量也往往需要将其转换为相应模拟信号才能为执行机构所接受。
这样,就需要一种能在模拟信号与数字信号之间起桥梁作用的电路-模数和数模转换器。
将模拟信号转换成数字信号的电路,称为模数转换器(简称a/d转换器或adc,analog to digital converter);将数字信号转换为模拟信号的电路称为数模转换器(简称d/a转换器或dac,digital to analog converter);a/d转换器和d/a转换器已成为信息系统中不可缺俚慕涌诘缏贰?br>为确保系统处理结果的精确度,a/d转换器和d/a转换器必须具有足够的转换精度;如果要实现快速变化信号的实时控制与检测,a/d与d/a转换器还要求具有较高的转换速度。
转换精度与转换速度是衡量a/d与d/a转换器的重要技术指标。
信号抽样与抽样定理

(1)信号在时域周期化,周期为 T ,则频谱离散化,
抽样间隔为 ω0=2π/T。 (2)信号在时域抽样,抽样间隔为 TS ,则频谱周期化,
重复周期为 ωS=2π/TS 。
四、频域抽样与频域抽样定理
矩形单脉冲信号的频谱 F ( ) E Sa 0
2
m0 Sa 2 m
( ns m0 )
四、频域抽样与频域抽样定理
f 0 t
E
F0 ( )
E
2
0
a
E
2
t
2
0
2
f1 t
b
F1
E 0
T 0
2
T
c
E
2
t
2
0
2
d
f s t
E 0 Ts
T
Fs
二、时域抽样定理
时域抽样定理:一个频谱受限的信号 f (t) ,如果频谱只占据 , m m
的范围,则信号 f (t)可以用等间隔的抽样值
样间隔 Ts 不大于 2f
1
m
f (nTs ) 唯一地表示,只要抽
,其中 f m为信号的最高频率,
或者说,抽样频率 f s 满足条件
通常把满足抽样定理要求的最低抽样频率 f s 2 f m 称为奈奎斯特频率, 1 1 把最大允许的抽样间隔 Ts 称为奈奎斯特间隔 。 fs 2 fm
如何从抽样信号中恢复原连续信号,以及在什么条件下才可以无失
真地由抽样信号恢复原连续信号。著名的抽样定理对此作了明确而精 辟的回答。
抽样定理在通信系统、信息传输理论、数字信号处理等方面占有十 分重要的地位,该定理在连续时间信号与系统和离散时间信号与系统、 数字信号与系统之间架起了一座桥梁。该定理从理论上回答了为什么 可以用数字信号处理手段解决连续时间信号与系统问题。
抽样定理简介

出在一根模拟传输线上传输信号时,当抽样率大于一定值后, 可以近乎无失真地还原信号。
Kotelnikov(科捷利尼科夫)第一个证明了低通信号和带通信 号的抽样定理。
H.Raabe在博士论文中阐述了抽样定理,后被Bennet引用
1948年
Shanno(香农)引用了Bennet论文,并总结,从而被广泛接 受。同期的Someya(日本人)在《信号传输》中阐述了抽样 定理,所有也叫Someya抽样定理。
物联网技术基础知识系列 ——抽样定理简介
Dr. SHEN
连续信号的抽样定理
模拟 信号
A/D D/A
数字 信号
问题1
采样(抽样):将连续信号转换为离散信号,便于采 用数字系统进行处理.连续信号被取样后,是否保 留了原信号的所有信息?即在什么条件下,可以从 取样的信号还原出原始信号?
函数插值重建
采样信号
冲激函数序列在实际中无法取得,实际中,采用周期 脉冲抽样,其抽样结果为
fs (t) f (t) PTs (t)
下面分析 fs (t) 中是否包含 f (t) 的全部信息
PTs
(t)
2
Ts
n
Sa
ns
2
(
ns )
F[
fs (t)]
1
2
F
f
(t) F PTs
(t)
F[
fs (t)]
1
2
F (
域
域
抽
周
样
Ts
相
s
卷
s
期 重
复
乘
积
信号恢复
fs (t)
fs (t) 理想低通 f (t)
滤波器h(t)
f (t)
抽样定理
抽样定理词义就是对时间连续的信号隔一定的时间间隔T抽取一个瞬时幅度值分类时域抽样定理、频域抽样定理基本定义所谓抽样,就是对时间连续的信号隔一定的时间间隔T 抽取一个瞬时幅度值(样值),抽样是由抽样门完成的。
在一个频带限制在(0,f h)内的时间连续信号f(t),如果以小于等于1/(2 f h)的时间间隔对它进行抽样,那么根据这些抽样值就能完全恢复原信号。
或者说,如果一个连续信号f(t)的频谱中最高频率不超过f h,这种信号必定是个周期性的信号,当抽样频率f S≥2 f h时,抽样后的信号就包含原连续信号的全部信息,而不会有信息丢失,当需要时,可以根据这些抽样信号的样本来还原原来的连续信号。
根据这一特性,可以完成信号的模-数转换和数-模转换过程。
意义介绍抽样定理指出,由样值序列无失真恢复原信号的条件是f S≥2 f h ,为了满足抽样定理,要求模拟信号的频谱限制在0~f h之内(fh为模拟信号的最高频率)。
为此,在抽样之前,先设置一个前置低通滤波器,将模拟信号的带宽限制在fh以下,如果前置低通滤波器特性不良或者抽样频率过低都会产生噪声。
例如,话音信号的最高频率限制在3400HZ,这时满足抽样定理的最低的抽样频率应为fS=6800HZ,为了留有一定的防卫带,CCITT规定话音信号的抽样率fS=8000HZ,这样就留出了8000-6800=1200HZ作为滤波器的防卫带。
应当指出,抽样频率fS不是越高越好,太高时,将会降低信道的利用率(因为随着fS升高,数据传输速率也增大,则数字信号的带宽变宽,导致信道利用率降低。
)所以只要能满足fS≥2f h,并有一定频带的防卫带即可。
以上讨论的抽样定理实际上是对低通信号的情况而言的,设模拟信号的频率范围为f0~fh,带宽B=fh - f0.如果f0<B,称之为低通型信号,例如,话音信号就是低通型信号的,弱f0>B,则称之为带通信号,载波12路群信号(频率范围为60~108KHZ)就属于带通型信号。
信号与系统第3章 傅里叶变换
P
f
2 (t) 1 T1
t0 T1 t0
f
2 (t)d t
a0 2
1 2
n1
(an
2
bn 2 )
2
Fn _____ 帕塞瓦尔定理
n
结论:周期信号的平均功率等于傅里叶级数展开 式中基波分量及各谐波分量有效值的平方 和,即时域和频域的能量守恒。
五. 周期信f号(t)的频c0 谱 (c三n c角os函(n数1t形 式n )) n1
(1) 偶函数 f (t) f (t)
4
an T1
T1
2 0
f (t) cos(n1t)dt
Fn
Fn
an 2
bn 0
傅里叶级数中不会含有正弦项, 只可能含有直流项和余弦项。
(2) 奇函数 f (t) f (t)
a0 0 , an 0
bn
4 T1
T1
2 0
f (t) sin(n1t)d t
e j n1t
T1 n 2
画频谱图:
c0
a0
E
T1
an
2E
T1
Sa
n1
2
, n
1,2,
cn an
1)令 m
2
得
2
m
即在
2
m,m为整数处有零点。
2)
2
2
T1
T1
零点间谱线个数
3) c n值为正,相位为0,值为负,相位为π
4)谱线间隔为 1 带宽
2
T1
,第一个过零点带宽定义为信号的
1 3
s in31t
1 4
sin41t
E
1 n1
抽样信号与抽样定理
? b0 a0
离散系统的转移算子
r(k ) ? H ( S )e(k )
例2:画出下面差分方程的模拟图
y(k ? 2) ? a1 y(k ? 1) ? a2 y(k) ? b2e(k ? 2) ? b1e(k ? 1) ? b0e(k)
分析:
H (s) ?
y(k ) ? e(k )
b2 S 2 ? b1S ? b0 S 2 ? a1S ? a0
0
FT
Fs (? )
1
Ts
t
??
0
?
特点:理想抽样后的频谱,是将连续信号的频谱进行周 期延拓,延拓的周期是采样频率
三 香农抽样定理
设f(t)是一个带限信号,在|? |> ? m时,F(j? )=0。如果抽 样频率? s>2 ? m ,其中? s =2? /Ts , 那f(t) 就唯一地由其样 本 fs(t)所确定。
差分方程阶数:差分方程的阶定义为响应最大移序与最小移 序之差;
初始条件:解差分方程也必须有初始条件,初始条件的个 数必须等于差分方程的阶数;
线性时不变系统:与连续时间系统中的结论相似,可以用一 个常系数差分方程描述。
数值解:因为差分方程可以很方便地用计算机求其数 值解,所以很多微分方程可以近似为差分方程 求近似数值解。
分析:假设y(k)代表第k个月兔子的总对数,则:
? 老兔子
y(k
?
? 老兔子
2)? ?
新生儿
y(k
?
1)? ?
新生儿
y(k )
解:y(k+2)=y(k)+y(k+1)
y(k+2)-y(k+1)- y(k)=0 y(k)-y(k-1)- y(k-2)=0
抽样信号的傅立叶变换
❖ 第二步,用自适应噪声抵消方法从ECG 信号中消除较强的低频干扰。
Yeldman 等人的研究表明,仅仅运用自适 应噪声抵消方法而又没有任何预处理滤 波器,要消除所有ECG信号干扰是不可 能的。
43
一种基于LMS算法的数字式 自适应滤波器
44
特点
❖ 因为同时存在两个不同的干扰,所以采用双参考信 道
(5)
25
应用上述五点结论推导权系数更新表达式 应用(1)结论有: 再应用(2)(3)(4)(5)结论,有
26
❖ 由此可见,当迭代次数无限增加时,权
系数向量的数学期望值可收敛至Wiener
解,其条件是对角阵
的所有对
角元素均小于1,即
❖或
27
基本LMS自适应算法 (软件实现)
28
LMS自适应滤波器(硬件实现)
或其统计特性是随时间变化的.
因此,用维纳或卡尔曼滤波器实现不了最优滤波. 在此情况下,自适应滤波能够提供优良的滤波性能。
3
引言
自适应滤波概念
利用前一时刻已获得的滤波器参数等 结果,自动地调节(更新)现时刻的滤波 器参数,以适应信号和噪声未知的统计特 性,或者随时间变化的统计特性,从而实 现最优滤波。
29
第二节 自适应噪声抵消器
❖ 自适应噪声抵消的目的是:
主信号由有用信号和背景噪声组成;
去除主信号中的背景噪声;
背景噪声与参考信号中的噪声相关;
因此,自适应噪声抵消技术主要依赖于从主信号 和噪声中获取参考信号。
30
8.2.1 自适应噪声抵消原理
最佳噪声抵消器
❖ 其中 ❖ 估计误差 e (n)
31
低通滤波器。采用LMS算法。
64
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
s(t )
x(t )
H ( j)
x(t )
H ( j)
T
c 0 c
n
(t nT )
理想低通滤波器的频率响应和单位 冲激响应为:
H ( j) T [u( c ) u( c )]
h(t ) T
T
c
c
h(t )
x(nT )Sa[
c
(t nT )]
12
动态演示
xs (t )
1 T
X s ( j)
T 0
T 2T
t
s m0 m s
2s
T
c
c
h(t )
T
c
H ( j)
0
t
c 0
c
xs (t )
1
X ( j )
T 0
T 2T
t
m
Re{X ( j)}e jt d 2e t
试求:x(t)。
八、设y(t)=x(t)cost,且已知Y(jΩ)=u(Ω+2)-u(Ω-2),试求:x(t)。
九、设y(t)=2x1(t).x2(t),且已知: x1 (t )
1 Sa[ (t 1)] 2 2
3 3 x2 (t ) Sa[ (t 1)] 试求下列各式: y(t )e jt dt , y (t ) Sa(t ) 2 2
xs (t )
s(t )
xs (t ) x(t ) s(t )
信号s(t)称为开关信号。上式关系可以用右图表示。
根据开关信号的不同,可以产生不同的抽样信号。这里只介绍 两种常见的抽样信号:理想抽样与自然抽样。 理想抽样是不能实现的,但它在说明抽样定理时,有重要的理 论价值,我们会经常用到它。 自然抽样是一种现实的抽样,它不仅有理论价值,还有实用价 值。
2
二、理想抽样
上述开关函数s(t)若是单位冲 激序列,抽样称为理想抽样。 于是,理想抽样信号为
x(t )
s(t )
n
xs (t )
(t nT )
xs (t ) x(t ) T (t ) x(t )
设信号x(t)的傅里叶变换为
FT x(t ) X ( j)
ℱ {T (t )}
T
0
T
2T
t
2s s
s 2s
xs (t )
1 T
X s ( j)
T
0
T
2T
t
动态演示
2s m m 2s s
4s
10
当满足抽样定理时,让抽样信号通过截止频率为Ωc的理想低通 滤波器(Ωm<Ωc<Ωs-Ωm),就可以恢复原信号。
§3-8 抽样信号的傅里叶变换与抽样定理
一、抽样信号
抽 样 保 持 量 化 编 码 解 滤
码
波
A/D
x(t )
D/A
s (t )
xs (t )
0
t
x(t )
s (t )
1
xs (t )
3T 2T T
0
T
2T
3T
t
3T 2T T
T
2T
3T
t
1
这里“抽样”的实现可以描述为
x(t )
1 T
X s ( j)
T 0
T 2T
t
s
0
s
2s
4
三、自然抽样
上述开关函数s(t)若是周期性矩形脉冲,抽样称为自然抽样。 于是,信号抽样的图形如下:
x(t )
X ( j )
0
t
0
S ( j)
(s )
s (t )
1
3T 2T T
T
2T
3T
t
s
T
s
X s ( j)
X ( j) 0 , m
f s 2 f m ( s 2m )
8
x(t )
X ( j )
0
t
m
m
T (t )
(1)
ℱ {T (t )}
( s )
T 2T
T 0
t
s
0
s
2s
xs (t )
1 T
X s ( j)
T 0
T 2T
t
s m0 m s
14
第三章测试题 (1,2题各5分,其他每小题10分)
一、一实值连续时间信号x(t),基波周期T=8,已知其非0傅里叶系数:
A1 A1 2
* A3 A3 j 4
2 5 t ) 4 sin( t ) ,求出Ω1,并将其写成指数级数形式。 3 3
n
3
s 1 X s ( j) X ( j) ( k s ) 2 T k
k
X [ j ( k
X ( j )
s
)]
x(t )
0
t
0
ℱ {T (t )}
T (t )
(1)
( s )
T 2T
T 0
t
s
0
s
2s
xs (t )
2c c Sa(ct ) Sa ( c t ) s
0
c
t
11
X ( j) X s ( j) H ( j)
根据卷积定理
X s ( j)
1 T
s m0 m s
2s
x(t ) xs (t ) h(t )
[ x(nT )(t nT )]
2s
xs (t )
n
x(nT )(t nT )
1 X s ( j) Tk Biblioteka X [ j ( k )]
s
9
如果不满足抽样定理,此时
x(t )
fs 2 fm
( s 2m )
X ( j )
1
0
t
m
m
T (t )
(1)
( s )
n
(t nT )
n
x(nT )(t nT )
由傅里叶变换的频域卷积定理,抽样信号的傅里叶变换为
1 xs (t ) X s ( j) X ( j) s ( k s ) 2 k FT
( s
2 ) T
2s
xs (t )
3T 2T T
0
T
2T
3T
t
s
s
2s
5
自然抽样信号及其傅里叶变换式
xs (t ) x(t ) s(t )
1 X s ( j ) X ( j ) s Sa(k s ) ( k s ) 2 2 k
十、试利用傅里叶变换,证明: sin t dt t
十一、已知:x(t ) Sa(ct ) cos0t ,使其通过如下带通滤波器,求其输出y(t)。
H ( j)
1
(设Ω0>>Ωc)
16
( 0 )t0
(0 c ) 0
( 0 )t0
0 c 00 c
n
H ( j)
T
2c Sa(ct ) s
c 0
c
n
x(nT )(t nT )
2c Sa(ct ) s
X ( j )
1
2c s
m
c
m
n
x(nT )Sa[ (t nT )]
x(t )
n
若Ωs=2Ωc =2Ωm ,
写出指数形式和三角形式的傅里叶级数展开式,并画出双边与单边频谱图。 二、已知
x(t ) 2 cos(
n 三、设系统的频率响应:H ( j) 4Sa(4) ,已知: x(t ) [2 (1) u (t 4n)] 1
试求系统响应y(t)。 四、两系统对输入ej5t的响应分别是ej5(t-1)与cos5t,试问哪个系统是非线性的? 五、一RL电路如图,输入为电流源is(t),输出是电感中
is (t ) io (t )
1H
的电流io(t),试:列出电路的输入输出方程,求出其
频率响应,若输入x(t)=cost,求输出的时间函数。 六、周期性三角脉冲如图所示,试求其傅里叶级数展开式。
1
E
T T 2
x(t )
T 2
15 T
t
七、设一实值因果信号x(t)的傅里叶变换为X(jΩ),已知:
s X ( j) Sa(k s )( k s ) 2 2 k
T
Sa(k s 2 ) X [ j ( k s )] k
6
四、抽样定理
x(2T )
x(T ) x(3T )
x(0)
x(2T )
2T
T T
x(T )
m
x(t )
n
x(nT )Sa[ (t nT )]
c
X ( j) X s ( j) H ( j)
13
┌┼──┼┐┌──╯─╮┌─┐┐┌┐ ──┼─ ┌───┼┤┌┬┐┼─┐ └──┘ │────│┌─┴┴┴┐└─┬┼┬┘├─┐ │ │ │ │ ┌──┼─┐┌──┌─┐│┌──┐│ │││ │ │ │ │ │ │ └──┼─┘│ │ │││ ││ │││ │ │ ││ │ │ │ ┌──┼─┐│ │ ││└──╯│╭ │││┐│ │ ├┘ │ │ │ ─┘ └──├─╯└╯ ╰┘└─╯┘└╯╯└╯└╰┘└┴╯╯─╯,
