理论力学静力学第二章习题答案
理论力学习题答案

第三章 空间力系
一、是非题判断题
3.1.1对一空间任意力系,若其力多边形自行封闭,则该力系的主矢为零。 (∨)
平面力系中,若其力多边形自行闭合,则力系平衡。(×)
3.1.2只要是空间力系就可以列出6 个独立的平衡方程。 (×)
2.3.4悬臂式吊车的结构简图如图所示,由DE、AC二杆组成,A、B、C为铰链连接。已知P1=5kN,P2=1kN,不计杆重,试求杆AC杆所受的力和B点的支反力。
(答案:FBx=3.33kN,FBy=0.25kN,FAC=6.65kN)
2.3.5由AC和CD构成的组合粱通过铰链C连接,它的支承和受力如图所示,已知均布载荷强度q=10kN/m,力偶矩M=40kN.m,不计梁重,求支座A、B、D的约束反力和铰链C处所受的力。
3.1.3若由三个力偶组成的空间力偶系平衡,则三个力偶矩矢首尾相连必构成自行封闭的三角形。(∨)
3.1.4空间汇交力系平衡的充分和必要条件是力系的合力为零;空间力偶系平衡的充分和必要条件是力偶系的合力偶矩为零。(∨)
二、填空题
3.2.1若一空间力系中各力的作用线平行于某一固定平面,则此力系有5个独立的平衡方程。
3.3.3如图所示,三圆盘A、B、C的半径分别为15cm、10cm、5cm,三根轴OA、OB、OC在同一平面内,∠AOB为直角,三个圆盘上分别受三个力偶作用,求使物体平衡所需的力F和α角。
3.3.4某传动轴由A、B两轴承支承。圆柱直齿轮的节圆直径d=17.3cm,压力角 =20º,在法兰盘上作用一力偶矩为M=1030N.m的力偶,如轮轴的自重和摩擦不计,求传动轴匀速转动时A、B两轴承的约束反力。(答案:FAx=4.2kN,FAz=1.54kN,FBz=7.7kN,FBz.=2.79kN)
理论力学习题及答案(全)

第一章静力学基础一、是非题1.力有两种作用效果,即力可以使物体的运动状态发生变化,也可以使物体发生变形。
()2.在理论力学中只研究力的外效应。
()3.两端用光滑铰链连接的构件是二力构件。
()4.作用在一个刚体上的任意两个力成平衡的必要与充分条件是:两个力的作用线相同,大小相等,方向相反。
()5.作用于刚体的力可沿其作用线移动而不改变其对刚体的运动效应。
()6.三力平衡定理指出:三力汇交于一点,则这三个力必然互相平衡。
()7.平面汇交力系平衡时,力多边形各力应首尾相接,但在作图时力的顺序可以不同。
()8.约束力的方向总是与约束所能阻止的被约束物体的运动方向一致的。
()二、选择题1.若作用在A点的两个大小不等的力F1和F2,沿同一直线但方向相反。
则其合力可以表示为。
①F1-F2;②F2-F1;③F1+F2;2.作用在一个刚体上的两个力F A、F B,满足F A=-F B的条件,则该二力可能是。
①作用力和反作用力或一对平衡的力;②一对平衡的力或一个力偶。
③一对平衡的力或一个力和一个力偶;④作用力和反作用力或一个力偶。
3.三力平衡定理是。
①共面不平行的三个力互相平衡必汇交于一点;②共面三力若平衡,必汇交于一点;③三力汇交于一点,则这三个力必互相平衡。
4.已知F1、F2、F3、F4为作用于刚体上的平面共点力系,其力矢关系如图所示为平行四边形,由此。
①力系可合成为一个力偶;②力系可合成为一个力;③力系简化为一个力和一个力偶;④力系的合力为零,力系平衡。
5.在下述原理、法则、定理中,只适用于刚体的有。
①二力平衡原理;②力的平行四边形法则;③加减平衡力系原理;④力的可传性原理;⑤作用与反作用定理。
三、填空题1.二力平衡和作用反作用定律中的两个力,都是等值、反向、共线的,所不同的是。
2.已知力F沿直线AB作用,其中一个分力的作用与AB成30°角,若欲使另一个分力的大小在所有分力中为最小,则此二分力间的夹角为度。
理论力学习题答案

理论力学习题答案(总26页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--2第一章 静力学公理和物体的受力分析一、是非判断题在任何情况下,体内任意两点距离保持不变的物体称为刚体。
( ∨ ) 物体在两个力作用下平衡的必要与充分条件是这两个力大小相等、方向相反,沿同一直线。
( × ) 加减平衡力系公理不但适用于刚体,而且也适用于变形体。
( × ) 力的可传性只适用于刚体,不适用于变形体。
( ∨ ) 两点受力的构件都是二力杆。
( × ) 只要作用于刚体上的三个力汇交于一点,该刚体一定平衡。
( × ) 力的平行四边形法则只适用于刚体。
( × ) 凡矢量都可以应用平行四边形法则合成。
( ∨ ) 只要物体平衡,都能应用加减平衡力系公理。
( × ) 凡是平衡力系,它的作用效果都等于零。
( × ) 合力总是比分力大。
( × ) 只要两个力大小相等,方向相同,则它们对物体的作用效果相同。
( × )若物体相对于地面保持静止或匀速直线运动状态,则物体处于平衡。
( ∨ )当软绳受两个等值反向的压力时,可以平衡。
( × )静力学公理中,二力平衡公理和加减平衡力系公理适用于刚体。
( ∨ )静力学公理中,作用力与反作用力公理和力的平行四边形公理适用于任何物体。
( ∨ )凡是两端用铰链连接的直杆都是二力杆。
( × )如图所示三铰拱,受力F ,F 1作用,其中F 作用于铰C 的销子上,则AC 、BC 构件都不是二力构件。
( × )图3二、填空题力对物体的作用效应一般分为 外 效应和 内 效应。
对非自由体的运动所预加的限制条件称为 约束 ;约束力的方向总是与约束所能阻止的物体的运动趋势的方向 相反 ;约束力由 主动 力引起,且随 主动 力的改变而改变。
理论力学第二章力系简化习题解

第二章 力系的简化习题解[ 习题 2-1] 一钢构造节点 , 在沿 OA,OB,OC 的方向上遇到三个力的作用, 已知 F 1 1kN ,F 2 1.41kN , F 32kN , 试求这三个力的协力 .解:F 1 x0 F1 y1kNF 21350F 3F 2 x 1.41 cos451( kN ) F 2 y 1.41sin 45 1(kN )F 3 x2kNF3 yO 9003F 1F RxF xi0 1 2 1(kN )i 03FRyFyi1 1 0i 0F R F Rx 2R Ry 21 作用点在 O 点 , 方向水平向右 .[ 习题 2-2]计算图中已知F 1 , F 2 , F 3 三个力分别在 x, y, z 轴上的投影并求协力. 已知F 1 2kN , F 2 1kN , F 33kN .解:zF1 x 2kNF1yF1zF2 xF 2 sin 450 cos13 0.424( kN ) F 15 F2 yF 2 sin 450 sin14 0.567( kN )A45 05F 2 sin 4505yF2 z10.707( kN)OF 2F 3F3 xF3 y0 F3 z3kN334F RxF xi20 2.424( kN )xi 03F RyF yi0 0.567(kN )i 03F RzF zi3 3.707(kN )i 0协力的大小 :F R FRx2FRy2FRz220.567 224.465(kN )方向余弦 :cosFRxF RcosFRyF RF RzcosF R作用点 : 在三力的汇交点A.[ 习题 2-3]已知 F 1 2 6N ,F 2 2 3N ,F 3 1N F 4 4 2N ,F 5 的结果 ( 提示 : 不用开根号 , 可使计算简化 ).解:zF 1 x 0 F 1y 0 F 1z 2 6NF 2 x 0 F 2 y2 3N F 2 zF 1F3 x 1N F 3 y 0F3z0 F 4F4 xF 4 cos450cos604 22 1 2(N ) 45A2260 0F 3F 4 yF 4 cos 450 sin 6004 2 2 3 2 3(N)22F4 zF 4 sin 4504 22 4(N)253F5 xF 5 sin cos74232 (2 6) 2 3(N)5 F5 yF 5 sin sin75 44232(2 6) 2 4(N)5F5 zF 5 cos72 62 6(N)4232(2 6 )25F RxF xi 001234(N)i 05FRyF yi0230234 4(N)i 05FRz Fzi26004264(N)i 0协力的大小 :F RFRx2FRy2FRz24 24242 4 3 6.93(N)方向余弦 :cosFRx4 3F R4 3 37 N , 求五个力合成F 52 6F 2y34xF Ry 4 3cos433F RFRz4 3cos4 33F Rarccos3540 44'8"3作用点 : 在三力的汇交点 A.[ 习题 2-4] 沿正 六面 体的 三棱 边作用 着三 个力 , 在平 面 OABC 内作 用一个 力偶 .已 知F 1 20N , F 2 30N , F 3 50 N , M 1N m . 求力偶与三个力合成的结果 .AzF 1B150mmMOyO 1EF 2xF 3150mmD200mmC解:把 F 1, F 2 , F 3向O 1平移, 获得: 题 24图主矢量 :F RF 3 F 1 F 25020 30 0M x ( F 1 ) F 1204( N m)M y ( F 1 ) 0 M z ( F 1 ) 0M x ( F 2 ) F 2 30 6( N m) M y ( F 2 ) F 2304.5(N m)M z ( F 2 ) 0 M x ( F 3 ) 0M y ( F 3 ) F 37.5( N m)M z ( F 3 )M 的方向由 E 指向 D.MOCM O 1(F 1)M O 1(F 3)8.25( N m)M xM sin12000.8( N m)2002150 2OE150M yM cos10.6( N m)O 12002 1502M 900DCM z3M xM x (F i ) M x 4 6 0 0.89.2( N m)i 13M y M y (F i ) M y3.6( N m) i 1 3M zi 1 M z (F i ) M z00000主矩 :M O (M x )2 (M y ) 2 (M z ) 2( 9.2)2( 3.6)202 9.88( N m)方向余弦 :cosM xM 0cosM yM 0cosM zM 0[习题 2-5]一矩形体上作用着三个力偶 (F 1,F 1') , (F 2,F 2') , (F 3,F 3') .已 知F 1F 1 ' 10N , F 2F 2 '16N , F 3 F 3 '20N , a 0.1m , 求三个力巧合成的结果 .解:先把 F 1 在正 X 面上平行挪动到 x 轴 .则应附带力偶矩 :zM x ( F 1 ) F 1a 101( N m)F 'Mx1M x (F 1 ) 1(N m)1'aM y1F 1 2a 102( N m)F 2Mz1y把 F 2 沿 y, z 轴上分解 :F 2F 3FF cos450 1611.314( N )2 y22aF F sin 4501611.314( N )'F 12 z2Mx2 0F 3xa题 2 5图M y2 F 2z 2a2.263( N m)M z2 F 2 y 2a2.263( N m)M x3 0 My3Mz3F 3 a 20 2( N m)3M xM xi 1 0 0 1i 13M yMyi24.263(N m)i 1 3M zMzi2 0.263( N m)i 1主矩 :M O (M x ) 2(M y ) 2(M z ) 212( 4.263) 2 0.263 24.387(N m)方向余弦 :zcosM x1100mmM 0100mm2NM y2Ncos2NM 05N7NM zcosyOM 0[ 习题 2-6] 试求图诸力合成的结果 .4N4N解:3N1200主矢量 :3NF R 5 2 7 0竖 M x (5N ) 0的向 M x (7N )7力 矩产M x (2N ) 2生 面 顶M x1底 Mx 2面斜 M x3 3sin 60 0面x习题2 6图M y M z (5N ) 0M yM z ( 7N ) 0 M y (2 N ) 0M z ( 2N ) 0M y10 M x1My20 Mx2M y3M x33 cos 600主矩 :M O ( M x ) 2( M y ) 2( M z ) 2( 0.76) 2221.086( N m)方向余弦 :M xcosM 0cosM yM 0cosM zM 0[ 习题 2-7]柱子上作有着 F1,F2, F3三个铅直力,已知 F1 80kN , F2 60kN ,F3 50kN ,三力地点以下图. 图中长度单位为mm ,求将该力系向O点简化的结果.zF1F3A( 0, 250, ZA )F2C( 170,150,0)yOB(170,150,0)解:主生竖向的力矩产主矩 :矢量:x习题27图F R8060 50190(kN ) M x (F1 )800.25 20M y (F1 )0M z (F1 )0M x (F2 )609M y (F2 )60M z (F2 )0M x (F3 )50M y (F3 )50M z (F3 )0M O(M x ) 2( M y ) 2(M z ) 22 1.7 202 3.891( N m)方向余弦 :cosM xM 0cosM yM 0cosM z0M 0[ 习题 2-8]求图示平行力系合成的结果( 小方格边长为100mm)7kNyo(0,0)7kN3kN9kNB(400,200)12kNA(450,0)D(300,600)x 解:C(600,500)习题28图1277390主矢量:F RA M x (3kN)0M y ( 3kN )3B M x (9kN)9M y ( 9kN )9C M x (12kN )6M y (12kN )12D M x (7kN)7M y (7kN )7主矩 :M O(M x )2( M y ) 28.4 2( 4.35)29.46(kN m)方向余弦 :cosM x M 0cosM y M 0[ 习题 2-9]平板 OABD上作用空间平行力系以下图, 问x, y应等于多少才能使该力系协力作用线经过板中心 C.解:主矢量 :F R7 8 5 6 430(kN )由协力矩定理可列出以下方程:4 y5 8 8 83044 y 40 64120y 4(m)长度单位 : m4x 5 6 6 6 303x 6( m)[ 习题 2-10] 一力系由四个力构成。
工程力学(静力学答案)

第一章习题下列习题中,凡未标出自重的物体,质量不计。
接触处都不计摩擦。
1-1试分别画出下列各物体的受力图。
1-2试分别画出下列各物体系统中的每个物体的受力图。
1-3试分别画出整个系统以及杆BD,AD,AB(带滑轮C,重物E和一段绳索)的受力图。
1-4构架如图所示,试分别画出杆HED,杆BDC及杆AEC的受力图。
1-5构架如图所示,试分别画出杆BDH,杆AB,销钉A及整个系统的受力图。
1-6构架如图所示,试分别画出杆AEB,销钉A及整个系统的受力图。
1-7构架如图所示,试分别画出杆AEB,销钉C,销钉A及整个系统的受力图。
1-8结构如图所示,力P作用在销钉C上,试分别画出AC,BCE及DEH部分的受力图。
参考答案1-1解:1-2解:1-3解:1-4解:1-5解:1-6解:1-7解:1-8解:第二章 习题参考答案2-1解:由解析法,23cos 80RX F X P P Nθ==+=∑12sin 140RY F Y P P Nθ==+=∑故: 22161.2R RX RY F F F N=+=1(,)arccos2944RYR RF F P F '∠==2-2解:即求此力系的合力,沿OB 建立x 坐标,由解析法,有123cos45cos453RX F X P P P KN ==++=∑13sin 45sin 450RY F Y P P ==-=∑故: 223R RX RY F F F KN=+=方向沿OB 。
2-3解:所有杆件均为二力杆件,受力沿直杆轴线。
(a ) 由平衡方程有:0X =∑sin 300ACAB FF -=0Y =∑cos300ACFW -=联立上二式,解得:0.577AB F W=(拉力)1.155AC F W=(压力)(b ) 由平衡方程有:0X =∑cos 700ACAB FF -=0Y =∑sin 700ABFW -=联立上二式,解得:1.064AB F W=(拉力)0.364AC F W=(压力)(c ) 由平衡方程有:0X =∑cos 60cos300ACAB FF -=0Y =∑sin 30sin 600ABAC FF W +-=联立上二式,解得:0.5AB F W=(拉力)0.866AC F W=(压力)(d ) 由平衡方程有:0X =∑sin 30sin 300ABAC FF -=0Y =∑cos30cos300ABAC FF W +-=联立上二式,解得:0.577AB F W=(拉力)0.577AC F W=(拉力)2-4解:(a)受力分析如图所示:由x=∑22cos45042RAF P=+15.8RAF KN∴=由Y=∑22sin45042RA RBF F P-=+7.1RBF KN∴=(b)解:受力分析如图所示:由0x =∑3cos 45cos 45010RA RB F F P ⋅--= 0Y =∑1sin 45sin 45010RA RB F F P ⋅+-=联立上二式,得:22.410RA RB F KN F KN==2-5解:几何法:系统受力如图所示三力汇交于点D ,其封闭的力三角形如图示所以: 5RA F KN=(压力)5RB F KN=(与X 轴正向夹150度)2-6解:受力如图所示:已知,1R F G = ,2AC F G =由x =∑cos 0AC r F F α-=12cos G G α∴=由0Y =∑sin 0AC N F F W α+-=22221sin N F W G W G G α∴=-⋅=--2-7解:受力分析如图所示,取左半部分为研究对象由x =∑cos 45cos 450RA CB P F F --=0Y =∑sin 45sin 450CBRA F F '-=联立后,解得:0.707RA F P=0.707RB F P=由二力平衡定理 0.707RB CB CBF F F P '===2-8解:杆AB ,AC 均为二力杆,取A 点平衡由x =∑cos 60cos300AC AB F F W ⋅--=0Y =∑sin 30sin 600ABAC FF W +-=联立上二式,解得:7.32ABF KN=-(受压)27.3ACF KN=(受压)2-9解:各处全为柔索约束,故反力全为拉力,以D,B点分别列平衡方程(1)取D点,列平衡方程由x=∑sin cos0DBT Wαα-=DBT Wctgα∴==(2)取B点列平衡方程由0Y =∑sin cos 0BDT T αα'-=230BDT T ctg Wctg KN αα'∴===2-10解:取B 为研究对象:由0Y =∑sin 0BC F P α-=sin BC PF α∴=取C 为研究对象:由x =∑cos sin sin 0BCDC CE F F F ααα'--=由0Y =∑sin cos cos 0BC DC CE F F F ααα--+=联立上二式,且有BCBC F F '= 解得:2cos 12sin cos CE P F ααα⎛⎫=+ ⎪⎝⎭取E 为研究对象:由0Y =∑cos 0NH CEF F α'-=CECE F F '=故有:22cos 1cos 2sin cos 2sin NH P PF ααααα⎛⎫=+= ⎪⎝⎭2-11解:取A 点平衡:0x =∑sin 75sin 750ABAD FF -=0Y =∑cos 75cos 750ABAD FF P +-=联立后可得:2cos 75AD AB PF F ==取D 点平衡,取如图坐标系:0x =∑cos5cos800ADND F F '-=cos5cos80ND ADF F '=⋅由对称性及ADAD F F '=cos5cos5222166.2cos80cos802cos 75N ND AD PF F F KN'∴===⋅=2-12解:整体受力交于O 点,列O 点平衡由x=∑cos cos300RA DCF F Pα+-=Y=∑sin sin300RAF Pα-=联立上二式得:2.92RAF KN=1.33DCF KN=(压力)列C点平衡x=∑405DC ACF F-⋅=Y=∑305BC ACF F+⋅=联立上二式得:1.67ACF KN=(拉力)1.0BCF KN=-(压力)2-13解:(1)取DEH 部分,对H 点列平衡0x =∑05RD REF F '-= 0Y =∑05RD F Q -=联立方程后解得: 5RD F Q =2REF Q '=(2)取ABCE 部分,对C 点列平衡0x =∑cos 450RERA FF -= 0Y =∑sin 450RBRA FF P --=且RE REF F '=联立上面各式得: 22RA F Q =2RB F Q P=+(3)取BCE 部分。
理论力学习题及答案(全)

第一章静力学基础一、是非题1.力有两种作用效果,即力可以使物体的运动状态发生变化,也可以使物体发生变形。
()2.在理论力学中只研究力的外效应。
()3.两端用光滑铰链连接的构件是二力构件。
()4.作用在一个刚体上的任意两个力成平衡的必要与充分条件是:两个力的作用线相同,大小相等,方向相反。
()5.作用于刚体的力可沿其作用线移动而不改变其对刚体的运动效应。
()6.三力平衡定理指出:三力汇交于一点,则这三个力必然互相平衡。
()7.平面汇交力系平衡时,力多边形各力应首尾相接,但在作图时力的顺序可以不同。
()8.约束力的方向总是与约束所能阻止的被约束物体的运动方向一致的。
()二、选择题1.若作用在A点的两个大小不等的力F1和F2,沿同一直线但方向相反。
则其合力可以表示为。
①F1-F2;②F2-F1;③F1+F2;2.作用在一个刚体上的两个力F A、F B,满足F A=-F B的条件,则该二力可能是。
①作用力和反作用力或一对平衡的力;②一对平衡的力或一个力偶。
③一对平衡的力或一个力和一个力偶;④作用力和反作用力或一个力偶。
3.三力平衡定理是。
①共面不平行的三个力互相平衡必汇交于一点;②共面三力若平衡,必汇交于一点;③三力汇交于一点,则这三个力必互相平衡。
4.已知F1、F2、F3、F4为作用于刚体上的平面共点力系,其力矢关系如图所示为平行四边形,由此。
①力系可合成为一个力偶;②力系可合成为一个力;③力系简化为一个力和一个力偶;④力系的合力为零,力系平衡。
5.在下述原理、法则、定理中,只适用于刚体的有。
①二力平衡原理;②力的平行四边形法则;③加减平衡力系原理;④力的可传性原理;⑤作用与反作用定理。
三、填空题1.二力平衡和作用反作用定律中的两个力,都是等值、反向、共线的,所不同的是。
2.已知力F沿直线AB作用,其中一个分力的作用与AB成30°角,若欲使另一个分力的大小在所有分力中为最小,则此二分力间的夹角为度。
理论力学习题及解答1
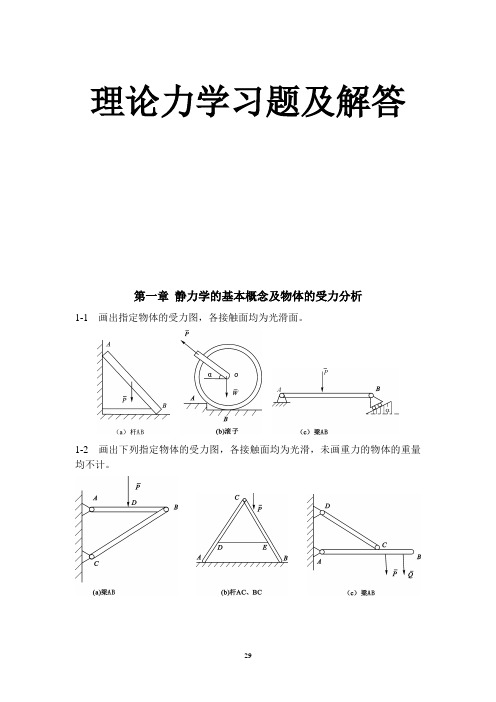
理论力学习题及解答第一章静力学的基本概念及物体的受力分析1-1 画出指定物体的受力图,各接触面均为光滑面。
1-2 画出下列指定物体的受力图,各接触面均为光滑,未画重力的物体的重量均不计。
1-3 画出下列各物体以及整体受力图,除注明者外,各物体自重不计,所有接触处均为光滑。
(a) (b)(c) (d)(e) (f)第二章平面一般力系2-1 物体重P=20kN,用绳子挂在支架的滑轮B上,绳子的另一端接在铰车D 上,如图所示。
转动铰车,物体便能升起,设滑轮的大小及滑轮转轴处的摩擦忽略不计,A、B、C三处均为铰链连接。
当物体处于平衡状态时,试求拉杆AB和支杆CB所受的力。
2-2 用一组绳悬挂重P=1kN的物体,求各绳的拉力。
2-3 某桥墩顶部受到两边桥梁传来的铅直力P1=1940kN,P2=800kN及制动力T=193kN,桥墩自重W=5280kN,风力Q=140kN。
各力作用线位置如图所示,求将这些力向基底截面中心O简化的结果,如能简化为一合力,试求出合力作用线的位置。
2-4 水平梁的支承和载荷如图所示,试求出图中A、B处的约束反力。
2-5 在图示结构计算简图中,已知q=15kN/m,求A、B、C处的约束力。
2-6 图示平面结构,自重不计,由AB、BD、DFE三杆铰接组成,已知:P=50kN,M=40kN·m,q=20kN/m,L=2m,试求固定端A的反力。
图2-6 图2-72-7 求图示多跨静定梁的支座反力。
2-8 图示结构中各杆自重不计,D、E处为铰链,B、C为链杆约束,A为固定端,已知:q G=1kN/m,q=1kN/m,M=2kN·m,L1=3m,L2=2m,试求A、B、C 处约束反力。
图2-8 图2-92-9 支架由两杆AO、CE和滑轮等组成,O、B处为铰链,A、E是固定铰支座,尺寸如图,已知:r=20cm,在滑轮上吊有重Q=1000N的物体,杆及轮重均不计,试求支座A和E以及AO杆上的O处约束反力。
胡汉才编著理论力学课后习题答案第2章力系的简化

力系的简化第二章,的力F,5)两点(长度单位为米),且由A指向B.通过A(3,0,0),B(0,42-1 。
,对z轴的矩的大小为在z轴上投影为22 /5。
答:F / ;6 F上和y,c,则力F在轴z2-2.已知力F的大小,角度φ和θ,以及长方体的边长a,b的矩x ;F对轴;Fy= 的投影:Fz=F 。
)= M ( x)··()(··;-··;cos=FFz=F答:φsinφbFy=θFsincosφφcosφ+cMxFcos41-图2 图2-40F,则该力,若F=100N,4)两点(长度单位为米)),B(0,2-3.力4通过A(3,4、0 。
,对x轴的矩为在x轴上的投影为320N.m;答:-60NAE内有沿对角线,在平面ABED2-4.正三棱柱的底面为等腰三角形,已知OA=OB=a °,则此力对各坐标轴之矩为:α=30的一个力F,图中。
)= );M(F= ((MF)= ;MF zYx6Fa/4 =(F);M)=0,(F)=-Fa/2MF答:M(zxy2-5.已知力F的大小为60(N),则力F对x轴的矩为;对z轴的矩为。
答:M(F)=160 N·cm;M(F)=100 N·cmzx43-图2 2图-42O2-6.试求图示中力F对点的矩。
M(F)=Flsinα解:a: O M(F)=Flsinαb: Oα+ Flcos)sinc: M(F)=F(l+lα2O13??22?lM?Fl?Fsin d: 2o1。
轴的力矩M1000N2-7.图示力F=,求对于z z图题2-8 7题2-图。
试求=40N,M=30N·m=40N2-8.在图示平面力系中,已知:F=10N,F,F321其合力,并画在图上(图中长度单位为米)。
解:将力系向O点简化=30N F=F-R12X40N -=R=-F3V R=50N ∴m )··3+M=300N+FF主矩:Mo=(+F312d=Mo/R=6mO合力的作用线至点的矩离iiRR0.8-=),(cos,=0.6),(cos合力的方向:iR )=-53,°08'(iR ,')(=143°08,内作用一力偶,其矩M=50KNGA转向如图;又沿·m,2-9.在图示正方体的表面ABFE2RR =50。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2-3 在图示结构中,二曲杆重不计,曲杆AB 上作用有主动力偶M 。
试求A 和C 点处的约束力。
解:BC 为二力杆(受力如图所示),故曲杆AB 在B 点处受到约束力的方向沿BC 两点连线的方向。
曲杆AB 受到主动力偶M 的作用,A 点和B 点处的约束力必须构成一个力偶才能使曲杆AB 保持平衡。
AB 受力如图所示,由力偶系作用下刚体的平衡方程有(设力偶逆时针为正):
0=∑M 0)45sin(100=-+⋅⋅M a F A θ a
M F A 354.0=
其中:31
tan =θ。
对BC 杆有:a
M F F F A B C 354.0=== A ,C 两点约束力的方向如图所示。
2-4
解:机构中AB 杆为二力杆,点A,B 出的约束力方向即可确定。
由力偶系作用下刚体的平衡条件,点O,C 处的约束力方向也可确定,各杆的受力如图所示。
对BC 杆有: 0=∑M
030sin 20=-⋅⋅M C B F B
对AB 杆有: A B
F F =
对OA 杆有: 0=∑M
01=⋅-A O F M A
求解以上三式可得:m N M ⋅=31, N F F F C O AB 5===,方向如图所示。
//
2-6求最后简化结果。
解:2-6a
坐标如图所示,各力可表示为:
j F i F F ρ
ρρ23211+=, i F F ρρ=2, j F i F F ρρρ2
3213+-=
先将力系向A 点简化得(红色的): j F i F F R ρρρ3+=, k Fa M A ρ
ρ2
3=
方向如左图所示。
由于A R M F ρ
ρ⊥,可进一步简化为一个不过
A 点的力(绿
色的),主矢不变,其作用线距A 点的距离a d 4
3=
,位置如左图所示。
2-6b
同理如右图所示,可将该力系简化为一个不过A 点的力(绿色的),主矢为:
i F F R ρρ2-=
其作用线距A 点的距离a d
4
3=
,位置如右图所示。
简化中心的选取不同,是否影响最后的简化结果?
2-13
解:整个结构处于平衡状态。
选择滑轮为研究对象,受力如图,列平衡方程(坐标一般以水平向右为x 轴正向,竖直向上为y 轴正向,力偶以逆时针为正):
∑=0x F 0sin =+Bx F P α
∑=0y F 0cos =--αP P F By
选梁AB 为研究对象,受力如图,列平衡方程:
∑=0x F
0=-Bx Ax F F ∑=0y F
0=-By Ay F F
0=∑A M
0=⋅-l F M By A
求解以上五个方程,可得五个未知量A By Bx Ay Ax M F F F F ,,,,分别为:
αsin P F F Bx Ax -==(与图示方向相反) )cos 1(α+==P F F By Ay (与图示方向相同)
l P M A )cos 1(α+= (逆时针方向)
2-18
解:选AB 杆为研究对象,受力如图所示,列平衡方程: 0=∑A M
0cos cos 2
cos =⋅-⋅-⋅
αααl F l
G a N D
∑=0y F 0cos =--F G N D α
求解以上两个方程即可求得两个未知量α,D N ,其中:
31
])2()(2arccos[l
G F a G F ++=α
未知量不一定是力。
2-27
解:选杆AB 为研究对象,受力如下图所示。
列平衡方程:
0=∑y M
0tan sin cos tan 2
1
=⋅-⋅-⋅αθθαc F c F c P BC BC
N F BC 6.60=
0'=∑x M
0sin 2
1
=⋅-⋅-⋅a F c F a P BC B θ
N F B 100=
由∑=0y
F 和∑=0z F 可求出Az Ay F F ,。
平衡方程0=∑x M 可用来校核。
思考题:对该刚体独立的平衡方程数目是几个?
2-29
解:杆1,2,3,4,5,6均为二力杆,受力方向沿两端点连线方向,假设各杆均受压。
选板ABCD 为研究对象,受力如图所示,该力系为空间任意力系。
采用六矩式平衡方程: 0=∑DE M 045cos 02=⋅F 02=F
0=∑AO M
045cos 45cos 45cos 0006=⋅-⋅-a F a F
F F 2
26-
=(受拉) 0=∑BH M 045cos 45cos 0604=⋅-⋅-a F a F F F 2
24=(受压) 0=∑AD M
045sin 45cos 0061=⋅-⋅+⋅a F a F a F
F F 2
211+=
(受压)
0=∑CD M
045sin 031=⋅-⋅+⋅a F a F a F
F
F 213-=(受拉)
0=∑BC M
045cos 0453=⋅-⋅+⋅a F a F a F
05=F
本题也可以采用空间任意力系标准式平衡方程,但求解代数方程组非常麻烦。
类
似本题的情况采用六矩式方程比较方便,适当的选择六根轴保证一个方程求解一个未知量,避免求解联立方程。
2-31 力偶矩cm N M
⋅=1500
解:取棒料为研究对象,受力如图所示。
列平衡方程:
⎪⎩⎪
⎨⎧∑=∑=∑=000
O
y x M F F
⎪⎪⎩⎪⎪⎨⎧=-⋅+=+-=-+02
)(045sin 045cos 2110
2201
M D
F F N p F N p F 补充方程:⎩⎨
⎧
==2211N f F N f F s s
五个方程,五个未知量s f N F N F ,2211,,,,可得方程:
02222=+⋅⋅-⋅M f D p f M S S
解得491.4,223.021==S S f f 。
当491.42=S f 时有:
0)
1(2)
1(2
221<+-=
S S f f p N 即棒料左侧脱离V 型槽,与提议不符,故摩擦系数223.0=S f 。
2-33
解:当045=α时,取杆AB 为研究对象,受力如图所示。
列平衡方程:
⎪⎩⎪
⎨⎧∑=∑=∑=000A
y x M F F
⎪⎪⎩⎪
⎪
⎨⎧
=⋅
-⋅-⋅=-+=-0sin 2
cos sin sin cos 0cos 0sin ααθαθθθB
A p C A T C A T p T F T F S
N 附加方程:N S S F f F =
四个方程,四个未知量s S N f T F F ,,,,可求得646.0=s f 。
2-35
解:选棱柱体为研究对象,受力如图所示。
假设棱柱边长为a ,重为P ,列平衡方程:
⎪⎩⎪
⎨⎧∑=∑=∑=000x
B A F M M
⎪⎪
⎪
⎩
⎪
⎪⎪⎨⎧
=-+=+⋅+⋅-=+⋅-⋅0sin 032sin 2cos 032sin 2cos αα
αααP F F a P a P a F a P a P a F B A NA NB 如果棱柱不滑动,则满足补充方程⎩⎨⎧==NB
s B NA s A F
f F F f F 21时处于极限平衡状态。
解以上五个方程,可求解五个未知量α,,,,NB B NA A F F F F ,其中:
3
2)(3tan 1221+-+=
s s s s f f f f α
(1)
当物体不翻倒时0≥NB
F ,则:
060tan ≤α
(2)
即斜面倾角必须同时满足(1)式和(2)式,棱柱才能保持平衡。
