陈省身杯2011真题
第一届至第九届(2010-2018年)陈省身杯全国高中数学奥林匹克试题及答案【PDF版】

第九届陈省身杯全国高中数学奥林匹克1.已知锐角△ABC 的外接圆为⊙O ,边BC 、CA 、AB 上的高的垂足分别为D 、E 、F ,直线EF 与⊙O 的 AB 、AC 分别交于点G 、H ,直线DF 与BG 、BH 分别交于点K 、L ,直线DE 与CG 、CH 分别交于点M 、N .证明:K 、L 、M 、N 四点共圆,且该圆的直径为2222()b c a +-,其中,BC =a ,CA =b ,AB =c .证明 如图1,因为B 、C 、E 、F 四点共圆,所以,AFE ACB ∠=∠.图1°°2GB HA AFE 注意到,+∠=, °°°22AB AG GB ACB +∠==. 从而, HA AG =,即AG AH =.因为C 、A 、F 、D 四点共圆,所以,=BFD ACB AFE BFG ∠=∠∠=∠.从而,直线GH 与直线DK 关于直线AB 对称.由 °°AG AH =, 知GBA ABH ∠=∠.从而,直线BK 与直线BH 关于直线AB 对称.因此,点K 、H 关于直线AB 对称,即AK =AH .类似地:点L 、G 关于直线AB 对称,即AL =AG ;G 、N 关于直线AC 对称,即AG =AN ;M 、H 关于直线AC 对称,即AM =AH .综上,AL =AN =AG =AH =AK =AM .因此,K 、L 、M 、N 四点共圆,且圆心为A ,半径为AG ,记该圆为⊙A . 设⊙O 的半径为R ,⊙O 的直径AQ 与GH 交于点P .如图2.图2则∠AGQ=90°,且AP ⊥GH .由射影定理得2AG AQ AP =⋅.注意到,sin =cos sin AP AF AFE AC CAB ACB .=⋅∠⋅∠⋅∠2222222cos sin =22AQ AP R AC CAB ACBb c a b c a AB AC bc 故.⋅=⋅∠⋅∠+-+-=⋅⋅ 因此,2222b c a AG +-=,⊙A 的直径为2222()b c a +-.。
历届陈省身杯重要知识点-数论(答案)

六年级历届陈省身杯重要知识点数论专题高频考点一、05~10陈省身杯数论模块重要知识点约、倍、质、合、整除位值原则余数(中国剩余,同余)个位率常用方法1.翻译?!2.分解3.位值4.题型特点—方法(同余、奇偶性…)【例1】(2010年陈省身杯第4题)三个相邻的自然数的乘积是3360,这三个自然数分别是________、________和________。
5=⨯⨯⨯=⨯⨯,所以三个自然数为14、15、16。
33602357141516【例2】(2008年13题)用5、6、7、8四个数字(每个数字恰好用一次)可组成24个不同的四位数,其中有________个数能被11整除。
5+8=6+7,当奇数位是5、8时:2×2=4(种)。
当奇数位是6、7时:2×2=4(种)。
共有8(种)。
【例3】(2009年12题)A、B、C、D都是小于100的合数,并且A、B、C、D两两互质,则A+B+C+D的最大值为_______。
由于此题求和的最大值,所以我们要使每个数尽量大,且保证其两两互质,故分别取99,95,94,91,和为379。
【例4】(2011年4题)一个数是质数,+10 +14 都是质数,求这个数是几?这个数为3。
【例5】(2011年6题)A是大于0的最小自然数,B是质数中唯一的偶数,C是最小的奇质数,C和D的和是70,问:A+B×C×D×(B+C)=_______。
A=1,B=2,C=3,D=67;A+B×C×D×(B+C)=2011【例6】(2011年14题)有一个三位数,各个数位都不为0,且不相同,把这三个数交换位置,形成5个不同的三位数,其平均数为这三位数,求这三个数最大数多少?设此三位数为abc ,则形成的5个三位数在加上原数就是原数的6倍 则有:222()6a b c abc ++=,37()abc a b c =++;三位数各不相同,最大629符合要求。
第二届陈省身杯数学奥林匹克第6题_省略_广_兼谈一类二次齐次不等式的证法

当 y=- 5 x , z =2 x 时, 左端等号成立; 当 y=槡 5 x , z =2 x 槡 时, 右端等号成立. 所以 5 5 x y+2 y z 槡 , 最大值为 槡 . 2 2 2 的最小值为 - 2 2 +y +z x
评注: 这类问题以往通常是利用待定系数法与均值不等 式的知识解决, 以上锁定主元, 巧用判别式的方法不仅解法 直观简单, 而且给出了这类不等式问题的共同渊源与命制背 景. 其实在运用中我们也不需要死死记住这个结论, 只要理 解以上推广的证明思路, 这类试题的解决便不在话下.
参考文献 [ 1 ]李建泉, 李宝毅, 丁云龙, 潘铁, 宋强. 第二届陈省身杯全国高中 数学奥林匹克[ J ] . 中等数学, 2 0 1 1 ( 9 ) : 2 8-3 2 . [ 2 ]贺斌, 贺聪. 第二届陈省身杯数学奥林匹克第 6题的推广[ J ] . 中 等数学, 2 0 1 2 ( 2 ) : 1 1-1 2 . [ 3 ]张. 两个“ 怪异”不等式的统一简证[ J ] . 中学数学教学参考, 2 0 1 2 ( 7 ) : 3 1 . [ 4 ]李锋. 一类二次齐次不等式证法的探究过程 [ J ] . 数 学 教 学, 2 0 1 3 ( 5 ) : 2 4-2 5 . [ 5 ]张同语, 王兆臣. 一道考题的自觉分析[ J ] . 数学教学, 2 0 1 3 ( 4 ) : 4 4-4 5 .
2 2 2 2 2 2 z , 有m ( x +y +z ) x y +b y z +c z x ( x +y +z ) ∈R a n
恒成立, 则 m的最大值 m 的最小值 n m a x与 n m i n 分别为关于 f
小学数学竞赛陈省身杯2009-2011年六年级真题
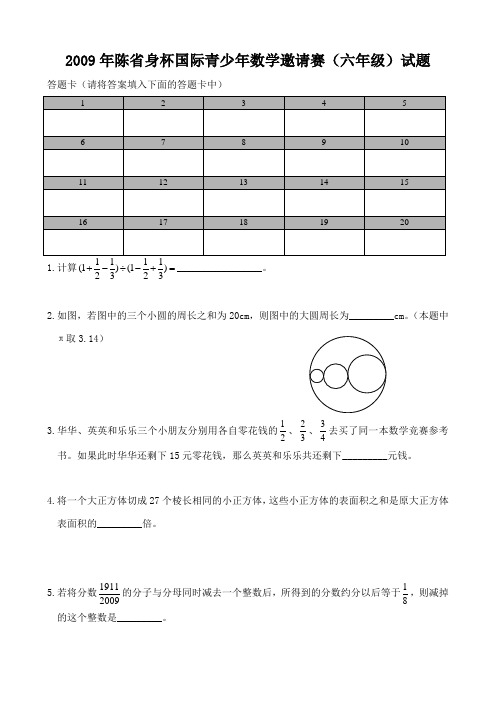
2009年陈省身杯国际青少年数学邀请赛(六年级)试题答题卡(请将答案填入下面的答题卡中)1.计算(1)(1)2323+-÷-+=_________________。
2.如图,若图中的三个小圆的周长之和为20cm,则图中的大圆周长为_________cm。
(本题中π取3.14)3.华华、英英和乐乐三个小朋友分别用各自零花钱的12、23、34去买了同一本数学竞赛参考书。
如果此时华华还剩下15元零花钱,那么英英和乐乐共还剩下_________元钱。
4.将一个大正方体切成27个棱长相同的小正方体,这些小正方体的表面积之和是原大正方体表面积的_________倍。
5.若将分数19112009的分子与分母同时减去一个整数后,所得到的分数约分以后等于18,则减掉的这个整数是_________。
6.如图中,一个小正六边形内接于一个圆,一个大正六边形外切于同一个圆。
若大正六边形的面积为10平方厘米,则其中小正六边形的面积为_________平方厘米。
7.1000以内的自然数,有些数不能被2整除,有些数不能被3整除,有些数不能被5整除,那么,这样的数共有_________个。
8.在下面的算式中,不同的汉子代表不同的数字,则其中四位数“我要加参”最小是_________。
比赛+ 陈省身我要参加.9.有三批货物共值152万元,第一、二、三批货物按重量比为2:4:3,按单价比为6:5:2,这三批货物分别值_________万元、_________万元和_________万元。
10.将2009除以一个两位数,所得的余数为7,则满足条件的两位数共有_________个。
11.计算1119111243234++++++=__________________。
12.A、B、C、D都是小于100的合数,并且A、B、C、D两两互质,则A+B+C+D的最大值为_________。
13.如图,两个正方形的中心相同,其对应边成45度角,若两个阴影三角形的面积分别为362cm和50362cm,则其中较大正方形的面积为_________2cm。
第九届陈省身杯全国高中数学奥林匹克竞赛(浙江预赛)试题及解答

令 f x
x
3
x 1
2
x
2
2 1 x 1 x2
x
3
x 1
2
2 1 x 1
0 ,则
x
2
2 1 x 1 x2
2
由于 x
2 1 x 1 0 。 2 1 x 1 0 的判别式小于 0 ,则该方程无实根。
1 1 2 , t
2 2 1 1 2 1 f t 3 2 t 1 2 3 t 0 ,因此函数 f t 为凸函数,由琴生不等 t t t t
L, M , N , K ,则四面体 LMNK 的内切球的半径为
答
。
3 2 。 2
设四面体 LMNK 的内切球的半径为 r ,因为 NLK LNM 90 ,所以
1 2 2 。 S LMN S LNK 1 2 2 4
又因为 MLK MNK 90 ,所以 S LMK S MNK
5, 43+19
2 11 14 。
x 1 x 0 x 1 ,若 f x 的最大值为 f x0 x3 x 1
,则 x0
6.设函数 f x 。 答
2 1 2 2 1 。 2
x 4 2 x3 x 2 2 x 1
式可得 f x f y 2 f
3 3
x y 2f 2
1 1 125 。当 x y 时等号成立,因此 4 2 2
125 1 1 。 x y 的最小值为 4 x y
2022-2023学年小学六年级奥数典型题测评卷14《等积变形》(解析版)

【六年级奥数举一反三—全国通用】测评卷14《等积变形》试卷满分:100分考试时间:100分钟姓名:_________班级:_________得分:_________一.选择题(共5小题,满分15分,每小题3分)1.(2014•迎春杯)如图,大正六边形内部有7个完全一样的小正六边形,已知阴影部分的面积是180平方厘米.那么大正六边形的面积是()平方厘米.A.240 B.270 C.300 D.360【分析】按题意,显然可以将图进行分割,分割后阴影部分有六个面积相等的小正六边形,而空白部分是3个面积相等的小正六边形,利用面积之比不难求得大正六边形的面积.【解答】解:如图所示,将图分割成面积相等的小正三角形,显然,图中的空白部分的面积和等于3个小正六边形.而阴影部分由6个小正六边形组成,所以,大正六边形是由9个小正六边形组成的.一个小正六边形的面积为:180÷6=30(平方厘米),大正六边形的面积为:30×9=270(平方厘米),故选:B.2.(2014•迎春杯)如图,大正方形的边长为14,小正方形的边长为10,阴影部分的面积之和是()A.25 B.40 C.49 D.50【分析】按题意,将图①逆时针旋转90°,阴影部分可拼成一等腰直角三角形,不难求得阴影部分的面积.【解答】解:根据分析,如下图所示,图①逆时针旋转90°,阴影部分可拼成一等腰直角三角形,S=142÷4=49故选:C.3.(2006•创新杯)图中,将两个正方形放在一起,大、小正方形的边长分别为10,6,则图中阴影部分面积为()A.42 B.40 C.38 D.36【分析】由图意可知:阴影部分的面积就等于两个正方形的面积和减去两个空白三角形的面积,利用正方形和三角形的面积公式即可求解.【解答】解:10×10+6×6﹣6×(10+6)÷2﹣10×10÷2=100+36﹣48﹣50=38答:阴影部分的面积是38.故选:C。
植树问题学生版

植树问题综合运用本讲说明:主要介绍两端都种、只种一端、两端都不种和封闭图形四种基本类型的植树问题,以及锯木头、爬楼梯、敲钟三个植树拓展。
对于植树问题而言,“段数”是核心,解决植树问题的基本思路即判断植树类型,确定“段数”和“棵树”之间的关系,拓展题目部分有些涉及到与容斥原理的综合等题目,难度稍大,老师可结合班级情况选择性讲解。
【基本公式】段数= 总长÷每段长每段长= 总长÷段数总长= 每段长×段数四大类型1.两端都种(两端都没有障碍物):棵数=段数+12.只种一端(一端有障碍物):棵树=段数3.两端都不种(两端都有障碍物):棵树=段数-14.封闭图形:棵树=段数常 1.已知棵数,及每段长(即题目中两棵树的距离)锯木头:刀数=段数-1注:锯木头问题,钱和时间都花在刀数上。
爬楼梯:住的层数=爬的层数+1(一楼敲钟:间隔=点数-1(时间花在敲钟间隔里)温馨小贴士:植树问题的核心是“段数”:路长----段数----棵数& 棵数----段数----路长;“两边”、“两侧”、“两旁”,先看一边。
1. (2010年第十一届“中环杯” 三年级决赛)在长120米的直道上,从距离起点4米处开始,依次重复地轮换插上红、黄、蓝三种彩旗,相邻的两面彩旗间间隔4米。
问:距离起点88米的地方插不插旗?如果插,插的是什么颜色的旗?2. (2009年第十届“中环杯” 三年级决赛)小林与小胖比赛爬楼梯,小林跑到第6楼时,小胖恰好跑到第5楼。
以这样的速度,小林跑到第31楼时,小胖跑到第()楼。
【例1】【例1】为了优化居住环境,大头儿子一家进行了轰轰烈烈的植树活动。
(1)大头儿子的任务是要在家门口600米长的公路一边每隔4米种一棵树,那么他需要种多少棵树?(2)小头爸爸负责家门口到邻居家的一段路。
路长200米,每隔4米种一棵树,小头爸爸需要种多少棵树?(3)大头儿子和爸爸要一起在家门口长1000米的路上每隔10米装一盏路灯,一共要装多少盏?(4)围裙妈妈要在后院周长为200米的水池周围种树,每隔4米种一棵,求围裙妈妈一共要种多少棵树?【例2】【例2】(1)一个湖泊周长1800米,沿湖泊周围每隔3米栽一棵柳树,每两棵柳树中间栽一棵桃树,湖泊周围栽柳树()棵,栽桃树()棵。
五年级组“陈省身杯”模拟题试卷教案:促进教师专业发展

本文主要介绍五年级组“陈省身杯”模拟题试卷教案的制作过程,着重探讨该教案如何能促进教师的专业发展。
一、教案制作的背景与意义良好的教案不仅能够提高课堂教学质量,还能够促进教师的专业发展。
一份优质的教案不仅要符合教学大纲和教材要求,更需要体现教师的教学特色和个性思维。
在教案制作时,教师需要先了解学生的学习状况,再根据学生的实际情况设计相应教学内容,使其更加符合学生的需求和特点。
五年级组“陈省身杯”模拟题试卷教案是为了促进教师专业发展而制作的。
该教案对五年级的学生群体进行了深入调研,分析了其学习特点和学习习惯,注重探究学生的兴趣点和思维方式。
在教学内容的设计过程中,注重贯彻“以学生为中心”的教育理念,注重发挥学生参与性,激发学生的学习热情和积极性,从而达到促进教师专业发展的目的。
二、主要思路和教学实施2.1 教学目标通过该教案,能够使学生进一步了解自我,提升自信心,促进个人发展。
同时,也引导他们更好地了解司法、理解法治社会,增强对法律的敬畏和遵守守规划定的意识。
2.2 教学内容(1) 以“守法学习、弘扬小学生社会主义核心价值观”为主线,设计相关教学任务。
(2) 开设相关习惯变得更加有纪律和有条理,使学生养成良好的学习习惯和行为规范,并通过阅读法律知识图书等,使学生在学习中渐渐领悟出遵纪守法的重要性。
(3)引导学生关注家渊及身边的社会公德,培养家渊公益意识。
2.3 教学方法(1)以情境教学的方法实现教学内容的生动化,清晰的教育形象引发学生的学习兴趣。
(2)采取多元化的教育方式,如游戏式教学等,引导学生积极参与。
(3)以案例分析和角色扮演等教学方式,引导学生从实际中学习,加深对法律值的认识。
2.4 教学评价在教学过程中,采用多元化的教学评价方式。
注重通过考试、作业及课堂讨论等评估学生的学习态度、学习成果及思想观念。
三、教案效果五年级组“陈省身杯”模拟题试卷教案专注于促进教师专业发展,按照“以学生为中心”的教育理念,注重简化知识点,突出教学重点,通过丰富多彩的教学方式,激发学生的学习兴趣和主动性,使学生在轻松愉悦中获得学习成就。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2011年“陈省身数学周”六年级组真题
1.在下面的四个数3.14,314%,3.1415和π中,最大的是_____,最小的是_____。
2.一份稿件,甲需要6天才能完成打印,乙需要10天才能完成打印,那么两人合打3天
共完成这份稿件的_____。
3.如下图,已知正方形的边长为2cm,则阴影部分的周长为_____cm。
(π取3.14)
第3题图第5题图第9题图
4.有一个质数,用它分别加上10与14以后,所得和仍为质数,这个质数是_____。
5.如上图表示的长方体(单位:dm),其长和宽都是3dm,体积是36dm³,则这个长方形
的表面积是_____dm²。
6.已知A是大于0的最小自然数,B是质数中唯一的一个偶数,C是最小的奇质数,C和
D的和等于70,那么()_____
A B C D B C
+⨯⨯⨯+=。
7.一个分数的分子与分母之和是100。
将它的分子、分母都减去6后约分得1
3
,那么原来
的分数是_____。
8.把同一段铁丝围城一个正方形后,又改围成一个圆形,发现按照面积公式得出的二者面
积之比为4:5,那么在计算圆面积时,圆周率π的取值为______。
9.一个六位数能被99整除,竖式如图所示,则这个六位数最小可以是______。
10.搬运一批货物,甲车单独运要运6次,乙车每次可运7.2吨。
现在甲、乙两车合运,运
的次数相同,完成任务时,甲、乙两车搬运货物重量的比是5:3,这批货物共有_____吨。
11. 计算111111111335192124_____11111111111123234345192021
++++
++++=1⨯⨯⨯⨯⨯⨯⨯⨯ 。
12. 甲、乙两班期末考试平均成绩的统计表如图所示,已知甲、乙两班的女生人数相同,那么这两个班全体同学的平均成绩是_____分。
平均分 甲班 乙班 男生 86
95 女生
94 88 全体
89
92
13. 从1至2011中任取若干个数,并且保证其中任意5个数之和都是15的倍数,最多可以
取出_____个数。
14. 如下图,将边长8厘米和12厘米的两个正方形并放在一起,那么图中阴影三角形的面
积是____平方厘米。
第14题图 第16题图 第18题图
15. 一个底面内半径为6厘米的圆柱形容器中盛有水,水面高4.8厘米,在其中放入一个长
和宽分别为4厘米和3厘米的长方形铁块后,长方形的上表面刚好露出水面,那么长方体的高是_____厘米。
(π取3)
16. 请将1~9这九个数字各一个填入上图中的圆圈中,使得图中每个小正方形顶点的4个数
字之和都等于S ,且大正方形顶点所填的4个数是连续的自然数(其中两个为5和6已填出),则S 是_____。
17. 一个三位数,各位数字非零且互不相同,经过调换各位数字的顺序得到5个新的三位数,
其平均数恰好等于原来的三位数,那么原来的三位数最大是_____。
18. 如图,甲圆和乙圆的面积之和是丙圆面积的五分之三,甲圆内阴影部分面积占甲圆面积
的三分之一,乙圆内阴影部分面积占乙圆面积的二分之一,丙圆内阴影部分面积占丙圆面积的四分之一,那么甲、乙两圆面积之比为_____。
19. 一次测验共有10道题,每道题完全答对可以得5分,答对一半可以得3分,答错或不
答不得分,至少有_____人参加比赛才能保证有3人的得分相同。
20.沿着东湖河岸绕湖一周是22千米,甲、乙二人从湖边某一地点同时出发反向而行。
甲
以4千米/小时的速度每走1小时后休息5分钟,乙以6千米/小时的速度每走50分钟
后休息10分钟。
则两人出发到第一次相遇用_____分钟。
