材料力学附录(截面特性)
§A-2 静矩、形心及相互关系
任意平面几何图形如图A-1所 示。在其上取面积微元dA，该微 元在Oxy坐标系中的坐标为x、 y。定义下列积分：
（A-1）
分别称为图形对于x轴和y轴的截 面一次矩或静矩，其单位为
。 如果将dA视为垂直于图形平面的
化，而当α=α0时，二者分别为极大值和极小值。
定义 过一点存在这样一对坐标轴，图形对于其惯性积等于零，这一对坐标轴便称为过这一点 的主轴。图形对主轴的惯性矩称为主轴惯性矩，简称主惯性矩。显然，主惯性矩具有极大或极 小的特征。
根据式(A-20)和(A-21)，即可得到主惯性矩的计算式
(A-23) 需要指出的是对于任意一点(图形内或图形外)都有主轴，而通过形心的主轴称为形心主轴，图
和惯性积，相加(空洞时则减)后便得到整个图形的 、
和
。
·应用式(A-21)和(A-22)确定形心主轴的位置，即形心主轴与x轴的夹角α0。
·利用转轴定理或直接应用式(A-23)计算形心主惯性矩
和
。
file://D:\收藏\专业相关\附录A平面图形的几何性质.htm
2005-8-23
附录A平面图形的几何性质
,
(A-14)
根据式(A-10)、(A-11)，注意到圆形对于通过其中心的任意两根轴具有相同的惯性矩，便可得 到圆截面对于通过其中心的任意轴的惯性矩均为
对于外径为D、内径为d的圆环截面,
(A-15)
(A-16)
应用上述积分，还可以计算其他各种简单图形对于给定坐标轴的惯性矩。 必须指出，对于由简单几何图形组合成的图形，为避免复杂数学运算，一般都不采用积分的方 法计算它们的惯性矩。而是利用简单图形的惯性矩计算结果以及图形对于平行轴惯性矩之间的 关系，由求和的方法求得。
设
、
为形心坐标，则根据合力之矩定理
(A-2) 或
页码，3/14
(A-3)
这就是图形形心坐标与静矩之间的关系。 根据上述定义可以看出： 1.静矩与坐标轴有关，同一平面图形对于不同的坐标轴有不同的静矩。对某些坐标轴静矩为 正；对另外某些坐标轴为负；对于通过形心的坐标轴，图形对其静矩等于零。
2.如果已经计算出静矩，就可以确定形心的位置；反之，如果已知形心位置，则可计算图形的
因为组合图形都是由一些简单的图形(例如矩形、正方形、圆形等)所组成，所以在确定其形 心、形心主轴以至形心主惯性矩的过程中，均不采用积分，而是利用简单图形的几何性质以及 移轴和转轴定理。一般应按下列步骤进行。
·将组合ห้องสมุดไป่ตู้形分解为若干简单图形，并应用式(A-5)确定组合图形的形心位置。
·以形心为坐标原点，设Ozy坐标系x、y轴一般与简单图形的形心主轴平行。确定简单图形对 自身形心轴的惯性矩，利用移轴定理(必要时用转轴定理)确定各个简单图形对x、y轴的惯性矩
页码，12/14
可以看出，确定形心主惯性矩的过程就是综合应用本章§A-2～§A-6全部知识的过程。
§A-8 例题
例题A-1 截面图形的几何尺寸如图A-7所示。试求图中具有断面线部分的Ix、Iy。 解: 根据积分定义，具有断面线的图形对于x、y轴的惯性矩，等于高为h、宽为b的矩形对于 x、y轴的惯性矩减去高为 的矩形对于相同轴的惯性矩，即
静矩。
实际计算中，对于简单的、规则的图形，其形心位置可以直接判断。例如矩形、正方形、圆 形、正三角形等的形心位置是显而易见的。对于组合图形，则先将其分解为若干个简单图形 (可以直接确定形心位置的图形)；然后由式(A-2)分别计算它们对于给定坐标轴的静矩，并求 其代数和；再利用式(A-3),即可得组合图形的形心坐标。即:
file://D:\收藏\专业相关\附录A平面图形的几何性质.htm
2005-8-23
附录A平面图形的几何性质
力，则ydA和zdA分别为dA对于z
轴和y轴的力矩；
和
则分别为dA对z轴和y轴之矩。图 A-1图形的静矩与形心图形几何 形状的中心称为形心,若将面积 视为垂直于图形平面的力，则形 心即为合力的作用点。
为图形对于点O的截面二次极矩或极惯性矩。 定义积分
为图形对于通过点O的一对坐标轴x、y的惯性积。 定义
(A-7) (A-8)
(A-9)
, 分别为图形对于x轴和y轴的惯性半径。 根据上述定义可知：
file://D:\收藏\专业相关\附录A平面图形的几何性质.htm
2005-8-23
附录A平面图形的几何性质
2005-8-23
附录A平面图形的几何性质
轴的惯性矩、惯性积，求图形对另一对坐标轴的惯性矩与惯性积。 下面推证二者间的关系。 根据平行轴的坐标变换
页码，7/14
将其代人下列积分 ,
得
展开后,并利用式(A-2)、(A-3)中的定义，得
(A-17)
如果x、y轴通过图形形心，则上述各式中的
=
=0。于是得
§A-5 惯性矩与惯性积的转轴定理
所谓转轴定理是研究坐标轴绕原点转动时， 图形对这些坐标轴的惯性矩和惯性积的变化 规律。
图A-5所示的图形对于x、y轴的、惯性矩和惯
性积分别为 、
和
。
现将Oxy坐标系绕坐标原点。反时针方向转过 α角，得到一新的坐标系，记为Ox1y1。要考察
的是图形对新坐标系的
、
、
与、 、
与
相加，不难得到
这表明：图形对一对垂直轴的惯性矩之和与α角无关，即在轴转动时，其和保持不变。
上述式(A-19)、(A-20)，与移轴定理所得到的式(A-18)不同，它不要求x、y通过形心。当然， 对于绕形心转动的坐标系也是适用的，而且也是实际应用中最感兴趣的。
§A-6主轴与形心主轴、主矩与形心主矩
从式(A-19)的第三式可以看出，对于确定的点(坐标原点)，当坐标轴旋转时，随着角度α的改 变，惯性积也发生变化，并且根据惯性积可能为正，也可能为负的特点，总可以找到一角度α0 以及相应的x0、y0轴，图形对于这一对坐标轴的惯性积等于零。为确定α0，令式(A-19)中的第
,
(A-12) (A-13)
式中，D为圆环外径；d为内径。 4.根据惯性矩的定义式(A-6)、(A-7)，注意微面积的取法(图A-3所示)，不难求得矩形对于平 行其边界的轴的惯性矩：
file://D:\收藏\专业相关\附录A平面图形的几何性质.htm
2005-8-23
附录A平面图形的几何性质
页码，6/14
上述方法称为负面积法。用于图形中有挖空部分 的情形，计算比较简捷。
心主惯性矩。
例题A-2 T形截面尺寸如图A-8a所示。试求其形
解：1.分解为简单图形的组合。
将T形分解为如图A-8b所示的两个矩形I和II。
2.确定形心位置
首先，以矩形I的形心C1为坐标原点建立如图A-8b所示的C1xy坐标系。因为y轴为T字形的对称 轴，故图形的形心必位于该轴上。因此，只需要确定形心在y轴上的位置，即确定yc。根据式 (A-5)的第二式，形心C的坐标
矩、惯性矩、惯性半径、极惯性矩、惯性 学
积、主轴等）的概念。 目
2、 能正确计算组合图形的形心、形心 的 主轴、形心主惯性矩。
重 重点：形心、静矩、惯性矩、惯性半径、
极惯性矩、惯性积、主轴等概念及其计 点
算。 和
难点：惯性矩与惯性积的转轴公式及主惯 难 性矩的计算。
点
教学 以常见的圆形、圆环、矩形、T形、常见型
file://D:\收藏\专业相关\附录A平面图形的几何性质.htm
2005-8-23
附录A平面图形的几何性质
三式为零， 即
页码，10/14
由此解得
(A-21) 或
如果将式(A-20)对α求导数并令其为零，即
(A-22)
，
同样可以得到式(A-21)或(A-22)的结论。这表明:当α改变时,
、
的数值也发生变
file://D:\收藏\专业相关\附录A平面图形的几何性质.htm
2005-8-23
附录A平面图形的几何性质
页码，2/14
方法 钢截面的组合圆形为主。 作业
附录A 平面图形的几何性质
§A-1 引言
不同受力形式下杆件的应力和变形，不仅取决于外力的大小以及杆件的尺寸，而且与杆件截面 的几何性质有关。当研究杆件的应力、变形，以及研究失效问题时，都要涉及到与截面形状和 尺寸有关的几何量。这些几何量包括：形心、静矩、惯性矩、惯性半径、极惯性短、惯性积、 主轴等，统称为“平面图形的几何性质”。
file://D:\收藏\专业相关\附录A平面图形的几何性质.htm
2005-8-23
附录A平面图形的几何性质
页码，13/14
3.确定形心主轴
因为对称轴及与其垂直的轴即为通过二者交点的主轴，所以以形心C为坐标原点建立如图A-12c 所示的Cx0y0坐标系，其中y0通过原点且与对称轴重合，则x0、y0即为形心主轴。
形的惯性积，二者数值相等，但反号。所以，整个图形对于x、y轴的惯性积 对称轴为主轴x、y为主轴。又因为C为形心，故x、y为形心主轴。
=0，故图A-6
§A-7组合图形的形心、形心主轴
工程计算中应用最广泛的是组合图形的形心主惯性矩，即图形对于通过其形心的主轴之惯性 矩。为此必须首先确定图形的形心以及形心主轴的位置。
页码，5/14
1.惯性矩和极惯性矩恒为正；而惯性积则由于坐标轴位置的不同，可能为正，也可能为负。三
者的单位均为
或
。
2.因为
=
+
，所以由上述定义不难得出
=+
(A-10)
3.根据极惯性矩的定义式(A-8)，以及图A-2中所示的微面积取法，不难得到圆截面对其中心的 极惯性矩为
材料力学截面特性汇总
材料力学截面特性汇总一、引言材料力学截面特性是材料在应力作用下的力学性能表现。
在工程设计和结构分析中，了解材料力学截面特性对于确保结构的稳定性和安全性至关重要。
本文将对常见材料的力学截面特性进行汇总和总结，以供工程师和设计师参考和应用。
二、材料力学截面特性的概念材料力学截面特性是指材料在截面上的力学性能。
根据截面特性的研究对象的不同，可以分为以下几个方面：1. 截面形状特性截面形状特性是指截面的几何形状对其力学性能的影响。
截面形状特性包括截面面积、截面惯性矩、截面备战半径等。
例如，在梁的设计中，截面形状特性可以用来计算梁的承载能力和抗弯刚度。
2. 材料特性材料特性是指材料的物理和力学性质对其截面性能的影响。
材料特性包括杨氏模量、泊松比、屈服强度等。
在结构设计过程中，需要结合材料特性来计算结构的应变和应力分布。
3. 比例限制特性比例限制特性是指截面受应力作用时，截面形变受限的程度。
比例限制特性包括平面内应变、截面扭转等。
在设计中，比例限制特性能够预测结构在加载过程中的变形情况，从而优化结构设计。
三、常见材料的力学截面特性1. 钢材钢材是一种广泛应用于工程和建筑领域的材料，具有良好的力学性能和强度。
常见的钢材力学截面特性包括：•弹性模量：钢材的弹性模量通常较高，能够承受较大的应力而不发生塑性变形。
•屈服强度：钢材的屈服强度表示了钢材能够承受的最大应力，超过屈服强度后，钢材会发生塑性变形。
•剪切模量：剪切模量描述了钢材在剪切应力作用下的变形程度。
•截面惯性矩：截面惯性矩用于计算梁的扭转刚度和截面的抗扭能力。
2. 混凝土混凝土是一种常用于建筑结构的材料，具有较高的抗压强度和耐久性。
混凝土的力学截面特性包括：•压力区形状特性：混凝土在受压作用下会出现压力区，该区域的形状对混凝土的抗压承载能力有影响。
•弯曲形变特性：混凝土在受弯曲作用下会产生变形，在设计过程中需要考虑混凝土的弯曲刚度和变形限制。
•截面抗剪特性：混凝土的截面抗剪特性影响着结构的抗剪能力，在设计中需要选择适当的截面形状和钢筋布置来增强抗剪能力。
附录 截面的几何性质(材料力学)
b b( y ) ( h y ) h
b(y )
S x A y d A 0
b bh2 (h y ) y d y h 6
h
dy
材 料 力 学 Ⅰ 电 子 教 案
例 试确定图示截面心 C 的位置。 解：将截面分为 1，2 两个矩形。 取 x 轴和 y 轴分别与截面 的底边和左边缘重合 y
10
1
x1
C( y, x )
y1
o
2
y2
10
x2
80
x
材 料 力 学 Ⅰ 电 子 教 案
思考： 求下图所示截面的形心位置
50
10 A1
z
60
A2
10
y
12
yc1 A1 yc 2 A2 yc A1 A2
材 料 力 学 Ⅰ 电 子 教 案
例 半径为r的半圆：求半圆的形心。 解 在距 z 轴任意高度 y 处取狭长条 作为微面积，即
分别称为截面图形对于z轴和y 轴的惯性矩。 惯性矩的数值恒为正，常用单位为m4 。
14
dA
y x
材 料 力 学 Ⅰ 电 子 教 案
二、极惯性矩
y
I p 2 dA
A
称为截面图形对O点的极惯性矩。
x
dA y x
2 x2 y 2
I p 2dA x 2 y 2 dA x 2dA y 2dA I y I x
A
y
z y A o
A
A
y
dA z
y
ydA S A z A A
求静矩的另一公式：
Sy x A
5
Sx y A
材料力学
bh3 bh2 12 h 6 2
h
y
z
实心圆
空心圆
z y
z C y d
D
Iz
D 4
64
Iz
D 4 d 4
64 64
4
Wz
D 3
32
d Wz (1 ) D 32
D 3
41
箱形截面
y
Iz Wz ymax
BH bh 12 12 H 2
3 3
x y
y
y
min
xy
x
2 一点处有三个主应力，按代数 值大小排列分别记为 1，2， 3
2 0、（2 0 ） 0、（ 0 ）
x
max
1 2 3
极值剪应力
x y 2 2 max max min ( ) xy 2 2 min
P P P d Pbs t
挤压面
有效挤压面积 dt
双剪——有两个剪切面
Q=P/2
Q
P/2 P P P P/2 二个剪切面 P
Q
三、实用计算及强度条件
实用计算
1、假定剪切面上的应力分布规律；
2、确定破坏应力的试验，所用试件的形状及受力 情况与实际构件相似或相同。
强度条件 剪切强度条件 剪断条件
m=Q/Am [m]
1 2
max
1 3
2
3
2 1
12
2 2 3 23 2 1 3 13 2
五、 复杂应力状态下应力应变关系
1 x x y E
1 y y x E
y
截面特性值
截面特性值
sax对x轴的面积矩；say对y轴的面积矩
ixx,iyy,ixy分别是对x轴的惯性矩，y轴惯性矩，xy的截面惯性积，对应于材料力学
帮助文件说明如下：
Asy：单元局部坐标系y轴方向的有效抗剪面积(Effective Shear Area)。
Asz：单元局部坐标系z轴方向的有效抗剪面积(Effective Shear Area)。
Ixx：对单元局部坐标系x轴的扭转惯性距(Torsional Resistance)。
Iyy：对单元局部坐标系y轴的惯性距(Moment of Inertia)。
Izz：对单元局部坐标系z轴的惯性距(Moment of Inertia)。
Cyp：沿单元局部坐标系+y轴方向，单元截面中和轴到边缘纤维的距离。
Cym：沿单元局部坐标系-y轴方向，单元截面中和轴到边缘纤维的距离。
Czp：沿单元局部坐标系+z轴方向，单元截面中和轴到边缘纤维的距离。
Czm：沿单元局部坐标系-z轴方向，单元截面中和轴到边缘纤维的距离。
Qyb：沿单元局部坐标系z轴方向的剪切系数。
Qzb：沿单元局部坐标系y轴方向的剪切系数。
Peri:O ：截面外轮廓周长。
Peri:I ：箱型或管型截面的内轮廓周长。
Cent:y ：从截面最左侧到形心轴的距离。
Cent:z ：从截面最下端到形心轴的距离。
y1、z1：截面左上方最边缘点的y、z坐标。
y2、z2：截面右上方最边缘点的y、z坐标。
y3、z3：截面右下方最边缘点的y、z坐标。
y4、z4：截面左下方最边缘点的y、z坐标。
材料力学--附录A截面的几何性质
y
A
其中： 为截面面积 为截面面积， 、 其中：A为截面面积，x、 y轴为形心轴， x1、 y1为 轴为形心轴， 轴为形心轴 分别与x、 轴平行的轴 轴平行的轴， 分别与 、y轴平行的轴， a、b分别为相应平行轴之 、 分别为相应平行轴之 间的距离。 间的距离。
O a O1 b
z
附录A 附录
截面的几何性质
附录A 附录
截面的几何性质
静矩、 g 静矩、形心及其相互关系 惯性矩、极惯性矩、惯性积、 g 惯性矩、极惯性矩、惯性积、惯性半径 g 惯性矩与惯性积的平行移轴定理 g 惯性矩与惯性积的转轴定理 主轴与形心主轴、 g 主轴与形心主轴、主惯性矩与形心主惯性矩 组合图形形心、 g 组合图形形心、形心主轴和形心主矩的计算
试确定等腰梯形面积的形心和对底边的静矩。 试确定等腰梯形面积的形心和对底边的静矩。
y
【解】 截面对底边的静矩
Sz = A y1 + A y2 1 2
b C1
h
1 2 1 h = bh⋅ h + ah⋅ 2 3 2 3
C C2
=
h (a+2b) 6
2
O a
z
形心位置
zC = 0
Sz h a +2b yC = = ⋅ A 3 a +b
120
C1（0,0） 负面积 C2（5,5） C2 C1 C
10 80
z
yC = −20.3mm
形心C坐标为（ 形心 坐标为（-20.3， -20.3）。 坐标为 ， ）。
这两种方法所得到的形心坐标不同 是由于选择不同的坐标系引起的。 是由于选择不同的坐标系引起的。
附录A 附录 【例2】 】
截面的几何性质
《材料力学》附录I 截面的几何性质 习题解
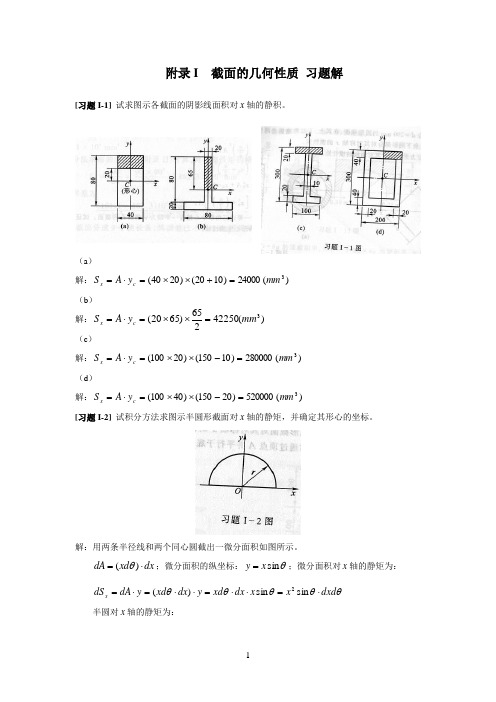
附录I 截面的几何性质 习题解[习题I-1] 试求图示各截面的阴影线面积对x 轴的静积。
（a ）解：)(24000)1020()2040(3mm y A S c x =+⨯⨯=⋅=（b ）解：)(42250265)6520(3mm y A S c x =⨯⨯=⋅= （c ）解：)(280000)10150()20100(3mm y A S c x =-⨯⨯=⋅=（d ）解：)(520000)20150()40100(3mm y A S c x =-⨯⨯=⋅=[习题I-2] 试积分方法求图示半圆形截面对x 轴的静矩，并确定其形心的坐标。
解：用两条半径线和两个同心圆截出一微分面积如图所示。
dx xd dA ⋅=)(θ；微分面积的纵坐标：θsin x y =；微分面积对x 轴的静矩为： θθθθθdxd x x dx xd y dx xd y dA dS x ⋅=⋅⋅=⋅⋅=⋅=sin sin )(2半圆对x 轴的静矩为：32)]0cos (cos [3]cos []3[sin 33003002r r x d dx x S r rx =--⋅=-⋅=⋅=⎰⎰πθθθππ因为c x y A S ⋅=，所以c y r r ⋅⋅=232132π π34ry c = [习题I-3] 试确定图示各图形的形心位置。
（a ） 解：解：[习题I-4] 试求图示四分之一圆形截面对于x 轴和y 轴的惯性矩x I 、y I 和惯性积xy I 。
解：用两条半径线和两个同心圆截出一微分面积如图所示。
dx xd dA ⋅=)(θ；微分面积的纵坐标：θsin x y =；微分面积对x 轴的惯性矩为： θθθθθdxd x dx xd x dx xd y dA y dI x ⋅=⋅⋅=⋅==232222sin sin )(四分之一圆对x 轴的惯性矩为： ⎰⎰⎰-⋅==2/0042/02322c o s 1]4[s i n ππθθθθd x d dx x I r rx)]2(2cos 21[2142/02/04θθθππd d r ⎰⎰-⋅= }]2[sin 212{82/04πθπ-=r 164r ⋅=π由圆的对称性可知，四分之一圆对y 轴的惯性矩为：164r I I x y ⋅==π微分面积对x 轴、y 轴的惯性积为：xydA dI xy =8)42(21]42[21)(21444042222022r r r x x r dx x r x ydx xdx I r rx r rxy =-=-=-==⎰⎰⎰- [习题I-5] 图示直径为mm d 200=的圆形截面，在其上、下对称地切去两个高为mm 20=δ的弓形，试用积分法求余下阴影部分对其对称轴x 的惯性矩。
材料力学 附录 截面的几何性质
(Properties of Plane Areas) 三、组合截面的静矩和形心 (The first moments ¢roid of a composite area)
由几个简单图形组成的截面称为组合截面.
截面各组成部分对于某一轴的静矩之代数和，等于该截 面对于同一轴的静矩.
(Properties of Plane Areas)
§1-1 截面的静矩和形心 (The first moment of the area & centroid of
an area)
一、静矩(The first moment of the area ）
截面对 y , z 轴的静矩为
z
S y
zdA
A
Sz
ydA
A
dA z
静矩可正，可负，也可能等于零.
1
矩形 2
A2 10 80 800mm2
y2
10
80 2
50mm
z2 5mm
所以 y A1 y1 A2 y2 23mm A1 A2
z A1z1 A2z2 38mm A1 A2
y1
z1
2 z2
10
O y2
y
90
(Properties of Plane Areas)
方法2 用负面积法求解，图形分割及坐标如图(b)
yC , zC￣ 过截面的形心 C 且与 y, z轴平行
的坐标轴(形心轴）
z
Iy , Iz , Iyz — 截面对 y, z 轴的惯性矩和惯性积.
zC
IyC , IzC , IyCzC￣ 截面对形心轴 yC , zC的惯性矩
n
Ai zi
z
材料力学附录(截面特性)
设
、
为形心坐标，则根据合力之矩定理
(A-2) 或
页码，3/14
(A-3)
这就是图形形心坐标与静矩之间的关系。 根据上述定义可以看出： 1.静矩与坐标轴有关，同一平面图形对于不同的坐标轴有不同的静矩。对某些坐标轴静矩为 正；对另外某些坐标轴为负；对于通过形心的坐标轴，图形对其静矩等于零。
2.如果已经计算出静矩，就可以确定形心的位置；反之，如果已知形心位置，则可计算图形的
,
(A-12) (A-13)
式中，D为圆环外径；d为内径。 4.根据惯性矩的定义式(A-6)、(A-7)，注意微面积的取法(图A-3所示)，不难求得矩形对于平 行其边界的轴的惯性矩：
file://D:\收藏\专业相关\附录A平面图形的几何性质.htm
2005-8-23
附录A平面图形的几何性质
页码，6/14
(A-18)
file://D:\收藏\专业相关\附录A平面图形的几何性质.htm
2005-8-23
附录A平面图形的几何性质
页码，8/14
此即关于图形对于平行轴惯性矩与惯性积之间关系的移轴定理。其中，式(A-18)表明： 1.图形对任意轴的惯性矩，等于图形对于与该轴平行的形心轴的惯性矩，加上图形面积与两平 行轴间距离平方的乘积。
之间的关系。
根据转轴时的坐标变换：
于是有
file://D:\收藏\专业相关\附录A平面图形的几何性质.htm
2005-8-23
附录A平面图形的几何性质
页码，9/14
将积分记号内各项展开，得
改写后，得
(A-19)
上述式(A-19)和(A-20)即为转轴时惯性矩与惯性积之间的关系。
（A-20）
若将上述
材料力学课后复习习题集
第二章 轴向拉伸与压缩1、试求图示各杆1-1和2-2横截面上的轴力,并做轴力图。
（1） （2）2、图示拉杆承受轴向拉力F =10kN ，杆的横截面面积A =100mm 2。
如以α表示斜截面与横截面的夹角，试求当α=10°,30°,45°,60°,90°时各斜截面上的正应力和切应力,并用图表示其方向。
3、一木桩受力如图所示。
柱的横截面为边长200mm 的正方形,材料可认为符合胡克定律,其弹性模量E =10GPa 。
如不计柱的自重，试求：(1)作轴力图；(2)各段柱横截面上的应力； (3)各段柱的纵向线应变；(4)柱的总变形。
4、(1)试证明受轴向拉伸(压缩)的圆截面杆横截面沿圆周方向的线应变d ε,等于直径方向的线应变d ε。
(2)一根直径为d =10mm 的圆截面杆,在轴向拉力F 作用下,直径减小0.0025mm 。
如材料的弹性摸量E =210GPa ，泊松比ν=0.3,试求轴向拉力F 。
(3)空心圆截面钢杆,外直径D =120mm,内直径d =60mm,材料的泊松比ν=0.3。
当其受轴向拉伸时, 已知纵向线应变ε=0.001,试求其变形后的壁厚δ。
5、图示A和B两点之间原有水平方向的一根直径d=1mm的钢丝,在钢丝的中点C加一竖直荷载F。
已知钢丝产生的线应变为ε=0.0035,其材料的弹性模量E=210GPa，钢丝的自重不计。
试求：(1) 钢丝横截面上的应力(假设钢丝经过冷拉,在断裂前可认为符合胡克定律)；(2) 钢丝在C点下降的距离∆；(3) 荷载F的值。
6、简易起重设备的计算简图如图所示.一直斜杆AB应用两根63mm×40mm×4mm不等边角钢组[σ=170MPa。
试问在提起重量为P=15kN的重物时,斜杆AB是否满足强度成,钢的许用应力]条件?7、一结构受力如图所示,杆件AB,AD均由两根等边角钢组成。
已知材料的许用应力[σ=170MPa，试选择杆AB,AD的角钢型号。
截面特性查询
目前，很多门窗软件附带型材截面特性的计算功能，但采用AutoCAD查询型材截面特性操作还是比较方便一、型材惯性矩、抵抗矩的物理参数查询1、从CAD中调出门窗校核对象中主受力构件梃（或组合构件）的截面图（制图比例必须为1：1）；2、在你的CAD中调出“实体”快捷键，其中包括“差集”、“并集”；3、取截面的面域：点击“面域”－>用鼠标选取整个截面轮廓；4、验证选取面域是否成功：点击每个轮廓线时都是连续的、封闭的，说明成功，否则，需要检查截面图，找出不连续位置后修改，再重复选择面域；5. 差集（将实体中的空缺删除，仅保留实体部分）：下图为是4个截面的组合，每个截面中间都有空腔，因此必须作4个截面各自的差集：选择“差集”，先左击第一个截面的外轮廓线，右击确定后，再左击该截面的内轮廓线（有几个内轮廓线，就左击几个），右击完成；再接着作下一个截面的差集；6、验证差集是否成功：点击一个截面上任意一点，显示该截面上所有内外轮廓线；7、并集（将所有实体合并为一个整体）：选择“并集”连续左击每个实体，右击完成。
鼠标左击截面，右击完成。
二、查询1、选择“工具”－>“查询”－>“面域/质量特性”2、点击截面任意处，弹出查询结果。
3、选择惯性矩值Ix：下图是查询结果表，其中的“惯性矩”，是该截面相对于世界坐标“0，0”的惯性矩值，“主力拒与值心的X-Y方向”的两个值才是我们需要的惯性矩，注意两个惯性矩的受力方向：第一个是沿着【1.0000 0.0000】，即x=1.0000，y=0.0000，画一个坐标，显然受力方向是沿x轴的；同理，第二个的受力方向是沿y轴的。
本例中的构件受力方向（风压方向）显然是沿y轴的，因此取惯性矩为：Ix＝387464mm4=38.7464cmm44、计算抵抗矩：由材料力学论证定义：抵抗矩Wx=Ix/YmanxYmanx是材料截面的中性轴距离材料截面轮廓线的最大垂直距离。
计算方法1：在查询表中，已经给出“边界框”的两组坐标和“质心”的坐标，具体位置如右图所示。