材料力学截面的几何性质答案
材料力学 截面的几何性质
录
附录Ⅰ
§Ⅰ-1 §Ⅰ-2 §Ⅰ-3 §Ⅰ-4
截面的几何性质
截面的静矩和形心位置 惯性矩、惯性积和惯性半径 平行移轴公式 转轴公式 主惯性矩
静矩与形心
一、静矩的定义(与力矩类似)（也称面积矩或一次矩） 截面对z轴的静矩： y 截面对y轴的静矩：
Sz Sy
dS
A A
z
ydA
A
3
z 100
I
C
CI
a1 a2
I y I yI I yII 443 10 768 10
4
4
y
1211 104 mm 4
由于z轴是对称轴 ，故图形对两轴的惯性积为
140 103.3
CII
II
y
I yz 0
20
I z y 2 dA 2h y 2 bdy
3
附
录
组合截面形心
组合截面：如果截面的图形是由几个简单图形(如矩形、圆形 等）组成的，这种截面称为组合截面。 组合截面对X、Y轴静矩的计算：
S x Ai yci Ayc
i
n
S y Ai xci Axc
i
n
Ai——任一简单图形的面积； xci，yci——任一简单图形的形心坐标； n——全部简单图形的个数。 确定组合截面形心位置的公式：
C H/2
X
1 h 1 h yc 1 y1 ( y1 ) ( y1 ) 2 2 2 2
h 1 h S x Ayc 1 b( y 1 ) ( y 1 ) 2 2 2
b
b 2 2 (h 4y1 ) 8
例2、图形对 x 轴的静矩为
(材料力学)截面几何性质习题及参考答案
截面几何性质 作业专业班级 姓名 学号1. 判断题（1）任意平面图形至少有1对形心主惯性轴，等边三角形有3对形心主惯性轴。
（ × ） （2）平面图形的几何性质中，静矩和惯性矩的值可正、可负、可为零。
（ × ） （3）平面图形中，使静矩为零的轴必为对称轴。
（ × ） 2. 选择题（1）若截面图形有对称轴，则该图形对其对称轴的（ A ）。
A. 静矩为零，惯性矩不为零B. 静矩和惯性矩均不为零C. 静矩和惯性矩均为零D. 静矩不为零，惯性矩为零（2）设图形具有三个以上（含三个）对称轴时，对某一形心轴的惯性矩I 1 ，对某一对正交形心轴的惯性积为I 2。
则当形心轴绕形心旋转时（ A ）。
A. I 1值不变，I 2恒等于零B. I 1 值不变，I 2不恒等于零C. I 1值变化，I 2恒等于零D. I 1值变化，I 2不恒等于零（3）任意图形的面积为A ，x C 轴通过形心C ，x 1轴和x C 轴平行，并相距a ，已知图形对x 1轴的惯性矩是I 1，则对x C 轴的惯性矩为（ A ）。
A. 21xC I I Aa =-B. 0xC I =C. 21xC I I Aa =+D. 1xC I I Aa =+C x 1（4）图示等底等高的矩形和平行四边形，对其形心轴y 的惯性矩I a 和I b 满足（ A ）。
A. I a = I bB. I a > I bC. I a < I bD. 不能确定（a ）（b ）（5）设矩形对其对称轴z 的惯性矩为I ，当其长宽比保持不变，面积增加1倍时，该矩形对其对称轴z 的惯性矩将变为（ A ）。
A. 4IB. 2IC. 8ID. 16I（6）图示任意形状图形，形心轴z 将图形分为两部分，则一定成立的是（ A ）。
A. S z 1 + S z 2 = 0B. I z 1 = I z 2C. A 1 = A 2D. S z 1 = S z 2（7）图形对通过某点的所有轴的惯性矩中，图形对主惯性轴的惯性矩一定（ A ）。
材料力学(金忠谋)第六版答案-附录
材料力学(金忠谋)第六版答案-附录附录I 截面图形的几何性质I-1 求下列截面图形对z 轴的静矩与形心的位置。
解：（a ）)2)2((2)2(2h t h b t h ht t h bt s z ++=⋅++=hb h t h b h b t h t h b t A s y zc +++=+++==2)2()()2)2((22（b ）322332219211)}2)4()43()41()43(32(])4()43[(2{4442DD D D D D D D D D s z =--⨯-+⨯⨯-=ππDD D D D DAs y z c 1367.0])2()43[(2)44(219211223=-⨯+⨯==π（c ）]22)[(22)(2h t t b t h ht t t t b s z +⋅-=⨯+⨯⨯-=tb)(2)(2t b h h t t b A s y z c -++-==I-2 试求（1）图示工字形截面对形心轴 y 及 z 的惯性矩zI 与I y 。
（2）图示 T 字形截面对形心轴的惯矩zI 与I y 。
解(a)12)2)((12)2)((123333t h t b bh t h t b bh J z ---=---=12))2(2(12))(2(1222333t t h b t t t h tb J y -+=-+=(b) cmy c 643.9)520515(2)515(552522=⨯+⨯-⨯+⨯=(b433423231615121551252010186520)643.91025(12205515)5.2643.9(12515cm J cm J y z =⨯+⨯==⨯⨯--+⨯+⨯⋅-+⨯=I-3 求图示椭圆截面对长轴的惯矩、惯性半径与对形心的极惯矩。
解：θθcos ,sin ⋅=⋅=a z b yθθd b dy cos = ⎰⎰--⋅==∴b bbbz zdyy dA y J 222322223224cos sin 2cos cos sin 2ab d abd b a b J bb z πθθθθθθθππ==⋅=⎰⎰--)(4)(42422333b a ab b a ab J J J b ab ab AJ i y z p zz +=+=+====ππππI-4 试求图示的41的圆面积（半径a ）对于z ，yyy 轴的惯性积zyI 。
材料力学 截面图形几何性质
（此为平行移轴公式 ）
注意： •式中的a、b代表坐标值，有时可能取负值。
•等号右边各首项为相对于形心轴的量。
9
材料力学Ⅰ电子教案
2.组合截面的惯性矩和惯性积
根据惯性矩和惯性积的定义易得组合截面对于某 轴的惯性矩（或惯性积）等于其各组成部分对于同一 轴的惯性矩（或惯性积）之和：
n
Ix
i1
I
xi
n
Iy
1
材料力学Ⅰ电子教案
二、形心公式：
yc
Sz A
; zc
Sy A
.
三、组合截面的静矩：n个简单图形组成的截面，其静矩为：
n
Sz Ai yci; i 1
n
S y Ai zci; i 1
n
四、组合截面形心公式：
Ai yci
yc
i 1 n
;
Ai
i 1
例5-1 求图示T形截面形心位置。
n
Ai zci
(20010) (5 150) 2 (10 300) 0 20010 2 (10 300)
38.8 mm
由于对称知： xc=0
3
y y1 200
C O
10 150 yC x1
x
目录
材料力学Ⅰ电子教案
求图示半径为r的半圆形对其直径轴x的静矩及其形心坐标yC。
解：过圆心O作与x轴垂直的y轴，在距x任意高度y处取一个与x 轴平行的窄条，
y
d A 2 r2 y2 • d y
dA
dy
yC
所以
Sx
A
yd
A
r
0
y( 2
r2 y2 )d y 2 r3 3
Cr
y
第26讲第五章 材料力学(九)
第五节截面图形的几何性质一、静矩与形心对图所示截面静矩的量纲为长度的三次方。
对于由几个简单图形组成的组合截面形心坐标显然，若z轴过形心，y c=0，则有S z=0，反之亦然：若y轴过形心，z c=0，则有S y=0，反之亦然。
【真题解析】5—30（2007年真题）图所示矩形截面，m-m线以上部分和以下部分对形心轴z的两个静矩( )。
(A)绝对值相等，正负号相同(B)绝对值相等，正负号不同(c)绝对值不等，正负号相同(D)绝对值不等，正负号不同解：根据静矩定义，图示矩形截面的静矩等于m-m线以上部分和以下部分静矩之和，即，又由于z轴是形心轴，Sz=0，故答案：(B)二、惯性矩、惯性半径、极惯性矩、惯性积对图所示截面，对z轴和y轴的惯性矩为惯性矩总是正值，其量纲为长度的四次方，也可写成i z、i y称为截面对z、y轴的惯性半径，其量纲为长度的一次方。
截面对0点的极惯性矩为因=y2+z2，故有I p=I z+I y，显然I p也恒为正值，其量纲为长度的四次方。
截面对y、z轴的惯性积为I yz可以为正值，也可以为负值，也可以是零，其量纲为长度的四次方。
若y、z两坐标轴中有一个为截面的对称轴，则其惯性积I yz恒等于零。
例6图(a)、(b)所示的两截面，其惯性矩关系应为哪一种？A.(I y)1>(I y)2,(I z)1=(I z)2B. (I y)1=(I y)2, (I z)1>(I z)2C.(I y)1=(I y)2,(I z)1<(I z)2D. (I y)1<(I y)2,(I z)1=(I z)2解：两截面面积相同，但图 (a)截面分布离z轴较远，故I z较大。
对y轴惯性矩相同。
答案：B2016—63真题面积相同的两个如图所示，对各自水平形心轴 z 的惯性矩之间的关系为（）。
提示：图（ a ）与图（ b ）面积相同，面积分布的位置到 z 轴的距离也相同，故惯性矩I za=I zb而图（ c ）虽然面积与（ a ）、（ b ）相同，但是其面积分布的位置到 z 轴的距离小，所以惯性矩I zc也小。
材料力学课后习题答案
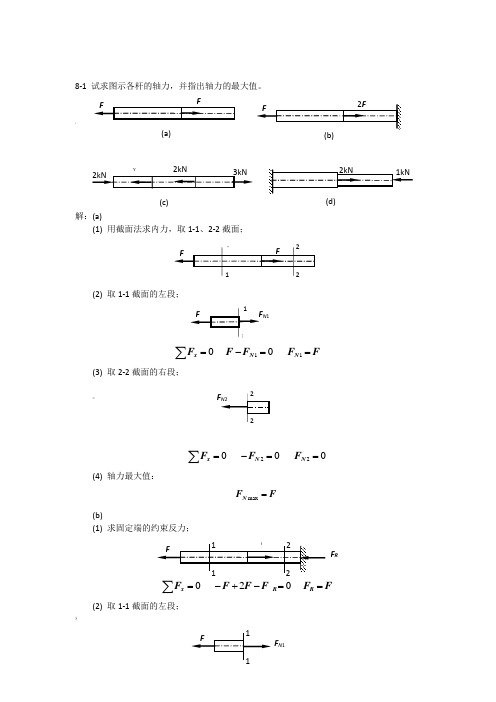
8-1 试求图示各杆的轴力，并指出轴力的最大值。
`解：(a)(1) 用截面法求内力，取1-1、2-2截面；(2) 取1-1截面的左段； 110 0 xN N FF F F F =-==∑(3) 取2-2截面的右段；>220 0 0xN N FF F =-==∑(4) 轴力最大值：max N F F =(b)(1) 求固定端的约束反力；0 20 xR R FF F F F F =-+-==∑(2) 取1-1截面的左段； 》(a)(c) ￥ (d)N 1F RF N 1110 0 xN N FF F F F =-==∑(3) 取2-2截面的右段；220 0 xN R N R FF F F F F =--==-=-∑(4) 轴力最大值：max N F F =(c) '(1) 用截面法求内力，取1-1、2-2、3-3截面；(2) 取1-1截面的左段；110 20 2 xN N FF F kN =+==-∑(3) 取2-2截面的左段；220 230 1 xN N FF F kN =-+==∑(4) 取3-3截面的右段；330 30 3 xN N FF F kN =-==∑(5) 轴力最大值：max 3 N F kN =,【F N 211#N 2F N 3(1) 用截面法求内力，取1-1、2-2截面；。
(2) 取1-1截面的右段；|110 210 1 xN N FF F kN =--==∑(2) 取2-2截面的右段；*220 10 1 xN N FF F kN =--==-∑(5) 轴力最大值：max 1 N F kN =8-2 试画出8-1所示各杆的轴力图。
解：(a) 、(b)《(c)F N 1F N 2FNF NFF N:(d)<8-5 图示阶梯形圆截面杆，承受轴向载荷F 1=50 kN 与F 2作用，AB 与BC 段的直径分别为d 1=20mm 和d 2=30 mm ，如欲使AB 与BC 段横截面上的正应力相同，试求载荷F 2之值。
材料力学 3 截面的几何性质
大小：正，负，0。
y
量纲：[长度]3
二、截面的形心 几何形心=等厚均质薄片重心 z 形心坐标公式：
yc
C
zc
yc zc
y dA A z dA
A
A
Sz A Sy A
O
A
y
S y A zc
S z A yc
结论： 若 S z 0 yc 0 z 轴通过形心。反之，亦成立。
转轴公式
sin 2 I yz cos2
I y1 I z1 I y I z
二、形心主轴和形心主惯性矩 1、主轴和主惯性矩：坐标旋转到= 0 时，
Ix y
0 0
Ix I y 2
sin20 I xy cos 20 0
tan 2 0
2 I xy Ix Iy
z1
I yzc y1 z1 dA
A
a
O
z
yc
I z A y 2dA A (b y1 )2 dA
2 A ( y1 2by1 b 2 )dA
y
zc 为形心轴， S zc Ayc 0
I zc 2bS zc b 2 A
I zc b 2 A
2
a
2677710 .52 cm 4
平 衡 项 惯 性 矩 6686481 . 857.8 单 个 形 心 惯 性 矩 779.53
组合截面可以大大提高截面惯性矩。
I y Iz 2 cos2 I yz sin 2 cos2 I yz sin 2
I y Iz 2
I y Iz 2
当＝0时，
dI y1 d
工程力学2(材料力学)习题解答
《工程力学2习题解答》建筑1001班陈飞力学教研室编著1-2. 试求图示结构mm 和nn 两截面上的内力，并指出AB 和BC 两杆属何种基本变形。
解：（1）求约束反力：取杆AB 为研究对象∑∑∑=⨯-⨯==-+===0233 003 000BCABCAAN M N Y Y X X 解得：kN Y kN N A BC 1 2==（2）求m-m 截面内力：将杆AB 沿截面m-m 截开, 取左半部分kNm Y M kN Y Q A m-m A m m 11 1=⨯===-AB 杆发生弯曲变形。
（3）求n-n 截面内力：取杆BC 为研究对象，截开n-n 截面kN N N BC n n 2==-BC 杆发生拉伸变形1-3. 拉伸试件A 、B 两点的距离l 称为标距，在拉力作用下，用引伸仪量出两点距离的增量为Δl =5×10-2mm 。
若l 的原长为l =10cm ，试求A 、B 两点间的平均应变。
解：平均应变为42105100105Δ--⨯=⨯==l l m ε1-4. 图示三角形薄板因受外力而变形。
角点B 垂直向上的位移为0.03mm ，但AB和BC 仍保持为直线。
试求沿OB 的平均应变，并求AB 、BC 两边在B 点夹角的变化。
解：（1） 求OB 方向的平均线应变n4105.212003.0Δ120-⨯=====l l mmOA OB m ε （2）求AB 与BC 两边的角应变4105.2'22-⨯=-=OB AO arctg πγ2-1. 试求图示各杆1-1、2-2、3-3截面的轴力， 并作轴力图。
解: (a)（1）求约束反力kNR R X 500203040 0==-++-=∑（2）求截面1-1的轴力kNN NR X 500011==+-=∑（3）求截面2-2的轴力kNN NR X 10040 022==++-=∑（4）求截面3-3的轴力(a) (b)kNN NR X 2003040 033-==+++-=∑（5）画轴力图(b)（1）求截面1-1的轴力01=N（2）求截面2-2的轴力 PN4022==（3）求截面3-3的轴力PN P P NX 304 033==-+=∑（4）画轴力图2-2. 作用图示零件上的拉力P=38kN ，试问零件内最大拉应力发生于哪个横截面上？并求其值。
截面的几何性质—平行移轴公式(材料力学)
1、平行移轴公式
右图任意截面，zc、yc 轴为通过截面形心C的一对正交轴，z、y轴为分别与zc、yc 轴平行的轴，
两平行轴之间的距离分别为a和b。
根据定义，图形对zc、yc 轴的惯性矩和惯性积分别为
Izc yc2dA, I yc zc2dA, Izc yc yc zcdA
I zy
i 1
I yzi
Izi， Iyi
,Iyz i
----指第
i个简单截面对
y, z
轴的惯性矩，惯性积。
例题 求T形截面对其形心轴 zC 的惯性矩（单位为mm）。
解：将截面分成两个矩形截面。 截面的形心必在对称轴 y 上。
取过矩形2的形心且平行于底边的轴作为参考轴记作z轴。
A1
20140
2800mm2 ,
Iz c
I1 zc
I2 zc
7.68106
4.43106
12.11106 mm4
20 140
yc
20
1
a1 zc
y1 a2 yc z
2
100
a2A b2A
c
I zy I zc yc abA
上式即为惯性矩和惯性积的平行移轴公式。
y
z yc
b
zc
dA
C
yc
a y zc
O
z
2、组合截面的惯性矩、惯性积
组合截面对某轴的惯性矩、惯性积，等于各简单图形对此轴的惯性矩、惯性积的代数和。
n
Iz Iz i
i 1
n
I y I y
i1 i
n
ycdA a2
dA
A
A
A
A
A
A
材料力学截面图形的几何性质习题
附录Ⅰ 截面图形的几何性质
I-1 填空题： I-1(1) 当一个正方形的边长和一个圆形的直径相等时，两图形对 其形心轴的惯性矩之比应为 16 。
3π
I-1(2) 若已知图示平面图形对 A 轴的惯性矩为 27 bh3 ，则图 4
形对 C 轴的惯性矩为 3 bh3 ，对 D 轴的惯性矩为 9 bh3 。
y xC
−α
0
α
= 2 R3 sin α 。 3
x Oα C
R
A = R 2α 。
xC
=
2R3 sin α 3R 2α
=
2 R sinα 3α
。
题 I-4 图
I-5 如图的截面由一个直径为 D 的半圆和一个矩形组成。如果图形的形心位于半圆的水
平直径处，求矩形的高 a。
解：上半圆对形心轴的静矩：
S1
=
12
-1-
B
A
题 I-1(6) 图
工程力学习题解答
I-2 单选题：
I-2(1) 边长为 4a 的正方形，在如图位置挖去一个边长为 a
的小正方形，余下的阴影图形对坐标轴 x、y、x′、y′的静
矩分别为 S x , S y , S x′ , S y′ ，其中只有 C 是对的。
A． S x
=
a3 2
B． S y =
C． I x = I x′ + (a2 + a′2 ) A D． I x = I xC + (a + a′)2 A E． I x = I x′ + 2aa′A + a2 A F． I x = I x′ + 2aSx′ + a2 A
b′ C a′
材料力学 截面的几何性质
O1 O 2
O
x
O3
x 1
C
课堂练习
I.
&
任意图形，若对某一对正交坐标轴的惯性积为零， 则这一对坐标轴一定是该图形的（ ）。
B
A. 形心轴； B. 主轴 C. 主形心轴 D. 对称轴 在图示开口薄壁截面图形中，当（ 为一对主轴。
y
）时，y-z轴始终保持
A. y轴不动，x轴平移； B. x轴不动，y轴平移； C. x轴不动，y轴任意移动；
y b C 1x C 2x O a x
æ 1 öæ 2 ö æ 1 öæ h ö = ç bh ÷ç h ÷ + ç ah ÷ç ÷ è 2 øè 3 ø è 2 øè 3 ø
h 2 = (a + 2 b ) 6
形心位置
h
x = 0
h 2 (a + 2 b ) h a + 2 b S x y = = பைடு நூலகம்· = 6 A h 3 a + b (a + b ) 2
主惯性矩:
图形对主轴的惯性矩,称主惯性矩
形心主轴:
过形心的主轴称为形心主轴
形心主矩:
图形对形心主轴的惯性矩称为形心主矩
课堂练习
I.
&
在下列关于平面图形的结论中，（
）是错误的。
A.图形的对称轴必定通过形心； B.图形两个对称轴的交点必为形心； C.图形对对称轴的静矩为零； D.使静矩为零的轴必为对称轴。 在平面图形的几何性质中，（
y
dA y
ü2、惯性矩和极惯矩永远为正，
惯性积可能为正、为负、为零。
x 1
ü3、任何平面图形对于通过其形
材料力学 附录 截面的几何性质
(Properties of Plane Areas) 三、组合截面的静矩和形心 (The first moments ¢roid of a composite area)
由几个简单图形组成的截面称为组合截面.
截面各组成部分对于某一轴的静矩之代数和，等于该截 面对于同一轴的静矩.
(Properties of Plane Areas)
§1-1 截面的静矩和形心 (The first moment of the area & centroid of
an area)
一、静矩(The first moment of the area ）
截面对 y , z 轴的静矩为
z
S y
zdA
A
Sz
ydA
A
dA z
静矩可正，可负，也可能等于零.
1
矩形 2
A2 10 80 800mm2
y2
10
80 2
50mm
z2 5mm
所以 y A1 y1 A2 y2 23mm A1 A2
z A1z1 A2z2 38mm A1 A2
y1
z1
2 z2
10
O y2
y
90
(Properties of Plane Areas)
方法2 用负面积法求解，图形分割及坐标如图(b)
yC , zC￣ 过截面的形心 C 且与 y, z轴平行
的坐标轴(形心轴）
z
Iy , Iz , Iyz — 截面对 y, z 轴的惯性矩和惯性积.
zC
IyC , IzC , IyCzC￣ 截面对形心轴 yC , zC的惯性矩
n
Ai zi
z
长沙理工大学材料力学练习册答案1-5章
材料力学 分析与思考题集第一章 绪论和基本概念一、选择题1.关于确定截面内力的截面法的适用范围，有下列四种说法：【D.适用于不论等截面或变截面、直杆或曲杆、基本变形或组合变形、横截面或任意截面的普通情况。
2.关于下列结论的正确性：【C 1.同一截面上正应力τσ与剪应力必须相互垂直3.同一截面上各点的剪应力必相互平行。
】3.下列结论中那个是正确的：【B.若物体各点均无位移，则该物体必定无变形】4.根据各向同性假设，可认为构件的下列量中的某一种量在各方向都相同：【B 材料的弹性常数】5.根据均匀性假设，可认为构件的下列量中的某个量在各点处都相同：【C 材料的弹性常数】6.关于下列结论：【C 1.应变分为线应变ε和切应变γ 2.应变为无量纲量 3.若物体的各部分均无变形，则物体内各点的应变均为零】7.单元体受力后，变形如图虚线所示，则切应变γ为【B 2α】二、填空题1.根据材料的主要性能作如下三个基本假设 连续性假设 ， 均匀性假设 和 各向同性假设 。
2.构件的承载能力包括强度、刚度和稳定性三个方面。
3.图示结构中，杆1发生轴向拉伸变形，杆2发生轴向压缩变形，杆3发生弯曲变形。
4.图示为构件内A 点处取出的单元体，构件受力后单元体的位置为虚线表示，则称dx du /为A 点沿x 方向的线应变，dy dv /为【A 点沿y 方向的线应变】，)(21a a +为【A 在xy 平面内的角应变】。
5.认为固体在其整个几何空间内无间隙地充满了物质，这样的假设称为连续性假设。
根据这一假设，构件的应力、应变和位移就可以用坐标的连续性函数来表示。
6.在拉（压）杆斜截面上某点处分布内力集度称为应力(或全应力），它沿着截面法线方向的分量称为正应力，而沿截面切线方向的分量称为切应力。
第二章 杆件的内力分析一、选择题1.单位宽度的薄壁圆环受力如图所示，p 为径向压强，其n-n 截面上的内力N F 有四个答案：【B 2/pD 】2.梁的内力符号与坐标系的关系是：【B 剪力、弯矩符号与坐标系无关】3.梁的受载情况对于中央截面为反对称（如图）。
材料力学 第五版 i 截面的几何性质+习题答案
附录I 截面的几何性质 习题解[习题I-1] 试求图示各截面的阴影线面积对x 轴的静积。
（a ）解：)(24000)1020()2040(3mm y A S c x =+⨯⨯=⋅=（b ）解：)(42250265)6520(3mm y A S c x =⨯⨯=⋅= （c ）解：)(280000)10150()20100(3mm y A S c x =-⨯⨯=⋅=（d ）解：)(520000)20150()40100(3mm y A S c x =-⨯⨯=⋅=[习题I-2] 试积分方法求图示半圆形截面对x 轴的静矩，并确定其形心的坐标。
解：用两条半径线和两个同心圆截出一微分面积如图所示。
dx xd dA ⋅=)(θ；微分面积的纵坐标：θsin x y =；微分面积对x 轴的静矩为： θθθθθdxd x x dx xd y dx xd y dA dS x ⋅=⋅⋅=⋅⋅=⋅=sin sin )(2半圆对x 轴的静矩为：32)]0cos (cos [3]cos []3[sin 33003002r r x d dx x S r rx =--⋅=-⋅=⋅=⎰⎰πθθθππ因为c x y A S ⋅=，所以c y r r ⋅⋅=232132π π34ry c = [习题I-3] 试确定图示各图形的形心位置。
（a ） 解：习题I-3(a): 求门形截面的形心位置矩形 Li Bi Ai Yci AiYci Yc 离顶边上 400 20 8000 160 1280000 左 150 20 3000 75 225000 右150 20 3000 75 225000140001730000Ai=Li*Bi Yc=∑AiYci/∑Ai(b)解：(c)解：[习题I-4]试求图示四分之一圆形截面对于x轴和y轴的惯性矩x I、y I和惯性积xy I。
解：用两条半径线和两个同心圆截出一微分面积如图所示。
dx xd dA ⋅=)(θ；微分面积的纵坐标：θsin x y =；微分面积对x 轴的惯性矩为： θθθθθdxd x dx xd x dx xd y dA y dI x ⋅=⋅⋅=⋅==232222sin sin )(四分之一圆对x 轴的惯性矩为： ⎰⎰⎰-⋅==2/0042/02322cos 1]4[sin ππθθθθd x d dx x I r rx)]2(2cos 21[2142/02/04θθθππd d r ⎰⎰-⋅= }]2[sin 212{82/04πθπ-=r 164r ⋅=π由圆的对称性可知，四分之一圆对y 轴的惯性矩为：164r I I x y ⋅==π微分面积对x 轴、y 轴的惯性积为：xydA dI xy =8)42(21]42[21)(21444042222022r r r x x r dx x r x ydx xdx I r rx r rxy =-=-=-==⎰⎰⎰- [习题I-5] 图示直径为mm d 200=的圆形截面，在其上、下对称地切去两个高为mm 20=δ的弓形，试用积分法求余下阴影部分对其对称轴x 的惯性矩。
材料力学习题答案1
材料力学习题答案12.1 试求图各杆1-1、2-2、3-3 截面上的轴力，并作轴力图。
解：(a) ()1140302050F kN -=+-=，()22302010F kN -=-=，()3320F kN -=- (b) 11F F -=，220F F F -=-=，33F F -= (c) 110F -=，224F F -=，3343F F F F -=-= 轴力图如题2. 1 图( a) 、( b ) 、( c) 所示。
2.2 作用于图示零件上的拉力F=38kN ，试问零件内最大拉应力发生在哪个截面上? 并求其值。
解 截面1-1 的面积为()()21502220560A mm =-⨯=截面2-2 的面积为()()()2215155022840A mm =+-=因为1-1截面和2-2 截面的轴力大小都为F ，1-1截面面积比2-2 截面面积小，故最大拉应力在截面1-1上，其数值为：()3max11381067.9560N F F MPa A A σ⨯====2.9 冷镦机的曲柄滑块机构如图所示。
镦压工件时连杆接近水平位置，承受的镦压力F=1100kN 。
连杆截面是矩形截面，高度与宽度之比为 1.4h b=。
材料为45钢，许用应力[]58MPa σ=，试确定截面尺寸h 及b 。
解 连杆内的轴力等于镦压力F ，所以连杆内正应力为F Aσ=。
根据强度条件，应有[]F F A bh σσ==≤，将 1.4hb=代入上式，解得()()0.1164116.4b m mm ≥≤== 由 1.4h b=，得()162.9h mm ≥所以，截面尺寸应为()116.4b mm ≥，()162.9h mm ≥。
2.12 在图示简易吊车中，BC 为钢杆，AB 为木杆。
木杆AB 的横截面面积21100A cm =，许用应力[]17MPa σ=；钢杆BC的横截面面积216A cm =，许用拉应力[]2160MPa σ=。
材料力学 截面性质
(Ai 和xi , yi分别为第i个简单图形的面积及其形心坐标）
5. 组合截面的形心坐标公式
n
将 S y Ai xi i1
n
S x Ai yi i1
代入 S y A x Sx A y
解得组合截面的形心坐标公式为：
n
Ai xi
x
i 1 n
Ai
i 1
n
Ai yi
y
i 1 n
Ai
i 1
（注：被“减去”部分图形的面积应代入负值）
例 试计算图示三角形截面对x轴的静矩。
y
dy
h
b(y)
y
O
b
x
解：取平行于x轴的狭长条，易求 b( y) b (h y)
因此 d A b (h y) d y
ห้องสมุดไป่ตู้
h
所以对x轴的静矩为
h hb
bh2
S x
y d A (h y)y d y
A
0h
6
2
4
I2 xc yc
x
I x1 A y12 d A
y
Ix1
cos2
y2 d A sin2
A
x2 d A
A
2sin cos A xy d A
I x cos2 I y sin2 2I xy sin cos
利用二倍角函数代入上式，得转轴公式 ：
I x1
Ix
2
Iy
Ix
Iy 2
cos2
I xy sin 2
n
Ix
i1
I
xi
n
Iy
i1
I
yi
n
I xy I i1 xyi
截面图形的几何性质-材料力学
yC
Sz A
558000 9000
62
Sz Sz1 Sz2 120 40 20 140 30110 558000
A A1 A2 120 40 140 30 9000
120
I
CI
C
CII
II
y 30
参考轴
z 40
yC
zC 140
注意
① 由两块组成组合图形，其复合图形形心一定位于两个子图的形心连线上。 ② 组合图形形心计算公式也适用于负面积情况， 但要记住面积为负号。
z
I
C1 C
s
C2
II
b
y1 h
y
y2
t
典型例题
例3 已知组合截面尺寸t=20mm，h=140mm，b=100mm。试求截面图
形对形心轴 y 的惯性矩。
t
解： 由平行移轴定理
矩形1对y轴的惯性矩：
I (1) y
I y1
b12 A1
矩形2对y轴的惯性矩：
I (2) y
I y2
b22 A2
整个截面的惯性矩：
Iz
y 2 dA
A
h y2bdy 0
b
y3 3
/
h 0
bh3 3
y
h b
dy y
z
典型例题
例2 试求图示截面对形心轴zC轴的惯性矩。
IzC
y 2 dA
A
h
2 h
y2bdy
2
b
y3 3
h
/
2
h
2
bh3
12
I yC
z 2dA
A
y
yC
hb3 =
(完整版)材料力学习题册答案-附录平面图形几何性质
附录 截面图形的几何性质一、是非判断题⒈ 图形对某一轴的静矩为零，则该轴必定通过图形的形心。
（ √ ）⒉ 图形在任一点只有一对主惯性轴。
（ × ）⒊ 有一定面积的图形对任一轴的轴惯性矩必不为零。
（ √ ）⒋ 图形对过某一点的主轴的惯性矩为图形对过该点所有轴的惯性矩中的极值。
（ √ ）二、填空题⒈ 组合图形对某一轴的静矩等于 各组成图形对同一轴静矩 的代数和。
⒉ 图形对任意一对正交轴的惯性矩之和，恒等于图形对 两轴交点的极惯性矩 。
⒊ 如果一对正交轴中有一根是图形的对称轴，则这一对轴为图形 主惯性轴 。
⒋ 过图形的形心且 图形对其惯性积等于零 的一对轴为图形的形心主惯性轴。
三、选择题⒈ 图形对于其对称轴的（ A ）A 静矩为零，惯性矩不为零；B 静矩和惯性矩均为零C 静矩不为零，惯性矩为零；D 静矩和惯性矩均不为零⒉ 直径为d 的圆形对其形心主轴的惯性半径=（ C ）。
i A d/2 B d/3 C d/4 D d/8⒊ 图示截面图形中阴影部分对形心主轴的惯性矩=（ C ）。
z Z I A B123234dD D -π63234dD D -π C D 126434dD D -π66434dD D -πz四、计算题1、求图示平面图形中阴影部分对z 轴的静矩。
232.0)2.06.0(4.0bh h h h b S Z =+⋅⋅=()8842422222bh h H B h h b h H h h H B S Z +-=⋅⋅+⎪⎭⎫ ⎝⎛-+⋅-⋅=2、求图示平面图形对z 、y 轴的惯性矩。
4523231023.251040121040251040123010mm I I I II I Z ⨯=⋅⋅+⋅+⋅⋅+⋅=+=由于图形对称，451023.2mm I I Z Y ⨯===3、试求图示平面图形的形心主惯性轴的位置，并求形心主惯性矩。
mm y C 7.5610020201401010020902010=⋅+⋅⋅⋅+⋅⋅=4723231021.17.46200.1012201003.33201401214020mm I I I II I Z ⨯=⋅⋅+⋅+⋅⋅+⋅=+=46331076.112100201220140mm I Y ⨯=⋅+⋅=z zz。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
~
15-1(I-8) 试求图示三角形截面对通过顶点A并平行于底边BC的轴的惯性矩。
解：已知三角形截面对以BC边为轴的惯性矩是，利用平行轴定理，可求得截面对形心轴的惯性矩
所以
再次应用平行轴定理，得
返回
)
15-2(I-9) 试求图示的半圆形截面对于轴的惯性矩，其中轴与半圆形的底边平行，相距1 m。
解：知半圆形截面对其底边的惯性矩是，用
平行轴定理得截面对形心轴的惯性矩
再用平行轴定理，得截面对轴的惯性矩
/
返回
15-3(I-10) 试求图示组合截面对于形心轴的惯性矩。
解：由于三圆直径相等，并两两相切。
它们的圆心构成一个边长为的等边三角形。
该等边三角形的形心就是组合截面的形心，因此下面两个圆的圆心，到形心轴的距离是
上面一个圆的圆心到轴的距离是。
利用平行轴定理，得组合截面对轴的惯性矩如下：
{
返回
15-4(I-11) 试求图示各组合截面对其对称轴的惯性矩。
解：（a）22a号工字钢对其对称轴的惯性矩是。
利用平行轴定理得组合截面对轴的惯性矩
（b）等边角钢的截面积是，其形心距外边缘的距离是 mm，求得组合截面对轴的惯性矩如下：
：
返回
15-5(I-12) 试求习题I-3a图所示截面对其水平形心轴的惯性矩。
关于形心位置，可利用该题的结果。
解：形心轴位置及几何尺寸如图
所示。
惯性矩计算如下：
返回
15-6(I-14) 在直径的圆截面中，开了一个的矩形孔，如图所
示，试求截面对其水平形心轴和竖直形心轴的惯性矩
和。
解：先求形心主轴的位置
！
即
返回
15-7(I-16) 图示由两个20a号槽钢组成的组合截面，若欲使截面对两对称轴的惯性矩和相等，则两槽钢的间距应为多少
（
解：20a号槽钢截面对其自身的形心轴、的惯性矩是，；横截面积为；槽钢背到其形心轴的距离是。
根据惯性矩定义和平行轴定理，组合截面对
，轴的惯性矩分别是
；
若
即
等式两边同除以2，然后代入数据，得
于
是
所以，两槽钢相距。