分布列三角函数立体几何小测
三角函数、立体几何及概率专项训练题.docx
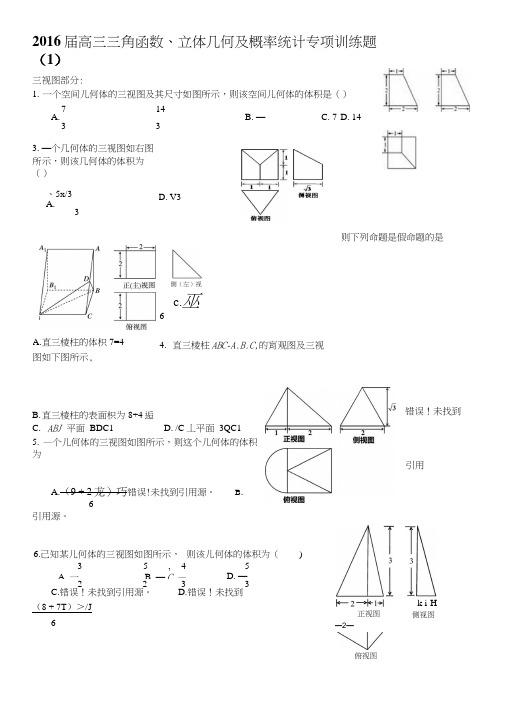
2016届高三三角函数、立体几何及概率统计专项训练题(1)三视图部分:1. 一个空间儿何体的三视图及其尺寸如图所示,则该空间儿何体的体积是()7 14 A. -B. —C. 7D. 14333. —个几何体的三视图如右图所示,则该几何体的体积为() 、5x/3 A. --------3c.巫64. 直三棱柱ABC-A.B.C,的肓观图及三视图如下图所示,B. 直三棱柱的表面枳为8+4逅C. ABJ 平面 BDC1D. /C 丄平面 3QC1 5. —个儿何体的三视图如图所示,则这个儿何体的体积为A.(9 + 2龙)巧错误!未找到引用源。
B .6引用源。
C.错误!未找到引用源。
D.错误!未找到 (8 + 7T )>/J6D. V36.己知某儿何体的三视图如图所示, 则该儿何体的体积为()3 5 ,4 5A. 一B. —C.—D. — 2 2 3 3则下列命题是假命题的是A.直三棱柱的体枳7=4 侧(左)视图错误!未找到引用源。
正视图k i-H侧视图—2—俯视图球内接几何体:1.一个三棱锥P-ABC的三条侧棱刃、PB、PC两两互相垂直,且长度分别为1、乔、3,则这个三棱锥的外接球的表面积为()A. 16/rB. 32%C. 36〃D. 64龙2.平面a截球O的球面所得関的半径为1,球心O到平面a的距离为2迈,则此球的体积为()A. 27兀B. 36龙C. 4届D. 6希龙3.如图所示,正四棱锥P-ABCD底面的四个顶点A、B、C、D在球0的同一个大圆上,点P在球面上.如果v®=¥,则球0的表面积是()A. 4nB. 16兀C. 12“D・ 8 n4.已知正四棱锥的各棱棱长都为3血,贝怔四棱锥的外接球的表血积为_____空间中的点、线、面的位置关系1.设表示三条直线,ci , b , g表示三个平而,给出下列四个命题:①若/丄Q,加丄G,贝0////7?: ②若m u卩,〃是/在b内的射影,加丄则加丄〃;③若加ua, mH n ,则nil a \④若a丄g, bdg,则a // b .其中真命题为()A.①②B.①②③C.②③④D.①③④2.设Q,0是两个不同的平面,/是一条直线,以下命题正确的是A.若/丄丄0,贝I"u0B.若llla.al ![3 ,贝ij/u0C.若/丄a,a//0,贝强丄“D.若11 la.a丄0,贝I” 丄0文科解答题:E1.在长方体中,AA=AD=2 , E是棱C/Q上的一点.(1)求证:BE丄出D;(2)若E是棱C/),的中点,在棱AA f±是否存在点使得D,P//平而⑦<E?若存在,求出线段的长;若不存在,请说明理由.2 •如图四棱锥P-ABCD中,底面MBCD是平行四边形,ZACB = 90(), P/1丄平面ABCD,PA = BC = l f AE =近,F 是BC 的中点.⑴求证:D4丄平面PAC ;(2)若点G是"的中点,证明:CG //平面PAF ,并求三棱锥A-CDG的体积.3.如图,在多面体ABCDEF中,底而ABCD是边长为2的正方形, 平面/BCD BF=3, G和H分别是CE和CF的中点.(1 )求证:/C丄平而BDEF;(II )求多血体ABCDEF的体积. 四边形BDEF是矩形,平而8DEF丄P4.如图,长方体力G中,AB4D的中点为P,DP的中点为H・(I)证明EH//平面FG坊;Di F C1 (II)求四而体EFG目的体积.5•如图,在三棱柱ABC —佔G中,B]B = B}A = AB = BC = 21的BC = 9()° ,。
三角函数及解三角形测试题(含答案)

三角函数及解三角形测试题(含答案)三角函数及解三角形1.在锐角三角形ABC中,角A的对边为a,角B的对边为b,角C的对边为c。
根据正弦定理,$\frac{a}{\sinA}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R$,其中R为三角形外接圆的半径。
根据余弦定理,$c^2=a^2+b^2-2ab\cos C$。
根据正切的定义,$\tan A=\frac{a}{b}$。
根据余切的定义,$\cotA=\frac{b}{a}$。
根据正割的定义,$\sec A=\frac{c}{a}$。
根据余割的定义,$\csc A=\frac{c}{b}$。
2.选择题:1.设$\alpha$是锐角,$\tan(\frac{\pi}{4}+\alpha)=3+\sqrt{22}$,则$\cos\alpha=\frac{2\sqrt{22}}{36}$。
2.一艘船向XXX,看见正西方向有相距10海里的两个灯塔恰好与它在一条直线上,继续航行半小时后,看见一灯塔在船的南偏西60°,另一灯塔在船的南偏西75°,则这艘船的速度是每小时5海里。
4.已知函数$f(x)=3\sin\omega x+\cos\omega x$,$y=f(x)$的图象与直线$y=2$的两个相邻交点的距离等于$\pi$,则$f(x)$的单调递增区间是$(\frac{k\pi}{2}-\frac{\pi}{12},\frac{k\pi}{2}+\frac{5\pi}{12})$,其中$k\in Z$。
5.圆的半径为4,$a,b,c$为该圆的内接三角形的三边,若$abc=162$,则三角形的面积为$22$。
6.已知$\cos\alpha=-\frac{4}{\pi}$,且$\alpha\in(\frac{\pi}{4},\frac{\pi}{2})$,则$\tan(\alpha+\frac{\pi}{4})=-\frac{7}{7}$。
数列三角函数立体几何习题

数列三角函数立体几何习题一.选择题(共3小题)1.记S n 为等差数列{a n }的前n 项和.若a 4+a 5=24,S 6=48,则{a n }的公差为( )A .1B .2C .4D .82.等差数列{a n }的首项为1,公差不为0.若a 2,a 3,a 6成等比数列,则{a n }前6项的和为( )A .﹣24B .﹣3C .3D .83.已知数列{a n }为等差数列,S n 其前n 项和,且a 2=3a 4﹣6,则S 9等于( )A .25B .27C .50D .54二.填空题(共3小题)4.设等比数列{a n }满足a 1+a 2=﹣1,a 1﹣a 3=﹣3,则a 4= .5.在等差数列{a n }中,若a 4+a 6+a 8+a 10+a 12=120,则2a 10﹣a 12的值为 .6.公差不为0的等差数列{a n }中,a 1+a 3=8,且a 4为a 2和a 9和等比中项,则a 5= .三.解答题(共10小题)7.记S n 为等比数列{a n }的前n 项和.已知S 2=2,S 3=﹣6.(1)求{a n }的通项公式;(2)求S n ,并判断S n +1,S n ,S n +2是否成等差数列.8.设数列{a n }的前n 项和为S n ,且a 1=1,a n +1=2S n +1,数列{b n }满足a 1=b 1,点P (b n ,b n +1)在直线x ﹣y +2=0上,n ∈N *.(1)求数列{a n },{b n }的通项公式;(2)设,求数列{c n }的前n 项和T n .9.如图,四棱锥P ﹣ABCD 中,侧面PAD 为等边三角形且垂直于底面ABCD ,AB=BC=AD ,∠BAD=∠ABC=90°.(1)证明:直线BC ∥平面PAD ;(2)若△PCD面积为2,求四棱锥P﹣ABCD的体积.10.如图,圆锥的轴截面为三角形SAB,O为底面圆圆心,C为底面圆周上一点,D为BC的中点.(I)求证:平面SBC⊥平面SOD;(II)如果∠AOC=∠SDO=60°,BC=2,求该圆锥的侧面积.11.如图,在四棱锥P﹣ABCD中,AD⊥平面PDC,AD∥BC,PD⊥PB,AD=1,BC=3,CD=4,PD=2.(Ⅰ)求异面直线AP与BC所成角的余弦值;(Ⅱ)求证:PD⊥平面PBC;(Ⅲ)求直线AB与平面PBC所成角的正弦值.12.已知函数f(x)=cos(2x﹣)﹣2sinxcosx.(I)求f(x)的最小正周期;(II)求证:当x∈[﹣,]时,f(x)≥﹣.13.已知函数f(x)=4tan(x+)cos2(x+)﹣1.(Ⅰ)求f(x)的定义域与最小正周期;(Ⅱ)讨论f(x)在区间(0,)上的单调性.14.已知函数f(x)=sin(2x+)+sin2x.(1)求函数f(x)的最小正周期;(2)若函数g(x)对任意x∈R,有g(x)=f(x+),求函数g(x)在[﹣,]上的值域.15.已知函数f(x)=sin(x﹣)cosx+1.(Ⅰ)求函数f(x)的最小正周期;(Ⅱ)当x∈[,]时,求函数f(x)的最大值和最小值.16.已知函数f(x)=sinωx•cosωx﹣cos2ωx(ω>0)的最小正周期为2π(Ⅰ)求ω的值;(Ⅱ)在△ABC中,sinB,sinA,sinC成等比数列,求此时f(A)的值域.数列三角函数立体几何习题参考答案与试题解析一.选择题(共3小题)1.记S n为等差数列{a n}的前n项和.若a4+a5=24,S6=48,则{a n}的公差为()A.1 B.2 C.4 D.8【解答】解:∵S n为等差数列{a n}的前n项和,a4+a5=24,S6=48,∴,解得a1=﹣2,d=4,∴{a n}的公差为4.故选:C.2.等差数列{a n}的首项为1,公差不为0.若a2,a3,a6成等比数列,则{a n}前6项的和为()A.﹣24 B.﹣3 C.3 D.8【解答】解:∵等差数列{a n}的首项为1,公差不为0.a2,a3,a6成等比数列,∴,∴(a1+2d)2=(a1+d)(a1+5d),且a1=1,d≠0,解得d=﹣2,∴{a n}前6项的和为==﹣24.故选:A.3.已知数列{a n}为等差数列,S n其前n项和,且a2=3a4﹣6,则S9等于()A.25 B.27 C.50 D.54【解答】解:设数列{a n}的首项为a1,公差为d,因为a2=3a4﹣6,所以a1+d=3(a1+3d)﹣6,所以a5=3.所以S9=9a5=27.故选B.二.填空题(共3小题)4.设等比数列{a n}满足a1+a2=﹣1,a1﹣a3=﹣3,则a4=﹣8.【解答】解:设等比数列{a n}的公比为q,∵a1+a2=﹣1,a1﹣a3=﹣3,∴a1(1+q)=﹣1,a1(1﹣q2)=﹣3,解得a1=1,q=﹣2.则a4=(﹣2)3=﹣8.故答案为:﹣8.5.在等差数列{a n}中,若a4+a6+a8+a10+a12=120,则2a10﹣a12的值为24.【解答】解:∵a n为等差数列且a4+a6+a8+a10+a12=5a1+35d=120∴a1+7d=24∵2a10﹣a12=2a1+18﹣a1﹣11d=a1+7d=24故答案为:246.公差不为0的等差数列{a n}中,a1+a3=8,且a4为a2和a9和等比中项,则a5= 13.【解答】解:设等差数列{a n}的公差d≠0,∵a1+a3=8,且a4为a2和a9和等比中项,∴2a1+2d=8,,解得a1=1,d=3.则a5=1+3×4=13.故答案为:13.三.解答题(共10小题)7.记S n为等比数列{a n}的前n项和.已知S2=2,S3=﹣6.(1)求{a n }的通项公式;(2)求S n ,并判断S n +1,S n ,S n +2是否成等差数列.【解答】解:(1)设等比数列{a n }首项为a 1,公比为q ,则a 3=S 3﹣S 2=﹣6﹣2=﹣8,则a 1==,a 2==,由a 1+a 2=2,+=2,整理得:q 2+4q +4=0,解得:q=﹣2,则a 1=﹣2,a n =(﹣2)(﹣2)n ﹣1=(﹣2)n ,∴{a n }的通项公式a n =(﹣2)n ;(2)由(1)可知:S n ===﹣(2+(﹣2)n +1), 则S n +1=﹣(2+(﹣2)n +2),S n +2=﹣(2+(﹣2)n +3),由S n +1+S n +2=﹣(2+(﹣2)n +2)﹣(2+(﹣2)n +3)=﹣[4+(﹣2)×(﹣2)n +1+(﹣2)2×+(﹣2)n +1],=﹣[4+2(﹣2)n +1]=2×[﹣(2+(﹣2)n +1)],=2S n ,即S n +1+S n +2=2S n ,∴S n +1,S n ,S n +2成等差数列.8.设数列{a n }的前n 项和为S n ,且a 1=1,a n +1=2S n +1,数列{b n }满足a 1=b 1,点P (b n ,b n +1)在直线x ﹣y +2=0上,n ∈N *.(1)求数列{a n },{b n }的通项公式;(2)设,求数列{c n }的前n 项和T n .【解答】解:(1)由a n +1=2S n +1可得a n =2S n ﹣1+1(n ≥2),两式相减得a n +1﹣a n =2a n ,a n +1=3a n (n ≥2).又a 2=2S 1+1=3,所以a2=3a1.故{a n}是首项为1,公比为3的等比数列.所以a n=3n﹣1.由点P(b n,b n+1)在直线x﹣y+2=0上,所以b n+1﹣b n=2.则数列{b n}是首项为1,公差为2的等差数列.则b n=1+(n﹣1)•2=2n﹣1(2)因为,所以.则,两式相减得:.所以=.9.如图,四棱锥P﹣ABCD中,侧面PAD为等边三角形且垂直于底面ABCD,AB=BC=AD,∠BAD=∠ABC=90°.(1)证明:直线BC∥平面PAD;(2)若△PCD面积为2,求四棱锥P﹣ABCD的体积.【解答】(1)证明:四棱锥P﹣ABCD中,∵∠BAD=∠ABC=90°.∴BC∥AD,∵AD⊂平面PAD,BC⊄平面PAD,∴直线BC∥平面PAD;(2)解:四棱锥P﹣ABCD中,侧面PAD为等边三角形且垂直于底面ABCD,AB=BC=AD,∠BAD=∠ABC=90°.设AD=2x,则AB=BC=x,CD=,O是AD的中点,连接PO,OC,CD的中点为:E,连接OE,则OE=,PO=,PE==,△PCD面积为2,可得:=2,即:,解得x=2,PE=2.=×(BC+AD)×AB×PO==4.则V P﹣ABCD10.如图,圆锥的轴截面为三角形SAB,O为底面圆圆心,C为底面圆周上一点,D为BC的中点.(I)求证:平面SBC⊥平面SOD;(II)如果∠AOC=∠SDO=60°,BC=2,求该圆锥的侧面积.【解答】证明:(Ⅰ)由题意知SO⊥平面OBC,又BC⊂平面OBC,∴SO⊥BC,在△OBC中,OB=OC,CD=BD,∴OD⊥BC,又SO∩OD=O,∴BC⊥平面SOD,又BC⊂平面SBC,∴平面SBC⊥平面SOD.解:(Ⅱ)在△OBC中,OB=OC,CD=BD,∵∠AOC=60°,∴∠COD=60°,∵CD=,∴OD=1,OC=2,在△SOD中,∠SDO=60°,又SO⊥OD,∴SO=,在△SAO中,OA=OC=2,∴SA=,∴该圆锥的侧面积为.11.如图,在四棱锥P﹣ABCD中,AD⊥平面PDC,AD∥BC,PD⊥PB,AD=1,BC=3,CD=4,PD=2.(Ⅰ)求异面直线AP与BC所成角的余弦值;(Ⅱ)求证:PD⊥平面PBC;(Ⅲ)求直线AB与平面PBC所成角的正弦值.【解答】解:(Ⅰ)如图,由已知AD∥BC,故∠DAP或其补角即为异面直线AP与BC所成的角.因为AD⊥平面PDC,所以AD⊥PD.在Rt△PDA中,由已知,得,故.所以,异面直线AP与BC所成角的余弦值为.证明:(Ⅱ)因为AD⊥平面PDC,直线PD⊂平面PDC,所以AD⊥PD.又因为BC∥AD,所以PD⊥BC,又PD⊥PB,所以PD⊥平面PBC.解:(Ⅲ)过点D作AB的平行线交BC于点F,连结PF,则DF与平面PBC所成的角等于AB与平面PBC所成的角.因为PD⊥平面PBC,故PF为DF在平面PBC上的射影,所以∠DFP为直线DF和平面PBC所成的角.由于AD∥BC,DF∥AB,故BF=AD=1,由已知,得CF=BC﹣BF=2.又AD⊥DC,故BC⊥DC,在Rt△DCF中,可得.所以,直线AB与平面PBC所成角的正弦值为.12.已知函数f(x)=cos(2x﹣)﹣2sinxcosx.(I)求f(x)的最小正周期;(II)求证:当x∈[﹣,]时,f(x)≥﹣.【解答】解:(Ⅰ)f(x)=cos(2x﹣)﹣2sinxcosx,=(co2x+sin2x)﹣sin2x,=cos2x+sin2x,=sin(2x+),∴T==π,∴f(x)的最小正周期为π,(Ⅱ)∵x∈[﹣,],∴2x+∈[﹣,],∴﹣≤sin(2x+)≤1,∴f(x)≥﹣13.已知函数f(x)=4tan(x+)cos2(x+)﹣1.(Ⅰ)求f(x)的定义域与最小正周期;(Ⅱ)讨论f(x)在区间(0,)上的单调性.【解答】解:(Ⅰ)函数f(x)=4tan(x+)cos2(x+)﹣1.∵正切函数的定义域满足,x+,可得:x≠,k∈Z∴函数f(x)的定义域为{x|x≠,k∈Z},函数f(x)化简可得:f(x)==2sin(2x+)﹣1∴f(x)的最小正周期T=;(Ⅱ)∵f(x)=2sin(2x+)﹣1,由2x+,k∈Z得:,∵x∈(0,)上时,令k=0,可得f(x)在区间(0,]上是单调增区间.由2x+,k∈Z.得:,∵x∈(0,)上,令k=0,可得f(x)在区间[,)上是单调减区间.∴f(x)在区间(0,)上时,(0,]是单调增区间,[,)上是单调减区间.14.已知函数f(x)=sin(2x+)+sin2x.(1)求函数f(x)的最小正周期;(2)若函数g(x)对任意x∈R,有g(x)=f(x+),求函数g(x)在[﹣,]上的值域.【解答】解:(1)f(x)=sin(2x+)+sin2x==sin2x+cos2x+sin2x=sin2x+=sin2x+1﹣=sin2x+,∴f(x)的最小正周期T=;(2)∵函数g(x)对任意x∈R,有g(x)=f(x+),∴g(x)=sin2(x+)+=sin(2x+)+,当x∈[﹣,]时,则2x+∈,则≤sin(2x+)≤1,即×≤g(x),解得≤g(x)≤1.综上所述,函数g(x)在[﹣,]上的值域为:[,1].15.已知函数f(x)=sin(x﹣)cosx+1.(Ⅰ)求函数f(x)的最小正周期;(Ⅱ)当x∈[,]时,求函数f(x)的最大值和最小值.【解答】解:(Ⅰ)==,∴函数f(x)的最小正周期.(Ⅱ)由(Ⅰ)知,∵,∴,∴,故当时,函数f(x)的最大值为.当时,函数f(x)的最小值为.16.已知函数f(x)=sinωx•cosωx﹣cos2ωx(ω>0)的最小正周期为2π(Ⅰ)求ω的值;(Ⅱ)在△ABC中,sinB,sinA,sinC成等比数列,求此时f(A)的值域.【解答】解:(Ⅰ)∵函数f(x)=sinωx•cosωx﹣cos2ωx=sin(2ωx﹣)(ω>0)的最小正周期为=2π,∴ω=,f(x)=sin(x﹣).(Ⅱ)在△ABC中,∵sinB,sinA,sinC成等比数列,∴sin2A=sinBsinC,∴a2=bc.∵cosA==≥,∴A∈(0,],∴A﹣∈(﹣,],求此时f(A)=sin(A﹣)∈(﹣,].。
三角函数+数列+立体几何小测

三角函数+数列+立体几何小测PS:1~3题12分一题,4~9题14分一题,满分120分.(72分及格)-----茶 1.已知函数1sin 226y x π⎛⎫=+ ⎪⎝⎭,∈x R . (1)求它的振幅、周期、初相; (2)用五点法作出它的简图;(3)该函数的图象可由x y sin =(∈x R )的图象经过怎样的平移和伸缩变换得到?2.已知两个向量(cos ,sin )θθ=m ,sin ,cos )θθ=+n ,其中),23(ππθ--∈,且满足1⋅=m n .(1)求)4sin(πθ+的值 (2)求)127cos(πθ+的值3.在△ABC 中,内角A ,B ,C 对边的边长分别是c b a ,,,已知3,2π==C c .(1)若△ABC 的面积等于3,求a ,b ;(2)若A A B C 2sin 2)sin(sin =-+,求△ABC的面积.4.已知等差数列{}na 满足:37a=,5726aa +=.{}na 的前n 项和为nS .(1)求na 及nS ;(2)令211nn b a =-(n N +∈),求数列{}nb 的前n 项和nT .5.已知数列{}n a 满足a a =1,1(46)41021n n n a n a n ++++=+(n *∈N )..(1)判断数列221n a n +⎧⎫⎨⎬+⎩⎭是否为等比数列?若不是,请说明理由;若是,试求出通项n a ;.(2)如果1a =时,数列{}n a 的前n 项和为n S ,试求出n S .6.已知数列{}n a 的前n 项和为n S ,且585n n S n a =--,*n N ∈(1)证明:{}1n a -是等比数列;(2)求数列{}n S 的通项公式,并求出使得1n n S S +>成立的最小正整数n .俯视图侧视图正视图EDCA P7.如图SA ⊥面ABC ,∠ABC =90°,AE ⊥SB ,且SB ∩AE =E ,AF ⊥SC ,且AF ∩SC =F ,求证:(1) BC ⊥面SAB ;(2) AE ⊥面SBC ;(3) SC ⊥EF .8.已知一四棱锥P -ABCD 的三视图如下,E 是侧棱PC 上的动点。
三角函数立体几何练习

绝密★启用前三角函数立体几何练习一、解答题1.已知函数f(x)=2sinxcosx+√+2.(1)求f(x)的单调递增区间;(2)求函数f(x)在区间[−π3,π3]上的最小值和最大值.2.已知cos(π6−α)=√33.(1)求cos(5π6+α)的值;(2)求sin(2π3−α)的值.3.已知函数f(x)=cosx(sinx−√+√32,x∈R (Ⅰ)求f(x)的最小正周期和单调递增区间;(Ⅱ)若函数g(x)=f(x+a)为偶函数,求|a|的最小值.4.在ΔABC 中,角A 、B 、C 所对的边分别为a 、b 、c ,且满足2acosB =2c −b .(1)求角A 的大小;(2)若c =2b ,求角B 的大小.5.在ABC ∆中,角A ,B ,C 的对边分别为a ,b ,c ,已知5a b +=,6.在ABC ∆中,a ,b ,c 分别为角A ,B ,C 所对的边,S 为ABC ∆的面积,且(I )求角A 的大小;(II ,b c >,D 为BC 的中点,且,求sin C 的值.7.如图,四棱锥中P−ABCD,∠ABC=∠BAD=90°,BC=2AD,ΔPAB与ΔPAD都是边长为2的等边三角形,E是BC的中点.(Ⅰ)求证:AE//平面PCD;(Ⅱ)证明:平面PCD⊥平面PBD.8.如图,在四棱锥P−ABCD中,底面ABCD为平行四边形, E为侧棱PA的中点.(Ⅰ)求证: PC∥平面BDE(Ⅱ)若PC⊥PA,PD=AD,求证:平面BDE⊥平面PAB9.如图,四边形ABCD为梯形,AB//CD,PD⊥平面ABCD,∠BAD=∠ADC=90∘,DC= 2AB=2a,DA=√3a,E为BC的中点.(1)求证:平面PBC⊥平面PDE;(2)线段PC上是否存在一点F,使PA//平面BDF?若存在,请求出具体位置,并进行证明;若不存在,请分析说明理由.。
高中数学三角函数立体几何题目原题素材

三角函数立体几何题目原题1、已知函数(1)求5()4f π的值; (2)设,求的值。
2、已知n S 为数列{}n a 的前n 项和,且有111,1n n a S a +=+=(*n ∈N ).(Ⅰ) 求数列{}n a 的通项n a ;(Ⅱ) 若nn a nb 4=,求数列{}n b 的前n 项和n T ;3设()ln -4f x a x x =+,其中a R ∈,曲线()y f x =在点(1,(1))f 处的切线垂直于y 轴. (Ⅰ) 求a 的值;(Ⅱ) 求函数()f x 的极值.604、设函数⎪⎭⎫⎝⎛π-+=2sin sin )(x x x f ωω,R ∈x . (Ⅰ) 若21=ω,求)(x f 的最大值及相应的x 的取值集合; (Ⅱ)若8π=x 是)(x f 的一个零点,且100<<ω,求ω的值和)(x f 的最小正周期.5、如图,在三棱锥P ABC -中,PA ⊥平面ABC ,AC BC ⊥,D 为侧棱PC 上一点, 它的正(主)视图和侧(左)视图如图所示. (Ⅰ)证明:AD ⊥平面PBC ;(Ⅱ)在ACB ∠的平分线上确定一点Q ,使得PQ ∥平面ABD ,并求此时PQ 的长.侧(左)视图正(主)视图PDCBA6、已知函数32()39f x x x x a =-+++,定义域为D . (1)若(,)D =-∞+∞,求()f x 的单调递减区间;(2)若[3,2]D =-,且()f x 的最大值为19,求()f x 的最小值.7.已知向量)1,(sin ),31cos ,3(x b x a =-= ,函数b a x f•=)(.将函数()yf x 的图象上各点的纵坐标保持不变,横坐标先缩短到原来的12,把所得到的图象再向左平移3π个单位,得到函数()yg x 的图象.(Ⅰ)求函数f(x)的单调递增区间;(Ⅱ)若b a⊥,求()yg x 的值。
8.在三棱锥ABC P -中,侧棱长均为297,底边32,2,4===BC AB AC ,E D 、分别为BC PC 、的中点.(Ⅰ)求三棱锥ABC P -的体积; (Ⅱ)求二面角E DA C --的平面角.9.已知数列{}n a ,{}n b ,11=a ,112--+=n n n a a ,111+-+=n n n n a a a b ,n S 为数列{}n b 的前n 项和,n T 为数列{}n S 的前n 项和. (Ⅰ)求数列{}n a 的通项公式;EDCBAPD CFBEA(Ⅱ)求数列{}n b 的前n 项和n S ;10、某工厂生产甲、乙两种产品,甲产品的一等品率为80%,二等品率为20%;乙产品的一等品率为90%,二等品率为10%;生产1件甲产品,若是一等品,则获利4万元,若是二等品,则亏损1万元;生产1件乙产品,若是一等品,则获利6万元,若是二等品,则亏损2万元.两种产品生产的质量相互独立.(1)设生产1件甲产品和1件乙产品可获得的总利润为X (单位:万元),求X 的分布列; (2)求生产4件甲产品所获得的利润不少于10万元的概率.11、 如图一,△ABC 是正三角形,△ABD 是等腰直角三角形,AB=BD=2.将△ABD 沿边AB 折起, 使得△ABD 与△ABC 成30o的二面角C AB D --,如图二,在二面角C AB D --中.(1) 求D 、C 之间的距离;(2) 求CD 与面ABC 所成的角的大小.12、已知向量(sin ,3),(1,cos )a x b x =-= (1)若x 是三角形的一个内角,且,a b ⊥求x ;(2)若函数()f x a b m =⋅+的最大值为3,求m 的值,并确定()f x 的单调区间. 13现在用甲、乙、丙三种食物配成100kg 混合食物,并使混合食物内至少含有56000单位维生素A 和63000单位维生素B ,问:分别用甲、乙、丙三种食物各多少kg ,才能使这100kg 混合食物的成本最低?其最低成本为多少元?14、如图,在直二面角E AB D --中,四边形ABCD 是边长为2的正方形,EB AE =,F 为CE 上的点,且BF ⊥平面ACEBDC图一 图二A BCDP (1)求证:AE ⊥平面BCE ;(2)求二面角E AC B --的正弦值.15、已知a 为正实数,函数36)2(23)(23-++-=x x a ax x f (1)当1a =时,求函数)(x f 的极小值;(2)试讨论曲线)(x f y =与x 轴的公共点的个数。
三角函数测试题及答案
三角函数测试题及答案本文将为您提供一系列的三角函数测试题及其详细答案解析。
在完成测试题之前,请确保您对基本的三角函数概念以及三角函数的性质和应用有一定的了解。
请按照每道题目的要求进行思考和解答,并参考我们提供的答案解析进行对比和巩固。
题目一:已知一个角的正弦值为0.6,求该角的余弦值。
答案解析:由于正弦值为0.6,我们可以根据三角函数的定义得到:sinθ = 0.6。
根据三角函数的性质,我们知道正弦函数和余弦函数是相关的,即sinθ = cos(π/2 - θ)。
因此,我们可以得到cos(π/2 - θ) = 0.6。
进一步求解可得:cos(π/2 - θ) = cosarcsin(0.6) ≈ 0.8。
所以该角的余弦值约为0.8。
题目二:已知一个角的余弦值为0.4,求该角的正切值。
答案解析:由于余弦值为0.4,我们可以根据三角函数的定义得到:cosθ = 0.4。
然后我们可以利用三角函数的性质,即tanθ = sinθ / cosθ,求解正切值。
将已知的cosθ代入公式可得:tanθ = sinθ / 0.4。
由已知的cosθ = 0.4,我们可以利用三角函数的定义得到:sinθ = √(1 - cos²θ) =√(1 - 0.4²) ≈ √(1 - 0.16) ≈ √0.84 ≈ 0.917。
将sinθ = 0.917代入公式可得:tanθ = 0.917 / 0.4 ≈ 2.292。
所以该角的正切值约为2.292。
题目三:已知一条直角边的长度为5,另一条直角边的长度为12,求该直角三角形的正弦值、余弦值、正切值。
答案解析:已知一条直角边的长度为5,另一条直角边的长度为12。
我们可以利用直角三角形中的三角函数定义和性质来求解。
根据已知条件,我们可以得到斜边的长度:√(5² + 12²) ≈ √(25 + 144) ≈ √169 = 13。
然后,我们可以利用定义求解三角函数的值:sinθ = 对边/斜边= 5/13 ≈ 0.385,cosθ = 临边/斜边= 12/13 ≈ 0.923,tanθ = 对边/临边= 5/12 ≈0.417。
三角函数相关几何计算训练(附参考答案).docx
三角函数相关几何计算训练1. (2011・南宁)如图,在AABC 中,ZACB=90° , ZA=15° , AB 二8,则 AC ・BC 的值为()D. 16AD=3: 2, ZADB=60° ,那么 cosA 的值等于(3+V63. (2013*遵义模拟)如图,AABC 内接于00, AD 为O0的直径,交BC 于点E,若DE 二2, 0E 二3,则tanC*tanB=()4•路边路灯的灯柱BC 垂直于地面,灯杆BA 的长为2m,灯杆与灯柱BC 成120度角,锥形灯罩轴线AD 与灯杆AB 垂肓,且灯罩轴线AD 正过道路路面的中心线(D 在屮心线上),已经点C 与D 点之间的距离为12m,则BC 的高()5.如图,在等腰直角三角形ABC 中,ZC 二90° , D 为BC 的中点,将AABC 折叠,使点A 与点D 重合,EF 为折痕, 则sinZBED 的值是( )B. 12D. 12V3-216雄2.如图,在口ABCD 中,AB : m .6. (2011-西城区一模)如图,点A在半径为3的00内,0A=<3, P为00±一点,当Z0PA取最大值时,PA的长等于()9. (2007-临沂)如图,客轮在海上以30km/h 的速度由B 向C 航行,在B 处测得灯塔A 的方位角为北偏东80° ,测 得C 处的方位角为南偏东25° ,航行1小时后到达C 处,在C 处测得A 的方位角为北偏东20° ,贝UC 到A 的距离10. (2004*武汉)已知:如图,OOi 与002外切于C 点,AB —条外公切线,A 、B 分别为切点,连接AC 、BC.设(DO 】 的半径为R, 002的半径为r,若tanZABC=V2,则卫的值为()r11•如图在梯形 ABCD 中,AD/7BC, AD 丄CD, BC=CD=2AD, E 是 CD 上一点,ZABE=45° ,贝ij tanZAEB的值等于(c-书7.将一副直角三角板中的两块按如图摆放,连AD,贝ij tanZDAC 的值为(B. <6D.2^3B 警 :響 在AABC 中,ZA=30° , E 为 AC 上一点,且 AE : EC=3: 1, EF 丄AB 于 F,连接 FC, D.2^2+1 则tanZCFB 等于(D. B. 15近 kmC. 15(V6+V2) kmD. 5 (^6+3^2) kmC. 2D. 3A .2V3 "1Z 如图, 8.A .是( )12. (2008-资阳)如图,已RtAABC^Rt ADEC, ZE 二30° , D 为AB 的中点,AC=1,若ADEC 绕点D 顺时针旋转, 使ED, CD 分别与RtAABC 的直角边BC 相交于M, N.则当△DMX 为等边三角形时,AM 的值为( )15. (2013・道里区三模)如图,在Z\ABC 中,ZO90° , AC 二16, AB 的垂直平分线交AC 于点D,连接BD,若cosZBDC 三,5则BC 的长是 _____________ .16. __________________________________________________________________________________ 如图,在 RtAABC 屮,ZC=90° , ZA-300 ,在 AC 上取一点 D,使得 CD=BC,则sinZABD= _________________________A. 3B. 2C ・ID.B.2A /31"D. 113. (2014-奉贤区二模)如图, 在四边形ABCD 中,E 、F 分别是AB 、AD 的中点,若EF 二2, BC=5, CD 二3,则tanC 二17. (2013・宝应县二模)如图,在AABC 中,AB=10, AO6, BC 二8,为AABC 的内切圆,点D 是斜边AB 的中点, 则 tanZODA= ___________ .18. (2013-成都一模)如图,P 为圆外一点,PA 切圆于A, PA 二8,直线PCB 交圆于C 、B,且PC 二4,连接AB 、AC,RS 上的点,且ZMPN=30°・若△PMN 为等腰三角形,且面积为1,21- SBC 中,D 为 AC 边中点,ZEDF=9。
三角函数、数列、立体几何试卷学生用
三角函数、数列立体几何试题一、选择题1.函数()sin()(0,0,0)f x A x A ωϕωϕπ=+>><<的图象如图所示,为了得到()cos g x A x ω=-的图象,可以将()f x 的图象( )A .向右平移12π个单位长度 B .向右平移512π个单位长度 C .向左平移12π个单位长度 D .向左平移512π个单位长度2.在ABC ∆中,角,,A B C 所对边分别为,,a b c , 且(2)cos cos b a C c A -= , 3c =,sin sin sin A B A B +=,则ABC ∆的面积为( )A .8B .2C .2D .43.设n S 是等差数列{}n a 的前n 项和,若==5935,95S S a a 则( ) A .1 B .1- C .2 D .21 4.已知数列{}n a 的前n 项和为n S ,若321n n S n =++,则n a =( )A .16,123,2n n n a n -=⎧=⎨⨯≥⎩ B .123n n a -=⨯ C .1232n n a -=⨯+ D .16,1232,2n n n a n -=⎧=⎨⨯+≥⎩ 5.如图,四棱锥P ABCD -中,90ABC BAD ∠=∠=,2BC AD =,PAB ∆和PAD ∆都是等边三角形,则异面直线CD 与PB 所成角的大小为A .90B .75C .60D .456.如图,空间四边形ABCD 的对角线AC =8,BD =6,M 、N 分别为AB 、CD 的中点,并且AC 与BD 所成的角为90°,二、填空题7.已知函数()sin 26f x x π⎛⎫=+ ⎪⎝⎭.若()(0)2y f x πϕϕ=-<<是偶函数,则ϕ= .8.函数()cos sin 222x x x f x ⎛⎫= ⎪⎝⎭的最小正周期为 .9.若数列{}n a 满足212332n a a a a n n =++⋅⋅⋅⋅⋅⋅⋅,则数列{}n a 的通项公式为___________.10.已知数列{}n a 满足113,2n n a a a n +=-=, 则_____n a =.11.已知数列{}n a 的首项是11a =,前n 项和为n S ,且1231(*)n n S S n n N +=++∈,设2log (3)n n c a =+,若存在常数k ,使不等式1(*)(25)n nc k n N n c -≥∈+恒成立,则k 的最小值为 .12.已知数列}{n a 的前n 项的和n S 满足n S n =+)1(log 2,则n a = .13.用一个平面截半径为25 cm 的球,截面面积是225π2cm ,则球心到截面的距离为_____cm .14.如图,四边形ABCD 和ADPQ 均为正方形,它们所在的平面互相垂直,M ,E ,F 分别为PQ ,AB ,BC 的中点,则异面直线EM 与AF 所成的角的余弦值是 .三、解答题15.(本小题满分12分)在ABC ∆中,设角,,A B C 的对边分别为,,a b c ,且1cos 2a C c b +=. (1)求角A 的大小;(2)若4a b ==,求边c 的大小.16.(本题满分12分)在ABC ∆中,角A 、B 、C 所对的边分别为,,a b c ,且34C π=,sin A = (1)求sin B 的值;(2)若5c a -=-ABC ∆的面积。
高考立体几何、数列、三角函数、不等式、平面向量综合经典试题练习(含答案)
cos
x
0
2
的部分图象如图所示,f
x0
f
0 ,
则正确的选项是( )
试卷第 2页,总 9页
A.
6
,
x0
1
C.
3
,
x0
1
B.
6
,
x0
4 3
D.
3
,
x0
2 3
20.已知 | a | 1,| b | 2, a 与 b 的夹角为 600,若 a kb 与 b 垂直,则 k 的值为( )
B. 2 2
C. 3 2
D.1
22 . . 设 G 是 ABC 的 重 心 , 且
(56 sin A)GA (40 sin B)GB (35 sin C)GC 0 ,则角 B 的大小为
()
A.45° B.60° C.30° D.1 5°
23.在△ABC 中,a=2,b=2 ,B=45°,则 A 等于( )
CC1 c 则A1B
(A) a+b-c
(B) a–b+c
(C)-a+b+c.
(D)-a+b-c
18.函数 f x sin 2 x
3
sin
x
cos
x
在区间
4
,
2
上的最大值为(
)
(A) 3 2
(B)1 3
(C)1
(D) 1 3 2
19.已知函数
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.A ,B ,C ,D ,E 五人并排站成一排,如果B 必须站在A 的右边,(A ,B 可以不相邻)那么不同的排法有( )
A .24种
B .60种
C .90种
D .120种
2.一工厂生产的100个产品中有90个一等品,10个二等品,现从这批产品中抽取4个,则其中恰好有一个二等品的概率为( )
A.41004901C C -
B.4100390110490010C C C C C +
C.4100
110C C D.4100390110C C C .
3下列函数中,最小正周期为且图象关于原点对称的函数是( )
()cos(2)2A y x π=+ ()sin(2)2
B y x π
=+ ()sin 2cos 2C y x x =+ ()sin cos D y x x =+
4.某四棱台的三视图如图所示则该四棱台的体积是
( )
A .4B
.6
5.在ABC △中,4a =,5b =,6c =,则sin 2sin A C = .
6.有6名学生,其中有3名会唱歌,2名会跳舞,1名既会唱歌也会跳舞.现从中选出2名会唱歌的,1名会跳舞的去参加文艺演出,则共有选法 种.
正视图 俯视图 侧视图
第5题图
7.将4个不同的球放入4个不同的盒子内,(1)共有几种放法?
(2)恰有一个盒子未放球,共几种放法?(3)恰有一个盒子内有2球,共几种放法?(4)恰有两个盒子内未放球,共有几种放法?
8.甲、乙、丙三人分别独立的进行某项技能测试,已知甲能通过测试的概率是2
5
,甲、乙、
丙三人都能通过测试的概率是3
20
,甲、乙、丙三人都不能通过测试的概率是
3
40
,且乙通
过测试的概率比丙大。
(Ⅰ)求乙、丙两人各自通过测试的概率分别是多少;(Ⅱ)求测试结束后通过的人数 的分布列。
9.设()2sin cos cos 4f x x x x π⎛
⎫=-+ ⎪⎝⎭
. (Ⅰ)求()f x 的单调区间;
(Ⅱ)在锐角ABC ∆中,角,,A B C 的对边分别为,,a b c ,若0,12A f a ⎛⎫==
⎪⎝⎭,求ABC ∆面积的最大值.
10.设ABC ∆的内角A ,B ,C 的对边分别为a ,b ,c ,tan a b A =,且B 为钝角.
(1)证明:2B A π
-=;
(2)求sin sin A C +的取值范围.。
