第11章 习题课
辽宁工业大学高数习题课11-1

an ≥ 0
正项级数
二,判别常数项级数收敛的解题方法
的敛散性, 判别常数项级数∑an的敛散性,应先考察是否有
n=1
liman = 0 成立.若不成立,则可判定级数发散; 成立.若不成立,则可判定级数发散;
n→∞
若成立,则需作进一步的判别. 若成立,则需作进一步的判别.
此时可将常数项级数分为两大类,即正项级数与任意项级数. 此时可将常数项级数分为两大类,即正项级数与任意项级数. 对于正项级数,可优先考虑应用比值法或根值法. 对于正项级数,可优先考虑应用比值法或根值法.若此 二方法失效,则可利用比较法(或定义)作进一步判别; 二方法失效,则可利用比较法(或定义)作进一步判别; 对于任意项级数, 是否收敛. 对于任意项级数,一般应先考虑正项级数 ∑ an 是否收敛. 若收敛,则可判定原级数收敛,且为绝对收敛; 若收敛,则可判定原级数收敛,且为绝对收敛;
n=1
∞
问题是熟练掌握一批已知正项级数的敛散性(如几何级数, 问题是熟练掌握一批已知正项级数的敛散性(如几何级数,
p 级数等),然后根据 an 的特点,进行有针对性的放缩. 级数等), ),然后根据 的特点,进行有针对性的放缩.
a nn! 的收敛性. 【例6】判别级数 ∑ nn 的收敛性. 】 n =1
un+1 ∵ = un e >1 1 n (1 + ) n
∴ un+1 > un lim un ≠ 0
n →∞
所以,原级数发散. 所以,原级数发散. 的因子时, 注:在级数一般项 un 中,若含有形如 nk , an , n!, nn 的因子时, 适于使用比值审敛法. 适于使用比值审敛法.
1 的敛散性. 【例7】判断级数∑ [ln(n + 1)]n 的敛散性 】 n =1
大学物理 磁学习题课

( I 1 I 2 ) ln 2
第11章 恒定电流的磁场
17
MN上电流元I3dx所受磁力:
0 I1
a M
dx N
c I2
d F I 3 B d x I 3 [ 2(r x) 2(2r x) ] d x
r
0 I1
I3 r Or b
r d
x
F I3 [
0
0 I1
2(r x)
0I2
2(2r x)
]d x
0I3
S
B
圆面
Φm
2 B S BR cos
1 B d S B R 2 2
n
60°
R
B
任意曲面
S
S
很多漏掉负号 类似本页二.1(1)磁通量
12
第11章 恒定电流的磁场
P42 一选择1.
H dl 2 I L1
H dl I L2
1
第11章 恒定电流的磁场
16
P44 二1、如图所示,载有电流I1和I2的长直导线ab和cd相互平行,相距为
3r,今有载有电流I3的导线MN = r,水平放置,且其两端MN分别与I1、I2 的距离都是r,ab、cd和MN共面,求导线MN所受的磁力大小和方向.
载流导线MN上任一点处的磁 感强度大小为: I 0 I 2 0 1 I1 B 2( r x ) 2( 2r x )
1
B
•直导线延长线上
a
第11章 恒定电流的磁场
P
6
2.
圆电流轴线上某点的磁场
B
大小:
11章马尔可夫链习题课

pN ,1 p,
p1,N q,
第19页,共20页。
例5 试证Wiener过程B(t)是马尔可夫过程 .
证明
p{B(t s) y | B(s) x, B(u)(0 u s)} p{B(t s) B(s) y x | B(s) x,
B(u)(0 u s)} p{B(t s) B(s) y x} 独立增量性 p{B(t s) B(s) y | B(s) x}
为马氏链在时刻 m处于状态ai条件下,在时刻
m n转移到状态a m, m n) 1, i 1,2,.
j1
由转移概率组成的矩阵 P(m, m n)(Pij (m, n n))
称为马氏链的转移概率矩阵.
它是随机矩阵.
第7页,共20页。
马氏链的n步转移概率
马尔可夫链.
简记为: { Xn X (n),n 0,1,2,}
第5页,共20页。
齐次马尔可夫链
当转移概率Pij (m, n n)只与i, j及时间间距n
有关时, 称此链是齐次的或时齐的.
第6页,共20页。
转移概率、转移概率矩阵
称条件概率 Pij (m, n n) P{ X mn a j | X m ai }
第18页,共20页。
例4 一质点在圆周上做随机 游动,圆周上共有N格, 质点以概率 p顺时针移动一格 ,以概率 q 1 p逆时 针移动一格,试用马尔可夫链描述游 动过程,确定状 态空间和转移概率矩阵 .
解 状态空间为 S 1, 2, , N
pi,i1 p, i 1, 2, , N 1, pi,i1 q, i 2, , N .
j1
第11页,共20页。
三、典型例题
例1 艾伦非斯特(Ehrenfest)模型 设一个坛子装有 c个球,它们或是红色的,或
机械设计 螺纹连接 习题课讲解

注:此题用图解法求解。
N 1000
900
800
700600F500F0F0
F
400
F’
300
F”
200
60°
100
30° 45°
45°
F”
变形
机械设计 第11章 螺纹联接习题课
10
BIGC 例4 一钢板采用三个铰制孔螺栓联接,下列三个方案哪个最好?
BIGC
机械设计 第11章 螺纹联接习题课
11
FL 2a
机械设计 第11章 螺纹联接习题课
4
(二)工作条件分析
1、保证结合面不滑移
F s z k f H 又:F F c2 V
c1 c2 z
2、受力最大螺栓轴向载荷
F 1 ( k f H c2 V )
z s c1 c2
=5662.5N
取: kf =1.3 μs=0.13
Q
解: 一)受力分析
R
Q
T
R=Q/2=10000 N T=R×300=3000000 N.mm
Q
FSR
FST FSR
FSR FST
FST FSR FST
BIGC
机械设计 第11章 螺纹联接习题课
7
R使各螺栓受到横向工作载荷FSR: FSR=R/4=2500( N )
T也使各螺栓受到横向工作载荷FST,方向与形心连线垂直。
BIGC
机械设计 第11章 螺纹联接习题课
1
一、螺栓组计算
螺栓联接习题课
螺栓 组受 力分 析
轴向力
横向力
受拉 F k f FR
F=FQ/z
s m z
(完整版)理论力学课后习题答案第11章达朗贝尔原理及其应用
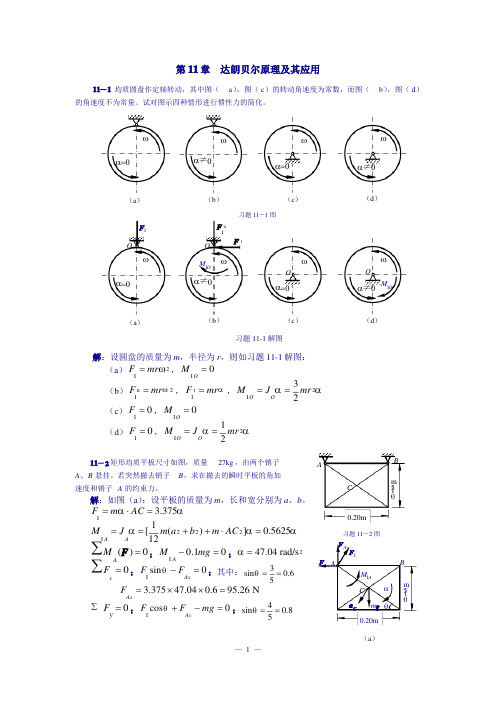
第11章达朗贝尔原理及其应用11-1均质圆盘作定轴转动,其中图(a ),图(c )的转动角速度为常数,而图(b ),图(d )的角速度不为常量。
试对图示四种情形进行惯性力的简化。
ωα=0α≠0ωα=0ωα≠0ω(a )(b )习题11-1图(c )(d )F I OOF InF Itωα=0M I OωOωOωα≠0M I Oα≠0α=0(a )(b )(c )(d )习题11-1解图解:设圆盘的质量为m ,半径为r ,则如习题11-1解图:2(a )F I=mr ω,MI O=0(b )F I =mr ω,F I=mr α,MI O=J O α=(c )F I=0,MI O=0(d )F I=0,MI O=J O α=11-2矩形均质平板尺寸如图,质量27kg ,由两个销子A 、B 悬挂。
若突然撤去销子B ,求在撤去的瞬时平板的角加速度和销子A 的约束力。
n2t32mr α212mr α2ACB解:如图(a ):设平板的质量为m ,长和宽分别为a 、b 。
F I=m α⋅AC =3.375α0.20m习题11-2图.15m1M I A =J A α=[m (a 2+b 2)+m ⋅AC 2]α=0.5625α122α=47.04rad/s M -0.1mg =0;;M (F )=0I A∑A F AyF IF Ax AM I A C a CBαm g θ∑F y=0;F I cos θ+F Ay -mg =0;sin θ=4=0.850.20m (a ).15m∑Fx=0;F I sin θ-F Ax=0;其中:sin θ=3=0.65F Ax=3.375⨯47.04⨯0.6=95.26NF Ay=27⨯9.8-3.375⨯47.04⨯0.8=137.6N11-3在均质直角构件ABC 中,AB 、BC 两部分的质量各为 3.0kg ,用连杆AD 、DE 以及绳子AE 保持在图示位置。
若突然剪断绳子,求此瞬时连杆AD 、BE 所受的力。
第十一章反常积分习题课

第十一章 反常积分习题课一 概念叙述 1.叙述()dx x f a⎰+∞收敛的定义.答:()dx x f a⎰+∞收敛⇔()()lim+∞→+∞=⎰⎰uaau f x dx f x dx 存在.⇔()lim0+∞→+∞=⎰uu f x dx .2.叙述()b af x dx ⎰(a 是暇点)收敛的定义.答:()ba f x dx ⎰收敛⇔()()lim +→=⎰⎰b buau a f x dx f x dx 存在.⇔0,0,εδ∀>∃>当δ<<+a u a ,有()()ε-<⎰⎰b buaf x dx f x dx .3. 叙述()dx x f a⎰+∞收敛的柯西准则.答:无穷积分()dx x f a⎰+∞收敛的柯西准则是:任给0ε>,存在0M >,只要12,u u M >,便有()()()2121u u u aau f x dx f x dx f x dx ε-=<⎰⎰⎰.4. 叙述()b af x dx ⎰(a 是暇点)收敛的柯西准则.答:瑕积分()dx x f ba ⎰(瑕点为a )收敛的充要条件是:任给0ε>,存在0δ>,只要()12,,u u a a ∈+δ,总有()()()2121b bu u u u f x dx f x dx f x dx -=<ε⎰⎰⎰.二 疑难问题1.试问⎰+∞adx x f )(收敛与0)(lim =+∞→x f x 有无联系?答:首先,0)(lim =+∞→x f x 肯定不是⎰+∞adx x f )(收敛的充分条件,例如01lim=+∞→x x ,但⎰+∞11dx x发散.那么0)(lim =+∞→x f x 是否是⎰+∞adx x f )(收敛的必要条件呢?也不是!例如⎰+∞12sin dx x ,⎰+∞12cos dx x ,⎰+∞14sin dxx x 都收敛,因为前两个无穷积分经换元2t x =得到⎰+∞12sin dx x 1+∞=⎰,21cos x dx +∞=⎰=dt tt ⎰+∞12cos ,则⎰+∞12sin dx x ,⎰+∞12cos dx x 是条件收敛,对于第三个无穷积分,经换元2t x =而得⎰+∞14sin dx x x =⎰+∞12sin 21dt t ,它也是条件收敛的. 从这三个无穷积分的收敛性可以看到,当x →+∞时被积函数即使不趋于零,甚至是无界的,无穷积分仍有可能收敛.注:若lim ()0x f x A →+∞=≠,则⎰+∞ax x f d )(发散.注:1)若⎰+∞ax x f d )(收敛,且lim ()x f x A →+∞=存在, 则定有0)(lim =+∞→x f x ;2)若⎰+∞a x x f d )(收敛,且f 在[)+∞,a 上为单调,则0)(lim =+∞→x f x ;3)若⎰+∞a x x f d )(收敛,且f 在[)+∞,a 上一致连续,则0)(lim =+∞→x f x ;4)若⎰+∞ax x f d )(收敛,且()d af x x +∞'⎰收敛,则0)(lim =+∞→x f x .证:1)设A x f x =+∞→)(lim .若0≠A (不妨设0A >),则由极限保号性,M a ∃>,当x M ≥时满足 于是有()()2MaAf x dx u M ≥+-⎰, 于是 而这与⎰+∞ax x f d )(收敛相矛盾,故0A =.2)不妨f 在[)+∞,a 上单调增,若f 在[)+∞,a 上无上界,则0A ∀>,M a ∃>,当x M ≥时,使A x f ≥)(.类似于1)的证明,推知⎰+∞+∞=a dx x f )(,矛盾.所以f 在[)+∞,a 上单调增而有上界,于是由单调有界定理知A x f x =+∞→)(lim 存在.依据已证得的命题1),0)(l i m =+∞→x f x .3)由f 在[)+∞,a 上一致连续,则0,0εδ∀>∃>,(设)δε≤[),,x x a '''∀∈+∞ x x δ'''-<只要时,就有()()2f x f x ε'''-<.又因⎰+∞adx x f )(收敛,故对上述,M a δ∃>,当12,x x M >时,有212()2x x f x dx δ<⎰.现对任何x M >,取12,x x M >,且使1221,.x x x x x δ<<-=此时由 便得(),.f x x M ε<>这就证得.0)(lim =+∞→x f x4)因为()d af x x +∞'⎰收敛,则()()()lim()d lim uau u f x x f u f a →+∞→+∞'=-⎰存在,于是()lim u f u →+∞存在,由1)得证.2.()af x dx +∞⎰收敛,与|()|af x dx +∞⎰收敛,2()af x dx +∞⎰收敛的关系?答:1)因为绝对收敛⇒收敛,反之不对,条件收敛的例子都是反例,则|()|af x dx +∞⎰收敛()af x dx +∞⎰收敛.2)()af x dx +∞⎰2()af x dx +∞⎰收敛,例1+∞⎰条件收敛,但 21111sin 1cos 21cos 2222xx x dx dx dx dx x x x x+∞+∞+∞+∞-==-⎰⎰⎰⎰,112dx x +∞⎰发散,1cos 22x dx x+∞⎰发散,则21sin x dx x +∞⎰发散. 例 211dx x +∞⎰收敛,但11dx x+∞⎰发散. 3)()af x dx +∞⎰收敛2()af x dx +∞⎰收敛,例 ()2441,10,1n n x n n f x n x n n ⎧≤<+⎪⎪=⎨⎪+≤<+⎪⎩,对ε∀,总存在1M >,使当n M >时,都有41221n n nn dx n ε+=<⎰. 故但对于()2f x ,例302sin x dx x+∞⎰绝对收敛,即302sin x dx x+∞⎰收敛,因为312sin x dx x+∞⎰绝对收敛,即312sin x dx x+∞⎰收敛,而1302sin x dx x⎰,0是暇点,取12p =,则3322sin lim lim 1ppx x x x x x xx++→→==,因为112p =<收敛. 因为2133330010sin 1cos 21cos 21cos 2222x x x x dx dx dx dx x x x x+∞+∞+∞---==+⎰⎰⎰⎰, 311cos 22xdx x +∞-⎰收敛.1301cos 22x dx x -⎰,0是暇点,取1p = ,则23300141cos 22lim lim 122p p x x xx x x x x ++→→-==, 因为1p =,则发散.例 211dx x +∞⎰收敛,但11dx x+∞⎰发散. 3.()baf x dx ⎰(a 为瑕点)收敛,与|()|baf x dx ⎰收敛 ,2()baf x dx ⎰收敛的关系?答:1)|()|baf x dx ⎰收敛()baf x dx ⎰收敛.因为绝对收敛⇒收敛,反之不对,条件收敛的例子都是反例. 2)()baf x dx ⎰收敛2()baf x dx ⇒⎰收敛,()baf x dx ⎰收敛2()baf x dx ⇒⎰收敛.反例1⎰收敛,但101dx x ⎰发散.3)若2()b af x dx ⎰(a 为瑕点)收敛,则|()|baf x dx ⎰(a 为瑕点)收敛.证 因()()212f x f x +≤,则由比较原则,可得|()|b a f x dx ⎰收敛,从而()b a f x dx ⎰收敛.3.下列说法对吗?1)因为sin xx 在0没有定义,则10sin x dx x⎰是瑕积分;2)因为ln 1xx -在1x =没有定义,则1x =是10ln 1x dx x-⎰的暇点.答:若被积函数f 在点a 的近旁是无界的,这时点a 称为f 的瑕点.1)错误,因为0sin lim 1x x x +→=,则s i n xx在0的近旁有界,因此不是瑕点,10sin x dx x ⎰是定积分.若()x f 在(]b a ,上连续,()A x f ax =+→lim (常数),则()⎰badx x f 可看成正常积分,事实上,定义()()(]⎩⎨⎧∈==.,,,,b a x x f a x A x F 知()x F 在[]b a ,上连续,即()⎰badxx F 存在,而()()()⎰⎰⎰-→-→++==ba ba b adx x F dx x f dx x f εεεε00lim lim ,由于()x F 在[]b a ,上连续,知变下限函数()()⎰-=ba dx x F G εε在[]a b -,0上连续,有()()()⎰==+→ba dx x F G G 0limεε,即()().⎰⎰=b a b a dx x F dx x f 故()⎰ba dx x f 可看成正常积分。
第11章习题课·数学苏科版七下-课课练
在我们的生活中,不等关系更为普遍.习㊀题㊀课1.解不等式组:(1)2x -1>x +1,x +8<4x -1;{(2)x -3(x -2)ɤ4,①1+2x 3>x -1.㊀②{2.求满足不等式组2x +5>1,3x -8ɤ10{①②的整数解.3.解不等式组3x -2<x +2,8-x ȡ1-3(x -1).{4.某小区前坪有一块空地,现想建成一块面积大于48平方米,周长小于34米的矩形绿化草地,已知一边长为8米,设其邻边长为x 米,求x 的整数解.(第4题)七年级数学(下)5.如图所示的矩形包书纸中,虚线是折痕,阴影是裁剪掉的部分,四个角均为大小相同的正方形,正方形的边长为折叠进去的宽度.(1)设课本的长为a c m,宽为b c m,厚为c c m,如果按如图所示的包书方式,将封面和封底各折进去3c m,用含a,b,c的代数式,分别表示满足要求的矩形包书纸的长与宽; (2)现有一本长为19c m,宽为16c m,厚为6c m的字典,你能用一张长为43c m,宽为26c m的矩形纸,按如图所示的方法包好这本字典,并使折叠进去的宽度不小于3c m 吗?请说明理由.(第5题)6.筹建中的城南中学需720套课桌椅,光明厂承担了这项生产任务,该厂生产桌子的必须5人一组,每组每天可生产12张;生产椅子的必须4人一组,每组每天可生产24把.已知学校筹建组要求光明厂6天完成这项生产任务.(1)问光明厂平均每天要生产多少套单人课桌椅?(2)学校筹建组要求至少提前1天完成这项生产任务,光明厂生产课桌椅的员工增加到84名,试给出一种分配生产桌子㊁椅子的员工数的方案.7.小明利用课余时间回收废品,将卖得的钱去购买5本大小不同的两种笔记本,要求共花钱不超过28元,且购买的笔记本的总页数不低于340页,两种笔记本的价格和页数如下表所示:大笔记本小笔记本价格(元/本)65页数(页/本)10060为了节约资金,小明应选择哪一种购买方案?请说明理由.习㊀题㊀课1.(1)第一个不等式解得x >2,第二个不等式解得x >3,得到x >2,x >3.{所以原不等式组的解集为x >3.(2)由①,得x -3x +6ɤ4,-2x ɤ-2,x ȡ1.由②,得1+2x >3x -3,-x >-4,x <4.ʑ㊀原不等式组的解集为1ɤx <4.2.由①,得x >-2.由②,得x ɤ6.ʑ㊀-2<x ɤ6.ʑ㊀满足不等式组的整数解为-1,0,1,2,3,4,5,6.3.-2ɤx <24.依题意,得8x >48,2(x +8)<34.{解得6<x <9,当x 为整数时,取值为7,8.5.(1)矩形包书纸的长为(2b +c +6)c m ,矩形包书纸的宽为(a +6)c m .(2)设折叠进去的宽度为x c m ,分两种情况:①当字典的长与矩形纸的宽方向一致时,根据题意,得19+2x ɤ26,16ˑ2+6+2x ɤ43.{解得x ɤ2.5.所以不能包好这本字典.②当字典的长与矩形纸的长方向一致时,同理可得x ɤ-6.所以不能包好这本字典.综上,所给矩形纸不能包好这本字典.6.(1)ȵ㊀720ː6=120,ʑ㊀光明厂平均每天要生产120套单人课桌椅.(2)设x 人生产桌子,则(84-x )人生产椅子,则x 5ˑ12ˑ5ȡ720,84-x 4ˑ24ˑ5ȡ720.{解得60ɤx ɤ60,ʑ㊀x =60,80-x =24.ʑ㊀生产桌子60人,生产椅子24人.7.设买大笔记x 本,由题意,得6x +5(5-x )ɤ28,100x +60(5-x )ȡ340.{解得1ɤx ɤ3.又㊀x 为正整数,ʑ㊀x =1,2,3.所以购买的方案有三种:方案一:购买大笔记本1本,小笔记本4本;方案二:购买大笔记本2本,小笔记本3本;方案三:购买大笔记本3本,小笔记本2本.方案一花费的费用为6ˑ1+5ˑ4=26元;方案二花费的费用为6ˑ2+5ˑ3=27元;方案三花费的费用为6ˑ3+5ˑ2=28元.所以选择方案一省钱.。
高中物理第11章电路及其应用4串联电路和并联电路第2课时习题课串并联电路的应用新人教版必修第三册
探究 测电表内阻的两种方法
测电表内阻与测纯电阻阻值的原理相同,对于电表的“身份”我们 进行一下转换:认为它是一个“会说话的电阻”,会说自己的电压值(电 压表)或电流值(电流表),我们需要做的工作就是想办法测量另一未知的 物理量。
1.半偏法 (1)半偏法测电流表内阻 ①原理:如图所示,闭合 S1,断开 S2,调节滑动变阻器 R1,使电流 表示数达到满偏值 Ig;保持 R1 不变,闭合 S2,调节电阻箱 R2,使电流表 的示数等于I2g,然后读出 R2 的值,则有 Rg=R2。
2.常用的简化方法 (1)电流分支法 ①先将各节点用字母标出; ②判定各支路元件中的电流方向(若原电路无电压或电流,可假设在 总电路两端加上电压后判定); ③按电流流向,自左到右将各元件、节点分支逐一画出; ④将画出的等效图加工整理,如图所示。
(2)等势点排列法 ①将各节点用数字或字母标出,如图甲中S断开时,1、2两个节点 可视为同一个节点,3、4两个节点可视为同一个节点; ②判定各节点电势的高低,图甲中有φ12>φ34>φ5; ③对各节点按电势高低自左到右排列,再将各节点间的支路画出; ④将画出的简化图加工整理,得到如图乙所示的等效电路。
具 体 地 说 就 是 最 小 分 度 末 位 是 “1” 的 仪 器 , 读 数 时 应 估 读 到 下 一 位。例如,最小分度是1 mm的刻度尺,读出的数以mm为单位,小数点 后应有1位数(如28.3 mm);最小分度是0.1 A的电流表,读出的数以A为 单位,小数点后应有2位数(如0.36 A)。
答案2.5 A
方法点拨:进行电路计算,首先要简化电路,简化电路的一般规则 如下:
(1)无阻导线可缩成一点,一点也可延展成无阻导线; (2)几个等势点都可合成一点,连接在等势点之间的导体因其中没有 电流,可将其摘去; (3)电路中的电表没有特别说明可按理想电表处理 ,理想电压表 RV→∞,可将其摘去(视为断路),理想电流表RA=0,可将其用导线取 代。
《高数》第十一章-习题课:级数的收敛、求和与展开
概念:
为收敛级数
若
收敛 , 称
若
发散 , 称
绝对收敛 条件收敛
Leibniz判别法: 若
且
则交错级数
收敛 , 且余项
4
例1. 若级数
均收敛 , 且
证明级数
收敛 .
证: 0 c n a n bn a n (n 1 , 2 , ), 则由题收敛
(1)n
n0
x2n ,
x (1,1)
arctan
x
x
01
1 x2
d
x
(1)n x2n1, n02n 1
x [1,1]
于是
f (x) 1 (1)n x2n (1)n x2n2
n1 2n 1
n02n 1
25
f
a 1 时收敛 ; a 1 时发散.
s 1 时收敛;
a 1 时, 与 p 级数比较可知 s 1 时发散.
7
P257 题3. 设正项级数 和 都收敛, 证明级数
也收敛 .
提示:
因
lim
n
un
lim
n
vn
0
,存在
N
>
0, 当n
>N
时
又因
2( un2 vn2 )
思考: 如何利用本题结果求级数
提示: 根据付式级数收敛定理 , 当 x = 0 时, 有
e 1 1
2 n1
f (0 ) f (0 ) 1
2
2
28
作业
P257 6 (2); 7 (3); 9(1) ; 10 (1) ;
第七章无穷级数习题课(二) - 第十一章无穷级数习题课(一)
− 故此幂级数的收敛域为 [−2, 2]。
( −1) n−1 【例4】求幂级数 ∑ 】
( −1) n −1 ∑
n =1
∞
∞
∞
n =1
2 2 n −1 2 n −1 x 的和函数, 的和函数,并求 2n − 1
1 的和。 的和。 2n − 1
n −1
解:记 S ( x ) = ∑ ( −1)
n =1
∞ ( −1) n 1 该级数收敛。 当 x = − 时,级数为 ∑ 2 ,该级数收敛。 n +1 2 n =1 1 1 − 故此幂级数的收敛域为 [− , ] 。 2 2
∞
【例2】求幂级数 ∑ 】
n =1
∞
1 n
( x − 2)n 的收敛域。 的收敛域。
∞
解:令 x − 2 = t ,原级数变为∑
an xn 型、 求幂级数的收敛域,通常有三种基本类型, 求幂级数的收敛域,通常有三种基本类型,即∑
∞ n=0
an ( x − x0 )n 型和缺幂型,还有一种特殊的非幂函数型。 型和缺幂型,还有一种特殊的非幂函数型。 ∑
n=0
∞
对于 ∑an x 型,通过求 ρ = lim n→∞
n n=0
∞
an+1 1 ,得半径 R = , an ρ
un+1 ( x ) x 2n+1 n4 n 1 2 1 = lim ⋅ 2 n −1 = x = x 2 lim n → ∞ ( n + 1)4 n + 1 n→ ∞ u ( x ) 4 4 x n
1 2 级数收敛。 当 x < 1 ,即 x < 2 时,级数收敛。 4 1 2 级数发散。 当 x > 1 ,即 x > 2 时,级数发散。 4
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(1)
n1
n1
un 收敛 ,
7
例4. 设常数 a > 0 , 讨论级数
n 1
1 n 的敛散性。 1 a
a 解 当 0 a 1 , n 时, 0 ,
n
1 n 1 0 , ∴级数发散。 1 a 1 1 0 级数发散。 当 a 1时, n 1 a 2 1 n 1 1 ( ) , 当 a 1 时, n a 1 a an 1 n 1 收敛, 收敛。 ∵ ( ) n n 1 1 a n 1 a
1 1 1 1 1 , x x 3 x 1 3 , ∵ 3 1 n 2 3 4 12 x 4 ,x x ... x (... 2,4) x n x x 收敛域 x 1 x n 0 25
x 3.将函数 f ( x ) 2 展开成 x 的幂级数。 2 x x x 1 1 ) f ( x) ( 解 3 1 x 2 x
1 n2 1 n n lim (1 ) lim(1 ) n n n n
e
e
1
n 1 0 e
因此级数在端点发散 ,
1 1 故收敛区间为 ( , 17 ) . e e
解:
lim
n
un1 ( x )
un ( x )
lim n lim n
x 2
2
x2 当 1 , 即 2 x 2 时, 级数收敛; 2 当 x 2 时, 一般项 un n 不趋于0,级数发散;
故收敛区间为 ( 2 , 2 ) .
18
三、幂级数和函数的求法
• 求部分和式极限
•
•
初等变换法:
分解、套用公式
an x n n 0
微积分变换法 (在收敛区间内)
n
不满足
发散
2.
正项级数审敛法
满足
un1 比值审敛法 lim u n n 1
根值审敛法
部分和极限 比较审敛法
lim n un
n
不定
用它法判别
积分判别法
1
收 敛 发
1
散
5
比较判别法 设 (1)若
vn
则
则
v n 收敛,
发散,
也收敛;
(2)若
v n 也发散.
10 10
解
x
lim
lim
x
10ln x
x 1
9
lim
n
lim n 10
n
ln n
12
级数
1 n 发散,
原级数 发散.
(3)
n 1
a s n
n
(a 0, s 0).
解
lim
n
an n ns
lim
n
a
(n n )
s
a
根据根值判别法可知: a 1 时收敛 ; a 1 时发散.
(1)
n1
1 1 1 n1 ( 1) 发散, n n1 n( n 1) n1
∵
n1
an an1 和 均收敛, 2 2 n1
n1
an an1 收敛. 4 2
一、数项级数的审敛法
1. 利用部分和数列的极限 判别级数的敛散性 必要条件 lim u 0 n
23
四、函数的幂级数和付式级数展开法
1. 函数的幂级数展开法 • 直接展开法 — 利用泰勒公式 • 间接展开法 — 利用已知展式的函数及幂级数性质
练习: 1. 将函数 解:
展开成 x 的幂级数.
n 0
x 2n
n
n
两边对x求导
1 (2 x )2
n 0
x 2n
n 0
n n1 x n 2
发散 . 发散 .
因
单调递减,
且
由Leibniz判别法知级数收敛 ; 所以原级数条件收敛 14 .
sin 1 1 n1 n 1 n 1 n 1 ( ) ( 1) 因 解(3) n 1 1 n1 ( ) 收敛 故 原级数绝对收敛 . un1 解(4) 因 un
第十一章 习题课 级数的收敛、求和与展开
一、数项级数的审敛法 二、幂级数收敛域的求法
三、幂级数和函数的求法
四、函数的幂级数
1
n , 则级数的 例1. 已知级数 un 的前n 项和 Sn 2n 1 n1 1
通项 un=
4n 1
2
.
n n 1 解 un S n Sn1 2n 1 2n 1 2n2 n 2n2 n 1 4n 2 1 1 2 4n 1
2
例2.设级数
u
n1 n
n
收敛, 则必收敛的级数为(
( 1) ( A) un n n1
( B) ( D)
u
n1 n1
D
)
2 n
(C )
(u
n1 n1
2 n1
u2 n )
(u
n
un1 )
解 ∵
u
n1
n
和 un1 均收敛,
n1 n
直接用比值法或根值法
例9. 求下列级数的敛散区间:
标准形
非标准形
16
解:
1 1 1 R , 即 x 时原级数收敛. e e e 1 当 x 时, un e 1 n 1 (1 ) e n 1 1 e (1 1 )n1 n
1 n n (1 ) n
8
cos n 条件收敛 例5. 级数 的敛散性是 n 0 2n 1 cos n ( 1)n 解 cos n 1 n 2n 1 (1) 2n 1 , n 0 n 0 1 1 2n 1 发散 ∵ lim 2n 1 0 , n n 0
1 1 n x ( ( 1)n x n n x ) 2 n 0 2 3 n 0 1 1 n n1 ] x n1 [( 1) 2 3 n 0 1 x 1 由 1 x 1 x 1 1 2
26
4. 设 x 的幂级数, 并求级数 解:
2
2
x ( 1) 2 2 x 202
2
求幂级数
的和函数。
解
收敛域为 [1,1]
设和函数为
21
求幂级数
的和函数。
解法2 和函数
22
例3.求幂级数
解 先求出收敛区间
的和函数 设和函数为
x 2 1 x S ( x ) sin x cos x , 2 2
X=1
x sin x 2 sin1 cos1 S (1) 2
。
由莱布尼兹定理, 交错级数条件收敛。
9
例6.若级数
均收敛,且
证:
n1
收敛 . 证明级数 ( n 1 , 2 , ), 0 c n a n bn a n
(b
n
a n ) bn
n1
收敛
(c
n1
n
a n ) 收敛
n1
(c
n1
24
1 x 展开成(x—1)的幂级数。 2. 将 f ( x ) 2 x 1 1 x 1 解 f ( x ) ( x 1) 3 ( x 1) 3 1 x 1 3 x 1 n x 1 n (1) ( 3 ) 3 n 0 n 1 ( x 1) ( x 1)n n ( 1)n1 ( 1) n 1 n 0 3 3n n 1
a
n 0
n
x
n
逐项求导或求积分
难
求和 对和求积分或求导
S( x)
数项级数求和
S ( x)
*
直接求和: 直接变换, 求部分和等 间接求和: 转化成幂级数求和, 再代值
19
例10.
求下列幂级数的和函数:
解: 容易求出级数 的收敛域为 设和函数为 则
2 x 2x 2 2 (2 x 2) 2 x 2 2 (2 x )
且 n
un lim
极限形式 设 当 0 l 时, 若 若
vn
l
v n 收敛 ,则 v n 发散 , 则
也收敛. 也发散.
6
3. 一般项级数审敛法
设级数 收敛
若 若
收敛 , 则称 发散 , 则称
绝对收敛 ;
条件收敛 ;
且 lim un 0 n
Leibniz判别法: 若
则交错级数
27
, 将 f (x)展开成
的和. ( 01考研 )
1 2 1 x
( 1)
n 0
n
x
2n
x ( 1,1) x [1,1]
arctan x
于是
f ( x) 1
n 1
n 0
2 1
n 0 n 1
1
n 1
n 1
(u
un1 ) 收敛。
3
例3.
设级数
a
n 1
则( n 收敛,
( A) (C )
解
aa
n1 n1
n1
a
D
n
)
n
n
收敛,
