多体系统传递矩阵法及其应用(芮筱亭[等]著)思维导图
绪论

出生日期: 1831年06月13日 逝世日期: 1879年11月5日 职业: 物理学家
Harbin Engineering University
3 公因子和最大公因子
公因子的定义
• 相同列数的两个多项式矩阵间可以定义右公因子(是多项式 矩阵).假定N(s)和D(s)列数相同,若 N ( s) N ( s) R( s)
D(s) D (s) R(s) 则R(s)称为N(s)和D(s)的右公因子.
认识他们吗??
Edward John Routh :1831年1月20日出 生在加拿大的魁北克。
Routh 11岁那年回到英国,在de Morgan指导下学 习数学。在剑桥学习的毕业考试中,他获得第一名。并 得到了“Senior Wrangler”的荣誉称号。 毕业后Routh开始从事私人数学教师的工作。从 1855年到1888年Routh教了600多名学生,其中有27位获 得“SEnior Wrangler”称号。建立了无可匹敌的业绩。
Harbin Engineering University
哈罗德·史蒂芬·布莱克( Harold Stephen Black)
Harold Stephen Black (April 14, 1898 – December 11, 1983) was an American electrical engineer, who revolutionized the field of applied electronics by inventing the negative feedback amplifier in 1927. To some, his invention is considered the most important breakthrough of the twentieth century in the field of electronics, since it has a wide area of application. However, a negative feedback amplifier can be unstable such that it may oscillate. Once the stability problem is solved, the negative feedback amplifier is extremely useful in the field of electronics. Black published a famous paper, Stabilized feedback amplifiers, in 1934.
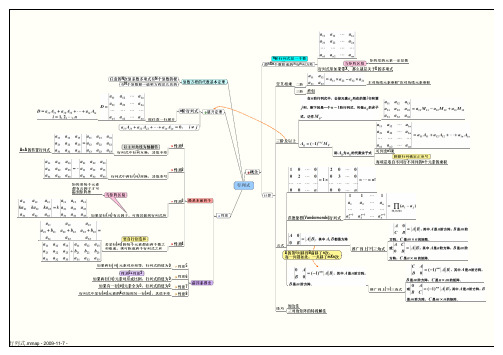
线性代数思维导图全6页及其总结
组成得向量组为对应齐次方程组的通解
求非齐次线性方程 组的通解
一组基中向量的个数称为子空间的维数
向量组A与B等价的充要条件是L(A)=L(B), 向量A组可由向量组B线性表示的充要条件
是 L(A)属于L(B) 其中L(A)表示由A生成的子空间
初等变换
第二章
通过行初等变化,可得阶梯形矩阵 通过行初等变换和列初等变换,可得等价标准型
注意:A必须是方阵且只可以进行行初等变换
等价标准型 A是可逆矩阵
A的秩等于n
detA不等于零
对于n阶矩阵A(方阵),下列条件等价
矩阵经初等变换之后秩不变,且称变换之前的矩 阵和变换之后的矩阵等价
A可表示为有限个初等矩阵的积
a的每个特征值对应的线性无关的特征向量的最大个数等于该特征值的重数注意p的逆矩阵在前施密特正交法将给定的一组基转化成正交基将给定的一个向量组变为单位正交的向量组先用施密特正交法将其正交化再将其单位化求齐次方程组的解空间w的正交基并将其扩充参见p95例58若矩阵a与其转置矩阵的乘积为单位矩阵则称a为正交矩阵即a的逆矩阵与其转置矩阵相等a为正交矩阵的充要条件是其列行向量组是rn中的单位正交基若a为正交矩阵则a的逆矩阵也为正交矩阵若ab为同阶正交矩阵则ab也为正交矩阵若a为正交矩阵则deta1实对称矩阵一定能与对角矩阵相似可对角化并且相似变换矩阵可取为正交矩阵实对称矩阵的特征值都是实数实对称矩阵的不同特征值对应的特征向量必定正第四章线性表示向量b可由向量a1a2???am线性表示的充要条件是ranka1a2???amranka1a2???am向量b可由向量a1a2???am惟一线性表示的充要条件是ranka1a2???amranka1a2???am注意将其与非齐次线性方程组联系起来线性相关当向量组构成的齐次线性方程组只有惟一解零解时向量组线性无关当向量组构成的齐次线性方程组有无数非零解时向量组线性相向量组线性相关含有零向量的向量组线性相关仅含一个向量a的向量组线性相关的充要条件是若n维向量组线性无关那么把每个向量任意添加s个分量后所得向量组也线性无关向量组线性相关的充要条件是其中至少有一个向量可由向量组织其他向量线性表示若n维向量组线性相关那么取这些向量的前r个分量rn组成的向量组也是线性相关的注意这条例题的思想相册内有清晰版与齐次线性方程组联系起来有n维向量组a若它的一个部分向量组a1线性无关且a1与a等价称a1是a的最大线性无关a1是a的最大线性无关组的充要条件rankaranka1r任意a1包含r个向量r同时称为向量组a的秩有向量组a和向量组bb可由a线性表示的充要条brankaa与b等价的充要条件是rankbrankaranka若b可由a线性表示则rankb小于等于ranka求齐次线性方程组的一个基础解系齐次方程组的一个基础解系是由一组线性无关的向量组成先用行初等变换简化系数矩阵得到同解方程组再令x1x2x3
索力振动测量的传递矩阵法

索力振动测量的传递矩阵法刘志军;芮筱亭;杨富锋;于海龙;姜世平【摘要】振动法测量拉索张力需要准确描述索力与自振频率的关系,在建立拉索振动的离散模型基础上应用传递矩阵法计算拉索固有频率,通过求解特征方程建立了索力与振动频率的关系;然后将计算得到的模态频率与测试得到的模态频率比较,通过修正拉索张力计算值使计算频率与实测频率误差最小,最后修正的拉索张力则为拉索实际张力.通过对实际工程的测试结果分析表明,该方法具有准确、实用和易编程的特点,完全能满足工程应用要求.%The relation between cable tension and natural vibration frequencies needs to be defined accurately for measurement of cable tension with vibration method. Transfer matrix method of a multibody system was used to compute natural vibration frequencies of a cable based on a cable-vibration discrete model. The relation between cable tension and natural vibration frequencies was described by solving a characteristic equation. The computed value of cable tension was modified until the difference between the theoretical calculation frequencies and the measured ones reached the minimum. The final computed value of cable tension was regarded as the actual cable tension. The field measurement results were analyzed and it was indicated that the proposed method has higher computational efficiency because of lower order of system matrices and can effectively satisfy the requirements for measurement precision of cable tension.【期刊名称】《振动与冲击》【年(卷),期】2011(030)010【总页数】4页(P270-273)【关键词】传递矩阵法;索力;固有频率【作者】刘志军;芮筱亭;杨富锋;于海龙;姜世平【作者单位】南京理工大学发射动力学研究所,南京210094;南京理工大学发射动力学研究所,南京210094;南京理工大学发射动力学研究所,南京210094;南京理工大学发射动力学研究所,南京210094;南京理工大学发射动力学研究所,南京210094【正文语种】中文【中图分类】U448.27拉索作为结构的主要承重构件在工程中得到了广泛应用,拉索张力的大小直接关系到结构的受力状况。
现代控制理论-传递矩阵

λi Pi = APi
称pi为特征向量。
4. 4 状态方程的线性变换
选取不同的状态变量有不同形式的状态方程, 两组状态变量之间存在着线性变换。
x& = Ax + bu y = cx
x = px
x& = Ax + bu y = cx
= G(s)U(s) 【传递函数矩阵】
对于多输入多输出系统,初始条件为零时,输出 的拉氏变换与输入的拉氏变换之比,称为传递函数矩 阵,简称传递矩阵。
这里: G(s) = C(sI − A)−1B + D
(sI − A)−1 = adj[sI − A] sI − A
对于r维输入m维输出系统:
⎡Y1(s)⎤ ⎡G11(s) G12(s) L G1r(s)⎤⎡U1(s)⎤
b) 若A阵为友矩阵,且有n个互不相同的实数特 征值λi
⎡0 1 0 L 0 ⎤
⎢ ⎢
0
01
⎥ ⎥
A=⎢ ⎢ ⎢
O
⎥
1
⎥ ⎥
⎢⎣−a0 −a1 L
−an−1 ⎥⎦
sI − A = 0
λi
3
2011-3-10
则下边的范德蒙特矩阵使A对角化
⎡1 1 L 1⎤
⎢ ⎢
λ1
λ2
L
λn
⎥ ⎥
P
=
⎢ ⎢ ⎢
λ12 M
P变换,
变换矩阵: p = [ p1 p2 L pn ]
x = px x& = px& = Ax + bu = Apx + bu
x& = p−1Apx + p−1bu = Ax + bu
一种压杆稳定计算的通用算法

一种压杆稳定计算的通用算法
作者:崔清洋, 郭少春
作者单位:崔清洋(盐城工学院建工系,盐城,224003), 郭少春(宁夏大学土木与水利学院,银川,750021)
1.李青宁几种常用变截面杆元的传递矩阵和传递载常数[会议论文]-1999
2.刘开国变截面高层框筒结构的矩阵传递法[期刊论文]-力学与实践2004,26(4)
3.倪晓博.许笛.NI Xiao-bo.XU Di自重压杆稳定性问题分析[期刊论文]-企业技术开发(学术版)2010,29(1)
4.李黎.刘耀宗.郁殿龙基于传递矩阵法的局域共振Timoshenko梁振动特性研究[会议论文]-2006
5.何斌.陈树辉连续梁瞬态振动离散时间精细传递矩阵法[会议论文]-2007
6.杨韧关于细长压杆稳定性问题的讨论[期刊论文]-硅谷2010(2)
7.芮筱亭.陆毓淇多体系统动力学离散时间传递矩阵法[会议论文]-1998
8.李青宁高层框-桁结构传递矩阵法计算[会议论文]-2001
9.陈玉骥.CHEN Yuji提高能量法确定压杆临界荷载精度的一种方法[期刊论文]-力学与实践2005,27(6)
10.魏泽丽基于Riccati传递矩阵法的桥梁结构概率损伤识别方法研究[学位论文]2003
本文链接:/Conference_6152889.aspx。
离散数学4.4-等价和偏序关系

4.4.3 集合的划分
集合的划分
定义4.21 设A为非空集合, 若A的子集族 ( P(A)) 满 足下面条件: (1) (2) xy (x,y∈∧x≠y→x∩y=) (3) ������∈������ ������=A 则称是A的一个划分, 称 中的元素为A的划分块. 例3 设A={a, b, c, d}, 给定 1, 2, 3, 4, 5, 6如下: 1={{a, b, c},{d}}, 2={{a, b},{c},{d}} 3={{a},{a, b, c, d}}, 4={{a, b},{c}} 5={,{a, b},{c, d}}, 6={{a,{a}},{b, c, d}} 则 1和 2 是A的划分, 其他都不是A的划分. 12
4.4.4 偏序关系
相关概念
定义4.23 x与 y可比 设R为非空集合A上的偏序关系, x, yA, x与 y 可比 x≼y ∨ y≼x. 对IA, A上的元素可比吗? 不可比 定义4.24 非空集合A上的反自反和传递的关系,称为A 上的拟序关系,简称为拟序,记作≺. 求证:如果一个关系是拟序,那么它一定是反对称的。 证:如果不是反对称的,则 ∃x, y, 使 x≺y, 且 y≺x成立。 根据传递性,有 x≺x, 与反自反性矛盾。 19 得证
4.4.1 等价关系
模3等价关系的关系图
设 A={1, 2, …, 8}, R={ <x,y>| x,y∈A∧x≡y (mod 3) } R 的关系图如下:
4
4.4.1 等价关系
注: (1) 关系图的特点: ① 不连通 ② 在每个连通分支中是完全图 (2) 关系矩阵的特点: 修改排列顺序后为对角块矩阵,对角块为全”1”矩阵 1 4 7 2 5 8 3 6 1 1 1 1 0 0 0 0 0 4 1 1 1 0 0 0 0 0 7 1 1 1 0 0 0 0 0 2 0 0 0 1 1 1 0 0 5 0 0 0 1 1 1 0 0 8 0 0 0 1 1 1 0 0 3 0 0 0 0 0 0 1 1 6 0 0 0 0 0 0 1 1
线性代数及其应用(阎慧臻主编)PPT模板

第1章行列式
1.1行列式的定义
1.1.12阶和3阶行 列式
1.1.2n阶行列式的 定义
第1章行列式
1.2行列式的性质
1.2.1行列式的性质
1.2.2利用行列式的 性质计算行列式
第1章行列 式
1.3行列式按行(列)展 开
5.1.2特征值 与特征向量 的计算
5.1.1特征值 与特征向量 的概念
5.1.3特征值 与特征向量 的性质
第5章相似矩阵与二次型
5.2相似矩阵与矩阵的对角化
5.2.1相似矩阵的概 念
5.2.2相似矩阵的性 质
5.2.3矩阵对角化的 条件
第5章相似矩 阵与二次型
5.3实对称矩阵的对角 化
A
5.3.1向量的内积、 正交向量组和正交
02
6.4.2线性方程 组
第6章线性代数的 M AT L A B 实 现
6.5矩阵的特征值与二次 型
1
6.5.1特征值与特征向量
2
6.5.2相似变换及二次型
07 参考答案
参考答案
08 参考文献
参考文献
感谢聆听
关系
第3章n维向量组
3.5向量空间
3.5.1向量空 间
3.5.2向量空 间的基与维数
3.5.3基变换 与坐标变换
04 第4章线性方程组
第4章线性方程组
4.1线性方程组的消元法
4.1.1线性方程组相关
概念及其矩阵表示
1
4.1.2线性方程组的Ga uss消元法
4.3非齐次线性方程组
3
2
4.2齐次线性方程组
提高多管火箭射击密集度新技术

s no lpel n hrc e ss m ( R )w s n lzd Th eh dt rv r gd p ro i f o mut l a c k t yt i u o e ML Si s i
关键 词 :机 械 学;多管火箭 系 统;火箭 弹;射 击顺序 ;射击 时间 间隔 ;密集度 中图 分类号 :T 33 J9 文献 标志 码 :A 文章编 号 :10.0 320 )200.5 0019 (06 0.3 10
A w c o o y t m pr vng Fii s r in o Ne Te hn lg o I o i rngDipe so f
b p i z gf ig o d ra d f ig itra sp ee td yo t mii i n r e n i n n ev lwa rs ne .U s g ta se ti to fmut・ n r r i rn frmarx meh do l n i b d y tm n a n h d n mi t e r , t erlt n ewe n t ef ig o d ra d f ig itra S o ys se a dlu c y a c h o y h ea i sb t e h i n r e n i n e l . o r r n v V p ro ma c fM LRS wee etbi e .Th e tc n lg sd v lp d b p i zn iig o d r ef r n eo r sa l h d s en w e h oo y i e e e yo t o miig f n r e r a dfr g itr a fM L n ii n ev 1 RS.Th etrs l h w h tfr g ds es n o. L po e . n o ets eut s o t a i n ip ri fM RS i i rv d s i o sm Ke rs y wo d :meh nc ;mut l a n h rc e y tm ;r c e ;fr g o d r iig itr a;ds e — c a is l pelu c o k ts se i o k t i n r e ;f n n e v l ip r i r
